昆明理工大学考研试题运筹学(2012-2016年)

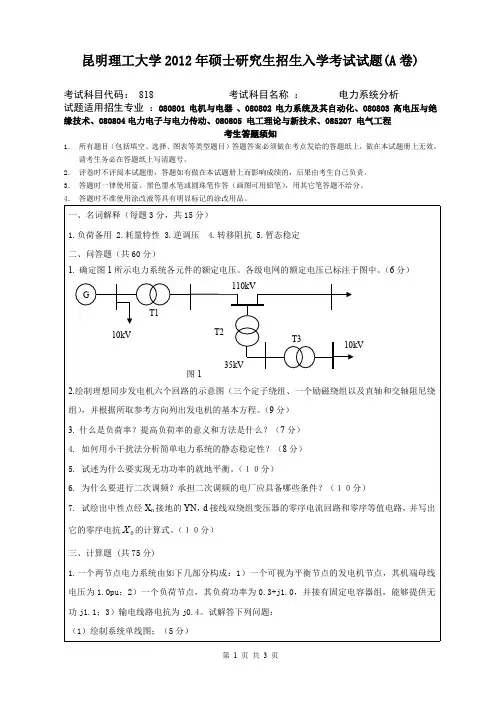
昆明理工大学2012年硕士研究生招生入学考试试题(A卷)考试科目代码：818 考试科目名称：电力系统分析试题适用招生专业：080801 电机与电器、080802 电力系统及其自动化、080803 高电压与绝缘技术、080804电力电子与电力传动、080805 电工理论与新技术、085207 电气工程考生答题须知1．所有题目（包括填空、选择、图表等类型题目）答题答案必须做在考点发给的答题纸上，做在本试题册上无效。

请考生务必在答题纸上写清题号。

2．评卷时不评阅本试题册，答题如有做在本试题册上而影响成绩的，后果由考生自己负责。

3．答题时一律使用蓝、黑色墨水笔或圆珠笔作答（画图可用铅笔），用其它笔答题不给分。

4．答题时不准使用涂改液等具有明显标记的涂改用品。

昆明理工大学2013年硕士研究生招生入学考试试题(A 卷)考试科目代码：819 考试科目名称 ：电力系统分析考生答题须知1． 所有题目（包括填空、选择、图表等类型题目）答题答案必须做在考点发给的答题纸上，做在本试题册上无效。

请考生务必在答题纸上写清题号。

2． 评卷时不评阅本试题册，答题如有做在本试题册上而影响成绩的，后果由考生自己负责。

3． 答题时一律使用蓝、黑色墨水笔或圆珠笔作答（画图可用铅笔），用其它笔答题不给分。

4． 答题时不准使用涂改液等具有明显标记的涂改用品。

一、 名词解释 （每小题3分，共15分）1.正序等效定则2.日负荷率3.电磁环网4. 平衡节点5. 热备用 二、 问答题（60分）1.什么是电晕现象？如何避免？（5分）2.输电线路何时作为无功电源、何时作为无功负荷？（5分）3.试以单变量非线性方程为例，结合图示解释牛顿拉夫逊法的一般思路。

（8分）4.请问什么是发电机的一、二次调频？一次调频能使频率保持不变吗？是否所有机组都进行一次调频？二次调频能否使频率保持不变？是否所有机组都担负二次调频？（10分）5.简述双绕组变压器分接头选择的步骤，双绕组升压变压器与降压变压器分接头选择有何区别？（8分）6. 为什么要引入暂态电动势和暂态电抗？它们具有怎样的物理意义？（8分）'q E 'd x 7.如图1所示的简单电力系统在f 点发生三相短路，作图说明快速切除故障提高同步发电机并列运行稳定性的原理。

昆明理工大学2013年硕士研究生招生入学考试试题(A卷)
考试科目代码：825 考试科目名称：物流工程学
试题适用招生专业：物流工程与管理（0823Z1）
考生答题须知
1．所有题目（包括填空、选择、图表等类型题目）答题答案必须做在考点发给的答题纸上，做在本试题册上无效。

请考生务必在答题纸上写清题号。

2．评卷时不评阅本试题册，答题如有做在本试题册上而影响成绩的，后果由考生自己负责。

3．答题时一律使用蓝、黑色墨水笔或圆珠笔作答（画图可用铅笔），用其它笔答题不给分。

4．答题时不准使用涂改液等具有明显标记的涂改用品。

第 1 页共14 页。

历年运筹学考研试题及答案试题：一、单项选择题（每题2分，共10分）1. 线性规划问题的标准形式是：A. 所有变量非负B. 目标函数为最小化C. 约束条件为等式D. 所有变量非负，约束条件为等式和不等式2. 在单纯形法中，如果某个非基变量的检验数为负，则：A. 该变量不能进入基B. 该变量可以进入基C. 该变量必须进入基D. 以上都不对3. 对于运输问题，当供应量等于需求量时，我们称其为：A. 平衡运输问题B. 不平衡运输问题C. 线性运输问题D. 非线性运输问题4. 在动态规划中，最优子结构性质意味着：A. 问题的最优解包含子问题的最优解B. 问题的所有解都包含子问题的最优解C. 问题的一个解包含子问题的最优解D. 以上都不对5. 网络最大流问题中，Ford-Fulkerson算法的核心思想是：A. 寻找增广路径B. 寻找最短路径C. 寻找最长路径D. 寻找最小割二、简答题（每题10分，共20分）1. 简述线性规划的几何意义及其在实际问题中的应用。

2. 解释什么是灵敏度分析，并说明其在解决线性规划问题中的作用。

三、计算题（每题15分，共30分）1. 假设有以下线性规划问题：Max Z = 3x + 4ySubject to:2x + y ≤ 6x + 2y ≤ 7x, y ≥ 0请用图解法找到该问题的最优解。

2. 给定一个网络流问题，网络中有三个节点A, B, C，以及三条边(A,B), (B, C), (A, C)，每条边的容量分别为10, 5, 8。

要求从节点A到节点C的最大流量。

使用Ford-Fulkerson算法求解。

四、论述题（每题20分，共20分）1. 论述动态规划与分治法在解决组合优化问题时的异同，并给出一个适合使用动态规划法解决的实际问题例子。

答案：一、单项选择题1. D2. C3. A4. A5. A二、简答题1. 线性规划的几何意义是在n维空间中寻找一个多边形的顶点，这个多边形由约束条件定义，而目标函数则定义了一个目标方向。

昆明理工大学2012年秋季入学博士研究生招生考试试题
考试科目代码：2153 考试科目名称：运筹学
试题适用招生专业：管理科学与工程、信息管理与信息系统、决策科学与决策支持系统、系统工程、项目管理与持续创新发展、科教管理与知识创新、工业工程
考生答题须知
1．所有题目（包括填空、选择、图表等类型题目）答题答案必须做在考点发给的答题纸上，做在本试题册上无效。

请考生务必在答题纸上写清题号。

2．评卷时不评阅本试题册，答题如有做在本试题册上而影响成绩的，后果由考生自己负责。

3．答题时一律使用蓝、黑色墨水笔或圆珠笔作答（画图可用铅笔），用其它笔答题不给分。

4．答题时不准使用涂改液等具有明显标记的涂改用品。

第 1 页共2 页。

昆明理工大学2020年硕士研究生招生入学考试试题(A卷) 考试科目代码：711 考试科目名称：单考数学考生答题须知1．所有题目（包括填空、选择、图表等类型题目）答题答案必须做在考点发给的答题纸上，做在本试题册上无效。

请考生务必在答题纸上写清题号。

2．评卷时不评阅本试题册，答题如有做在本试题册上而影响成绩的，后果由考生自己负责。

3．答题时一律使用蓝、黑色墨水笔或圆珠笔作答（画图可用铅笔），用其它笔答题不给分。

4．答题时不准使用涂改液等具有明显标记的涂改用品。

昆明理工大学2016年硕士研究生招生入学考试试题(A卷) 考试科目代码：711 考试科目名称：单考数学考生答题须知5．所有题目（包括填空、选择、图表等类型题目）答题答案必须做在考点发给的答题纸上，做在本试题册上无效。

请考生务必在答题纸上写清题号。

6．评卷时不评阅本试题册，答题如有做在本试题册上而影响成绩的，后果由考生自己负责。

7．答题时一律使用蓝、黑色墨水笔或圆珠笔作答（画图可用铅笔），用其它笔答题不给分。

8．答题时不准使用涂改液等具有明显标记的涂改用品。

昆明理工大学2018年硕士研究生招生入学考试试题(A卷) 考试科目代码：711 考试科目名称：单考数学考生答题须知9．所有题目（包括填空、选择、图表等类型题目）答题答案必须做在考点发给的答题纸上，做在本试题册上无效。

请考生务必在答题纸上写清题号。

10．评卷时不评阅本试题册，答题如有做在本试题册上而影响成绩的，后果由考生自己负责。

11．答题时一律使用蓝、黑色墨水笔或圆珠笔作答（画图可用铅笔），用其它笔答题不给分。

12．答题时不准使用涂改液等具有明显标记的涂改用品。

昆明理工大学2009年硕士研究生招生入学考试试题(A卷)考试科目代码：711考试科目名称：单考数学试题适用招生专业：单考考生答题须知13．所有题目（包括填空、选择、图表等类型题目）答题答案必须做在考点发给的答题纸上，做在本试题册上无效。

昆明理工大学2012年硕士研究生招生入学考试试题(A卷)考试科目代码：502 考试科目名称：《规划设计作图》试题适用招生专业：城乡规划学考生答题须知1．请按《准考证》和《招生简章》规定的作图纸进行答题，考生姓名和考生编号写在图纸底部的右下角，写在其它地方的按作弊卷处理，后果由考生自己负责。

2．请使用规定的作图用笔进行答题，没有特殊要求的全部用铅笔进行绘制。

3．不准使用涂改液等具有明显标记的涂改用品。

设计题目：某城市中心区商务、居住综合地块规划设计(150分)(一).基地概述：某城市拟在中心区一地块建设包括办公、商业服务与居住相结合的综合功能区块，基地东、南、北三侧与不同级别的城市道路相邻，西侧、西北部与现有一高层、多层结合的住宅组相邻；用地现状及范围见地形图，用地面积9.53ha。

(二（二）.规划设计要求：1．项目要求: 本综合功能区规划地上总建筑面积26万--29万平方米，主要面积功能为：办公写字楼建筑面积10万平方米; 商业服务、餐饮、休闲及相关的配套服务设施建筑面积8万平方米，其中需要设一座建筑面积3.8万平方米左右的多层主力商业建筑; 住宅建筑面积9万平方米（户型建筑面积80-130平方米）; 住宅限高:70米，住宅日照间距按1:1控制；写字楼高度体量和其它建筑的体量、形式可根据规划设计构思自行考虑。

2．城市规划要求: 1)基地建筑限高:150米;2)基地容积率小于3.0; 3)建筑退让道路红线不小于20米;4)建筑密度小于38%，5)绿地率大于30%，6)停车泊位：平均按建筑面积每100平方米0.5个车位考虑，地面停车泊位不小于120个；其中:小客车停车位70个，大客车停车位50个，另须考虑自行车停放问题。

3.设计要求：总平面规划设计应认真考虑基地环境因素，协调好综合区建筑空间与周边环境的关系，合理布局，合理组织空间与交通，塑造一个人性化、环境优美并具有特色的商务、居住综合区环境。

总平面设计和表达应满足题目要求和国家现行相关技术规范要求。

昆明理工大学2012年硕士研究生招生入学考试试题(A 卷)考试科目代码：813 考试科目名称 ：运筹学试题适用招生专业 ：120121 工业工程、085236 工业工程（专业学位）考生答题须知1． 所有题目（包括填空、选择、图表等类型题目）答题答案必须做在考点发给的答题纸上，做在本试题册上无效。

请考生务必在答题纸上写清题号。

2． 评卷时不评阅本试题册，答题如有做在本试题册上而影响成绩的，后果由考生自己负责。

3． 答题时一律使用蓝、黑色墨水笔或圆珠笔作答（画图可用铅笔），用其它笔答题不给分。

4． 答题时不准使用涂改液等具有明显标记的涂改用品。

一、单项选择题（每题1分，共10分）1.若某线性规划问题中，变量的个数为n ，基变量的个数为m(m<n)，则该问题基解的最大数目为A.C m n m -B. C n n m -C. C m nD. C n m2.在有最优解的线性规划问题中，如果存在C j 是惟一最优解时最终单纯形表里的基变量X j 的目标函数中的系数，如果C j 发生变化，则下列要发生变动的是A.所有基变量的检验数B.最优解C.该变量的检验数D.非基变量的检验数 3.动态规划问题中最优策略具有性质A.每个阶段的决策都是最优的B.当前阶段以前的各阶段决策是最优的C.无论初始状态与初始决策如何，对于先前决策所形成的状态而言，其以后的所有决策应构成最优策略D.它与初始状态无关 4.下面命题正确的是A.线性规划的最优解是基本可行解B.基本可行解不一定是基本解C.线性规划一定有可行解D.线性规划的最优值至多有一个5.在运输问题中，每次迭代时，如果有某非基变量的检验数等于零，则该运输问题 A.无最优解 B.有无穷多个最优解 C.有唯一最优解 D.出现退化解6.在箭线式网络图中，任何活动A.需要消耗一定的资源，占用一定的时间B.可能消耗资源，但不一定占用时间C.资源和时间至少消耗其一D.不一定耗费资源也不一定占用时间 7.原问题与对偶问题具有相同的最优A.解 B ．目标值 C ． 解结构 D ．解的分量个数 8.网络计划技术一章中所述的网络图分为两种,即 A.加工图和示意图B.装配图和示意图C.加工图和装配图D.箭线式网络图和结点式网络图9. 有n 个村镇要架设电线，问要怎样架线才能使架设的线路最短。

运筹学考研考试试题及答案# 运筹学考研考试试题及答案## 一、选择题（每题2分，共20分）1. 线性规划问题的标准型中，目标函数和约束条件的系数应满足以下哪个条件？A. 目标函数为线性，约束条件为非线性B. 目标函数和约束条件均为线性C. 目标函数为非线性，约束条件为线性D. 目标函数和约束条件均为非线性答案：B2. 在单纯形法中，如果某个非基变量的系数在目标函数中为负，这表示什么？A. 该变量可以增加目标函数值B. 该变量可以减少目标函数值C. 该变量不影响目标函数值D. 无法确定答案：A3. 以下哪个不是网络流问题的特点？A. 存在源点和汇点B. 每条边都有容量限制C. 每条边的流量可以为负D. 网络中的流量满足守恒定律答案：C4. 动态规划的基本思想是什么？A. 将问题分解为多个阶段B. 利用已知解求解未知问题C. 利用递归关系求解问题D. 所有上述选项答案：D5. 整数规划与线性规划的主要区别在于：A. 目标函数的线性性B. 约束条件的线性性C. 变量的取值范围D. 求解方法的复杂性答案：C## 二、简答题（每题10分，共30分）1. 简述线性规划的图解法解决线性规划问题的步骤。

- 首先，确定问题的可行域。

- 其次，将目标函数转化为直线方程。

- 然后，画出目标函数在可行域内的图形。

- 最后，找到可行域边界上使目标函数值最大化的点。

2. 解释什么是灵敏度分析，并说明其在运筹学中的应用。

- 灵敏度分析是评估模型参数变化对模型结果的影响。

- 在运筹学中，灵敏度分析用于评估最优解对数据变化的敏感度，帮助决策者了解在不同情况下的决策效果。

3. 描述单纯形法的基本思想及其求解过程。

- 单纯形法是一种求解线性规划问题的算法，其基本思想是从一个初始可行解出发，通过迭代，逐步改善解，直到达到最优解。

- 求解过程包括：选择进入基的非基变量，计算离开基的基变量，更新基和解，重复上述步骤直到满足最优性条件。

## 三、计算题（每题25分，共50分）1. 给定以下线性规划问题：\[ \text{Maximize } z = 3x_1 + 4x_2 \]\[ \text{Subject to } \begin{cases} 2x_1 + x_2 \leq 6 \\ x_1 + 2x_2 \leq 4 \\ x_1, x_2 \geq 0 \end{cases} \] 求解该问题，并给出最优解和最大值。

1、B2、B3、A4、C5、D6对7对8 错9 对10 对11 标准化（用对偶单纯型法解）MAX Z=-5X1 -2X2 -4X3ST-3X1-X2-2X3+X4 = -4-6X1-3X2-5X3 +X5 = -10X1…X5>=0B (-4，-10) 含负数，不是最优解确定进基MIN()=MIN(Zi/x5)=2/3 所以进基X2单纯型表迭代B (-2/3，10/3) 含负数，不是最优解再迭代一次确定离基变量MIN (X4,X2)=MIN(-2/3,-10/3)=-2/3 所以X4 为离基确定进基MIN()=MIN(Zi/x5)=2/3 所以进基X1单纯型表迭代先X2行除以A11=-1每行-AI1*X1Z’=-26/3 所以Z=26/3 X=(2/3,10/3,0,0,0)对偶问题MAX W=4Y1+10Y2ST3Y1+6Y2<5Y1+3Y2<=2Y1+5Y2<=4Y1,Y2>=0最优解就是松弛变量Y1=2 Y2=4/312题表作业法此题是产销平衡问题检验σ不能小于0A11 =4-4+3-2=1A24=9-3+4-11=-1 24不通过,不是最优解检验31，没有标记的格子A31=8-5+6-11+4-3+2=1检验22，没有标记的格子A22=10-3+4-11+6-5=1最小的σ24=-1，需要变换对奇数转角变量减去A14 ,对偶数转角变量加上A14,本身不变于是运费为2×8+2×3+4×12+5×14+6×8+11×4。

一、 解： 121284x x x +=⎧⎨=⎩ ⇒ 1242x x =⎧⎨=⎩ *243214Z =⋅+⋅= 1212233x x x x +=⎧⎨+=⎩ ⇒ 123212x x ⎧=⎪⎪⎨⎪=⎪⎩ *33192224Z =+⋅=二、（10分）证明：若ˆX 、ˆY 分别是原问题和对偶问题的可行解。

那么ˆˆ0s s YX Y X ==,当且仅当ˆX、ˆY 为最优解。

证明：min ,0,0S S S S max z CX Yb AX X b YA Y C X X Y Y ω==+=-=≥≥设原问题和对偶问题的标准关系是原问题对偶问题将原问题目标函数中的系数向量C 用C=Y A-YS 代替后，得到 z =(YA − YS )X =YAX − YSX将对偶问题的目标函数中系数列向量b ，用b =AX +XS 代替后，得到 w =Y (AX +XS )=YAX +YXSˆˆˆˆˆˆˆˆ;,4,4ˆˆ2152160,0S SSSY X 0,YX 0Yb YAX CX X Y CX YAX YbYXY X ======--==若则由性质（），可知是最优解。

又若分别是原问题和对偶问题的最优解，根据性质（），则有由（），（）式可知，必有三、1）（5分）写出下列线性规划问题的对偶问题123123123123123Min z x x 2x 2x 3x 5x 23x x 7x 3s.t x 4x 6x 5x ,x ,x 0=++++≥⎧⎪++≤⎪⎨++≤⎪⎪≥⎩解：123123123123123Max w 2y 3y 5y 2y 3y y 13y y 4y 1s.t 5y 7y 6y 2y 0,y ,y 0=++++≥⎧⎪++≥⎪⎨++≥⎪⎪≥≤⎩ 2）（5分）试写出下述非线性规划的Kuhn-Tucker 条件并求解2()(4)15Minf x x x =-≤≤解：先将该非线性规划问题写成以下形式212min ()(4)()10()50f x x g x x g x x ⎧=-⎪=-≥⎨⎪=-≥⎩写出其目标函数和约束函数的梯度：12()2(4),()1, ()1f x xg x g x ∇=-∇=∇=-对第一个和第二个约束条件分别引入广义拉格朗日乘子，设K-T 点为X*，则可以得到该问题的K-T 条件。

昆明理工大学硕士研究生招生入学考试试题(B卷)考试科目代码：813 考试科目名称：运筹学一、单项选择题。

将正确的答案选择出来。

（每题1分，共10分）1.线性规划的可行域的形状取决于A.目标函数B.约束函数的个数C.约束函数的系数D.约束条件的个数和系数2.线性规划一般模型中，自由变量可以代换为两个非负变量的A.和B.差C.积D.商3.若运输问题已求得最优解，此时所求出的检验数一定是全部A.大于或等于零B.大于零C.小于零D.小于或等于零4.在线性规划模型中，没有非负约束的变量称为A.多余变量B.松弛变量C.自由变量D.人工变量5.在产销平衡运输问题中，设产地为m个，销地为n个，那么解中非零变量的个数A.不能大于(m+n-1)B.不能小于(m+n-1)C.等于(m+n-1)D.不确定6．若原问题中x i为自由变量，那么对偶问题中的第i个约束一定为A.等式约束B.“≤”型约束C.“≥”约束D.无法确定7.总运输费用最小的运输问题，若已得最优运输方案，则其中所有空格的检验数A.大于或等于0B.小于或等于0C.大于0D.小于08.在箭线式网络图中，任何活动A.需要消耗一定的资源，占用一定的时间B.可能消耗资源，但不一定占用时间C.资源和时间至少消耗其一D.不一定耗费资源也不一定占用时间9.某人要从上海乘飞机到奥地利首都维也纳，他希望选择一条航线，经过转机，使他在空中飞行的时间尽可能短。

该问题可转化为A.最短路线问题求解B.最大流量问题求解C.最小枝杈树问题求解D.树的生成问题求解10.在运输方案中出现退化现象，是指数字格的数目A.等于m+nB.大于m+n-1C.小于m+n-1D.等于m+n-1二、下列线性规划模型的单纯形表的最终表如表1所示：（15分）⎪⎩⎪⎨⎧≥=++=-++=0,,225max 32132121321x x x cx x x bx x ax x x z试根据单纯形各部分之间的关系完成下列问题：1. 此单纯形表最终表的=-1B？2. 求出a 、b 、c 、d 、e 、f 的值。

见面课：运筹帷幄之初识运筹1、问题:下面关于运筹学的说法，错误的是（）。

选项：A:运筹学追求整体最优B:运筹学一般建立数学模型C:运筹学整体最优中也达到了局部最优D:运筹学不是对各子系统的决策行为孤立评价答案: 【运筹学整体最优中也达到了局部最优】2、问题:下面哪些属于运筹学的分支（）。

选项：A:线性规划B:非线性规划C:决策论D:图论答案: 【线性规划;非线性规划;决策论;图论】3、问题:下面哪些职业跟运筹学有关（）选项：A:百度地图的路径优化算法师B:京东物流的仓储规划师C:投资银行的投资分析师D:民航航班计划工程师答案: 【百度地图的路径优化算法师;京东物流的仓储规划师;投资银行的投资分析师;民航航班计划工程师】4、问题:运筹学起源于第二次世界大战。

（）选项：A:对B:错答案: 【对】见面课：运筹帷幄之理论基础1、问题:线性规划中关于解的描述，说法正确的是（）选项：A:可能有唯一最优解B:若存在两个最优解，那么一定有无穷多个最优解C:可能无解D:可能有无界解答案: 【可能有唯一最优解;若存在两个最优解，那么一定有无穷多个最优解;可能无解;可能有无界解】2、问题:若线性规划模型求得最优解，那么最优解（）选项：A:一定是基可行解B:一定是可行解C:可能为无界解D:一定在可行域顶点处得到答案: 【一定是基可行解;一定是可行解;一定在可行域顶点处得到】3、问题:原问题和对偶问题的关系中，下面错误的是（）选项：A:原问题和对偶问题互为对偶B:原问题和对偶问题最优值相等时各自取得最优解，最优解相等C:原问题有最优解，对偶问题一定有最优解D:对偶问题的解其实是对应资源的影子价格答案: 【原问题和对偶问题最优值相等时各自取得最优解，最优解相等】4、问题:若某种资源有剩余，那么它的影子价格为0。

（）选项：A:对B:错答案: 【对】5、问题:b的变化一般不会引起解的变化。

（）选项：A:对B:错。