《1.3 函数的基本性质》测试题

《函数的基本性质---奇偶性》同步测试题（一） ----主要涉及奇偶性的判断、求值和解析式一．选择题(在每小题给出的四个选项中，只有一项是符合题目要求的） 1．下列函数中，既不是奇函数也不是偶函数的是( ) A ．()21f x x =+B ．()3f x x =C ．()33xxf x -=+ D ．()21x f x x =-2．下列函数中，是奇函数的是（ ） A ．2y x x =+B ．21y x =+C ．3y x x =+D ．23=+y x x3．下列函数是偶函数的是： （ ） A ．y x =B ．223y x =-C ．12y x = D ．2,[0,1]y x x =∈4．已知()f x 是定义在[]2,2-上的奇函数，当(]0,2x ∈时，()21x f x =-，则()()20f f -+=（ ）A ．3-B ．2C ．3D ．2-5．已知函数2()()F x f x x =+是奇函数，且(2)1f =，则(2)f -=（ ） A ．9B ．9-C ．7-D ．76．已知()f x 是奇函数，当0x >时()(1)f x x x =-+，当0x <时，()f x 等于（ ） A ．(1)x x --B ．(1)x x -C ．(1)x x -+D ．(1)x x +7．对于定义在R 上的任意奇函数()f x ，均有（ ） A ．()()0f x f x --> B ．()()0f x f x --≤ C ．()()0f x f x ⋅->D ．()()0f x f x ⋅-≤8．设函数()f x 为奇函数，当0x >时，22f x x ，则()()1f f =（ ）A ．-1B ．-2C ．1D ．29．已知()21f x ax bx =-+是定义域为[a ，a +1]的偶函数，则2b a a -＝（ ）A ．0B ．34C D ．410．若函数()21f x ax bx =++是定义在[]1,2a a --上的偶函数，则该函数的最大值为（ ） A ．5B ．4C ．3D ．211．设函数3()1f x ax bx =+-，且(1)3f -=，则(1)f 等于（ ） A ．3-B ．3C ．5-D ．512．设2()2f x ax bx =++是定义在[1,1]a +上的偶函数，则2+a b =( ) A ．0 B ．2 C ．2- D ．12二．填空题13．已知函数()f x 是定义域为R 的奇函数，当0x ≥时，()22f x x x a =+-，则()1f -=___.14．已知53()8f x x ax bx =++-，若(3)10f -=，则(3)f =_______. 15．若2()21xf x a =-+是奇函数，则a =_______. 16．已知函数()f x 是定义在R 上的奇函数，且当0x >时， ()31f x x x =++，则()f x 在R 上的解析式为__________.三．解答题(解答应写出文字说明、证明过程或演算步骤) 17．判断下列函数的奇偶性： （1）f （x ）＝x 3＋x ；（2）()f x =；（3）222()1x xf x x +=+；（4）1,0()0,0,1,0x x f x x x x -<⎧⎪==⎨⎪+>⎩18．已知函数()4f x x x=-(1)判断函数的奇偶性,并说明理由: (2)证明:函数()f x 在()0,+∞上单调递增; (3)求函数()4f x x x=-,[]4,1x ∈--的值域．19．已知函数()f x 是定义域为R 的奇函数，当0x >时，()22f x x x =-.（1）求出函数()f x 在R 上的解析式； （2）画出函数()f x 的图像，并写出单调区间；（3）若()y f x =与y m =有3个交点，求实数m 的取值范围.20．若函数()f x 的定义域是R ,且对任意,R x y ∈,都有()()()f x y f x f y +=+成立.试判断()f x 的奇偶性.21．已知()f x 是定义在R 上的奇函数，当0x >时，()24f x x x =-，（1）求()f x 的解析式； （2）求不等式()f x x >的解集.22．已知函数()f x 是定义在R 上的偶函数，且当0x ≥时，()22f x x x =-.（1）求()0f 及()()1ff 的值；（2）若关于x 的方程()0f x m -=有四个不同的实数解，求实数m 的取值范围.参考答案一．选择题(在每小题给出的四个选项中，只有一项是符合题目要求的）二．填空题 13．3- 14．-26 15．116．331,0()0,01,0x x x f x x x x x ⎧++>⎪==⎨⎪+-<⎩三．解答题(解答应写出文字说明、证明过程或演算步骤) 17.【解析】（1）函数的定义域为R ，关于原点对称． 又f (－x )＝(－x )3＋(－x )＝－(x 3＋x )＝－f （x ）， 因此函数f （x ）是奇函数．（2）由221010x x ⎧-≥⎨-≥⎩ 得x 2＝1，即x ＝±1. 因此函数的定义域为{－1，1}，关于原点对称．又f （1）＝f (－1)＝－f (－1)＝0，所以f （x ）既是奇函数又是偶函数． （3）函数f （x ）的定义域是(－∞，－1)∪(－1，＋∞)， 不关于原点对称，所以f （x ）既不是奇函数也不是偶函数． （4）函数f （x ）的定义域为R ，关于原点对称．f (－x )＝1,00,01,0x x x x x ---<⎧⎪-=⎨⎪-+->⎩，于是有f (－x )＝－f （x ）．所以f （x ）为奇函数．18.【解析】（1）证明:定义域为(,0)(0,)-∞+∞;444()()f x x x x f x x x x ⎛⎫-=--=-+=--=- ⎪-⎝⎭,()f x ∴为奇函数. （2）证明:对任意的()12,0,x x ∈+∞,且12x x <,()()12112244x x f x f x x x ⎛⎫=--- ⎝-⎪⎭()121244x x x x ⎛⎫=--- ⎪⎝⎭()()1212124x x x x x x -=-+()121241x x x x ⎛⎫=-+ ⎪⎝⎭120x x <<,12120,0x x x x ∴-<>,()()120f x f x ∴-<，()()12f x f x ∴< ()x f ∴在()0,+∞上单调递增.（3）f x 为奇函数且在()0,+∞上是增函数,则()f x 在(),0-∞上是增函数,()x f ∴在[]4,1--上是增函数,()()()41f f x f -≤≤-,即()33f x -≤≤,所以函数()4f x x x=-,[]4,1x ∈--的值域为[]3,3-- 19.【解析】（1）①由于函数()f x 是定义域为R 的奇函数，则()00f =； ②当0x <时，0x ->，因为()f x 是奇函数，所以()()f x f x -=-． 所以()()()()22[2]2f x f x x x x x =--=----=--．综上：()222,00,02,0x x x f x x x x x ⎧->⎪=⎨⎪--<⎩＝．（2）图象如下图所示：．单调增区间：(][),1,1,-∞-+∞ 单调减区间：()1,1-． （3）因为方程()f x m =有三个不同的解， 由图像可知， 11m -<<，即()1,1m ∈-．20.【解析】令==0x y 得(00)(0)(0)f f f +=+,即(0)0f =.(0)()()()0f f x x f x f x ∴=-=+-=,()()f x f x ∴-=-,()f x ∴为奇函数.21.【解析】（1）∵()f x 是定义在R 上的奇函数，∴()00f =. 又当0x <时，0x ->，∴22()(4)4()f x x x x x ---=+-=.又()f x 为奇函数，∴()()f x f x -=-，∴()()240f x x x x --<=，∴2240()0040x x x f x x x x x ⎧->⎪==⎨⎪--<⎩. （2）当0x >时，由()f x x >得24x x x ->，解得5x >； 当0x =时，()f x x >无解；当0x <时，由()f x x >得24x x x -->，解得5x 0-<<. 综上，不等式()f x x >的解集用区间表示为(5,0)(5,)-⋃+∞. 22.【解析】（1）()f x 是定义在R 上的偶函数， 且当0x ≥时，()22f x x x =-，()()1(1)(1)1(0)0,f f f f f ==-==-；（2）函数()f x 是定义在R 上的偶函数， 关于x 的方程()0f x m -=有四个不同的实数解， 只需0x >时，()f x m =有两个解， 当0x ≥时，()222(1)1f x x x x =-=--，所以10m -<<。

高一数学《函数的基本性质》单元测试题 班次 学号 姓名一、选择题：1.下列函数中，在区间),0(+∞上是增函数的是 （ ）A.42+-=x yB.x y -=3C.x y 1=D.x y = 2.若函数)()(3R x x x f ∈=，则函数)(x f y -=在其定义域上是 （ ）A.单调递减的偶函数B.单调递减的奇函数C.单调递增的偶函数D.单调递增的奇函数3.函数x x x f +=2)(的奇偶性为 ( )A.奇函数B.偶函数C.既是奇函数又是偶函数D.既不是奇函数有不是偶函数4.若)(x f y =在[)+∞∈,0x 上的表达式为)1()(x x x f -=，且)(x f 为奇函数，则(]0,∞-∈x 时)(x f 等于 （ ）A.)1(x x --B. )1(x x +C. )1(x x +-D. )1(-x x5.已知定义在R 上的奇函数)(x f 满足)()2(x f x f -=+，则)6(f 的值为 （ ）A.1-B.0C.1D.26．已知函数()()0f x x a x a a =+--≠，()()()2200x x x h x x x x ⎧-+>⎪=⎨+≤⎪⎩， 则()(),f x h x 的奇偶性依次为 （ ） A ．偶函数，奇函数 B ．奇函数，偶函数 C ．偶函数，偶函数D ．奇函数，奇函数7．已知3()4f x ax bx =+-其中,a b 为常数，若(2)2f -=，则(2)f 的值等于 ( )A ．2-B ．4-C ．6-D ．10-8．下列判断正确的是 （ ） A ．函数22)(2--=x x x x f 是奇函数 B．函数()(1f x x =- C．函数()f x x = D ．函数1)(=x f 既是奇函数又是偶函数9．若函数2()48f x x kx =--在[5,8]上是单调函数，则k 的取值范围是 （ ）A ．(],40-∞B ．[40,64]C ．(][),4064,-∞+∞D ．[)64,+∞10．已知函数()()2212f x x a x =+-+在区间(]4,∞-上是减函数，则实数a 的取值范围是（ ） A ．3a ≤- B ．3a ≥- C ．5a ≤ D ．3a ≥11．若)(x f 是偶函数，其定义域为()+∞∞-,，且在[)+∞,0上是减函数，则)252()23(2++-a a f f 与的大小关系是 （ ） A ．)23(-f >)252(2++a a f B ．)23(-f <)252(2++a a f C ．)23(-f ≥)252(2++a a f D ．)23(-f ≤)252(2++a a f 12．设()f x 是奇函数，且在(0,)+∞内是增函数，又(3)0f -=，则()0x f x ⋅<的解集是（ ） A ．{}|303x x x -<<>或 B ．{}|303x x x <-<<或 C ．{}|33x x x <->或 D ．{}|3003x x x -<<<<或二、填空题： 13.设函数)(x f y =是奇函数，若3)2()1(3)1()2(++=--+-f f f f ，则=+)2()1(f f ____________________；14．已知定义在R 上的奇函数()f x ，当0x >时，1||)(2-+=x x x f ，那么0x <时，()f x = ； 15．若函数2()(32)f x k k x b =-++在R 上是减函数，则k 的取值范围为__________；16．若函数2()(2)(1)3f x k x k x =-+-+是偶函数，则)(x f 的递减区间是 .三、解答题：17．判断并证明下列函数的奇偶性：（1）21)(x x x f +=；（2）x x x f 2)(2+=；（3）x x x f 1)(+=；（4）()22f x x =+-. 18.已知3)1()2()(2+-+-=x k x k x f 是偶函数，求)(x f 的递减区间。

1 1.3函数的基本性质练习题（2）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内。

1．（2010浙江理）设函数的集合211()log (),0,,1,1;;1,0,122P f x x a b a b ìü==++=-=-íýîþ，平面上点的集合11(,),0,,1,1;;1,0,122Q x y x y ìü==-=-íýîþ，则在同一直角坐标系中，P 中函数()f x 的图象恰好．．经过Q 中两个点的函数的个数是（A ）4 4 （（B ）6 6 （（C ）8 8 （（D ）102.（2010重庆理）(5) (5) 函数函数()412x xf x +=的图象A. A. 关于原点对称关于原点对称关于原点对称 B. B. B. 关于直线关于直线y=x 对称对称 C. C. C. 关于关于x 轴对称轴对称 D. D. D. 关于关于y 轴对称3.（2010广东理）3．若函数f （x ）=3x+3-x与g （x ）=3x-3-x的定义域均为R ，则A. )(x f 与)(x g 与均为偶函数与均为偶函数 B. B.)(x f 为奇函数，)(x g 为偶函数C. )(x f 与)(x g 与均为奇函数与均为奇函数 D. D.)(x f 为偶函数，)(x g 为奇函数4.（2010山东理）（4）设f(x)f(x)为定义在为定义在R 上的奇函数，当x ≥0时，时，f(x)=f(x)=2x+2x+b(b 为常数)，则f(-1)=(A) 3 (B) 1 (C)-1 (D)-35.（2010湖南理）8.用{}min ,a b 表示a ，b 两数中的最小值。

若函数(){}min ||,||f x x x t =+的图像关于直线x=12-对称，则t 的值为A ．-2B -2 B．．2C 2 C．．-1D -1 D．．16. .若f(x)是R 上周期为5的奇函数，且满足f(1)=1，f(2)=2，则f(3)-f(4)= （A ）-1 (B) 1 (C) -2 (D) 2 7. （2009全国卷Ⅰ理）函数()f x 的定义域为R ，若(1)f x +与(1)f x -都是奇函数，则( )A.()f x 是偶函数B.()f x 是奇函数C.()(2)f x f x =+ D.(3)f x +是奇函数8. 对于正实数a ，记M a 为满足下述条件的函数f （x ）构成的集合：12,x x "ÎR 且2x ＞1x ,有212121()()()()x x f x f x x x a a --<-<-，下列结论正确的是，下列结论正确的是（A ）若1212(),(),()()f x M g x M f x g x M a a a a ×ÎÎ×Î则 （B ）1212()(,()()0,()f x f x M g x M g x Mg x a a a a ÎιÎ若）且则（C ）1212(),(),()()f x M g x M f x g x M a a a a +ÎÎ+Î若则（D ）若()()12,a f x M g x M a ÎÎ1()f x M a Î，2()g x M a Î，且12a a >，则()()12.f x g x M a a --Î9. (2009山东卷理山东卷理))函数xxx x e ey e e--+=-的图像大致为的图像大致为10. (2009山东卷理山东卷理))定义在R 上的函数f(x )满足f(x)=îíì>---£-0),2()1(0),1(log 2x x f x f x x ， 则f （2009）的值为）的值为( ) A.-1 B. 0 C.1 D. 2 11. (2009山东卷文山东卷文))已知定义在R 上的奇函数)(x f ，满足(4)()f x f x -=-,且在区间[0,2]上是增函数,则( ).A.(25)(11)(80)f f f -<<B. (80)(11)(25)f f f <<-C. (11)(80)(25)f f f <<-D. (25)(80)(11)f f f -<< 12. （2009全国卷Ⅱ文）函数y=x -(x £0)的反函数是的反函数是（ ）（A ）2y x =（x ³0） （B ）2y x =-（x ³0）1x y 1O A xyO 11B xyO 1 1 C x y 1 1 D O（B ）2y x =（x £0） （D ）2y x =-（x £0） 13. （2009全国卷Ⅱ文）函数22log 2xy x-=+的图像的图像 （ ）（A ） 关于原点对称关于原点对称 （B ）关于主线y x =-对称对称 （C ） 关于y 轴对称轴对称 （D ）关于直线y x =对称对称 14. （2009全国卷Ⅱ文）设2lg ,(lg ),lg ,a e b e c e ===则（ ）（A ）a b c >> （B ）a c b >> （C ）c a b >> （D ）c b a >> 15. （2009江西卷理）设函数2()(0)f x ax bx c a =++<的定义域为D ，若所有点(,())(,)s f t s t D Î构成一个正方形区域，则a 的值为的值为( ) A ．2-B ．4-C ．8-D ．不能确定16. （2009安徽卷理）设a ＜b,b,函数函数2()()y x a x b =--的图像可能是的图像可能是（ ）17.（2009福建卷理）函数()(0)f x ax bx c a =++¹的图象关于直线2b x a=-对称。

1.3 函数的基本性质1．已知()f x 是定义(),-∞+∞上的奇函数，且()f x 在[)0,+∞上是减函数．下列关系式中正确的是 ( )Ａ．()()55f f >- Ｂ．()()43f f > Ｃ．()()22f f ->Ｄ．()()88f f -≥2．如果奇函数()f x 在区间[3，7]上是增函数且最小值为5，那么()f x 在区间[]7,3--上是 ( )Ａ．增函数且最小值为5- Ｂ．增函数且最大值为5- Ｃ．减函数且最小值为5-Ｄ．减函数且最大值为5-3．下列函数中，在区间(0，2)上为增函数的是 ( )A ．1y x =-+B ．y =C ．245y x x =-+D ．2y x=4．对于定义域是R 的任意奇函数()f x 有 ( ) A ．()()0f x f x --≥ B ．()()0f x f x --≤ C ．()()0f x f x -≤D ．()()0f x f x -≥5．求函数()211y x xx =--≤≤的最大值，最小值．6．将长度为l 的铁丝分成两段，分别围成一个正方形和一个圆，要使正方形与圆的面积之和最小，正方形的周长应为__________．7．函数()()0f x kx b k =+≠的单调性是____________．8．函数()f x 是偶函数，而且在()0,+∞上是减函数，判断()f x 在(),0-∞上是增函数还是减函数，并加以证明．9．如果二次函数()()215f x x a x =--+在区间1,12⎛⎫⎪⎝⎭上是增函数，求()2f 的取值范围．10．求函数3y =-的最大值． 11．已知函数()1f x x x=+．判断()f x 在区间(0，1]和[1，+∞)上的单调性，说明理由．12．已知函数()f x 是偶函数，且0x ≤时，()1.1xf x x+=-．求 (1) ()5f 的值， (2) ()0f x =时x 的值； (3)当x >0时，()f x 的解析式．13．作出函数()21y x x =-+的图象，并根据函数的图象找出函数的单调区间．参考答案。

函数的基本性质练习题一、选择题：1．下面说法正确的选项A．函数的单调区间可以是函数的定义域B．函数的多个单调增区间的并集也是其单调增区间C．具有奇偶性的函数的定义域定关于原点对称D．关于原点对称的图象一定是奇函数的图象2．在区间(,0)上为增函数的是A．y1B．y（）（）某21某C．y某22某1D．y1某23．函数y某2b某c(某(,1))是单调函数时，b的取值范围A．b2B．b2C．b2D．b24．如果偶函数在[a,b]具有最大值，那么该函数在[b,a]有A．最大值B．最小值5．函数y某|某|p某，某R是A．偶函数B．奇函数A．f(某1)f(某2)C．f(某1)f(某2)A．[3,8]B．[7,2]（）（）C．没有最大值D．没有最小值（）C．不具有奇偶函数D．与p有关B．f(某1)f(某2)D．无法确定（）C．[0,5]D．[2,3]（）6．函数f(某)在(a,b)和(c,d)都是增函数，若某1(a,b),某2(c,d)，且某1某2那么（）7．函数f(某)在区间[2,3]是增函数，则yf(某5)的递增区间是8．函数y(2k1)某b在实数集上是增函数，则A．k11B．kC．b0D．b0229．定义在R上的偶函数f(某)，满足f(某1)f(某)，且在区间[1,0]上为递增，则（）A．f(3)f(2)f(2)B．f(2)f(3)f(2)（）C．f(3)f(2)f(2)D．f(2)f(2)f(3)10．已知f(某)在实数集上是减函数，若ab0，则下列正确的是A．f(a)f(b)[f(a)f(b)]C．f(a)f(b)[f(a)f(b)]D．f(a)f(b)f(a)f(b)11．若loga2A．0b>1D．b>a>1二、填空题：请把答案填在题中横线上.12．函数f(某)在R上为奇函数，且f(某)某1,某0，则当某0，f(某).213．函数y某|某|，单调递减区间为，最大值和最小值的情况为.B．f(a)f(b)f(a)f(b)14.函数f(某)＝lg(某－1)＋4－某的定义域为________15．函数y＝loga(某＋2)＋3(a＞0且a≠1)的图象过定点________．16．函数y＝log1(－某2＋4某＋12)的单调递减区间是________．317.命题“某0,某20”的否定是18．已知f(某)(某2)2,某[1,3]，函数f(某1)单调递减区间是________17．已知f(某)某2005a某3b8，f(2)10，f(2)=________某1.3函数的基本性质练习题（1）（答案）一、CBAABDBAAD二、11．y某1；12．[1,0]和[,)，21214；13．(某)(某)；214．y某2,某R；三、15．解：函数f(某1)[(某1)2]2(某1)2某22某1，某[2,2]，故函数的单调递减区间为[2,1].16．解①定义域(,0)(0,)关于原点对称，且②定义域为{f(某)f(某)，奇函数.1}不关于原点对称。

1.3 函数的基本性质专题训练-解答题一．选择题（共12小题）1．（2016•蚌埠一模）在定义域内既是奇函数又是减函数的是（）A．y=B．y=﹣x+C．y=﹣x|x|D．y=2．（2016•昆明校级模拟）已知函数f（x）为奇函数，且在（0，+∞）上单调递增，则以下结论正确的是（）A．函数|f（x）|为偶函数，且在（﹣∞，0）上单调递增B．函数|f（x）|为奇函数，且在（﹣∞，0）上单调递增C．函数f（|x|）为奇函数，且在（0，+∞）上单调递增D．函数f（|x|）为偶函数，且在（0，+∞）上单调递增3．（2016•北海一模）若函数f（x）=ln（x+）为奇函数，则a=（）A．﹣1 B．0 C．1 D．﹣1或14．（2016•昆明一模）若函数f（x）=为奇函数，则实数a=（）A．0 B．C．1 D．25．（2016•东城区二模）已知函数g（x）=f（x）﹣x是偶函数，且f（3）=4，则f（﹣3）=（）A．﹣4 B．﹣2 C．0 D．46．（2016•广州模拟）已知f（x）在R上是奇函数，且满足f（x+4）=f（x），当x∈（0，2）时，f（x）=2x2，则f（7）=（）A．2 B．﹣2 C．﹣98 D．987．（2016•广州模拟）已知f（x）在R上是奇函数，且满足f（x+4）=f（x），当x∈（0，2）时，f（x）=2x2，则f（7）=（）A．2 B．﹣2 C．﹣98 D．988．（2016•浙江模拟）定义在R上的函数f（x）满足f（x+1）=2f（x），且当0≤x≤1时，f（x）=x2﹣x，则=（）A．B．C．D．9．（2016•镇江一模）设f（x）=，若f（x）=9，则x=（）A．﹣12 B．±3 C．﹣12或±3 D．﹣12或310．（2016•长沙一模）已知定义在R上的函数f（x）满足f（x+1）=﹣f（x），且f（x）=，则下列函数值为1的是（）A．f（2.5）B．f（f（2.5））C．f（f（1.5））D．f（2）11．（2016•陕西一模）设函数f（x）=则f[f（﹣8）]=（）A．4 B．﹣4 C．2 D．﹣212．（2016•新余三模）若f（x）=x2+2（a﹣1）x+2在区间（4，+∞）上是增函数，那么实数a的取值范围是（）A．a≥3 B．a≥﹣3 C．a≤﹣3 D．a≤5二．解答题（共18小题）13．（2016•衡阳校级模拟）已知二次函数f（x）满足条件f（0）=1和f（x+1）﹣f（x）=2x．（1）求f（x）；（2）求f（x）在区间[﹣1，1]上的最大值和最小值．14．（2016•嘉定区一模）设函数f（x）=k•a x﹣a﹣x（a＞0且a≠1）是奇函数．（1）求常数k的值；（2）设a＞1，试判断函数y=f（x）在R上的单调性，并解关于x的不等式f（x2）+f（2x﹣1）＜0．15．（2016•岳阳校级三模）已知函数（1）求f（x）的定义域与值域；（2）判断f（x）的奇偶性并证明；（3）研究f（x）的单调性．16．（2016•江西模拟）已知函数f（x）的定义域为（0，+∞），且对任意的正实数x，y都有f（xy）=f（x）+f（y），且当x＞1时，f（x）＞0，f（4）=1，（1）求证：f（1）=0；（2）求f（）；（3）解不等式f（x）+f（x﹣3）≤1．17．（2016•江西模拟）已知f（x）=x2+2（a﹣2）x+4，（1）如果对一切x∈R，f（x）＞0恒成立，求实数a的取值范围；（2）如果对x∈[﹣3，1]，f（x）＞0恒成立，求实数a的取值范围．18．（2016春•高安市校级期末）已知：f（x）=ax2+（b﹣8）x﹣a﹣ab，当x∈（﹣3，2）时，f（x）＞0；x∈（﹣∞，﹣3）∪（2，+∞）时，f（x）＜0（1）求y=f（x）的解析式；（2）c为何值时，ax2+bx+c≤0的解集为R．19．（2016春•泉州期中）已知函数f（x）=a﹣是定义在（﹣1，1）上的奇函数．（1）求a的值；（2）试判断函数f（x）在（﹣1，1）上的单调性并证明；（3）若f（x﹣1）+f（x）＜0，求x的取值集合．20．（2016春•杭锦后旗校级期中）设常数a≥0，函数f（x）=是奇函数．（1）求a的值；（2）求f（x）＞3成立的x的取值范围．21．（2016春•保山校级期中）定义在实数集上的函数y=f（x）是偶函数，当x≥0时，f（x）=﹣x2+4x．（1）求f（x）在R上的表达式；（2）求y=f（x）的最大值，并写出f（x）在R上的单调区间（不必证明）．22．（2016春•临沂期中）已知函数f（x）=，（1）求f（2）+f（），f（3）+f（）的值；（2）归纳猜想一般性结；（3）求值：f（1）+f（2）+f（3）+…+f（2016）+f（）+f（）+…+f（）．23．（2015秋•甘谷县校级期末）设函数y=f （x），对任意实数x，y都有f （x+y）=f （x）+f （y）+2xy．（1）求f （0）的值；（2）若f （1）=1，求f （2），f （3），f （4）的值；（3）在（2）的条件下，猜想f （n）（n∈N*）的表达式．24．（2015秋•丰台区期中）已知f（x）=．（1）证明f（x）是奇函数；（2）证明f（x）是增函数．25．（2015秋•北京校级期中）已知（Ⅰ）求f（﹣1），f（1）的值；（Ⅱ）求f（a）+f（﹣a）的值；（Ⅲ）判别并证明函数f（x）的单调性．26．（2015秋•双鸭山校级期中）已知f（x）是定义在实数集R上的奇函数，且当x＞0时，f（x）=x2﹣4x+3，（Ⅰ）求f[f（﹣1）]的值；（Ⅱ）求函数f（x）的解析式．27．（2014•中山市校级三模）已知函数f（x）在定义域（0，+∞）上为增函数，且满足f（xy）=f（x）+f（y），f（3）=1（1）求f（9），f（27）的值（2）解不等式f（x）+f（x﹣8）＜2．28．（2014秋•珠海期末）已知函数．（1）求证：不论a为何实数f（x）总是为增函数；（2）确定a的值，使f（x）为奇函数．29．（2014秋•广州期末）已知函数f（x）=a x+，且f（1）=．（1）求a的值；（2）判定f（x）的奇偶性，并说明理由；（3）令函数g（x）=f（x）﹣5，且g（a）=8，求g（﹣a）的值．30．（2013秋•沙坪坝区校级期末）已知二次函数y=f（x）满足f（0）=f（1）=1，且，求：（Ⅰ）f（x）的解析式；（Ⅱ）f（x）在（0，1）上的值域．1.3 函数的基本性质专题训练-解答题参考答案与试题解析一．选择题（共12小题）1．（2016•蚌埠一模）在定义域内既是奇函数又是减函数的是（）A．y= B．y=﹣x+C．y=﹣x|x| D．y=【解答】解：A.在定义域内没有单调性，∴该选项错误；B.时，y=，x=1时，y=0；∴该函数在定义域内不是减函数，∴该选项错误；C．y=﹣x|x|的定义域为R，且﹣（﹣x）|﹣x|=x|x|=﹣（﹣x|x|）；∴该函数为奇函数；；∴该函数在[0，+∞），（﹣∞，0）上都是减函数，且﹣02=02；∴该函数在定义域R上为减函数，∴该选项正确；D.；∵﹣0+1＞﹣0﹣1；∴该函数在定义域R上不是减函数，∴该选项错误．故选：C．2．（2016•昆明校级模拟）已知函数f（x）为奇函数，且在（0，+∞）上单调递增，则以下结论正确的是（）A．函数|f（x）|为偶函数，且在（﹣∞，0）上单调递增B．函数|f（x）|为奇函数，且在（﹣∞，0）上单调递增C．函数f（|x|）为奇函数，且在（0，+∞）上单调递增D．函数f（|x|）为偶函数，且在（0，+∞）上单调递增【解答】解：函数f（x）为奇函数，且在（0，+∞）上单调递增，不妨令f（x）=x，则|f（x）|=|x|，f（|x|）=|x|；∴函数|f（x）|为偶函数，且在（﹣∞，0）上单调递减，∴命题A、B错误；函数f（|x|）为偶函数，且在（0，+∞）上单调递增，∴命题C错误、D正确．故选：D．3．（2016•北海一模）若函数f（x）=ln（x+）为奇函数，则a=（）A．﹣1 B．0 C．1 D．﹣1或1【解答】解：函数f（x）=ln（x+）为奇函数，f（﹣x）+f（x）=ln（﹣x+）+ln（x+）=lna=0恒成立，解得a=1，故选：C．4．（2016•昆明一模）若函数f（x）=为奇函数，则实数a=（）A．0 B．C．1 D．2【解答】解：由函数f（x）=为奇函数，可得f（0）==0，求得a=1，故选：C．5．（2016•东城区二模）已知函数g（x）=f（x）﹣x是偶函数，且f（3）=4，则f（﹣3）=（）A．﹣4 B．﹣2 C．0 D．4【解答】解：函数g（x）=f（x）﹣x是偶函数，可知g（3）=g（﹣3），可得f（3）﹣3=f（﹣3）+3，即4﹣3=f（﹣3）+3，f（﹣3）=﹣2．故选：B．6．（2016•广州模拟）已知f（x）在R上是奇函数，且满足f（x+4）=f（x），当x∈（0，2）时，f（x）=2x2，则f（7）=（）A．2 B．﹣2 C．﹣98 D．98【解答】解：∵f（x+4）=f（x），∴函数的周期是4，∵f（x）在R上是奇函数，且当x∈（0，2）时，f（x）=2x2，∴f（7）=f（7﹣8）=f（﹣1）=﹣f（1）=﹣2，故选：B7．（2016•广州模拟）已知f（x）在R上是奇函数，且满足f（x+4）=f（x），当x∈（0，2）时，f（x）=2x2，则f（7）=（）A．2 B．﹣2 C．﹣98 D．98【解答】解：∵f（x）在R上是奇函数，且满足f（x+4）=f（x），当x∈（0，2）时，f（x）=2x2，∴f（7）=f（﹣1）=﹣f（1）=﹣2．故选：B．8．（2016•浙江模拟）定义在R上的函数f（x）满足f（x+1）=2f（x），且当0≤x≤1时，f（x）=x2﹣x，则=（）A．B．C．D．【解答】解：∵定义在R上的函数f（x）满足f（x+1）=2f（x），且当0≤x≤1时，f（x）=x2﹣x，当﹣2≤x≤﹣1时，0≤x+2≤1，由题意f（x）=f（x+1）=f（x+2）=（x+2）[（x+2）﹣1]，∴f（﹣）==﹣．故选：D．9．（2016•镇江一模）设f（x）=，若f（x）=9，则x=（）A．﹣12 B．±3 C．﹣12或±3 D．﹣12或3【解答】解：∵f（x）=，f（x）=9，∴当x≤﹣1时，﹣x﹣3=9，解得x=﹣12；当﹣1＜x＜2时，x2=9，解得x=±3，不成立；当x≥2时，3x=9，解得x=3．∴x=﹣12或x=3．故选：D．10．（2016•长沙一模）已知定义在R上的函数f（x）满足f（x+1）=﹣f（x），且f（x）=，则下列函数值为1的是（）A．f（2.5）B．f（f（2.5））C．f（f（1.5））D．f（2）【解答】解：由f（x+1）=﹣f（x），得f（x+2）=﹣f（x+1）=f（x），则函数的周期是2，则f（2.5）=f（2+0.5）=f（0.5）=﹣1，f（f（2.5））=f（﹣1）=f（﹣1+2）=f（1）=﹣1f（f（1.5））=f（f（2﹣0.5））=f（f（﹣0.5））=f（1）=﹣1，f（2）=f（0）=1，即列函数值为1的f（2），故选：D．11．（2016•陕西一模）设函数f（x）=则f[f（﹣8）]=（）A．4 B．﹣4 C．2 D．﹣2【解答】解：∵f（x）=，∴f（﹣8）=﹣（﹣8）=2，f[f（﹣8）]=2+﹣7=﹣4．故选：B．12．（2016•新余三模）若f（x）=x2+2（a﹣1）x+2在区间（4，+∞）上是增函数，那么实数a的取值范围是（）A．a≥3 B．a≥﹣3 C．a≤﹣3 D．a≤5【解答】解：二次函数f（x）=x2+2（a﹣1）x+2是开口向上的二次函数，对称轴为x=1﹣a，∴二次函数f（x）=x2+2（a﹣1）x+2在[1﹣a，+∞）上是增函数，∵在区间（4，+∞）上是增函数，∴1﹣a≤4，解得：a≥﹣3．故选B．二．解答题（共18小题）13．（2016•衡阳校级模拟）已知二次函数f（x）满足条件f（0）=1和f（x+1）﹣f（x）=2x．（1）求f（x）；（2）求f（x）在区间[﹣1，1]上的最大值和最小值．【解答】解：（1）设f（x）=ax2+bx+c，则f（x+1）﹣f（x）=a（x+1）2+b（x+1）+c﹣（ax2+bx+c）=2ax+a+b∴由题恒成立∴∴f（x）=x2﹣x+1（2）f（x）=x2﹣x+1=在[﹣1，]单调递减，在[，1]单调递增∴，f（x）max=f（﹣1）=314．（2016•嘉定区一模）设函数f（x）=k•a x﹣a﹣x（a＞0且a≠1）是奇函数．（1）求常数k的值；（2）设a＞1，试判断函数y=f（x）在R上的单调性，并解关于x的不等式f（x2）+f（2x﹣1）＜0．【解答】解：（1）函数f（x）的定义域为R，f（x）是奇函数；∴f（0）=k﹣1=0；∴k=1；（2）由（1），f（x）=a x﹣a﹣x，设x1，x2∈R，且x1＜x2，则：；∵a＞1，x1＜x2；，又；∴f（x1）﹣f（x2）＜0；即f（x1）＜f（x2）；∴函数f（x）在R上是单调递增函数；由f（x2）+f（2x﹣1）＜0，得f（x2）＜﹣f（2x﹣1）；即f（x2）＜f（1﹣2x）；f（x）在R上单调递增；∴x2＜1﹣2x，即x2+2x﹣1＜0；解得；∴原不等式的解为．15．（2016•岳阳校级三模）已知函数（1）求f（x）的定义域与值域；（2）判断f（x）的奇偶性并证明；（3）研究f（x）的单调性．【解答】解：原函数化为：．（1）令分母4x+1≠0，该不等式恒成立，故定义域为R函数的解析式可以变为，由于4x+1＞1，故0＜＜1故0＜＜2，∴f（x）的值域是（﹣1，1）（2）函数是一个奇函数，证明如下，故是一个奇函数．（3）f（x）在（﹣∞，+∞）是一个增函数，证明如下由于，在（﹣∞，+∞）上，2x+1递增且函数值大于0，在（﹣∞，+∞）上是减函数，故在（﹣∞，+∞）上是增函数．16．（2016•江西模拟）已知函数f（x）的定义域为（0，+∞），且对任意的正实数x，y都有f（xy）=f（x）+f（y），且当x＞1时，f（x）＞0，f（4）=1，（1）求证：f（1）=0；（2）求f（）；（3）解不等式f（x）+f（x﹣3）≤1．【解答】解：（1）证明：令x=4，y=1，则f（4）=f（4×1）=f（4）+f（1）．∴f（1）=0．（2）f（16）=f（4×4）=f（4）+f（4）=2，f（1）=f（×16）=f（）+f（16）=0，故f（）=﹣2．（3）设x1，x2＞0且x1＞x2，于是f（）＞0，∴f（x1）=f（×x2）=f（）+f（x2）＞f（x2）．∴f（x）为x∈（0，+∞）上的增函数．又∵f（x）+f（x﹣3）=f[x（x﹣3）]≤1=f（4），∴⇒3＜x≤4．∴原不等式的解集为{x|3＜x≤4}．17．（2016•江西模拟）已知f（x）=x2+2（a﹣2）x+4，（1）如果对一切x∈R，f（x）＞0恒成立，求实数a的取值范围；（2）如果对x∈[﹣3，1]，f（x）＞0恒成立，求实数a的取值范围．【解答】解：（1）∵对一切x∈R，f（x）＞0恒成立，根据二次函数的图象和性质可得△=4（a﹣2）2﹣16＜0⇒0＜a＜4；（2）∵对x∈[﹣3，1]，f（x）＞0恒成立，∴讨论对称轴与区间[﹣3，1]的位置关系得或或，解得a∈ϕ或1≤a＜4或，∴a的取值范围为．18．（2016春•高安市校级期末）已知：f（x）=ax2+（b﹣8）x﹣a﹣ab，当x∈（﹣3，2）时，f（x）＞0；x∈（﹣∞，﹣3）∪（2，+∞）时，f（x）＜0（1）求y=f（x）的解析式；（2）c为何值时，ax2+bx+c≤0的解集为R．【解答】解：（1）∵不等式f（x）＞0的解集为x∈（﹣3，2），∴﹣3，2是方程ax2+（b﹣8）x﹣a﹣ab=0的两根，∴，且a＜0，可得，∴f（x）=﹣3x2﹣3x+18．（2）由a＜0，知二次函数y=ax2+bx+c的图象开口向下，要使不等式﹣3x2+5x+c≤0的解集为R，只需△≤0，即25+12c≤0，故c≤﹣．∴当c≤﹣时，不等式ax2+bx+c≤0的解集为R．19．（2016春•泉州期中）已知函数f（x）=a﹣是定义在（﹣1，1）上的奇函数．（1）求a的值；（2）试判断函数f（x）在（﹣1，1）上的单调性并证明；（3）若f（x﹣1）+f（x）＜0，求x的取值集合．【解答】解：（1）由题意得；（2）由（1）可知，函数f （x）在区间（﹣1，1）上为增函数；证明如下：设﹣1＜x1＜x2＜1，则：f （x1）﹣f （x2）===；∵﹣1＜x1＜x2＜1；∴；∴f（x1）＜f（x2）；∴f（x）在（﹣1，1）上为增函数；（3）f（x﹣1）+f（x）＜0⇔f（x﹣1）＜﹣f（x）因为f（x）为奇函数，所以﹣f（x）=f（﹣x）；则不等式可变形为f（x﹣1）＜f（﹣x），因为f（x）在（﹣1，1）上为增函数；所以；解得；∴x的取值集合为．20．（2016春•杭锦后旗校级期中）设常数a≥0，函数f（x）=是奇函数．（1）求a的值；（2）求f（x）＞3成立的x的取值范围．【解答】解：（1）∵f（x）为奇函数，∴f（﹣x）=﹣f（x），∴=﹣，∴a=1（﹣1舍去）；（2）f（x）＞3，即＞3，∴1＜2x＜2，解得0＜x＜1．21．（2016春•保山校级期中）定义在实数集上的函数y=f（x）是偶函数，当x≥0时，f（x）=﹣x2+4x．（1）求f（x）在R上的表达式；（2）求y=f（x）的最大值，并写出f（x）在R上的单调区间（不必证明）．【解答】解：（1）∵定义在实数集上的函数y=f（x）是偶函数，当x≥0时，f（x）=﹣x2+4x=﹣（x﹣2）2+4，设x＜0时，则﹣x＞0，故f（x）=f（﹣x）=﹣（﹣x）2+4（﹣x）=﹣x2﹣4x=﹣（x+2）2，综上可得，f（x）=．（2）根据函数的解析式可得，当x=±2时，y=f（x）取得最大值为4，结合f（x）的图象写出f（x）在R上的单调增区间为（﹣∞，﹣2]、[0，2]；减区间为[﹣2，0]、[2，+∞）．22．（2016春•临沂期中）已知函数f（x）=，（1）求f（2）+f（），f（3）+f（）的值；（2）归纳猜想一般性结论，并给出证明；（3）求值：f（1）+f（2）+f（3）+…+f（2016）+f（）+f（）+…+f（）．【解答】解（1）∵f（x）=，∴f（2）+f（）===1，…（2分）f（3）+f（）=+=+=1．…（4分）（2）由（1）猜想f（x）+f（）=1，…（6分）证明：f（x）+f（）=+=+=1．…（8分）（3）由（2）可得，原式=f（1）+[f（1）+f（）]+[f（3）+f（）]+…+[f（2016）+f（）]=f（1）+2015==．…（12分）23．（2015秋•甘谷县校级期末）设函数y=f （x），对任意实数x，y都有f （x+y）=f （x）+f （y）+2xy．（1）求f （0）的值；（2）若f （1）=1，求f （2），f （3），f （4）的值；（3）在（2）的条件下，猜想f （n）（n∈N*）的表达式并用数学归纳法证明．【解答】解：（1）令x=y=0，得f（0+0）=f（0）+f（0）+2×0×0，得f（0）=0．…（2分）（2）由f（1）=1，得f（2）=f（1+1）=f（1）+f（1）+2×1×1=4．f（3）=f（2+1）=f（2）+f（1）+2×2×1=9．f（4）=f（3+1）=f（3）+f（1）+2×3×1=16．…（5分）（3）由（2）可猜想f（n）=n2，…（7分）用数学归纳法证明：（i）当n=1时，f（1）=12=1显然成立．…（8分）（ii）假设当n=k时，命题成立，即f（k）=k2，…（10分）则当n=k+1时，f（k+1）=f（k）+f（1）+2×k×1=k2+1+2k=（k+1）2，故当n=k+1时命题也成立，…（12分）由（i），（ii）可得，对一切n∈N*都有f（n）=n2成立．…（14分）24．（2015秋•丰台区期中）已知f（x）=．（1）证明f（x）是奇函数；（2）证明f（x）是增函数．【解答】解：（1）证明：任取x∈R，都有：=﹣f（x），∴f（x）是定义域R上的奇函数；（2）证明：令x1＜x2，则，∵x1＜x2，∴，∴，则f（x1）＜f（x2），∴f（x）在R上是增函数．25．（2015秋•北京校级期中）已知（Ⅰ）求f（﹣1），f（1）的值；（Ⅱ）求f（a）+f（﹣a）的值；（Ⅲ）判别并证明函数f（x）的单调性．【解答】解：（Ⅰ）∵，∴f（﹣1）==，f（1）==；（Ⅱ）f（a）+f（﹣a）=+=+=1；（Ⅲ）函数f（x）是定义域R上的单调增函数，证明如下：任取x1、x2∈R，且x1＜x2，∴＜，（1+）（1+）＞0，∴f（x1）﹣f（x2）=﹣=＞0，即f（x1）＜f（x2），∴函数f（x）是定义域R上的单调增函数．26．（2015秋•双鸭山校级期中）已知f（x）是定义在实数集R上的奇函数，且当x＞0时，f（x）=x2﹣4x+3，（Ⅰ）求f[f（﹣1）]的值；（Ⅱ）求函数f（x）的解析式．【解答】解：（Ⅰ）因为f（x）是定义在实数集R上的奇函数，f（0）=0，当x＞0时，f（x）=x2﹣4x+3，f[f（﹣1）]=f[﹣f（1）]=f（0）=0…4′（Ⅱ）因为f（x）是定义在实数集R上的奇函数，∴f（0）=0，且当x＞0时，f（x）=x2﹣4x+3，x＜0时f（x）=﹣f（﹣x）=﹣（x2+4x+3）=﹣x2﹣4x﹣3∴ (12)27．（2014•中山市校级三模）已知函数f（x）在定义域（0，+∞）上为增函数，且满足f（xy）=f（x）+f（y），f（3）=1（1）求f（9），f（27）的值（2）解不等式f（x）+f（x﹣8）＜2．【解答】解：（1）f（9）=f（3）+f（3）=2，f（27）=f（9）+f（3）=3（2）∵f（x）+f（x﹣8）=f[x（x﹣8）]＜f（9）而函数f（x）是定义在（0，+∞）上为增函数，∴即原不等式的解集为（8，9）28．（2014秋•珠海期末）已知函数．（1）求证：不论a为何实数f（x）总是为增函数；（2）确定a的值，使f（x）为奇函数．【解答】解：（1）∵f（x）的定义域为R，设x1＜x2，则=（4分）∵x1＜x2，∴，∴f（x1）﹣f（x2）＜0，（6分）即f（x1）＜f（x2），所以不论a为何实数f（x）总为增函数．（7分）（2）∵f（x）为奇函数，∴f（﹣x）=﹣f（x），即，解得：．∴．（12分）29．（2014秋•广州期末）已知函数f（x）=a x+，且f（1）=．（1）求a的值；（2）判定f（x）的奇偶性，并说明理由；（3）令函数g（x）=f（x）﹣5，且g（a）=8，求g（﹣a）的值．【解答】解：（1）因为，所以，所以a=3；（2）由（1）得，所以f（x）的定义域为（﹣∞，+∞），，所以f（x）=f（﹣x），所以f（x）为偶函数；（3）因为g（x）=f（x）﹣5，g（a）=8，所以f（x）=g（x）+5，所以f（a）=g（a）+5=13因为f（x）为偶函数，所以f（﹣a）=g（﹣a）+5=13，所以g（﹣a）=8．30．（2013秋•沙坪坝区校级期末）已知二次函数y=f（x）满足f（0）=f（1）=1，且，求：（Ⅰ）f（x）的解析式；（Ⅱ）f（x）在（0，1）上的值域．【解答】解：（Ⅰ）设f（x）的一般式y=ax2+bx+c，∵f（0）=f（1）=1，且，∴解得∴f（x）=x2﹣x+1…..…（6分）（Ⅱ）f（x）=x2﹣x+1的解析式可化为：；当时，；当x=1时，f（1）=1，综上，f（x）在（0，1）上的值域是…（13分）第21页（共21页）。

更上一层楼基础·巩固·达标1.下列函数中，在区间（0，2）上为增函数的是（ ）A.y=3-xB.y=x 2+1C.y=x 1 D.y=-|x| 思路解析：y=3-x ，y=x 1，y=-|x|，在（0，2）上都是减函数，y=x 2+1在（0，2）上是增函数. 答案：B2.已知函数f （x ）=x3，则下列区间不是递减区间的是（ ） A.（0，+∞） B.（-∞，0）C.（-∞，0）∪（0，+∞）D.（1，+∞）思路解析：f （x ）=x3的递减区间有两个，即（-∞，0），（0，+∞）. 答案：C3.设函数f （x ）=（2a-1）x+b 是R 上的减函数，则有（ ）A.a ≥21 B.a ≤21 C.a ＞-21 D.a ＜21 思路解析：由已知f （x ）为一次函数，且2a-1＜0，解得a ＜21. 答案：D4.小刚离家去学校由于怕迟到，所以一开始就跑步，跑累了再走余下的路程.在下图所示中，纵轴表示离校的距离，横轴表示出发后的时间，则下列四个图象中较符合小刚走法的是（ ）答案：D5.函数f （x ）=2x 2-mx+3，当x ∈［-2，+∞）时为增函数，x ∈（-∞，-2］时为减函数，则f（1）等于（ ）A.-3B.13C.7D.由m 而定思路解析：二次函数的对称轴为x=4m ，由条件，得4m =-2，所以m=-8.所以f （x ）=2x 2+8x+3，所以f （1）=2+8+3=13.答案：B6.(经典回放)g （x ）=x （2-x ）的递增区间依次是（ ）A.(-∞，0]，(-∞,1]B.(-∞，0]，［1，+∞)C.［0，+∞)，(-∞，-1]D.［0，+∞］，［1，+∞］思路解析：由于f(x)=|x|=⎩⎨⎧>-≥.0,,0,x x x x g(x)=-(x-1)2+1，结合图象易知选C.答案：C7.已知函数f （x ）在区间（-1，1）上是减函数，且f （a 2-1）＜f （a-1），则a 的取值范围是______________________.思路解析：∵1>a 2-1>-1得0＜a ＜2或-2＜a ＜0.又由1>a-1>-1得0＜a ＜2，所以，要使f （a 2-1）、f （a-1）有意义，则0＜a ＜2 ① 又f （x ）在（-1，1）上是减函数，由f （a 2-1）＜f （a-1）得a 2-1>a-1,即a>1或a ＜0 ② 综合①②可得，1＜a ＜2.答案：1＜a ＜28.当|x|≤1时，函数y=ax+2a+1的值有正也有负，则实数a 的取值范围是_______________. 思路解析：∵f （x ）=ax+2a+1在［-1，1］时，f （x ）有正也有负，∴f （-1）·f （1）＜0，即（a+1）（3a+1）＜0.∴-1＜a ＜-31. 答案：（-1，-31） 综合·应用·创新9.已知f （x ）满足f （-x ）=f （x ），定义域为R 且当x ≥0时单调递增，若f （π）＜f （m ），则m 的取值范围是__________________.思路解析：f （x ）满足f （-x ）=f （x ），定义域为R ，且x ≥0时递增，则x ＜0时递减，又f （π）＜f （m ），∴π＜|m|，即m>π或m ＜-π.答案：（-∞，-π）∪（π，+∞）10.（经典回放）f(x)=a|x-b|+2在[0,+∞]上为增函数,则实数a 、b 的取值范围是____________. 答案：a>0且b ≤011.已知A=［1，b ］（b ＞1），对于f （x ）=21（x-1）2+1，若x ∈A ，f （x ）∈A ，试求b 的取值范围.答案：∵f （x ）=21（x-1）2+1的图象是抛物线，21>0，∴开口向上，顶点坐标是（1，1）. 当x ∈［1，b ］时，f （x ）单调递增.当x=b 时，f （x ）max =f （b ）∈［1，b ］.∴f （b ）≤b ， 即21（b-1）2+1≤b ，b 2-4b+3≤0.解得1≤b ≤3. ∵b>1，∴1＜b ≤3为所求. 12.已知函数f （x ）=x+x 1， （1）求函数的定义域；（2）证明f （x ）在（0，1］上是减函数，在［1，+∞）上为增函数；（3）求函数f （x ）在区间（0，+∞）上的最小值；（4）根据以上函数的性质作出f （x ）在区间（0，+∞）上的图象.（1）解：函数的定义域为（-∞，0）∪（0，+∞）.（2）证明：设x 1、x 2是（0，1）上的任意两个实数，且x 1＜x 2，则f （x 2）-f （x 1）=（x 2+21x ）-（x 1+11x ）=（x 2-x 1）+（21x -11x ）=（x 2-x 1）+2121x x x x =（x 2-x 1）（1-211x x ）. ∵x 1、x 2∈（0，1］，∴0＜x 1x 2＜1，211x x ＞1. ∴1-211x x ＜0. 又∵x 2-x 1＞0，∴f （x 2）-f （x 1）＜0，即f （x 2）＜f （x 1）.∴函数f （x ）=x+x1在（0，1）上是减函数. 同理可证f （x ）=x+x1在［1，+∞］上是增函数. （3）解：∵函数f （x ）=x+x 1在（0，1］上是减函数， ∴当x=1时，函数取最小值y min =f （1）=1+1=2.又∵f （x ）=x+x1在［1，+∞）上是增函数，∴当 x=1时，也取最小值y min =f （1）=1+1=2 . 综上所述，函数在（0，+∞）上的最小值为2.（4）解：函数的图象如下图：。

高中数学必修一1.3函数的基本性质练习题及答案 一：单项选择题： (共10题,每小题5分,共50分)1. 已知函数)127()2()1()(22+-+-+-=m m x m x m x f 为偶函数，则m 的值是（ ） A.1 B.2 C.3 D.42. 若偶函数)(x f 在(]1,-∞-上是增函数，则下列关系式中成立的是（ ） A.)2()1()23(f f f <-<- B.)2()23()1(f f f <-<- C.)23()1()2(-<-<f f f D.)1()23()2(-<-<f f f3. 如果奇函数)(x f 在区间[3,7] 上是增函数且最大值为5，那么)(x f 在区间[]3,7--上是（ ）A.增函数且最小值是5-B.增函数且最大值是5-C.减函数且最大值是5-D.减函数且最小值是5-4. 设)(x f 是定义在R 上的一个函数，则函数)()()(x f x f x F --=在R 上一定是（ ）A.奇函数B.偶函数C.既是奇函数又是偶函数D.非奇非偶函数5. 函数)11()(+--=x x x x f 是（ ）A.是奇函数又是减函数B.是奇函数但不是减函数C.是减函数但不是奇函数D.不是奇函数也不是减函数6. 下列函数既是奇函数，又在区间上单调递减的是（ ） A. B. C. D.7. 设函数|| + b + c 给出下列四个命题： ①c = 0时，y是奇函数 ②b 0 , c >0时，方程0 只有一个实根 ③y 的图象关于(0 , c)对称 ④方程0至多两个实根其中正确的命题是（ ）A ．①、④B ．①、③C ．①、②、③D ．①、②、④8. 已知函数f(x)=3-2|x|,g(x)=x 2-2x,构造函数F(x),定义如下:当f(x)≥g(x)时,F(x)=g(x);当f(x)<g(x)时,F(x)=f(x).那么F(x) ( )A．有最大值7-2,无最小值 B．有最大值3,最小值-1 C．有最大值3,无最小值 D．无最大值,也无最小值9.已知函数是定义在上的奇函数，当时，的图象如图所示，则不等式的解集是（）A ．B ．C ．D ．10.设定义域为R的函数f（x ）满足，且f（－1）＝，则f（2006）的值为（）A．1 B．1 C．2006 D ．二：填空题：(共2题,每小题10分,共20分)1.设奇函数)(xf的定义域为[]5,5-，若当[0,5]x∈时，)(xf的图象如右图,则不等式()0f x<的解是.2.若函数2()(2)(1)3f x k x k x=-+-+是偶函数，则)(xf的递减区间是____________三：解答题：(共2题,每小题10分,共20分)1.判断y=1-2x3在(-)上的单调性，并用定义证明。

1．3函数性质测试题一、选择题（每小题4分，共40分）1、在区间)0,(-∞上为增函数的是 （ ）A ．2)1(--=x yB ．21x y +=C ．x y -=D ．xx y -=1 2、若)(),(R x x f y ∈=是奇函数，则下列坐标表示的点一定在)(x f y =的图象上的是 （ ）A ．))(,(a f a -B ．))(,(a f a --C ．))(,(a f a ---D ．))(,(a f a -3、函数)22(),(2≤≤-=x a x f y 是奇函数，由实a 数的值是 （ ） A ．2- B ．2 C ．22-或 D ．无法确定4、函数)(x f ，则下列命题正确的是 （ ）A ．若)(x f 在)0.(-∞和),0(+∞上是增函数，则)(x f 是增函数；B ．若)(x f 在)0.(-∞和),0(+∞上是减函数，则)(x f 是减函数；C 。

若)(x f 是偶函数，在)0.(-∞上是增函数，则)(x f 在),0(+∞上也是增函数；D ．若)(x f 是奇函数，在)0.(-∞上是增函数，则)(x f 在),0(+∞上也是增函数。

5、已知偶函数)(x f 在],0[π上是增函数，那么)2(),2(),32(---f f f ππ的大小关系 A ．)32(π-f >)2(π-f >)2(-f B ．)32(π-f )2(-f >>)2(π-f C ．)2(π-f >)2(-f >)32(π-f D ．)2(-f >)2(π-f >)32(π-f 6、如奇函数)(x f 在区间]7,3[上是增函数且最小值为5，那么)(x f 在]3,7[--上是A ．增函数且最小值为-5B ．增函数且最大值为-5C ．减函数且最小值为-5D ．减函数且最大值为-57、若)(x f 为偶函数，)(x g 为奇函数且它们都不恒为零，它们的定义域的交集为非空集合，则)()(x g x f ⋅是A ．偶函数B ．奇函数C ．非奇非偶函数D ．既是奇函数，又是偶函数8、函数)(x f 为奇函数，且∈x )0.(-∞时，)1()(-=x x x f ，则∈x ),0(+∞时，)(x f 为A ．)1(+-x xB ．)1(+--x xC ．)1(+-x xD ．)1(-x x9、若函数2)1(2)(2+-+=x a x x f 在区间]4,(-∞上是减函数，那么实数工a 的取值范围是A ．3≥aB ．3-≥aC ．3-≤aD ．5≤a10、定义在),(+∞-∞的奇函数)(x f 为增函数；偶函数)(x g 在区间),0[+∞的图象与)(x f 的图象重合，设0>>B a ，给出下列不等式①)(b f -)(a f ->)(a g -)(b g - ②)(b f -)(a f -<)(a g -)(b g - ③)(a f -)(b f ->)(b g -)(a g - ④)(a f -)(b f -<)(b g -)(a g - 其中成立的是A ．①与③B ．②与③C ．①与④D ．②与④二、填空题（每小题5分，共20分）11、函数x x y -+=1的减区间是 ；12、若)(x f y =为奇函数，则=)0(f ；13、函数,,(3)(3R b a bx ax x f ∈-+= 且不同时为零）若4)3(-=f ，则=-)3(f ；14、奇函数)(x f 满足)()2(x f x f =+，且10<<x 时，则=)5.7(f 。

1.3函数的基本性质 练习试卷一、选择题（共6小题；共30分）1. 下列函数中，在区间 (0,+∞) 上是增函数的是 ( )A. y =−x 2B. y =x 2−2C. y =(12)xD. y =log 21x2. 设 f (x ) 是 R 上的任意函数，则下列叙述正确的是 ( ) A. f (x )⋅f (−x ) 是奇函数 B. f (x )⋅∣f (−x )∣ 是奇函数 C. f (x )−f (−x ) 是偶函数D. f (x )+f (−x ) 是偶函数3. 函数 f (x )=x 2−3x 的图象为曲线 C 1，函数 g (x )=4−x 2 的图象为曲线 C 2，过 x 轴上的动点 M (a,0)(0≤a ≤3) 作垂直于 x 轴的直线分别交曲线 C 1，C 2 于 A,B 两点，则线段 AB 长度的最大值为 ( )A. 2B. 4C. 5D. 418 4. 函数 y =x 2+2(a −5)x −6 在 (−∞,−5) 上是减函数，则 a 的范围是 ( )A. a ≥0B. a ≤0C. a ≥10D. a ≤105. 定义在区间 (−∞,+∞) 上的奇函数 f (x ) 为增函数；偶函数 g (x ) 在 [0,+∞) 上的图象与 f (x ) 的图象重合．设 a >b >0，给出下列不等式： ① f (b )−f (−a )>g (a )−g (−b ) ② f (b )−f (−a )<g (a )−g (−b ) ③ f (a )−f (−b )>g (b )−g (−a ) ④ f (a )−f (−b )<g (b )−g (−a ) 其中成立的是 ( )A. ①④B. ②④C. ①③D. ②③6. 设 Ω 为平面直角坐标系 xOy 中的点集，从 Ω 中的任意一点 P 作 x 轴、 y 轴的垂线，垂足分别为 M ，N ，记点 M 的横坐标的最大值与最小值之差为 x (Ω)，点 N 的纵坐标的最大值与最小值之差为 y (Ω)．如果 Ω 是边长为 1 的正方形，那么 x (Ω)+y (Ω) 的取值范围是 ( )A. [√2,2√2]B. [2,2√2]C. [1,√2]D. [1,2√2]二、填空题（共3小题；共15分） 7. 函数 f (x )=x 2+1x(12≤x ≤2) 的值域是 ．8. 已知函数 f (x ) 是定义 R 上的减函数，如果 f (a )>f (x +1) 在 x ∈[1,2] 上恒成立，那么实数 a 的取值范围是 ．9. 已知函数 f (x ) 是 R 上的奇函数，且 f (x +2) 为偶函数，若 f (1)=1，则 f (8)+f (9)= ． 三、解答题（共4小题；共52分）10. 已知函数 f (x )=1x−2 .Ⅰ 求 f (x ) 的定义域；Ⅱ 证明：函数 f (x ) 在 (0,+∞) 上为减函数． 11. 选做题：已知 f (x )=2x −12x +1(x ∈R )，Ⅰ 证明 f (x ) 是奇函数； Ⅱ 证明 f (x ) 是增函数． 12. 已知函数 f (x )=x 2−2x −1．Ⅰ 当 x ∈[−3,0] 时，求 f (x ) 的最大值和最小值； Ⅱ 当 x ∈[−3,2] 时，求 f (x ) 的最大值和最小值． 13. 用定义法证明 f (x )=1x+1 在 (−1,+∞) 上是减函数．答案第一部分1. B2. D3. D4. D5. C6. B 第二部分7. [2,52]8. {a ∣a <2} 9. 1 第三部分10. （1） f (x ) 的定义域是 {x ∈R ∣x ≠0} .（2） 证明：设 x 1，x 2 是 (0,+∞) 上的两个任意实数，且 x 1<x 2，则 Δx =x 1−x 2<0，Δy =f (x 1)−f (x 2)=1x 1−2−(1x 2−2)=1x 1−1x 2=x 2−x 1x 1x 2.因为 x 2−x 1=−Δx >0，x 1x 2>0，所以 Δy >0． 因此 f (x )=1x −2 是 (0,+∞) 上的减函数． 11. （1） 因为 f (x )=2−x −12−x +1=12x −112x+1=1−2x1+2x =−f (x )．所以 f (x ) 为奇函数．（2） 令 x 1<x 2，f (x 1)−f (x 2)=2(2x 1−2x 2)(2x 1+1)(2x 2+1)，因为 x 1<x 2， 所以 2x 1<2x 2， 所以 2x 1−2x 2<0， 所以 f (x 1)<f (x 2)，所以 f (x ) 在 R 上是增函数．12. （1） f (x )=x 2−2x −1=(x −1)2−2，因为 x ∈[−3,0]，所以当 x =−3 时，f (x ) 有最大值，最大值是 14，当 x =0 时，f (x ) 有最小值，最小值是 −1．（2） f (x )=x 2−2x −1=(x −1)2−2，因为 x ∈[−3,2]，当 x =−3 时，f (x ) 有最大值，f (x ) 的最大值是 14，当 x =1 时，f (x ) 有最小值，最小值是 −2． 13. 设 x 1，x 2∈(−1,+∞)且x 1<x 2，则 f (x 1)−f (x 2)=1x 1+1−1x 2+1=x 2−x 1(x 1+1)(x 2+1)，因为 x 1,x 2∈(−1,+∞)， 所以 x 1+1>0，x 2+1>0， 所以 x 1<x 2． 所以 x 2−x 1>0， 所以 x 2−x 1(x1+1)(x 2+1)>0，即 f (x 1)>f (x 2)，所以f(x)=1在(−1,+∞)上是减函数．x+1。

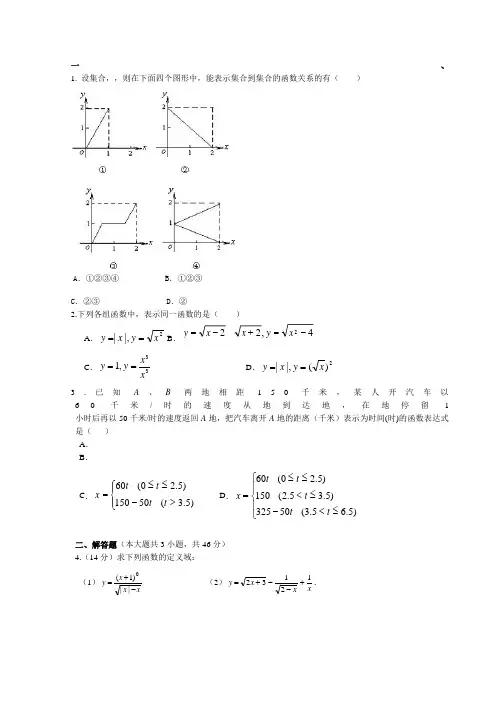
一、 1. 设集合，，则在下面四个图形中，能表示集合到集合的函数关系的有（ ）

A．①②③④ B．①②③ C．②③ D．② 2.下列各组函数中，表示同一函数的是（ ）

A．2|,|xyxy B．

C．33,1xxyy D．2)(|,|xyxy 3.已知A、B两地相距150千米，某人开汽车以 60千米/时的速度从地到达地，在地停留1 小时后再以50千米/时的速度返回A地，把汽车离开A地的距离（千米）表示为时间(时)的函数表达式是（ ） A． B．

C． D．

二、解答题（本大题共3小题，共46分） 4.（14分）求下列函数的定义域：

（1）xxxy||)1(0 （2）xxxy12132．

4 , 2 2 2      x y x x y  

 

      ) 5 . 3 ( 50 150 ) 5 . 2 0 ( 60 t t t t

x

 

 



        ) 5 . 6 5 . 3 ( 50 325 ) 5 . 3 5 . 2 ( 150) 5 . 2 0 ( 60 t tt t tx 一、选择题 1.C 解析：由函数的定义知①中的定义域不是，④中集合中有的元素在集合中对应两个函数值不符合函数定义，故不对，只有②③成立．故选C． 4.A 解析：B、C、D三个选项中的两个函数的定义域不相同,不表示同一个函数，A选项中的两个函数的定义域与对应关系都相同，表示相同的函数.故选A.

5.D 解析；从Ａ地到Ｂ地用了1502.560(时),因此当02.5t时, tx60.

因为在B地停留1小时,所以当2.53.5t时, 150x. 经3.5小时开始返回,由B地到A地用了150350（时）,因此当3.56.5t时,

150503.532550.xtt

综上所述, 三、解答题

10.解 ：（1）由,0||,01xxx得,0,1xx 故函数xxxy||)1(0的定义域是{x|x<0，且x≠1}．

1.3 函数的基本性质1．已知()f x 是定义(),-∞+∞上的奇函数，且()f x 在[)0,+∞上是减函数．下列关系式中正确的是( )Ａ．()()55f f >-Ｂ．()()43f f > Ｃ．()()22f f -> Ｄ．()()88f f -≥2．如果奇函数()f x 在区间[3，7]上是增函数且最小值为5，那么()f x 在区间[]7,3--上是( )Ａ．增函数且最小值为5-Ｂ．增函数且最大值为5- Ｃ．减函数且最小值为5- Ｄ．减函数且最大值为5-3．下列函数中，在区间(0，2)上为增函数的是 ( )A ．1y x =-+B ．y =C ．245y x x =-+D ．2y x= 4．对于定义域是R 的任意奇函数()f x 有 ( )A ．()()0f x f x --≥B ．()()0f x f x --≤C ．()()0f x f x -≤D ．()()0f x f x -≥ 5．求函数()211y x x x =--≤≤的最大值，最小值．6．将长度为l 的铁丝分成两段，分别围成一个正方形和一个圆，要使正方形与圆的面积之和最小，正方形的周长应为__________．7．函数()()0f x kx b k =+≠的单调性是____________．8．函数()f x 是偶函数，而且在()0,+∞上是减函数，判断()f x 在(),0-∞上是增函数还是减函数，并加以证明．9．如果二次函数()()215f x x a x =--+在区间1,12⎛⎫ ⎪⎝⎭上是增函数，求()2f 的取值范围．10．求函数3y =11．已知函数()1f x x x=+．判断()f x 在区间(0，1]和[1，+∞)上的单调性，说明理由． 12．已知函数()f x 是偶函数，且0x ≤时，()1.1x f x x +=-．求 (1) ()5f 的值，(2) ()0f x =时x 的值；(3)当x >0时，()f x 的解析式．13．作出函数()21y x x =-+的图象，并根据函数的图象找出函数的单调区间．参考答案。

(完整版)《函数的基本性质》练习题一、选择题1. 设函数 f(x) = 3x^2 + 2x + 1，在区间 [-2, 2] 上，f(x) 的最小值出现在区间的哪个点？A. x = -2B. x = -1C. x = 0D. x = 1E. x = 2答案：C. x = 02. 若函数 g(x) 的定义域为实数集，且对任意 x，g(x) = g(x + 1)，则函数 g(x) 的图像具有什么样的性质？A. 对称性B. 周期性C. 单调性D. 渐近性E. 不对称性答案：B. 周期性二、填空题1. 设函数 h(x) = 2^(x - 1)，则 h(0) = ____答案：12. 设函数i(x) = √(x^2 - 9)，则定义域为 ____ 的实数集。

答案：[-∞, -3] 并[3, +∞]三、解答题1. 证明函数 f(x) = x^3 - 6x^2 + 9x + 2 在整个实数集上是递增的。

解答：首先，计算 f'(x) = 3x^2 - 12x + 9。

我们可以使用求函数的导数的方法证明 f(x) 的递增性。

根据二次函数的性质，当 3x^2 - 12x + 9 > 0 时，即 x^2 - 4x + 3 > 0 时，函数 f(x) 在该区间上是递增的。

化简方程得到 (x - 1)(x - 3) > 0，所以 f(x) 在 (-∞, 1)U(3, +∞) 上是递增的。

因此，函数 f(x) 在整个实数集上是递增的。

2. 设函数 g(x) = |x + 3| - 2x，求函数 g(x) 的定义域以及其在定义域上的单调区间。

解答：对于函数 g(x) 来说，|x + 3| 在定义域内的取值范围为 x+ 3 ≥ 0 和 x + 3 < 0 两种情况，即x ≥ -3 或 x < -3。

同时，2x 在定义域内的取值范围为 x 属于实数集。

综合两种情况，g(x) 的定义域为x 属于实数集。