流体力学 2-1_静力学
- 格式:ppt
- 大小:852.00 KB
- 文档页数:24



第二章 流体静力学§2-1作用在流体上的力、表面力、质量力在运动的实际流体中任取一块流体,其体积为V ,表面积为A ,在这块流体上任取一微元面积δA ,作用在其表面上的力为δF ,分解为⎩⎨⎧切向力法向力τδδF F n ,则法向力: AF p A δδδn 0lim →= (N/m 2)切向力:AF A δδτδτ0lim →= (N/m 2)在这块流体上,取一流体微团,其体积为δV,由于地球引力的作用,产生的重力为ρg δV 。
由于流体存在加速度a,根据达朗贝尔原理,虚加的惯性力为-ρδVa。
所以,流体所受的力为:⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧惯性力重力或体积力质量力一般情况不考虑和表面张力摩擦力切向应力压力法向应力表面力)()()()(στP 表面力―是指作用在流体中的所取某部份流体体积表面上的力,也就是该部分体积周围的流体(既可是同一种类的流体,也可是不同种类的流体)或固体通过接触面作用在其上的力。
质量力―是指作用在流体内部所有流体质点上并与流体的体积或质量成正比的力,又称体积力。
通常,单位质量流体的质量力用→f 表示,在笛卡尔直面坐标系中:k j i zyxf f f f →→→→++=流体静力学―研究流体处于静止状态时各种物理量的分布规律及在工程实际中的应用。
所谓流体的静止状态是指流体对选用的坐标系无相对运动的状态。
δF§2-2流体的静压强及其特性在静止的流体中,任取一块流体。
当δA →0时,p 就定义为空间某点的静压强:AP p A δδδlim→=静压强的两个特性:① 流体静压强指向作用面的内法线方向。
② 流体中任意点静压强的大小只是位置的函数,即p=f (x ,y ,z )与其作用面的方向无关,又称作静压强各向同性。
证①:流体中任意点所受的力均可分为切应力和压应力。
因总体静止,0d d =yu, 故切应力0=τ,所以,只存在法向应力,当然垂直于作用面。
又:流体在拉力作用下,要发生运动,因为静止,故只存在压应力。





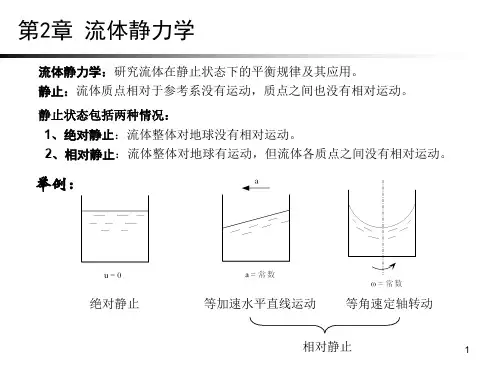
第二章 流体静力学2-1 将盛有液体的U 形小玻璃管装在作水平加速运动的汽车上(如图示),已知L =30 cm ,h =5cm ,试求汽车的加速度a 。
解:将坐标原点放在U 形玻璃管底部的中心。
Z 轴垂直向上,x 轴与加速度的方向一致,则玻璃管装在作水平运动的汽车上时,单位质量液体的质量力和液体的加速度分量分别为0,0,,0,0x y z x y z g g g ga a a a ===-===代入压力全微分公式得d (d d )p a x g z ρ=-+ 因为自由液面是等压面,即d 0p =,所以自由液面的微分式为d d a x g z =- 积分得:a z x c g =-+,斜率为a g -,即a g h L = 解得21.63m/s 6g a g h L ===2-2 一封闭水箱如图示,金属测压计测得的压强值为p =4.9kPa(相对压强),测压计的中心比A 点高z =0.5m ,而A 点在液面以下h =1.5m 。
求液面的绝对压强和相对压强。
解:由0p gh p gz ρρ+=+得相对压强为30() 4.91010009.81 4.9kPa p p g z h ρ=+-=⨯-⨯⨯=-绝对压强0( 4.998)kPa=93.1kPa abs a p p p =+=-+2-3 在装满水的锥台形容器盖上,加一力F =4kN 。
容器的尺寸如图示,D =2m ,d =l m ,h =2m 。
试求(1)A 、B 、A ’、B ’各点的相对压强;(2)容器底面上的总压力。
解:(1)a 20 5.09kP 4πd F A F p ==,由0p p gh ρ=+得: a 0B A 5.09kP P P P ===a a a 0B A kP 24.7P 29.81000kP 5.09ρgh P P P =⨯⨯+=+==''(2) 容器底面上的总压力为2'24.7kPa 77.6kN 4A D P p A π==⨯=2-4 一封闭容器水面的绝对压强p 0=85kPa ,中间玻璃管两端开口,当既无空气通过玻璃管进入容器、又无水进人玻璃管时,试求玻璃管应该伸入水面下的深度h 。
