下载文档原格式
一、填空题1、设A B, C为三个事件，则下列事件“ B发生而A与C至少有一个发生”，“A，B, C中至少有两个发生”，“A, B, C中至少有一个发生”，“A，B, C中不多于一个发生”，“A，B, C中恰好有一个发生” ，“ A , B , C中恰好有两个发生”分别可表示丿为、、、、、。
参考答案：B ( A+C AB+AC+BCA + B+C, AC + BC +AB , AB C +AC B + A BC, ABC + ABC +ABC考核知识点：事件的关系及运算2、从0, 1, 2,…，9这10个数中可重复取两个数组成一个数码，则“两个数之和为3”、“两个数之和为17”、“两个数相同”的概率分别为___________ 、______ 、______ 。
参考答案：，，考核知识点：古典型概率3、同时抛掷3枚均匀的硬币，则3枚正面都向上的概率为_____________ ，恰好有2枚正面向上的概率为__________________ 。
参考答案：1/8 , 3/8考核知识点：古典型概率4、箱中有60个黑球和40个白球，从中任意连接不放回取出k个球，则第k次取出黑球的概率为_____________________ 。
参考答案：考核知识点：古典型概率5、假设某商店获利15万元以下的概率为，获利10万元以下的概率为，获利5万元以下的概率为，则该商店获利5~10万元的概率为_____________ ，获利U 10~15万元的概率为_____________ 。
参考答案：，考核知识点：概率的性质6、设袋中有6个球，其中4白2黑。
用不放回两种方法取球，则取到的两个球都是白球的概率为______________ ;取到的两个球颜色相同的概率为_____________ ;取到的两个球中至少有一个是白球的概率为_____________ 。
参考答案：,7/15, 14/15考核知识点：古典型概率和概率的性质7、设事件A,B互不相容，已知P( A= ,P( B)二，则P( A+B= ________ ; P( A +B) = _______ ；P( A B) = _______ ；P( AB) = _______ 。
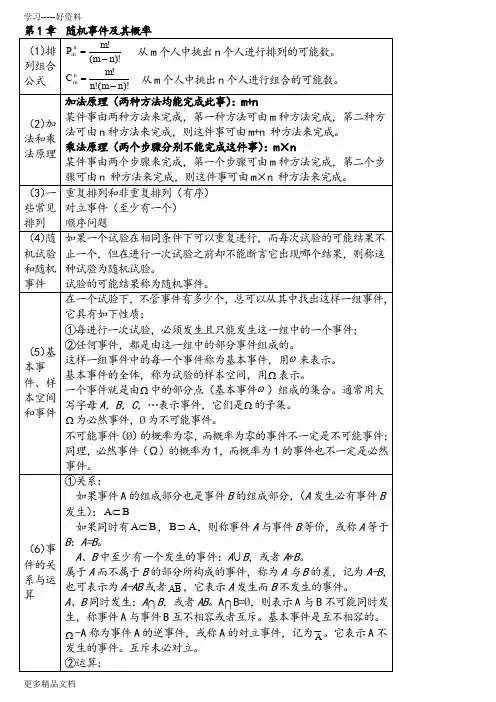
古典概型例子 摸球模型例1：袋中有a 个白球，ｂ个黑球，从中接连任意取出m (m ≤a +ｂ)个球，且每次取出的球不再放回去，求第m 次取出的球是白球的概率;分析：本例的样本点就是从a +ｂ中有次序地取出m 个球的不同取法；第m 次取出的球是白球意味着：第ｍ次是从a 个白球中取出一球，再在a +ｂ-1个球中取出m-1个球。
解：设B ＝｛第m 次取出的球是白球｝样本空间的样本点总数： mb a A n +=事件B 包含的样本点： 111--+=m b a a A C r ，则 b a a A aA n r B P mba mb a +===+--+11)( 注：本例实质上也是抽签问题，结论说明按上述规则抽签，每人抽中白球的机会相等，同抽签次序无关。
例2：袋中有4个白球，5个黑球，6个红球，从中任意取出9个球，求取出的9个球中有1 个白球、3个黑球、5个红球的概率.解：设B ＝｛取出的9个球中有1个白球、3个黑球、5个红球｝样本空间的样本点总数： 915C n ==5005事件B 包含的样本点： 563514C C C r ==240，则 P (B )=120/1001=0.048 占位模型例：n 个质点在N 个格子中的分布问题.设有n 个不同质点，每个质点都以概率1/N 落入N 个格子(N ≥n)的任一个之中，求下列事件的概率：(1) A ={指定n 个格子中各有一个质点}；(2) B ={任意n 个格子中各有一个质点}； (3) C ={指定的一个格子中恰有m (m ≤n )个质点}.解：样本点为n 个质点在N 个格子中的任一种分布，每个质点都有N 种不同分布，即n 个质点共有N n 种分布。
故样本点总数为：N n(1)在n 个格子中放有n 个质点，且每格有一个质点，共有n !种不同放法；因此，事件A 包含的样本点数：n!，则 n Nn A P !)(=(2)先在N 个格子中任意指定n 个格子，共有nN C 种不同的方法；在n 个格子中放n 个质点，且每格一个质点，共有n !种不同方法；因此，事件B 包含的样本点数： n NnN A C n =!，则n nNNA B P =)((3)在指定的一个格子中放m (m ≤n )个质点共有mn C 种不同方法；余下n-m 个质点任意放在余下的N-1个格子中,共有m n N --)1(种不同方法.因此，事件C 包含的样本点数：mn C m n N --)1(, 则mn m m n nm n mn N N N C N N C C P ---=-=)1()1()1()( 抽数模型例：在0～9十个整数中任取四个，能排成一个四位偶数的概率是多少？解：考虑次序.基本事件总数为：410A =5040，设B ={能排成一个四位偶数} 。
《概率论与统计原理》课程期末复习资料《概率论与统计原理》课程讲稿章节目录：第一章事件的概率§1.1 随机事件和样本空间1.1.1 随机现象与随机试验1.1.2 随机事件1.1.3 样本空间§1.2 事件的关系和运算1.2.1 事件的关系和运算1.2.2 事件与集合的关系1.2.3 事件的运算性质§1.3 随机事件的概率1.3.1 概率的统计定义1.3.2 古典型概率1.3.3 几何型概率§1.4 概率的公理化定义1.4.1 概率的三条公理（概率的公理化定义）1.4.2 概率的性质§1.5 条件概率和事件的独立性1.5.1 条件概率1.5.2 乘法公式1.5.3 全概率公式1.5.4 贝叶斯公式1.5.5 事件的独立性第二章随机变量及其分布§2.1 随机变量及其分布函数2.1.1 随机变量2.1.2 随机变量的分布函数§2.2 离散型随机变量2.2.1离散型随机变量及其分布2.2.2 常用离散型概率分布§2.3 连续型随机变量2.3.1 连续型随机变量的定义2.3.2 常用连续型概率分布§2.4 随机变量函数的分布2.4.1 离散型随机变量函数的分布2.4.2 连续型随机变量函数的分布§2.5 多维随机变量简介2.5.1 多维随机变量的定义2.5.2 二维随机变量的联合分布函数2.5.3 边缘分布函数2.5.4 随机变量的独立性第三章随机变量的数字特征§3.1 随机变量的数学期望3.1.1 数学期望的定义3.1.2 随机变量函数的数学期望3.1.3 数学期望的性质§3.2 随机变量的方差3.2.1 方差和标准差的定义3.2.2 方差的性质3.2.3 切比雪夫不等式§3.3 常用分布的数学期望和方差3.3.1 常用离散型分布的数学期望和方差3.3.2 常见连续型分布的数学期望和方差§3.4 随机变量的矩第四章极限定理§4.1 大数定律4.1.1随机变量列的极限4.1.2 大数定律§4.2 中心极限定理4.2.1 列维-林德伯格定理4.2.2 棣莫佛-拉普拉斯（De Moivre-Laplace）定理第五章统计原理§5.1 数理统计的基本概念5.1.1 总体和样本5.1.2 统计量5.1.3 经验分布函数§5.2 抽样分布5.2.1 χ2分布5.2.2 t分布5.2.3 正态总体的抽样分布§5.3 参数估计5.3.1 统计估计的概念5.3.2 参数的点估计5.3.3 正态总体参数的区间估计§5.4 假设检验5.4.1 一个总体均值的假设检验5.4.2 一个正态总体方差σ2的假设检验5.4.3 一个总体比率的假设检验（大样本）一、客观部分：（单项选择）★考核知识点: 事件的关系和运算考核知识点解释：“事件A与事件B至少有一个发生”的事件，称为事件A与事件B的和（或并），记作A∪B或A+B。
《概率统计》、《概率论与数理统计》、《随机数学》课程期末复习资料注：以下是考试的参考内容，不作为实际考试范围，考试内容以教学大纲和实施计划为准；注明“了解”的内容一般不考。
1、能很好地掌握写样本空间与事件方法，会事件关系的运算，了解概率的古典定义2、能较熟练地求解古典概率；了解概率的公理化定义3、掌握概率的基本性质和应用这些性质进行概率计算；理解条件概率的概念；掌握加法公式与乘法公式4、能准确地选择和运用全概率公式与贝叶斯公式解题；掌握事件独立性的概念及性质。
5、理解随机变量的概念，能熟练写出(0—1)分布、二项分布、泊松分布的分布律。
6、理解分布函数的概念及性质，理解连续型随机变量的概率密度及性质。
7、掌握指数分布(参数λ)、均匀分布、正态分布，特别是正态分布概率计算8、会求一维随机变量函数分布的一般方法，求一维随机变量的分布律或概率密度。
9、会求分布中的待定参数。
10、会求边缘分布函数、边缘分布律、条件分布律、边缘密度函数、条件密度函数，会判别随机变量的独立性。
11、掌握连续型随机变量的条件概率密度的概念及计算。
12、理解二维随机变量的概念，理解二维随机变量的联合分布函数及其性质，理解二维离散型随机变量的联合分布律及其性质，理解二维连续型随机变量的联合概率密度及其性质，并会用它们计算有关事件的概率。
13、了解求二维随机变量函数的分布的一般方法。
14、会熟练地求随机变量及其函数的数学期望和方差。
会熟练地默写出几种重要随机变量的数学期望及方差。
15、较熟练地求协方差与相关系数.16、了解矩与协方差矩阵概念。
会用独立正态随机变量线性组合性质解题。
17、了解大数定理结论，会用中心极限定理解题。
18、掌握总体、样本、简单随机样本、统计量及抽样分布概念，掌握样本均值与样本方差及样本矩概念，掌握2分布(及性质)、t分布、F分布及其分位点概念。
19、理解正态总体样本均值与样本方差的抽样分布定理；会用矩估计方法来估计未知参数。
概率论与数理统计期末复习重要知识点及公式整理2010-2011学年第一学期期末复习资料概率论与数理统计期末复习重要知识点第二章知识点：1.离散型随机变量：设X是一个随机变量，如果它全部可能的取值只有有限个或可数无穷个，则称X为一个离散随机变量。
2.常用离散型分布：（1）两点分布（0-1分布）：若一个随机变量XP{X x1}p,P{X x2}1p只有两个可能取值，且其分布为(0p1)，则称X服从x1,x2处参数为p的两点分布。
两点分布的概率分布：两点分布的期望：（2）二项分布：P{X x1}p,P{X x2}1p(0p1) E(X)p；两点分布的方差：D(X)p(1p)若一个随机变量X的概率分布由式给出，则称X服从参数为n,p的二项分布。
记为X~b(n,p)(或B(n,p)).两点分布的概率分布：二项分布的期望：（3）泊松分布：P{x k}Cnp(1p)kkn kkkn k,k0,1,...,n. P{x k}Cnp(1p),k0,1,...,n. E(X)np；二项分布的方差：D(X)np(1p)kP{X k} e若一个随机变量X的概率分布为数为的泊松分布，记为X~P () k!,0,k0,1,2,...，则称X服从参P{X k} e泊松分布的概率分布：泊松分布的期望：4.连续型随机变量：kk!,0,k0,1,2,... E(X)；泊松分布的方差：D(X)如果对随机变量X的分布函数F(x)，存在非负可积函数F(x)P{X x}f(x)，使得对于任意实数x，有xf(t)dt，则称X为连续型随机变量，称f(x)为X的概率密度函数，简称为概率密度函数。
2010-2011学年第一学期期末复习资料5.常用的连续型分布：（1）均匀分布：1,若连续型随机变量X的概率密度为f(x)b a 0,a x b其它，则称X在区间（a,b）上服从均匀分布，记为X~U(a,b)1,均匀分布的概率密度：f(x)b a0,a b2a xb 其它均匀分布的期望：（2）指数分布：E(X)；均匀分布的方差：D(X)(b a)122e xf(x)0若连续型随机变量X的概率密度为x00，则称X服从参数为的指数分布，记为X~e ()x0e xf(x)0指数分布的概率密度：指数分布的期望：（3）正态分布：E(X)1；指数分布的方差：D(X)2f(x)(x)222x若连续型随机变量X的概率密度为则称X服从参数为和22的正态分布，记为X~N(,)(x)222f(x)正态分布的概率密度：正态分布的期望：E(X)xD(X)x22；正态分布的方差：（4）标准正态分布：0,21(x)，2(x)xet22标准正态分布表的使用：（1）x0(x)1(x)2010-2011学年第一学期期末复习资料X~N(0,1)P{a x b}P{a x b}P{a x b}P{a x b}(b)(a)X~N(,),Y2（2）X（3）P{a X b}P{a~N(0,1),F(x)P{X x}P{X故b}(b)(a)x(x) Y2Y定理1：设X~N(,),则X~N(0,1)6.随机变量的分布函数：设X是一个随机变量，称分布函数的重要性质：0F(x) 1P{x1X x2}P{X x2}P{X x1}F(x2)F(x1)x1x2F(x1)F(x2)F()1,F()0F(x)P{X x}为X的分布函数。
一、填空题1、设A ，B ，C 为三个事件，则下列事件“B 发生而A 与C 至少有一个发生”，“A ，B ，C 中至少有两个发生”，“A ，B ，C 中至少有一个发生”，“A ，B ，C 中不多于一个发生”，“A ，B ，C 中恰好有一个发生”，“A ，B ，C 中恰好有两个发生”分别可表示为 、 、 、 、 、 。
参考答案：B （A+C ，AB+AC+BC ，A +B +C ，C A +C B +B A ，AB C +AC B +A BC ，BC A +C B A +C AB 考核知识点：事件的关系及运算，参见P92、从0，1，2，…，9这10个数中可重复取两个数组成一个数码，则“两个数之和为3”、“两个数之和为17”、“两个数相同”的概率分别为 、 、 。
参考答案：0.04，0.04，0.1考核知识点：古典型概率，参见P113、箱中有60个黑球和40个白球，从中任意连接不放回取出k 个球，则第k 次取出黑球的概率为 。
参考答案：0.6考核知识点：古典型概率，参见P134、假设某商店获利15万元以下的概率为0.9，获利10万元以下的概率为0.5，获利5万元以下的概率为0.3，则该商店获利5~10万元的概率为 ，获利10~15万元的概率为 。
参考答案：0.2，0.4考核知识点：概率的性质，参见P16~P175、设袋中有6个球，其中4白2黑。
用不放回两种方法取球，则取到的两个球都是白球的概率为 ；取到的两个球颜色相同的概率为 ；取到的两个球中至少有一个是白球的概率为 。
参考答案：0.4，7/15，14/15考核知识点：古典型概率和概率的性质，参见P18~P19 6、设事件A ，B 互不相容，已知P （A ）= 0.6，P （B ）= 0.3，则P （A+B ）= ；P （A +B ）= ；P （A B ）= ；P （B A ）= 。
参考答案：0.9，0.4，0.3，0.1考核知识点：概率的性质，参见P197、甲、乙、丙三人各射一次靶子，他们各自中靶与否相互独立，且已知他们各自中靶的概率分别为0.5，0.6，0.8，则恰有一人中靶的概率为 ；至少有一人中靶的概率为 。
参考答案：（1）0.26；（2）0.96考核知识点：事件的独立性，参见P298~P30 8、每次试验的成功率为p （0< p <1），则在5次重复试验中至少成功一次的概率为 。
参考答案：5)1(1p --考核知识点：事件的独立性，参见P299、设随机变量X ~N （1，4），则P{0 ≤X ＜1.6}= ；P{X ＜1}= 。
参考答案：0.3094，0.5考核知识点：正态分布，参见P6110、设随机变量X ～B （n ，p ），已知E X =0.6，D X =0.48，则n = ，p = 。
参考答案：3，0.2考核知识点：随机变量的数学期望和方差，参见P111，P120~P121 11、设随机变量X 服从参数为（100，0.2）的二项分布，则E X = ， D X = 。
参考答案：20，16考核知识点：随机变量的数学期望和方差，参见P111，P120~P121 12、设随机变量X 服从正态分布N （-0.5，0.52），则E X 2= ，D （2X -3）= 。
参考答案：0.5，1考核知识点：随机变量的数学期望和方差及其性质，参见P113， P12213、设由来自正态总体)9,(2μN 的容量为9的简单随机样本，得样本均值X =5，则未知参数μ的最大似然估计值为 ，μ的置信度为0.95的置信区间为 。
参考答案：5，（-0.88，10.88）考核知识点：正态总体参数的极大似然估计以及区间估计，参见P185~P186，P19414、设由来自正态总体)10,(2μN 的容量为25的简单随机样本，得样本均值X =15，则未知参数μ的最大似然估计值为 ，μ的置信度为0.95的置信区间长度为 。
参考答案：15，7.84考核知识点：正态总体参数的极大似然估计以及区间估计，参见P185~P186，P194~P19515、设总体X 服从正态分布),(2σμN ，从X 中随机抽取一个容量为36的样本，设X 为样本均值，S 2为样本方差。
当总体方差σ2已知时，检验假设H 0：μ=μ0的统计量为 ，当总体方差σ2未知时，检验假设H 0：μ=μ0的统计量为 。
参考答案：36/0σμ-X ，36/0S X μ-考核知识点：正态总体均值的假设检验，参见P21216、设总体X 服从正态分布),(2σμN ，从X 中随机抽取一个容量为n 的样本，设S 2为样本方差，则检验假设H 0：202σσ=的统计量为 。
参考答案：222)1(σχS n -=考核知识点：正态总体方差的假设检验，参见P21817、假设检验时若增大样本容量，则犯两类错误的概率都将 。
参考答案：减少考核知识点：假设检验的两类错误，参见P 210~P211二、单项选择题1、下列数字中不可能是随机事件概率的是（ ）。
A ．- 1/3B ．0 Ｃ．0.3 Ｄ．1 参考答案：A考核知识点：概率的公理化定义，参见P162、某产品共有10件，其中3件为次品，其余为正品。
用不放回方法从中任取两次，一次一件，则第二次取到的是正品的概率为（ ）。
A ．107 B ．103C ．92D ．151参考答案：B考核知识点：古典型概率，参见P133、设某厂的甲、乙、丙三个车间生产同一种产品，记A 1为“产品是由甲车间生产的”， A 2为“产品是由乙车间生产的”， A 3为“产品是由丙车间生产的”， B 为“产品是次品”。
今从即将出厂的该种产品中任取一件，则取到的是甲车间生产的次品的概率为（ ）。
A ．P (C A 1) B ．P (C 2A ) C ．P (B A 2) D ．P (A 1B )参考答案：D考核知识点：概率的表示与条件概率，参见P214、设某厂的甲、乙、丙三个车间生产同一种产品，记A 1为“产品是由甲车间生产的”， A 2为“产品是由乙车间生产的”， A 3为“产品是由丙车间生产的”， B 为“产品是次品”。
今从次品中任取一件，则它是由甲车间生产的的概率为（ ）。
A ．P (C A 1) B ．P (C 2A ) C ．P (B A 2) D ．P (B A 1) 参考答案：D考核知识点：概率的表示与条件概率，参见P215、任何连续型随机变量的概率密度f (x ) 一定满足（ ）。
A ．1)(0≤≤x fB ．在定义域内单调不减C ．在定义域内右连续D ．⎰∞+∞-=1)(dx x f参考答案：D考核知识点：概率密度的性质，参见P526、设随机变量X ~N （2，1002），且P{0<X <4}=0.3，则P{X <0}=（ ）。
A ．0.25B ．0.35C ．0.65D ． 0.95 参考答案：B考核知识点：正态分布，参见P617、设X 是随机变量，x 0为任意实数，E X 是X 的数学期望，则（ ）。
A ．220)E E()E(X X x X -=- B ．220)E E()E(X X x X -≥- C ．220)E E()E(X X x X -≤- D ．0)E(20=-x X参考答案：B考核知识点：方差的性质，参见P1238、设假设总体X 服从参数为p （0<p <1）的0-1分布，p 未知。
（X 1，X 2，…，X 5）是来自X 的简单随机样本，则下面的（ ）是统计量。
A ．X 1+pX 3B ．X 5+2p （X 5 -X 2）C ．min （X 1，X 2，…，X 5）D ．X 2-E X 4 参考答案：C考核知识点：统计量的定义，参见P 1609、设总体X 的均值μ与方差2σ都存在，且均为未知参数，而n X X X ,,,21 为该总体的一个样本，∑==ni i X n X 11，则总体均值μ的矩估计量为（ ）．A ．∑=n i i X n 121B ．∑=-n i i X X n 12)(1C ．∑=-n i i X n 12)(1μ D ．∑=-n i i X X n 1)(1参考答案：A考核知识点：参数的矩估计，参见P 180~P18110、设总体X 的均值μ与方差2σ都存在，且均为未知参数，而n X X X ,,,21 为该总体的一个样本，∑==n i i X n X 11，则总体方差2σ的矩估计量为（ ）．A ．∑=n i i X n 121B ．∑=-n i i X X n 12)(1C ．∑=-n i i X n 12)(1μ D ．∑=-n i i X X n 1)(1参考答案：B考核知识点：参数的矩估计，参见P 180~P18111、从估计量的有效性是指（ ）。
A ．估计量的抽样方差比较小B ．估计量的抽样方差比较大C ．估计量的置信区间比较宽D ．估计量的置信区间比较窄 参考答案：A考核知识点：评价估计量的标准，参见P 19012、在一次假设检验中，当显著性水平为0.01时原假设被拒绝。
当显著性水平为0.05时，则（ ）。
A ．可能会被拒绝B ．就不会被拒绝C ．也一定会被拒绝D ．需要重新检验 参考答案：C考核知识点：假设检验的显著性水平，参见P 20913、假设检验时若增大样本容量，则犯两类错误的概率（ ）。
A ．一个增大，一个减少B ．都增大C ．都不变D ．都减少 参考答案：D考核知识点：假设检验的两类错误，参见P 210~P21114、假设检验中，一般情况下，（ ）错误。
A ．只犯第一类B ．只犯第二类C ．既可能犯第一类也可能犯第二类D ．既不犯第一类也不犯第二类 参考答案：C考核知识点：假设检验的两类错误，参见P 210~P21115、要求次品率低于10%才能出厂，在检验时原假设应该是（ ）。
A. 1.0:0≥p H B.1.0:0=p H C. 1.0:0≤p H D.1.0:0<p H 参考答案：A考核知识点：单边假设检验，参见P 221~P224三、计算题1、写出下列随机试验的样本空间及下列事件的样本点。
（1）E 1：掷一颗均匀对称的骰子，观察出现的点数；A ={掷出偶数点}。
（2）E 2：记录一段时间内某城市110报警次数；B ={报警次数小于5次}。
（3）E 3：在一批灯泡中任意抽取一只，观察其使用寿命（单位：小时）；C ={使用寿命超过500小时}。
（4）E 4：向半径为10的平面区域D ={（x ，y ）：x 2 +y 2≤100}内随机投掷一点（假设点必落在D 内），观察落点的坐标；C={落点在半径为5的同心圆内}。
参考答案：（1）Ω1 = {1，2，…，6}；A = {2，4，6}（2）Ω2 ={0，1，2，…}；B ={0，1，2，3，4} （3）Ω3 =（0，∞ ）；C =（500，∞）（4）Ω4 = {100:),(22≤+y x y x }，D ={25:),(22≤+y x y x } 考核知识点：用集合表示随机试验的样本空间和随机事件，参见P4~P52、已知P （A ）=P （B ）=P （C ）=1/4，P （AC ）=P （AB ）=1/16，P （BC ）= 0，求事件“A ，B ，C 至少有一个发生”和事件“A ，B ，C 都发生”的概率。
