2017.3.10每周一练1

胶州市大同小学三年级第 3 周“周周清”
一、根据算式填空。

1.计算40×3＝？时，我是这样想的：（）个（）乘（），得（）个（），就是（）。

2．计算32×4＝？时，我是这样想的：2乘（）等于（），（）乘以4等于（），（）加上（）等于（），所以32×4＝（）。

3. 1 2
× 3
6……（）○（）
3 0……（）О（）
3 6……（）О（）
二、 2 7
× 2 3
81
积的十位上为什么是8？
---------------------------------
-------------------------------------
考点题
三、选一选。

认真学好每一课，每天进步一点点
1．要使□4×3的积是三位数，□里可填（）。

①比2大的数②比3小的数③任何数都行
2．要使□5×3的积是二位数，□里可填（）。

①比3小的数②比3大的数③任何数
3.一个两位数乘9，积是（）。

①两位数②三位数③两位数或三位数
四、比较大小。

42×5○200 57×8○8×67
97×0○97 1＋48○48×1
41×5○5×83 50×8○7×60
1．□ 9 □4
× 3 ×□
8 □ 5 1 8
□83□
×□× 7
1□ 8 □□5
胶州市大同小学三年级第 3 周“周周清”
认真学好每一课，每天进步一点点。

乡镇（街道） 学校 班级 姓名 学号 ………密……….…………封…………………线…………………内……..………………不……………………. 准…………………答…. …………题…乌海市小学三年级数学上学期每周一练试卷 含答案题 号 填空题 选择题 判断题 计算题 综合题 应用题 总分 得 分考试须知：1、考试时间：90分钟，满分为100分（含卷面分2分）。

2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。

3、不要在试卷上乱写乱画，卷面不整洁扣2分。

一、用心思考，正确填空（共10小题，每题2分，共20分）。

1、换算。

7000千克=（ ）吨 8千克=（ ）克 23吨=（ ）千克 5200千克－200千克=（ ）吨 2、小明从一楼到三楼用8秒，照这样他从一楼到五楼用（ ）秒。

3、体育老师对第一小组同学进行50米跑测试,成绩如下小红9秒,小丽11秒,小明8秒,小军10秒。

( )跑得最快,( )跑得最慢。

4、□45÷5，要使商是两位数，□里最大可填（ ）；要使商是三位数，□里最小应填（ ）。

5、46÷9=5……1中，被除数是（ ），除数是（ ），商是（ ），余数是（ ）。

6、分针走1小格，秒针正好走（ ），是（ ）秒。

分针走1大格是（ ），时针走1大格是（ ）。

7、小林晚上10：00睡觉，第二天早上7：00起床，他一共睡了（ ）小时。

8、把一根绳子平均分成6份，每份是它的（ ），5份是它的（ ）。

9、量出钉子的长度。

10、劳动课上做纸花，红红做了2朵纸花，4朵蓝花，红花占纸花总数的（ ），蓝花占纸花总数的（ ）。

二、反复比较，慎重选择（共8小题，每题2分，共16分）。

1、四边形（ ）平行四边形。

A.一定B.可能C.不可能2、一个长方形花坛的宽是4米，长是宽的3倍，花坛的面积是（ ）平方米。

A 、12 B 、16 C 、483、用7、3、9三个数字可组成（ ）个三位数。

A 、3 B 、4 C 、64、最小三位数和最大三位数的和是（ ）。

乡镇（街道） 学校 班级 姓名 学号 ………密……….…………封…………………线…………………内……..………………不……………………. 准…………………答…. …………题…大庆市小学三年级数学上学期每周一练试题 附答案题 号 填空题 选择题 判断题 计算题 综合题 应用题 总分 得 分考试须知：1、考试时间：90分钟，满分为100分（含卷面分2分）。

2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。

3、不要在试卷上乱写乱画，卷面不整洁扣2分。

一、用心思考，正确填空（共10小题，每题2分，共20分）。

1、小林晚上10：00睡觉，第二天早上7：00起床，他一共睡了（ ）小时。

2、劳动课上做纸花，红红做了2朵纸花，4朵蓝花，红花占纸花总数的（ ），蓝花占纸花总数的（ ）。

3、体育老师对第一小组同学进行50米跑测试,成绩如下小红9秒,小丽11秒,小明8秒,小军10秒。

( )跑得最快,( )跑得最慢。

4、你出生于（ ）年（ ）月（ ）日，那一年是（ ）年，全年有（ ）天。

5、小明从一楼到三楼用8秒，照这样他从一楼到五楼用（ ）秒。

6、小红家在学校（ ）方（ ）米处；小明家在学校（ ）方（ ）米处。

7、量出钉子的长度。

8、在进位加法中，不管哪一位上的数相加满（ ），都要向（ ）进（ ）。

9、□÷8＝138……○，余数最大填（ ），这时被除数是（ ）。

10、□45÷5，要使商是两位数，□里最大可填（ ）；要使商是三位数，□里最小应填（ ）。

二、反复比较，慎重选择（共8小题，每题2分，共16分）。

1、把一根长60厘米的铁丝围城一个正方形，这个正方形的面积是（ ）。

A.225平方分米 B.225平方厘米 C.360平方厘米2、学校开设两个兴趣小组，三（1）27人参加书画小组，24人参加棋艺小组，两个小组都参加的有3人，那么三（1）一共有（ ）人参加了书画和棋艺小组。

A 、51 B 、54 C 、48 D 、303、最大的三位数是最大一位数的（ ）倍。

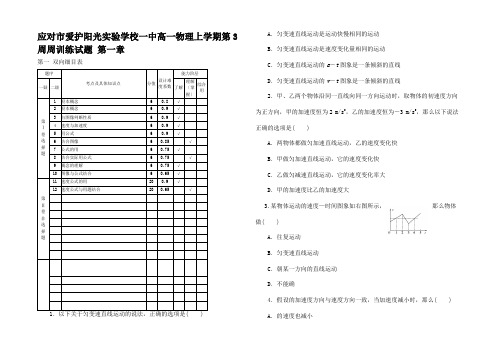
应对市爱护阳光实验学校一中高一物理上学期第3周周训练试题第一章第一双向细目表题序考点及具体知识点分值设计难度系数能力阶层一疑二级了解理解〔掌握〕综合用第Ⅰ卷选择题1 根本概念 6 0.8 √2 根本概念 6 0.9 √3 由图像判断性质 6 0.9 √4 速度与加速度 6 0.9 √5 用公式6 0.9 √6 结合图像 6 0.85 √7 公式的用 6 0.75 √8 结合实际用公式 6 0.75 √9 概念的理解 6 0.75 √10 图像与公式结合 6 0.65 √第Ⅱ卷非选择题11 速度公式的用20 0.9 √12 速度公式与用题结合20 0.65 √1．以下关于匀变速直线运动的说法，正确的选项是( )A．匀变速直线运动是运动快慢相同的运动B．匀变速直线运动是速度变化量相同的运动C．匀变速直线运动的a－t图象是一条倾斜的直线D．匀变速直线运动的v－t图象是一条倾斜的直线2．甲、乙两个物体沿同一直线向同一方向运动时，取物体的初速度方向为正方向，甲的加速度恒为2 m/s2，乙的加速度恒为－3 m/s2，那么以下说法正确的选项是( )A．两物体都做匀加速直线运动，乙的速度变化快B．甲做匀加速直线运动，它的速度变化快C．乙做匀减速直线运动，它的速度变化率大D．甲的加速度比乙的加速度大3．某物体运动的速度—时间图象如右图所示，那么物体做( )A．往复运动B．匀变速直线运动C．朝某一方向的直线运动D．不能确4．假设的加速度方向与速度方向一致，当加速度减小时，那么( )A．的速度也减小B．的速度仍在增加C．当加速度减小到零时，静止D．当加速度减小到零时，的速度到达最大5．一辆匀加速行驶的，经过路旁的两根电线杆共用5 s时间，的加速度为2 m/s2，它经过第二根电线杆时的速度是15 m/s，那么经过第一根电线杆的速度为( )A．2 m/s B．10 m/sC．2.5 m/s D．5 m/s6．如以下图所示，用闪光照相的方法记录某同学的运动情况，假设规向右的方向为正方向，那么以下图象能大体描述该同学运动情况的是( ) 7．物体做匀加速直线运动，第1 s末的速度为6 m/s，第2 s末的速度为8 m/s，那么以下结论中正确的选项是( )A．物体的初速度为3 m/sB．物体的加速度为2 m/s2C．任何1 s内物体速度的变化都为2 m/sD．第1 s内物体的平均速度为6 m/s8．甲和乙两个物体在同一直线上运动，它们的v－t图象分别如右图中的a和b所示．在t1时刻( )A．它们的运动方向相同B．它们的运动方向相反C．甲的速度比乙的速度大D．乙的速度比甲的速度大9．跳伞运发动做低空跳伞表演，当飞机离地面某一高度静止于空中时，运发动离开飞机自由下落，运动一段时间后翻开降落伞，翻开伞后运发动以5 m/s2的加速度匀减速下降，那么在运发动减速下降的任意一秒内( ) A．这一秒末的速度比前一秒初的速度小5 m/sB．这一秒末的速度是前一秒末的速度的0.2倍C．这一秒末的速度比前一秒末的速度小5 m/sD．这一秒末的速度比前一秒初的速度小10 m/s10.如右图所示是某质点的v－t图象，那么( )A．前2 s物体做匀加速运动，后3 s物体做匀减速运动B．2～5 s内物体静止C．前2 s和后3 s内速度的增量均为 5 m/sD．前2 s的加速度是2.5 m/s2，后3 s 的加速度是－53m/s2 11．以54 km/h的速度匀速行驶．(1)假设以0.5 m/s2的加速度加速，那么10 s后速度能到达多少？(2)假设以3 m/s2的加速度减速刹车，那么10 s后速度为多少？12．卡车原来以10 m/s的速度在平直公路上匀速行驶，因为路口出现红灯，司机从较远的地方开始刹车，使卡车匀减速，当车减速到2 m/s时，交通灯转为绿灯，司机当即停止刹车，并且只用了减速过程的一半时间就加速到原来的速度，从刹车开始到恢复原速过程用了12 s．求：(1)减速与加速过程中的加速度大小；(2)开始刹车后2 s末及10 s末的瞬时速度．。

八年级年级数学每周一练（1）《第十六章》单元练习班级____________ 学号 ______________ 姓名 ______________ 得分 __________一、选择题：（每题3分，满分18分）1 •如果丁3口冇意义，那么实数d 的取值范围是（ 2A. G A —32.在下列二次根式中，最简二次根式是（3.与盯是同类二次根式的是（6. 如果d 、b 是实数，下列各式中一定成立的是（A.(V^ + 7^)2=a + b B.丽-丽= a-b C^(a 2+b 2)2=a 2+b 2二、填空题：（每题2分，满分24分）7. _________________________________________ 已知半径为r 的圆的而积是27兀，则r= ______________________________________________10. _________________________________________________ 如果VTT5-UV2是同类二次根式，那么兀的值可以是 __________________________________ （只需写出一个）. 11. 化为最简二次根式：牡= ______________ • 12. 若XV ）,化简如亍= ______________ . 13. 当 a<-5 时，化简 J/ +]0d + 25 =D, a>-2A. 74 - 4xB. J(x_y)(x+y)C. J1 — 2x + /D. JO ・5abA.C.V75D.V244•.若依与厉是同类二次根式, 则兀可以是（A. 0.05B. 0.5C. 50D. 1250B.x > 2C.x WD.x 2 3.D. yj(a + b)2 = a + b C. a >-3 5.等式成立的条件是（14.比较大小：2A/5___ 515.y 二 + 贝W 二____________ .16.如果最简二次根式g — b与J3d + 7b是同类二次根式，那么f平方根是h17.计算：』4xy •』9xy ( x> >' >0) = _________ .1 &把JR 化简为最简二次根式是______________ •三、简答题：(每题6分，满分18分)19.G为怎样的实数时，下列各式在实数范围内有意义？(1)J—3a(2) J5 — 2d20.d为怎样的实数时，下列各式在实数范围内有意义?⑵E +亠a 7a _221.化简二次根式:⑴(2)7(124四、综合题：（每题8分，满分40分）23. 计算J 宀占+ 2的值，其中24. 如果J 百+ ” + 1| = 0,求的值.22 •化简:25. 先观察下列各式，再回答问题。

广东省清远市清城区三中高三第一学期第一次周考数学（理）试题本卷满分150分，时间120分钟一、选择题（60分，每题5分）1.设全集I R =，集合2{|log 2}A y y x x ==>，{|B x y ==，则（ ）A ．AB A = B ．A B ⊆C ．A B =∅D ．()I A C B ≠∅2.知2()f x ax bx =+是定义在[1,3]a a -上的偶函数，那么a b +=（ ）A ．14-B ．14C ．12D ．12- 3.知3{(,)|3}2y M x y x -==-，{(,)|20}N x y ax y a =++=，且M N =∅，则a =（ ） A ．2或-6 B ．-6 C ．-6或-2 D ．-2 4.设命题:P 函数1y x=在定义域上是减函数；命题:,(0,)q a b ∃∈+∞，当1a b +=时，113a b+=，以下说法正确的是（ ） A ．P q ∨为真 B ．P q ∧为真 C ．P 真q 假 D ．.P q 均为假 5.函数2lg(2)y x x a =-+的值域不可能是（ ） A ．(,0]-∞ B ．[0,)+∞ C ．[1,)+∞ D ．R6.设246(0)()6(0)x x x f x x x ⎧++≤=⎨-+>⎩则不等式()(1)f x f <-的解集是（ ）A ．(3,1)(3,)--+∞ B ．(3,1)(2,)--+∞ C ．(3,)-+∞ D ．(,3)(1,3)-∞--7.若[1,2]x ∈，[2,3]y ∈时，22210ax y xy+->，恒成立，则a 的取值范围（ ） A ．(1,)-+∞ B ．(,1)-∞- C ．[1,)-+∞ D ．(,1)-∞- 8.函数()x f x x a=+的图像关于点(1,1)对称，()lg(101)xg x bx =++是偶函数，则a b +=（ ） A ．12-B ．12C ．32D ．32-9.函数2log (2)a y x ax =-+在区间(,1]-∞上是减函数，则a 的取值范围是（ ） A ．[2,)+∞ B ．[1,)+∞ C ．[2,3) D. (2,3)10.知21()21x x f x -=+，则不等式2(2)(4)0f x f x -+-<的解集为（ ）A ．(-1,6)B ．(-6,1)C ．(-2,3)D ．(-3,2)11.设集合2{|230}A x x x =+->，2{|2100}B x x ax a =--≤>，若A B 中恰含有一个整数，则实数a 的取值范围是（ ）A ．3(0,)4B ．34[,)43C ．3[,)4+∞ D ．(1,)+∞12.设()f x 是定义在R 上的偶函数，任意实数x 都有(2)(2)f x f x -=+，且当[0,2]x ∈时，()22xf x =-，若函数()()log (1)(0,1)a g x f x x a a =-+>≠，在区间(1,9]-内恰有三个不同零点，则a 的取值范围是（ ）A ．1(0,)(7,)9+∞ B ．11(,)(1,3)95 C ．11(,)(3,7)95 D ．11(,)(3,7)73二、填空题（20分，每题5分）13．（5分）设满足不等式组，若的最大值为，最小值为，则实数的取值范围为 ______________.14．（5分）已知直线l ⊥平面α，直线m ⊂平面β，则下列四个命题： ①α∥β⇒l ⊥m ； ②α⊥β⇒l ∥m ； ③l ∥m ⇒α⊥β； ④l ⊥m ⇒α∥β 其中正确命题的序号是____________________．15．已知曲线y=x+lnx 在点（1，1）处的切线与曲线y=ax 2+（a+2）x+1相切，则a 的值为_________________.16．若线性回归方程为y ＝2－3.5x ，则变量x 增加一个单位，变量y 平均 减少__________个单位.三、解答题（70分）17.设a R ∈,函数2()22f x ax x a =--，若()0f x >的解集为A ，{12},B x x =<<,AB =∅求实数a 的取值范围（10分）18. （本小题满分12分）某工厂在试验阶段大量生产一种零件。

石景山区2017年高三统一练习数学（文）试卷第一部分（选择题 共40分）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．已知集合{210}A x x =-<，{}01B x x =≤≤，那么A B 等于（ ） A ．{}0x x ≥ B ．{}1x x ≤C ．102x x ⎧⎫<<⎨⎬⎩⎭ D ．102x x ⎧⎫≤<⎨⎬⎩⎭ 2．以(1,1)-为圆心且与直线0x y -=相切的圆的方程是（ ） A ．22(1)(1)2x y ++-= B ．22(1)(1)4x y ++-= C ．22(1)(1)2x y -++= D ．22(1)(1)4x y -++= 3．下列函数中，偶函数是（ ） A ．122xx y =-B ．sin y x x =C ．cos x y e x =D ．2sin y x x =+4．设R θ∈，“s i n c o s θθ=”是“cos 20θ=”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件5．我国南宋数学家秦九韶（约公元1202—1261年）给出了求(N )n n *∈次多项式1110n n n n a x a x a x a --++++ 当0x x =时的值的一种简捷算法，该算法被后人命名为“秦九韶算法”． 例如，可将3次多项式改写为：323210a x a x a x a +++3210(())a x a x a x a =+++然后进行求值． 运行如图所示的程序框图，能求得多项式（ ）的值．A ．432234x x x x ++++ B ．4322345x x x x ++++ C ．3223x x x +++ D ．32234x x x +++ 6．某三棱锥的三视图如图所示，则该三棱锥的表面积是（ ）A ．2+．4．2+．57．如图，在矩形ABCD 中，AB =，2BC =，点E 为BC 的中点，点F 在边CD 上，若AB AF = ，则AE BF的值是（ ）A．2．1 C．28．21个人按照以下规则表演节目：他们围坐成一圈，按顺序从1到3循环报数，报数字“3”的人出来表演节目，并且表演过的人不再参加报数．那么在仅剩两个人没有表演过节目的时候，共报数的次数为（ ）A ．19B ．38C ．51D ．57第二部分（非选择题 共110分）二、填空题共6小题，每小题5分，共30分．9．若复数1a ii+-是纯虚数，则实数a = ． 10．已知实数,x y 满足236000x y x y -+≥⎧⎪≤⎨⎪≥⎩，那么z y x =-的最大值是 ．11．若抛物线22y px =的焦点与双曲线2214x y -=的右顶点重合，则p = ． 12．已知函数22,0(),0x x x f x x x x ⎧+≥⎪=⎨-<⎪⎩．若()(2)f a f a >-，则a 的取值范围是 ． 13．若函数sin()(0)y x ωϕω=+>的部分图象如图所示，则ω= ．14．在环境保护部公布的2016年74城市PM2.5月均浓度排名情况中，某14座城市在74城的排名情况如下图所示，甲、乙、丙为某三座城市．从排名情况看，① 在甲、乙两城中，2月份名次比1月份名次靠前的城市是 ； ②在第1季度的三个月中，丙城市的名次最靠前的月份是 ．三、解答题共6小题，共80分．解答应写出文字说明、演算步骤或证明过程．15．数列{}n a 中，12a =，12n n n a a c +=+ （c 是常数，1,2,3n = ），且1a ，2a ，3a 成公比不为1的等比数列． （Ⅰ）求c 的值；（Ⅱ）求{}n a 的通项公式．16．已知,,a b c 分别是ABC ∆的三个内角,,A B C 的三条对边，且222c a b ab =+-． （Ⅰ）求角C 的大小；（Ⅱ）求cos cos A B +的最大值．17．“累积净化量（CCM ）”是空气净化器质量的一个重要衡量指标，它是指空气净化器从开始使用到净化效率为50%时对颗粒物的累积净化量，以克表示．根据GB/T18801-2015《空气净化器》国家标准，对空气净化器的累计净化量（CCM ）有如下等级划分：为了了解一批空气净化器（共2000台）的质量，随机抽取n 台机器作为样本进行估计，已知这n 台机器的累积净化量都分布在区间(]4,14中．按照(]4,6，(]6,8，(]8,10，(]10,12，(]12,14均匀分组，其中累积净化量在(]4,6的所有．．数据有：4.5，4.6，5.2，5.3，5.7和5.9，并绘制了如下频率分布直方图：（Ⅰ）求n 的值及频率分布直方图中的x 值；（Ⅱ）以样本估计总体，试估计这批空气净化器（共2000台）中等级为P2的空气净化器有多少台？ （Ⅲ）从累积净化量在(]4,6的样本中随机抽取2台，求恰好有1台等级为P2的概率．18．如图，在ABC ∆中，C ∠为直角，4AC BC ==．沿ABC ∆的中位线DE ，将平面ADE 折起，使得90ADC ∠=，得到四棱锥A BCDE -．（Ⅰ）求证：BC ⊥平面ACD ； （Ⅱ）求三棱锥E ABC -的体积；（Ⅲ）M 是棱CD 的中点，过M 做平面α与平面ABC 平行，设平面α截四棱锥A BCDE -所得截面面积为S ，试求S 的值． 19．已知函数()xf x e =．（Ⅰ）过原点作曲线()y f x =的切线，求切线方程；（Ⅱ）当0x >时，讨论曲线()y f x =与曲线2(0)y mx m =>公共点的个数．20．已知椭圆2222:1(0)x y E a b a b +=>>过点(0,1)（Ⅰ）求椭圆E 的方程； （Ⅱ）设直线1:2l y x m =+与椭圆E 交于A 、C 两点，以AC 为对角线作正方形ABCD ．记直线l 与x 轴的交点为N ，问B 、N 两点间距离是否为定值？如果是，求出定值；如果不是，请说明理由．试卷答案一、选择题1-5：DABAA 6-8：CCD二、填空题9．1 10．3 11．4 12．1a > 13．3 14．乙，二月份三、解答题15．解：（Ⅰ）∵12a =，12n n n a a c +=+ ∴2122a a c c =+=+，232226a a c c =+=+ ． 依题意，1a ，2a ，3a 成公比不为1 的等比数列， ∴2213a a a =，即：2(22)2(26)c c +=+， 化简，得：20c c -=， 解得，0c =或1c =．由于公比不为1，因此，1c =． （Ⅱ）由（Ⅰ）可知：12n n n a a +=+． 因此，212a a =+2322a a =+3432a a =+112n n n a a --=+，（2n ≥，且N n *∈） “叠加”：23112222n n a a -=+++++ 12(12)2212n n --=+=-（2n ≥，且N n *∈）．∵12a =∴1n =时也满足2n n a =．故，数列{}n a 的通项公式为：2n n a =（N n *∈）．16．解：（Ⅰ）因为222c a b ab =+-，所以2221cos 22a b c C ab +-==．又因为(0,)C π∈，所以3C π=．（Ⅱ）由（Ⅰ）知3C π=，又A B C π++=，所以23B A π=-且2(0,)3A π∈， 故2cos cos cos cos()3AB A A π+=+-22cos coscos sin sin 33A A A ππ=++1cos sin()226A A A π=+=+． 又2(0,)3A π∈，5(,)666A πππ+∈， 所以当62A ππ+=即3A π=时，cos cos A B +的最大值为1．17．解：（Ⅰ）因为(]4,6之间的数据一共有6个，再由频率分布直方图可知：落在(]4,6之间的频率为0.0320.06⨯=． 因此，61000.06n ==． (0.030.120.140.15)21x ++++⨯=∴0.06x =．（Ⅱ）由频率分布直方图可知：落在(]6,8之间共：0.12210024⨯⨯=台， 又因为在(]5,6之间共4台， ∴落在(]5,8之间共28台，故，这批空气净化器等级为2P 的空气净化器共有560台． （Ⅲ）设“恰好有1台等级为2P ”为事件B依题意，落在(]4,6之间共有6台．记为：12345,6,,,,A A A A A A ，属于国标2P 级有4台，我们记为：345,6,,A A A A ，则从(]4,6中随机抽取2个，所有可能的结果有15种，它们是：121314(,),(,),(,),A A A A A A 151623(,),(,),(,),A A A A A A 242526(,),(,),(,),A A A A A A 343536(,),(,),(,),A A A A A A 454656(,),(,),(,)A A A A A A ，而事件B 的结果有8种，它们是：131415(,),(,),(,),A A A A A A 162324(,),(,),(,),A A A A A A 2526(,),(,)A A A A ．因此事件B 的概率为8()15P B =． 18．（Ⅰ）证明：因为//DE BC ，且90C ∠=， 所以DE AD ⊥，同时DE DC ⊥， 又AD DC D = ，所以DE ⊥面ACD ． 又因为//DE BC ，所以BC ⊥平面ACD ．（Ⅱ）由（Ⅰ）可知：BC ⊥平面ACD ，又AD ⊂平面ADC ， 所以AD BC ⊥，又因为90ADC ∠=，所以AD DC ⊥．又因为BC DC C = ，所以AD ⊥平面BCDE ．所以，13E ABC A EBC EBC V V S AD --∆==⨯． 依题意，1142422EBC S BC CD ∆=⨯=⨯⨯=．所以，184233E ABC V -=⨯⨯=．（Ⅲ）分别取,,AD EA AB 的中点,,N P Q ，并连接,,,MN NP PQ QM ，因为平面//α平面ACD ，所以平面α与平面ACD 的交线平行于AC ，因为M 是中点，所以平面α与平面ACD 的交线是ACD ∆的中位线MN ．同理可证，四边形MNPQ 是平面α截四棱锥A BCDE -的截面．即：MNPQ S S =．由（Ⅰ）可知：BC ⊥平面ACD ，所以BC AC ⊥， 又∵//QM AC ，//MN BC ∴QM MN ⊥． ∴四边形MNPQ 是直角梯形．在Rt ADC ∆中，AD CD 2==∴AC =12MN AC ==112NP DE ==，1()32MQ BC DE =+=．∴1(13)2S =+=19．解：（Ⅰ）由题意，设切点为00(,)M x y ，由题意可得0000'()0y f x x -=-，即00x x e e x =，解得01x =，即切点(1,)M e ． 所以010e k e -==-，所以切线方程为y ex =． （Ⅱ）当0x >，0m >时，曲线()y f x =与曲线2(0)y mx m =>的公共点个数 即方程2()f x mx =根的个数．由2()f x mx =得2xe m x=．令2()x e g x x =，则4(2)'()x xe x g x x -=，令'()0g x =，解得2x =．随x 变化时，'()g x ，()g x 的变化情况如下表：其中2(2)4e g =．所以(2)g 为2()xe g x x =在(0,)+∞的最小值．所以对曲线()y f x =与曲线2(0)y mx m =>公共点的个数，讨论如下：当2(0,)4e m ∈时，有0个公共点；当24e m =时，有1个公共点；当2(,)4e m ∈+∞时，有2个公共点．20．解：（Ⅰ）设椭圆的半焦距为c ．因为点(0,1)在椭圆E 上，所以1b =．故221a c -=．又因为c e a ==，所以c =2a =． 所以椭圆E 的标准方程为：2214x y +=．（Ⅱ）设11(,)A x y ，22(,)C x y ，线段AC 中点为00(,)M x y ． 联立12y x m =+和22440x y +-=，得：222220x mx m ++-=．由222(2)4(22)840m m m ∆=--=->，可得m <<所以122x x m +=-，21222x x m =-．所以AC 中点为1(,)2M m m -．弦长AC === 又直线l 与x 轴的交点(2,0)N m -，所以MN ==所以222BN BM MN =+221542AC MN =+=．所以B 、N 两点间距离为定值2． 【注：若有其它解法，请酌情给分】。

乡镇（街道） 学校班级 姓名学号 ………密……….…………封…………………线…………………内……..………………不……………………. 准…………………答…. …………题…绝密★启用前西藏重点小学三年级数学【上册】每周一练试题 附答案题 号 填空题 选择题 判断题 计算题 综合题 应用题 总分得 分考试须知：1、考试时间：90分钟，满分为100分（含卷面分2分）。

2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。

3、不要在试卷上乱写乱画，卷面不整洁扣2分。

一、用心思考，正确填空（共10小题，每题2分，共20分）。

1、劳动课上做纸花，红红做了2朵纸花，4朵蓝花，红花占纸花总数的（ ），蓝花占纸花总数的（ ）。

2、在进位加法中，不管哪一位上的数相加满（ ），都要向（ ）进（ ）。

3、小明从一楼到三楼用8秒，照这样他从一楼到五楼用（ ）秒。

4、在里填上适当的数。

5、小林晚上10：00睡觉，第二天早上7：00起床，他一共睡了（ ）小时。

6、常用的长度单位有（ ）、（ ）、（ ）、（ ）、（ ）。

7、换算。

7000千克=（ ）吨 8千克=（ ）克 23吨=（ ）千克 5200千克－200千克=（ ）吨8、□÷8＝138……○，余数最大填（ ），这时被除数是（ ）。

9、分针走1小格，秒针正好走（ ），是（ ）秒。

分针走1大格是（ ），时针走1大格是（ ）。

10、你出生于（ ）年（ ）月（ ）日，那一年是（ ）年，全年有（ ）天。

二、反复比较，慎重选择（共8小题，每题2分，共16分）。

1、下面现象中属于平移现象的是（ ）。

A 、开关抽屉B 、拧开瓶盖C 、转动的风车2、下列3个图形中，每个小正方形都一样大，那么（ ）图形的周长最长。

3、一个长方形长6厘米，宽4厘米，它的周长是（ ）厘米。

A 、10 B 、20 C 、24 D 、484、平均每个同学体重25千克，（ ）名同学重1吨。

A 、40 B 、4 C 、400 D 、40005、时针从上一个数字到相邻的下一个数字，经过的时间是（ ）。

乡镇（街道）学校 班级姓名 学号 ………密……….…………封…………………线…………………内……..………………不……………………. 准…………………答…. …………题…绝密★启用前西藏重点小学三年级数学【上册】每周一练试卷 附答案题 号 填空题 选择题 判断题 计算题 综合题 应用题 总分 得 分考试须知：1、考试时间：90分钟，满分为100分（含卷面分2分）。

2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。

3、不要在试卷上乱写乱画，卷面不整洁扣2分。

一、用心思考，正确填空（共10小题，每题2分，共20分）。

1、小明从一楼到三楼用8秒，照这样他从一楼到五楼用（ ）秒。

2、□÷8＝138……○，余数最大填（ ），这时被除数是（ ）。

3、在进位加法中，不管哪一位上的数相加满（ ），都要向（ ）进（ ）。

4、□45÷5，要使商是两位数，□里最大可填（ ）；要使商是三位数，□里最小应填（ ）。

5、小林晚上10：00睡觉，第二天早上7：00起床，他一共睡了（ ）小时。

6、在里填上适当的数。

7、小红家在学校（ ）方（ ）米处；小明家在学校（ ）方（ ）米处。

8、劳动课上做纸花，红红做了2朵纸花，4朵蓝花，红花占纸花总数的（ ），蓝花占纸花总数的（ ）。

9、看图写分数，并比较大小。

10、换算。

7000千克=（ ）吨 8千克=（ ）克 23吨=（ ）千克 5200千克－200千克=（ ）吨二、反复比较，慎重选择（共8小题，每题2分，共16分）。

1、平均每个同学体重25千克，（ ）名同学重1吨。

A 、40 B 、4 C 、400 D 、40002、要使“□21÷9”的商是三位数，“□”里只能填（ ）。

A 、9 B 、8 C 、73、四边形（ ）平行四边形。

A.一定B.可能C.不可能 4、按农历计算，有的年份（ ）有13个月。

A.一定 B.可能 C.不可能 5、最小三位数和最大三位数的和是（ ）。

2017年高中学业水平语文考试每周一考（三）2016 / 11 /111．下列各组词语中，加点字的读音完全正确的一项是A．湖泊(pō) 淡泊(bó) 谄(chǎn)媚之颜毛骨悚(sù)然B．游说(shui) 劝说(shuō) 彤(t6ng)云密布诡谲(jú)多变C．角(jiǎo)度角(jué)色瞠(chēng)目结舌聒(guā)噪刺耳D．横(héng)扫蛮横(hèng) 梦寐(mèi)以求面面相觑(qù)2．下列各组词语中，没有错别字的一项是A．慰藉辐射相形见拙贻笑大方B．修葺玷辱哗众取宠肢离破碎C．契据收讫杯水车薪焕然一新D．鞭挞斑驳急功进利谈笑风生3．下列句子中，标点符号使用正确的一项是A．到红光制衣厂的公交车有：8路、18路、28路、32路等，停车点离厂门口不到100米。

B．本化工厂招聘运输部主管一名；需从事过运输调度工作一年以上，司机两名；需有三年以上驾驶经验。

C．不绝于耳的争议提醒我们，应该对改革进行认真的反思和总结，明确改革是要进?还是要退?如果要进，哪些应该坚持，哪些需要调整?D．在杭州举行的“城镇和风景区水环境治理国际研讨会”上，建设部官员在主题报告中对《无极》剧组污染香格里拉的行为提示了严厉批评。

4．依次填入下列各句横线处的词语，恰当的一组是①做生意，当然要讲_________，借此让家乡脱贫，更是我们的愿望。

②当叶笃正从国家主席胡锦涛手中接过“奖金500万元”的奖牌时，全场掌声雷动，这位9l岁的老人表情却十分________。

③5月lO日，黄花岗公园_______为国家级爱国主义教育基地，200多名市民和游客参加了挂牌仪式。

A．盈利安静进升B．营利安详晋升C．营利安详进升D．盈利安静晋升5．下列各句中，加点的词语使用正确的一项是A．让大家难以理解的是，我班读书角的报刊杂志常常不胫而走。

B．事情紧迫，已是燃眉之急了，我们还不动手，更待何时啊!C．提起我们车间的张师傅，谁不称赞?他可是班门弄斧，技术高得很哩!D．李老师说笑话真有本事，每次都说得大家笑个不停，他还是道貌岸然地说下去。

数学周练第一章测试一、选择题（3×10=30）1.下面计算中正确的是： ( ) A.2226)3(b a ab = B.4224)2(a a -=- C.1055m m m =+ D.35)()(a a -÷-2.若159338)2(b a ba n m=+成立,那么 ( )A.m=3, n=2B.m=n=3C.m=6, n=2D.m=3, n=5 3.3)41(--的值是 ( )A. 64-B. 641- C. 64- D. 644.下列计算不能使用平方差公式的是( )A.)2)(2(b a b a +-B.)2)(2(-+a aC. )3)(3(a b b a +---D.)23)(32(m n n m -- 5.若229)3(x y y x M -=-⋅,则M 是（ ）A. )3(y x +-B. x y 3+-C. y x +3D.y x -3 6.下列各式计算正确的是（ ）A. 22294)32(b a b a -=- B. 22224)2(b ab a b a +-=- C. 2229341)321(n mn m n m +-=- D. 22422469)23(y y x x y x ++=- 7.若xy y x N y x ++=+-222)(成立，则N 为（ ） A. xy B. xy 2 C. xy 3 D. xy - 8.计算)5()4(5222ab bc a b a -÷-⋅等于（ ） A. c b a 234- B. c b a 234 C.bc a 234 D. bc a 254- 9.[]1)2()2(22=÷+--M a b b a ，则M 为（ ）A. ab 8B. ab 8-C. ab 4D. ab 4- 10.已知3=-b a ，1=ab ，则22b a +为（ ） A. 5 B. 7 C. 9 D. 11 二、填空题（3×10=30） 11.若1312=-x ，则=x12.若34=m，52=n，则nm -22=13.若一个单项式与233y x -的积是5712y x ，则这个单项式为 14.若32=na，那么126-n a =15.若53=a ，34=b ，则86b a -=16.矩形的宽是324y x ，长是)3(22y xy x -，那么矩形的面积是 17.若)21)((+-+x m x 是的结果中不含有x 的一次项，那么m 的值为 18.若0432=+-x x ，那么x x 622+-的值为19.若172=a ，416=c ，则a c （用大于、小于、等于填空）20.代数式)120121()131)(121(222-⋅⋅⋅--= 1 2 3 4 5 6 7 8 9 1011. 12. 13. 14. 15.16 17. 18. 19 20三、计算题（3×8=24） 四、解答题（4×4=16）。

每日一练第一周 周一1．(2020·北京大兴区模拟)在△ABC 中，c ＝1，A ＝2π3，且△ABC 的面积为32. (1)求a 的值；(2)若D 为BC 上一点，且________，求sin ∠ADB 的值．从①AD ＝1，②∠CAD ＝π6这两个条件中任选一个，补充在上面问题中并作答． 解 (1)由于c ＝1，A ＝2π3，S △ABC ＝12bc sin A ＝32， 所以b ＝2，由余弦定理a 2＝b 2＋c 2－2bc cos A ，解得a ＝7.(2)选①：当AD ＝1时，在△ABC 中，由正弦定理b sin B ＝a sin ∠BAC ， 即2sin B ＝732，所以sin B ＝217. 因为AD ＝AB ＝1，所以∠ADB ＝∠B .所以sin ∠ADB ＝sin B ，即sin ∠ADB ＝217. 选②：当∠CAD ＝π6时， 在△ABC 中，由余弦定理知cos B ＝a 2＋c 2－b 22ac ＝7＋1－427×1＝277. 因为A ＝2π3，所以∠DAB ＝π2， 所以∠B ＋∠ADB ＝π2， 所以sin ∠ADB ＝cos B ，即sin ∠ADB ＝277.周二2．已知正数数列{a n}的前n项和为S n，满足a2n＝S n＋S n－1(n≥2)，a1＝1.(1)求数列{a n}的通项公式；(2)设b n＝(1－a n)2－a(1－a n)，若{b n}是递增数列，求实数a的取值范围．解(1)a2n＝S n＋S n－1(n≥2)，a2n－1＝S n－1＋S n－2(n≥3)．相减可得a2n－a2n－1＝a n＋a n－1，∵a n>0，a n－1>0，∴a n－a n－1＝1(n≥3)．当n＝2时，a22＝a1＋a2＋a1，∴a22＝2＋a2，a2>0，∴a2＝2.因此n＝2时，a n－a n－1＝1成立．∴数列{a n}是等差数列，公差为1.∴a n＝1＋n－1＝n.(2)b n＝(1－a n)2－a(1－a n)＝(n－1)2＋a(n－1)，∵{b n}是递增数列，∴b n＋1－b n＝n2＋an－(n－1)2－a(n－1)＝2n＋a－1>0，即a>1－2n恒成立，∴a>－1.∴实数a的取值范围是(－1，＋∞)．周三3．(2020·宁德模拟)甲、乙、丙三人投篮的命中率各不相同，其中乙的命中率是甲的2倍，丙的命中率等于甲与乙的命中率之和．若甲与乙各投篮一次，每人投篮相互独立，则他们都命中的概率为0.18.(1)求甲、乙、丙三人投篮的命中率；(2)现要求甲、乙、丙三人各投篮一次，假设每人投篮相互独立，记三人命中总次数为X，求X的分布列及均值．解(1)设甲的命中率为p，则依题意可得p×2p＝0.18，解得p＝0.3，故甲、乙、丙三人投篮的命中率分别为0.3,0.6,0.9.(2)X的可能取值为0,1,2,3，则P(X＝0)＝(1－0.3)×(1－0.6)×(1－0.9)＝0.028，P(X＝1)＝0.3×(1－0.6)×(1－0.9)＋(1－0.3)×0.6×(1－0.9)＋(1－0.3)×(1－0.6)×0.9＝0.306，P(X＝2)＝0.3×0.6×(1－0.9)＋(1－0.3)×0.6×0.9＋0.3×(1－0.6)×0.9＝0.504，P(X＝3)＝0.3×0.6×0.9＝0.162，则X 的分布列为 X 0 1 2 3 P0.028 0.306 0.504 0.162故E (X )＝0×0.028＋1×0.306＋2×0.504＋3×0.162＝1.8.周四4.如图，四棱锥P －ABCD 的底面是矩形，PD ⊥平面ABCD ，E 为AB 的中点．(1)证明：平面P AD ⊥平面PCD ；(2)若AD ＝1，AB ＝PD ＝2，求二面角B －EC －P 的余弦值．(1)证明 因为四边形ABCD 是矩形，所以AD ⊥CD .因为PD ⊥平面ABCD ，AD ⊂平面ABCD ，所以PD ⊥AD ，又CD ∩PD ＝D ，PD ，CD ⊂平面PCD ，所以AD ⊥平面PCD .因为AD ⊂平面P AD ，所以平面P AD ⊥平面PCD .(2)解 以D 为坐标原点，DA ，DC ，DP 所在直线分别为x 轴，y 轴，z 轴，建立空间直角坐标系，如图所示，则P (0,0,2)，E (1,1,0)，C (0,2,0)，所以PE →＝(1,1，－2)，EC →＝(－1,1,0)．设平面PCE 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧ PE →·n ＝0，EC →·n ＝0，即⎩⎪⎨⎪⎧x ＋y －2z ＝0，－x ＋y ＝0，令x ＝1，得n ＝(1,1,1)．易知平面BCE 的一个法向量为m ＝(0,0,1)，所以cos 〈n ，m 〉＝n ·m |n |·|m |＝33， 由图可知二面角B －EC －P 为钝角，故二面角B －EC －P 的余弦值为－33. 周五5.如图所示，椭圆x 22＋y 2b 2＝1(0<b <2)的离心率为22，过点P (2,0)作直线l 交椭圆于不同两点A ，B .(1)求椭圆的方程；(2)①设直线l 的斜率为k ，求出与直线l 平行且与椭圆相切的直线方程(用k 表示)； ②若C ，D 为椭圆上的动点，求四边形ACBD 面积的最大值．解 (1)在椭圆x 22＋y 2b 2＝1(0<b <2)中， ∵a ＝2，c ＝2－b 2，∴椭圆的离心率为e ＝c a ＝2－b 22＝22，解得b ＝1， ∴椭圆的方程为x 22＋y 2＝1. (2)①设切线方程为y ＝kx ＋m ，代入x 22＋y 2＝1，可得(1＋2k 2)x 2＋4kmx ＋2m 2－2＝0， 由Δ＝0，可得m 2＝1＋2k 2，故切线方程为y ＝kx ±1＋2k 2.②要使得四边形ACBD 的面积最大，需满足C ，D 两点到直线l 的距离之和最大，即两条切线间的距离d ＝2|m |1＋k 2＝21＋2k 21＋k 2最大． 设A (x 1，y 1)，B (x 2，y 2)，直线l 的方程为y ＝kx －2k ，联立⎩⎪⎨⎪⎧x 22＋y 2＝1，y ＝kx －2k ，整理得 (1＋2k 2)x 2－8k 2x ＋8k 2－2＝0，Δ＝64k 4－4(1＋2k 2)(8k 2－2)>0，∴1－2k 2>0，－22<k <22， 则x 1＋x 2＝8k 21＋2k 2，x 1x 2＝8k 2－21＋2k 2， 故|AB |＝1＋k 2|x 1－x 2|＝1＋k 2·(x 1＋x 2)2－4x 1x 2＝22(1－2k 2)1＋2k2·1＋k 2， 故四边形ACBD 的面积S ≤12d ·|AB |＝1＋2k 21＋k2·22(1－2k 2)1＋2k 2·1＋k 2 ＝22(1－2k 2)1＋2k 2＝22·－(1＋2k 2)＋21＋2k 2 ＝22·－1＋21＋2k 2≤22， 当且仅当k ＝0，且C (0,1)，D (0，－1)或C (0，－1)，D (0,1)时等号成立． 故所求最大值为2 2.周六6．(2020·黄山模拟)已知曲线f (x )＝mx －m e x 在点(1，f (1))处的切线斜率为－1e. (1)求m 的值，并求函数f (x )的极小值；(2)求证：当x ∈(0，π)时，e x sin x －x ＋e x －2＋1>e x x cos x .(1)解 由题意，f (x )的定义域为R .∵f ′(x )＝m (2－x )e x ，∴f ′(1)＝m e ＝－1e， ∴m ＝－1，∴f (x )＝1－x e x ，∴f ′(x )＝x －2ex ， 当x >2时，f ′(x )>0，f (x )单调递增；当x <2时，f ′(x )<0，f (x )单调递减，∴x ＝2是f (x )的极小值点，f (x )的极小值为f (2)＝－1e2. (2)证明 要证e x sin x －x ＋e x －2＋1>e x x cos x ，两边同除以e x ，只需证1－x e x ＋1e 2>x cos x －sin x 即可．即证f(x)＋1e2>x cos x－sin x.由(1)可知，f(x)＋1e2在x＝2处取得最小值0，设g(x)＝x cos x－sin x，x∈(0，π)，则g′(x)＝cos x－x sin x－cos x＝－x sin x，∵x∈(0，π)，∴g′(x)<0，∴g(x)在区间(0，π)上单调递减，从而g(x)<g(0)＝0，∴f(x)＋1e2>x cos x－sin x，即当x∈(0，π)时，e x sin x－x＋e x－2＋1>e x x cos x．。

乡镇（街道） 学校班级 姓名 学号 ………密……….…………封…………………线…………………内……..………………不……………………. 准…………………答…. …………题…三明市小学三年级数学上学期每周一练试卷 附答案题 号 填空题 选择题 判断题 计算题 综合题 应用题 总分 得 分考试须知：1、考试时间：90分钟，满分为100分（含卷面分2分）。

2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。

3、不要在试卷上乱写乱画，卷面不整洁扣2分。

一、用心思考，正确填空（共10小题，每题2分，共20分）。

1、时针在7和8之间，分针指向7，这时是（ ）时（ ）分。

2、劳动课上做纸花，红红做了2朵纸花，4朵蓝花，红花占纸花总数的（ ），蓝花占纸花总数的（ ）。

3、把一根绳子平均分成6份，每份是它的（ ），5份是它的（ ）。

4、看图写分数，并比较大小。

5、小明从一楼到三楼用8秒，照这样他从一楼到五楼用（ ）秒。

6、在里填上适当的数。

7、□÷8＝138……○，余数最大填（ ），这时被除数是（ ）。

8、分针走1小格，秒针正好走（ ），是（ ）秒。

分针走1大格是（ ），时针走1大格是（ ）。

9、小林晚上10：00睡觉，第二天早上7：00起床，他一共睡了（ ）小时。

10、常用的长度单位有（ ）、（ ）、（ ）、（ ）、（ ）。

二、反复比较，慎重选择（共8小题，每题2分，共16分）。

1、时针从上一个数字到相邻的下一个数字，经过的时间是（ ）。

A. 60秒 B. 60分 C. 60时 D. 无法确定2、下面的结果刚好是250的是（ ）。

A.1500-500B.2500-2250C.150+1503、下列3个图形中，每个小正方形都一样大，那么（ ）图形的周长最长。

4、下面现象中属于平移现象的是（ ）。

A 、开关抽屉B 、拧开瓶盖C 、转动的风车 5、四边形（ ）平行四边形。

A.一定B.可能C.不可能6、用7、3、9三个数字可组成（ ）个三位数。