当前位置：文档之家 › 微波技术基础7-阻抗匹配

微波技术基础7-阻抗匹配

  • 格式：ppt
  • 大小：485.50 KB
  • 文档页数：30

下载文档原格式

  / 30

合集下载

阻抗匹配

阻抗匹配
2 2 2 Z ( R − Z ) t − 2 X Z t + ( R Z − R − X { 0 L 0} L 0 L 0 L L) = 0
m X ± R ( Z − R ) 2 + X 2 o/ c . Z0 L L L Lu 0 c m rf . RL − Z 0 ww t= w XL − 2Z0
2 RL + ( X L + Z 0t ) 2
RL (1 + t ) 2 RL + ( X L + Z 0t ) 2
2
B=
RL t + ( X L t − Z 0 ) ( X L + Z 0t )
2 2 Z0 R + ( X + Z t ) L 0 L
单支节并联调配器（续一）
选d 使G＝Y0＝1/Z0 可得关于t (tgβz)的方程：
例2.6-1 设计一L节匹配网络，在500MHz使负载阻抗 ZL=200-j100Ω与特性阻抗Z0＝100Ω的传输线匹配。
归一化阻抗为：zL=ZL/Zo = 2-j2 在1+jx圆内，a 方案。 (1)归一化ZL 并在图中标出 (2)由于要计算并联转换成导纳较为方便 —— 将zL旋 om c . 转180度得出yL=0.4+j0.2; 如果加 上jb可使总电导落在 cu -m f r . w 1+jb的圆周上（电阻1+jx ），则可能 串 接 jx 达 到匹配 w w (3)在0.4圆上转到y(1+jy圆周）y＝yL+j0.3=0.4+j0.5 (4)再变回z ＝1－j1.2 (转180度) (5)显见只要串接x＝j1.2即可匹配。
匹配时多次反射 可能造成相位叠 加——功率增大

微波技术基础7-阻抗匹配

微波技术基础7-阻抗匹配

2
L
设计指数线匹配器的一般步骤是： ①先根据上式，通过给定的中心频率和带宽要求选定过渡段长度L； ②由两端的阻抗求变换比R，从而得指数线特性阻抗变化规律
0 z 0elnR/Lz
③根据传输线的类型，按特性阻抗公式算出横截面尺寸的变化规律。
编辑ppt
26
作业 5.23，5.31，5.32
编辑ppt
和
g
为Z L 实数，即
Xg X成L 立0)
★注意：共轭匹配时，线上可能存在反射波，反射系数 不为零，但经多次反射后，负载所得到的功率比无反 射匹配负载时还要大。
编辑ppt
6
传输线的电路理论—阻抗匹配
负载匹配的其它优点
传输线的功率容量最大 传输线的效率最高 微波源工作较稳定
负载失配，产生“频率”、“功率”牵 引，导致工作不稳定。
用图解法计算：串联单支节与计算并联单支节 完全类似，但这时应在阻抗圆图上进行。
用解析法计算：采用并联支节相似的分析（此 时用阻抗而不用导纳），可得串联支节接入位置
dlm in4 gcos11 1 S S
串联支节长度为
l g tg1 1 S
2 S
编辑ppt
20
传输线的电路理论—阻抗匹配
双支节匹配器与三支节匹配器
的反射。 实际情况：负载不匹配而产生反射波，但波源匹配将
不产生二次反射。
编辑ppt
2
传输线的电路理论—阻抗匹配
共轭匹配
特点：负载吸收最大功率的匹配。 匹配条件：传输线上任一参考面T向负载看去的输入 阻抗与向波源看去的输入阻抗互为共轭，即
如图：
T右＝T左
T处向负载看去：
in R in jX in 0 0 L j j L 0 t tg g

微波技术传输线的阻抗匹配ppt课件

微波技术传输线的阻抗匹配ppt课件
21
本章小结
1. 微波传输线是一维分布参数电路。传输线可用于 传输微波信号能量及构成各种微波元器件。
2. 传输线方程可由传输线的等效电路导出，它是传
输线理论中的基本方程。
均匀无耗传输线方程：
d
2U( dz 2
z)
2
U(
z)
0
d
2
I( z
)
dz2
2
I(z)
0
其通解为(以终端为坐标原点)：
U(z)
(5)阻抗匹配可提高传输线的功率容量(
Pbr
1 2
Ubr Z0
2
K
)。
1
2. 阻抗匹配问题
1). 共轭匹配
目的：使信号源的功率输出最大。
条件：
Zin
Z
* g
( Rin Rg , Xin X g )
满足共轭匹配条件的信号源输出的最大功率为:
2
Pmax
Eg
Rin
2
Zg Zin
2
Eg
4Rg
2
`.
10
2. 支节调配器
支节调配器是在距终端负载的某一处并联或串联短
路或开路支节。有单支节、双支节或多支节匹配器，常
用并联调配支节。 1). 单支节匹配器 并联单支节匹配器是在距
Y~in
d
~ Y~0
Y~2 Y~1 Y~0
Y~L
负载 d 处并联长度为 l 的短路
Y~0
支节，利用调节 d 和 l 来实现
线、带状线等传输
线十分不便，解决
的办法是采用双支
节匹配器。
~l ~l
~l~E lF
0.25 0.25
~ lF B~ F

A 第2.6章 阻抗匹配

A 第2.6章 阻抗匹配

∵ f =500MHz
b ∴ C = 2p fZ = 0.92( pF ) 0 L= xZ 0 = 38.8(nH ) 2p f
如果是向下半圆移动交1+jb于yA=0.4-j0.5, 则并联电纳b=-0.7，转换至阻抗圆则得 z=1+j1.2,则串联电抗为x=-1.2。即为并联 电感L和串联电容C的匹配网络。 在f = 500MHz时，
式中
yL = 1 zL
即rL>1
Z0
jX jB ZL
图a. zL在1+jx圆内用
jX
Z0
jB
ZL
图b.zL在1+jx圆外用
例1
设计一个L节匹配网络，在500MHz使负载阻抗
Z L 200 j100与特性阻抗 Z 0 100 的传输线匹配。
解：归一化阻抗：
zL Z L 200 j100 2 j1 Z0 100
选择d使G=Y0=1/Z0，代入可得t的二次方程：
2 2 Z 0 (RL Z 0 )t 2 2 X L Z 0t (RL Z0 RL X L ) 0
解得
X R [(Z R ) 2 X 2 ] / Z L 0 L L 0 L , RL Z 0 RL Z 0 t X L , RL Z 0 2Z 0
图a. zL在1+jx圆内用
即应在r =1的电阻圆上；而从zA到zin需 在r=1的圆上沿等电阻圆移动一段距离；
Q
1 y A = = g A + jbA zA
在圆图上为zA旋转180⁰,即gA<1
而zA为jb与yL的并联后的阻抗，当yL与jb并联时，即在 圆图上沿等电导圆移动相应的距离， yA = jb + yL = g L + jb + bL g + jbA 即gL=gA<1

阻抗匹配——精选推荐

阻抗匹配——精选推荐

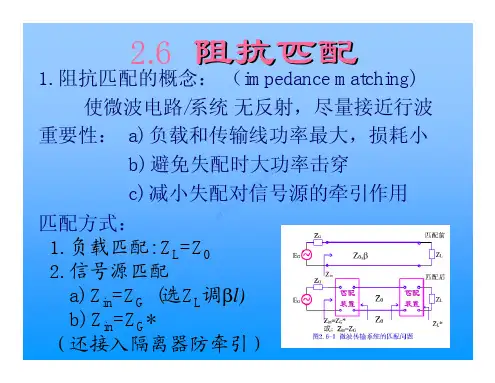
阻抗匹配阻抗匹配是指信号源或者传输线跟负载之间的⼀种合适的搭配⽅式。

阻抗匹配分为低频和⾼频两种情况讨论。

阻抗匹配主要有两点作⽤，调整负载功率和抑制信号反射。

{扩展：我们可以把⼀个实际电压源，等效成⼀个理想的电压源跟⼀个电阻r串联的模型。

假设负载电阻为R，电源电动势为U，内阻为r，那么我们可以计算出流过电阻R的电流为：I=U/(R+r)，可以看出，负载电阻R越⼩，则输出电流越⼤。

负载R上的电压为：Uo=IR=U/[1+(r/R)]，可以看出，负载电阻R越⼤，则输出电压Uo越⾼。

再来计算⼀下电阻R消耗的功率为：P = I2×R=[U/(R+r)]2×R = U2×R/(R2+2×R×r+r2)= U2×R/[(R-r)2+4×R×r]= U2/{[(R-r)2/R]+4×r}对于⼀个给定的信号源，其内阻r是固定的，⽽负载电阻R则是由我们来选择的。

注意式中[(R-r)2/R]，当R=r时，[(R-r)2/R]可取得最⼩值0，这时负载电阻R上可获得最⼤输出功率Pmax=U2/(4×r)。

即，当负载电阻跟信号源内阻相等时，负载可获得最⼤输出功率，这就是我们常说的阻抗匹配之⼀。

}如果我们需要输出电流⼤，则选择⼩的负载R；如果我们需要输出电压⼤，则选择⼤的负载R；如果我们需要输出功率最⼤，则选择跟信号源内阻匹配的电阻R。

有时阻抗不匹配还有另外⼀层意思，例如⼀些仪器输出端是在特定的负载条件下设计的，如果负载条件改变了，则可能达不到原来的性能，这时我们也会叫做阻抗失配。

在⾼频电路中，我们还必须考虑反射的问题。

当信号的频率很⾼时，则信号的波长就很短，当波长短得跟传输线长度可以⽐拟时，反射信号叠加在原信号上将会改变原信号的形状。

如果传输线的特征阻抗跟负载阻抗不相等（即不匹配）时，在负载端就会产⽣反射。

为什么阻抗不匹配时会产⽣反射以及特征阻抗的求解⽅法，牵涉到⼆阶偏微分⽅程的求解，在这⾥我们不细说了，有兴趣的可参看电磁场与微波⽅⾯书籍中的传输线理论。

关于阻抗匹配

关于阻抗匹配

关于阻抗匹配来源: kmmzs 发布时间: 2014-12-26 14 次浏览大小: 16px 14px 12px 阻抗匹配（Impedance matching）是微波电子学里的一部分，主要用于传输线上，来达至所有高频的微波信号皆能传至负载点的目的，几乎不会有信号反射回来源点，从而提升能源效益。

大体上，阻抗匹配有两种，一种是透过改变阻抗力（用于集中参数电路），另一种则是调整传输线的波长（用于传输线）。

要匹配一组线路，首先把负载点的阻抗值，除以传输线的特性阻抗值来归一化，然后把数值划在史密斯图上匹配条件①负载阻抗等于信源内阻抗，即它们的模与辐角分别相等，这时在负载阻抗上可以得到无失真的电压传输。

②负载阻抗等于信源内阻抗的共轭值，即它们的模相等而辐角之和为零。

这时在负载阻抗上可以得到最大功率。

这种匹配条件称为共轭匹配。

如果信源内阻抗和负载阻抗均为纯阻性，则两种匹配条件是等同的。

阻抗匹配是指负载阻抗与激励源内部阻抗互相适配，得到最大功率输出的一种工作状态。

对于不同特性的电路，匹配条件是不一样的。

在纯电阻电路中，当负载电阻等于激励源内阻时，则输出功率为最大，这种工作状态称为匹配，否则称为失配。

当激励源内阻抗和负载阻抗含有电抗成份时，为使负载得到最大功率，负载阻抗与内阻必须满足共扼关系，即电阻成份相等，电抗成份绝对值相等而符号相反。

这种匹配条件称为共扼匹配。

阻抗匹配（Impedance matching）是微波电子学里的一部分，主要用于传输线上，来达至所有高频的微波信号皆能传至负载点的目的，不会有信号反射回来源点，从而提升能源效益。

史密夫图表上。

电容或电感与负载串联起来，即可增加或减少负载的阻抗值，在图表上的点会沿着代表实数电阻的圆圈走动。

如果把电容或电感接地，首先图表上的点会以图中心旋转180度，然后才沿电阻圈走动，再沿中心旋转180度。

重覆以上方法直至电阻值变成1，即可直接把阻抗力变为零完成匹配。

共轭匹配在信号源给定的情况下，输出功率取决于负载电阻与信号源内阻之比K，当两者相等，即K=1时，输出功率最大。

阻抗匹配

阻抗匹配
它是通过附加反射来抵消传输线上原存在的反射波达到匹配的目的。 常用并联电抗性元件的方法。
• 支节调配器：是由距离负载的某位置上的并联或串联终端短路或开
路的传输线（又称支节）构成的。支节数可以是一条、两条、三条或更多。 讨论 (1)单支节调配器、(2)双支节调配器、(3)三支节调配器。
l
ZL
三、阻抗匹配的方法——并联支节调配器法
但Zg和Zl一般为复阻抗，无耗传输线Z0为纯阻抗，很难同时满足匹配
为实现匹配一般在信号源和终端负载处分别加始端和终端匹配装置 （一）信号源端的阻抗匹配 一般采用去耦衰减器或隔离器以实现信号源端匹配（吸收反射波）
前者使被信号源再反射的二次反射波由于两次通过衰减器，已微不足道。 但也会消耗输往负载的入射功率，不适合大功率微波源。 后者是一个非互易器件，只允许入射波通过而吸收掉反射波，即保证了功 率的有效传输，又可消除信号源的内反射，构成匹配源
(1) 归一化负载阻抗 zL=ZL/Z0=2+j4 对应A点，电长度为：0.218 (2) 找波腹点B或波节点C 可读得ρ 11 (3) 求所接λ /4传输线的Z01
( Z 01 ) R
m ax
ZC
Z01
Zin = =>
ZC
λ /4
d
Z 0 R m ax
Z0 Z0 Z0
249
传输线功率容量最大。 o 阻抗失配时传输大功率信号易导致击穿； 信号源可能被破坏。 行波状态时信号源工作稳定 o 避免频率牵引和输出功率变化 o 匹配源的输出功率是固定不变的
三、阻抗匹配的方法
阻抗匹配：ZL＝Z0、Zg＝Z0、 Zin＝Z0* 只有当Zg＝ZL＝ZC都为纯电阻时，才能同时实现匹配。

微波射频学习笔记7.阻抗匹配

微波射频学习笔记7.阻抗匹配

阻抗匹配
1.阻抗匹配的目的
阻抗匹配主要用于传输线上，以此来达到所有高频的微波信号均能传递至负载点的目的，而且几乎不会有信号反射回来源点，从而提升能源效益。

Ps：波的反射会造成驻波，从这点看来：插损一部分是介质和导体本身带来的系统损耗，还有一部分就是阻抗失配带来的VSWR，反射功率是要会抵消部分发射功率。

所以我应该大概可以认为VSWR不好，使设计问题，这时候的插损是可以通过优化设计改善，但如果驻波已经很好了，说明阻抗匹配，插损也就差不多了。

2.阻抗匹配的几种方法
（1）L网络（集总元件匹配）
使用场景：频率f≤1GHz
构造：串联电感L同时并联电容C/串联电容C同时并联电感L；
①输入电阻R0＜负载电阻R1，两个元件适合先串联后并联；
②输入电阻R0＞负载电阻R1，两个元件适合先并联后串联。

特点：成本低（只有两个元件）、Q值低（BW宽，选频性能差，挤滤波能力差），还有π型/T型网络都可以分解成两个L型网络分析，咱也看不懂，咱就不学了，都是利用了LC谐振。

计算方法：网上找小工具...
（2）短截线调谐
阻抗匹配的过程被称为调谐（大概），波导中常用，以下省略500字。

（3）四分之一波长变换器
当Z
in =Z
，波长为λ/4的奇数倍时，反射系数Γ=0，完全匹配，此时馈线上
没有驻波，不过λ/4匹配段内会有驻波存在，所以λ/4波长可用作阻抗变换；
注意：只能在一个频点获得完全匹配，附近频点越远，失配越严重。

①单节四分之一波长变换，匹配段的特征阻抗：Z
1= √（Z
Z
L
），相对带宽：
（f
2-f
1
）/f
0 。

微波技术传输线的阻抗匹配详解

微波技术传输线的阻抗匹配详解
2 Z0
2. 阻抗匹配问题 1). 共轭匹配 目的：使信号源的功率输出最大。 * 条件： Zin Z g ( Rin Rg , X in X g ) 满足共轭匹配条件的信号源输出的最大功率为:
2
Pmax
E g Rin Z g Z in
2

Eg
2
4 Rg
2) 无反射匹配
目的：使传输线上无反射波，即工作于行波状态。 条件：Zg= ZL= Z0 。 实际中传输线的始端和终端很难做到无反射匹配， 通常在信号源输出端接入隔离器以吸收反射波，而在传 输线与负载之间使用匹配装置用来抵消反射波。 信号源
隔离器
匹配器
负载
隔离器又称单向器，是非互易器件，只允许入射 波通过而吸收掉反射波，使信号源端无反射, 以稳定 信号源的工作状态。
二、阻抗匹配的方法 阻抗匹配的方法是 在负载与传输线之间接 入匹配器，使其输入阻
Z0 Z0
匹 配 器
~ ZL
抗作为等效负载与传输线的特性阻抗相等。 匹配器是一个两端口的微波元件，要求可调以适应 不同负载，其本身不能有功率损耗，应由电抗元件构成。 匹配阻抗的原理是产生一种新的反射波来抵消实际 负载的反射波(二者等幅反相)，即“补偿原理”。 常用的匹配器有l/4 阻抗变换器和支节匹配器。
第六节 传输线的阻抗匹配
一、阻抗匹配的概念 阻抗匹配是使微波系统无反射、载行波尽量接近行 波状态的技术措施。 1. 阻抗匹配的重要性 (1) 匹配时传输功率最大，功率损耗最小； (2) 阻抗匹配可改善系统的信噪比； (3) 功率分配网络(如天线阵的馈源网络)中的阻抗匹 配将降低幅度和相位的误差； (4) 阻抗匹配可保持信号源工作的稳定性； 2 (5)阻抗匹配可提高传输线的功率容量( Pbr 1 U br K )。

微波技术传输线的阻抗匹配讲解

微波技术传输线的阻抗匹配讲解

线十分不便，解决
的办法是采用双支
节匹配器。

~l ~l

~ l~E lF
0.25 0.25
~ lF B~ F
C G~ 1
0.25
D

B~
E
~
lE
~l
导纳园图
2). 双支节匹配器 在单支节匹配器中改变d 是为了找到归一化电导分量
为1的参考面。由：
Y~in

1 Z~in

1 Z~L
(5)阻抗匹配可提高传输线的功率容量(
Pbr

1 2
Ubr Z0
2

K
)。
2. 阻抗匹配问题
1). 共轭匹配
目的：使信号源的功率输出最大。
条件：
Zin

Z
* g
( Rin Rg , X in X g )
满足共轭匹配条件的信号源输出的最大功率为:
2
Pmax
Eg Rin
2
Zg Zin
d2 = l/4 时，
盲区为 G~ 1。
0
G~ 2 0.25
d2= l/8 双支节匹配器的盲区
3). 三支节匹配器
C
B
A
d3
d2
d1
~ Y~0
Y~L
Y~0
C’
Y~0
B’ Y~0
A’
l3
l2
l1
三支节匹配器为二支节匹配器的组合。l1、l2 为一组，
l2、l3 为一组。首先， l3 = l /4 (闲置)，由l1、l2 调配；若

L0 , C0

2p , lp
vp

阻抗匹配定义及实现简介

阻抗匹配定义及实现简介

1.阻抗的定义在具有电阻、电感和电容的电路里，对电路中的电流所起的阻碍作用叫做阻抗。

阻抗常用Z表示，是一个复数，实部称为电阻，虚部称为电抗，其中电容在电路中对交流电所起的阻碍作用称为容抗,电感在电路中对交流电所起的阻碍作用称为感抗，电容和电感在电路中对交流电引起的阻碍作用总称为电抗;阻抗的单位是欧姆。

阻抗的公式是：Z= R+j(ωL–1/（ωC）)其中，负载是电阻、电感的感抗、电容的容抗三种类型的复物，复合后统称“阻抗”，写成数学公式即是：阻抗Z= R+j(ωL–1/（ωC）)。

其中R为电阻，ωL为感抗，1/（ωC）为容抗。

（1）如果(ωL–1/ωC) > 0，称为“感性负载”；（2）反之，如果(ωL–1/ωC) < 0称为“容性负载”。

2.阻抗匹配阻抗匹配是指信号源或者传输线跟负载之间的一种合适的搭配方式。

匹配条件包括：①负载阻抗等于信源内阻抗，即它们的模与辐角分别相等，这时在负载阻抗上可以得到无失真的电压传输。

②负载阻抗等于信源内阻抗的共轭值，即它们的模相等而辐角之和为零。

这时在负载阻抗上可以得到最大功率。

这种匹配条件称为共轭匹配。

如果信源内阻抗和负载阻抗均为纯阻性，则两种匹配条件是等同的。

我们先从直流电压源驱动一个负载入手。

由于实际的电压源，总是有内阻的，我们可以把一个实际电压源，等效成一个理想的电压源跟一个电阻r串联的模型。

假设负载电阻为R，电源电动势为U，内阻为r，那么我们可以计算出流过电阻R的电流为：I=U/(R+r)，可以看出，负载电阻R越小，则输出电流越大。

负载R上的电压为：Uo=IR=U/[1+(r/R)]，可以看出，负载电阻R越大，则输出电压Uo越高。

再来计算一下电阻R消耗的功率为：P=I2×R=[U/(R+r)]2×R=U2×R/(R2+2×R×r+r2)=U2×R/[(R-r)2+4×R×r]=U2/{[(R-r)2/R]+4×r}对于一个给定的信号源，其内阻r是固定的，而负载电阻R则是由我们来选择的。

微波技术与天线-阻抗匹配

微波技术与天线-阻抗匹配

Zg g
Z
g
g
Z
g
g
Zg Zi*n g *in
信号源有 最大 输出功率， 并通过传输线提供给 负载 。
Zg Eg
Zin in
Z0
Zl
Z
in
in
Zl
l
信号源输出最大资用功率
T1
T2
T3
Pmax Eg2 / 8Rg
Zg
传输线任意参考面等效信源 Eg
阻抗与等效负载阻抗共轭
Z
g
Z
g
Zin = 传Z输in 线 +负载 Zl
Y2 jb
Yin 在匹配圆轨迹。通过传输线λ/8 (即向负载方向转90°)，构成 Y4 轨迹。
Y2 l2
辅助圆
(在双枝节匹配中，Y4轨迹称为辅助圆)。
Y3 Yl gl jbl
0
Y1 jbl
按等 gl 圆旋转到辅助圆上，由此算出 Y1 jbl 。
Y4
Y3
Yl
Y1 l1
i Y4 轨迹
等 g l圆
电压波节点 Z0 Z0 K
dumin l / 4 0.25
Z0
Z0 g / 4 dumax Zl
Z0
Z
0
g / 4
dumin
Zl
g
3108 300 106
1m
2 2
Z0
g
1
1
21
Yl
Zl
200
j250
1025
j 410
1
Yin jY0 c tan lmin - j 410
lmin 0.11m
Eg
Eg
Zg Zin* g in*
此时传输线与负载不一定匹配

第7次 阻抗匹配

第7次 阻抗匹配

短路支节长度为：
l1 0.318 0.25 0.068
l2 0.25 0.182 0.432
yL
j 2.2 , 0.318

2 Z 01 Z0 阻抗匹配时：Z in ( ) 4 RL

Z 01 Z 0 RL
分析：优缺点，能否匹配复阻抗？
Anhui University
3. 支节调配器
(a).单支节调配器
串联支节
并联支节
l, d ?
Anhui University
归一化负载阻抗
Z L 25 j 75 zL Z0 50 0.5 j1.5
ZG Z0 G ZG Z0
L
ZL Z0 Z L ቤተ መጻሕፍቲ ባይዱ Z0
Anhui University
EG Z 0 e j l j d j d V (d ) (e L e ) 2 j l ZG Z 0 1 L G e
j (l d ) j (l d ) j (3l d ) u0 e L u0 e L G u0 e j (3l d ) 2 2 j (5l d ) 2 u e L G 0 L G u0 e
Anhui University
2.6阻抗匹配
阻抗匹配(impedance matching)：使微波电路或系统无反射、载行波或尽量接
近行波状态的技术措施。是微波电路和系统设计时必须考虑的重要问题之一。 一. 阻抗匹配的概念： 1. 阻抗匹配的意义： （1）.传输效率：阻抗匹配时传输给传输线和负载的功率最大，且馈线中 的功率损耗最小。 2
Anhui University
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

传输线的电路理论—阻抗匹配
常用的匹配方法
g 4 阻抗变换器
臵于特性阻抗不同的均匀传输线之间或 传输系统与负载之间起阻抗匹配作用。
情形 I
情形 II
传输线的电路理论—阻抗匹配
对于该图所示的结构，容易推导要使T处 in 0
0 L 0
g / 4阻抗变 由于无耗传输线的特性阻抗是实数，因此， 换器原则上只用于匹配纯电阻负载，即 L RL，所以
向波源看去：
g Rg jX g
传输线的电路理论—阻抗匹配
根据电路理论，图中 L吸收最大功率的条件为:
L g
即：
RL Rg X L X g
两者的电阻应相等，电抗的数值相等， 而性质相反。
传输线的电路理论—阻抗匹配

匹配下的负载吸收功率情况
RL 1 1 PL Re VL I L Eg 2 Rg )2 ( X L X g )2 2 2 ( RL
sin L 1 ln R 2 L
sin L 1 ln R 2 L
设计指数线匹配器的一般步骤是：
①先根据上式，通过给定的中心频率和带宽要求选定过渡段长度L；
②由两端的阻抗求变换比R，从而得指数线特性阻抗变化规律
0 z 0e
ln R / L z
③根据传输线的类型，按特性阻抗公式算出横截面尺寸的变化规律。
并联单支节匹配器
设计并联单支节匹配器的任务在于确定负载 到参考面的距离d和支节长度L。可采用解析法或 图解法来计算。
传输线的电路理论—阻抗匹配
解析法
该方法计算较为复杂，可根据负载的具体情况，分两类讨论： 第一种情况： YL为纯阻负载，即 YL GL 支节接入位臵： g G 1 d cos 1 L 4 GL 1 支节长度：
(可以3个同学为1组(自愿组合),参加讨论,用 图形曲线表示并打印,给出结论. 本周5交)
传输线的电路理论—阻抗匹配
单支节匹配器 单支节匹配器是在距离负载d处并联或串联长 度为L的终端短路或开路的短截线构成。调节d和L 就可以实现阻抗调配，从而达到阻抗匹配目的。
并联支节
串联支节
传输线的电路理论—阻抗匹配
传输线的电路理论—阻抗匹配
在最佳频响特性下，两节变换器的特性阻抗分别为:
4 01 4 3 R R 0 0 L 3 02 4 RL 0 1/ RRL
其中：
RL R Z0
称为变换比。
传输线的电路理论—阻抗匹配
课后设计作业:
请用matlab计算并讨论带宽问题, 特性阻抗50欧姆,负载阻抗800欧姆,分别 用单支节和双支节四分之一波长阻抗变 换器给出计算结果并比较带宽(驻波≤1.2), 中心频率可以任意选定。
ln 0 ( z) ln 0 bz
当z=L时
ln 0 ( L) ln RL ln 0 bL
因此
1 RL 1 b ln ln R L 0 L
（R为阻抗变换比）
最后可得
1 L j 2 z d ln R 1 j L sin L e z ln 0 dz e ln R 0 2 dz L 2 L
g 1 1 S l tg 2 S
传输线的电路理论—阻抗匹配
双支节匹配器与三支节匹配器
优点： 匹配不同负载时，只需调节支节长度 L，无需调节d; 三支节匹配器克服了双支节匹配区存在“匹配禁区” 的缺点。
传输线的电路理论—阻抗匹配
g / 4 线与 g / 4 支节联合匹配器
图解法
求解较为简单，可分为两个步骤。 1. 找出负载归一化导纳值在导纳圆图中的对应点M 作等反射系数圆交G 1 的匹配圆与A、B 读出点M顺时转至A、B的长度 d1 、 d2 读出A、B处得导纳值 1 jb 、1 jb
2. 在 d1 处并联一个短路支节： 由导纳圆图中的短路点C 顺时转至 jb 点D 的距离即为支节归一化电长度。 在 d2处并联一个短路支节： 由导纳圆图中的短路点C 顺时转至 jb 点 的距离即为支节归一化电长度。
作业 5.23，5.30，5.31
负载吸收功率可表示为：
无反射匹配情况
Z g Z0 Z L
Rg 1 1 2 PLm Re VL I L Eg 2 8 Rg 2 X g 2
可见负载吸收的功率为源输出功率的一半，而另一半消 耗在内阻 Rg 上。
传输线的电路理论—阻抗匹配
共轭匹配情况
, RL Rg X g X L
特性阻抗 Z0=50欧姆
相对带宽 5.5%
相对带宽 15.6%
传输线的电路理论—阻抗匹配
g 4
阻抗变换器带宽
特性阻抗 Z0=50欧姆
负载阻抗越接近特性阻抗,匹配效果越好
传输线的电路理论—阻抗匹配
g / 4阻抗匹配器属于点频匹配，即使考虑一定的反射容 限，相对带宽也较窄,特别是在阻抗变换比较大的情况下。 多节 g / 4 阻抗变换器，可获得更宽的工作频带 两节g / 4 阻抗变换器由两节不同特性阻抗的传输线段级 联而成。
传输线的功率容量最大 传输线的效率最高 微波源工作较稳定
负载失配，产生“频率”、“功率” 牵引，导致工作不稳定。 实际工程上的匹配是指在某一给定频 率范围内，反射系数或驻波系数小于某规 定值。
传输线的电路理论—阻抗匹配
阻抗匹配的方法
匹配网络的要求： ①简单、易行、可靠； ②附加损耗小； ③频带宽； ④可调节,用以匹配可变的负载阻抗（仅用于测量系 统）。
g 1 GL l tg 2 1 GL
传输线的电路理论—阻抗匹配
YL GL jL为复数 第二种情况：
思路：先计算出波节的位臵 lmin ，接入点处的输入导纳 值便为实数。最后可算出： g g 1 S S 1 d min d0 min cos 1 l tg 4 S 1 2 1 S
0 RL 0
传输线的电路理论—阻抗匹配
阻抗匹配时，则
0102 0
若负载值为复数，仍可使用g / 4阻抗变换器，只需将接 入点选在电压波节或电压波腹处。
通常选在电压波节处接入为宜，可使 变换器的特性阻抗小于主传输线的特性阻 抗。
传输线的电路理论—阻抗匹配
g 4
阻抗变换器带宽
传输线的电路理论—阻抗匹配
0 ( z ) d 0 0 ( z ) d 0 1 1 d d z d ln 0 ( z ) ln 0 ( z) dz 0 ( z ) d 0 0 ( z ) 2 0 ( z ) 2 2 dz
此反射系数对渐变线输入端总反射系数的贡献为
工作原理：当工作频率为中心频率时，支节不
起作用，匹配器等效为阻抗变换器。当频率偏离 中心频率时，阻抗变换器引起的反射由支节产生 的反射来抵消，从而使频带增宽。
传输线的电路理论—阻抗匹配
渐变传输线匹配器
当 / 4 阻抗匹配器节数增加时，两节之间阻抗变 换就较小；当节数无限多的极限情况下，就变成 了连续的渐变传输线。可实现较宽频带内的匹配。
传输线的电路理论
阻抗匹配
阻抗匹配的重要性： 使微波传输系统能将波源的功率有效地传给负载； 关系到系统的传输效率、功率容量与工作稳定性； 关系到微波元器件的性能以及微波测量的系统误差 和测量精度。 阻抗匹配的分类：
无反射匹配 共轭匹配
传输线的电路理论—阻抗匹配

无反射匹配
负载匹配—负载与传输线之间的匹配； 匹配条件：L 0 匹配后传输线状态：负载经匹配后不产生波的反射， 传输线上呈行波状态。 波源匹配—波源与传输线之间的匹配； 匹配条件：g 0 匹配后传输线状态：波源经匹配后对传输线不产生波 的反射。 实际情况：负载不匹配而产生反射波，但波源匹配将 不产生二次反射。
PLcm
PLcm PLm
可见
1 Eg 8Rg
2
（等号仅在传输线无耗，Z g 和 Z L 为实数，即 X g X L 0 成立) ★ 注意：共轭匹配时，线上可能存在反射波，反射系数 不为零，但经多次反射后，负载所得到的功率比无反 射匹配负载时还要大。
传输线的电路理论—阻抗匹配
负载匹配的其它优点
传输线的电路理论—阻抗匹配

共轭匹配
特点：负载吸收最大功率的匹配。 匹配条件：传输线上任一参考面T向负载看去的输入 阻抗与向波源看去的输入阻抗互为共轭，即
如图：
T右＝T左
T处向负载看去：
L j 0tg in Rin jX in 0 0 j Ltg
C、D间
C点与该点
传输线的电路理论—阻抗匹配
串联单支节匹配器
用图解法计算：串联单支节与计算并联单支 节完全类似，但这时应在阻抗圆图上进行。 用解析法计算：采用并联支节相似的分析 （此时用阻抗而不用导纳），可得串联支节接入 位臵
g 1 S d lmin cos 1 4 1 S
串联支节长度为
d d z e j 2 z 1 j 2 z d e ln 0 ( z ) dz 2 dz
于是
1 L dz
传输线的电路理论—阻抗匹配
例如
0 ( z) 0 (0)ebz 0ebz