初中物理 杠杆经典例题讲解学习

一、初中物理杠杆平衡条件的应用问题1．在我国古代书籍《墨经》中，对杠杆有精辟论述，并有许多巧妙的应用．如下图所示是在井上汲水的桔槔，下列对其在使用中正确的解释是A．桔槔是等臂杠杆，不省力也不费力B．向井内放送水桶时，人用的力气一定小于水桶的重力，所以省力C．桔槔是不等臂杠杆，动力臂小于阻力臂，是费力杠杆D．往上提水时，人用的力气一定小于桶与水的总重，所以省力【答案】D【解析】【分析】杠杆的分类：①省力杠杆，动力臂大于阻力臂；②费力杠杆，动力臂小于阻力臂；③等臂杠杆，动力臂等于阻力臂；要使杠杆平衡，作用在杠杆上的两个力（用力点、支点和阻力点）的大小跟它们的力臂成反比。

【详解】AC．由图可见，桔槔是不等臂杠杆，动力臂大于阻力臂，是省力杠杆，故AC错误；B．向井内放送水桶时，人用的力通过杠杆原理，与石头的重力相关，一般比木桶的重力要大，故B错误；D．往上提水时，因为有石头帮忙，人的力气比水和桶的总重力小，故D正确。

故选D。

【点睛】此题主要考查了对简单机械的认识，要掌握杠杆的要素。

2．如图所示，杠杆挂上钩码后刚好平衡，每个钩码的质量相同，在下列情况中，杠杆还能平衡的是A．左右钩码各向支点移一格B．左右各减少一个钩码C．左右各减少一半钩码D．左右各增加两个钩码【答案】C【解析】设杠杆的分度值为 L，一个钩码的重为G．原来4G×2L=2G×4L；左、右钩码各向支点移动一格，左边=4G×L=4GL，右边=2G×3L=6GL，左边＜右边，杠杆向右端下沉，A不符合题意；左右各减少一个钩码，左边=3G×2L=6GL，右边=G×4L=4GL，左边＞右边，杠杆向左下沉，B 不符合题意；左、右钩码各减少一半法码，左边=2G×2L=4GL，右边=G×4L=4GL，左边=右边，杠杆平衡；C符合题意；左右各增加两个钩码，左边=6G×2L=12GL，右边=4G×4L=16GL，左边＜右边，杠杆右边下沉，D不符合题意，故选C．3．生活中，小华发现有如图甲所示的水龙头，很难徒手拧开，但用如图乙所示的钥匙，安装并旋转钥匙就能正常出水（如图丙所示）．下列有关这把钥匙的分析中正确的是A．在使用过程中可以减小阻力臂B．在使用过程中可以减小阻力C．在使用过程中可以减小动力臂D．在使用过程中可以减小动力【答案】D【解析】【详解】由图可知，安装并旋转钥匙，阻力臂不变，阻力不变，动力臂变大，根据杠杆平衡的条件F1L1=F2L2可知，动力变小，故选D。

杠杆考题归类点拨题型一：会确认并画出杠杆的力臂点拨:例1如图1甲所示的钢丝钳，其中A为剪钢丝处，B为手的用力点，O为转动轴（支点），图乙为单侧钳柄及相连部分示意图，请在图乙中画出剪钢丝时的动力F1、阻力F2、动力臂L1、阻力臂L2 .点拨:画力臂时必须注意力臂是“支点到力的作用线的距离”,而不是“支点到力的作用点的距离”.力的作用线是通过力的作用点并沿力的方向所画的直线.答案:如图丙所示。

例2如图2所示杠杆中，动力臂用L表示,图中所画力臂正确的是（）点拨:动力臂是“支点到动力的作用线的距离"，画动力臂时应从支点向动力的作用线作垂线。

四个图中只有D 是正确的。

答案：D题型二：判断是省力杠杆还是费力杠杆例3下列工具中，属于省力杠杆的是( ）A．夹邮票用的镊子B．理发师修剪头发用的剪刀C．剪铁丝用的钢丝钳D．钓鱼用的鱼竿点拨：根据杠杆平衡条件，我们把杠杆分为三类：省力杠杆、费力杠杆和等臂杠杆。

如果动力臂比阻力臂长,就是省力杠杆;如果动力臂比阻力臂短,就是费力杠杆；如果动力臂和阻力臂相等，就是等臂杠杆。

上面例子的实质都是考查的杠杆的分类。

A、B、D三种杠杆均是阻力臂大于动力臂,所以它们都是费力杠杆.答案：C例4人体的运动系统相当复杂，但最基本的运动形式是，骨骼在肌肉提供的动力作用下绕关节转动。

如图3所示是手端起茶杯的情景,其前臂骨骼相当于杠杆，肱二头肌收缩提供动力.由图3可以看出,这是一个（）A．费力、省距离的杠杆B．省力、费距离的杠杆 C．既费力，也费距离的杠杆D．既省力，也省距离的杠杆点拨：本题与生活实际相联系,由于人的前臂相当于杠杆，动力臂和阻力臂已经固定，且阻力臂大于动力臂，是一个费力杠杆。

根据杠杆平衡条件可知:在动力臂和阻力臂确定的情况下，手托起的物体越重，肌肉提供的动力越大，感觉越累。

答案：A例5杠杆在我国古代就有了许多巧妙的应用。

护城河上安装使用的吊桥就是一个杠杆，由图4可知它的支点是______点（填“A”、B”或“C”),在匀速拉起时，它属于一个______杠杆（填“省力”或“费力”），并在图中画动力臂L1。

杠杆题目经典例题
一、题目
有一个杠杆，它的动力臂长为1米，阻力臂长为0.2米。

现在我们要抬起一个重为500牛的物体，问至少需要用多大的力？
二、解题思路（超口语化讲解）
1. 首先呢，咱们得知道杠杆原理的公式，那就是动力×动力臂 = 阻力×阻力臂。

这个就像是一个跷跷板的规则一样，你这边使多大劲儿（动力）乘以你这边的杠杠长度（动力臂），就等于对面多重（阻力）乘以对面的杠杠长度（阻力臂）。

2. 在这道题里呀，阻力就是那个要被抬起的物体的重力，也就是500牛，阻力臂是0.2米，动力臂是1米。

我们要求的是动力，也就是我们得使多大的劲儿。

3. 根据公式动力 = （阻力×阻力臂）÷动力臂。

4. 把数字带进去，那就是（500牛×0.2米）÷1米。

先算括号里的，500牛乘以0.2米等于100牛·米，再除以1米，最后得出动力是100牛。

所以呀，至少需要用100牛的力才能抬起这个物体。

这就像是你在玩一个很长动力臂和很短阻力臂的跷跷板，对面虽然有个500牛重的“大胖子”，但是你这边杠杠长，所以你用100牛的劲儿就能把他翘起来啦。

初中物理简单机械例题及详细解析【典型例题】 类型一、杠杆 1、在探究杠杆平衡条件的实验中，如果杠杆右侧高左侧低，则可将左侧的平衡螺母向 调节，使其在水平位置平衡。

如图所示，在支点左侧20cm 刻度处挂3个重均为0.5N 的钩码，在支点右侧15cm 刻度处用弹簧测力计拉杠杆，使其水平平衡。

要使弹簧测力计示数最小，弹簧测力计的拉力应沿 方向，此时读数为 N 。

【思路点拨】（1）实验前杠杆右侧高左侧低，原因是右侧的力和力臂乘积小于左侧的力和力臂乘积，根据杠杆的平衡条件可知，可将左侧的平衡螺母向右调节，减小左侧的力和力臂乘积，使杠杆在水平位置平衡；（2）当把支点到作用点的连线作为动力臂（施力方向与连线垂直）时，动力臂最长、最省力（弹簧测力计示数最小）；（3）知道阻力、阻力臂和动力臂，利用杠杆的平衡条件求动力。

【答案】右；竖直（或竖直向下）； 2【解析】杠杆在调节过程中右侧高，左侧低，可将左侧的平衡螺母向右调；在阻力和阻力臂及动力作用点一定的条件下，力的作用方向与杠杆垂直时，力臂最大，所用力最小，根据杠杆平衡条件可得F=2N 。

【总结升华】本题考查探究杠杆平衡条件的实验，要求学生平时重视实验能力的培养，重视自己动手实验，要学会利用杠杆平衡条件解决简单的实际问题。

举一反三：【变式】（2015•南宁）如图所示，在使用相同的钩码进行“探究杠杆的平衡条件”的实验中，要使调好的杠杆重新在水平位置平衡，应在A 处悬挂钩码的个数是（ ） A ．1个 B ．2个 C ．3个 D ．6个【答案】B类型二、滑轮2、如图所示，用水平方向的力F 拉绳子的一端P ，使物体A 以2m/s 的速度向左匀速运动，303020201010此时弹簧测力计的示数为8N。

不计滑轮、绳、弹簧的测力计的重力及绳与滑轮间的摩擦，则物体A与水平面的摩擦力及2秒内P端移动的距离分别为（）A．8N，4m B．8N，8m C．16N，4m D．16N，8m【思路点拨】要解决此题需要搞清此滑轮的种类，是动滑轮。

一、初中物理杠杆平衡条件的应用问题1．如图，粗细均匀木棒AB 长为1m ，水平放置在O 、O '两个支点上．已知AO 、O'B 长度均为0.25m 。

若把B 端竖直向上稍微抬起一点距离，至少需要用力40N ；则木棒的重力为（ ）A ．160NB ．120NC ．80ND ．4ON【答案】B【解析】【分析】【详解】设木棒AB 的重心在C 点，抬起B 端时的支点为O ，由于AO ＝0.25m ，则抬B 端的力的力臂OB ＝AB −AO ＝1m−0.25m ＝0.75m木棒AB 的重心距离支点的距离，即重力的力臂 111m 0.25m 0.25m 22OC O C AB AO '=-⨯-＝＝＝ 木棒平衡，则有 F ×OB ＝G ×OC木棒的重力40N 0.75m =120N 0.25mF OBG OC ⨯⨯=＝ 故B 正确。

故选B 。

2．AC 硬棒质量忽略不计，在棒的B 、C 两点施加力F 1、F 2，F 2的方向沿OO'线，棒在图所示位置处于静止状态，则（ ）A ．F 1<F 2B ．F 1=221s F s C ．F 1力臂等于s 1D ．F 2方向沿OO '线向上【答案】D【解析】【详解】AC ．由图知，F 2的方向沿OO ′线，其力臂最长，为s 2；而F 1的方向竖直向下，所以其力臂L 1是从A 点到F 1的垂线段，小于s 1，更小于s 2， 由F 1L 1=F 2L 2知，L 1＜s 2，所以F 1一定大于F 2，故AC 不符合题意；B ．由F 1L 1=F 2L 2知，F 1L 1=F 2s 2，即2211F s F L故B 不符合题意； D ．已知F 1的方向是竖直向下的，为保持杠杆平衡，F 2的方向应该沿OO′向上，故D 符合题意。

3．如图所示为等刻度轻质杠杆，A 处挂4牛的物体，若使杠杆在水平位置平衡，则在B 处施加的力（ ）A ．可能为0.5牛B ．一定为2牛C ．一定为3牛D ．可能是4牛【答案】D【解析】【分析】【详解】设杠杆每小格的长度为L ，若在B 点用垂直OB 竖直向下的力使杠杆在水平位置平衡，此时所用的力最小，根据杠杆平衡条件1122Fl F l =可得min 42F L G L ⋅=⋅则有min 24N22N 44G L F L ⋅⨯=== 若在B 点斜拉使杠杆在水平位置平衡，由杠杆平衡条件1122Fl F l =可知 2211F l F l =则此时杠杆左边的阻力与阻力臂的乘积不变，动力臂减小，故动力将增大，故若使杠杆在水平位置平衡，在B 点施加的力2N F ≥故选D 。

原创：杠杆典型题及解题技巧杠杆的知识即是对前几章力学知识的延续，也是后面要学习滑轮等简单机械的基础知识。

今天阿辉老师通过五种题型，用十四道典型例题及变式题，总结出八个答题技巧，希望对同学们有所帮助。

一、画图例1、如图1，画出下列各力的力臂解析；因为力臂是支点到力的作用线的垂直距离，所以画力臂时，一是先找到支点，二是画线（力的作用线）三是定距离（力臂的长）答案如右图。

技巧一、画力臂时，先把笔点到支点上，往力的作用线引垂线。

若力的作用线不够长，先沿力的方向用虚线正向或反向延长即可。

例2、如图2，画出图中缺少的力解析：图中给出F1缺少F2，根据L2可画出F2，因为力臂与力的作用线垂直，所以画出与L2垂直的一条线与杠杆相交的点即是F2的作用点，又因为支点在两力之旁，两力方向应相反，所以往上画实线标出方向。

下面的线用虚线表示即可。

答案如右图。

技巧二、画力时，先画出与力臂垂直的一条线，这条线与杠杆相交的点就是力的作用点，再根据支点的位置，画出力。

技巧三、若支点在动力与阻力之间，则两个力的方向相同；若支点在动力与阻力之旁，则两个力的方向相反。

例3、如图3，画出使杠杆平衡的最小的力解析：此题还差一个动力未画出，根据杠杆的平衡条件，阻力和阻力臂一定，要使动力最小，必使动力臂最长。

答案如右图。

技巧四、要画使杠杆平衡的最小的力，先把支点与杠杆各点相连，最长的那条线段就是所要求画力的力臂，与杠杆相交的点就是力的作用点，通过力的作用点画与力臂垂直的线，即力作用线，再根据支点的位置，画出力的方向即可。

变式题一、如图所示，用一根硬棒撬一个大石块，棒的上端Ａ是动力作用点．（1）在图上标出：当动力方向向上时，杠杆的支点01；当动力方向向下时，杠杆的支点02、（2）在图上画出撬动石块动力F为最小时的力的方向．解析：（1）因为阻力的方向向下，而动力的方向向上，两力的方向相反，根据技巧三，支点应在两力之旁，所以支点O1如图所示。

当动力方向向下时，与阻力的方向向相同，则支点应在两力之间，所以支点O2如图所示。

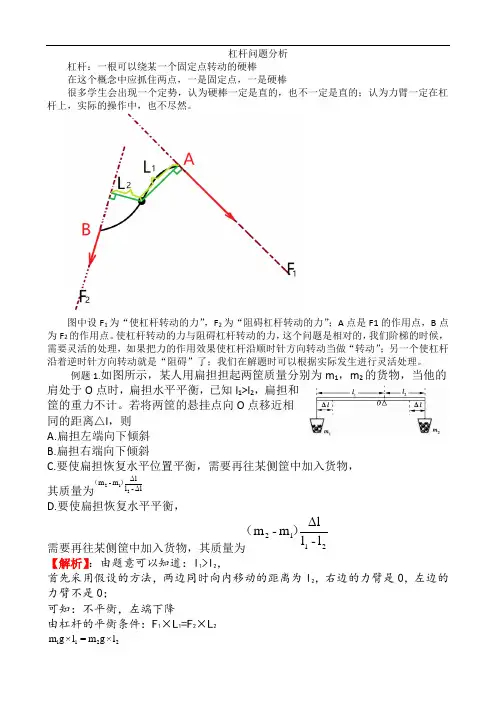
杠杆问题分析杠杆：一根可以绕某一个固定点转动的硬棒在这个概念中应抓住两点，一是固定点，一是硬棒很多学生会出现一个定势，认为硬棒一定是直的，也不一定是直的；认为力臂一定在杠杆上，实际的操作中，也不尽然。

图中设F 1为“使杠杆转动的力”，F 2为“阻碍杠杆转动的力”；A 点是F1的作用点，B 点为F 2的作用点。

使杠杆转动的力与阻碍杠杆转动的力，这个问题是相对的，我们阶梯的时候，需要灵活的处理，如果把力的作用效果使杠杆沿顺时针方向转动当做“转动”；另一个使杠杆沿着逆时针方向转动就是“阻碍”了；我们在解题时可以根据实际发生进行灵活处理。

例题1.如图所示，某人用扁担担起两筐质量分别为m 1，m 2的货物，当他的肩处于O 点时，扁担水平平衡，已知l 1>l 2，扁担和筐的重力不计。

若将两筐的悬挂点向O 点移近相同的距离△l ，则A.扁担左端向下倾斜B.扁担右端向下倾斜C.要使扁担恢复水平位置平衡，需要再往某侧筐中加入货物，其质量为l -l lm -m 212∆∆）（ D.要使扁担恢复水平平衡，需要再往某侧筐中加入货物，其质量为2112l -l lm -m ∆）（【解析】：由题意可以知道：l 1>l 2，首先采用假设的方法，两边同时向内移动的距离为l 2，右边的力臂是0，左边的力臂不是0；可知：不平衡，左端下降由杠杆的平衡条件：F 1×L 1=F 2×L 2 2211l ×g m =l ×gm）l △-l （×g ）m △+m （=）l △-l （×g m 2211展开以后，可以知道：ll lm m m 212∆-∆-=∆）（答案：A C例题2.如图所示，杠杆处于平衡状态，若在两边的钩码下，各加一个同样的钩码，则（ ）A.杠杆仍然保持平衡B.杠杆A 端下降C.杠杆B 端下降D.无法判断【解析】由图可以看到左边的钩码是3个，力臂是2格；右边的钩码是2个，力臂是3格；力臂都是选择在杠杆上直接读取的；整体的杠杆是平衡的。

杠杆原理训练题及详细解析【典型例题】类型一、杠杆的概念及力臂1、（2016春•南京校级月考）下列关于杠杆的说法中正确的是（）A．杠杆的力臂一定在杠杆上B．支点到阻力作用线的距离就是阻力臂C．支点到动力作用点的距离就是动力臂D．力臂的长度不可能为零【思路点拨】杠杆是能在力的作用下绕着固定点转动的硬棒；根据对杠杆的支点、力臂和作用力的了解可逐一做出判断。

【答案】B【解析】A、杠杆的力臂是从支点到力的作用线的距离，力臂不一定在杠杆上，故A错误；B、根据力臂的概念，支点到阻力作用线的距离就是阻力臂，故B正确；C、支点到动力作用线的距离就是动力臂，而不是到动力作用点的距离，故C错误；D、当力的作用线通过支点时，力臂的长度正好为零，故D 错误，故选B。

【总结升华】熟知并正确理解杠杆的定义和五个要素，是我们学习杠杆最基本的要求。

举一反三：【变式】关于力臂，下列说法不准确的是（）A 力臂一定在杠杆上B 支点到动力的作用线的距离叫动力臂C 支点到阻力的作用线的距离叫阻力臂D力的作用线通过支点，这个力的力臂为零【答案】A2、如图所示，轻质杠杆的支点在O点，在杠杆A点用力F1竖直向上拉。

请画出拉力F1的力臂和作用在杠杆上阻力F2的示意图。

【答案】如图所示【解析】杠杆A点用力F1竖直向上拉，那么F1就是动力，物体的重力G 就是阻力F2。

【总结升华】画力臂的步骤：首先在杠杆的示意图上，确定支点O，再从支点O向力的作用线作垂线，画出垂足，则支点到垂足的距离就是力臂。

力臂用虚线表示，支点到垂足用大括号勾出，并用字母L1表示是动力臂。

注意力臂是从支点到力的作用线的垂直距离，不要错误地理解为从支点到力的作用点的距离。

举一反三：【变式】如图所示，杠杆AO在力F1、F2的作用下处于静止状态，L1是力F1的力臂，在图中画出力F1。

【答案】类型二、杠杆的平衡条件3、小明在做“研究杠杆平衡条件”实验时进行了如下实验步骤：把杠杆的中点支在支架上；把钩码挂在杠杆的两边,改变钩码的位置使杠杆平衡；记下两边钩码的重量,并用尺量出它们的力臂,分别填入实验数据的表格内；改变力和力臂的数值,做三次实验；求出各次实验的动力乘以动力臂和阻力乘以阻力臂的数值。

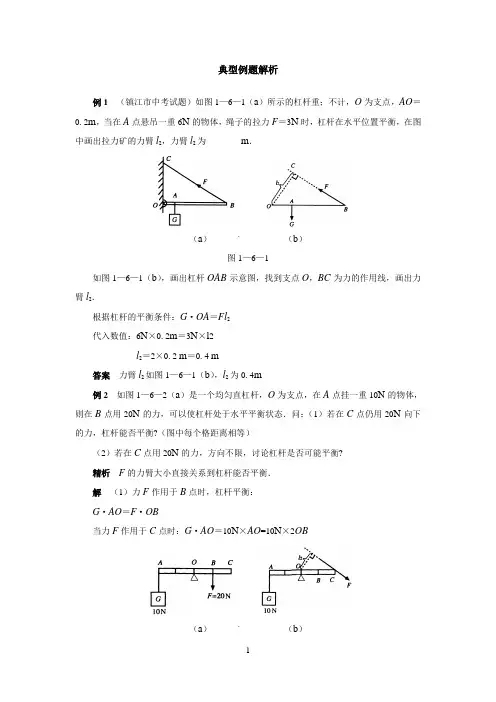
典型例题解析例1（镇江市中考试题）如图1—6—1（a）所示的杠杆重；不计，O为支点，AO＝0.2m，当在A点悬吊一重6N的物体，绳子的拉力F＝3N时，杠杆在水平位置平衡，在图中画出拉力矿的力臂l2，力臂l2为________m．（a）`（b）图1—6—1如图1—6—1（b），画出杠杆OAB示意图，找到支点O，BC为力的作用线，画出力臂l2．根据杠杆的平衡条件：G·OA＝Fl2代入数值：6N×0.2m＝3N×l2l2＝2×0.2 m＝0.4 m答案力臂l2如图1—6—1（b），l2为0.4m例2如图1—6—2（a）是一个均匀直杠杆，O为支点，在A点挂一重10N的物体，则在B点用20N的力，可以使杠杆处于水平平衡状态．问：（1）若在C点仍用20N向下的力，杠杆能否平衡?（图中每个格距离相等）（2）若在C点用20N的力，方向不限，讨论杠杆是否可能平衡?精析F的力臂大小直接关系到杠杆能否平衡．解（1）力F作用于B点时，杠杆平衡：G·AO＝F·OB当力F作用于C点时：G·AO＝10N×AO=10N×2OB（a）`（b）图1—6—2F·OC＝20 N×20BF·OC＞G·AO∴杠杆不能平衡，C端下沉．（2）根据上面的讨论，若C点用力为20N，但方向不限的话，我们可以采取减小力臂的方法，使杠杆重新平衡．如图1—6—2（b）．当F斜着用力时，力臂减小为l2．若此时F＝20N，l2＝OB大小，则杠杆可以再次平衡．答案不能平衡，可能平衡例3（哈尔滨市中考试题）下图中可视为费力杠杆的是（如图l—6—3）（）A BC D图1—6—3精析起重机，l1＜l2，F l＞F2为费力杠杆．其他：手推车、瓶启子、撬杠均是l1＞l2，为省力杠杆．答案A例4（乌鲁木齐市中考试题）如图1—6—4（a）所示，杠杆A处挂一重为40N的物体，杠杆在拉力F作用下保持平衡．O是杠杆的支点．请画出拉力F的力臂L．并写出杠杆平衡时的表达式．（a ） （b ）（c ） （d ）图1—6—4 如图1—6—4（b ）F 的力臂为L ．杠杆平衡时：G ·OA ＝F ·L ．扩展：若CB ＞AO ＞OC ，当F 方向垂直于CB 时，F 的力臂为L ′＞OA ，F ＜G ． 当F 沿CB 方向时，如图1—6—4（d ）．F 的力臂为L ″，当L ″＜OA 时，F ＞G ． 答案 如图1—6—4（b ）（d ），平衡时：G ·OA ＝F ·L例5 （苏州市中考题）杠杆OA 在力F A 、FB 的作用下保持水平静止状态，如图1—6—5（a ）．杠杆的自重不计，O 为杠杆的支点，FB 的方向与OA 垂直，则下列关系式中一定正确的是 （ ）A ．F A ·OA ＝FB ·OB B ．F A ·OA ＜F B ·OBC ．B A F F ＝OBOA D ．F A ＞OA OB F B ⋅（a ） （b ）图1—6—5 精析 此题是考查学生对杠杆平衡条件的理解和能否正确地找出力臂．如图1—6—5（b ），画出力F A 的力臂为l A ，F A 和OA 的夹角为θ。

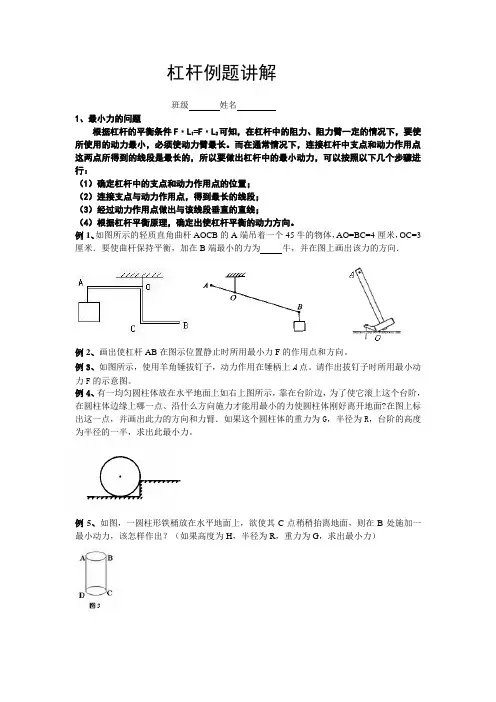
杠杆例题讲解班级 姓名1、最小力的问题根据杠杆的平衡条件F ·L 1=F ·L 2可知，在杠杆中的阻力、阻力臂一定的情况下，要使所使用的动力最小，必须使动力臂最长。

而在通常情况下，连接杠杆中支点和动力作用点这两点所得到的线段是最长的，所以要做出杠杆中的最小动力，可以按照以下几个步骤进行：（1）确定杠杆中的支点和动力作用点的位置； （2）连接支点与动力作用点，得到最长的线段； （3）经过动力作用点做出与该线段垂直的直线；（4）根据杠杆平衡原理，确定出使杠杆平衡的动力方向。

例1、如图所示的轻质直角曲杆AOCB 的A 端吊着一个45牛的物体，AO=BC=4厘米，OC=3厘米．要使曲杆保持平衡，加在B 端最小的力为 牛，并在图上画出该力的方向．例2、画出使杠杆AB 在图示位置静止时所用最小力F 的作用点和方向。

例3、如图所示，使用羊角锤拔钉子，动力作用在锤柄上A 点。

请作出拔钉子时所用最小动力F 的示意图。

例4、有一均匀圆柱体放在水平地面上如右上图所示，靠在台阶边，为了使它滚上这个台阶，在圆柱体边缘上哪一点、沿什么方向施力才能用最小的力使圆柱体刚好离开地面?在图上标出这一点，并画出此力的方向和力臂．如果这个圆柱体的重力为G ，半径为R ，台阶的高度为半径的一半，求出此最小力。

例5、如图，一圆柱形铁桶放在水平地面上，欲使其C 点稍稍抬离地面，则在B 处施加一最小动力，该怎样作出？（如果高度为H ，半径为R ，重力为G ，求出最小力）例6、如图所示，用撬棒撬起大石头，向上、向下用力都可以，农民伯伯想用最省力的方法撬起大石头，请你在图中画出这个力的示意图。

2、杠杆的动态平衡问题杠杆动态平衡是指构成杠杆的某些要素发生变化,而杠杆仍处于静止状态或匀速转动状态，分析杠杆的动态平衡时，一般是动中取静，根据杠杆平衡条件，分析比较，得出结论。

下面就杠杆动态平衡问题归类分析。

一、阻力一定，判断动力的变化情况1、1l 不变，2l 变化例1、如图1所示，轻质杠杆可绕O 转动，在A用于杠杆的力，在从A 转动A / 位置时，力F 将（ A 、变大 B 、变小C 、先变大，后变小 D2、2l 不变，1l 变化例2、如图2所示，轻质杠杆OA 的B 在圆环M 下，此时OA 恰成水平且A 点与圆弧形架么当环M 从P 点逐渐滑至Q 点的过程中，绳对A A 、保持不变 B 、逐渐增大 C 、逐渐减小 D 、由大变小再变大3、1l 与2l 同时变化，但比值不变例3、用右图3所示的杠杆提升重物，设作用在A 下，在将重物慢慢提升到一定高度的过程中，F A 、保持不变 B 、逐渐变小 C 、逐渐变大 D 、先变大，后变小BG4、1l 与2l 同时变化例4、如图4所示，一个直杠杆可绕轴O 转动，在直杆的中点挂一重物， 在杆的另一端施加一个方向始终保持水平的力F ，将直杆从竖直位置 慢慢抬起到水平位置过程中，力F 大小的变化情况是( ) A 、一直增大 B 、一直减小 C 、先增大后减小 D 、先减小后增大习题：1.如图1，一根重木棒在水平动力(拉力)F 的作用下以O 点为轴，由竖直位置逆时针匀速转到水平位置的过程中，若动力臂为L ，动力与动力臂的乘积为M ，则（ ） A.F 增大,L 减小，M 增大．B.F 增大,L 减小，M 减小．C.F 增大,L 增大，M 增大．D.F 减小,L 增大，M 增大．2、如图所示，将一根粗细均匀的硬棒从水平地面抬起，所用的力F 始终与棒垂直，请画出 图示位置的动力臂（l 1）和阻力臂（l 2）。

杠杆知识点1、杠杆定义：在力的作用下绕着固定点转动的硬棒叫杠杆。

说明：①杠杆可直可曲，形状任意。

②有些情况下，可将杠杆实际转一下，来帮助确定支点。

如：鱼杆、铁锹。

2、杠杆五要素组成杠杆示意图。

①支点：杠杆绕着转动的点。

用字母O表示。

②动力：使杠杆转动的力。

用字母F i表示。

③阻力：阻碍杠杆转动的力。

用字母F 2表示。

说明：动力、阻力都是杠杆的受力，所以作用点在杠杆上。

动力、阻力的方向不一定相反，但它们使杠杆的转动的方向相反④动力臂：从支点到动力作用线的距离。

用字母l i表示。

⑤阻力臂：从支点到阻力作用线的距离。

用字母12表示。

画力臂方法：一找支点、二画线、三连距离、四标签⑴找支点Q⑵画力的作用线（虚线）；⑶画力臂（虚线，过支点垂直力的作用线作垂线）；⑷标力臂（大括号）。

3、研究杠杆的平衡条件：杠杆平衡是指：杠杆静止或匀速转动。

实验前：应调节杠杆两端的螺母，使杠杆在水平位置平衡。

这样做的目的是：可以方便的从杠杆上量出力臂。

⑴ 结论：杠杆的平衡条件（或杠杆原理）是：动力X动力臂=阻力X阻力臂。

写成公式F i l 1=F212也可写成：F i / F 2=1 2 / 1 1⑵ 解题指导：分析解决有关杠杆平衡条件问题，必须要画出杠杆示意图；弄清受力与方向和力臂大小；然后根据具体的情况具体分析，确定如何使用平衡条件解决有关问题。

（如：杠杆转动时施加的动力如何变化，沿什么方向施力最小等。

）⑶ 解决杠杆平衡时动力最小问题：此类问题中阻力X阻力臂为一定值，要使动力最小，必须使动力臂最大，要使动力臂最大需要做到①在杠杆上找一点，使这点到支点的距离最远；②动力方向应该是过该点且和该连线垂直的方向。

4、应用：说明：应根据实际来选择杠杆，当需要较大的力才能解决问题时，应选择省力杠杆，当为了使用方便，省距离 时，应选费力杠杆。

经典考题1、图5是环卫工人用的一种垃圾夹的结构示意图。

拉绳的一端固定在手把上，另一端穿过空心管杆与两夹爪的一端 相连。

初中物理杠杆作图题归类例析一、杠杆力臂的作法一找点，二画线（必要时反向延长或正向延长力的作用线），三作垂线段（力臂用虚线或实线表示），四标符号（标上直角符号和大括号，并标上力臂的字母）。

点拨：杠杆的支点、动力作用点和阻力作用点都必须在杠杆上，力臂和力的作用线必须垂直例：如图所示，作出图中各杠杆的动力和阻力的力臂。

二、最大动力臂和最小动力的作法例1：为使杠杆OA保持静止，画出在A点所加最小力F1的示意图和阻力F2的力臂l2．例2：如图丙所示，用螺丝刀撬起图钉．请在图上画出螺丝刀受到图钉阻力F2的力臂；并画出作用在螺丝刀柄上A点的最小动力F1的示意图．例3：如图3所示，一重力可忽略不计的杠杆，支点为O，A端挂一重物G，若要杠杆在图示位置平衡，要在C点加最小的力，这个力的方向怎样？三、根据力臂画力的作法例1：如图所示，轻质杠杆可绕O转动，杠杆上吊一重物G，在力F作用下杠杆静止在水平位置，l为F的力臂，请在图中作出力F的示意图及重物G所受重力的示意图。

例2：如图6所示，杠杆在力、作用下处于平衡状态，为的力臂。

请在图中作出力。

四、情境设置题作图例1：画出作用在压水泵摇柄上力的力臂。

例2：杠杆在我国古代就有了许多巧妙的应用，护城河上安装的吊桥（图3）就是一个杠杆，它的支点是C点，画出绳对吊桥的拉力及拉力的力臂。

例3：请你在图3—1中画出使用剪刀时，杠杆AOB所受动力的示意图。

例4：小华在动物园参观时，看到了如上图所示的场景，为使小熊猫不致与石头相撞而受伤害，请你在杠杆AOB上作出使杠杆AOB在图所示位置静止时的最小力的示意图，图中O为旋转点。

例5：如图所示，使用羊角锤拔钉子，动力作用在锤柄上A点。

请作出拔钉子时所用最小动力的示意图。

（注意：请在图上保留为确保作图准确所画的辅助线）杠杆分类（1）L1＞L2时，叫省力杠杆，其特点是省了力但费了距离。

如开瓶盖的起子、铡刀、老虎钳、道钉撬等。

（2）L1＜L2时，叫费力杠杆，其特点是费了力但省了距离。

《杠杆》典例解析DIV.MyFav_1329359512746 P.MsoNormal{TEXT-JUSTIFY: inter-ideograph; FONT-SIZE: 10.5pt; MARGIN: 0cm 0cm 0pt; FONT-FAMILY: "Times New Roman"; TEXT-ALIGN: justify}DIV.MyFav_1329359512746LI.MsoNormal{TEXT-JUSTIFY: inter-ideograph;FONT-SIZE: 10.5pt; MARGIN: 0cm 0cm 0pt; FONT-FAMILY: "Times New Roman"; TEXT-ALIGN:justify}DIV.MyFav_1329359512746DIV.MsoNormal{TEXT-JUSTIFY: inter-ideograph;FONT-SIZE: 10.5pt; MARGIN: 0cm 0cm 0pt; FONT-FAMILY: "Times New Roman"; TEXT-ALIGN:justify}DIV.MyFav_1329359512746P.MsoPlainText{TEXT-JUSTIFY: inter-ideograph;FONT-SIZE: 10.5pt; MARGIN: 0cm 0cm 0pt; FONT-FAMILY: 宋体; TEXT-ALIGN: justify}DIV.MyFav_1329359512746 LI.MsoPlainText{TEXT-JUSTIFY: inter-ideograph;FONT-SIZE: 10.5pt; MARGIN: 0cm 0cm 0pt; FONT-FAMILY: 宋体; TEXT-ALIGN: justify}DIV.MyFav_1329359512746 DIV.MsoPlainText{TEXT-JUSTIFY: inter-ideograph; FONT-SIZE: 10.5pt; MARGIN: 0cm 0cm 0pt; FONT-FAMILY: 宋体; TEXT-ALIGN: justify}DIV.MyFav_1329359512746DIV.Section1{page: Section1}1．关于杠杆的下列说法中正确的是（）A．杠杆必须是一根直棒B．杠杆不一定要有支点C．杠杆可以是直的，也可以是弯的D．作用在杠杆上的两个力总是使杠杆向相反的方向转动思路解析：根据杠杆的定义，杠杆使能绕固定点（支点）转动的硬棒，因此一定要有支点，并且两个力反向并能使杠杆转动，而且可直可弯，因此AB不对，应选CD。