第五章对流传热分析..
- 格式:doc
- 大小:484.00 KB
- 文档页数:14

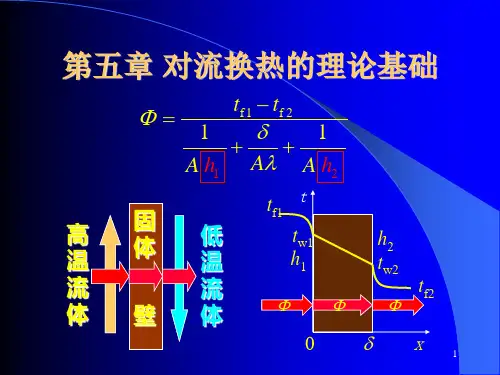








第五章对流换热思考题1、在对流换热过程中,紧靠壁面处总存在一个不动的流体层,利用该层就可以计算出交换的热量,这完全是一个导热问题,但为什么又说对流换热是导热与对流综合作用的结果。
答:流体流过静止的壁面时,由于流体的粘性作用,在紧贴壁面处流体的流速等于零,壁面与流体之间的热量传递必然穿过这层静止的流体层。
在静止流体中热量的传递只有导热机理,因此对流换热量就等于贴壁流体的导热量,其大小取决于热边界层的厚薄,而它却受到壁面流体流动状态,即流动边界层的强烈影响,故层流底层受流动影响,层流底层越薄,导热热阻越小,对流换热系数h也就增加。
所以说对流换热是导热与对流综合作用的结果。
2、试引用边界层概念来分析并说明流体的导热系数、粘度对对流换热过程的影响。
答:依据对流换热热阻主要集中在热边界层区域的导热热阻。
层流边界层的热阻为整个边界层的导热热阻。
紊流边界层的热阻为层流底层的导热热阻。
导热系数越大,将使边界层导热热阻越小,对流换热强度越大;粘度越大,边界层(层流边界层或紊流边界层的层流底层)厚度越大,将使边界层导热热阻越大,对流换热强度越小。
3、由对流换热微分方程知,该式中没有出现流速,有人因此得出结论:表面传热系数h与流体速度场无关。
试判断这种说法的正确性?答:这种说法不正确,因为在描述流动的能量微分方程中,对流项含有流体速度,即要获得流体的温度场,必须先获得其速度场,“流动与换热密不可分”。
因此表面传热系数必与流体速度场有关。
4、试引用边界层概念来分析并说明流体的导热系数、粘度对对流换热过程的影响。
答:依据对流换热热阻主要集中在热边界层区域的导热热阻。
层流边界层的热阻为整个边界层的导热热阻。
紊流边界层的热阻为层流底层的导热热阻。
导热系数越大,将使边界层导热热阻越小,对流换热强度越大;粘度越大,边界层(层流边界层或紊流边界层的层流底层)厚度越大,将使边界层导热热阻越大,对流换热强度越小。
5、对管内强制对流换热,为何采用短管和弯管可以强化流体的换热?答:采用短管,主要是利用流体在管内换热处于入口段温度边界层较薄,因而换热强的特点,即所谓的“入口效应”,从而强化换热。

第五章对流换热分析通过本章的学习,读者应熟练掌握对流换热的机理及其影响因素,边界层概念及其应用,以及在相似理论指导下的实验研究方法,进一步提出针对具体换热过程的强化传热措施。
5.1 内容提要及要求5.1.1 对流换热概述1.定义及特性对流换热指流体与固体壁直接接触时所发生的热量传递过程。
在对流换热过程中,流体内部的导热与对流同时起作用。
牛顿冷却公式q h(t w t f ) 是计算对流换热量的基本公式,但它仅仅是对流换热表面传热系数h 的定义式。
研究对流换热的目的是揭示表面传热系数与影响对流换热过程相关因素之间的内在关系,并能定量计算不同形式对流换热问题的表面传热系数及对流换热量。
2.影响对流换热的因素(1)流动的起因:流体因各部分温度不同而引起密度差异所产生的流动称为自然对流,而流体因外力作用所产生的流动称为受迫对流,通常其表面传热系数较高。
(2)流动的状态:流体在壁面上流动存在着层流和紊流两种流态。
(3)流体的热物理性质:流态的热物性主要指比热容、导热系数、密度、粘度等,它们因种类、温度、压力而变化。
(4)流体的相变:冷凝和沸腾是两种最常见的相变换热。
(5)换热表面几何因素:换热表面的形状、大小、相对位置及表面粗糙度直接影响着流体和壁面之间的对流换热。
综上所述,可知表面传热系数是如下参数的函数h f u, t w , t f , , c p , ,,, l这说明表征对流换热的表面传热系数是一个复杂的过程量,不同的换热过程可能千差万别。
3.分析求解对流换热问题分析求解对流换热问题的实质是获得流体内的温度分布和速度分布,尤其是近壁处流体内的温度分布和速度分布,因为在对流换热问题中“流动与换热是密不可分”的。
同时,分析求解的前提是给出正确地描述问题的数学模型。
在已知流体内的温度分布后,可按如下的对流换热微分方程获得壁面局部的表面传热系数由上式可有h xtt x yW/(m 2 K)w,x其中为过余温度,h xxyW/(m 2 K)w,x对流换热问题的边界条件有两类,第一类为壁温边界条件,即壁温分布为已知,待求的是流体的壁面法向温度梯度;第二类为热流边界条件,即已知壁面热流密度,待求的是壁温。
(0-4)第五章 对流传热分析q = h (t w — t f ) W/m 2 =h (t w — t f ) A W、流动的起因和流动状态、流体的热物理性质本书采用国际单位制,各热物性的单位)如下: 1 •密度 p , k g / m 3; 2 •定压比热容C p , kJ /(k g K); 3.动力黏度Ns / m 2或 kg /( s m)u / y运动黏度=卩/pm 2/s4. 体积膨胀系数 ,1/ K;比体积v ,m 3/kg1v1v TpT P理想气体 =1/T ,对液体或蒸汽,由实验测定,可查附录物性表。
5.热导率入,W /(m K) ; a , m 2/s 。
第一节对流传热概述图5-1几种常见的换热设备示意图、流体的相变四、换热表面几何因素h f u,t w, t f, ,C p, , , ,l (5-1)第二节对流传热微分方程组、对流传热过程微分方程式式中图5-3连续性方程的推导x 方向:M x udyM x M x dx M x x dxxy 方向:M y vdxM y M y dy M ydyy (5-3)、动量微分方程式tq xy w ,xW/m 2(1)q xh x (t wt f )xh x t x⑵th x tt xy w,x(5-2a)t t wh x ---------------------------Xy w,x(5-2b)其中wf x't f t w 01、连续性方程Y 卅严霧如图5-4动量微分方程的推导dxdy DUd(1) 微元体的质量X加速度:Du u u u= u v——d x yDv v v v= u v——d x y(2) 微元体所受的外力:体积力:X dx dyY dx dy表面力:(——-——汪)dx dyx y(—y——y ) dx dyy xu u u x yx x 方向:P ( u v ) = X + ----------------------------x y x yx y yx22z uuu 、p u u P (u v ) =X —+ 2 2 x yxxy22,vv v 、p v v P (uv ):=Y —+22 xyyxy(1)(2) (3)⑷vvvy xyy 方向: P ( u v ) = 丫 + —(5-4a)(4)黏滞x方向导入的净能量三(x+ x dx ) xy方向导入的净能量三2ydx dyx方向热对流传递的净能量三x—(x+ x dx) xdx dy⑴惯性力项,即质量与加速度之积;(2)体积力;⑶压强梯度; 力。
第五章 对流换热分析通过本章的学习,读者应熟练掌握对流换热的机理及其影响因素,边界层概念及其应用,以及在相似理论指导下的实验研究方法,进一步提出针对具体换热过程的强化传热措施。
5.1内容提要及要求5.1.1 对流换热概述1.定义及特性对流换热指流体与固体壁直接接触时所发生的热量传递过程。
在对流换热过程中,流体内部的导热与对流同时起作用。
牛顿冷却公式w f ()q h t t =-是计算对流换热量的基本公式,但它仅仅是对流换热表面传热系数h 的定义式。
研究对流换热的目的是揭示表面传热系数与影响对流换热过程相关因素之间的内在关系,并能定量计算不同形式对流换热问题的表面传热系数及对流换热量。
2.影响对流换热的因素(1)流动的起因:流体因各部分温度不同而引起密度差异所产生的流动称为自然对流,而流体因外力作用所产生的流动称为受迫对流,通常其表面传热系数较高。
(2)流动的状态:流体在壁面上流动存在着层流和紊流两种流态。
(3)流体的热物理性质:流态的热物性主要指比热容、导热系数、密度、粘度等,它们因种类、温度、压力而变化。
(4)流体的相变:冷凝和沸腾是两种最常见的相变换热。
(5)换热表面几何因素:换热表面的形状、大小、相对位置及表面粗糙度直接影响着流体和壁面之间的对流换热。
综上所述,可知表面传热系数是如下参数的函数()w f p ,,,,,,,,h f u t t c l λραμ=这说明表征对流换热的表面传热系数是一个复杂的过程量,不同的换热过程可能千差万别。
3.分析求解对流换热问题分析求解对流换热问题的实质是获得流体内的温度分布和速度分布,尤其是近壁处流体内的温度分布和速度分布,因为在对流换热问题中“流动与换热是密不可分”的。
同时,分析求解的前提是给出正确地描述问题的数学模型。
在已知流体内的温度分布后,可按如下的对流换热微分方程获得壁面局部的表面传热系数2x x w,xW/(m K)t h t y λ∆⎛⎫∂=-⋅ ⎪∂⎝⎭由上式可有2x x w,xW/(m K)h y λθ∆θ⎛⎫∂=-⋅ ⎪∂⎝⎭其中θ为过余温度,t t θ=-。
对流换热问题的边界条件有两类,第一类为壁温边界条件,即壁温分布为已知,待求的是流体的壁面法向温度梯度;第二类为热流边界条件,即已知壁面热流密度,待求的是壁温。
由于对流换热问题的分析求解常常要求解包括连续性方程、动量微分方程和能量微分方程在内的一系列方程,因此它的求解过程比导热问题要困难得多。
5.1.2 对流换热微分方程组1.连续性方程二维常物性不可压缩流体稳态流动连续性方程:0u x yυ∂∂+=∂∂ 2.动量微分方程式动量微分方程式描述流体速度场,可从分析微元体的动量守恒中建立。
它又称纳斯-斯托克斯方程,简称N·S 方程。
2222u u u pu u u X x y x x y ρυμτ⎛⎫⎛⎫∂∂∂∂∂∂++=-++ ⎪ ⎪∂∂∂∂∂∂⎝⎭⎝⎭2222pu Y x y y x y υυυυυρυμτ⎛⎫⎛⎫∂∂∂∂∂∂++=-++ ⎪ ⎪∂∂∂∂∂∂⎝⎭⎝⎭3.能量微分方程式能量微分方程式描述流体的温度场,由能量守恒原理分析进出微元体的各项能量来建立。
22p 22t t t t t c u x y x y ρυλτ⎛⎫⎛⎫∂∂∂∂∂++=+ ⎪ ⎪∂∂∂∂∂⎝⎭⎝⎭5.1.3 边界层分析及边界层换热微分方程组1.边界层的概念由于对流换热的热阻大小主要取决于紧靠壁面附近的流体流动状况,而该区域中速度和温度的变化最为剧烈。
因此,将固体壁面附近流体速度急剧变化的薄层称为流动边界层,而将温度急剧变化的薄层称为热边界层。
流动边界层的厚度δ通常规定为在壁面法线方向达到主流速度99%处的距离,即0.99u u ∞=。
而热边界层的厚度t δ为沿该方向达到主流过余温度99%处的距离,即f 0.99θθ=。
t δ不一定等于δ,两者之比决定于流体的物性。
读者应熟练掌握流动边界层和热边界层的特点及两者的区别,这是进行边界层分析的前提。
2.边界层的特性 (1)边界层极薄,其厚度δ、t δ与壁面尺寸相比都是很小的量。
(2)边界层内法线方向速度梯度和温度梯度非常大。
(3)边界层内存在层流和紊流两种流态。
(4)引入边界层的概念后,流场可分为边界层区和主流区。
边界层区是流体粘性起作用的区域,而主流区可视为无粘性的理想流体。
(建议增加关于管内(受限空间)流动时的边界层分析,因为学生容易误解,管内流动情况下边界层也很薄。
)3.边界层微分方程组二维稳态无内热源层流边界层对流换热方程组由动量微分方程、连续性方程、能量微分方程组成,即221d d u u p u u x y x yυνρ∂∂∂+=-+∂∂∂ 0u x yυ∂∂+=∂∂ 22t t t u a x y yυ∂∂∂+=∂∂∂ 利用边界层理论,可将原本需整个流场求解的问题,转化为可分区(主流区和边界层区)求解的问题。
其中,主流区按理想流体看待,而边界层区用边界层微分方程组求解。
4.外掠平板层流换热边界层微分方程式分析求解 由常物性流体外掠平板层流边界层换热微分方程组22u u u u x y yυν∂∂∂+=∂∂∂ 0u x yυ∂∂+=∂∂ 22t t t u a x y yυ∂∂∂+=∂∂∂ x w,xΔt h t y λ⎛⎫∂=- ⎪∂⎝⎭可求解得到如下结论:(1)边界层厚度及局部摩擦系数1/2x5.0Re xδ-= 1/3tPr δδ-= f,x 1/2x0.332Re 2C -= (2)常壁温平板局部表面传热系数1/21/32x x0.332Re Pr W/(m K)h xλ=⋅1/21/3Nu 0.332Re Pr=其中普朗特准则Pr aν=,反映流体物性对换热影响的大小;努谢尔特准则Nu hlλ=,反映对流换热强弱的程度。
5.1.4 边界层换热积分方程组及求解1.概述分析平板层流边界层换热问题的一种近似方法是,通过分析流体流过边界层任一微元宽度时的质量、动量及能量守恒关系,导出边界层积分方程组。
它与边界层微分方程组的不同在于,它不要求对边界层内每一微元都满足守恒定律,而是只要求包括固体边界及边界层外边界在内的有限大小的控制容积满足守恒定律即可。
2.边界层积分方程组 (1)边界层动量积分方程式00d d()d ()d d d w u u u u y u u y x x δδρρτ∞∞∞-+-=⎰⎰ (2)边界层能量积分方程式f 0w d()d d t u t t y a x y δ⎛⎫∂-= ⎪∂⎝⎭⎰ 3.求解结果常物性流体外掠平板层流边界层速度分布曲线33122u y y u δδ∞⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭无量纲温度分布3w f w f t t 3122t t y y t t θθδδ⎛⎫⎛⎫-==- ⎪ ⎪-⎝⎭⎝⎭离平板前沿x 处的流动边界层厚度的无量纲表达式1/2x4.64Re xδ=局部摩擦系数f,x 1/2x0.323Re 2C -= 离平板前沿x 处的热边界层厚度的无量纲表达式1/3t1/2x4.52Pr Re xδ-=局部表面传热系数1/21/32x x0.332Re Pr W/(m K)h xλ=⋅1/21/3Nu 0.332Re Pr=(建议增加积分解与分析解结果的比较,说明今后在计算过程中如何选取公式)5.1.5 动量传递和热量传递的类比紊流总粘滞应力为层流粘滞应力与紊流粘滞应力之和,即()2t m d N/m d l u yτττρνε=+=+紊流总热流密度为层流导热量和紊流传递热量之和,即()2t p h d W/m d l t q q q c a yρε=+=-+柯比朋类比律2/3x f,x Pr /2St C ⋅=(建议说明为什么可以类比、类比的原则是什么)5.1.6 相似理论基础1.相似原理 研究对流换热的主要方法是在相似理论指导下的实验方法,相似理论使个别的实验数据上升到能够代表整个相似群(?)的高度。
(建议再展开一些,许多学生不明白相似原理的用途)(1)相似性质1)用相同形式且具有相同内容的微分方程式所描述的现象称为同类现象。
只有同类现象才能谈相似问题。
(边界条件是否要相同)2)彼此相似的现象,其相关的物理量场分别相似。
3)彼此相似的现象,其同名相似准则必定相等。
(2)相似准则间的关系1)物理现象中的各物理量不是单个起作用,而是由各准则数组成联合作用。
因此方程的解只能是由这些准则组成的函数关系式,称为准则关联式。
2)按准则关联式的内容整理实验数据,就能得到反映现象变化规律的实用关联式,从而解决了实验数据如何整理的问题。
(3)判别相似的条件凡同类现象,单值性条件(几何条件、物理条件、边界条件、时间条件等)相似,同名的已定准则相等,现象必定相似。
学习相似理论时,读者应深入理解并充分掌握以下问题,如怎样安排实验、测量什么参数、如何整理实验数据,如何推广应用所得的实验关联式。
对于同一组实验数据,不同人采用不同的准则关系式形式,完全可能得到不同的实验关联式。
衡量一个实验关联式的好坏应该考虑该公式是否将所有实验数据拟合后的偏差最小,同时其参数范围是否广泛等。
教材中介绍的所有实验关联式都是前人经过大量实验研究并用相似理论方法整理出来的研究成果,学习时要充分理解并注意其使用方法及参数范围。
2.对流换热常用准则数及其物理意义 (1)雷诺准则,Re ulν=,它表示流体流动时惯性力与粘滞力的相对大小。
(2)格拉晓夫准则,32ΔGr g t l αν=,它表示浮升力与粘滞力的相对大小。
(3)普朗特准则,Pr aν=,它表示流体的动量传递能力与热量传递能力的相对大小。
(4)努谢尔特准则,Nu hlλ=,它表示壁面法向无量纲过余温度梯度的大小。
在受迫对流换热问题中,引入无量纲准则数后,原本影响因素众多的表面传热系数就变为Nu =f (Re ,Pr)。
由此可知,根据准则数安排实验,可大大减少实验次数,并减少实验的盲目性。
(关于准则的物理意义,建议稍微展开一点解释,因为教材中关于此问题的解释不容易被学生理解。
许多学生是死记硬背下来的)3.实验数据的整理方法通常,对流换热问题的准则关联式可表示为如下形式Nu (Re,Pr,Gr)f =-----5.2公式小结5.2.1 外掠平板层流换热流动边界层厚度1/2x4.64Re xδ=热边界层厚度1/3t1/2x4.52Pr Re xδ-=局部摩擦系数f,x 1/2x0.323Re 2C -= 局部表面传热系数1/21/32x x 0.332Re PrW/(m K)h xλ=⋅1/21/3x x Nu 0.332Re Pr= 平均表面传热系数1/21/320.664Re Pr W/(m K)h lλ=⋅1/21/3Nu 0.664Re Pr =5.2.2外掠平板紊流换热局部摩擦系数1/5f,x x0.0592Re C -= 局部表面传热系数关联式4/51/3x x Nu 0.0296Re Pr= 平均表面传热系数关联式0.81/3Nu (0.037Re 870)Pr =-5.3习题解析(以下几式中的矩形符号表示“正比于”或“相当于”的意思)例5.1 利用数量级分析的方法,对流体外掠平板的流动,从动量微分方程可导出边界层厚度有如下的变化关系式Re xδ试证明之。