Mathematica表达式及其运算规则解读
- 格式:ppt
- 大小:583.00 KB
- 文档页数:45

mathematica逻辑运算Mathematica是一种强大的计算机代数系统,可以进行各种数学运算和逻辑推理。
它不仅可以进行简单的算术运算,还可以处理复杂的逻辑问题。
在本文中,我们将探讨一些常见的逻辑运算及其在Mathematica中的应用。
我们来介绍一下Mathematica中的逻辑运算符。
Mathematica支持以下逻辑运算符:与(&&)、或(||)、非(!)、等于(==)、不等于(!=)、大于(>)、小于(<)、大于等于(>=)和小于等于(<=)。
这些运算符可以用于对布尔值进行逻辑运算,也可以用于比较数字和表达式的大小关系。
逻辑运算符的使用非常简单。
例如,我们可以使用与运算符(&&)来判断两个条件是否同时成立。
如果两个条件都为真,则结果为真;否则结果为假。
类似地,使用或运算符(||)可以判断两个条件中是否至少有一个为真。
非运算符(!)用于取反,将真变为假,将假变为真。
除了基本的逻辑运算符,Mathematica还提供了一些更高级的逻辑函数,如And、Or和Not。
这些函数可以用于对多个条件进行逻辑运算。
例如,And函数可以判断多个条件是否同时成立,如果所有条件都为真,则结果为真;否则结果为假。
类似地,Or函数可以判断多个条件中是否至少有一个为真。
Not函数用于取反,将真变为假,将假变为真。
在Mathematica中,我们可以使用逻辑运算符和逻辑函数来解决各种逻辑问题。
例如,我们可以使用逻辑运算符来判断一个数是否为偶数。
首先,我们可以使用求余(%)运算符来判断一个数除以2的余数是否为0。
如果余数为0,则该数为偶数;否则该数为奇数。
另一个常见的逻辑问题是判断一个年份是否为闰年。
根据闰年的定义,如果一个年份能够被4整除,但不能被100整除,或者能够被400整除,那么该年份就是闰年。
在Mathematica中,我们可以使用逻辑运算符和条件语句来判断一个年份是否为闰年。
1表达式的含义M athematica 能处理数学公式,表以及图形等多多种数据形式。
尽管他们从形式上看起来不一样,但在Mathematica内部都被看成同种类型,即都把他们当作表达式的形式。
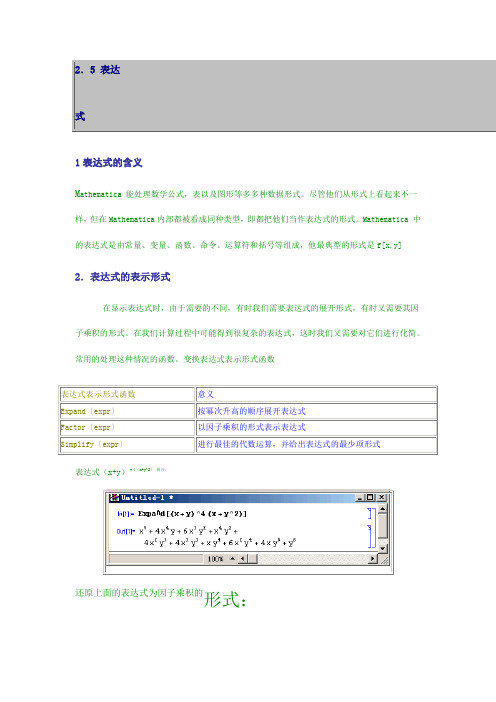
Mathematica 中的表达式是由常量、变量、函数、命令、运算符和括号等组成,他最典型的形式是f[x,y] 2.表达式的表示形式在显示表达式时,由于需要的不同,有时我们需要表达式的展开形式,有时又需要其因子乘积的形式。
在我们计算过程中可能得到很复杂的表达式,这时我们又需要对它们进行化简。
常用的处理这种情况的函数。
变换表达式表示形式函数表达式(x+y)^4(x+y^2)展开:还原上面的表达式为因子乘积的形式:多项式表达式的项数较多,比较复杂,在显示时显得比较杂乱,而且在计算过程中没有必要知道全部的内容;或表达式的项很有规律,没有必要打印全部的表达式的结果,Mathematica提供了一些命令,可将它缩短输出或不输出将表达式(1+x)^30展开,并仅显示一行有代表项的式子:将上式分成三行的形式展开:把代数表达式变换到你所需要的形式没有一种固定的模式,一般情况下,最好的办法是进行多次实验,尝试不同的变换并观察其结果,再挑出你满意的表示形式。
3.关系表达式与逻辑表达式我们已经知道“=”表示给变量赋值。
现在我们来学习一些其它的逻辑与关系算子。
关系表达式是最简单的逻辑表达式,我们常用关系表达式表示一个判别条件。
例如:x>0,y=0。
关系表达式的一般形式是:表达式+关系算子+表达式。
其中表达式可为数字表达式、字符表达式或意义更广泛的表达式,如一个图形表达式等。
在我们实际运用中,这儿的表达式常常是数字表达式或字符表达式。
下面出Mathematica中的各种关系算子。
给变量x,y赋值,输出后以变量的值,如:下面是比较两个表达式的大小用一个关系式只能表示一个判定条件,要表示几个判定条件胡组合,必须用逻辑运算符将关系表达式组织在一起,我们称表示判定条件的表达式为逻辑表达式。

mathematica中表达式运算的结合次序
Mathematica是一种强大的数学计算软件,它能够处理各种复杂的数值计算和符号计算任务。
在Mathematica中,表达式的运算是按照一定的结合次序进行的,这是确保计算的正确性
的重要因素。
在Mathematica中,运算的结合次序遵循通常的数学规则。
具体来说,Mathematica按照以下次序进行运算:
1. 指数运算:Mathematica首先计算指数运算,即计算表达式中的幂。
2. 乘法和除法:Mathematica接下来计算乘法和除法运算,按照表达式中出现的顺序进行计算。
3. 加法和减法:Mathematica最后计算加法和减法运算,同样按照表达式中出现的顺序进行计算。
需要注意的是,Mathematica会自动识别和处理括号和其他运算符。
如果表达式中使用了括号,则括号中的计算会优先进行。
此外,Mathematica还提供了控制运算次序的特殊符号和函数。
例如,可以使用符号“!”表示
阶乘运算,在计算过程中优先进行。
另外,可以使用函数Table、Sum和Product等来计算针对特定变量的迭代运算。
为了进一步控制运算次序,Mathematica还提供了不同级别的规则函数,例如:优先级运算规则、结合性运算规则和替换运算规则。
这些规则函数可以帮助用户自定义算法和优化运算过程。
总之,在Mathematica中,表达式的运算按照指数运算、乘法和除法运算,以及加法和减法运
算的顺序进行。
用户可以通过括号、特殊符号和函数,以及规则函数等来进一步控制运算次序,以满足复杂计算任务的需求。

Mathematica 软件使用简介Mathematica 是一个功能强大的常用数学软件, 它是由美国物理学家Stephen Wolfram领导的Wolfram Research公司用C语言开发的数学系统软件。
不但可以解决数学中的数值计算问题, 还可以解决符号演算问题, 并且能够方便地绘出各种函数图形。
这里介绍的命令可以适用于Windows操作系统的Mathematica2.2以上版本运行。
一、Mathematica 的进入/退出如果你的计算机已经安装了Mathematica 软件, 系统会在Windows【开始】菜单的【程序】子菜单中加入启动Mathematica命令的图标:图1.1 启动Mathematica用鼠标单击它就可以启动Mathematica系统进入Mathematica系统工作界面:图1.2 Mathematica2.2工作界面图图1.3 Mathematica4.0工作界面图Mathematica系统工作界面是基于Windows 环境下的Mathematica 函数或程序运行与结果显示的图形用户接口, 是Mathematica的工作屏幕。
界面上方的主菜单和工具条的功能类似于Windows中的Word软件。
其中的空白位置称为Notebook用户区, 在这里可以输入文本、实际的Mathematica命令和程序等来达到使用Mathematica的目的。
在用户区输入的内容被 Mathematica用一个具有扩展名为“.ma” (Mathematica2.2)或“.mb”(Mathematica4.0)在的文件名来纪录,该文件名是退出Mathematica时保存在用户区输入内容的默认文件名,一般是文件名:“Newnb-1.ma”或“Newnb-1.mb”。
退出Mathematica系统像关闭一个Word文件一样, 只要用鼠标点击Mathematica系统集成界面右上角的关闭按钮即可。
关闭前, 屏幕会出现一个对话框, 询问是否保存用户区的内容, 如果单击对话框的“否(N)”按钮, 则关闭Notebook窗口, 退出Mathematica系统; 如果单击对话框的“是(Y)”按钮, 则先提示你用一个具有扩展名为 .ma或.mb的文件名来保存用户区内的内容, 再退出Mathematica系统。

mathematica对数运算摘要:1.Mathematica 简介2.对数运算的定义与性质3.Mathematica 中的对数运算函数4.Mathematica 中对数运算的实例5.总结正文:【1.Mathematica 简介】Mathematica 是一款功能强大的数学软件,广泛应用于科学研究、工程设计以及教育等领域。
它具有丰富的函数库和强大的计算能力,可以方便地处理各种复杂的数学问题。
【2.对数运算的定义与性质】对数运算是数学中一种重要的运算方式,主要包括自然对数、常用对数和余对数等。
对数运算具有如下性质:1) 幂与对数的互反性:a^log_a(x) = x,其中a 为底数,x 为指数;2) 对数的乘法法则:log_a(x*y) = log_a(x) + log_a(y),其中a 为底数,x 和y 为指数;3) 对数的除法法则:log_a(x/y) = log_a(x) - log_a(y),其中a 为底数,x 和y 为指数;4) 对数的幂运算法则:log_a(x^n) = n*log_a(x),其中a 为底数,x 为指数,n 为整数。
【3.Mathematica 中的对数运算函数】在Mathematica 中,对数运算主要通过以下函数实现:1) 自然对数函数:Log[x],表示以自然常数e 为底,x 的对数;2) 常用对数函数:Log10[x],表示以10 为底,x 的对数;3) 余对数函数:LogMod[x, y],表示x 除以y 的余数,其中x 和y 均为正整数。
【4.Mathematica 中对数运算的实例】以下是Mathematica 中对数运算的一些实例:1) 计算自然对数:Log[27] = 3,表示27 的自然对数为3;2) 计算常用对数:Log10[1000] = 3,表示1000 的常用对数为3;3) 计算余对数:LogMod[13, 4] = 1,表示13 除以4 的余数为1;4) 对数运算法则的验证:Log[2^3] = 3*Log[2],表示对数的乘法法则成立;Log[6] - Log[3] = Log[2],表示对数的除法法则成立。
Mathematica是一种强大的数学符号计算系统,它可以进行符号运算、数值计算、绘图和数据分析等多种数学操作。
作为一种专业的数学软件,Mathematica在科学研究、工程设计和教育教学中被广泛应用,它为用户提供了丰富的功能和简洁的操作界面。
本文将介绍Mathematica中的符号运算功能,包括基本运算、方程求解、微积分计算、矩阵运算等内容,帮助读者更好地了解和使用这一强大的数学工具。
一、基本运算在Mathematica中,可以使用基本的运算符号进行加减乘除等计算。
输入表达式"a + b",Mathematica会自动进行加法运算并给出结果。
除了基本的四则运算外,Mathematica还支持幂运算、取余运算等操作,可以满足用户在数学计算中的各种需求。
二、方程求解Mathematica能够对各种类型的方程进行求解,包括线性方程、二次方程、多项式方程、常微分方程等。
用户可以通过输入方程表达式,使用Solve或NSolve等函数进行求解,得到方程的解析解或数值解。
Mathematica还支持对方程组进行求解,可以解决多元方程的求解问题。
三、微积分计算微积分是数学中重要的内容,Mathematica提供了丰富的微积分计算功能,包括求导、积分、极限、级数等操作。
用户可以通过输入函数表达式,使用D、Integrate、Limit等函数进行微积分计算,得到函数的导数、不定积分、定积分等结果。
这些功能在科学研究和工程设计中具有重要的应用价值。
四、矩阵运算矩阵运算是数学中常见的运算方式,Mathematica为用户提供了丰富的矩阵运算功能,包括矩阵乘法、转置、逆矩阵、特征值等操作。
用户可以通过输入矩阵表达式,使用Dot、Transpose、Inverse、Eigenvalues等函数进行矩阵运算,得到矩阵的乘积、转置矩阵、逆矩阵、特征值等结果。
这些功能上线性代数和数值分析中具有重要的应用价值。
第3章符号运算求解析解(公式解)的主要工具是符号运算,所谓符号运算是指运算的主要对象是符号、文字或变量。所进行的运算自然是指精确解公式中所需要的各种运算了。比如二次方程求根,被运算的主要对象是文字a、b、c,而不是具体的数值1、2、3,所进行的运算是加、减、乘、除、平方、开平方等。在符号运算中,表达式的变换是最基本的也是最常见的运算,例如对多项式进行展开、分解、集项或者化简等。
3.1 表达式的变换这里的表达式主要是指多项式与有理式(分式多项式),有时也可以是三角多项式等。
化简Simplify[表达式] 设法化简表达式,寻求等价的最简形式化简FullSimplify[表达式] 使用更广泛的变换化简表达式展开Expand[表达式] 展开分子,每项除以分母展开ExpandAll[表达式] 分子与分母完全展开分解Factor[表达式] 将表达式分解因式,表示为最简因式的乘积通分Together[表达式] 用于通分,把所有的项放在同一分母上,并化简约分Cancel[表达式] 用于约分,消去分式中分子和分母的公因式分项Apart[表达式] 将有理分式分解为一些最简分式之和集项Collect[表达式,某一个(或某几个)变量] 将表达式按照某一个(或某几个)变量的幂次进行集项【例1】化简下面各表达式。3.2 函数的极限求函数的极限需分为两种情况,一种是当x→a(a为一有限实数)时,函数f(x)→?,另一种是当x→∞(∞为无穷大记号,包括+∞与-∞)时f(x)→?,在数学里记为lim x→a f(x)=?与lim x→∞f(x)=?,而在Mathematica里记为Limit[f(x),x→a]与Limit[f(x),x →Infinity]。【例1】【例2】【例3】Note:(1)对某些函数,极限虽然存在,但利用Mathematica系统不一定能够求出来。(2)对某些函数,利用Mathematica系统虽然求出了极限,但却不能保证所得结果的正确性。3.3 导函数与偏导数3.3.1求导函数D[f(x),x]D[f(x),{x,n}]上面第一式是将f(x)对x求一阶导数,而第二式是将f(x)对x求n阶导数,式中的D是求导符号。3.3.2求偏导数D[f(x,y),x,y] 将f(x,y)先对x求导,再对y求导。D[f(x,y),{x,m},{y,n}] 将f(x,y)先对x求m 阶导数,再对y求n阶导数。3.4不定积分与定积分3.4.1不定积分求不定积分在数学里的符号是∫f(x)dx=F(x)+c在Mathematica系统中的符号是Integrate[f(x),x]=F(x) ( 将常数c略去不写 )式中Integrate是求不定积分的符号,f(x)为被积函数,x为积分变量。Note:在初等函数范围内,不定积分有时是不存在的,亦即当f(x)为初等函数,而∫f(x)dx却不一定是初等函数.Zhou er3.4.2 定积分Integrate[f(x),{x,a,b}]3.5 将函数展开为幂级数Series[f(x),{x,x0,n}]式中f(x)为给定的函数,x0为展开点的坐标,n为展开的项数Note: Normal[Expr] 去掉余项3.6 求和与求积求和 Sum[u n,{n,n1,n2}]求积 Product[u n,{n,n1,n2}]式中u n为通项,n为通项的项数,n1为起始项,n2为终止项,n2可以取有限数,也可以取Infinity(即+∞)。3.7 方程求根在Mathematica系统中为我们提供了求解各类代数方程精确解的求解函数Solve,它的调用格式如下Solve[代数方程(或方程组),未知量]3.8 常微分方程求解在Mathematica系统中,利用符号运算求解常微分方程的调用函数是DSolve,它的求解对象自然也是以线性常微分方程,特别是常系数线性常微分方程为主。利用DSolve函数求解微分方程的调用格式如下:求通解 DSolve[微分方程或方程组,未知函数,自变量]求特解 DSolve[{微分方程,初始条件},未知函数,自变量]3.9 偏微分方程求解(略)。