数独教程 数独选修课教材
- 格式:doc
- 大小:452.50 KB
- 文档页数:16

数独精品课件目录CONTENCT •数独简介与基本规则•初级解法与策略•中级解法与策略•高级解法与策略•难题挑战与解析•数独变种与拓展01数独简介与基本规则数独的起源与发展起源数独是一种源自18世纪瑞士的数学游戏。
发展日本将其发扬光大,并在20世纪80年代推出标准数独,使该游戏在全球流行开来。
现状数独已成为全球最受欢迎的智力游戏之一,拥有大量爱好者。
规则玩法目标基本规则与玩法介绍玩家需要根据已知的数字,通过逻辑推理和排除法,逐步填出所有空格的数字。
完成一个符合规则的数独盘面。
在9x9的盘面上,每行、每列和每个3x3的小宫格内均要填入1-9的数字,且不能重复。
候选数、区块、摒除法等。
术语常用技巧解题策略唯一解法、区块摒除法、数对占位法等。
先易后难,从可能性最少的空格入手,结合多种技巧进行推理。
030201术语解析及常用技巧02初级解法与策略应用场景当某个宫内的数字已经给出较多,剩余空格较少时,可以使用宫内排除法。
概念宫内排除法是指在某个宫内观察已经出现的数字,从而推断出该宫内其他空格应填的数字。
示例假设某宫内已经出现了数字1、2、3、4、6、7、8、9,那么该宫内剩余的空格就只能填数字5。
概念01行列排除法是指在某一行或某一列内观察已经出现的数字,从而推断出该行或该列内其他空格应填的数字。
应用场景02当某一行或某一列的数字已经给出较多,剩余空格较少时,可以使用行列排除法。
示例03假设某一行内已经出现了数字1、2、3、4、6、7、8,那么该行内剩余的空格就只能填数字5或9。
如果此时该行内还有一个空格位于一个宫内,且该宫内已经出现了数字5,那么该空格就只能填数字9。
概念应用场景示例区块排除法是指将数独盘面划分为3x3的区块,并在区块内观察已经出现的数字,从而推断出该区块内其他空格应填的数字。
当某个区块内的数字已经给出较多,剩余空格较少时,可以使用区块排除法。
假设某个区块内已经出现了数字1、2、3、4、6、7、8,那么该区块内剩余的空格就只能填数字5或9。




数独课程体系第一章:数独概述1.1 数独的定义和历史1.2 数独的基本规则1.3 数独的魅力和益智性第二章:数独基础技巧2.1 唯一候选数法2.1.1 唯一候选数的概念2.1.2 如何找到唯一候选数2.2 唯余候选数法2.2.1 唯余候选数的概念2.2.2 如何找到唯余候选数2.3 隐性唯余候选数法2.3.1 隐性唯余候选数的概念2.3.2 如何找到隐性唯余候选数 2.4 交叉排除法2.4.1 交叉排除法的概念2.4.2 如何应用交叉排除法第三章:数独进阶技巧3.1 块值排除法3.1.1 块值排除法的概念3.1.2 如何应用块值排除法 3.2 X-Wing法3.2.1 X-Wing法的概念3.2.2 如何应用X-Wing法3.3 XY-Wing法3.3.1 XY-Wing法的概念3.3.2 如何应用XY-Wing法 3.4 链数摒除法3.4.1 链数摒除法的概念3.4.2 如何应用链数摒除法第四章:高级数独技巧4.1 难题求解技巧4.1.1 多候选数法4.1.2 试错法4.1.3 隐性候选数法4.2 数独变体4.2.1 数独变体的种类和规则 4.2.2 如何解决数独变体第五章:数独解题策略5.1 解题思路和方法5.1.1 从易到难的解题顺序5.1.2 解题过程中的注意事项5.2 解题技巧和窍门5.2.1 如何快速解决数独难题5.2.2 如何提高解题效率第六章:数独竞赛技巧6.1 数独竞赛的要求和规则6.2 数独竞赛的解题策略6.2.1 如何在有限时间内解决难题6.2.2 如何应对竞赛中的压力6.3 数独竞赛的实战经验分享第七章:数独应用领域7.1 数独在教育中的应用7.1.1 数独对学生智力的培养作用7.1.2 如何在教学中引入数独7.2 数独在认知训练中的应用7.2.1 数独对认知能力的提升作用7.2.2 如何利用数独进行认知训练7.3 数独在老年人健脑中的应用7.3.1 数独对老年人脑功能的改善作用 7.3.2 如何在老年人中推广数独第八章:数独解题软件和工具8.1 数独解题软件的种类和功能8.2 如何选择和使用数独解题软件8.3 数独解题工具和技巧的介绍第九章:数独研究和创新9.1 数独研究的意义和价值9.2 数独创新的方法和途径9.3 数独研究和创新的案例分析第十章:数独乐趣和困惑10.1 数独给人们带来的乐趣和享受10.2 数独解题中常见的困惑和难点10.3 如何克服数独解题中的困惑通过以上的数独课程体系,学习者可以系统地学习和掌握数独的基础技巧、进阶技巧和高级技巧,了解数独的解题策略和方法,并深入研究数独在不同领域的应用。

数独教案基本项目课程名称:感受数独魅力授课对象:三到六年级学生课程类型:逻辑思维课,选修课教学材料:自编纲要教学时间:一学期,每周1课时,共18课时具体教学方案一、指导思想数学是神奇的世界,肯定有不少学生产生了浓厚的兴趣。
为此,训练学生的思维活动是重中之重。
数学思维活动在数学教学课堂中探求问题的思考、推理、论证的过程等一系列数学活动都是数学教学中实施思维训练的理论依据之一。
因此,开展校本数独课程,一是能更好的促进学生数学思维能力的发展,符合课改的要求;二是填补了我们课改中的弱项。
二、教学目标1、尊重学生的主体地位和主体人格,培养学生自主性、主动性,引导学生在掌握数学思维成果的过程中学会学习、学会创造。
2、将数学知识寓于游戏之中,教师适当穿针引线,把单调的数学过程变为艺术性的游戏活动,让学生在游戏中学习在玩中收获。
3、课堂上围绕“趣”字,把数学知识容于活动中,使学生在好奇中,在追求答案的过程中提高自己的观察能力,想象能力,分析能力和逻辑推理能力。
力求体现我们的智慧秘诀:“做数学,玩数学,学数学”。
三、教学措施1、结合教材,精选小学数学的教学内容,以适应社会发展和进一步学习的需要。
力求题材内容生活化,形式多样化,解题思路方程化,教学活动实践化。
2、教学内容的选编体现教与学的辨证统一。
教学内容呈现以心理学的知识为基础,符合儿童认知性和连续性的统一,使数学知识和技能的掌握与儿童思维发展能力相一致。
3、教学内容形式生动活泼,符合学生年龄特点,赋予启发性,趣味性和全面性,可以扩大学生的学习数学的积极性。
4、每次数学思维训练课都有中心,有讨论有交流有准备。
有阶段性总结和反思。
四、教学内容数独初级入门课程第一课数独的起源一、数独(sudoku)介绍是一种智力运动。
从字面意思来看,是“单独的数字”或“只出现一次的数字”,是一种以数字为表现形式的逻辑推理谜题。
数独 Sudoku(日语:数独すうどく)是一种源自18世纪末的瑞士,后在美国发展、并在日本得以发扬光大的数字智力拼图游戏。

数独教案第一章标准数独一、常见元素:盘面、格、行、列、宫、格的坐标、区二、规则:把数字1—9填入空格内,使每行、每列和每宫内的数字均不重复。
第二章宫内排除法利用排除原理,对每一个宫进行观察,选用某个相同的数字对同一个宫进行排除,最终得到该宫内只有一格可以填入该数字。
例题6 3 25 1 73 8 6 5 44 8 52 5 8 19 1 53 6 7 1 29 3 69 6 5第三章行列排除法利用排除原理,对一行或一列进行观察,选用某个相同的数字对同一行或同一列进行排除,最终得到该行或该列内只有一格可以填入该数字。
例题6 2 4 35 3 782 1 43 2 7 84 2 995 6 48 4 5 3第四章区块排除法利用排除原理,在某宫中形成一个区块(并排的2格或3格内比含有某个数字),再利用区块作为条件继续排除。
例题4 3 97 1 6 2 38 53 5 6 7 81 6 5 4 92 57 2 4 8 99 3 2第五章数对占位法数对(数组)的概念是同行、同列或同宫中,某两格(三格)内只能包含两个(三个)数字,而暂时还不能确定这两个(三个)数的具体位置,这时我们可以把这两个(三个)数字看做一个整体,占住那两格(三格),使其他数字不能填入这两格(三格),再用区块排除法填其他数字。
1、宫内隐形数对(数组)2、行列内隐形数对(数组)3、显性数对(数组)例题第六章唯一余数法唯一余数法简称唯余法,是利用同行、同列或同宫内数字不能重复的原理,使某一格内最终只剩下一个数字可填的方法。
具体情况是出现了8个不同的数字,且都对同一格影响,导致该格内不能再填这8个数,只能填入未出现的第9个数字。
1、行列唯余2、行或列与宫结合的唯余3、行、列、宫结合的唯一余数法例题第七章综合解法数独的解法和思路总的来说只划分为排除法和唯余法,而数对站位法等思路只是一种辅助构成可以运用排除或唯余的间接方法。
例题第八章模拟题第九章对角线数独第十章额外区域数独第十一章不规则数独第十二章奇数数独第十三章无马数独第十四章无缘数独第十五章同位数独第十六章杀手数独第十七章乘积数独第十八章模拟题。



数独教案第一章标准数独一、常见元素:盘而、格、行、列、宫、格的坐标、区二、规则:把数字1—9填入空格内,使每行、每列和每宫内的数字均不重复。
第二章宫内排除法利用排除原理,对每一个宫进行观察,选用某个相同的数字对同一个宫进行排除,最终得到该宫内只有一格可以填入该数字。
例题6 3 25 1 73 8 6 5 44 8 52 5 8 19 1 53 6 7 1 29 3 69 6 5第三章行列排除法利用排除原理,对一行或一列进行观察,选用某个相同的数字对同一行或同一列进行排除,最终得到该行或该列内只有一格可以填入该数字。
1 2 3 4 5 6 7 8 9A1 2 3 4 5 6 7 8 9例题第四章区块排除法利用排除原理,在某宫中形成一个区块(并排的2格或3格内比含有某个数字),再利用区块作为条件继续排除。
43 971 62 385 3 56 781 6 5 492 57 2 4 89 93 212 3 4 5 6 7 8 96 —61 2∣ 5∣6 A A O V OI第五章数对占位法数对(数组)的概念是同行、同列或同宫中,某两格(三格)内只能包含两个(三个)数字,而暂时还不能确定这两个(三个)数的具体位置,这时我们可以把这两个(三个)数字看做一个整体,占住那两格(三格),使其他数字不能填入这两格(三格),再用区块排除法填其他数字。
1、宫内隐形数对(数组)2、行列内隐形数对(数组)3. 显性数对(数组)例题第六章唯一余数法唯一余数法简称唯余法,是利用同行、同列或同宫内数字不能重复的原理,使某一格内最终只剩下一个数字可填的方法。
具体情况是出现了8个不同的数字,且都对同一格影响,导致该格内不能再填这8个数,只能填入未出现的第9个数字。
1、行列唯余2、行或列与宫结合的唯余3>行.列、宫结合的唯一余数法例题数独的解法和思路总的来说只划分为排除法和唯余法,而数对站位法等思路只是一种辅助构成可以运用排除或唯余的间接方法。
数独教案
第一章标准数独
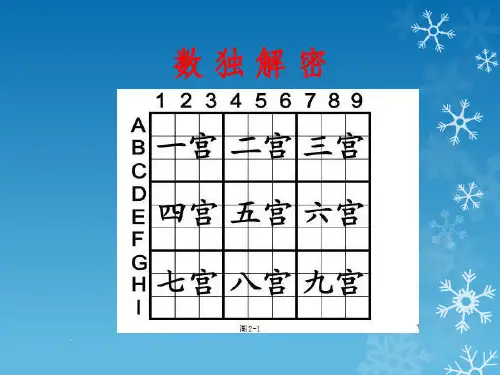
一、常见元素:盘面、格、行、列、宫、格的坐标、区
二、规则:把数字1—9填入空格,使每行、每列和每宫的数字均不
重复。
第二章宫排除法
利用排除原理,对每一个宫进行观察,选用某个相同的数字对同一个宫进行排除,最终得到该宫只有一格可以填入该数字。
第三章行列排除法
利用排除原理,对一行或一列进行观察,选用某个相同的数字对同一行或同一列进行排除,最终得到该行或该列只有一格可以填入该数字。
例题
第四章区块排除法
利用排除原理,在某宫中形成一个区块(并排的2格或3格比含有某个数字),再利用区块作为条件继续排除。
例题
第五章数对占位法
数对(数组)的概念是同行、同列或同宫中,某两格(三格)只能包含两个(三个)数字,而暂时还不能确定这两个(三个)数的具体位置,这时我们可以把这两个(三个)数字看做一个整体,占住那两格(三格),使其他数字不能填入这两格(三格),再用区块排除法填其他数字。
1、宫隐形数对(数组)
2、行列隐形数对(数组)
3、显性数对(数组)
例题
第六章唯一余数法
唯一余数法简称唯余法,是利用同行、同列或同宫数字不能重复的原理,使某一格最终只剩下一个数字可填的方法。
具体情况是出现了8个不同的数字,且都对同一格影响,导致该格不能再填这8个数,只能填入未出现的第9个数字。
1、行列唯余
2、行或列与宫结合的唯余
3、行、列、宫结合的唯一余数法
例题
第七章综合解法
数独的解法和思路总的来说只划分为排除法和唯余法,而数对站位法等思路只是一种辅助构成可以运用排除或唯余的间接方法。
例题
第八章模拟题
第九章对角线数独第十章额外区域数独
第十一章不规则数独第十二章奇数数独第十三章无马数独第十四章无缘数独第十五章同位数独第十六章杀手数独第十七章乘积数独第十八章模拟题。