材料力学(2)阶段性作业11.doc

第一章测试1【判断题】(10分)强度问题为构件抵抗破坏的能力。

A.错B.对2【判断题】(10分)材料力学的基本任务为强度、刚度和稳定性。

A.对B.错3【判断题】(10分)杆件的四种基本变形为轴向受拉、轴向受压、扭转和弯曲。

A.对B.错4【判断题】(10分)外力作用在杆件轴线上时发生轴向拉压变形。

A.错B.对5【单选题】(10分)材料力学的研究对象为？A.质点系B.刚体C.质点D.可变形固体6【单选题】(10分)在荷载作用下，构件应不至于破坏（断裂或失效），即具有抵抗破坏的能力。

这一问题属于？A.稳定性问题B.刚度问题C.强度问题7【单选题】(10分)在荷载作用下，构件所产生的变形应不超过工程上允许的范围，即具有抵抗变形的能力。

这一问题属于？A.稳定性问题B.强度问题C.刚度问题8【单选题】(10分)承受荷载作用时，构件在其原有形态下的平衡应保持为稳定的平衡。

这一问题属于？A.刚度问题B.强度问题C.稳定性问题9【单选题】(10分)构件的强度、刚度和稳定性问题均与所用材料的什么有关？A.受力状态B.构件体系特点C.力学性能10【多选题】(10分)材料力学的基本任务为？A.强度问题B.稳定性问题C.刚度问题第二章测试1【判断题】(10分)杆件轴力图的绘制方法可采用截面法，截面法步骤可分为一截二代三平衡，其中平衡方程中力的正负号与轴力正负号规定准则一致。

A.错B.对2【判断题】(10分)轴力图可以清晰展示轴力沿着杆件各个横截面内力的分布规律。

A.对B.错3【判断题】(10分)弹性模量的单位为帕A.错B.对4【判断题】(10分)拉压超静定问题求解过程中需补充变形协调方程。

A.错B.对5【判断题】(10分)静定结构构件体系在温度作用下也会产生温度内力和应力。

A.错B.对6【单选题】(10分)轴向拉压变形时，哪个截面上的切应力最大。

A.45度斜截面上B.横截面C.60度斜截面上D.30度斜截面上7【单选题】(10分)屈服阶段的强度指标为?A.屈服应力B.比例极限C.弹性极限D.强度极限8【单选题】(10分)轴向拉压变形会在横截面上产生何种应力分量？A.正应力B.全应力C.切应力9【多选题】(10分)轴向拉压变形时，斜截面应力分量包含有？A.切应力B.正应力10【多选题】(10分)低碳钢单轴拉伸时，应力应变关系曲线的弹性阶段包含？A.非比例阶段B.强化阶段C.线性比例阶段D.颈缩阶段第三章测试1【判断题】(10分)薄壁圆筒扭转时横截面形状与大小均发生变化A.错B.对2【判断题】(10分)圆轴扭转时，圆周线大小、形状和间距均保持不变。

第二章轴向拉(压变形[习题2-1]试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。

（a）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（b）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（c）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（d）解：（1）求指定截面上的轴力（2）作轴力图中间段的轴力方程为：轴力图如图所示。

[习题2-2]试求图示等直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。

若横截面面积，试求各横截面上的应力。

解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（3）计算各截面上的应力[习题2-3] 试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。

若横截面面积，，，并求各横截面上的应力。

解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（3）计算各截面上的应力[习题2-4] 图示一混合屋架结构的计算简图。

屋架的上弦用钢筋混凝土制成。

下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个的等边角钢。

已知屋面承受集度为的竖直均布荷载。

试求拉杆AE和EC横截面上的应力。

解：（1）求支座反力由结构的对称性可知：（2）求AE和EG杆的轴力①用假想的垂直截面把C铰和EG杆同时切断，取左部分为研究对象，其受力图如图所示。

由平衡条件可知：②以C节点为研究对象，其受力图如图所示。

由平平衡条件可得：（3）求拉杆AE和EG横截面上的应力查型钢表得单个等边角钢的面积为：[习题2-5] 石砌桥墩的墩身高，其横截面面尺寸如图所示。

荷载，材料的密度，试求墩身底部横截面上的压应力。

解：墩身底面的轴力为：墩身底面积：因为墩为轴向压缩构件，所以其底面上的正应力均匀分布。

[习题2-6]图示拉杆承受轴向拉力，杆的横截面面积。

如以表示斜截面与横截面的夹角，试求当时各斜截面上的正应力和切应力，并用图表示其方向。

解：斜截面上的正应力与切应力的公式为：式中，，把的数值代入以上二式得：轴向拉/压杆斜截面上的应力计算题目编号10000 100 0 100 100.0 0.0 习题2-6100 30 100 75.0 43.310000100 45 100 50.0 50.010000100 60 100 25.0 43.310000100 90 100 0.0 0.010000[习题2-7]一根等直杆受力如图所示。

材料力学性能课后习题答案1弹性比功：金属材料吸收弹性变形功的能力，一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。

2．滞弹性：金属材料在弹性范围内快速加载或卸载后，随时间延长产生附加弹性应变的现象称为滞弹性，也就是应变落后于应力的现象。

3．循环韧性：金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。

4．xx效应：金属材料经过预先加载产生少量塑性变形，卸载后再同向加载，规定残余伸长应力增加；反向加载，规定残余伸长应力降低的现象。

5．解理刻面：这种大致以晶粒大小为单位的解理面称为解理刻面。

6．塑性：金属材料断裂前发生不可逆永久（塑性）变形的能力。

韧性：指金属材料断裂前吸收塑性变形功和断裂功的能力。

7.解理台阶：当解理裂纹与螺型位错相遇时，便形成一个高度为b的台阶。

8.河流花样：解理台阶沿裂纹前端滑动而相互汇合,同号台阶相互汇合长大,当汇合台阶高度足够大时,便成为河流花样。

是解理台阶的一种标志。

9.解理面：是金属材料在一定条件下，当外加正应力达到一定数值后，以极快速率沿一定晶体学平面产生的穿晶断裂，因与大理石断裂类似，故称此种晶体学平面为解理面。

10.穿晶断裂：穿晶断裂的裂纹穿过晶内，可以是韧性断裂，也可以是脆性断裂。

沿晶断裂：裂纹沿晶界扩展，多数是脆性断裂。

11.韧脆转变：具有一定韧性的金属材料当低于某一温度点时，冲击吸收功明显下降，断裂方式由原来的韧性断裂变为脆性断裂，这种现象称为韧脆转变12.弹性不完整性：理想的弹性体是不存在的，多数工程材料弹性变形时，可能出现加载线与卸载线不重合、应变滞后于应力变化等现象,称之为弹性不完整性。

弹性不完整性现象包括包申格效应、弹性后效、弹性滞后和循环韧性等金属的弹性模量主要取决于什么因素？为什么说它是一个对组织不敏感的力学性能指标？答：主要决定于原子本性和晶格类型。

合金化、热处理、冷塑性变形等能够改变金属材料的组织形态和晶粒大小，但是不改变金属原子的本性和晶格类型。

第一章轴向拉伸与压缩一、填空题1-1杆件轴向拉伸或压缩时，其受力特点是：作用于杆件外力的合力的作用线与杆件轴线相________。

1-2轴向拉伸或压缩杆件的轴力垂直于杆件横截面，并通过截面________。

1-3当杆件受到轴向拉力时,其横截面轴力的方向总是________截面指向的。

1-4杆件轴向拉伸或压缩时,其横截面上的正应力是________分布的。

1-5在轴向拉伸或压缩杆件的横截面上的正应力相等过是由平面假设认为杆件各纵向纤维的变形大小都________而推断的。

1-6一铸铁直杆受轴向压缩时，其斜截面上的应力是________分布的。

1-7在轴向拉，压斜截面上，有正应力也有剪应力，在正应力为最大的截面上剪应力为________。

1-8杆件轴向拉伸或压缩时，其斜截面上剪应力随截面方位不同而不同，而剪应力的最大值发生在与轴线间的夹角为________的斜截面上。

1-9杆件轴向拉伸或压缩时，在平行于杆件轴线的纵向截面上，其应力值为________。

1-10胡克定律的应力适用范围若更精确地讲则就是应力不超过材料的________极限。

1-11杆件的弹必模量E表征了杆件材料抵抗弹性变形的能力，这说明杆件材料的弹性模量E值越大，其变形就越________。

1-12在国际单位制中，弹性模量E的单位为________。

1-13在应力不超过材料比例极限的范围内，若杆的抗拉（或抗压）刚度越________，则变形就越小。

1-14金属材料圆截面试样上中间等直部分试验段的长度L称为________，按它与直径d的关系l=5d者称短度样，而l=________d者称长试样。

1-15低碳钢试样据拉伸时，在初始阶段应力和应变成________关系，变形是弹性的，而这种弹性变形在卸载后能完全消失的特征一直要维持到应力为________极限的时候。

1-16在低碳钢的应力—应变图上，开始的一段直线与横坐标夹角为α，由此可知其正切tgα在数值上相当于低碳钢________的值。

2022-2023学年苏科版七年级数学上册第二次阶段性（1.1-6.1）综合训练题（附答案）一、单选题（共18分）1．下列运算正确的是（）A．﹣1+2＝3B．3×（﹣2）＝1C．﹣1﹣2＝﹣3D．﹣12020＝12．下列说法正确的是（）A．是单项式B．是单项式C．是单项式D．（a﹣b）2是单项式3．过度包装既浪费资源又污染环境．据测算，如果全国每年减少10%的过度包装纸用量，那么可减排二氧化碳3120000吨，把数3120000用科学记数法表示为（）A．3.12×105B．3.12×106C．31.2×105D．0.312×1074．已知关于y的方程y+3m＝24与y+4＝1的解相同，则m的值是（）A．9B．﹣9C．7D．﹣85．下面四个几何体中，同一个几何体的主视图和俯视图相同的共有（）A．1个B．2个C．3个D．4个6．如图所示，圆的周长为4个单位长度，在圆的4等分点处标上数字0，1，2，3，先让圆周上数字0所对应的点与数轴上的数﹣2所对应的点重合，再让圆沿着数轴按顺时针方向滚动，那么数轴上的数﹣2017将与圆周上的哪个数字重合（）A．0B．1C．2D．3二、填空题（共30分）7．比较大小：﹣．8．在x﹣3y＝3中，用含x的代数式表示y，得．9．已知a、b、c三个数在数轴上对应点的位置如图所示，下列几个判断：①a＜c＜b；②﹣a＜b；③a+b＞0；④c﹣a＜0中，错误的是（写序号）10．若m﹣n＝﹣1，则（m﹣n）2﹣2m+2n＝．11．若（a﹣2）x|a|﹣1﹣2＝0是关于x的一元一次方程，则a＝．12．一台电器原价是a元，按8折优惠出售，用式子表示现价为元．13．如图，将五角星沿虚线折叠，使得A，B，C，D，E五个点重合，得到的立体图形是．14．一个正方体的数字魔方的平面展开图如图所示，将它折成正方体，若每组对立面的代数式相等，则A＝．15．如图所示的某种玩具是由两个正方体用胶水黏合而成的，它们的棱长分别为1dm和2dm，为了美观，现要在其表面喷涂油漆，如果喷涂1dm2需用油漆4g，那么喷涂这个玩具共需油漆g．16．已知（a+1）2+|b+5|＝b+5，且|2a﹣b﹣1|＝1，则ab＝．三、解答题（共72分）17．计算：（1）﹣9+5﹣（﹣12）+（﹣3）；（2）8﹣（﹣4）÷22×3．18．解方程：（1）5（x﹣1）﹣2（1﹣x）＝3+2x．（2）﹣1＝．19．实数a、b在数轴上的位置如图所示，则化简2|a+b|﹣|a﹣b|．20．小王在解关于x的方程2a﹣2x＝15时，误将﹣2x看作+2x，得方程的解x＝3，求原方程的解．21．如图，是由7个棱长为1的小正方体组合成的简单几何体．（1）请画出这个几何体的三视图；（注：所画线条用黑色签字笔描黑）（2）该几何体的表面积（含下底面）为；（直接写出结果）（3）如果在这个几何体上再添加一些相同的小正方体，并保持这个几何体的主视图和俯视图不变，那么最多可以再添加个小正方体．22．如图，A、B、C、D四点不在同一直线上，读句画图．（1）画射线DA；（2）画直线BD；（3）连接BC；（4）延长BC，交射线DA的反向延长线于E；（5）在直线BD上找一点P，使得P A+PC的和最小，并简要说明理由．（保留作图痕迹）23．用一元一次方程解决问题：小芳的爸爸买了一箱苹果回家，小芳想分给家里的每一个人，如果每人分3个，就剩下3个苹果分不完，如果每人分4个，则还差2个苹果才够分，问小芳家有几个人？爸爸买了多少个苹果？24．定义：对于一个有理数x，我们把[x]称作x的对称数．若x≥0，则[x]＝x﹣2；若x＜0，则[x]＝x+2．例：[1]＝1﹣2＝﹣1，[﹣2]＝﹣2+2＝0．（1）求[]，[﹣1]的值；（2）已知有理数a＞0，b＜0，且满足[a]＝[b]，试求代数式（b﹣a）3﹣2a+2b的值；（3）解方程：[2x]+[x+1]＝1．25．一辆快车从甲地驶往乙地，一辆慢车从乙地驶往甲地，两车同时出发相向而行，并以各自的速度匀速行驶．1.5小时后两车相距70km；2小时后两车相遇．相遇时快车比慢车多行驶40km．（1）甲乙两地之间相距km；（2）求快车和慢车行驶的速度；（3）若快车到达乙地后立刻返回甲地，慢车到达甲地后停止行驶，快车出发多长时间，两车相距35km？26．在数轴上，点A表示的数为a，点B表示的数为b，且a、b满足|a+5|+（b﹣7）2＝0．其中O为原点，如图：（1）直接写出：a＝，b＝，A，B两点之间的距离为；（2）在数轴上有一动点M，若点M到点A的距离是点M到点B的距离的2倍，求点M 对应的数；（3）在数轴上有一动点P，动点P从点A出发第一次向左运动1个单位长度；然后在此位置进行第二次运动，向右运动2个单位长度；然后在此位置进行第三次运动，向左运动3个单位长度…；按照如此规律不断地进行左右运动，当运动到2021次时，求此时点P所对应的有理数．参考答案一、单选题（共18分）1．解：A、原式＝+（2﹣1）＝1，不符合题意；B、原式＝﹣3×2＝﹣6，不符合题意；C、原式＝﹣（1+2）＝﹣3，符合题意；D、原式＝﹣1，不符合题意．故选：C．2．解：A选项，分母中有未知数，不是整式，不是单项式，故该选项不符合题意；B选项，单独的一个数字是单项式，故该选项符合题意；C选项，是多项式，故该选项不符合题意；D选项，（a﹣b）2是多项式，故该选项不符合题意；故选：B．3．解：将3120000用科学记数法表示为：3.12×106．故选：B．4．解：y+4＝1，解得y＝﹣3，把y＝﹣3代入y+3m＝24，得3+3m＝24．解得m＝9，故选：A．5．解：圆柱主视图、俯视图分别是长方形、圆，主视图与俯视图不相同；圆锥主视图、俯视图分别是三角形、有圆心的圆，主视图与俯视图不相同；球主视图、俯视图都是圆，主视图与俯视图相同；正方体主视图、俯视图都是正方形，主视图与俯视图相同．共2个同一个几何体的主视图与俯视图相同．故选：B．6．解：圆在旋转的过程中，圆上的四个数，每旋转一周即循环一次，则与圆周上的0重合的数是﹣2，﹣6，﹣10…，即﹣（﹣2+4n），同理与3重合的数是：﹣（﹣1+4n），与2重合的数是﹣4n，与1重合的数是﹣（1+4n），其中n是正整数．而﹣2017＝﹣（1+4×504），∴数轴上的数﹣2017将与圆周上的数字1重合．故选：B．二、填空题（共30分）7．解：∵﹣＜0，＞0，∴﹣＜．故答案为：＜．8．解：∵x﹣3y＝3，∴y＝，故答案为：．9．解：由数轴上右边表示的数总大于左边表示的数，可知a＜c＜b．①正确；②a＜﹣2，则﹣a一定大于2，而b＜1，所以﹣a＞b，错误；③∵a＜0，b＞0，|a|＞|b|，∴a+b＜0，③错误；④∵a＜c，∴c﹣a＞0，错误．故答案为②③④．10．解：∵m﹣n＝﹣1，∴（m﹣n）2﹣2m+2n＝（m﹣n）2﹣2（m﹣n）＝（﹣1）2﹣2×（﹣1）＝1+2＝3．故答案为：3．11．解：（a﹣2）x|a|﹣1﹣2＝0是关于x的一元一次方程，∴a﹣2≠0，|a|﹣1＝1，解得a＝﹣2．故答案为：﹣2．12．解：由题意得：现价为：0.8a元，故答案为：0.8a．13．解：底面是五边形，侧面是三角形，实际上是正五棱锥的展开图，所以是正五棱锥．故答案为正五棱锥．14．解：∵每组对立面的代数式相等，∴x＝5，A＝3x﹣y，﹣x+2y＝3，∴y＝4，∴A＝3x﹣y＝3×5﹣4＝11．故答案为：11．15．解：玩具的表面积为：6×（2×2）+4×（1×1）＝28平方分米，所以喷涂这个玩具共需油漆28×4＝112克．故答案为：112．16．解：∵（a+1）2≥0，|b+5|≥0，∴b+5≥0，∴（a+1）2＝0，解得，a＝﹣1，则|﹣2﹣b﹣1|＝1，即|﹣b﹣3|＝1，∴﹣b﹣3＝±1，解得，b＝﹣4或﹣2，∴ab＝2或4，故答案为：2或4．三、解答题（共72分）17．解：（1）﹣9+5﹣（﹣12）+（﹣3）＝﹣9+5+12+（﹣3）＝5；（2）8﹣（﹣4）÷22×3＝8﹣（﹣4）÷4×3＝8+1×3＝8+3＝11．18．解：（1）去括号得：5x﹣5﹣2+2x＝3+2x，移项合并得：5x＝10，解得：x＝2；（2）去分母得：x+1﹣2＝2﹣3x，移项合并得：4x＝3，解得：x＝0.75．19．解：由数轴可知a＜0＜b，∵|b|＞|a|，∴b＞﹣a，∴a+b＞0，∴2|a+b|﹣|a﹣b|＝2（a+b）﹣（b﹣a）＝2a+2b﹣b+a＝b+3a．20．解：根据题意得：2a+6＝15，a＝，原方程为：9﹣2x＝15原方程的解是：x＝﹣3．21．解：（1）如图所示：；（2）（4×2+6×2+4×2）×（1×1）＝（8+12+8）×1＝28×1＝28故该几何体的表面积（含下底面）为28；（3）由分析可知，最多可以再添加2个小正方体．故答案为：28；2．22．解：图形如图所示．理由：两点间线段最短23．解：设小芳家有x个人，根据题意得3x+3＝4x﹣2，解得x＝5．3x+3＝3×5+3＝18．答：小芳家有5个人，爸爸买了18个苹果．24．解：（1）[]＝﹣2＝﹣，[﹣1]＝﹣1+2＝1；（2）a＞0，b＜0，[a]＝[b]，即a﹣2＝b+2，解得：a﹣b＝4，故（b﹣a）3﹣2a+2b＝（b﹣a）3﹣2（a﹣b）＝（﹣4）3﹣8＝﹣72；（3）当x≥0时，方程为：2x﹣2+x+1﹣2＝1，解得：x＝；当﹣1≤x＜0时，方程为：2x+2+x+1﹣2＝1，解得：x＝0（舍弃）；当x＜﹣1时，方程为：2x+2+x+1+2＝1，解得：x＝﹣；故方程的解为：x＝．25．解：（1）70÷（2﹣1.5）×2＝70÷0.5×2＝280（km）．答：甲乙两地之间相距280km；（2）（280÷2+40÷2）÷2＝160÷2＝80（km/h），（280÷2﹣40÷2）÷2＝120÷2＝60（km/h），故快车行驶的速度80 km/h，慢车行驶的速度60km/h．（3）设快车出发x小时，两车相距35km，①两车相遇前，相距35km，则有80x+35+60x＝280，解得x＝；②两车相遇后，相距35km，则有80x﹣35+60x＝280，解得x＝；③快车到达乙地后，慢车到达甲地前，相距35km，则有80x﹣280+35＝60x，解得x＝，因为慢车走完全程需要小时，＞，所以不合题意，舍去；④慢车到达甲地后，相距35km，则有80x+35＝280×2，解得x＝综上所述，小时或小时或小时，两车相距35km．故答案为：280．26．解：（1）由非负数的意义得：a+5＝0，b﹣7＝0，解得：a＝﹣5；b＝7，∴AB＝7﹣（﹣5）＝7+5＝12，故答案为：﹣5，7，12；（2）设点M对应的数为t，①当t＜﹣5时，AM＝2BM，此种情况不成立；②当﹣5≤t≤7时，AM＝2BM，则t+5＝2（7﹣t），解得：t＝3，③当t＞7时，AM＝2BM，则t+5＝2（t﹣7），解得：t＝19，综上，点M对应的数是3或19；（3）由题意得：﹣5﹣1+2﹣3+•﹣2021＝﹣5+（﹣1+2）+（﹣3+4）+•+（﹣2019+2020）﹣2021＝﹣5+1+1+•+1﹣2021＝﹣5+1010﹣2021＝﹣1016．此时点P所对应的有理数是﹣1016．。

东北农业大学网络教育学院材料力学网上作业题（2015更新版）绪论一、名词解释1.强度2. 刚度3. 稳定性4. 变形5. 杆件6.板或壳7.块体二、简答题1．构件有哪些分类？2. 材料力学的研究对象是什么？3. 材料力学的任务是什么？4. 可变形固体有哪些基本假设？5. 杆件变形有哪些基本形式？6. 杆件的几何基本特征？7.载荷的分类？8. 设计构件时首先应考虑什么问题？设计过程中存在哪些矛盾？第一章轴向拉伸和压缩一、名词解释1.内力2. 轴力3.应力4.应变5.正应力6.切应力7.伸长率8.断面收缩率9. 许用应力 10.轴向拉伸 11.冷作硬化二、简答题1.杆件轴向拉伸或压缩时，外力特点是什么？2.杆件轴向拉伸或压缩时，变形特点是什么？3. 截面法求解杆件内力时，有哪些步骤？4.内力与应力有什么区别？5.极限应力与许用应力有什么区别？6.变形与应变有什么区别？7.什么是名义屈服应力？8.低碳钢和铸铁在轴向拉伸时，有什么样的力学特性？9.强度计算时，一般有哪学步骤？10.什么是胡克定律？11.表示材料的强度指标有哪些？12.表示材料的刚度指标有哪些？13.什么是泊松比？14. 表示材料的塑性指标有哪些？15.拉压杆横截面正应力公式适用范围是什么？16.直杆轴向拉伸或压缩变形时，在推导横截面正应力公式时，进行什么假设？三、计算题1. 试用截面法求下列各杆指定截面的轴力。

2. 试用截面法求下列各杆指定截面的轴力。

3. 试用截面法求下列各杆指定截面的轴力。

4. 试用截面法求下列各杆指定截面的轴力。

5. 试用截面法求下列各杆指定截面的轴力。

6. 试用截面法求下列各杆指定截面的轴力。

7 高炉装料器中的大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示；拉杆上端螺纹的小径d = 175 mm。

已知作用于拉杆上的静拉力F=850 kN，试计算大钟拉杆横截面上的最大静应力。

8 一桅杆起重机如图所示，起重杆AB为一钢管，其外径D = 20 mm，内径d≈18 mm；钢绳CB的横截面面积为10 mm2。

一．是非题：（正确的在括号中打“√”、错误的打“×”） （60小题）1．材料力学研究的主要问题是微小弹性变形问题，因此在研究构件的平衡与运动时，可不计构件的变形。

( √ )2．构件的强度、刚度、稳定性与其所用材料的力学性质有关，而材料的力学性质又是通过试验测定的。

( √ )3．在载荷作用下，构件截面上某点处分布内力的集度，称为该点的应力。

(√ ) 4．在载荷作用下，构件所发生的形状和尺寸改变，均称为变形。

( √ )5．截面上某点处的总应力p 可分解为垂直于该截面的正应力σ和与该截面相切的剪应力τ，它们的单位相同。

( √ )6．线应变ε和剪应变γ都是度量构件内一点处变形程度的两个基本量，它们都是无量纲的量。

( √ ) 7．材料力学性质是指材料在外力作用下在强度方面表现出来的性能。

( )8．在强度计算中，塑性材料的极限应力是指比例极限p σ，而脆性材料的极限应力是指强度极限b σ。

( ) 9．低碳钢在常温静载下拉伸，若应力不超过屈服极限s σ，则正应力σ与线应变ε成正比，称这一关系为拉伸（或压缩）的虎克定律。

( )10．当应力不超过比例极限时，直杆的轴向变形与其轴力、杆的原长成正比，而与横截面面积成反比。

( √ )11．铸铁试件压缩时破坏断面与轴线大致成450，这是由压应力引起的缘故。

( )12．低碳钢拉伸时，当进入屈服阶段时，试件表面上出现与轴线成45o的滑移线，这是由最大剪应力max τ引起的，但拉断时截面仍为横截面，这是由最大拉应力max σ引起的。

( √ )13．杆件在拉伸或压缩时，任意截面上的剪应力均为零。

( ) 14．EA 称为材料的截面抗拉（或抗压）刚度。

( √ )15．解决超静定问题的关键是建立补充方程，而要建立的补充方程就必须研究构件的变形几何关系，称这种关系为变形协调关系。

( √ )16．因截面的骤然改变而使最小横截面上的应力有局部陡增的现象，称为应力集中。

(√ )17．对于剪切变形，在工程计算中通常只计算剪应力，并假设剪应力在剪切面内是均匀分布的。

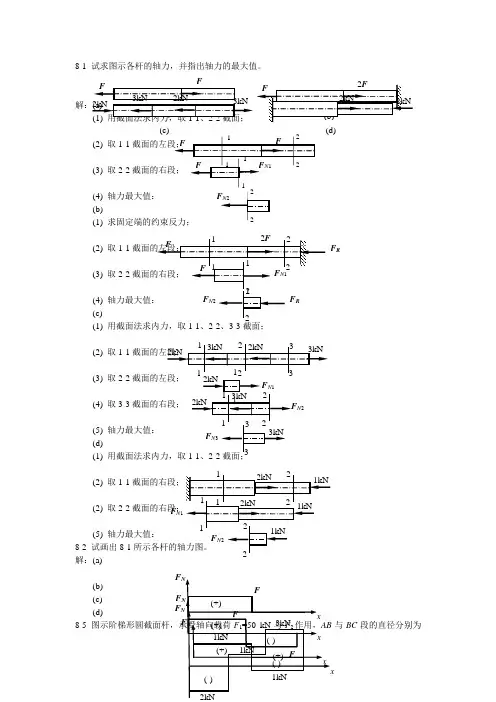
8-1 试求图示各杆的轴力，并指出轴力的最大值。

(2) 取1-1(3) 取2-2(4) 轴力最大值： (b)(1) 求固定端的约束反力； (2) 取1-1(3) 取2-2(4) (c)(1) 用截面法求内力，取1-1、2-2、3-3截面；(2) 取1-1(3) 取2-2 (4) 取3-3截面的右段；(5) 轴力最大值： (d)(1) 用截面法求内力，取1-1、(2) 取1-1(2) 取2-2(5) 轴力最大值： 8-2 试画出8-1解：(a) (b) (c) (d) 8-5与BC 段的直径分别为(c) (d)F RN 2F N 3 F N 1F F Fd 1=20 mm 和d 2=30 mm ，如欲使AB 与BC 段横截面上的正应力相同，试求载荷F 2之值。

解：(1) 用截面法求出(2) 求1-1、2-28-6 题8-5段的直径d 1=40 mm ，如欲使AB 与BC 段横截面上的正应力相同，试求BC 段的直径。

解：(1)用截面法求出1-1、2-2截面的轴力；(2) 求1-1、2-2截面的正应力，利用正应力相同；8-7 图示木杆，承受轴向载荷F =10 kN 作用，杆的横截面面积A =1000 mm 2，粘接面的方位角θ= 450，试计算该截面上的正应力与切应力，并画出应力的方向。

解：(1) (2) 8-14 2=20 mm ，两杆F =80 kN 作用，试校核桁架的强度。

解：(1) 对节点A(2) 列平衡方程 解得： (2) 8-15 图示桁架，杆1A 处承受铅直方向的载荷F 作用，F =50 kN ，钢的许用应力[σS ] =160 MPa ，木的许用应力[σW ] =10 MPa 。

解：(1) 对节点A (2) 84 mm 。

8-16 题8-14解：(1) 由8-14得到的关系；(2) 取[F ]=97.1 kN 。

8-18 图示阶梯形杆A 2=100 mm 2，E =200GPa ，试计算杆AC 的轴向变形 解：(1) (2) AC 8-22 图示桁架，杆1与杆2的横截面面积与材料均相同，在节点A 处承受载荷F 作用。

材料力学性能课后习题第一章1.解释下列名词①滞弹性：金属材料在弹性范围内快速加载或卸载后，随时间延长产生附加弹性应变的现象称为滞弹性，也就是应变落后于应力的现象。

②弹性比功：金属材料吸收弹性变形功的能力，一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。

③循环韧性：金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。

④包申格效应：金属材料经过预先加载产生少量塑性变形，卸载后再同向加载，规定残余伸长应力增加；反向加载，规定残余伸长应力降低的现象。

⑤塑性：金属材料断裂前发生不可逆永久（塑性）变形的能力。

⑥韧性：指金属材料断裂前吸收塑性变形功和断裂功的能力。

⑦加工硬化：金属材料在再结晶温度以下塑性变形时,由于晶粒发生滑移,出现位错的缠结,使晶粒拉长、破碎和纤维化,使金属的强度和硬度升高,塑性和韧性降低的现象。

⑧解理断裂：解理断裂是在正应力达到一定的数值后沿一定的晶体学平面产生的晶体学断裂。

2.解释下列力学性能指标的意义（1）E( 弹性模量）；（2）σp（规定非比例伸长应力）、σe（弹性极限）、σs（屈服强度）、σ0.2（规定残余伸长率为0.2%的应力）；（3）σb（抗拉强度）；（4）n（加工硬化指数）;（5）δ（断后伸长率）、ψ（断面收缩率）3.金属的弹性模量取决于什么？为什么说他是一个对结构不敏感的力学性能？取决于金属原子本性和晶格类型。

因为合金化、热处理、冷塑性变形对弹性模量的影响较小。

4.常用的标准试样有5倍和10倍，其延伸率分别用δ5和δ10表示，说明为什么δ5>δ10。

答：对于韧性金属材料，它的塑性变形量大于均匀塑性变形量，所以对于它的式样的比例，尺寸越短，它的断后伸长率越大。

5.某汽车弹簧，在未装满时已变形到最大位置，卸载后可完全恢复到原来状态；另一汽车弹簧，使用一段时间后，发现弹簧弓形越来越小，即产生了塑性变形，而且塑性变形量越来越大。

试分析这两种故障的本质及改变措施。