第4章光的偏振4(菲涅耳公式)_905507819

§1-6 菲涅耳公式一．菲涅耳公式电磁波通过不同介质的分界面时会发生反射和折射，在电动力学中将讲到入射、反射和折射三束波在分界面上振幅的大小和方向之间的关系，这一关系可由菲涅耳公式表达出来，上节提到的在反射过程中发生的半波损失问题，就可以用这个公式来解释，这一公式对以后讲到的许多光学现象，都能圆满地加以说明。

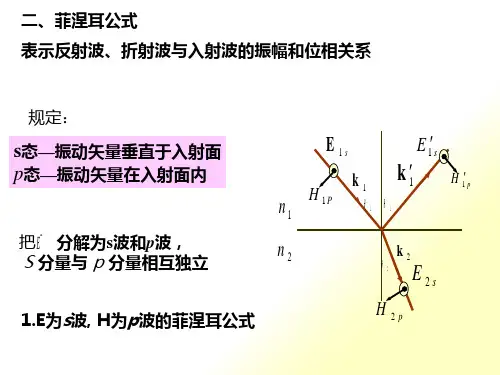
菲涅耳公式的内容说明如下：在任何时刻，我们都可以把入射波、反射波和折射波的电矢量分成两个分量，一个平行于入射面，另一个垂直于入射面。

有关各量的平等分量与垂直分量依次用指标P 和S 来表示。

以1i 、'1i 和2i 分别表示入射角、反射角和折射角，它们确定了各波的传播方向（在大多数情况下，只要注意各波的磁场矢量即可，因为知道了各个波的传播方向，各波的磁场矢量就可按右螺旋关系确定）。

以1A 、'1A 和2A 来依次表示入射波、反射波和折射波的电矢量的振幅，它们的分量相应就是1P A 、1'P A 、2P A 和1s A 、1's A 、2s A 。

由于三个波的传播方向各不相同，必须分别规定各分量的某一个方向作为正方向，这种规定当然是任意的。

但是只要在一个问题材的全部讨论过程中始终采取同一种正方向的选择，由此得到的各个关系式就具有普遍的意义，(a)(b)(图1-16)图1-16中xy 平面为两介质的分界面，z 轴为法线方向，xz 平面为入射面，规定电矢量的s 分量以沿着y +方向的为正，这对于入射、反射和折射三个波都相同，图中III II I 、、三个面依次表示入射、反射和折射三个波的波面。

电矢量的P 分量沿着这三个波面与入射面的交线，它们的正方向分别规定为如图1-16)()(b a 、所示，且S 分量、P 分量和传播方向三者构成右螺旋关系。

在传播过程中，电矢量的方向是在不断变化的，我们所注意的仅是在反射、折射过程这一瞬时的变化，所以菲涅耳公式所表示的有关各量的方向都是指紧靠两介质分界面O 点处而言的（在图中为清楚起见，将通过O 点的三个波面画III II I 、、画在离开O 点较远之处）。

菲涅尔积分公式
菲涅尔积分公式是光学和工程学中非常重要的公式之一，它用于描述光在两种不同介质之间反射和折射的过程。

这个公式是由物理学家和数学家奥古斯特·菲涅尔在19世纪初提出的，它基于光的波动理论，描述了光波在两种不同介质之间的传播行为。

菲涅尔积分公式包含两个部分：反射系数和折射系数。

反射系数用于描述光在两种不同介质之间的反射行为，而折射系数用于描述光在两种不同介质之间的折射行为。

这两个系数都与入射角、反射角和折射角有关，同时也与两种介质的折射率有关。

反射系数和折射系数的具体形式如下：
1. 反射系数R = (n2 * sinθi - n1 * sinθt) / (n2 * sinθi + n1 * sinθt)，其中n1 和n2 分别是两种介质的折射率，θi 和θt 分别是入射角和反射角。

2. 折射系数T = 2 * n1 * sinθi / (n2 * sinθt + n1 * sinθi)，其中n1 和n2 分别是两种介质的折射率，θi 和θt 分别是入射角和折射角。

在光学和工程学中，菲涅尔积分公式被广泛应用于计算光在各种不同介质之间的反射和折射行为。

这个公式对于光学设计、成像系统分析、光学仪器制造等领域非常重要。

除了菲涅尔积分公式外，还有许多其他公式和定理用于描述光的行为，例如斯涅尔定律、反射定理、折射定理等。

这些公式和定理都是基于光的波动理论或量子理论，是光学和工程学领域的重要工具。

综上所述，菲涅尔积分公式是一个重要的公式，用于描述光在两种不同介质之间反射和折射的行为。

它基于光的波动理论，包含反射系数和折射系数两个部分，对于光学设计和工程学领域非常重要。

大学物理光的偏振光在传播过程中，电矢量在垂直于传播方向上的两个相互垂直的分量分别称为水平分量H和垂直分量V，偏离这两个垂直分量的光波称为偏振光。

光波的偏振现象在光学中具有重要的应用价值。

自然光：具有垂直于传播方向的上、下两个偏振分量，两分量均在垂直于传播方向的平面内振动。

椭圆偏振光：在垂直于传播方向的平面内，除有一个与传播方向垂直的振动分量外，尚有与传播方向成一定夹角的振动分量。

圆偏振光：在垂直于传播方向的平面内，两个相互垂直的振动分量都与传播方向成一定夹角，且相位差为π/2。

尼科耳棱镜：其作用是将入射光从其他偏振状态转变成透过偏振片后的直线偏振光。

渥拉斯顿棱镜：其作用是将入射的非偏振光分成两束相干光波，其中一束光的振动方向与入射光的振动方向垂直，以透射光的形式出现；另一束光的振动方向与入射光的振动方向平行，以反射光的形式出现。

当两束偏振方向平行的线偏振光经过一个偏振片后，透射光为线偏振光，其偏振方向与入射光的偏振方向一致；当两束偏振方向垂直的线偏振光经过一个偏振片后，透射光为暗条纹。

当两束线偏振光的偏振方向既不平行也不垂直时，透射光将出现明暗相间的条纹，这种条纹称为椭圆偏振光的干涉条纹。

当两束椭圆偏振光的旋转方向相反时，透射光仍将出现明暗相间的条纹，且旋转方向相反。

当两束椭圆偏振光的旋转方向相透射光将出现圆偏振光的干涉条纹。

在物理学中，光的干涉是一个非常重要的概念，它描述了两个或多个光波叠加时产生的明暗条纹和相消干涉的现象。

这个概念最早由英国物理学家托马斯·杨在19世纪初提出，后来被广泛应用到光学、波动力学和其他领域。

光的干涉现象可以被分为两类：时间域干涉和空间域干涉。

时间域干涉指的是两个或多个光波在时间上同步抵达某一点，而空间域干涉则指的是两个或多个光波在空间中不同位置的叠加。

干涉现象的原理在于，当两个或多个光波的波峰或波谷完全重叠时，它们会相互增强，产生明亮的干涉条纹。

而当波峰与波谷相遇时，它们会相互抵消，产生暗的干涉条纹。

光学光的偏振和菲涅尔公式的实际应用在光学领域，光的偏振现象一直是一个备受关注的话题。

光的偏振是指光的电矢量在空间中的方向性特征。

而与偏振相关的菲涅尔公式则是描述光在介质边界上的反射和折射现象的重要公式。

本文将重点探讨光的偏振特性以及菲涅尔公式的实际应用。

一、光的偏振特性光的偏振是指光的电矢量在空间中的方向性特征。

正常情况下，自然光是无偏振光，其电矢量在各个方向上都有相同的强度和方向。

然而，通过特定的介质或装置，如偏振片或波片，可以将无偏振光转换成具有特定偏振方向的偏振光。

偏振光可以分为线偏振光和圆偏振光两种。

线偏振光是指光的电矢量在传播过程中只沿着一条直线方向振动的光。

通常，线偏振光可以分为水平偏振光、垂直偏振光、倾斜偏振光等几种。

线偏振光在许多领域有着广泛的应用，例如液晶显示器、偏振墨镜等。

圆偏振光是指光的电矢量在传播过程中绕光束方向旋转的光。

圆偏振光可以进一步分为左旋圆偏振光和右旋圆偏振光两种。

圆偏振光的独特性质使其在生物医学成像、光通信等领域有着重要的应用。

二、菲涅尔公式的实际应用菲涅尔公式是描述光在介质边界上的反射和折射现象的重要公式。

它由法国物理学家菲涅尔于19世纪提出，被广泛应用于光学测量、光学薄膜设计、遥感等领域。

1. 光学测量菲涅尔公式在光学测量中扮演着重要的角色。

例如，通过测量材料的反射光强度和入射光强度的变化，可以利用菲涅尔公式来计算材料的光学性质，例如折射率和厚度。

这种基于菲涅尔公式的测量方法在材料研究和光学器件表征中得到广泛应用。

2. 光学薄膜设计菲涅尔公式在光学薄膜设计中起到了关键作用。

光学薄膜是通过沉积一层或多层光学介质来改变光的传输特性。

通过菲涅尔公式可以计算出反射和透射的光强度以及相位差，从而实现对薄膜的设计和优化。

光学薄膜广泛应用于激光器、光学镜片以及太阳能电池等领域。

3. 遥感菲涅尔公式在遥感领域也有着重要应用。

遥感技术通过检测地面或大气中的光辐射信息，获取地质、气象等相关数据。

光的衍射与菲涅尔衍射公式光的衍射是指光通过一个或多个小孔后，产生的波的传播现象。

它是光的波动性质的一种表现，也是研究光的重要原理之一。

菲涅尔衍射公式是用来计算光的衍射现象的数学表达式，它是基于菲涅尔衍射原理和赫兹互衍原理推导得出的。

1. 衍射的基本原理光的衍射是基于光的波动性质，当光通过一个孔或者绕过一个物体时，波的振幅将发生变化，从而导致光的传播方向和强度的变化。

根据衍射的基本原理，可以推导出光的衍射公式。

2. 菲涅尔衍射公式的推导假设光通过一个孔或绕过一个物体后，在衍射屏上形成一系列衍射波阵列，每个波的振幅和相位都会受到影响。

根据菲涅尔衍射原理和赫兹互衍原理，可以得到菲涅尔衍射公式：A = (A1 + A2)e^(ikr)/r其中，A表示在衍射屏上的某一点的光强度（振幅的平方），A1和A2分别表示入射波和散射波的振幅，k是波矢量，r是衍射点到源点的距离。

3. 菲涅尔衍射公式的应用菲涅尔衍射公式可以用于计算不同形状和大小的开孔、物体或间隙对光的衍射效应。

通过将衍射公式应用于实际情况，我们可以计算光的衍射现象，并预测光的传播方向和强度的变化。

4. 衍射的实际应用光的衍射在许多领域都有重要的应用，例如光学显微镜、天文学、图像处理等。

通过掌握和应用衍射原理和衍射公式，人们可以改善光学仪器的性能，提高光学成像的分辨率，并且在物理学和工程学领域有更深入的研究。

5. 总结光的衍射是光的波动性质的一种表现，通过菲涅尔衍射公式可以定量地计算光的衍射效应。

菲涅尔衍射公式基于菲涅尔衍射原理和赫兹互衍原理推导而来，并广泛应用于光学领域的实际问题。

衍射现象的研究和应用有助于改善光学仪器性能，并在科学研究和工程实践中发挥重要作用。

（总字数：241）。