角动量守恒例题上课讲义

第四章角动量守恒定律基本要求：1. 明确力矩的物理涵义，掌握力矩的一般定义，并能从力矩的一般定义中得出力对某轴的力矩的表达式；2. 掌握质点的角动量的物理涵义，能熟练地推导在一般情况下的质点角动量定理，以及对轴的角动量定理；3. 理解角动量守恒定律的物理内容和定律的适用条件，并能运用这个定律解释有关现象。

§4-1力矩一、力矩的一般意义1、引入对于一个静止的质点来说, 当它受到力的作用时，将开始运动；但对于物体的转动而言, 当它受到外力作用时, 可能转动, 也可能不转动, 这决定于此外力是否产生力矩。

外力产生力矩，物体就转动, 不产生力矩，物体则不转动。

所以, 力矩对物体转动所起的作用, 与力对质点运动所起的作用是类似的。

2、定义在一般意义上，力矩是对某一参考点而言的。

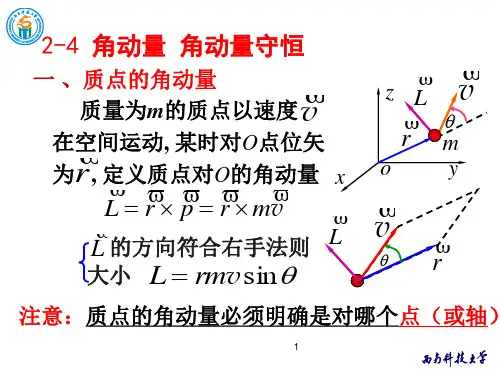
如果质点p在坐标系o-xyz中的位置矢量是r (见图4-1), 那么作用于质点的力f相对于参考点o所产生的力矩，就定义为(4-1)显然，m必定垂直于由矢量r和f所决定的平面, m的指向应由右手定则确定：右手的四指由r的方向经小于 π的角转向f的方向，伸直的拇指所指的方向就是力矩m的方向。

m的大小等于以r和f为邻边的平行四边形的面积，即(4-2)式中θ是r与f之间的夹角。

在国际单位制中，力矩的单位是n ⋅ m (牛顿⋅米)。

3、合力情况合力对某参考点o的力矩等于各分力对同一点力矩的矢量之和：由力矩的定义式(4-1)可以看到, 力矩m与质点的位置矢量r有关, 也就是与参考点o的选取有关。

对于同样的作用力f, 选择不同的参考点, 力矩m的大小和方向都会不同。

为了表示力矩m是相对于参考点o的, 所以一般在画图时总是把力矩m画在参考点o 上, 而不是画在质点p上, 如图4-1所表示的那样。

如果作用于质点上的力f是多个力的合力, 即f = f1+ f2 + …+ f n ,代入式(4-1)中, 得=r⨯f1+ r⨯f2+ … + r⨯f n= m1+ m2 + … + m n(4-3)这表示, 合力对某参考点o的力矩等于各分力对同一点力矩的矢量之和。

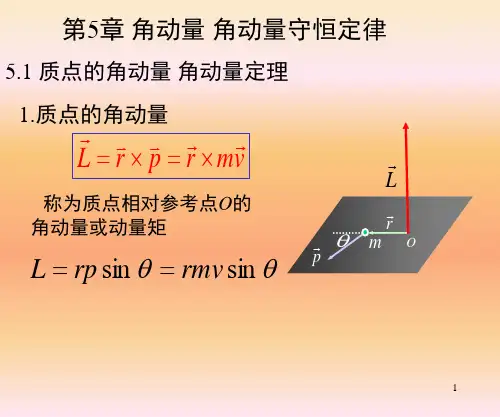
第四讲 角动量守恒定律 2018.10.25一、角动量的概念类似于力对转轴的矩（力矩），我们引入动量对轴的矩，称为动量矩，也称角动量。

如右图，质点对点O 的角动量为αs i n m r v p r J =⨯= 对于绕固定轴转动的刚体，如右图，设其在某时刻转动的角速度为ω，刚体上某一质点的质量为i m ，它到轴的距离为i r ，则其动量大小为ωi i r m ，则整个刚体对转轴的角动量为 ∑∑==⋅=ωωωI r m r m r J ii i i 2 二、角动量定理由刚体绕定轴转动的转动定理可知βI M =，则ωβ∆=∆=∆I t I t M上式中t M ∆描述了力矩对时间的累积效应，称为冲量矩，用L 表示。

由于刚体定轴转动时转动惯量I 为恒量，故J I I ∆=∆=∆)(ωω，所以J L ∆=上式表明，合外力对刚体的冲量矩等于这段时间内刚体角动量的增量，称为角动量定理。

角动量定理不仅适用于刚体，对非刚体也可采用，这时物体对转轴的转动惯量不是恒量，前式应写成 1122ωωI I L -=三、角动量守恒定律如果物体受到的合力矩为零，即∑=0M ，则其冲量矩也为零，这有恒量=J这就是说，一个物体（系统），如果所受的外力对固定轴的力矩之矢量和为零，则该物体（系统）对该固定轴的角动量不变，这就是角动量守恒定律。

需要注意的是，角动量守恒定律适用于惯性系和质心系，对其它非惯性系，要引入惯性力矩，一般角动量不守恒。

因而不能直接在非惯性系中应用角动量守恒定律。

[例1]如图所示，一个半径为R 、内表面光滑的半球面固定在地面上，开口水平朝上。

一小滑块在半球面内侧最高点处获得沿球面的水平速度0v 。

忽略空气阻力。

求滑块在此后运动过程中的最大速率。

[例2]如图所示，一质量分布均匀的刚性螺旋环的质量为m，半径为R，螺距H=πR，可绕竖直的对称轴OO′无摩擦地转动，连接螺旋环与转轴的两支撑杆的质量可忽略不计．一质量也为m的小球穿在螺旋环上并可沿螺旋环无摩擦地滑动，首先扶住小球使其静止于螺旋环上的某一点A，这时螺旋环也处于静止状态．然后放开小球，让小球沿螺旋环下滑，螺旋环便绕转轴OO′转动．求当小球下滑到离其初始位置沿竖直方向的距离为h时，螺旋环转动的角速度和小球对螺旋环作用力的大小．[练习]如图，在水平的光滑桌面上开有一小孔，一条绳穿过小孔，其两端各系一质量为m 的小球。

长为L 的均匀直棒，质量为M ，上端用光滑水平轴吊起静止下垂。

今有一质量为m 的子弹，以水平速度v 0 射入杆的悬点下距离为a 处而不复出。

（1）子弹刚停在杆中时杆的角速度多大？（2）子弹冲入杆的过程中（经历时间为Δt ），杆上端受轴的水平和竖直分力各多大？（3）要想使杆上端不受水平力，则子弹应在何处击中杆？解：把子弹和杆看作一个系统。

系统所受的力有重力和轴对杆的约束力。

在子弹射入杆的极短时间内，重力和约束力均通过轴，因而它们对轴的力矩均为零，系统的角动量守恒，于是有ω)31(220ma Ml a mv +=22033ma ML amv +=∴ω（2）解法1：对子弹与杆系统，根据动量定理，在水平方向有0p p t F x -=∆ωωmd lM mv Mv p mv p c +=+==2,00t vm t ma l M F x ∆-∆+=∴0)2(ω此即为轴在水平方对杆上端的作用力，与v 0的方向相反。

在竖直方向上有222)(ωωmd lM g m M F y +=+-)(222g d m Mg lM F y +++=∴ωω如略去m ，则 Mg l M F y +=22ω（2）解法2：子弹冲入杆的过程中，子弹受杆的阻力的大小为：t mv ma t mv mv f ∆-=∆-=00'ω杆受子弹的水平冲力为 t ma mv f f ∆-=-=ω0'对杆用质心运动定律t lM Ma f F C x ∆==+2ω )2(lt r a t t ∆==∆=∴∆=ωαωααωt v m t ma lM Ma f F C x ∆-∆+=+-=∴0)2(ω此即为轴在水平方对杆上端的作用力，与v 0的方向相反。

在竖直方向上有222)(ωωmd l M g m M F y +=+- )(222g d m Mg l M F y +++=∴ωω 如略去m ，则 Mg l M F y +=22ω（3）由0=∴x F 可得：m MLv a 20-=ω 将22033md ML amv +=ω代入得m Mlmd Ml ma a 23322-+=解得l a 32=。