数值计算流程与概况

第 1 卷 第 10 期 2006 年 4 月数值计算与工程仿真 Numerical Calculation and Engineering SimulationVol.1 No.10 Apr,2006《数值计算与工程仿真》改版公告清洁能源网——计算流体力学应用与工程仿真技术讨论区经过三年多的发 展，已经成为本领域内具有一定影响力的专题网络论坛。

而其内部交流刊物 《数值计算与工程仿真》电子期刊在广大会员的支持和鼓励下也已经成功发行 了九期，该期刊已经成为广大从事数值仿真的朋友共同学习，交流信息和沟通 思想的一个重要平台。

通过网络期刊，我们可以使一个共性的问题被完整而详 细的得到解释与记录；通过网络期刊，我们可以使讨论中出现的问题得到及时 地总结与固化，从而使不同的人，可以方便快捷的找到他所关心的问题；通过 网络期刊，我们可以使不同的人的经验与总结聚集在一起，从而使更多的人能 够分享到这种经验及总结，以及轻易解决相同问题后的喜悦和欢愉。

因此得到 了广大讨论区会员朋友的喜爱和支持，他们也都踊跃投稿，为网络期刊的发展 做出自己的一份贡献。

但是随着论坛的发展壮大和讨论的深入，我们的杂志也亟待迈向更高的目 标。

为了拓宽交流对象和讨论的内容，让更多的人参与到我们的学术讨论中 来，使《数值计算与工程仿真》真正地成为我们科研和学习的良师益友，也为 了更好地体现我们的办刊宗旨，切实提高国内 CFD 的应用水平。

我们将从第十 期开始对期刊进行全面改版，关于改版后的具体说明见下文。

一、栏目设置基于我们的办刊宗旨，栏目设置和内容选择力求实用性强、经验性强、工 程性强。

我们除根据前几期的成功经验，继续选择紧密围绕大家关心的典型问 题和共性问题展开外，每期还计划收录一些经典算例和对论坛上会员提出的经 典问题和答案的整理。

同时，改版后的期刊将增加基础理论，名师风采以及软 件介绍等栏目，使期刊内容更丰富，更正规。

栏目 基本概念 专家专访 企业动态（软件介绍） 特约稿件 论坛集萃 算例分析 理论进展（文献翻译） 栏目内容 基础性概念，理论 专家简介，及专家从事领域、专家推荐文章 企业仿真部门概况，软件最新进展 对外约稿 整理论坛讨论有深度的精华贴 某个问题计算过程中的经验总结 介绍理论上的研究进展— 1 — 清洁能源网版权所有第 1 卷 第 10 期 2006 年 4 月数值计算与工程仿真 Numerical Calculation and Engineering SimulationVol.1 No.10 Apr,2006由于改版后刊物增加了“特约稿件”的栏目，主要发表向论坛会员的约 稿。

油藏数值模拟培训_历史拟合的流程和⽅法历史拟合的流程和⽅法3.1历史拟合⽬的及意义应⽤数值模拟⽅法计算油藏动态时，由于⼈们对油藏地质情况的认识还存在着⼀定的局限性。

在模拟计算中所使⽤的油层物性参数，不⼀定能准确地反映油藏的实际情况。

因此，模拟计算结果与实际观测到的油藏动态情况仍然会存在⼀定的差异，有时甚⾄相差悬殊。

在这个基础上所进⾏的动态预测，也必定不完全准确，甚⾄会导致错误的结论。

为了减少这种差异，使动态预测尽可能接近于实际情况，现在在对油藏进⾏实际模拟的全过程中⼴泛使⽤历史拟合⽅法。

所谓历史拟合⽅法就是先⽤所录取的地层静态参数来计算油藏开发过程中主要动态指标变化的历史，把计算的结果与所观测到的油藏或油井的主要动态指标例如压⼒、产量、⽓油⽐、含⽔等进⾏对⽐，如果发现两者之间有较⼤差异，⽽使⽤的数学模型⼜正确⽆误，则说明模拟时所⽤的静态参数不符合油藏的实际情况。

这时，就必须根据地层静态参数与压⼒、产量、⽓油⽐、含⽔等动态参数的相关关系，来对所使⽤的油层静态参数作相应的修改，然后⽤修改后的油层参数再次进⾏计算并进⾏对⽐。

如果仍有差异，则再次进⾏修改。

这样进⾏下去，直到计算结果与实测动态参数相当接近，达到允许的误差范围为⽌。

这时从⼯程应⽤的⾓度来说，可以认为经过若⼲次修改后的油层参数，与油层实际情况已⽐较接近，使⽤这些油层参数来进⾏抽藏开发的动态预测可以达到较⾼的精度。

这种对油藏的动态变化历史进⾏反复拟合计算的⽅法就称为历史拟合⽅法。

综上所述历史拟合过程也是通过动态资料及数值模拟⽅法对油藏进⾏再认识的过程。

历史拟合流程图3.2基础数据及模型参数检查油藏模拟模型的数据很多，⼀般来说，少则⼏万，多则⼗⼏万到⼏⼗万数据。

出错的可能性很⼤，甚⾄是不可避免的。

在正式进⾏拟合之前对模型数据必须进⾏全⾯细致的检查。

模拟器⾃动检查：(1)各项参数上下界检查，发现某⼀参数越界打出错误信息。

(2)平衡检查。

在全部模拟井的产率(或注⼊率)都指定为零的情况下，进⾏⼀次模拟计算，模拟的时间应⼤于或等于油藏已经开发的时间(或历史拟合的时间)加上准备动态预测的时间。

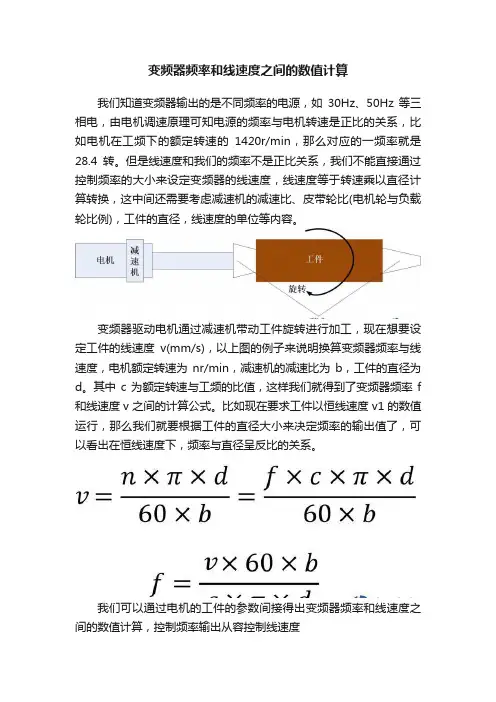
变频器频率和线速度之间的数值计算
我们知道变频器输出的是不同频率的电源，如30Hz、50Hz等三相电，由电机调速原理可知电源的频率与电机转速是正比的关系，比如电机在工频下的额定转速的1420r/min，那么对应的一频率就是28.4转。

但是线速度和我们的频率不是正比关系，我们不能直接通过控制频率的大小来设定变频器的线速度，线速度等于转速乘以直径计算转换，这中间还需要考虑减速机的减速比、皮带轮比(电机轮与负载轮比例)，工件的直径，线速度的单位等内容。

变频器驱动电机通过减速机带动工件旋转进行加工，现在想要设定工件的线速度v(mm/s)，以上图的例子来说明换算变频器频率与线速度，电机额定转速为nr/min，减速机的减速比为b，工件的直径为d。

其中c为额定转速与工频的比值，这样我们就得到了变频器频率f 和线速度v之间的计算公式。

比如现在要求工件以恒线速度v1的数值运行，那么我们就要根据工件的直径大小来决定频率的输出值了，可以看出在恒线速度下，频率与直径呈反比的关系。

我们可以通过电机的工件的参数间接得出变频器频率和线速度之间的数值计算，控制频率输出从容控制线速度。

§3 牛顿迭代法Newton Iteration————切线法牛顿迭代法是最著名的方程求根方法。

已经通过各种方式把它推广到解其他更为困难的非线性问题。

【例如】非线性方程组、非线性积分方程和非线性微分方程。

虽然牛顿法对于给定的问题不一定总是最好的方法，但它的简单形式和快的收敛速度常常使得解非线性问题的人优先考虑它。

迭代一般理论告诉我们，构造好的迭代函数可使收敛速度提高。

然而迭代函数的构造方法又各不相同，方法多样。

牛顿法是受几何直观启发，给出构造迭代函数的一条重要途径。

牛顿迭代的基本思想:方程f(x)=0的根，几何意义是曲线y=f(x)与ox轴y=0的交点。

求曲线与y=0的交点没有普遍的公式，但直接与0x 轴的交点容易计算。

用直线近似曲线y=f(x)，从而用直线方程的根逐步代替f(x)=0的根。

即把非线性方程逐步线性化。

方法：设x k是f(x)=0的一个近似根，把f(x)在x k处作一阶Taylor 展开，得到))(()()(k k k x x x f x f x f -'+≈ （19）设)(k x f '≠0，由于0)())(()(=≈-'+x f x x x f x f k k k所以求得解记为1+k x ，有牛顿迭代公式：（20） 按牛顿迭代计算称为牛顿迭代法。

牛顿法的几何意义：选初值x k 以后，过))(,(k k x f x p 点，作曲线y=f(x)的切线，其切线方程为))(()()(k k k x x x f x f x f -'+= (21)切线与ox 轴的交点，为1+k x ，则)(/)(1k k k k x f x f x x '-=+（22）牛顿迭代法也称为切线法。

迭代法的收敛性：如果取)(/)()(k k x f x f x x g '-=，则有x=g(x)，从而牛顿迭代公式就是)(1k k x g x =+因此就可以由考察g(x)的性质，来讨论迭代法的收敛性及收敛速度。

excel中如何准确复制公式计算出的数值
excel中，我们用公式计算出来的数据，一旦它的位置发生变化，数值也会变，比如数据求和，我们要想把求和的结果复制走，会发现数值变了，这时就是我们应该注意的地方。

方法/步骤
首先我们找到excel表格
双击打开它
我们找一组数据过来
然后全部选中，注意要多选中下方一个单元格，同时点击求和标志
我们可以发现每一列数据都得到了它们相应的数据之和
但当我们复制这个最后数据时，结果发生了变化，不是我们刚才得到的数值
现在我们就应该在粘贴的单元格中点击右键，在选项中我们点击选择性粘贴
会弹出如下对话框，我们选中数值，点击确定即可
最后我们看到的结果是我们刚才计算出来的数值了。

import java.awt.BorderLayout;import java.awt.Dimension;import java.awt.Toolkit;import java.awt.event.ActionEvent;import java.awt.event.ActionListener;import java.io.File;import java.io.FileNotFoundException;import java.io.FileReader;import java.text.NumberFormat;import java.util.Scanner;import javax.swing.JButton;import javax.swing.JFileChooser;import javax.swing.JFrame;import javax.swing.JPanel;import javax.swing.JTextArea;import javax.swing.filechooser.FileFilter;public class Sqrt{public static void main(String[] args){JFrame frame = new MatrixFrame_Sqrt ();frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);frame.setVisible(true);}}class MatrixFrame_Sqrt extends JFrame{public MatrixFrame_Sqrt (){setTitle("Solve the problem about matrix");setBounds((int) getScreenSize().width / 4, (int) getScreenSize().height / 4, (int) getScreenSize().width / 2, (int) getScreenSize().height / 2);JPanel southPanel = new JPanel();chooseButton = new JButton("Ñ¡Ôñ¾ØÕó");startButton = new JButton("¿ªÊ¼Çó½â");southPanel.add(chooseButton);southPanel.add(startButton);add(southPanel, BorderLayout.SOUTH);textArea = new JTextArea();textArea.setEditable(false);add(textArea, BorderLayout.CENTER);final NumberFormat myNumberFormat = NumberFormat.getInstance();myNumberFormat.setMinimumFractionDigits(3);myNumberFormat.setMaximumFractionDigits(3);fileChooser = new JFileChooser();fileChooser.setCurrentDirectory(new File("."));fileChooser.setFileFilter(new FileFilter(){public boolean accept(File f){return f.isDirectory() || f.getName().toLowerCase().endsWith(".txt");}public String getDescription(){return "txt files";}});chooseButton.addActionListener(new ActionListener(){public void actionPerformed(ActionEvent event){int result = fileChooser.showOpenDialog(null);if (result != JFileChooser.APPROVE_OPTION) return ;matrixFile = fileChooser.getSelectedFile();myMatrix = new MatrixInstance_Sqrt();matrix = myMatrix.getMatrix(matrixFile.getPath());StringBuilder line = new StringBuilder();for (int i = 0; i < matrix.length; i++){for (int j = 0; j < matrix[0].length; j++)line.append(matrix[i][j] + " ");textArea.append(line + "\n");line.setLength(0);}}});startButton.addActionListener(new ActionListener(){public void actionPerformed(ActionEvent event){double[][] temp = myMatrix.getLU_matrix(matrix);StringBuilder line = new StringBuilder("\n·Ö½âµÄϵÊý¾ØÕó\n");for (int i = 0; i < temp.length; i++){for (int j = 0; j < temp.length; j++)line.append(temp[i][j] + " ");textArea.append(line + "\n");line.setLength(0);}double[] answers = myMatrix.getAnswers(temp);line.append("\n(");for (int i = 0; i < answers.length; i++) line.append(answers[i] + ",");line.deleteCharAt(stIndexOf(","));line.append(")");textArea.append(line.toString());}});}private Dimension getScreenSize(){return Toolkit.getDefaultToolkit().getScreenSize();}private double[][] matrix;private MatrixInstance_Sqrt myMatrix;private File matrixFile;private JFileChooser fileChooser;private JButton chooseButton;private JButton startButton;private JTextArea textArea;}class MatrixInstance_Sqrt{public double[][] getMatrix(String name)try{Scanner in = new Scanner(new FileReader(name));if (!in.hasNextLine()) return null;String line = in.nextLine();int len = line.split(" ").length;matrix = new double[len - 1][len];int row = 0;String[] tokens = line.split(" ");for (int column = 0; column < tokens.length; column++){matrix[row][column] = Double.parseDouble(tokens[column]);}row += 1;while(in.hasNextLine()){line = in.nextLine();tokens = line.split(" ");for (int column = 0; column < tokens.length; column++){matrix[row][column] = Double.parseDouble(tokens[column]);}row += 1;}in.close();}catch (FileNotFoundException e){e.printStackTrace();}b = new double[matrix.length];for (int i = 0; i < matrix.length; i++) b[i] = matrix[i][matrix.length];return matrix;}public double[][] getLU_matrix(double[][] matrix){return LU_matrix = breakMatrix(matrix);}private double[][] breakMatrix(double[][] matrix){double[][] temp = new double[matrix.length][matrix.length];for (int j = 0; j < matrix.length; j++){for (int i = j; i < matrix.length; i++){temp[i][j] = matrix[i][j];for (int t = 0; t < j; t++) temp[i][j] -= temp[i][t] * temp[j][t];if (i == j) temp[i][j] = Math.sqrt(temp[i][j]);else temp[i][j] /= temp[j][j];}}for (int i = 0; i < matrix.length; i++)for (int j = i + 1; j < matrix.length; j++)temp[i][j] = temp[j][i];return temp;}public double[] get_y(double matrix[][]){double[] y = new double[b.length];for (int i = 0; i < b.length; i++){y[i] = b[i];for (int j = 0; j < i; j++) y[i] -= matrix[i][j] * y[j];y[i] /= matrix[i][i];}return y;}public double[] getAnswers(double[][] matrix){double[] y = get_y(matrix);double[] answers = new double[y.length];for (int i = y.length - 1; i >= 0; i--){answers[i] = y[i];for (int j = i + 1; j < y.length; j++) answers[i] -= matrix[i][j] * answers[j];answers[i] /= matrix[i][i];}return answers;}private double[] b;private double[][] LU_matrix;private double[][] matrix;}。

某场地强夯对边坡稳定性影响的数值模拟张明【摘要】结合拟建于高边坡坡顶的变电站工程,分析强夯施工振动的衰减规律与强夯引起建筑物破坏判据,确定了强夯施工振动的影响区域;采用FLAC软件建立强夯对边坡稳定性影响的数值模拟模型,分析计算不同夯击能条件下边坡关键监测点的水平振动速度、竖向振动速度和坡面的水平位移;根据强夯振动引起建筑物破坏判据,结合数值模拟计算结果,针对减少强夯对边坡稳定性的影响,提出强夯的范围及夯击能的合理取值.%Based on a substation engineering built on the top of high slope, the attenuation law of dynamic compaction vibration and the failure criterion of buildings caused by dynamic compaction were analyzed, respectively, and then the influencing regional of the dynamic compaction vibration was determined. A numerical simulation model of the influence of dynamic compaction on the slope stability was established using FLAC software, and some analysis and calculation were conducted in the numerical model, including the horizontal vibration velocity and vertical vibration velocity of the key monitoring points, and the horizontal displacement of the slope under different tamping energy. According to the failure criterion of buildings caused by the dynamic compaction vibration and the nu-merical results, the range of dynamic compaction and a reasonable value of tamping energy are put forward to reduce the influence of dynamic compaction on the slope stability.【期刊名称】《低温建筑技术》【年(卷),期】2018(040)001【总页数】4页(P130-133)【关键词】强夯;边坡稳定性;变电站;振动速度;数值模拟【作者】张明【作者单位】河南工程学院土木工程学院,郑州451191【正文语种】中文【中图分类】TU4351 项目概况1.1 工程概况拟建500kV变电站位于深圳市南山区长岭陂水库东南侧、福龙路白石岭隧道东侧、南坪快速路北侧，场地接近矩形，长247m，宽190m，面积约4.5万m2。

第39卷第3期Vol.39,No.32009年3月J OURNAL OF UNIVE RSITY OF SCIE NCE AND TECHNOLO GY OF CHINAMar.2009文章编号:025322778(2009)0320331206收稿日期:2006211213;修回日期:2007206228基金项目:国家自然科学基金(10632080,10572134)资助.作者简介:王峰,男,1976年生,博士.研究方向:计算力学.E 2mail :wangfeng0706@ 通讯作者:王肖钧,教授.E 2mail :xjwang @冲击力学有限元计算中的数值积分王　峰1,2,王肖钧1,卞　梁1,李建光1,劳　俊1(1.中国科学技术大学近代力学系,安徽合肥230027;2.解放军炮兵学院无人机和机械工程系,安徽合肥230031)摘要:在Lagrange 有限元基础上,介绍了计算运动方程中节点力的不同积分方法.单点积分方法具有较高的计算效率,为了控制沙漏变形,必须引入抗沙漏节点力;采用2×2×2高斯积分可以避免沙漏变形,并有较高的计算精度,但导致计算量增大;而采用局部2×2×2高斯积分则同时具有两者的优点.三维侵彻的计算结果表明局部2×2×2高斯积分能够很好地控制沙漏变形,并有较高的计算效率;一维应变波的模拟计算结果也表明,2×2×2高斯积分比单点积分更加接近理论值.这说明所述方法和所建程序的合理性和有效性,它为侵彻贯穿过程的数值分析提供了一种实用和有效的手段.关键词:爆炸力学;数值模拟;有限元;单点积分;高斯积分中图分类号:O385 文献标识码:ANumerical integration method of f inite elementcomputation in impact mechanicsWAN G Feng 1,2,WAN G Xiao 2jun 1,B IAN Liang 1,L I Jian 2guang 1,L AO J un 1(1.Depart ment of Modern Mechanics ,Universit y of S cience and Technology of China ,Hef ei 230027,China;2.Depart ment of Unmanned A erial V ehicle and Mechanical Engineering ,PL A A rtillery A cadem y ,Hef ei 230031,China )Abstract :Based on t he analysis of Lagrange finite element met hod ,numerical integration met hods to comp ute nodal force were briefly described.In order to cont rol hourglass deformations ,anti 2hourglass nodal forces have to be used for single point quadrat ure ,which has higher efficiency.The hourglass modes would be cont rolled and t he numerical accuracy raised effectively if 2×2×2Gaussian quadrat ure were adapted ,but t his would entail heavy comp utation.However ,partial 2×2×2Gaussian quadrat ure has t he merit s of two kinds of integration met hod.The numerical example of penet ration indicated t hat partial 2×2×2Gaussian quadrat ure could cont rol hourglass deformations effectively and has higher efficiency.And t he numerical simulations of one 2dimensional strain wave also shown t hat 2×2×2Gaussian quadrat ure is much better t han single point quadrat ure.It is concluded t hat t he met hod discussed and t he program we developed are reasonable and effective ,providing a usef ul met hod for t he numerical st udy of penet ration and perforation.K ey w ords :mechanics of explosion ;numerical simulation ;finite element ;single point quadrat ure ;Gaussian quadrat ure0　引言侵彻问题的理论与实验研究始终是新武器研制和高科技领域中的重要课题,无论是进攻或者防御,可靠预测侵彻效果、提高侵彻能力始终是新武器研究中的核心.传统的解析方法以及基于实验研究的经验或半经验方法已经远远不能满足现代高技术武器发展的需要.数值模拟方法,由于具有假设少、物理模型逼真、计算精度高等明显的优势,成为了高速侵彻理论研究中一种主要和广泛认同的方法[1,2].在有限元计算中,采用集中质量法后,守恒方程中的运动方程被离散为通过节点力表示的质量运动方程,节点力的计算需要通过一定的积分方法来实现.为了提高数值模拟侵彻过程的计算效率,通常采用单点积分法,但这种方法的直接后果是立方元被认为是常应力常应变单元,在某些情况下会导致网格相交,甚至网格翻转,计算中断,因此必须通过引入抗沙漏节点力的方法以控制沙漏变形.采用多点积分,如2×2×2高斯积分不但可以提高计算精度,还可以有效避免沙漏变形.然而采用2×2×2高斯积分所引起计算量的增大是侵彻贯穿数值计算中必须面对的现实问题.大量冲击力学数值计算的实例表明,出现网格严重畸变,导致沙漏变形发展失控的单元往往只是部分单元,甚至是个别单元,因此我们可以采用局部2×2×2高斯积分,将单点积分计算效率高和全高斯积分可以消除沙漏变形的优点结合起来.在数值模拟侵彻贯穿问题中,对部分网格严重畸变单元采用2×2×2高斯积分,而其他的绝大部分单元仍采用单点积分,计算实践表明,这一方法是有效的.本文对八节点立方元分别采用不同积分方法对平头弹侵彻靶板进行了数值模拟计算,表明局部2×2×2高斯积分能够很好地控制沙漏变形,精度接近2×2×2高斯积分,且具有较高的计算效率.还采用单点积分和2×2×2高斯积分分别计算了板中一维应变波的传播,并与理论解进行了比较,结果表明2×2×2高斯积分的计算结果明显优于单点积分.1　计算方法简介1.1　单点积分的沙漏变形与沙漏控制目前,在大多数冲击力学有限元程序里,为提高计算效率,在计算节点力时,通常采用的是单点积分法,对于八节点六面体立方元(图1)而言,即在自然坐标系里,在进行单元体积分时,积分点取为ξ=η=ζ=0.单点积分的直接后果是立方元被认为是常应力常应变单元,因此其对应的位移场只能是线性位移场,显然,单点积分无法描述非线性位移模态.当单元变形出现如图2所示的几种沙漏变形模态时,由单点积分定义的单元应变为零,这就是所谓零能模式.在这种变形模式中,相应的节点内力 f int i= 0.于是沙漏变形可以在无节点阻力的情况下任意发展,在数值计算中它将导致网格相交,甚至网格翻转,计算中断.针对单点积分中出现的这一问题,Belyt schko 等[3,4]提出了一种通过引入抗沙漏节点力的方法控制沙漏变形.其基本思想是根据沙漏变形模态引入相应的沙漏变形率,q iα=18v iIγαI.(1)式中,角标i表示空间坐标轴方向,I表示节点,α表示沙漏变形模态;v iI为节点速度分量,γαI为沙漏变形分量,定义为γαI=ΓαI-1VB iI x iJΓαJ.(2)式中,B iJ=5N I(x i)/5x i,ΓαI如表1所示.由虚功原理出发,可以建立抗沙漏节点力,f H G iI=18Q iαγαI.(3)233中国科学技术大学学报第39卷式中,Q i α是与沙漏变形相对应的沙漏应力,Q i α=k λ+2μ3B iI B iIVq i α,(4)k 为人工沙漏控制系数,λ和μ是拉梅常数.1.2　2×2×2高斯积分的计算过程单点积分所对应的位移场是线性位移场,实际上八节点立方元所设定的位移函数应包含若干非线性项,或者说在自然坐标系里,形函数应具有如下的形式,N I (ξ,η,ζ)=18(1+ξξI )(1+ηηI )(1+ζζI )= 18{ΣI +ξΛ1I +ηΛ2I +ζΛ3I +ηζΓ1I + ζξΓ2I +ξηΓ3I +ξηζΓ4I }.(5)式中,ξI ,ηI ,ζI ,ΣI ,Λ1I ,Λ2I ,Λ3I ,Γ1I ,Γ2I ,Γ3I ,Γ4I 分别表示与节点相对应的自然坐标取值,如表1所示,其中,Γ1I ,Γ2I ,Γ3I ,Γ4I 刻画了位移场的非线性模态.表1　节点的自然坐标取值T ab.1　N atural coordinates of nodes节点ξηζΣIΛ1I Λ2I Λ3I Γ1IΓ2IΓ3IΓ4I1-1-111-1-11-1-11121-1111-11-11-1-13111111111114-1111-1111-1-1-15-1-1-11-1-1-1111-161-1-111-1-11-1-11711-1111-1-1-11-18-11-11-11-1-11-11采用有限元方法离散运动方程时,通常取空间域和时间域分别离散的所谓半离散化思想,空间域采用有限元方法离散,时间域则按有限差分方法离散.由半离散化思想知,速度场可表示为v ( x ,t )=N ～( x )・ u (t ).(6)式中,N ～( x )是由形函数构成的3×24矩阵,N ～( x )=N 100…N 8000N 10…0N 800N 1…N 8;u (t )表示由节点速度构成的24×1列向量,u (t )=[u 11　u 21　u 31　u 12　u 22　u 32　…　u 18　u 28　u 38]T,u ij 表示第j 个节点i 方向的速度分量. u (t )只是时间t 的函数.于是,v ・( x ,t )=N ～( x )・ u ・(t ).(7) 应变率矢量可以表示成ε・= ε11 ε22ε33γ12γ23 γ31=55x 100055x 2055x 355x 255x 1055x 355x 255x 355x 1v 1(x ,t )v 2(x ,t )v 3(x ,t )=L ・ v (x ,t ).(8)式中, εii 为法向应变率, εii =5v i5x i; γij 为剪应变率, γij =5v i 5x j +5v j5x i; L 是由微分算子构成的矩阵,v i (x ,t )表示x i 方向上的速度分量.将式(6)代入式(8),有ε・= L ・N ～( x )・ u (t )= B ( x )・ u (t ).(9)式中, B 称为梯度矩阵,由形函数的空间导数构成,B ( x )= L ・N ～( x ).由式(5)可知,形函数N i (ξ,η,ζ)是由自然坐标给出的,根据偏微分法则,5N i 5ξ=5N i 5x 15x 15ξ+5N i 5x 25x 25ξ+5N i 5x 35x 35ξ.(10)对于其余两坐标(η,ζ),可以类似得到,写成矩阵形式有5N i5ξ5N i5η5N i 5ζ=5x 15ξ5x 25ξ5x 35ξ5x 15η5x 25η5x 35η5x 15ζ5x 25ζ5x 35ζ5N i5x 15N i 5x 25N i 5x 3=J 5N i 5x 15N i5x 25N i 5x 3(11)式中,J 称为雅可比矩阵,可记为5(x 1,x 2,x 3)5(ξ,η,ζ).在等参元里,空间坐标可以表示为x j =∑N ixji=N 1x j 1+N 2x j 2+…+N 8x j 8;i =1,2,…,8;j =1,2,3.(12)式中,x ji 表示第i 个节点j 方向的坐标值.利用式(12),J 可以显式地表现为自然坐标的函数,J ≡5(x 1,x 2,x 3)5(ξ,η,ζ)=333第3期冲击力学有限元计算中的数值积分∑5N i5ξx 1i ∑5N i5ξx 2i ∑5N i5ξx3i ∑5N i5ηx 1i ∑5N i5ηx 2i ∑5N i5ηx 3i ∑5N i5ζx 1i ∑5N i5ζx 2i ∑5N i5ζx 3i=5N 15ξ5N 25ξ…5N 85ξ5N 15η5N 25η…5N 85η5N 15ζ5N 25ζ…5N 85ζx 11x 21x 31x 12x 22x 32………x 18x 28x 38.(13)于是N i 对于(x 1,x 2,x 3)的偏导数可用自然坐标表示为5N i 5x 15N i 5x 25N i5x 3=J -15N i 5ξ5N i5η5N i5ζ.(14)式中,J -1是J 的逆矩阵.体积微元可以表示为d V =d ξ・(d η×d ζ).(15)式中,d ξ=5x 15ξd ξ i +5x 25ξd ξ j +5x 35ξd ξk ,d η=5x 1ηd η i +5x 2ηd η j +5x 3ηd η k ,d ζ=5x 15ζd ζ i +5x 25ζd ζ j +5x 35ζd ζ k ; i , j , k 是直角坐标的单位向量,于是d V =5x 15ξ5x 25ξ5x 35ξ5x 1η5x 2η5x 3η5x 15ζ5x 25ζ5x 35ζd ξd ηd ζ=|J |d ξd ηd ζ.(16) 节点内力可以表示为f inti (t )=∫ΩeB T i ( x ) σ( x ,t )d Ω= ∫VB T i (ξ,η,ζ) σ(ξ,η,ζ,t )d V = |J |∫1-1∫1-1∫1-1B Ti(ξ,η,ζ) σ(ξ,η,ζ,t )d ξd ηd ζ.(17)采用2×2×2高斯积分[5]后,式(17)可写为 f int i (t )=|J |∑2j =1∑2k =1∑2m =1HjH k H m B T i (ξj ,ηk ,ζm ) σ(ξj ,ηk ,ζm ,t ).(18)式中,B Ti σ=5N i5x 1005N i5x 205N i 5x 305N i5x 205N i 5x 15N i 5x 305N i 5x 305N i 5x 25N i 5x 1σ11σ22σ33σ12σ23σ31=5N i 5x 1σ11+5N i 5x 2σ12+5N i 5x 3σ315N i 5x 2σ22+5N i 5x 1σ12+5N i 5x 3σ235N i 5x 3σ33+5N i 5x 2σ23+5N i 5x 1σ31.(19)对于2×2×2高斯积分,H j =H k =H m =1,ξj =ηk =ζm =±0157735(j ,k ,m =1,2),将式(14)和式(18)代入式(17)可以计算得到节点内力.由于在每个坐标方向的积分点数取为n =2,数学上可以证明,2×2×2高斯积分的结果可以达到2×n -1=3阶的精度.也就是说,如果 B T i (ξ,η,ζ) σ(ξ,η,ζ)=∑ξi ηj ζk,且i ,j ,k ≤3,则式(18)将能给出积分的精确解.2　数值模拟计算及结果分析2.1　平头杆弹对靶板的三维侵彻计算为了考查沙漏变形对有限元计算过程的影响,我们对平头杆弹侵彻靶板进行了数值计算.弹体和靶板材料取为线性硬化体,其静水压力与体积变形之间用如下的Gruneisen 状态方程描述[6]:P =(K 1μ+K 2μ2+K 3μ3)(1-0.5γμ)+γρE.(20)式中,μ=V 0/V -1为压缩比,γ为Gruneisen 参数,E 为比内能.应力偏量服从增量型弹塑性应力应变关系,即d S ij =2G (de ij -d e p ij).(21)材料服从Mises 屈服准则,屈服强度取为线性硬化函数,Y =Y 0+(Y u -Y 0) εP / εu .(22)式中,Y 0为初始屈服应力,Y u 为极限屈服应力, εP433中国科学技术大学学报第39卷表2　材料参数T ab.2　P arameters of m aterialρ/(kg ・m -3)G /GPaY 0/GPaY u /GPaP σ/GPa εu状态方程参数/GPaK 1K 2K 3γ782377.5 1.43 2.50 1.700.011642945002.图3　不同积分方法下的侵彻图像Fig.3　Penetration conf igurations of different integration methods为等效塑性应变, εu 为极限应变.计算中用到的有关物理参数[6]和计算参数如表2所示.图3给出了平头杆弹以初速度V 0=1500m/s 侵彻靶板t =2710μs 时的应变及网格变形图像.可以看出,加入抗沙漏节点力的单点积分和2×2×2高斯积分都能够很好地控制沙漏变形,避免网格畸变,而取消抗沙漏节点力的单点积分则出现了网格的畸变和相交,严重影响了有限元计算的正常计算过程,这也进一步说明了上述计算方法的正确性.尽管2×2×2高斯积分的计算结果可以更为准确地给出杆弹靶板的物理图像,然而其计算量的增加依然是数值模拟高速侵彻和贯穿问题时不可忽视的因素.事实上,计算中我们发现,出现网格畸变严重导致沙漏变形模态发展的只是部分单元,这部分单元几乎全部集中在侵彻通道附近.为此我们开展了一组只对侵彻通道附近靶板单元采用2×2×2高斯积分,其余单元都采取不加抗沙漏节点力的单点积分,结果如图3(d )所示.由于充分利用了单点积分计算效率高、2×2×2高斯积分可以比较准确捕捉网格变形的物理细节等两者的长处,因此这种局部2×2×2高斯积分方法是非常有效的.图4是平头杆弹以初速度V 0=1500m/s 侵彻靶板时的平均侵彻速度与时间的关系曲线.可以看到,加入抗沙漏节点力的单点积分、2×2×2高斯积分和局部2×2×2高斯积分的模拟结果基本一致,而没有抗沙漏节点力的单点积分得到的平均侵彻速度在相同时刻远大于前两者,并且存在局部震荡,这是由于后者靶板单元产生过大的网格畸变而导致破图4　不同积分方法下的平均侵彻速度随时间的变化Fig.4　History of average velocity for different integration methods坏严重的缘故.表3给出了单点积分、2×2×2高斯积分和局部2×2×2高斯积分在不同的条件下所用CPU 机时的比较,可见与2×2×2高斯积分相比,局部2×2×2高斯积分的效率较高,且所用的计算时间只是稍大于单点积分.我们认为,以稍多的计算时间来换取更高的计算精度是值得的.表3　不同积分方法所用CPU 机时比较(单位:秒)T ab.3　CPU time used by different integration methods(unit :second)方法三维侵彻计算的靶板网格数12003000720010000单点积分5321896567696252×2×2高斯积分73531221073226354局部2×2×2高斯积分5952056601510463533第3期冲击力学有限元计算中的数值积分图5　脉冲载荷下单点积分和2×2×2高斯积分的应力波形Fig.5　Stress w aveform of single point qu adrature and2×2×2G aussian qu adrature in pulse load2.2　一维应变波的对比计算为确认上述积分方法的有效性和合理性,我们采用在此基础上开发的三维Lagrange有限元程序计算了脉冲载荷下半无限板中的弹塑性波的传播问题.设厚L=014m的半无限厚钢质平板上作用有脉冲载荷P,P=P0,t≤τ;0,t>τ.(23)式中,P0=5×109Pa,τ=10μs.当P0大于材料的屈服强度时,平板内部将产生弹塑性间断波的传播.平板材料的本构模型和相关参数同节211.图5给出了两种积分方法所得的计算结果和解析解的比较.当加载应力大于材料的初始屈服强度时将形成双波结构,较慢的塑性激波尾随在较快的弹性前驱波之后.随着时间的推移,弹性前驱波与塑性主波阵面逐渐拉开,而卸载时产生的弹性卸载波又对塑性波产生追赶卸载.由图5可见,单点积分的精度较低,尤其是在间断面上,其波形失真较大,间断面被过度地光滑化了.和单点积分相比,2×2×2高斯积分的计算精度有较大的改善,得到的波形更接近于理论波形.因此,通过数值计算方法模拟应力波演化过程时,最好放弃单点积分而采用全高斯积分方式.3　结论本文在Lagrange有限元数值计算方法的基础上,介绍了两种用于计算节点力的不同积分方法,并详细阐述了2×2×2高斯积分法的计算过程.单点积分计算效率高,但需要进行沙漏控制;2×2×2高斯积分可以避免沙漏变形,且计算精度较高,但计算量大;而采用局部2×2×2高斯积分则同时具有两者的优点.采用自建的三维有限元程序,对平头弹侵彻靶板进行了数值模拟计算,表明局部2×2×2高斯积分能够很好地控制沙漏变形,精度接近2×2×2高斯积分,且具有较高的计算效率.板中一维应变波传播的数值模拟对比计算也表明2×2×2高斯积分的计算结果明显优于单点积分.进一步的研究可以尝试采用其他的单元类型,例如四节点四面体单元,来进行网格的剖分,这样可以从根本上避免沙漏变形.当然,这会引起滑移面计算、积分方法等一系列计算方法的改变.参考文献(R eferences)[1]Znkas J A.High Velocity Impact Dynamics[M].NewY ork:Wiley,1990.[2]Camacho G T,Ortiz M.Adaptive Lagrangian modelingof ballistic penetration of metallic targets[J].Comput Meth Appl Mech Eng,1997,142(324):2692301.[3]Flanagan D P,Belytschko T.A uniform strainhexahedron and quadrilateral with orthogonal hourglass control[J].International Journal for Numerical Methods in Engineering,1981,17:6792706.[4]Belytschko T.Correction of article by D P Flanaganand T Belytschko[J].International Journal for Numerical Methods in Engineering,1983,19:4672468.[5]王勖成.有限单元法[M].北京:清华大学出版社,2003.[6]Robbins J R,Ding J L,Gupta Y M.Load spreadingand penetration resistance of layered structures:A numerical study[J].Int J Impact Eng,2004,30(6): 5932615.633中国科学技术大学学报第39卷。

第一章思考题(2012级本科学生作品)1、什么样的算法被称为不稳定算法？试列举一个例子进行说明。

在算法执行过程中，舍入算法对计算结果影响大的一类算法被称为数值不稳定的一种算法。

例如，假设初始数据有一点微小误差，就会对一个算法的数据结构产生很大的影响，造成误差扩散。

用计算公式ln 1ln n n =-，构造出的递推算法是一个数值不稳定的算法；而另一公式ln 1(1ln)/n -=-则可以构造出一个数值稳定的算法。

2、我们都知道秦九韶算法能够减少运算次数，高中也学过他的具体过程，请举出一个例子并用秦九韶算法计算。

答；一般的，一元n 次多项式的求值需要经过(1)/2n n +次乘法和n 次加法，而秦九韶算法只需要n 次乘法和n 次加法。

具体的不太会了。

3、为什么要设立相对误差的概念？答：相对误差是近似值误差与精确值的比值，用来衡量近似值的近似程度。

x=10±1，y=1000±5。

虽然x 的误差比y 的误差小，但y 的近似程度比x 更好。

这单用误差无法表现出来，而相对误差可以解决这个问题。

4、误差在生活中有什么作用？答：误差的作用不仅仅体现在数学课题研究中，在生活中误差的作用也非常大，比如在建筑行业中，设计图纸时必须要达到一定的精确度才行。

5、有效数字以及计算规则答：有效数字是指实际上能测量到的数值，在该数值中只有最后一位是可疑数字，其余的均为可靠数字。

它的实际意义在于有效数字能反映出测量时的准确程度。

例如，用最小刻度为0.1cm 的直尺量出某物体的长度为11.23cm ，显然这个数值的前3位数是准确的，而最后一位数字就不是那么可靠，医|学教育网搜集整理因为它是测试者估计出来的，这个物体的长度可能是11.24cm ，亦可能是11.22cm ，测量的结果有±0.01cm 的误差。

我们把这个数值的前面3位可靠数字和最后一位可疑数字称为有效数字。

这个数值就是四位有效数字。

在确定有效数字位数时，特别需要指出的是数字“0”来表示实际测量结果时，它便是有效数字。

５４Ｄｉｅ　ａｎｄ　Ｍｏｕｌｄ　Ｔｅｃｈｎｏｌｏｇｙ　Ｎｏ．６　２００４０引言随着现代化工业的发展，人们对机械零件的性能和可靠性的要求越来越高。

金属零件的内在性能和质量，除材料成份特征外，主要是在热加工过程中形成的。

材料热处理是保证零件内在质量的重要技术，由于热处理过程中零件自身的热传导、相变和应力的变化都无法直接观测，传统的热处理技术不可否认其不同程度的盲目性，与机械工业现代化的要求不相适应，现代计算机技术与热处理工艺的结合已成为当务之急。

１热处理过程数值模拟的基本原理和方法收稿日期：２００４－０９－１６基金项目：国家自然科学基金资助项目（５０２７５０９４）作者简介：宿德军（１９７７￣），男，硕士研究生。

１．１耦合关系模型热处理过程是温度、组织、应力／应变三方面交互作用的复杂过程，零件内部温度、组织、应力／应变的分布随加热、冷却产生和重新分布。

因此热处理过程的模拟必须采用温度、相变、应力／应变三者耦合的算法［１］。

整个耦合系统如图１所示。

文章编号：１００１－４９３４（２００４）０６－００５４－０４热处理过程数值模拟的研究现状和发展趋势宿德军，陈军（上海交通大学模具ＣＡＤ国家工程研究中心，上海２０００３０）摘要：热处理过程的数值模拟是一个复杂的过程，其复杂性源于热处理过程本身受多场量的影响，对热处理过程数值模拟的基本原理、研究方法进行了总结，介绍了温度场、组织场、应力／应变场的数值计算方法，分析了国内外的研究现状、存在的问题，同时展望了该技术今后的发展趋势。

关键词：热处理；数值模拟；温度场；应力场；相变中图分类号：ＴＧ１５１文献标识码：ＡＡｂｓｔｒａｃｔ：Ｎｕｍｅｒｉｃａｌ　ｓｉｍｕｌａｔｉｏｎ　ｏｎ　ｈｅａｔ　ｔｒｅａｔｍｅｎｔ　ｉｓ　ａ　ｃｏｍｐｌｅｘ　ｐｒｏｃｅｓｓ．　Ｔｈｅ　ｃｏｍｐｌｅｘｉｔｙ　ｉｓ　ｄｕｅ　ｔｏｍａｎｙ　ｆａｃｔｏｒｓ　ｗｈｉｃｈ　ｉｎｆｌｕｅｎｃｅ　ｔｈｅ　ｈｅａｔ　ｔｒｅａｔｍｅｎｔ．　Ｔｈｅ　ｐｒｉｎｃｉｐｌｅ　ａｎｄ　ｒｅｓｅａｒｃｈ　ｍｅｔｈｏｄ　ｏｆ　ｎｕｍｅｒｉｃａｌｓｉｍｕｌａｔｉｏｎ　ｏｎ　ｈｅａｔ　ｔｒｅａｔｍｅｎｔ　ａｒｅ　ｓｕｍｍａｒｉｚｅｄ．　Ｔｈｅ　ｎｕｍｅｒｉｃａｌ　ｃａｌｃｕｌａｔｉｎｇ　ｍｅｔｈｏｄｓ　ｏｆ　ｔｅｍｐｅｒａｔｕｒｅｆｉｅｌｄ，ｍｉｃｒｏｓｔｒｕｃｔｕｒｅ　ｆｉｅｌｄ　ａｎｄ　ｓｔｒｅｓｓ　ｆｉｅｌｄ　ａｒｅ　ｉｎｔｒｏｄｕｃｅｄ．　Ｔｈｅ　ｒｅｓｅａｒｃｈ　ｓｔａｔｕｓ　ａｎｄ　ｐｒｏｂｌｅｍｓ　ａｔ　ｈｏｍｅａｎｄ　ａｂｒｏａｄ　ａｒｅ　ａｎａｌｙｚｅｄ．　Ｔｈｅ　ｔｒｅｎｄ　ｉｎ　ｄｅｖｅｌｏｐｍｅｎｔ　ｏｆ　ｔｈｅ　ｔｅｃｈｎｏｌｏｇｙ　ｉｓ　ｐｒｅｓｅｎｔｅｄ．Ｋｅｙ　ｗｏｒｄｓ：ｈｅａｔ　ｔｒｅａｔｍｅｎｔ；ｎｕｍｅｒｉｃａｌ　ｓｉｍｕｌａｔｉｏｎ；ｔｅｍｐｅｒａｔｕｒｅ　ｆｉｅｌｄ；ｓｔｒｅｓｓ　ｆｉｅｌｄ；ｐｈａｓｅ　ｔｒａｎｓｆｏｒ－ｍａｔｉｏｎ模具技术２００４．Ｎｏ．６５５图１中①②为热处理介质流场、温度场与工件温度场的相互作用和影响；③为变形热，施加于物体表面或内部的应力会产生应变，部分能量会转化为热能，如发生了大的非弹性应变如锻压过程温升很明显，一般热处理过程中，塑性变形所产生的热量较小，可忽略不计；④为热应力，在热处理过程中，工件各部位由于加热或冷却不均匀产生了温度梯度，形成不协调膨胀，发生热应力；⑤相变潜热，由于相变产生组织的热焓值不同，相变过程必伴随潜热的释放与吸收既而影响温度场；⑥相变，温度是影响相变开始和过程的主要因素；⑦应力诱发相变，相变行为也受内部应力／应变的影响，如拉应力作用下珠光体相变时间会缩短；在应力作用下马氏体转变会在高于Ｍｓ点的温度下发生；⑧组织应力和相变塑性，由于新旧两相的比容不同，将产生体积膨胀的不均匀性，产生组织应力和应变，另外在相变发生时，在很低的应力水平下（远低于屈服应力）材料就会发生塑性变形，称为相变塑性；另外，化学成分的作用：化学成分的变化会引起材料热性能、物理性能及力学性能的改变，同时也会影响ＴＴＴ曲线和Ｍｓ点，从而对温度、组织、应力／应变情况都会产生影响。