当前位置：文档之家 › 第2章测试装置的基本特性2PPT课件

第2章测试装置的基本特性2PPT课件

  • 格式：ppt
  • 大小：1.99 MB
  • 文档页数：59

下载文档原格式

  / 59

合集下载

2测试装置的基本特性

2测试装置的基本特性

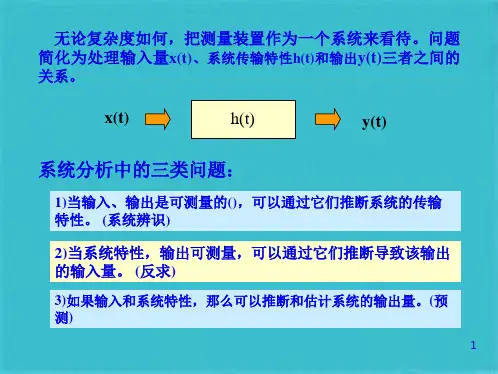
第二节 测试装置的静态特性
测试装置的静态特性是指静态测量情况下描述实际测试 装置与理想定常线性系统的接近程度。 •线性度 •灵敏度 •分辨力 •回程误差 •漂移
一、线性度
定义：测量装置输出、输入之间的关系与理想比例关系 的偏离程度。 线性误差的两种表达形式： * 静态标定所得输入、输出数据点与理想直线的最大偏差Δmax * 百分数表达
2 n H ( s) 2 2 s 2n s n
二、一阶、二阶系统的特性 （1）一阶系统
＋ u i(t ) － R ＋ C u o(t ) －
dxo RC xo xi dt
dy t a0 y t b0 x t 一般形式的一阶微分方程式： a1 dt dy t 改写为： T y t Sx t dt
（4）脉冲响应函数
已知： 若装置的输入为单位脉冲函数 由于 ，则有 。
对上式两边取拉氏逆变换，且令 则有
上式表明，单位脉冲函数的响应同样可描述测量系统的动态特性，它同 传递函数是等效的，不同的是一个在复频域 ，一个是在时间域，通常称 h(t) 为脉冲响应函数。脉冲响应函数可视为系统特性的时域描述。
T=a1/a0－系统时间常数 ; S=b0/a0－系统静态灵敏度 ; 为了分析方便，令S=1，
dy t T y t x t dt
一阶系统的特性
•传递函数： H ( s ) •频响函数：H ( )
1 Ts 1
1 jT 1

1 1 (T ) 2
x(t) 0 t0 t
测量装置实现测量不失真的频率特性
时域条件
y(t)= A0 x(t- t0)
式中：A0、t0均为常数。

机械工程测试基础_测量装置的基本特性

机械工程测试基础_测量装置的基本特性
dt n a n1
d n1 y t
dt n1
பைடு நூலகம் a1
dy t
dt
a
0
y
t
2－1
bm
d m xt
dt m bm1
d m1 x t
dt m1
b1
dx t
dt
b
0
x
t
测量装置的动态特性也可以用传递函数、频率响应函数 和单位脉冲响应函数表示：
传递函数： 频率响应函数： 脉冲响应函数：
H
实际标定过程如图2－2，主要考虑其他量不会严格保持不变。 测量装置的静态测量误差：测量装置自身和人为因素。
2、标准和标准传递
若标定结果有意义，输入和输出变量的测量必须精确； 用来定量输入、输出变量的仪器和技术统称为标准； 变量的测量精度以测量误差量化，即测量值与真值的差； 真值：用精度最高的最终标准得到的测量值； 标准传递和实例（图2－3）。
静态特性
测试装置的特性
动态特性 负载特性
抗干扰特性
说明：测试装置各特性是统一的，相互关联的。例如：动态特性方程
一般可视为线性方程，但考虑静态特性的非线性、迟滞等因素，就成 为非线性方程。
1、测试装置的静态特性
静态特性是由静态标定来确定的； 静态标定：是一个实验过程，只改变测量装置的一个输入量，其他所
s
Y s X s
bm s m an s n
b m1 s m1 b1 s b0 a n1 s n1 a1 s a 0
H
(
j)
bm an
j m j n
bm1 j m1 b1 j b0 an1 j n1 a1 j a0
输入量 x(t) (t)

第二章+测试装置基本特性

第二章+测试装置基本特性
3、 有关测试和测试装置的若干术语
1、测量、计量和测试 (1)测量：指以确定被测对象量值为目的全部操作。 例如：对一张纸的面积进行确定，一张纸有100平方厘米
2020/5/15
6
概述(6/7)
(2)计量：指实现单位统一和量值准确可靠的测量。 (3)测试：是测量和计量的综合（实验性质，多用于动态研究）。 2、测量装置的误差和准确度 (1)测量装置的误差：测量装置的示值和被测量的真值之间的差值 (2)测量装置的准确度(精确度):表示测量装置给出接近于被测值真值的 示值的能力 例：0~150V 电压表 示值100.0V 实际 99.4V，
的关系。如下图
系统
输入 (激励)
x(t)
X(s) X(ω)
h(t)
H(s) H(ω)
y(t)
Y(s) Y(ω)
输出 (响应)
• 如果x(t)、y(t)可以观察(已知)，则可推断h(t)。 • 如果h(t)已知，y(t)可测，则可推断x(t)。 • 如果x(t)和h(t)已知，则可推断和估计y(t)。
(2)比例性（均匀性）： 对任意常数a，必有 ax(t)-->ay(t)
(3)微分性：系统对输入导数的响应等于对原输入响应的导数 dx(t)/dt--->dy(t)/dt
(4)积分性：如果系统的初始状态均为零，则系统对输入积分的响应等同于
对原输入响应的积分
t
t
0 x(t)dt 0 y(t)dt
2020/5/15
例子：
量程为=±5v（给定的测量范围） 8位(8个01代码来表示）A/D卡: 10v/28=5/27=39.0625mv/bit（每一位所能表示的精度） 12位:10/212=5v/211=2.44140625mV/bit 16位:10v/216=5v/215=0.1525878906mV/bit

二测试装置的基本特性概要PPT课件

二测试装置的基本特性概要PPT课件

10
第二节测试装置的静态特性
根据(2-1)式，线性定常系统的静态特性：
y b0 x Sx a0
本章主要讨论测试装置及其与输入、输出的关系。
图 2-0 典型的测试装置
22
第一节 概述
一、对测试装置的基本要求 1、解决的问题 通常的工程测试问题总是处理输入量x(t)、装置(系统)的传输特性h(t)和输 出量y(t)三者之间的关系(图2·1)。即： ① 如果输入、输出是可以观察(已知)的量，则可以推断系统的传输特性； ② 如果系统特性已知，输出可测，则可以推断导致该输出的输入量； ③ 如果输入和系统特性已知，则可以推断和估计与该输出对应的系统输
(三)量程和测量范围
量程：测量装置的示值范围的上、下限之差的模。 测量范围：是指使该装置的误差处于允许极限内它所能测量的被测量值的 范围。对于用于动态测量的装置还标明在允许误差极限内所能测量的频率 (范四围)信。噪比
信噪比：信号功率与干扰(噪声)功率之比，记为SNR，单位为分贝(dB)。
SNR 10 lg Ns
测量装置的准确度反映测量装置的总误差。该总误差包括系统误差和 随机误差两部分。测量装置的随机误差分量可用对同一被测量在同一行程 方向连续进行多次测量，其示值的分散性来表述。通常这也称为测量装置 的重复性误差。
在实际工作中，往往使用到测量装置的引用误差一词。它是指测量装 置的示值绝对误差与引用值之比，并以百分数表示。引用值往往是指测量 装置的量程或示值范围的最高值。
。
静态测量：是指测量期间被测量值可认为是恒定的测量。
动态测量：是为确定量的瞬时值及(或)其随时间变化的量所进行的测量。 (二)测量装置的误差和准确度 装置的示值误差：测量装置的示值和被测量的真值之间的差值。若不会引 起混淆，可简称为测量装置的误差。

第2章 测试装置的基本特征2

第2章 测试装置的基本特征2

性曲线近似为一条水平线（斜率为零）；
高频段幅频特性曲线斜率为 -20dB/10 倍频
程，相频特性曲线渐进地接近-90°。
在幅频特性曲线渐近线的转折频率点处，
可求得时间常数τ=1/ωbreak。
2） 二阶系统
通常通过幅频特性曲线估计二阶系统的固有 频率和阻尼比。
(a)半功率点法
(b)幅值比较法
设有一个装置，其输出与输入满足下列 关系：
y(t ) A0 x(t t0 )
其中 A0和t0为常数。表明这个装置输出 的波形和输入的波形精确的一致，只是幅值 放大了A0和在时间上延迟了t0。测试装置实 现了不失真测量。
波形不失真复现பைடு நூலகம்
傅里叶变换后：
Y ( ) A0 e
jt 0
3.7.2 减轻负载效应的措施
• 提高后续环节（负载）的输入阻抗
• 减小输出阻抗；
• 在原来两个相连接的环节之中，插入高输入阻抗、
低输出阻抗的放大器，以便一方面减小从前环节
吸取能量，另一方面在承受后一环节（负载）后 又能减少电压输出的变化，从减轻负载效应。 • 使用反馈或零点测量原理，使后面环节几乎不从 前环节吸收能量。
3.8.4 接地设计
测量装置中的地线是所有公共的零电
平参考点。理论上，地线上任何位置上的
电平应该相同。然而，有地电流时，各点
之间连线电阻的影响，使得各个地点的电
位产生差异。
41
常用的接地方式有： 1.单点接地；无环路电流，相互干扰小；
2.串联接地；注意：信号电路靠近电源， 地线尽可能粗些；
3.多点接地；降低接地电阻
电 源 干 扰
测量系统
1) 电磁干扰：干扰以电磁波辐射方式 经空间串入测量系统。 2) 信道干扰：信号在传输过程中，通道中 各元件产生的噪声或非线性 畸变所造成的干扰。 3)电源干扰：这是由于供电电源波动对测 量电路引起的干扰。

第二 测试装置的基本特性(共53张PPT)

第二 测试装置的基本特性(共53张PPT)
在对动态物理量进行测试时，测试装置的输出变化是否能真 实地反映输入变化，则取决于测试装置的动态响应特性。
x(t)
h(t)
y(t)
属于：系统分析中的三类问题1
1)当输入、输出是可测量的(已知)，可以通过它们推断系统的传输 特性。 (系统辨识)
2)当系统特性已知，输出可测量，可以通过它们推断导致该输出的 输入量。 (反求)
域描述。h(t)=L-1[H(s)]
系统的传递函数、频率响应函数、脉冲响应函数分 别是系统的复域描述、频域描述和时域描述。
22
5
四、环节的串联和并联
n个环节Hi(s)串联组成的系统，总的传递函数H(s)为
n
H(s) Hi(s) i1
n个环节Hi(s)串联组成的系统，总的频率响应函数 H(j)为
率为-20dB/10倍频的直线，两直线相交于
=1/处。
28
〔二〕 二阶系统的特性
二阶系统的传递函数为
H(s)s2
n2 2nsn2
二阶系统的频率响应函数为
H(j)
[1(
1
)2]
j2
n
n
29
二阶系统的幅频和相频特性为
A( )
1
[1 ( ) 2 ]2 4 2 ( ) 2
n
n
2 ( )
( ) arctg
1. 稳态输出误差为零。
2. 系统固有频率n由系统的主要结构参数决定，
n越高，系统响应越快。
3. 阻尼比直接影响超调量和振荡次数。
4. 通常阻尼比选在0.6~0.8之间。
38
2.5 实现不失真测量的条件
设测试系统的输出y(t)与输入x(t)满足关系
y(t)=A0x(t-t0)
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

装置的传递函数与测量信号无关，也不能确定装置的物 理结构，只表示测量装置本身在传输和转换测量信号中 的特性或行为方式。
H(s)是对物理系统特性的一种数学描述，而与系统的具体 物理结构无关。所以同一传递函数可以表征具有相同传 输特性的不同物理系统。 例：液柱式温度计和RC低通滤 波器都是一阶系统。
•H(s)中的分母取决于系统的结构，而分子则表示系 统同外界之间的联系.分母中s的幂次n代表系统微分 方程的阶数，如当n=1 或n=2 时，分别称为一阶系 统或二阶系统。(n>m)
式中
Y(s) y(t)estdt X(s) x(t)estdt
0
0
sj,0, 复变数
s为拉氏变换算子: 和 皆为实变量
第二章 测试装置的基本特性
第三节 测试系统的动态响应特性
x
bmSmbm1Sm1 b1Sb0 anSnan1Sn1 a1Sa0
y
H(s) =
bmSmbm1Sm1 b1Sb0 anSnan1Sn1 a1Sa0
线性 y
线性 y
非线性y
x
x
x
第二章 测试装置的基本特性
第一节 概述
二.线性系统及其主要性质
1.微分方程:
系统输入x(t)和输出y(t)间的关系可以用常系数 线性微分方程来描述：
an dndytn(t)an1dndt1ny1 (t)a1dyd(tt)a0y(t) bmdm dtxm (t)bm1dm d t1m x(1t)b1dxd(tt)b0x(t)
第二章 测试装置的基本特性
本章学习要求： 1.建立测试系统的概念 2.了解测试系统的静态特性和动态特性 3.了解测试系统特性的测量方法及不失
真的条件
第二章 测试装置的基本特性
第一节 概述
一.测试系统基本要求
理想的测试系统应该具有单值的、确定的输入－ 输出关系。对于每一输入量都应该只有单一的输出量 与之对应。知道其中一个量就可以确定另一个量。其 中以输出和输入成线性关系最佳。
-----------------时不变系统或者定常系统
第二章 测试装置的基本特性
2.线性系统性质：
第一节 概述
a)叠加性
系统对各输入之和的输出等于各单个输入的输出之和
即
若
x1(t) → y1(t)，x2(t) → y2(t)
则
x1(t)±x2(t) → y1(t)±y2(t)
b)比例性
常数倍输入所得的输出等于原输入所得输出的常数倍，
第二节 测试装置的静态特性
如果测量时，测试装置的输入、输出 信号不随时间而变化或者随时间变化的极 慢，则称为静态测量。静态测量时，描述 理想定常线性系统与实际测试系统的接近 程度。
第二章 测试装置的基本特性
第二节 测试系统的静态特性
一. 线性度
测量装置输入、输出的关系与理想的直线的 偏离程度；即标定曲线与拟合直线的偏离程 度就是非线性度。
第二章 测试装置的基本特性
第三节 测试系统的动态响应特性
A(i)=Yi/Xi, (i)= i
第二章 测试装置的基本特性
第三节 测试系统的动态响应特性
第二章 测试装置的基本特性
第三节 测试系统的动态响应特性
一. 动态特性的数学描述
1. 传递函数 (Transfer function) H ( s )
传递函数的定义：x(t)、y(t)及其各阶导数的 初始值为零，系统输出信号的拉普拉斯变换 (拉氏变换)与输入信号的拉氏变换之比，记为
H (s) Y (s) X (s)
则
∫x(t)dt → ∫y(t)dt
e)频率保持性
若系统的输入为某一频率的谐波信号，则系统的稳态输
出将为同一频率的谐波信号，即
若
x(t)=Acos(ωt+φx)
则
y(t)=Bcos(ωt+φy)
线性系统的这些主要特性，特别是叠加 原理和频率保持性，在测量工作中具有重要 作用。
第二章 测试装置的基本特性
第二章 测试装置的基本特性
三. 回程误差
第二节 测试系统的静态特性
测试装置在输入量由小增大和由大减小的 测试过程中，对于同一个输入量所得到的两 个数值不同的输出量之间差值最大者为hmax。
第二章 测试装置的基本特性
四、分辨力
第二节 测试系统的静态特性
分辨力:指仪器可能检测出的输入信号最小 变化量。分辨力除以满量程称分辨率。
第二章 测试装置的基本特性
2. 频率响应函数
第三节 测试系统的动态响应特性ຫໍສະໝຸດ 第二章 测试装置的基本特性
第三节 测试系统的动态响应特性
传递函数与频率响应函数的区别
频率响应函数的求法：
1)已知H(S)求H(W):令：s=jw可得 2)初始条件为0情况下，同时测量输入
和输出，由傅里叶变化求: H（w）=Y(w)/x(w) 3)实验求法：
即:
若
x(t) → y(t)
则
kx(t) → ky(t)
c)微分性
系统对原输入信号的微分等于原输出信号的微分，即
若
x(t) → y(t)
则
x'(t) → y'(t)
第二章 测试装置的基本特性
第一节 概述
d)积分性
当初始条件为零时，系统对原输入信号的积分等于原
输出信号的积分，即
若
x(t) → y(t)
第二章 测试装置的基本特性
第三节 测试系统的动态响应特性
x(t)
h(t)
y(t)
系统分析中的三类问题
1)当输入、输出是可测量的(已知)，可以通过它们推断系统的传输特 性。 (系统辨识)
2)当系统特性已知，输出可测量，可以通过它们推断导致该输出的输 入量。 (反求)
3)如果输入和系统特性已知，则可以推断和估计系统的输出量。(预测 )
五. 静态响应特性的其他描述
漂 移:是指测试系统在输入不变的条件下,
输出随时间变化的趋势。 零点漂移:测量装置的输出零点偏离原始零点
的距离； 灵敏度漂移：材料性质的变化引起的输入输出 关系（斜率）的变化。
总误差=零点漂移+灵敏度漂移
第二章 测试装置的基本特性
第三节 测试系统的动态响应特性
在对动态物理量进行测试时，测试装置的输出 变化是否能真实地反映输入变化，则取决于测试 装置的动态响应特性。
线性误差= max/(Ymax-Ymin)×100%
标定曲线：静态标定
拟合直线：
1、端点法（最小值与最大 值连线）
2、最小二乘法（两者的 偏差Bi平方最小）
第二章 测试装置的基本特性
二. 灵敏度
第二节 测试系统的静态特性
当测试装置的输入x有一增量△x，引起输出y 发生相应的变化△y时，则定义:
S=△y/△x