过程控制工程过程动态特性分析

(一)概述1.过程控制概念：采用数字或模拟控制方式对生产过程的某一或某些物理参数进行的自动控制。

2.学科定位：过程控制是控制理论、工艺知识、计算机技术和仪器仪表知识相结合而构成的一门应用学科。

3.过程控制的目标：安全性，稳定性，经济性。

4.过程控制主要是指连续过程工业的过程控制。

5.过程控制系统基本框图：6.过程控制系统的特点:1)被控过程的多样性2)控制方案的多样性,包括系统硬件组成和控制算法以及软件设计的多样性。

3)被控过程属慢过程且多属参数控制4)定值控制是过程控制的主要形式5)过程控制有多种分类方法。

过程控制系统阶跃应曲线：7.衰减比η：衡量振荡过程衰减程度的指标，等于两个相邻同向波峰值之比。

即：8.衰减率ϕ：指每经过一个周期以后，波动幅度衰减的百分数，即：衰减比常用表示。

9.最大动态偏差y1：被控参数偏离其最终稳态值的最大值。

衡量过程控制系统动态准确性的指标10.超调量：最大动态偏差占稳态值的百分比。

11.余差：衡量控制系统稳态准确性的性能指标。

12.调节时间：从过渡过程开始到结束的时间。

当被控量进入其稳态值的范围内，过渡过程结束。

调节时间是过程控制系统快速性的指标。

13.振荡频率：振荡周期P的倒数，即：当相同，越大则越短；当相同时，则越高，越短。

因此，振荡频率也可衡量过程控制系统快速性。

被控对象的数学模型（动态特性）：过程在各输入量(包括控制量与扰动量)作用下，其相应输出量(被控量)变化函数关系的数学表达式。

14. 被控对象的动态特性的特点：1单调不振荡。

2具有延迟性和大的时间常数。

3具有纯时间滞后。

4具有自平衡和非平衡特性。

5非线性。

(二)过程控制系统建模方法机理法建模：根据生产过程中实际发生的变化机理，写出各种有关方程式，从而得到所需的数学模型。

测试法建模：根据工业过程的输入、输出的实测数据进行某种数学处理后得到的模型。

经典辨识法：测定动态特性的时域方法，测定动态特性的频域方法，测定动态特性的统计相关法。

1.过程控制系统的组成：被控对象，用于生产过程参数检测的检测与变送仪表，控制器，执行机构，报警、保护和连锁等其他部件。

2.控制参数：K（放大系数）、T（时间常数）、τ（纯延迟时间）3.一阶惯性环节的传递函数：G（s）=k/（Ts+1）4.流量特性：指流体流过阀门的相对流量Qr和相对开度Lr之间的函数关系，即Qr=f（Lr）。

理想流量特性：指阀前后压差保持不变的特性。

主要有直线、对数、抛物线、快开四中。

工作流量特性：指在实际生产中，调节阀前后压差总是变化的时候的流量特性。

工作流量特性与管道系统阻力有关。

（串联管道和并联管道的工作流量特性）流量系数的定义：温度为5到10摄氏度的水，在10*5 Pa的压降下，每小时流过调节阀水量的立方米数，以符号Kv表示。

流量系数对于选定控制阀的口径和结构有着重要作用。

5.建模的方法：机理法建模和测试法建模。

机理法：根据生产过程中实际发生的变化机理，写出各种有关的平衡方程。

测试法：根据工业过程的输入和输出的实际数据进行某种数学处理后得到的模型。

6.PID中的P、I、D的作用：比例调节成比例的反映控制偏差，偏差一旦产生，比例调节就立即发挥作用，以减小偏差；积分调节主要用于消除余差；微分作用反映偏差的变化趋势，并能在偏差信号变得太大前，在系统中引入一个有效的早期修正，从而加快系统的动作速度，减少调节时间。

7.分程控制：在反馈系统中，一台控制器的输出可能同时的去控制两个或两个以上的控制阀工作，这些控制阀在控制器的某个信号段内从全关到全开（或从全开到全关），因此需要将控制器输出信号分成若干个信号段，每一个信号段控制一个控制阀。

9.积分控制中积分饱和产生的原因：a.控制器具有积分作用b.控制器处于开环作用c.偏差信号长期存在抗积分饱和的措施：限幅法，外反馈法，积分切除法（限定PI调节器的输出，积分分离法，遇限削弱积分法）10.PID参数对系统稳定性的影响：a.比例度越大相当于加大调节系统的开环增益，导致系统激动振荡不稳定，反之比例越小越稳定b.控制系统的开环增益与积分时间成反比，积分时间越长系统越稳定c.微分调节作用总是力图抑制被调量的振荡，偏差变化越剧烈，由D调节器给出的作用就越大，从而及时的抑制偏差的增长，提高系统的稳定性.11.串级控制系统的作用及特点：a.串级控制系统对进入副回路的扰动有很强的克服作用；B.由于副回路的存在，减小了对象的时间常数，提高了系统的响应速度；c.提高系统的工作频率，改善了系统控制质量；D.串级系统有一定的自适应能力主副控制器的选择：A.主控制器必须具有积分作用，一般都采用PI控制器。

1过程控制的任务和要求要求三项：安全性经济性稳定性，过程控制的任务就是在了解掌握工艺流程和生产过程的静态和动态特性的基础上，根据上述三项要求，应用理论对控制系统进行分析和综合，最后采用适宜的技术手段加以实现。

过程控制的任务是由控制系统的设计和实现来完成的。

2常用过程控制系统分为哪几类三类1.反馈控制系统（根据被控参数与给定值的偏差进行控制的）2.前馈控制系统（根据扰动量的大小进行控制的，扰动是控制的依据）3.前馈-反馈控制系统（前馈控制的主要优点是能迅速及时克服主要扰动对被控量的影响，而前馈反馈能控制利用的反馈控制克服其他扰动，能够使被控量迅速而准确的稳定在给定值上，提高系统的控制质量）1过程控制系统在运行中状态有几种?过程控制系统时域性能指标包括哪些？它们分别反应系统哪些方面性能？两种，一种是稳态，此时系统没有收到任何外来干扰，同时设定值保持不变，因而被调量也不会随时间变化，整个系统处于稳定平衡的工况。

一种是动态，当系统收到外来干扰的影响或者在改变了设定值之后原来的稳态受到破坏，各部分输入输出都发现变化。

时域性能指标（衰减比和衰减率，最大动态误差和超调量，残余偏差，调节时间和振荡频率）衰减比是衡量一个振荡过程的衰减程度的指标，它相当于两个相邻的波峰值之比。

衡量震荡频率过程衰减程度的另一个指标是衰减率，指的是每经过一个周期，波动幅度衰减的百分数。

最大动态误差和超调量最大动态误差是指设定阶跃响应中，过度过程开始后第一个波峰超过其新稳态值的幅度，最大动态偏差占被调量稳态变化幅度的百分比称为超调量残余偏差是指过渡结束之后被调量新的稳态值Y（∞）与新设定值r之间的差值，它是控制系统稳态准确性的衡量指标调节时间和振荡频率调节时间是从过渡过程开始到结束所需的时间过渡过程的振荡频率也可以作为衡量控制系统快速性的一个指标那你。

2什么是被控过程的特性？什么是被控过程的数学模型？目前研究过程数学模型的主要方法有哪些？指被控过程是否容易控制。

动态系统稳定性及控制策略分析动态系统稳定性及控制策略分析是一个在控制工程领域中非常重要的主题。

在现代工业中，各种动态系统用于控制和调节各个过程，以达到稳定和优化的目标。

因此，了解动态系统的稳定性及采取合适的控制策略是非常关键的。

动态系统稳定性是指系统在一定范围内是否能保持稳定状态的性质。

对于一个动态系统来说，存在两种基本的稳定性：渐进稳定性和非渐进稳定性。

渐进稳定性是指系统在经过一段时间后，可以逐渐趋向于稳定状态。

这种稳定性是一种理想的性质，能够确保系统能够从干扰和变动中恢复，并保持在期望的状态。

对于渐进稳定性的动态系统，我们可以采用一系列的控制策略来保持其稳定性，例如比例积分控制器（PI控制），模型预测控制（MPC）等。

非渐进稳定性是指系统在存在干扰或变动时，可能不会逐渐恢复到稳定状态，而是会产生震荡或跃迁的现象。

这种稳定性通常是由系统本身的非线性特性或者外界环境因素所引起的。

对于非渐进稳定性的动态系统，我们需要采取一些特殊的控制策略来防止系统失控，例如模糊控制，滑模控制等。

在动态系统的控制策略分析中，我们需要考虑系统的特点和目标，并选择合适的控制器来实现稳定。

在实际应用中，选择合适的控制策略是一个非常关键的步骤，它会直接影响到系统的性能和稳定性。

在选择控制策略时，我们首先需要对系统进行建模和分析，了解系统的动态特性和稳定性。

建模可以基于物理原理、实验数据或者数学模型。

然后，我们可以通过系统的传递函数、状态空间模型或者差分方程来分析系统的稳定性，包括极点分析、根轨迹分析等。

接下来，我们可以根据系统的特点，选择适当的控制策略。

常见的控制策略包括比例控制，积分控制，微分控制，先进控制策略如模型预测控制、自适应控制等。

对于线性系统，可以使用经典控制理论，例如PID控制器。

而对于非线性系统，则需要采用非线性控制方法，例如模糊控制、滑模控制等。

最后，在实际应用中，我们还需要考虑到各种约束和限制条件。

例如，系统的动态响应时间、稳态误差、控制器的参数设定等。

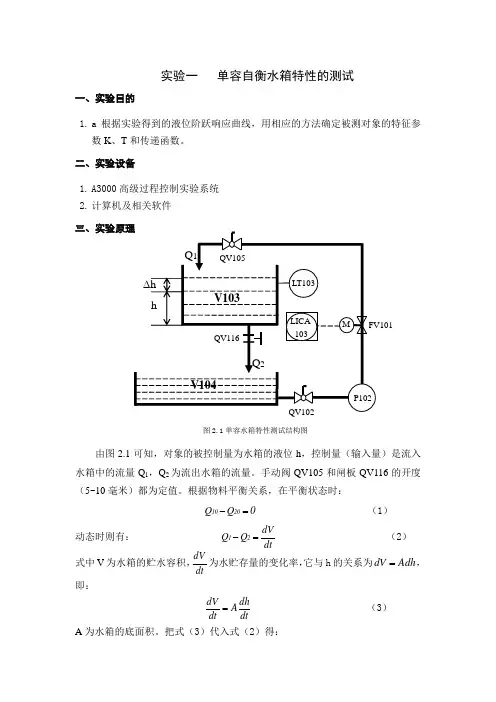
实验一 单容自衡水箱特性的测试一、实验目的1. a 根据实验得到的液位阶跃响应曲线，用相应的方法确定被测对象的特征参数K 、T 和传递函数。

二、实验设备1. A3000高级过程控制实验系统2. 计算机及相关软件 三、实验原理由图2.1可知，对象的被控制量为水箱的液位h ，控制量（输入量）是流入水箱中的流量Q 1，Q 2为流出水箱的流量。

手动阀QV105和闸板QV116的开度（5~10毫米）都为定值。

根据物料平衡关系，在平衡状态时：0Q Q 2010=- （1） 动态时则有： dtdVQ Q 21=- （2） 式中V 为水箱的贮水容积，dtdV为水贮存量的变化率，它与h 的关系为Adh dV =，即：dtdhA dt dV = （3） A 为水箱的底面积。

把式（3）代入式（2）得：QV116V104V103h∆h QV105QV102P102LT103LICA 103FV101MQ 1Q 2图2.1单容水箱特性测试结构图图2.2 单容水箱的单调上升指数曲线dtdhA=-21Q Q （4） 基于S 2R h Q =，R S 为闸板QV116的液阻，则上式可改写为dtdhA R h Q S =-1，即：或写作：1)()(1+=TS Ks Q s H （5） 式中T=AR S ，它与水箱的底积A 和V 2的R S 有关；K=R S 。

式（5）就是单容水箱的传递函数。

若令SR s Q 01)(=，R 0=常数，则式（5）可改为： TS KR S R K S R T S T K s H 0011/)(0+-=⨯+= 对上式取拉氏反变换得： )e -(1KR h(t)t/T0-= （6）当∞→t 时0KR )h(=∞，因而有=∞=0R )h(K 阶跃输入输出稳态值。

当t=T 时，则)h(KR )e-(1KR h(T) 001∞===-0.6320.632。

式（6）表示一阶惯性环节的响应曲线是一单调上升的指数函数，如图2.2所示。

什么是动态控制原理动态控制原理是指通过对系统的输入和输出进行监测和分析，从而实现对系统动态行为的控制和调节的一种控制理论。

动态控制原理在工程控制、自动化、机械设计等领域有着广泛的应用，它可以帮助我们更好地理解和控制各种动态系统的行为。

动态控制原理的核心思想是通过对系统的动态特性进行建模和分析，从而设计出合适的控制策略，实现对系统的稳定性、响应速度和鲁棒性等性能指标的优化。

在实际应用中，我们常常会遇到各种各样的动态系统，比如电机控制系统、飞行器姿态控制系统、汽车悬挂系统等，这些系统都具有复杂的动态特性，需要通过动态控制原理来实现对其行为的精确控制。

动态控制原理的基本方法包括建立系统的数学模型、分析系统的动态特性、设计控制器、实现控制器的参数调节和系统性能评估等步骤。

首先，我们需要通过物理定律或实验数据建立系统的数学模型，这通常包括微分方程、差分方程或状态空间方程等形式。

然后，我们可以通过对系统的动态特性进行分析，比如阶跃响应、频域特性等，来了解系统的稳定性、阻尼比、自然频率等重要参数。

接着，我们可以根据系统的动态特性设计合适的控制器，比如比例-积分-微分（PID）控制器、模糊控制器、神经网络控制器等。

通过对控制器参数的调节和优化，我们可以实现对系统性能的改善和优化。

最后，我们需要对控制系统进行性能评估，比如稳定性分析、鲁棒性分析、鲁棒稳定裕度分析等，从而确保控制系统能够在各种工况下稳定可靠地工作。

动态控制原理的研究和应用对于提高系统的稳定性、响应速度、抗干扰能力等性能指标具有重要意义。

通过对系统动态行为的深入理解和精确控制，我们可以实现对各种复杂系统的精确控制，从而提高系统的工作效率和可靠性。

同时，动态控制原理的研究也为我们提供了一种全新的思维方式，帮助我们更好地理解和应用各种动态系统，为工程技术的发展和创新提供了重要的理论支持。

总之，动态控制原理是一种重要的控制理论，它通过对系统的动态特性进行建模、分析和控制，帮助我们实现对各种复杂系统的精确控制。

过程控制实验报告液位控制系统参数整定实验概述⼀、PID调节器中各参数对控制结果的影响1 ⽐例作⽤⽐例作⽤即成⽐例的反应控制系统的偏差信号，⼀旦有偏差产⽣，控制器⽴即产⽣控制作⽤，使偏差向减⼩的趋势变化。

⽐例系数的作⽤在于加快系统的响应速度，提⾼系统调节精度。

越⼤，系统的响应速度越快，系统的调节精度越⾼，也就是对偏差的分辨率(重视程度)越⾼，将会产⽣超调，甚⾄导致系统不稳定。

取值过⼩，则会降低调节精度，尤其是使响应速度缓慢，从⽽延长调节时间，使系统静态、动态环节变坏。

2 积分作⽤积分作⽤的强弱取决于积分时间常数。

越⼤，积分作⽤越弱，反之则越强。

积分环节的作⽤在于消除系统的稳态误差，提⾼系统的⽆差度。

积分作⽤系数越⼤，系统静态误差消除越⼤，但积分作⽤系数过⼤，在响应过程的初期会产⽣积分饱和现象，从⽽引起响应过程的较⼤超调。

若积分作⽤系数过⼩，将使系统的静态误差难以消除，影响系统的调节精度。

3 微分作⽤微分环节是响应系统偏差变化的环节，其作⽤主要是在响应过程中抑制偏差向任何⽅向的变化，并能在偏差信号的值变得太⼤之前，在系统中引⼊⼀个有效的早期修正信号，从⽽加快系统的动作速度，减⼩调节时间，对偏差变化进⾏提前预报。

但微分作⽤太强，会引起被控参数⼤幅度变动，使过程产⽣振荡，微分作⽤太弱，导致静差较⼤。

因此，适当的加⼊微分作⽤不但会增加控制过程的稳定性，⽽且能使静差减⼩。

上⾯的分析表明，⽐例、积分、微分三者之间的关系是相互改善⼜相互制约的。

⽐例、积分、微分环节的综合作⽤使PID控制具有结构简单、物理意义明确、鲁棒性强及稳态⽆静差等优点。

因此，PID控制算法在⼯业控制中处于主导地位。

随着科学技术的发展特别是计算机的诞⽣和发展，涌现出许多新的控制⽅式，然⽽直到现在，PID控制仍有⾮常⼴泛的应⽤。

⼆、参数整定实验原理调节器在控制系统中将被调参数的测量值与给定值进⾏⽐较，得到偏差值，根据偏差进⾏逻辑判断和数学运算，产⽣⼀个使偏差减⼩甚⾄为零的控制信号，参数整定的实验⽬的就是根据被控过程的特性确定PID调节器的⽐例度δ，积分时间TI及微分时间TD的⼤⼩，以达到较好的控制效果在简单的过程控制系统中，调节器参数整定通常以系统瞬态响应的衰减率为主要指标，保证系统具有⼀定的稳定裕量。

第一章1.过程控制系统：是指工业生产过程中自动控制系统的被控量是温度、压力、流量、液位、成分等一些过程变量的系统2.控制系统均由测量元件、变送器、调节器、调节阀和被控过程等环节构成。

如果把测量元件、变送器、调节器、调节阀统称为过程检测控制仪表，则一个简单的过程控制系统是由被控过程和过程检测控制仪表两部分组成3.过程控制系统的分类：按被控参数名称，按控制系统完成的功能，按调节器的控制规律，按被控量的多少，按采用常规仪表和计算机按过程控制系统的结构特点来分类：1反馈控制系统：控制系统根据系统被控量的偏差进行工作，偏差值是控制的依据，最后达到消除或减小偏差的目的。

反馈控制系统可以是单回路，也可以是多个闭合回路的多回路控制系统。

2前馈控制系统：直接根据扰动量的大小进行工作按系统结构特点分 1）反馈控制系统 2）前馈控制系统 3）前馈—反馈控制系统按给定值信号特点 1）定制控制系统 2）程序控制系统 3）随动控制系统1-5采用DDZ-Ⅲ电动单元组合仪表。

氧气流量测量信号与供氧量给定值比较得其偏差值，经调节器按某种控制规律运算后输出控制信号，控制调节阀5的开度，改变供氧量的大小，达到控制供氧量的目的。

问：什么叫反馈？正/负反馈？反馈在控制系统中的意义？负反馈（negative feedback）：凡反馈信息的作用与控制信息的作用方向相反，对控制部分的活动起制约或纠正作用的，称为负反馈。

正反馈（positive feedback ）：凡反馈信息的作用与控制信息的作用方向相同，对控制部分的活动起增强作用的，称为正反馈前者使输出起到与输入相反的作用，使系统输出与系统目标的误差减小，系统趋于稳定第二章1被控过程－被控制的生产工艺设备（加热炉、贮罐）2.数学模型－被控过程在各输入量（控制量、扰动量）作用下，其相应输出量(被控量)变化函数关系的数学表达式。

非参数模型：曲线表示的。

如阶跃响应曲线等。

参数模型：用数学方程式或函数表示的。

控制作用μ干扰作用λ被调量G 0μ(s )G 0λ(s )图1-9 对象的输入、输出量第二节 热工控制对象的动态特性一、概述自动控制系统是由控制对象和自动控制设备组成的，控制对象是自动控制系统中的一个重要组成部分。

控制对象的输出就是控制系统的被调量，控制对象的输入信号是引起被调量变化的各种因素（包括扰动作用和控制作用），如图1-9所示。

要分析研究控制系统的工作质量，设计或改造自动控制系统，首先必须分析控制对象的动态特性，并根据它来正确地选择和使用自动控制设备，确定调节器的最佳整定参数，使控制设备与控制对象相互协调配合，构成一个合理的控制系统，才能获得预期的控制效果，对于机组运行人员来说，熟悉控制对象的动态特性，也是正确使用好控制系统的必要前提：所以，研究热工控制对象的动态特性，是研究控制系统、实现生产过程自动化的基础工作。

控制对象的动态特性就是控制对象在动态变化过程中各种输入信号与输出信号之间的关系。

对象的输入量至输出量的信号联系称之为通道；控制作用到输出量（被调量）的信号联系称为控制通道；干扰作用至输出量的信号联系称为干扰通道。

一般热工对象对于不同的输入信号所引起的被调量的变化特性是不同的，或者说同一对象的不同信号通道的传递函数（或微分方程）不同。

要全面了解对象的动态特性，就要了解各通道的动态特性，这往往是比较困难的。

由于控制通道在控制系统中的闭环以内，而控制作用又是经常、自动、反复地进行，所以它的动态特性较强地影响控制系统的稳定性。

影响控制对象输出的扰动分为外部扰动和内部扰动。

凡是来自控制系统之外，引起被调量发生变化的各种原因，都称为外扰，而控制系统内部的扰动称为内扰。

例如给水控制系统，给水流量和蒸汽流量的变化都会引起水位变化，但蒸汽流量的变化是用户需求变化引起的，调节系统本身无法控制，是系统的外扰，而给水母管压力变化引起的给水流量的变化是调节系统可以控制的，是系统的内扰。

外扰通道在控制系统的闭环以外，在一般情况下，外扰是随机的、短暂的、一次发生的，所以它的动态特性只影响调节过程中的被调量的幅值。