“隐圆”最值问题演示教学

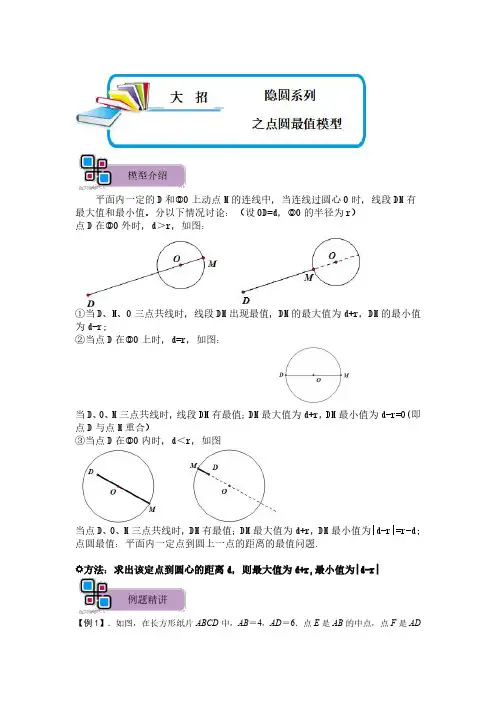
模型介绍平面内一定的D和⓪O上动点M的连线中，当连线过圆心O时，线段DM有最大值和最小值。

分以下情况讨论：（设OD=d，⓪O的半径为r）点D在⓪O外时，d＞r，如图：①当D、M、O三点共线时，线段DM出现最值，DM的最大值为d+r，DM的最小值为d-r;②当点D在⓪O上时，d=r，如图：当D、O、M三点共线时，线段DM有最值；DM最大值为d+r，DM最小值为d-r=0(即点D与点M重合）③当点D在⓪O内时，d＜r，如图当点D、O、M三点共线时，DM有最值；DM最大值为d+r，DM最小值为|d-r|=r-d;点圆最值：平面内一定点到圆上一点的距离的最值问题.方法：求出该定点到圆心的距离d，则最大值为d+r,最小值为|d-r|例题精讲【例1】．如图，在长方形纸片ABCD中，AB＝4，AD＝6．点E是AB的中点，点F是AD边上的一个动点．将△AEF沿EF所在直线翻折，得到△GEF．则GC长的最小值是（）A．B．C．2D．2解：以点E为圆心，AE长度为半径作圆，连接CE，当点G在线段CE上时，GC的长取最小值，如图所示根据折叠可知：GE＝AE＝AB＝2．在Rt△BCE中，BE＝AB＝2，BC＝6，∠B＝90°，∴CE＝＝2，∴GC的最小值＝CE﹣GE＝2﹣2．故选：A．变式训练【变式1-1】.如图，在平行四边形ABCD中，AB＝6，AD＝2，∠A＝45°，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A′MN，连接A′C，则A′C长度的最小值是．解：如图，连接MC；过点M作ME⊥CD，交CD的延长线于点E．∵四边形ABCD为平行四边形，∴AD∥BC，AD＝BC＝2，CD＝AB＝6，∵点M为AD的中点，∠A＝45°，∴DM＝MA＝，∠MDE＝∠A＝45°，∴ME＝DE＝DM＝1，∴CE＝CD+DE＝6+1＝7，由勾股定理得：CM2＝ME2+CE2，∴CM＝＝5；由翻折变换的性质得：MA′＝MA＝，点A′在以M为圆心，为半径的圆上显然，当折线MA′C与线段MC重合时，线段A′C的长度最短，此时A′C＝MC﹣MA′＝5﹣＝4，故答案为4．【变式1-2】．如图，矩形ABCD中，AB＝6，BC＝9，以D为圆心，3为半径作⊙D，E为⊙D上一动点，连接AE，以AE为直角边作Rt△AEF，使∠EAF＝90°，tan∠AEF＝，则点F与点C的最小距离为．解：如图取AB的中点G，连接FG．FC．GC．∵∠EAF＝90°，tan∠AEF＝，∴＝，∵AB＝6，AG＝GB，∴AG＝GB＝3，∵AD＝9，∴＝＝，∴＝，∵四边形ABCD是矩形，∴∠BAD＝∠B＝∠EAF＝90°，∴∠FAG＝∠EAD，∴△FAG∽△EAD，∴FG：DE＝AF：AE＝1：3，∵DE＝3，∴FG＝1，∴点F的运动轨迹是以G为圆心1为半径的圆，∵GC＝＝3，∴FC≥GC﹣FG，∴FC≥3﹣1，∴CF的最小值为3﹣1．故答案为3﹣1．【例2】.如图，△ABC中，AB＝AC，BC＝24，AD⊥BC于点D，AD＝5，P是半径为3的⊙A上一动点，连结PC，若E PC的中点，连结DE，则DE长的最大值为_______解：如图，连接PB，∵AB＝AC，AD⊥BC，∴CD＝DB＝BC＝12，∵点E为AC的中点，∴DE是△PBC的中位线，∴DE＝PB，∴当PB取最大值时，DE的长最∵P是半径为3的⊙A上一动点，∴当PB过圆心A时，PB最大，∵BD＝12，AD＝5，∴AB＝，∵⊙A的半径为3，∴PB的最大值为13+3＝16，∴DE长的最大值为8，故选：A．变式训练【变式2-1】.如图，在正方形ABCD中，AB＝2，F是BD边上的一个动点，连接AF，过点B作BE⊥AF于E，在点F变化的过程中，线段DE的最小值是．解：如图，∵BE⊥AF于E，∴E在以AB为直径圆心为O的圆上，∴当O、E、D三点共线的时候线段DE最小，∵AB＝2，四边形ABCD为正方形，∴AO＝1＝OE，AD＝2，∴OD＝＝，∴段DE最小值为OD﹣OF＝﹣1．故答案为：﹣1．【变式2-2】．如图，AB是⊙O的直径，点C在半圆的中点，且BC＝4cm，点D是上的一个动点，连接BD，过C点作CH⊥BD于H，连接AH，在点D的运动过程中，AH 长度的最小值是．解：连接AC，取BC的中点T，连接AT，TH．∵AB是直径，∴∠ACB＝90°，∵点C在半圆的中点，∴＝，∴AC＝CB＝4，∵CT＝TB＝2，∴AT＝＝＝2，∵CH⊥BD，∴∠CHB＝90°，∴点H在以BC为直径的圆上运动，∵CT＝TB，∴HT＝BC＝2，∵AH≥AT﹣HT＝2﹣2，∴AH的最小值为2﹣2，故答案为：2﹣2．1．如图，四边形ABCD为矩形，AB＝3，BC＝4，点P是线段BC上一动点，点M为线段AP上一点，∠ADM＝∠BAP，则BM的最小值为（）A．B．C．﹣D．﹣2解：如图，取AD的中点O，连接OB，OM．∵四边形ABCD是矩形，∴∠BAD＝90°，AD＝BC＝4，∴∠BAP+∠DAM＝90°，∵∠ADM＝∠BAP，∴∠ADM+∠DAM＝90°，∴∠AMD＝90°，∵AO＝OD＝2，∴OM＝AD＝2，∴点M在以O为圆心，2为半径的⊙O上，∵OB＝＝＝，∴BM≥OB﹣OM＝﹣2，∴BM的最小值为﹣2．故选：D．2．如图，△ABC为等边三角形，AB＝3．若P为△ABC内一动点，且满足∠PAB＝∠ACP，则线段PB长度的最小值为（）A．1.5B．C．D．2解：∵△ABC是等边三角形，∴∠ABC＝∠BAC＝60°，AC＝AB＝3，∵∠PAB＝∠ACP，∴∠PAC+∠ACP＝60°，∴∠APC＝120°，∴点P的运动轨迹是，设所在圆的圆心为O，当O、P、B共线时，PB长度最小，设OB交AC于D，如图所示：此时PA＝PC，OB⊥AC，则AD＝CD＝AC＝，∠PAC＝∠ACP＝30°，∠ABD＝∠ABC＝30°，∴PD＝，BD＝，∴PB＝BD﹣PD＝﹣＝．故选：B．3．如图，在Rt△ABC中，∠ACB＝90°，AB＝2，点D为线段AB的中点，将线段BC绕点B顺时针旋转90°，得到线段BE，连接DE，则DE最大值是．解：如图，将线段BD绕点B顺时针旋转90°，得到线段BP，连接PE，PD，则DB＝PB，∠DBP＝90°，∵将线段BC绕点B顺时针旋转90°，得到线段BE，∴BC＝BE，∠CBE＝90°，∴∠CBD＝∠EBP，∴△CBD≌△EBP（SAS），∴PE＝DC，∵在Rt△ABC中，∠ACB＝90°，AB＝2，点D为线段AB的中点，∴DB＝CD＝AB＝1，∴PE＝1，PB＝1，∴DP＝，∵PD+PE≥DE，∴DE≤+1，∴DE最大值为+1，故答案为：+1．4．如图，在边长为2的正方形ABCD中，E，F分别是边DC，CB上的动点，且始终满足DE＝CF，AE，DF交于点P，则∠APD的度数为90°；连接CP，线段CP的最小值为﹣1．解：∵四边形ABCD是正方形，∴AD＝CD，∠ADE＝∠DCF＝90°，在△ADE和△DCF中，，∴△ADE≌△DCF（SAS），∴∠DAE＝∠CDF，∵∠CDF+∠ADF＝∠ADC＝90°，∴∠ADF+∠DAE＝90°，∴∠APD＝90°，取AD的中点O，连接OP，则OP＝AD＝×2＝1（不变），根据两点之间线段最短得C、P、O三点共线时线段CP的值最小，在Rt△COD中，根据勾股定理得，CO＝＝＝，所以，CP＝CO﹣OP＝﹣1．故答案为：90°，﹣1．5．如图，在△ABC中，∠BAC＝90°，AC＝8，BC＝10，AD是BC边上的高，E、F分别为边DC，DA上的动点，且DE：DF＝4：3，射线AE与BF相交于点M，若连接CM，则线段CM的最小值为．解：如图1，连接EF，并延长EF交边AB于点G，∵在△ABC中，∠BAC＝90°，AC＝8，BC＝10，∴，∴AC：AB＝4：3，∴AC：AB＝DE：DF＝4：3，∴，∵∠BAC＝∠FDE＝90°，∴△BAC∽△FDE，∴∠GBE＝∠DFE，∵AD是BC边上的高，∴AD⊥BC，∴∠DFE+∠DEF＝90°，∴∠GBE+∠DEF＝90°，∴∠BGE＝90°，∴EG是△ABE的高，∵AD是△ABE的BE边上的高，∴BM是△ABE的AE边上的高，∴BM⊥AM，∴∠AMB＝90°，∴点M在线段AB为直径的上，如图2，作以线段AB为直径的，取圆心O，连接OC交于点N，则当点O、M、C 三点共线时，线段CM的最小值，如图3，∵AB＝6，点O是圆心，∴OA＝ON＝3，∵∠BAC＝90°，AC＝8，∴，∴线段CM的最小值即，故答案为：．6．如图，直角梯形ABCD中，AB∥DC，∠B＝90°，AB＝1，BC＝2，CD＝3，以B为圆心，半径为1的弧交BC于M，E是线段CD上一动点，EG⊥AD，垂足为G，F是弧AM 上一动点，则EG+EF的最小值为．解：作AH⊥CD于点H是矩形．DH＝CD﹣AB＝3﹣1＝2，AH＝BC＝2．则AH＝DH，△ADH是等腰直角三角形．则∠ADC＝45°．延长BC到M使CM＝BC＝2，作MN⊥AD于点N，交CD于点K．则当E到K时，EG+EF 取得最小值．∵∠ADC＝90°，MN⊥AD，∴△DNK是等腰直角三角形，∠NKD＝∠CKM＝45°，同理△CMK是等腰直角三角形．则CK＝CM＝2，KM＝CM＝2，∴DK＝CD﹣CK＝3﹣2＝1，∴NK＝DK＝．则MN＝MK+NK＝2+＝，则EG+EF的最小值是﹣1＝．故答案是：．7．如图，在△ABC中，∠ACB＝90°，AB＝4，点O是AB的中点，以BC为直角边向外作等腰Rt△BCD，连接OD，当OD取最大值时，则∠ODB的度数是．解：如图，将△ODB绕点B逆时针旋转90°，得到△ECB，连接CO，EO，∵将△ODB绕点B逆时针旋转90°，得到△ECB，∴OB＝BE，OD＝CE，∠BCE＝∠BDO，∠OBE＝90°∵CE≤OC+OE∴当点O在CE上时，CE有最大值，即OD取最大值，∵BE＝OB，∠ABE＝90°∴∠BOE＝45°∵点O是AB中点，∠ACB＝90°∴CO＝BO∴∠ECB＝∠CBO，∵∠EOB＝∠ECB+∠OBC＝45°∴∠ECB＝22.5°＝∠BDO故答案为：22.5°8．如图，正方形ABCD的边长为2，点E为正方形外一个动点，∠AED＝45°，P为AB中点，线段PE的最大值是．解：如图，若点E在正方形右侧，连接AC，BD交于点O，连接PO，EO，∵∠AED＝45°，∠ACD＝45°，∴A，C，E，D四点共圆，∵正方形ABCD的边长为2，∴OE＝OD＝BD＝，∵P为AB的中点，O是BD的中点，∴OP＝AD＝，∵PE≤OP+OE＝+，∴当点O在线段PE上时，PE＝OP+OE＝+，即线段PE的最大值为+，如图，点E在正方形ABCD上方，作斜边为AD的等腰直角△AOD，∠AOD＝90°，则点E在以O为圆心，OA为半径的圆上，∴当点P，点O，点E共线时，PE的值最大，过点O作ON⊥AB，交BA延长线于点N，∵AD＝2，AO＝DO，∠AOD＝90°∴AO＝，∠OAD＝45°，∵ON⊥AB，AD⊥AB∴∠NAO＝∠NOA＝45°∴AN＝NO＝∴PO＝＝＝∴PE最大值为+＞+，故答案为：+9．如图，在矩形ABCD中，AB＝4，BC＝6．（1）如图①，点E是AB的中点，点F是BC边上一点，将△BEF沿EF折叠，点B的对应点为点P，求CP的最小值；（2）如图②，若点P是矩形ABCD内部一点，且∠BPC＝90°，求PD取得最小值时，BP的长；（3）如图③，若点P是矩形ABCD内部一点，且∠PAD+∠PBC＝60°，求AP+BP的最大值.解：（1）如图1，∵点E是AB的中点，∴BE＝AB＝2，由折叠知，PE＝BE＝2，∴点P是在以E为圆心，2为半径的半圆上运动，当点E，P，C共线时，CP最小，∵四边形ABCD时矩形，∴∠ABC＝90°，∴CE＝＝＝2，＝CP′＝CE﹣EP′＝2﹣2；∴CP最小（2）如图2，∵∠BPC＝90°，∴点P在以BC为直径的半圆O上运动，当点D，P，O共线时，PD最小，在Rt△COD中，CD＝4，OC＝BC＝3，∴OD＝5，∴P′D＝OD﹣OP′＝5﹣3＝2，作P′Q⊥BC于Q，∵∠OQP′＝∠BCD＝90°，∠COD为公共角，∴△OQP′∽△OCD，∴，∴，∴OQ＝，QP′＝，在Rt△BQP′中，QP′＝，BQ＝OB+OQ＝3+＝，∴BP′＝＝，∴当PD取得最小值时，BP的长为：；（3）如图3，∵四边形ABCD是矩形，∴∠CAB＝∠BAD＝90°，∴∠CAB+∠BAD＝180°，∵∠PAD+∠PBC＝60°，∴（∠CAB+∠BAD）﹣（∠PAD+∠PBC）＝120°，∴∠PAB+∠PBA＝120°，在△ABP中，∠APB＝180°﹣120°＝60°，延长BP至E，使PE＝PA，∴∠E＝∠PAE，∵∠E+∠PAE＝∠APB＝60°，∴∠E＝30°，在AB的右侧作等边三角形ABO，以O为圆心，AB为半径作圆O，则点E优弧AEC上运动，当BE为直径时，即点P在点O处时，AP+BP最大，最大为直径BE′＝2AB＝8．10．如图，已知四边形ABCD为正方形，△AEF为等腰直角三角形，∠AEF＝90°，连接FC，G为FC的中点，连接GD，ED．（1）如图①，当点E在AB边上时，请直接写出DE，DG的数量关系；（2）如图②，将图①中的△AEF绕点A逆时针旋转，其他条件不变．①探究（1）中的结论是否成立？若成立，请证明；若不成立，请说明理由；②若AD＝4，AE＝1，求DG的最大值和最小值．解：（1）DE＝DG，理由如下：如图①，连接EG，延长EG交BC的延长线于M，连接DM．∵四边形ABCD是正方形，∴AD＝CD，∠B＝∠ADC＝∠DAE＝∠DCB＝∠DCM＝90°，∵∠AEF＝∠B＝90°，∴EF∥CM，∴∠CMG＝∠FEG，∵∠CGM＝∠EGF，GC＝GF，∴△CMG≌△FEG（AAS），∴EF＝CM，GM＝GE，∵AE＝EF，∴AE＝CM，∴△DCM≌△DAE（SAS），∴DE＝DM，∠ADE＝∠CDM，∴∠EDM＝∠ADC＝90°，∴DG⊥EM，DG＝GE＝GM，∴△EGD是等腰直角三角形，∴DE＝DG．（2）①结论成立，理由如下：如图②，连接EG，延长EG到M，使得GM＝GE，连接CM，DM，延长EF交CD于R．∵EG＝GM，FG＝GC，∠EGF＝∠CGM，∴△CGM≌△FGE（SAS），∴CM＝EF，∠CMG＝∠GEF，∴CM∥ER，∴∠DCM＝∠ERC，∵∠AER+∠ADR＝180°，∴∠EAD+∠ERD＝180°，∵∠ERD+∠ERC＝180°，∴∠DCM＝∠EAD，∵AE＝EF，∴AE＝CM，∴△DAE≌△DCM（SAS），∴DE＝DM，∠ADE＝∠CDM，∴∠EDM＝∠ADC＝90°，∵EG＝GM，∴DG＝EG＝GM，∴△EDG是等腰直角三角形，∴DE＝DG；②∵AE＝1，△AEF绕点A旋转，∴点E在以点A为圆心，1为半径的圆A上运动，如图③，当点A、E、D三点共线，且点E在点A的左侧时，DE最大，此时DE＝AD+AE＝4+1＝5，由①可知，DE＝DG，∴DG＝DE＝，即DG的最大值为；如图④，当点A、E、D三点共线，且点E在点A的右侧时，DE最小，此时DE＝AD﹣AE＝4﹣1＝3，由①可知，DE＝DG，∴DG＝DE＝，即DG的最小值为；综上所述，DG的最大值为，最小值为．11．（1）如图1，A、B是⨀O上的两个点，点P在⨀O上，且△APB是直角三角形，⨀O 的半径为1①请在图1中画出点P的位置；②当AB＝1时，∠APB＝30°；（2）如图2，⨀O的半径为5，A、B为⨀O外固定两点（O、A、B三点不在同一直线上），且OA＝9，P为⊙O上的一个动点（点P不在直线AB上），以PA和AB为作平行四边形PABC，求BC的最小值并确定此时点P的位置；（3）如图3，A、B是⊙O上的两个点，过A点作射线AM⊥AB，AM交⨀O于点C，若AB＝3，AC＝4，点D是平面内的一个动点，且CD＝2，E为BD的中点，在D的运动过程中，求线段AE长度的最大值与最小值．解：（1）①如图1，△APB、△AP′B是直角三角形；②在Rt△APB中，AB＝AP，∴∠APB＝30°，故答案为：30；（2）四边形PABC是平行四边形，∴BC＝AP，∴BC的最小值即AP的最小值，∵当P为OA与⊙O的交点时，AP最小，∴AP的最小值为9﹣5＝4，即BC的最小值为4；（3）连接BC，∵AM⊥AB，∴∠CAB＝90°，∴BC是⊙O的直径，∵点D是平面内的一个动点，且CD＝2，∴点D的运动路径为以C为圆心，以2为半径的圆，在直角△ABC中，BC＝＝＝5，∵O是直角△ABC斜边BC上的中点，∴AO＝BC＝，∵E是BD的中点，O是BC的中点∴OE＝CD＝1，∴AE的最小值是AO﹣OE＝，最大值是AO+OE＝．12．【问题提出】（1）如图①，四边形ABCD为正方形，以BC边为直径在BC上方作半圆O，P是上一点，若AB＝6，则DP的最小值为3﹣3；【问题探究】（2）如图②，在Rt△ABC中，∠ACB＝90°，BC＝4，AC＝3，CD是中线，将△ACD 沿CD折叠，得到△ECD，点A的对应点为E，连接AE，求AE的长；【问题解决】（3）如图③是一块矩形ABCD的场地，AB＝300m，AD＝600m，D为场地的出人口，点E在AD边上，且AE＝400m．按照规划，要在矩形内修建一个小型观光台P，且满足∠APE＝90°，在BC上修建休息亭M，并要在观光台P、休息台M以及出入口D之间规划道路PM，DM，为了节约成本，要使得线段PM，DM之和最短，试求PM+DM的最小值，并说明理由．（道路的宽度忽略不计）解：（1）如图1，连接OD，交⊙O于点P，则DP最小，∵四边形ABCD是正方形，∴∠BCD＝90°，CD＝BC＝AB＝3，在Rt△COD中，OC＝＝3，CD＝6，∴OD＝＝3，∴DP＝OD﹣OP＝3﹣3，故答案为：3﹣3；（2）设CD，AE交于点F，∵∠ACB＝90°，AC＝3，BC＝4，∴AB＝5，由折叠得：AE＝2AF，CD⊥AE，∵∠ACB＝90°，CD是中线，∴AD＝CD，∴∠ACD＝∠CAD，∵∠AFC＝∠ACB＝90°，∴△ACF∽△BAC，∴，∴＝，∴AF＝，∴AE＝2AF＝；（3）如图2，∵∠APE＝90°，∴点P在以AE为直径的⊙O上运动，作点D关于BC的对称点G，连接OG，交BC于M，交⊙O于P，则PM+DM最小，最小值为PG的长，∵四边形ABCD是矩形，∴CG＝CD＝AB＝300，∠ADC＝90°，在Rt△ODG中，DG＝CD+CG＝600，OD＝AD﹣OA＝600﹣200＝400，∴OG＝＝＝200，∴PG＝OG﹣OP＝200﹣200，∴PM+DM的最小值为：200﹣200．。

隐形圆（引圆）最值问题：我们首先要知道圆上一动点到平面内一定点距离的何时取得最小值和最大值；1》当定点在圆外时，如图所示动点P是在圆o上运动，定点C在圆o外，连接CO并延长，连接OP；我们令OC=d，OP=r；（1）当P，O，C三点不共线时P，O，C三点围成三角形，OC-OP<PC<OC+OP；即d-r<PC<d+r;（2）当P，O，C三点共线时，①P在P’处时，OC-OP=PC,即d-r=PC；②P在P1处时，OC+OP=PC,即d+r=PC；综上可得d-r≤PC≤d+r，PC min=d-r，PC max=d+r.2》当定点在圆内时（不与圆心重合）如图所示：动点P是在圆o上运动，定点C在圆o内，连接CO并双向延长，连接OP；我们令OC=d，OP=r；（1）当P，O，C三点不共线时P，O，C三点围成三角形，OP-OC<PC<OC+OP；即r-d<PC<d+r;（2）当P，O，C三点共线时，①P在P’处时，OP-OC=PC,即r-d=PC；②P在P1处时，OC+OP=PC,即d+r=PC；综上可得r-d≤PC≤d+r，PC min=r-d，PC max=d+r.1.折叠引圆：如图所示在矩形ABCD中，AB=4，AD=6.点E为AB边中点，F为边BC上一动点，以EF为折痕将三角形BEF折叠点B落在B’处，求线段DB’最小值.解析：由题中条件可知折痕EF 满足一定一动的特点，所以满足折叠引圆，根据折叠的性质我们可得到EB=EB ’=21AB=2,根据圆的定义可知，动点B ’是以E 为圆心，2为半径的圆上运动，而B ’的运动又与动点F 有关，我们如果我们将F 看成是从点B →C 的运动可得到B ’的轨迹，如下图所示，B ’的运动并不是完整的圆，而是一部分圆弧。

根据圆上一动点到圆外一定点的最小值分析可知，B ’D 取得最小值时，B ’，D ，E 三点共线，B ’在G 处；所以B ’D min =DE-EG,在直角三角形ADE 中，DE=，因为EG=EB=2，所以B ’D min =-2例1. 如图所示，四边形ABCD 是菱形，∠A=60o，AB=6，点E 是边AD 中点，动点F 是在线段AB 上由A →B 运动,到达B 点停止运动，102AE AD 22=+102连接EF，以EF为折痕将△AEF折叠，点A落在A’处.(1)求A’C长度最小值.(2)求A’的路径长.例2.如图所示矩形ABCD中，AB=8，AD=6，点E是AD边上的中点，点F是AB边上的动点，连接EF，以EF为折痕将△AEF折叠，点A落在A’处，求△A’BC的面积最小值.定角定弦引圆（隐圆）：如图所示，在平面内存在定点A，B.点P是平面内的一动点，且点∠P=a.像这类动点处存在一个角度恒为定角，且该角能放在一个三角形内，所对边为定边，那么该动点就是在圆上运动；这个定角就可以理解为圆周角，它所对的定边就是该圆周角所对的弦.（1）直角类型：如图1所示，在平面内存在定点A，B.点P是平面内的一动点，且点∠P=90o，根据上面定角定弦可知，∠P是圆周角，AB是它所对弦，因为∠P=90o，图1 图2（2）锐角类型:如图1所示，在平面内存在定点A，B.点P是平面内的一动点，且点∠P=a,且a<90o，根据上面定角定弦可知，∠P是圆周角，AB是它所对弦，此时的AB并不是直径，我们知道想要画出这个P所在的圆我们需要圆心和半径，或者找到直径；因为A，P，B三点都是圆上的点，∠A，∠B也是圆周角，点P在运动的时候∠A，∠B的大小是会发生改变的，，如图2所示.图1 图2（3）钝角类型：如图1所示，在平面内存在定点A，B.点P是平面内的一动点，且点∠P=a,且a>90o，根据上面定角定弦可知，∠P是圆周角，AB是它所对弦,此时我们发现钝角是无法构造到直角三角形中去的，那么我们就要想办法去转化，我们可以通过四点共圆的特点去转化，我们可以图1 图2图3例1. 如图所示，在矩形ABCD 中AB=8，AD=6，点Q 是边AD 边上一动点，连接CQ ，过点D 作DP ⊥CQ ，交CQ 于点P .(1) 求线段BP 最小值.(2) 如图2所示，点M 也是边AD 上的动点，求BM+PM 最小值.(3) 如图2所示，点M 是边AD 上的动点，求AM+PM 最小值21图1 图2例2.在三角形ABP中，AB=6，∠P=60o，求AP+BP最大值.例3.在等边三角形ABC中，D、E分别为边AC，AB上的动点，且AD=BE；BC=6，连接CE、BD交于点F.（1）.求∠CFD.（2）.求AF最小值.2.瓜豆原理引圆：瓜豆原理：从动点的运动状态与主动点吻合（主动点在直线上运动，从动点就会在直线上运动；主动点在圆上运动，从动点就会在圆上运动）(1)如图所示点A 、B 都是定点，点D 是圆B 上一动点，连接AD ，取AD 上一点E ，使=k ，此时点D 在圆B 上运动的时候就会带着点E 一起运动，那么点D 就是主动点，点E 就是从动点；（圆B 大小不变，k 为定值）∵=k （主动点与从动点之间的关联所在）∵点A 是定点∴我们可以将点E 所在图形是点D 所在图形关于点A 位似得到的如下图：圆的位似可以对其半径进行位似，即取AB 上一点C ，使=k ∵∠A=∠A ，==k ，∴△ABD ∽△ACE ，∴==k∴CE=kBD 为定值；所以点E 就是以点C 为圆心CE 为半径的圆上运动AD AEAD AEAB ACAD AE AB AC BD CE ABAC(2).如图所示，点A 、B 是平面内定点，点D 是圆B 上一动点，∠DAE=a ，=k ，此时点D 在圆B 上运动的时候就会带着点E 一起运动，那么点D 就是主动点，点E 就是从动点；（圆B 大小不变，k 为定值，a 角度为定值）这个可以看成（1）中图形旋转得到的；取AB 上一点C ，使=k ，将AC 以点A 为旋转中心逆时针旋转a得到C ’,易证△ACE ’∽△ABD ，所以==k ，即C ’E=kBD 所以点E 为C ’为圆心C ’E 为半径的圆上运动例1．如图，点A ，B 的坐标分别为(60)(06)A B C ，，，，为坐标平面内一点，BC M 为线段AC 的中点，连接OM ，当OM 取最大值时，点M 的坐标为__________________． AD AEAB ACBD E C'ABAC2．如图，△ACB中，CA＝CB＝4，∠ACB＝90°，点P为CA上的动点，连BP，过点A作AM⊥BP于M．当点P从点C运动到点A 时，线段BM的中点N运动的路径长为。

发现发现““隐形隐形””圆 巧求最小值在近几年的中考数学试题中，常有一些涉及到求线段最小值的问题.这些题目入手较难，得分率很低，分析其原因不难发现，学生对题目中运动变化的本质没有搞清楚.在这些蕴含运动变化的问题中，并没有显性的圆，但是仔细分析题目的条件，如果能发现某个点的运动路径是一个圆(或是一段弧)，可谓是“山重水复疑无路，柳暗花明又一村”，将会对问题的解决起着重要的作用.下面举例说明.一、翻折中的“隐形”圆例1 如图1，在Rt ABC ∆中，90,6,8C AC BC ∠=°==，点F在边AC 上，并且2CF =，点E 为边BC 上的动点，将CEF ∆沿直线EF 翻折，点C 落在点P 处，则点P 到边AB 距离的最小值是 .解 如图2，当点E 在BC 上运动时, PF 的长固定不变，即2PF CF ==.所以点P 在 以点F 为圆心，以2为半径的圆上运动.过点F 作FH AB ⊥交⊙F 于点P ，垂足为H ，此时PH 最短.由AFH ABC ∆∆:，得FH FA BC AB=.又由已知易得4,10AF AB ==.所以4810FH =，即165FH =.所以P 到AB 距离的最小值166255PH FH FP =−=−=.点评 本题关键的地方在于抓住无论点E 的位置在哪，翻折,FCE PF ∆的长度始终等 于FC 的长度，即2PF =.也就是说动点P 到定点F 的距离是定值2，所以点F 的运动路径是以点F 为圆心，2为半径的圆(或部分).如此，这个问题就最终转化为在圆上找一个到定直线距离最短的点.我们可以利用图3的模型1来作出直观解释.模型1 如图3，直线m 与⊙O 相离，过D 点O 作直线m 的垂线，垂足为点H ，交⊙O 与点P 、点Q ，则⊙O 上点P 到直线m 的距离最短，点Q 到直线m 的距离最长理由简述 在⊙O 上任意找一点P ′，过P ′作P H ′′⊥直线m ，垂足为点H ′.由三角形三边关系及直角三角形斜边大于直角边可得:OP P H OH OH ′′′′+>>，而OH OP PH =+,OP OP ′=，所以P H PH ′′>，所以点P 到直线m 的距离最短.类似的方法可以说明点P 到直线m 的距离最长.例2如图4，在边长为2的菱形ABCD 中，60,A M ∠=°对是AD 边的中点，N 是AB 边上一动点.将AMN ∆沿MN 所在的直线翻折得到A MN ′∆，连结A C ′，则A C ′长度的最小值是 .解 当点N 在AB 边上运动时，MA ′的长度固定不变，即1MA MA ′==，所以点A ′在以点M 为圆心，1为半径的圆上运动，如图5，连接CM ，与⊙M 交于点A ′，此时CA ′最短.过点C 作CG AD ⊥交AD 的延长线于点G .因为2,60CD CDG A =∠=∠=°，所以1,DG CG ==，在Rt CMG ∆中，由勾股定理，得CM == 点评 同例1，无论N 点在何处，沿MN 翻折后，线段MA ′的长度(1MA MA ′==)保持不变，而且点M 是定点，所以点A ′的运动轨迹是以M 为圆心，1为半径的圆(部分).要求A C ′的最小值，回归到模型1中，连结圆外定点C 与圆心M 与圆M 交于点A ′，此时A C ′的长度即为最小值.我们可以借助图6利用模型2来作出直观解释.模型2 如图6，点P 为⊙O 外一定点，连结PO 交⊙O 于点A ，延长线与⊙O 交于另一点B ，则PA 的长度为⊙O 外一点P 到⊙O 的最短距离，PB 的长度为⊙O 外一点P 到⊙O 的最长距离.理由简述 在⊙O 上再任意找一点A ′ ,连接PA ′，由三角形三边关系，可得OA PA OP ′′+>.又,OP OA AP OA OA ′=+=，所以PA PA ′>.类似的方法可以说明PB 的长度为⊙O 外一点P 到⊙O 的最长距离.例3 如图7，菱形ABCD 的边8,60AB B =∠=°,P 是AB 上一点，3,BP Q =是CD 边上一动点，将梯形APQD 沿直线PQ 折叠, A 的对应点为A ′.当 CA ′的长度最小时，CQ 的长为 .解 如图8，过C 作CE AB ⊥，连结AC .因为ABCD 是菱形，60B ∠=°，所以ABC ∆为等边三角形，所以84,3,12AE EB BP EP =====.要使CA ′的长度最小，则梯形APQD 沿直线PQ 折叠后A 的对应点A ′应落在CP 上，且对称轴PQ 应满足//PQ DE .由作图知，DEPQ 为平行四边形，所以1,817DQ EP CQ CD DQ ===−=−=.点评 点Q 在线段CD 上无论运动到何处，梯形APQD 沿直线PQ 折叠后PA ′的长度始终保持不变，因此A ′点的运动路径就是以点P 为圆心，PA 长为半径的圆.借助模型2，可知，当点A ′落在线段CP 与⊙P 的交点时，CA ′的长度最小.由PQ 平分,//APC CD AB ∠，可得CQ CP =.作CE AB ⊥，构造Rt CEP ∆，从而可以求出CP 的长.二、直角中的“隐形”圆例4 如图9，在正方形ABCD 中，动点,E F 分别从,D C 两点同时出发，以相同的速度在直线,DC CB 上移动.连结AE 和DF 交于点P ,由于点,E F 的移动，使得点P 也随之运动，请你画出点P 运动路径的草图.若2AD =,试求出线段CP 的最小值.解 由题意，可得DE CF =.又因为,90AD CD ADC DCB =∠=∠=°,所以ADE DCF ∆≅∆,所以DAE CDF ∠=∠.因为90ADP CDF ∠+∠=°，所以90DAE ADP ∠+∠=°.由于点P 在运动中保持90APD ∠=°.听以点P 的路径是一段以AD 为直径的弧.设AD 的中点为O ，连结OC 交弧于点P ，此时CP 的长度最小.在Rt ODC ∆中，OC ===，所以1CP OC OP =−=−. 点评 此题的本质是抓住动点,E F 在运动过程中，始终保持AE DF ⊥，即90APD ∠=°,这样点P 的运动路径就确定了，即点P 在以AD 为直径的圆弧上，再根据模型2求解即可.例5如图10, Rt ABC ∆中，,6,4,AB BC AB BC P ⊥==是ABC ∆内部的一个动点，且满足PAB PBC ∠=∠，则线段CP 长的最小值为 .解 因为90ABC ∠=°,所以90ABP PBC ∠+∠=°.又因为PAB PBC ∠=∠,所以90BAP ABP ∠+∠=°，即90APB ∠=°，所以点P 在以AB 为直径的⊙O 上.连结OC 交⊙O 于点P ，此时PC 最小，在Rt BCO ∆中，90,4,3OBC BC OB ∠=°==，可得5OC =,所以532PC OC OP =−=−=，即PC 最小值为2.点评 首先，根据题目的条件不难得出90APB ∠=°，从而可以证明点P 在以AB 直径的⊙O 上.利用模型2，连结OC ，与⊙O 交于点P ，此时PC 最小，利用勾股定理求出OC即可解决问题.以上例题说明，在求一类线段最值问题中，如果遇到动点的运动路径是圆时，只需利用上面提到的模型1或模型2就可以解决.然而难点在于如何知道动点的运动路径是圆，如何将这个隐身“圆”找出来?从以上例子中可以得出以下两种方法:①观察到定点的距离，即圆是到定点距离等于定长的点的集合;②“定弦对定张角”，如例5中线段AB是定值，当动点P在运动过程中，APB∠的大小不变等于90°(当然不一定为直角)，点P的运动路径也是圆(或弧).因此，教师在教学时，要让学生理解概念的本质，还要培养学生对常见模型的敏感性，从而在有限的考试时间内，能快速获得破解难题的策略.。

隐形圆圆有关问题第一讲“形”现“圆”形问题如图所示，在等腰直角三角形ABC中，AB= BC = 2,点P为等腰直角三角形ABC所在平面内一点，且满足PA丄PB,则PC的取值范围是圆是高中数学中一种简单但又非常重要的曲线，近几年高考题和高考模拟题中，经常会出现一类有关圆的题目，这类题目在条件中没有直接给出有关圆方面的信息，而是以隐性的形式出现，但我们通过分析和转化，最终都可以利用圆的知识求解.这类题目构思巧妙，综合性强，，充分考查了学生的数形结合、转化和化归等数学思想方法，处理这类题目关键在于能否把"隐形圆"找出来.圆作为几何图形，找“隐形圆”的一个角度可以从“形”的角度来发现.策略一由圆的定义(到定点的距离等于定长的点的轨迹)确定隐形圆例1 (1)如果圆(x —2a)2+ (y— a —3)2= 4上总存在两个点到原点的距离为1,则实数a的取值范围是________ .(2)( 2016 年南京二模)已知圆 O : x 2 + 寸=1,圆 M : (x — a)2 + (y — a + 4)2 = 1 •若圆M 上存在点P ,过点P 作圆O 的两条切线，切点为 A , B ,使得/ APB=60°则a 的取值范围为 ____________ .(3)( 2017年苏北四市一模)已知 A 、B 是圆C i : x 2 y 2 1上的动点,R ，直线 I : xcos + ysin = 2sin( + ) + 4 与圆 C : (x — m)2+6(y —掐m)2= 1均无公共点，则实数m 的取值范围是 ____________ .(5)( 2016年南通三模)在平面直角坐标系xOy 中，圆G ：x12 y 2 2 , 圆AB= .3 , P 是圆 C 2：(x 3)2 (y 4)21上的动点，贝U P A PB 的取值范围是(4)若对任意C2: x m 2 y m彳m2，若圆C2上存在点P满足：过点P向圆C1作两条切线PA、PB,切点为A、B, ABP的面积为1,则正数m的取值范围是策略二由动点P对两定点A、B张角是90°( k pA k pB 1，或PA PB 0)确定隐形圆例 2 ( 1)已知圆C：(x 3)2 (y 4)2 1 和两点A( m,0)，B(m,0) (m 0),若圆上存在点P,使得/ APB=90°,贝m的取值范围是________________•(2)(海安2016届高三上期末)在平面直角坐标系xOy中，已知点P(-1 , 0), Q(2, 1),直线I: ax by c 0其中实数a, b, c成等差数列，若点P在直线I上的射影为H,则线段QH的取值范围是______________ .(3)设m R，直线l i : x my 0与直线12 : mx y 2m 4 0 交于点P(X o,y°)，贝U x。

最值模型之隐圆模型模型一隐圆之定点定长型1、借助“隐圆”解决几何最值问题的理论依据有两个：①定圆的所有弦中，直径最长；②圆外一点与圆心的连线上，该点和此直线与圆的近交点距离最短、远交点距离最长.2、圆外的定点A与圆上动点B的距离AB的最值问题：当A、B、O三点共线时，AB有最大值或最小值。

如图2，AB最大值=OA+半径；如图3，AB最小值=OA-半径；定长模型(共顶点的三条等线段)若P为动点，但AB=AC=AP原理：圆A中，AB=AC=AP则B、C、P三点共圆，A圆心，AB半径备注：常转全等或相似证明出定长例题解析1如图，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上的一动点，将△AMN 沿MN所在直线翻折得到△A`MN，连接A`C，则A`C长度的最小值是．2如图，在矩形ABCD中，AB=2,AD=7，动点P在矩形的边上沿B→C→D→A运动．当点P不与点A、B重合时，将△ABP沿AP对折，得到△AB P，连接CB ，则在点P的运动过程中，线段CB 的最小值为．变式训练1如图，在矩形ABCD中，AB=2，AD=3，点E，F分别为AD、DC边上的点，且EF=2，G 为EF的中点，P为BC边上一动点，则PA+PG的最小值为？2如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，点F在边AC上，并且CF=2，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是．3如图，点A，B的坐标分别为A(6，0)，B(0，6)，C为坐标平面内一点，BC=22，M为线段AC的中点，连接OM，当OM取最大值时，点M的坐标为．△ABE沿BE翻折得到△FBE，连接GF．当GF最小时，AE的长是．EF，将四边形ABFE沿EF翻折，点A、B的对应点分别为A'、B'，连接A'D，则A'D的最小值为．模型二隐圆之定长定角型(1)直角圆周角模型固定线段AB所对动角∠C恒为90°原理：圆O中，圆周角为90°所对弦是直径则A、B、C三点共圆，AB为直径备注：常通过互余转换等证明出动角恒为直角解题技巧：若定角为90°，取定长AB的中点O为圆心，AB的一半为半径画辅助圆。

A专题04巧用隐圆妙解最值学校:___________姓名：___________班级：___________考号：___________模型背诵隐圆一:定弦定角，隐圆正好。

AB的长度固定不变（定弦），∠ABC=α不变（定角）。

这样的图形就是我们所谓的“定弦定角模型”。

若∠ACB=90°，则AB 为三点所在圆的直径。

（可以解决动点轨迹。

）隐圆二:等弦对等角，隐圆可以找。

(可以利用四点共圆证相似,角相等)若∠ADC=∠ABC，则A,B,C,D四点共圆。

在半角模型中,证四点共圆,主要利用了这类隐圆.隐圆二特殊.若∠ABC=∠ADC=90°，则A,B,C,D四点共圆，且AC为直径。

隐圆三:对角互补，四点共圆.若∠ADC+∠ABC=180°，则A,B,C,D四点共圆。

隐圆三特殊:若∠ABC=∠ADC=90°，则A,B,C,D四点共圆，且AC为直径。

隐圆四：定点定长，隐圆必现。

CA=CB=CP隐圆五、瓜豆原理之种圆得圆。

若Q为AP的中点，当P沿⊙O运动一周，则Q的运动轨迹为以 AO 中点M为圆心的圆。

（P为“主动点”，点Q为“从动点。

）典例分析如图1-1，点P（3,4），圆P半径为2，A（2.8,0），B（5.6,0），点M是圆P上的动点，点C是MB的中点，则AC的最小值是_______．【点睛】图1-2，M点为主动点，C点为从动点，B点为定点．考虑C是BM中点，可知C点轨迹：取BP 中点O，以O为圆心，OC为半径作圆，即为点C轨迹．图1-3：当A、C、O三点共线且点C在线段OA上时，AC取到最小值，根据B、P坐标求O，利用两点间距离公式求得OA，再减去OC即可．实战训练一、单选题1．如图，正方形ABCD的边长为4，点E是正方形ABCD内的动点，点P是BC边上的动点，且∠EAB=∠EBC．连结AE，BE，PD，PE，则PD+PE的最小值为（）A．2√13−2B．4√5−2C．4√3−2D．2√15−2【答案】A【详解】解：∵四边形ABCD是正方形，∴∠ABC=90°，∴∠ABE+∠EBC=90°，∵∠EAB=∠EBC，OyxA BCMPOOyxA BCMPOPMCBA xyO图1-1图1-2 图1-3∴∠EAB+∠EBA=90°，∴∠AEB=90°，∴点E在以AB为直径的半圆上移动，如图，设AB的中点为O，作正方形ABCD关于直线BC对称的正方形CFGB，则点D的对应点是F，连接FO交BC于P，交半圆O于E，根据对称性有：PD=PF，则有：PE+PD=PE+PF，则线段EF的长即为PE+PD的长度最小值，E∵∠G=90°，FG=BG=AB=4，∴OG=6，OA=OB=OE=2，∴OF=√FG2+OG2=2√13，∴EF=OF−OE=2√13−2，故PE+PD的长度最小值为2√13−2，故选：A．2．如图，⊙O的半径是√6，P是⊙O上一动点，A是⊙O内部一点，且AO=√3，则下列说法正确的是（）①PA的最小值为√6-√3；②PA的最大值为√6+√3；③当∠OAP=90°时，△PAO是等腰直角三角形；④△PAO面积最大为3．2则AM=√22AO=√2，在△ADE和△DCF中，{AD=CD∠ADE=∠DCFDE=CF，∴△ADE≌△DCF（SAS），∴∠DAG=∠CDF，∵∠ADG+∠CDF=90°，∴∠ADG+∠DAG=90°，∴∠AGD=90°，△ADG是直角三角形，∴OG=12AD=2，∵△AHG为等腰直角三角形，∴∠OAG+∠GAM=∠HAM+∠GAM，∴∠OAG=∠HAM，又∵AHAG =MAOA=√22，∴△AMH∽△AOG，∴MHOG =√22，∴MH=√2，∴点H的运动轨迹为以点M 为圆心，MH为半径的圆，如图，连接BM，交圆M于H′，过点M作MP⊥AB于点P，∵∠DAE+∠BAH=45°，∠OAG=∠MAH，∴∠PAM=∠MAH+∠BAH=45°，∴△APM为等腰直角三角形，∴∠BND=∠AND，∴DN平分∠ANB，∵DA⊥AN，过点D作DH⊥BN，∴DA=DH，∴DB=AB-AD=8-DH，在Rt△AND和Rt△HND中，{DN=DNDA=DH，∴Rt△AND≌Rt△HND（HL），∴AN=HN=6，在Rt△ABN中，AB=8，AN=6，∴BN=√AB2+AN2=10，∴BH=BN-HN=10-6=4，在Rt△DBH中，DB=8-DH，根据勾股定理得：DB2=DH2+BH2，∴（8-DH）2=DH2+42，解得DH=3，在Rt△ADN中，DH=DA=3，AN=6，根据勾股定理得：DN2=AD2+AN2，∴DN2=32+62=45，∴DN=3√5，∵∠A=∠NGC=90°，∠AND=∠GNC，∴∠ADN=∠NCG，∵sin∠ADN=ANDN =63√5=2√55，∴sin∠NCG=sin∠NCE=2√55．故选：D．7．如图，边长为1的小正方形网格中，点A,B,C,E在格点上，连接AE,BC，点D在BC上且满足AD⊥BC，则tan∠AED 的值是（）A．2√55B．2C．√55D．12【答案】D【详解】以O为圆心，1为半径作⊙O，连接OD．∵A,B,C,E在格点上．∴AC=OA=OE=OB=1∴A,B,E在⊙O上∵AD⊥BC∴∠ADB=90°又∵⊙O的直径是AB∴AB=2∵OA=OB∴OD=12AB=1∴点D在⊙O上∴∠AED=∠ABD∴tan∠AED=tan∠ABD=ACAB=12故选：D．二、填空题8．如图，正方形ABCD的边长为4，⊙B的半径为2，P为⊙B上的动点，则√2PC−PD的最大值是．【答案】2【详解】解法1如图：以PD为斜边构造等腰直角三角形△PDM，连接MC，BD，PD，∴∠PDM=45，DM=PM=√22∵四边形ABCD正方形=√2∴∠BDC=45°，DBDC又∵∠PDM=∠PDB+MDB，∠BDC=∠MDB+MDC∴∠PDB=∠MDC在△BPD与△MPC中【答案】9−3√3【详解】解：∵△ABD与△ACE是等腰直角三角形，∴∠BAD=∠CAE=90°，∴∠DAC=∠BAE，在△DAC与△BAE中，{AD=AB∠DAC=∠BAEAC=AE，∴△DAC≌△BAE(SAS)，∴∠ADC=∠ABE，∴∠PDB+∠PBD=90°，∴∠DPB=90°，∴P在以BC为直径的圆上，∵△ABC的外心为O，∠BAC=60°，∴∠BOC=120°，如图，当PO⊥BC时，OP的值最小，∵BC=18，∴BH=CH=9，OH=12OB∴BH=√OB2−OH2=√3OH ∴OH=3√3，PH=9，∴OP=9−3√3．则OP的最小值是9−3√3，故答案为：9−3√3．13．如图，正方形ABCD的边长为4，点E为边AD上一个动点，点F在边CD上，且线段EF＝4，点G为线段EF的中点，连接BG、CG，则BG+12CG的最小值为．【答案】5【详解】解：如图，在Rt△DEF中，G是EF的中点，∴DG＝12EF=2，∴点G在以D为圆心，2为半径的圆上运动，在CD上截取DI＝1，连接GI，∴DIDG ＝DGCD＝12，∴∠GDI＝∠CDG，∴△GDI∽△CDG，∴IGCG =DIDG＝12，∴IG＝12CG，当DB经过圆心O时，CD最小，最小值为4-（√3+1）=3-√3．故答案为：3−√3．15．如图，⊙O的半径为2，弦AB＝2，点P为优弧AB上一动点，AC⊥AP交直线PB于点C，则△ABC的最大面积是．【答案】√3【详解】解：连接OA、OB，如图1，∵OA=OB=2，AB=2，∴△OAB为等边三角形，∴∠AOB=60°，∠AOB=30°，∴∠APB=12∵AC⊥AP，∴∠C=60°，∵AB=2，要使△ABC的最大面积，则点C到AB的距离最大，作△ABC的外接圆D，∵∠ACB=60°，点C在⊙D上，∴∠ADB=120°，如图2，AB2=√3，当点C优弧AB的中点时，点C到AB的距离最大，此时△ABC为等边三角形，且面积为√34∴△ABC的最大面积为√3．故答案为：√3．16．如图，矩形ABCD中，AB=3，AD=5，点E为射线BA上一个动点，连接CE，以CE为对称轴折叠△BCE，得到△FCE，点B的对应点为点F，当点F落在直线AD上时，AF的长为．【答案】1或9【详解】解：∵在矩形ABCD中，则CD=AB=3,BC=AD=5，∠D=90°，由折叠的性质，则CF=BC=5，BE=EF，在Rt△CDF中，由勾股定理，得DF=√52−32=4；①当点E在线段AB上时，如图：∴AF=5−4=1，②当点E在BA的延长线上时，如图：∴AF=5+4=9，故答案为：1或9．17．如图，在矩形ABCD中，AB=3，BC=4，点P为边CD上一动点，连接AP交对角线BD于点E，过点E作EF⊥AP，EF交BC于点F，连接AF交BD于点G，在点P的运动过程中，△AEG面积的最小值为．【答案】4825【详解】解：在矩形ABCD中，AB=3，BC=4，∠BAD=90°，∴BD=5，如图，延长CB至点H，使BH=BD=5，∴∠H=∠BDH，∠DBC，∴∠H=12接AE．若AC=6，CD=5，则线段AE的长为．【答案】145/245/2.8【详解】解：如图，连接BE，延长CD交BE与点H，作CF⊥AB，垂足为F．∵在Rt△ABC中，∠ACB=90°，点D是边AB的中点，CD=5，∴AD=DB=CD=5，AB=10．∵AC=6，∴BC=√102−62=8．∵S△ABC=12AC⋅BC=12AB⋅CF，∴12×6×8=12×10×CF，解得CF=245．∵将△BCD沿直线CD翻折得到△ECD，∴BC=CE，BD=DE，∴CH⊥BE，BH=HE．∵AD=DB=DE，∴△ABE为直角三角形，∠AEB=90°，∴S△ECD=S△ACD，∴12DC⋅HE=12AD⋅CF，∵DC=AD，∴HE=CF=245．∴BE=2EH=485．∵∠AEB=90°，∴AE=√AB2−BF2=√102−(485)2=145．故答案为145．三、解答题19．在△ABC中，∠ACB=90°，CA＝2CB．将线段CA绕点C旋转得到线段CD．(1)如图1，当点D落在AB的延长线上时，过点D作DE⊥AD交AC的延长线于点E，若BC＝2，求DE的长；(2)如图2，当点D落在CB的延长线上时，连接AD，过点C作CF⊥AB于点F，延长CF交AD于点E，连接BE，求证：AB=CE+BE；(3)如图3，在（2）的条件下，将△ACF沿AC翻折得到△ACF′，M为直线AD上一个动点．连接BM，将△BDM沿BM翻折得到△BMD′．当D′F′最小时，直接写出F′D′FF′的值．【答案】(1)8√55(2)见解析(3)√85−58【详解】（1）解：∵CA＝2CB，BC＝2，∴CA＝4，∵∠ACB=90°，∴tanA=12．∵将线段CA绕点C旋转得到线段CD，∴AC=CD，∴∠CAD=∠ADC，∵DE⊥AD，∴∠ADE=90°，∴∠CAD+∠E=∠ADC+∠CDE=90°，∵∠CAD=∠ADC，∴∠E=∠CDE，∴CE=CD=CA=4，∴AE=AC+CE=8，∵CA=4，BC＝2，∠ACB=90°∴AB=√CA2+CB2=2√5，∴sinA=BCAB =22√5=√55，∵AE=8，∴DE=sinA×AE=8√55．（2）证明：过D作DG⊥CD交CE延长线于点G，∵线段CA绕点C旋转得到线段CD，∠ACB=90°，∴CD=CA，△ACD是等腰直角三角形．∵CA＝2CB，∴CD＝2CB，即CB=BD．∵CF⊥AB，∴∠AFC=90°，∴∠CAF+∠ACF=90°，∵∠FCB+∠ACF=90°，∴∠CAF=∠FCB．在△ACB与△CDG中，∵{∠CAB=∠GCDAC=CD∠ACB=∠CDG，∴△ACB≌△CDG（ASA）．∴CB=DG，∵CB=BD，∴BD=DG．∵DG⊥CD，∴∠CDG=90°，∵△ACD是等腰直角三角形，∴∠CDA=45°，∴∠EDG=∠EDB=45°．在△BED与△GED中，∵{BD=GD∠BDE=∠GDEED=ED，∴△BED≌△GED（SAS）．∴BE=EG，∴CE+BE=CE+EG=CG．∵△ACB≌△CDG，∴AB=CG，∴AB=CE+BE．（3）如图，过F′作F′K⊥BC交BC延长线于点K，以B为圆心，BC长为半径画圆，由题意得，D′在以B为圆心，BC长为半径的圆上运动，当F′，D′，B三点共线且D′在F′B之间时，D′F′最小．设CB=1，∵CA=2CB，∴FF′=85，∵F′D′=√85−55，∴F ′D′FF′=√85−58．20．已知，平面直角坐标系中有一个边长为6的正方形OABC，M为线段OC上的动点，将△AOM沿直线AM对折，使O点落在O′处．(1)如图①，当∠OAM=30°时，求点O′的坐标；(2)如图②，连接CO′，当CO′∥AM时．①求点M的坐标；②连接OB，求△AO′M与△AOB重叠部分的面积；(3)当点M在线段OC（不包括端点）上运动时，请直接写出线段O′C的取值范围．【答案】(1)O′(3√3,3).(2)①M(3,0)，②337.(3)6√2−6≤CO′<6.【详解】（1）解：如图，连接OO′,交AM于Q,过O′作O′N⊥OC于N,由对折可得：AO=AO′=6,OM=O′M,∠OAM=30°=∠O′AM,∴OO′⊥AM,OQ=O′Q,∴∠OAO′=60°,△OAO′是等边三角形，∴OO′=AO=6,∵∠AOM=90°,∴∠OMQ=90°−30°=60°,∵AM⊥OO′，∴∠O′ON=30°,∴ON=√3Q′N=3√3,∴O′(3√3,3).（2）①∵AM∥O′C,∴∠AMO=∠MCO′,∠AMO′=∠MO′C,而∠AMO=∠AMO′,∴∠MO′C=∠MCO,∴MO′=MC,∴OM=O′M=CM=3,∴M(3,0).②如图，连接OB,交AM于Q,交AO′于P,过Q作QD∥OA,交AO′于D,过O′E⊥OC于E,由①得：tan∠AMO=AOOM =2=tan∠O′CE=O′ECE,设CE=x,则ME=3−x,O′E=2x,∴32=(3−x)2+(2x)2,解得：x=65,（不符合题意的根舍去）∴O′E=2x=125,OE=6−x=245,∴O′(245,125),而A(0,6),设AO′为y=kx+6,则245k+6=125,解得：k=−34,(1)若AB=4，求AD的长度；(2)若将△BDE绕点B旋转到如图②所示的位置，请证明AF=DF，AF⊥DF；(3)如图③，在△BDE绕点B旋转的过程中，再将△ACF绕点A逆时针旋转60°到△AC′F′，连接BF′，若AB=4，请直接写出BF′的最大值．【答案】(1)2√5(2)见解析(3)2√3+√2+2【详解】（1）解：在等腰Rt△ABC中，∠BAC=90°，AB=4，AB=AC，∴BC=4√2，∠ABC=45°，∵点E为BC的中点，∴BE=2√2，在等腰Rt△BDE中，BDE=90°，BE=2√2，BD=DE，∴BD=DE=2，在Rt△BDA中，∠ABD=90°，AB=4，BD=2，∴AD=√AB2+BD2=√16+4=2√5；（2）证明：如图1，延长AF至G，使FG=AF，连接EG，DG，AD，∵点F是CE的中点，∴EF=CF，在△ACF和△GEF中，{CF=EF∠AFC=∠EFGAF=FG，∴△ACF≌△GEF(SAS)，∴AC=FG，∠ACF=∠FEG，∴AC∥EG，∵AB⊥AC，∴EG⊥AB，∵∠EDB=90°，∴∠DEG=∠ABD，∵AC=AB，∴EG=AB，在△ABD和△GED中，{AB=EG∠ABD=∠GEDBD=DE，∴△ABD≌△GED(SAS)，∴AD=DG，∠ADB=∠EDG，∴∠ADB−∠BDG=∠EDG−∠BDG，∴∠ADG=∠BDE=90°，∴△ADG是等腰直角三角形，（2）如图，连接CF∵M时BC中点，M是EM中点∴EM=MF，BM=CM∵∠BME=∠CMF∴△BEM≌△CFM∴BE=CF，∠EBM=∠MCF∴BE∥CF∵B、E、D共线，A、D、F共线∴BD∥CF∴∠AFC=∠BDA=90°∵AB=AC，∠CAF+∠BAD=∠BAD+∠ABD=90°∴∠CAF=∠BAD∴△ABD≌△CAF∴CF=AD∴CF=AD=BEEF∴AF=AD+DF=BE+√22∴√2AF=√2BE+EF.（3）连接DM，AM，延长AD交CF于N在直线DG 上？如存在，求出点P 的坐标，如不存在，并说明理由；(3)若第四象限有一动点E ，满足BE =OB ，过E 作EF ⊥x 轴于点F ，设F 坐标为(t,0)，0<t <4，△BEF 的内心为I ，连接CI ，直接写出CI 的最小值．【答案】(1)y =x 2-3x -4；点G 在此函数图像上，理由见解析； (2)P 的坐标为(3+√13,9+3√13)或(3−√13,9−3√13) (3)2√10−2√2【详解】（1）解：∵二次函数y =x 2+bx +c 的图象过点C (0，−4)和点D (2，−6)， ∴{c =−44+2b +c =−6， 解得{b =−3c =−4 ，∴y =x 2−3x −4．∵点G 与点D 关于坐标原点对称， ∴G (−2,6)，把x =2代入y =x 2−3x −4， 得y =(−2)2−3×(−2)−4=6， ∴G (−2,6)在此抛物线上．（2）设直线DG 的解析式为y =mx +n ， ∵D (2,−6)，G (−2,6)， ∴{2m +n =−6−2m +n =6，解得{m =−3n =0，∴直线DG 的解析式为y =−3x ．假设此抛物线上存在这样的点P (x,x 2−3x −4)，使得它关于x 轴，y 轴的对称点M ，N 恰好都在直线DG 上， ∵M (x,−x 2+3x +4)，N (−x,x 2−3x −4)， ∴x 2−3x −4=3x ， 解得x =3±√13，故所求点P 的坐标为(3+√13,9+3√13)或(3−√13,9−3√13)．（3）如图，连接BI ，OI ，EI ，作△OBI 的外接圆⊙M ，连接OM ，BM ，MI ，CM ，过M 作MH ⊥y 轴于H ，∵EF⊥x轴，∴∠BFE=90°，∴∠FBE+∠FEB=90°，∵△BEF的内心为I，∴BI，EI，分别平分∠FBE，∠FEB，∴∠IBE=12∠FBE，∠IEB=12∠FEB，∴∠IBE+∠IEB=12(∠FBE+∠FEB)=45°，∴∠BIE=135°，易证△BIO≌△BIE（SAS）∴∠BIO=∠BIE=135°，∵⊙M是△BIO的外接圆，∴∠OMB=2×（180°－∠BIO）=90°，∴OM=BM=√22OB=2√2，∴MI=OM=2√2，∴∠MOB=∠MOH=45°，∵MH⊥y轴，∴∠HOM=∠HMO=45°，∴OH=HM=√22OM=2，∴CH=OH+OC=2+4=6，∴CM=√HM2+CH2=2√10，∵CI≥CM－MI，当且仅当C、M、I共线时，CI取最小值，∴CI的最小值为2√10−2√2．25．如图，抛物线y=ax2−2ax−3a（a为常数，a<0）与x轴分别交于A，B两点（点A在点B的左侧），与y轴交于点C，且OB＝OC．(1)求a的值；(2)点D是该抛物线的顶点，点P（m，n）是第三象限内抛物线上的一个点，分别连接BD、BC、CD、BP，当∠PBA ＝∠CBD时，求m的值；(3)点K为坐标平面内一点，DK＝2，点M为线段BK的中点，连接AM，当AM最大时，求点K的坐标．【答案】(1)−1(2)−43(3)K(6√13+1313,4√13+5213)【详解】（1）∵y=ax2−2ax−3a=a(x2−2x−3)=a(x−3)(x+1)令y=0，解得x1=−1,x2=3令x=0，y=−3a∵抛物线y=ax2−2ax−3a（a为常数，a<0）与x轴分别交于A，B两点（点A在点B的左侧），与y轴交于点C，∴抛物线与x轴的交点为A(−1,0),B(3,0)C(0,−3a)∴OB=3∵OB=OC∴OC=3∴C(0,3)∴−3a=3解得a=−1（2）如图，过点P作PE⊥x轴于点E，∵y=−x2+2x+3=−(x−1)2+4∴D(1,4)∵B(3,0),C(3,0)∴CD=√12+12=√2,BC=√32+32=3√2,BD=√(3−1)2+42=2√5∴CD2+BC2=20,BD2=20∴CD2+BC2=BD2∴△BCD是直角三角形，且∠BCD=90°∵PE⊥AB∴∠PEB=∠PCD=90°又∵∠PBA=∠CBD∴△BCD∽△BEP∴CDPE=BCBE∵P(m,n)在抛物线y=−x2+2x+3上，∴n=−m2+2m+3∴PE=−n=m2−2m−3,BE=3−m∴√2m2−2m−3=3√23−m整理得(3m+4)(m−3)=0解得m1=−43,m2=3（舍）∵P(m,n)在第三象限，∴m<0∴m=−4 3（3）如图，连接BD ，取BD 的中点Q ，连接QM ,∴QM 是△BDK 的中位线∴QM =12DK =1 根据题意点K 在以D 为圆心，2为半径的圆上， 则M 在以Q 为圆心，1为半径的圆上运动，当A,Q,M 三点共线，且M 在AQ 的延长线上时，AM 最大，如图，∵B(3,0),D(1,4)∴Q(1+32,4+02)即Q (2,2)∵A(−1,0),Q(2,2)设直线AM 的解析式为y =kx +d ，代入点A(−1,0),Q(2,2)， 即{0=−k +d 2=2k +d解得{k =23b =23∴直线AM 的解析式为y =23x +23∵DK ∥QM要使得DE最小，则要使圆的半径最小，故直径PC最小，则当CP⊥AB时，PC最短，∵△ABC是等边三角形，∴∠B=60°,BP=3，∴CP=√3BP=3√3，∵∠DOP=60°，∴DE=2OD⋅sin∠DOP=9．227．如图，在矩形ABCD中，AB＝6，AD＝8，点E，F分别是边CD，BC上的动点，且∠AFE＝90°（1）证明：△ABF∽△FCE；（2）当DE取何值时，∠AED最大．【答案】（1）见解析；（2）103【详解】解：（1）证明：∵四边形ABCD是矩形，∴∠B＝∠C＝90°，∵∠AFE＝90°，∴∠AFB+∠EFC＝90°，∵∠EFC+∠FEC＝90°，∴∠AFB＝∠FEC，∴△ABF∽△FCE．（2）取AE的中点O，连接OD、OF．∵∠AFE＝∠ADE＝90°，∴OA＝OD＝OE＝OF，∴A、D、E、F四点共圆，∴∠AED＝∠AFD，∴当⊙O与BC相切时，∠AFD的值最大，∴BF＝CF＝4，∵△ABF∽△FCE，∴ABFC =BFEC，∴64=4EC，∴EC=83，∴DE=DC−CE=6−83=103，∴当DE=103时，∠AED的值最大．28．已知正方形ABCD与正方形AEFG，正方形AEFG绕点A旋转一周．(1)如图①，连接BG、CF，求CFBG的值；(2)当正方形AEFG旋转至图②位置时，连接CF、BE，分别取CF、BE的中点M、N，连接MN、试探究：MN与BE的关系，并说明理由；(3)连接BE、BF，分别取BE、BF的中点N、Q，连接QN，AE=6，请直接写出线段QN扫过的面积．【答案】（1）√2；（2）MN⊥BE;MN=12BE；（3）9π【详解】解：（1）连接AF、AC∵四边形ABCD和四边形AEFG是正方形∴AB=BC,AG=FG,∠BAD=∠GAE=∠CBA=∠AGF=90°∵AF、AC分别平分∠EAG,∠BAD∴∠BAC=∠GAF=45°∴∠BAC+∠CAG=∠GAF+∠CAG即∠BAG=∠CAF且ΔABC,ΔAGF都是等腰直角三角形∴ACAB=AFAG=√2∴ΔCAF∽ΔBAG∴CFBG=ACAB=√2（2）连接BM并延长使BM=MH，连接FH、EH∵M是CF的中点∴CM=MF又∠CMB=∠FMH∴ΔCMB≌ΔFMH∴BC=HF,∠BCM=∠HFM在四边形BEFC中∠BCM+∠CBE+∠BEF+∠EFC=360°又∠CBA=∠AEF=90°∴∠BCM+∠ABE+∠AEB+∠EFC=360°−90°−90°=180°即∠HFM+∠EFC+∠ABE+∠AEB=180°即∠HFE+∠ABE+∠AEB=180°∵∠BAE+∠ABE+∠AEB=180°∴∠HFE=∠BAE又四边形ABCD和四边形AEFG是正方形∴BC=AB=FH,EA=EF∴ΔBAE≌ΔHFE∴BE=HE.∠BEA=∠HEF∵∠HEF+∠HEA=∠AEF=90°∴∠BEA+∠HEA=90°=∠BEH∴三角形BEH是等腰直角三角形∵M、N分别是BH、BE的中点∴MN//HE,MN=12 HE∴∠MNB=∠HEB=90°,MN=12 BE∴MN⊥BE,MN=12 BE（3）取AB的中点O，连接OQ、ON，连接AF 在ΔABF中，O、Q分别是AB、BF的中点∴OQ=12 AFAE同理可得ON=12∵AF=√2AE=6√2∴OQ=3√2,ON=3所以QN扫过的面积是以O为圆心，3√2和3为半径的圆环的面积∴S=(3√2)2π−32π=9π．29．问题背景如图（1），△ABC为等腰直角三角形，∠BAC＝90°，直线l绕着点A顺时针旋转，过B，C两点分别向直线l作垂线BD，CE，垂足为D，E，此时△ABD可以由△CAE通过旋转变换得到，请写出旋转中心、旋转方向及旋转角的大小（取最小旋转角度）．尝试应用如图（2），△ABC为等边三角形，直线l绕着点A顺时针旋转，D、E为直线l上两点，∠BDA＝∠AEC＝60°．△ABD可以由△CAE通过旋转变换得到吗？若可以，请指出旋转中心O的位置并说明理由；拓展创新如图（3）在问题背景的条件下，若AB＝2，连接DC，直接写出CD的长的取值范围．【答案】（1）旋转中心为BC边的中点O，旋转方向为逆时针，旋转角度为90°；（2）可以，旋转中心为为等边△ABC三边垂直平分线的交点O，理由见解析；（3）√5−1≤CD≤√5+1【详解】解：问题背景（1）如图所示，作AO⊥BC，交BC于点O，由等腰直角三角形的性质可知：∠AOC=90°，OA=OC，∴点A是由点C绕点O逆时针旋转90°得到，同理可得，点B是由点A绕点O逆时针旋转90°得到，。

隐圆求最值例1（12年武汉中考）在坐标系中，点A的坐标为(3，0)，点B为y轴正半轴上的一点，点C是第一象限内一点，且AC=2．设tan∠BOC=m，则m的取值范围是_________．例2（13年武汉中考）如图,E、F是正方形ABCD的边AD上两个动点,满足AE＝DF.连接CF交BD于G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是.例3、如图,△ABC中,∠ABC＝90°,AB＝6,BC＝8,O为AC的中点,过O作OE⊥OF,OE、OF分别交射线AB、BC于E、F,则EF的最小值为.练习R t ABC中,∠C＝90°,∠ABC＝30°,AB＝6,点D在AB边上,点E是BC边上1、如图,△一点(不与点B、C重合),且DA＝DE,则AD的取值范围是.2、如图,已知边长为2的正△ABC,两顶点A、B分别在直角∠MON的两边上滑动,点C在∠MON内部,则OC的长的最大值为.3、如图,∠xOy＝45°,一把直角三角尺△ABC的两个顶点A、B分别在Ox、Oy上移动,其中AB＝10,那么点O到顶点A的距离最大值为,点O到AB的距离的最大值为.补充练习1、如图，在△R t ABC中，∠ACB=90°，AC=4，BC=3，点D是平面内的一个动点，且AD=2，M为BD的中点，在D点运动过程中，线段CM长度的取值范围是.2、如图，在△R t ABC中，∠C=90°，AC=6，BC=8，D为AB边上一点，过点D作CD的垂线交直线BC于点E，则线段CE长度的最小值是.3、如图，∠MON=90°，矩形ABCD的顶点A、B分别在边OM、ON上，当B在边ON上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D 到点O的最大距离为（）5D、A、21B、5C、145524、若在半径为1的圆O上任取两点A、B，再以AB为边向圆外作正方形，则OC的最大值和最小值分别为_______、________.5、如图，两同心圆半径分别为3、3，点A、B分别为两同心圆上的动点，以AB 为边作正方形ABCD，则OD的最大值为________.6、如图△ABC中，AB=3，AC=2，以BC为边的△BCP是等边三角形，则AP的最大值为（）A．3B．4C．5 D.67、如图所示，已知P是正方形ABCD外一点，且PA=3，PB=4，则PC的最大值是________.8、过边长为1的正方形的中心O引两条相互垂直的射线，分别与正方形的边交于A，B两点，则线段AB长的取值范围是________.8、如图，半径为1的圆0上有一定点M为圆O上的动点．在射线OM上有一动点B，A B=1，0B＞1．线段AB交圆O于另一点C，D为线段的OB中点．则线段CD长度的取值范围________．。