下载文档原格式
动能定理动能与功的关系动能定理是物理学中一个重要的原理，它描述了动能与功之间的关系。
在本文中，我们将探讨动能定理的概念以及它与功的关系。
一、动能的定义和计算方法动能是一个物体由于运动而具有的能量，是物体运动能量的量度。
根据经典力学，动能可以通过以下公式计算得出：动能（K）= 1/2 ×质量（m）×速度的平方（v²）其中，质量（m）是物体的质量，速度（v）是物体的速度。
二、功的定义和计算方法功是由力对物体所做的功效，是描述力对物体转移能量的物理量。
根据经典力学，功可以通过以下公式计算得出：功（W）= 力（F）×距离（d）× cosθ其中，力（F）是施加在物体上的力，距离（d）是力在物体运动方向上的位移，θ是力和位移之间的夹角。
三、动能定理的概念动能定理是描述动能与功之间关系的定理。
它表明，物体的动能的变化等于施加在物体上的净合外力所做的功。
即：ΔK = Wnet其中，ΔK表示动能的变化量，Wnet表示净合外力所做的功。
四、动能定理的示例应用为了更好地理解动能定理与功的关系，我们可以通过一个示例来说明。
假设有一个质量为2kg的物体以速度5m/s向前运动，受到一个由正方向施加的10N的恒力作用，并且恒力和物体的运动方向相同。
求物体在2s内的动能的变化量。
首先，根据动能的定义和计算方法，可以计算出物体在初始时刻（t=0）和终止时刻（t=2）的动能分别为：K1 = 1/2 × 2kg × (5m/s)² = 25JK2 = 1/2 × 2kg × (5m/s)² = 25J然后，计算净合外力所做的功。
根据功的计算方法，可以得到：Wnet = 力 ×距离× cosθ = 10N × 2m × 1 = 20J最后，根据动能定理，可以得到动能的变化量：ΔK = K2 - K1 = 25J - 25J = 0 J这说明在2s内，物体的动能没有发生变化。
动能定理与动能守恒动能定理和动能守恒定律是物理学中两个重要的基本原理，它们描述了物体在运动过程中动能的变化和守恒性质。
本文将介绍动能定理和动能守恒的概念、原理以及应用。
一、动能定理动能定理是描述物体动能变化的原理。
它表明，物体的动能变化等于物体所受的净外力沿着物体运动方向所做的功。
动能定理可以用以下公式表示：ΔKE = W其中，ΔKE表示动能的变化量，W表示净外力所做的功。
根据动能定理，当物体所受的净外力做功时，物体的动能将发生变化。
做正功的力会增加物体的动能，而做负功的力会减小物体的动能。
二、动能守恒动能守恒定律是描述物体在闭合系统内，动能守恒的性质。
它表明，在没有外力做功的情况下，物体系统的总动能保持不变。
动能守恒可以用以下公式表示：KE₀ = KE₁其中，KE₀表示初始状态下物体系统的总动能，KE₁表示最终状态下物体系统的总动能。
根据动能守恒定律，如果物体系统中没有外部力做功或者净外力所做的功为零，物体的总动能将保持不变。
三、应用举例动能定理和动能守恒定律在物理学中有广泛的应用。
以下是一些具体的应用举例：1. 自由落体运动：在自由落体运动中，一个物体在没有空气阻力的情况下，其总机械能保持不变。
在上升阶段，重力做负功，减小物体的动能；在下降阶段，重力做正功，增加物体的动能。
根据动能定理和动能守恒，可以计算物体在不同高度下的速度和位移。
2. 弹性碰撞：在弹性碰撞中，两个物体之间的动能可以互相转化，总动能保持不变。
通过应用动能守恒定律，可以计算碰撞前后物体的速度和动能变化。
3. 静止物体加速：当一个静止的物体受到恒定力作用时，可以利用动能定理计算物体的最终速度。
由于物体在初始状态时没有动能，因此动能定理可以简化为：物体所受的净外力所做的功等于物体最终动能。
总结：动能定理描述了物体动能的变化与外力做功之间的关系，而动能守恒定律则描述了动能在闭合系统内的守恒性质。
这两个原理在物理学中有着广泛的应用，可以帮助我们理解和计算物体运动中的各种现象。
动能定理运动中的能量转化在物理学中，动能定理是描述运动物体能量转化的重要原理。
它说明了物体的动能是由势能转化而来，并且这种能量转化是一个持续的过程。
本文将探讨动能定理以及在运动过程中的能量转化。
1. 动能定理的基本原理动能定理是描述物体在运动过程中能量转化的基本原理。
根据动能定理，物体的动能等于物体所受的净力所做的功。
具体表达式为：动能 = 功。
2. 动能的定义和公式动能是描述物体运动状态的物理量，它与物体的速度和质量有关。
动能的定义是：动能等于物体的质量乘以它的速度的平方再除以2。
动能的公式为：K.E. = 1/2mv²，其中K.E.表示动能，m表示物体的质量，v表示物体的速度。
3. 动能的转化过程动能在物体的运动过程中会发生转化。
主要的能量转化形式包括动能转化为势能、势能转化为动能以及动能转化为其他形式的能量。
3.1 动能转化为势能当物体处于高处或受到一定的外力作用时，物体的动能可以转化为势能。
例如，将一个物体从高处抛出，当物体上升到最高点时，它的动能减小，而势能增加。
这种转化也适用于弹簧等弹性体。
3.2 势能转化为动能当物体在其运动过程中下降或受到外力的施加时，势能可以转化为动能。
例如，当一个物体从高处自由下落时，势能逐渐减小，而动能逐渐增大。
这也适用于机械装置中的运动，如摆锤。
3.3 动能转化为其他形式的能量在一些情况下，动能也可以转化为其他形式的能量，如热能或声能等。
例如，当一个运动中的物体受到摩擦力时，部分动能会转化为热能，使物体发热。
4. 能量守恒定律与动能定理的关系动能定理是能量守恒定律的一个特例。
能量守恒定律指出，在一个封闭系统中，能量的总量保持不变。
动能定理是能量守恒定律在运动物体上的具体应用。
动能定理通过描述动能的转化，揭示了物体的能量如何在运动中相互转换。
它是解释和分析运动过程中能量变化的重要工具。
总结：动能定理是描述运动中能量转化的重要原理。
它通过动能和功的关系，描述了动能如何转化为势能、势能如何转化为动能以及动能如何转化为其他形式的能量。
动能定理与能量守恒动能定理和能量守恒定律是物理学中两个非常重要的概念。
动能定理描述了物体运动过程中动能的变化情况，而能量守恒定律则表明在一个封闭系统中，能量的总量是恒定的。
本文将分别介绍动能定理和能量守恒定律的基本原理、应用和重要性。
首先，我们来讨论动能定理。
动能定理指出，物体的动能的变化等于所有作用在物体上的力沿物体位移的总和。
动能定理可以用以下公式表示：$$\Delta KE = W_{\text{net}}$$其中，$\Delta KE$代表动能的变化，$W_{\text{net}}$代表外力对物体做的功。
根据该定理，当一个物体受到一系列力的作用时，物体的动能会发生变化。
如果外力对物体做正功，物体的动能将增加；如果外力对物体做负功，物体的动能将减小。
动能定理对于理解物体的运动过程、力的作用和能量转换具有重要意义。
动能定理的应用非常广泛。
例如，在机械领域中，动能定理可以用来分析机械设备的工作原理和效率。
在汽车行驶过程中，发动机产生的动力通过驱动轮对地面施加力，从而推动汽车前进。
根据动能定理，汽车的动能变化等于轮对地面所做的总功。
在物理实验中，动能定理也被广泛应用。
例如，当我们用弹簧秤测量物体的重力时，根据动能定理，物体沿竖直方向下降的距离与重力所做的功相等。
然而，动能定理只能描述物体动能的变化，而不能给出物体动能的具体数值。
要计算物体的动能，我们需要通过能量守恒定律来进一步分析。
能量守恒定律是基于宇宙中能量总量的恒定这一观察事实的。
在一个封闭系统中，能量既不能被创造也不能被销毁，只能从一种形式转化为另一种形式。
能量守恒定律可以用以下公式表示：$$E_{\text{initial}} = E_{\text{final}}$$其中，$E_{\text{initial}}$代表系统的初始总能量，$E_{\text{final}}$代表系统的最终总能量。
能量的转化包括各种形式的能量，如动能、势能、热能等。
九年级物理动能的知识点动能是物理学中一个重要的概念，它描述了物体在运动过程中所具有的能量。
在九年级物理课程中，学生将学习到关于动能的基本概念、计算方法和应用场景。
本文将围绕动能的概念、动能定理、动能与机械能的关系以及实际应用等方面进行探讨。
一、动能的概念动能是物体由于运动而具有的能量，它与物体的质量和速度相关。
当一个物体以一定的速度运动时，它所具有的动能与其质量成正比，与其速度的平方成正比。
动能的计算公式为：动能=1/2 ×质量 ×速度的平方。
这个公式展示了动能与质量、速度之间的关系。
二、动能定理动能定理是描述动能变化与力的关系的原理。
根据动能定理，物体所具有的动能的变化量等于物体所受的合外力所做的功。
简而言之，当物体受到力的作用时，它的动能将发生变化。
如果一个物体所受的合外力为正，那么它的动能将增加；如果合外力为负，那么动能将减小。
动能定理的数学表达为：动能的变化=力 ×距离。
三、动能与机械能的关系动能与机械能有着密切的联系。
在物理世界中，一个系统的机械能是由其动能和势能之和所决定的。
在不考虑摩擦和其他非保守力的情况下，一个系统的机械能守恒，即机械能的总量在运动过程中保持不变。
这意味着，当一个物体的动能增加时，它的势能相应减小，反之亦然。
动能和势能之间的转化是能量守恒定律的体现。
四、实际应用动能的理论不仅仅停留在课堂上，它也被广泛应用于工程和日常生活中。
例如，在交通运输行业，汽车的制动距离和能够行驶的最大距离是根据动能定理来计算的。
当汽车制动时，制动力减小汽车的速度，并通过摩擦将其动能转化为热能，从而减缓车辆的行驶距离。
另一个例子是弹射器。
弹射器的原理就是利用弹簧的弹性势能将物体加速，从而获得更大的动能，实现发射目标。
总结起来，九年级物理课程中关于动能的知识点主要围绕动能的概念、动能定理、动能与机械能的关系以及实际应用展开。
理解和熟练掌握这些知识将有助于学生理解物体在运动过程中的能量转化和运动规律，进一步提升对物理世界的认识。
动能定理能量守恒的基本原理动力学是物理学中的一个重要分支，研究物体的运动和受力情况。
其中，动能定理和能量守恒定律是描述物体运动过程中能量变化的基本原理。
一、动能定理动能定理是描述物体运动过程中动能变化的原理。
动能是物体运动的能量，定义为：动能 = 1/2 * m * v^2其中，m为物体的质量，v为物体的速度。
根据动能的定义，可以得出动能定理的表达式：物体的动能增量等于物体所受的净外力所做的功。
数学表达式为：ΔK = W其中，ΔK表示动能的增量，W表示净外力所做的功。
动能定理可以用来解释物体在外力作用下的运动状态和能量变化情况。
当物体受到力的作用时，外力对物体做功，使得物体的动能发生变化。
如果物体所受的外力为零，则根据动能定理得知物体的动能保持不变。
二、能量守恒定律能量守恒定律是自然界中一个普适的定律，描述了能量在一个封闭系统中的守恒性质。
能量守恒定律的表达式为：系统的总能量在封闭的过程中不变。
能量可以存在多种形式，包括动能、势能、热能等。
根据能量守恒定律，一个封闭系统中各种形式的能量可以相互转化，但总能量保持不变。
在物体运动过程中，动能和势能之间可以相互转化。
当物体处于高处时，具有势能；当物体运动时，其势能转化为动能，而动能定理也可以说明动能的变化量等于势能转化的大小。
能量守恒定律可以帮助我们理解许多物理现象，例如弹性碰撞、机械能转化等。
三、动能定理与能量守恒的关系动能定理和能量守恒定律在描述和分析物体的运动过程中密切相关。
首先，动能定理可以通过计算外力对物体做功的大小来描述物体动能的变化。
而能量守恒定律则表明，在一个封闭系统中，物体动能的变化可以转化为其他形式的能量，但总能量保持不变。
其次，动能定理和能量守恒定律都是适用于经典力学体系的基本原理，可以帮助我们理解和解释物态变化和能量转化的规律。
最后，动能定理和能量守恒定律的应用广泛，不仅适用于机械运动的问题，还可以推广到其他物理学领域，如热力学、电动力学等。
动能定理物体的动能与其质量和速度的平方成正比动能定理是物理学中一个重要的定理，它描述了物体的动能与其质量和速度的平方成正比的关系。
在本文中，我们将详细讨论动能定理的内容和应用。
一、动能定理的定义和表达式动能定理是描述物体动能与其质量和速度的平方成正比关系的定理。
根据动能定理，一个物体的动能等于其质量乘以速度的平方的一半。
动能定理的表达式可以用如下公式表示：K = (1/2) * m * v^2其中，K表示物体的动能，m表示物体的质量，v表示物体的速度。
二、动能的物理意义动能是一个物体所具有的做功能力，也是物体运动状态的度量。
当一个物体具有较大的质量和较高的速度时，它的动能也会较大。
三、动能定理的应用1. 动能定理在工程领域的应用在工程领域中，动能定理被广泛应用于机械设备和能源转化的研究中。
例如，在汽车碰撞测试中，可以利用动能定理来评估车辆发生碰撞时的动能转化情况，从而对车辆的安全性能进行评估和改进。
2. 动能定理在体育运动中的应用动能定理也在体育运动中有着重要的应用。
例如，当篮球运动员投篮时，球的速度和质量会影响投篮结果。
根据动能定理，投篮时加大球的速度或质量，可以提高球的动能，从而增加进球的可能性。
3. 动能定理在科研中的应用在科学研究中，动能定理经常被应用于研究物体的运动。
例如，在天文学中，科学家可以利用动能定理来研究行星和星系的运动，进一步了解宇宙的演化过程。
四、动能定理的局限性动能定理是在忽略其他因素的影响下建立起来的。
实际情况中，物体的运动受到了风阻、摩擦等力的影响，这些因素会改变物体的实际动能。
五、动能定理的实例分析为了更好地理解动能定理的应用和原理，我们以自行车骑行为例进行分析。
假设一个自行车的质量为10kg，骑手以10m/s的速度骑行。
根据动能定理，可以计算出自行车此时的动能：K = (1/2) * m * v^2 = (1/2) * 10 * 10^2 = 500J可以看出，自行车具有500焦耳的动能。
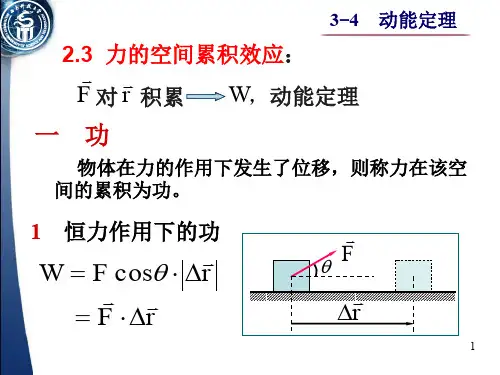
动能定理和功能原理 抛砖引玉 指点迷津 思维基础 学法指要 思维体操 心中有数 动脑动手 创新园地 一.教法建议
【】 抛砖引玉 在经典力学中，“动能定理”是“牛顿运动定律”的推论和发展，“功能原理”也是“牛顿运动定律”的进一步推导的结果。因此我们建议：教师不要把本单元的内容当作新知识灌输给学生，而是引导学生运用“牛顿运动定律”对下述的这个匀加速运动问题进行分析和推导，使学生自己获得新知识──“动能定理”和“功能原理”。 具体的教学过程请参考下列四个步骤：
第三步：运用牛顿第二定律和①、②两式导出“动能定理”。． m、所受之合外力为产生之加速度若已知物体的质量为、a 为。 则根据牛顿第
二定律可以写出： ③ 将①、②两式代入③式： 导出： ④ 若以W表示外力对物体所做的总功⑤ EEBA处时的动能 若以表示物体通过处时的动能，以表示物体通过ktko 则：⑥
⑦ 将⑤、⑥、⑦三式代入④式，就导出了课本中的“动能定理”的数学表达形式： WEE =－koktEEE －若以△表示动能的变化kokkt则可写出“动能定理”的一种简单
表达形式： E W=△k它的文字表述是：外力对物体所做的总功等于物体动能的变化。这个结
论叫做“动能定理”。 第四步：在“动能定理”的基础上推导出“功能原理”。 在推导“动能定理”的过程中，我们曾经写出过④式，现抄列如 下： ④ FS 为了导出“功能原理”我们需要对其中的下滑分力做功项进行分析推导。1． θFmg的关系如下：时，下滑分力和重力我们知道，当斜面的底角为1
将⑩式代入④式后进行推导：
若以代入⑾式，就导出了一种“功能原理”的数学表达形式： FsfsEE －=△+△PKFsfs之差(不包括重力做的功它的物理意义是：动力对物体
做功与物体克服阻力做功)，等于物体动能的变化量与势能的变化量之和。 若在⑾式基础上进行移项变化可导出下式： ⑿ 代入⑿式，就可以写为：若以． FsfsEE －－=t0再以代入上式就可以导出“功能原理”的另一种数学表 达形式：
EW =△F它的物理意义是：外力对物体对所做的总功W（不包括重力做的功），等于物体机械能的变化量F△E。（当W＞0时，△E＞0，机械能增加；当 FWE＜0，
机械能减少。＜0时，△ FWW是不相同的！我们将在后面的“指点 ：“功能原理”中的与“动能定理”中的(请读者注意F迷津”中进行说明。) WE最为简练，但在实用解题中在上面所推导出的关于“功能原理”的各数学表
达式中，虽以=△F以⑾、⑿两式最方便，在后讲述的“学海导航”和“智能显示”栏目中将会看到。 【】 指点迷津
下面我们推导“重力对物体做功”与“物体重力势能的变化”的数量关系：
由此可知：重力对物体的所做的功等于物体重力势能的变化。 上面推导出的这个结论是否只适用于竖直下落问题呢？不是的，它适用于重力对物体做功的各种情况，我们在后面的“学海导航”中还将通过例题说明其它情况。 3.“动能定理”和“功能原理”有什么联系和区别？在运用它们解题时需要注意什么？ 研究“外力对物体做功”和“物体机械能变化”的关系是力学中的重要问题之一。“动能定理”和“功能原理”都是表达这种关系的规律，只是表达的形式不同，但它们的本质是相同的。 在“动能定理”中只提动能而不提势能；在“功能原理”中既提动能也提势能。 在“动能定理”中包含重力所做的功；在“功能原理”中不包含重力所做的功。 在“动能原理”中所包含的重力对物体所做的功与在“功能原理”中所提到的物体重力势能的变化是对同一物理现象的不同表述。 某些力学问题，既可以用“动能定理”求解，也可以用“功能原理”求解。具体如何选择，往往要根据题意而定。选择恰当，不仅解题便捷，而且不易失误。（注：目前的高三物理课本只讲“动能定理”，但有关功能原理的思想也分布在课文之中了。如果学生的基础不太好，若为减轻负担，也可只学习和应用“动能定理”。） WE中不含在运用“动能定理”解题时应当注意：在公式势能的变化=△ KEWW。
但是在 中包含着重力做功(△),GPWE中既含动能的变化也含势能的变化，即在运用“功能原理”解题时应当注意：在公式=△FEEEWW。（注：也不包括重力分解出的下滑分力做功！） 中不包含△=△+△重力做功，但是在GKFPWWEE的区别。与
△ 的区别；△总之必须明确：与KF二.学海导航 【】 思维基础mABA处。物体通过的物体沿着光滑的斜面由所示：质量为处滑到如图 例题1.5－10 vhBvh。则在此过程中重力对物体所处时的速度为处时的速度为、高度为、高度
为;物体通过BABAW 做的功G 为：
思维基础：这是一个检查学生对概念规律的理解和应用能力的选择题，需掌握下列知识： 1.功的定义及其计算式。 2.“重力对物体做功”与“物体重力势能变化”的关系。 3.“动能定理”的物理意义及其应用。 4.建议：请学生阅读前面“教法建议”的内容后，参考其推理方法，先不看本题后面的解题思路和答案，自己进行解答，然后再进行核对，将会有较大的收获。 解题思路：在本题中物体只受重力和斜面的支持力(弹力)，又因斜面的支持力与物体的位移垂直而不做功，所以与解答本题无直接关系（因而在图中也未画出），因此只考虑重力做功与物体机械能的变化就可以了。 ，代入可得：F=mg，在本题中根据功的定义及其计算式
根据数学中的三角函数知识，可知在本题中 ，代入可得： mg分解出下滑分力, 附：若将然后据(，亦可得出同样结果。而重力的另一正压
分力 因与位移垂直不做功，只是与斜面支持力平衡，使物体在垂直于斜面方向保持) 根据“重力对物体做功等于物体重力势能的变化”(当重力对物体做正功时，物体的重力势能减少)，可以写出下式：
答案：[A、B、C、D] 解题后的思考： 你想到了本题的四个答案都是正确的吗？这四个答案之间有什么联系？1. 2.你能够运用功的计算式、匀变速运动公式及数学中的三角函数知识等推导出(C)、(D)两个答案吗？ f），那么(A)、(B)、(C)、3.如果在本题中斜面是不光滑的（物体与斜面间存在
着摩擦力(D)四个答案中哪些是正确的？哪些答案是不正确的？ 【】 学法指要 例题2.原来以7米/秒速度在水平轨道上直线行驶着的火车，在关闭气门停止动力后，滑行100米，车速减为5米/秒。问：继续滑行100米，车速将减为多少？（火车在滑行过程中阻力始终保持不变。） 启发性问题： 1.火车在滑行过程中处于何种做功状态？ 2.你打算用什么物理规律解答本题？ 3.你会用图示法分析物理问题吗？ 分析与说明： 1.在本题中，火车滑行时已停止了动力作用，所以只存在运动着的火车克服阻力做功火车将减速运动。 2.解答本题可有几种不同方法，但是对于学过“动能定理”的学生，往往想到使用这个规律。
求解过程： ，我们可以写出下列展开式：根据“动能定理”
=0、在本题中m，则：、设火车的质量为=fsW和=fs ⅡⅠ阻 对于s段可以写出下式：Ⅰ． 0－fs= ① Ⅰ s段可以写出下式：对于Ⅱ0－fs= ② Ⅱ在①、②两式中，已知s=s，所以两式的左方相等，因此两式的右方也应相等： ⅡⅠ ＝ 消去等式两边的可得 vv=5米/秒代入上式可得： 米将＝7/秒、01
秒。/米1车速将减为)米200即火车一共滑行了(米100答：火车继续滑行
【】 思维体操 “准备活动”(解题所需的知识与技能) 1.在本题中，由于汽车是加速运动，所以被提拉的物体也应是加速上升──这表明物体的动能和 重力势能都增加了。． 2.根据“功能原理”就可以求出绳的拉力对物体所做的W。(注：因为本题只要求绳的拉力对物体所做的功，所以就不必考虑汽车在运动过程中的牵引功F力和阻力等问题了。)
Bvh，据前面“准备活动”的分析，、上升的高度为设：汽车开到处时，物体上升
的即时速度为可以写下列二式：
QW，端拉力对物体做的功则：根据：“功能原理”，并将①、②两式代入进行推导，
就可求出绳F 具体过程如下：（注：物体的初速为零，初高定为零）．
“整理运动”（解题后的思考） 1.在本题的做功过程中，物体受到的是恒力还是变力？物体是匀加速上升还是变加速上升？ 2.请你用“动能定理”再将本题解答一次，并进行比较──你喜欢用哪种方法求解。
三.智能显示
【】 心中有数1.功和能的关系：各种不同形式的能可以通过做功来转化，能转化的多少通过功来量度，即功是能转化的量度。 W:动能定理：合力的功等于物体动能的增量，表达式为2.合=。
应用动能定理解题步骤： (1)分析物体的受力情况和运动情况； (2)分析各个力对物体做功的情况，计算时要把各已知功的正负号代入分式进行运算，若是未知功，W代入。 则用代号WFscosθ来求，可以应用动能定理来求。在公式中的功不要直接用(大小或方向改变)=变力(3) W表示。变力的功只能用代号
(4)如果物体运动有几个过程时，可以分段运用动能定理，也可以对全过程运用动能定理，即各个 力做功的代数和等于物体动能的增量： WWW= +……+n21【】 动脑动手(一).选择题
1.关于做功和物体动能变化的关系，下列说法中正确的是 A.只有动力对物体做功，物体的动能一定增加 B.只有物体克服阻力做功，物体的动能一定减少 C.外力对物体做功的代数和等于物体末动能与初动能之差。 D.动力和阻力都对物体做功，物体的动能一定变化 2.下面关于物体所受的合外力、合外力做功和物体动能变化的说法中正确的是
