中考试题专题之圆与圆的位置关系试题及答案

第六单元圆专题2 与圆有关的位置关系考点1 点和圆、直线和圆的位置关系1.已知平面内有⊙O和点A,B,若⊙O半径为2cm,线段OA=3cm,OB=2cm,则直线AB与⊙O的位置关系为( )A.相离B.相交C.相切D.相交或相切2.点P是非圆上一点，若点P到⊙O上的点的最小距离是4cm，最大距离是9 cm，则⊙O 的半径是___________.3.如图,直线a⊥b,垂足为H,点P在直线b上,PH=4cm,O为直线b上一动点.若以1cm为半径的⊙O与直线a相切,则OP的长为___________.考点2 切线的性质与判定1.如图,AB是⊙O的直径,BC是⊙O的切线,若∠BAC=35°,则∠ACB的大小为( )A.35°B.45°C.55°D.65°2.如图,PA,PB为圆O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交圆O于点D.下列结论不一定成立的是( )A.△BPA为等腰三角形B.AB与PD相互垂直平分C.点A，B都在以PO为直径的圆上D.PC为△BPA的边AB上的中线3.如图,菱形OABC的顶点A,B,C在⊙O上，过点B作⊙O的切线交OA的延长线于点D.若⊙O的半径为1,则BD的长为( )A.1B.2C.√2C.√34.如图,在▱ABCD中,AD=12,以AD为直径的⊙O与BC相切于点E,连接OC.若OC=AB,则▱ABCD 的周长为____________.5.如图,⊙O的半径OA=2,B是⊙O上的动点(不与点A重合),过点B作⊙O的切线BC,BC=OA,连接OC，AC.当△OAC是直角三角形时，其斜边长为_____________.6.如图,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C.连接BC,若∠P=36°,则∠B=___________.7.如图，PA是以AC为直径的⊙O的切线,切点为A,过点A作AB⊥OP,交⊙O于点B. (1)求证:PB是⊙O的切线;,求PO的长.(2)若CC=6,cos∠CCC=358.如图,AB为⊙O的直径,四边形ABCD内接于⊙O,对角线AC,BD交于点E,⊙O的切线AF交BD的延长线于点F,切点为A,且∠CAD=∠ABD.(1)求证:AD=CD;(2)若AB=4,BF=5,求sin∠BDC的值.̂上一点，连接AE并延长至点C，使9.已知:如图,AB是⊙O的直径,E为⊙O上一点，D是AE∠CBE=∠BDE,BD与AE交于点F.(1)求证:BC是⊙O的切线;(2)若BD平分∠ABE,求证:AD²=DF· DB.考点3 三角形的外接圆与内切圆1.如图,已知点O是△ABC的外心,∠A=40°,连接BO,CO,则∠BOC的度数是( )A.60°B.70°C.80°D.90°2.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD是⊙O的直径,若AD=3,则CC=( )C.2√3C.3√3 C.3D.43.设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h，r，R，则下列结论不正确的是( )A.h=R+rB.R=2rC.C=√34C C.C=√33C4.如图,△ABC内接于⊙O,∠A=50°,点D是BC的中点,连接OD,OB,OC,则∠BOD=_______.5.如图所示的网格由边长为1个单位长度的小正方形组成，点A，B，C在直角坐标系中的坐标分别为(3,6),(-3,3),(7,-2),则△ABC内心的坐标为_____________.6.已知△ABC的三边a,b,c满足b+|c-3|+C2−8C=4√C−1−19,则△ABC的内切圆半径=____________.专题检测一、选择题(每小题4分，共40分)1.平面内有两点P,O,⊙O的半径为5,若PO=4,则点P与⊙O的位置关系是( )A.点P在⊙O外B.点P在⊙O上C.点P在⊙O内D.无法判断2.已知⊙O的半径为5，点O到直线l的距离为3，则⊙O上到直线l的距离为2的点共有( )A.1个B.2个C.3个D.4个3.如图,AB是⊙O的弦,点C在过点B的切线上,OC⊥OA,OC交AB于点P.若∠BPC=70°,则∠ABC的度数等于( )A.75°B.70°C.65°D.60°̂上一点，则∠EPF的4.如图,⊙O是等边△ABC的内切圆,分别切AB,BC,AC于点E,F,D,P是DF度数是( )A.65°B.60°C.58°D.50°5.如图,PA,PB是⊙O的切线,A,B是切点,若∠P=70°,则∠ABO=( )A.30°B.35°C.45°D.55°6.如图,长方形ABCD中,AB=4,AD=3,圆B 半径为1，圆A与圆B内切，则点C、D与圆A的位置关系是( )A.点C在圆A外，点D在圆A内B.点C在圆A外，点D在圆A外C.点C在圆A上，点D在圆A内D.点C在圆A内，点D在圆A外7.如图,在等腰△ABC中, AB=AC=2√5,BC=8,按下列步骤作图：①以点A为圆心，适当的长度为半径作弧,分别交AB,AC于点E,F,再分EF的长为半径作弧相交于点H，作射线AH；别以点E，F为圆心，大于12AB的长为半径作弧相交于点M,N,作直线②分别以点A，B为圆心，大于12MN,交射线AH于点O;③以点O为圆心，线段OA长为半径作圆.则⊙O的半径为( )A.2√5B.10C.4D.58.如图,直线AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,若OB=6 cm,OC=8cm,则BE+CG的长等于( )A.13 cmB.12 cmC.11 cmD. 10 cm9.如图,AB为⊙O的直径,点P在AB的延长线上,PC,PD与⊙O相切,切点分别为C,D.若AB=6,PC=4,则sin∠CAD等于( )A.35B.23C.34D.4510.如图，点A的坐标为(-3，2),⊙A的半径为1,P为坐标轴上一动点,PQ切⊙A于点Q,在所有P点中，使得PQ长最小时，点P的坐标为( )A.( 0,2)B.( 0,3)C.( -2,0)D.( -3,0)二、填空题(每小题4分，共24分)11.点A(0,3),点B(4,0),则点O(0,0)在以AB为直径的圆 (填“内”“上”或“外”).12.如图,在△ABC中,D是边BC上的一点，以AD为直径的⊙O交AC于点E,连接DE.若⊙O与BC相切,∠ADE=55°,则∠C的度数为___________.13.点O是△ABC的外心,若∠BOC=110°,则∠BAC为 .14.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为 .15.如图,PA,PB是⊙O的切线,A,B是切点.若∠P=50°,则∠AOB= .16.如图，两个圆都是以点O为圆心，大圆的弦AB是小圆的切线，点P为切点，AB=10，则图中圆环的面积为 .三、解答题(共36分)17.(12分)阅读下列材料:平面上两点P₁(x₁,y₁),P₂(x₂,y₂)之间的距离表示为|P1P2|=√(x1−x2)2+(y1−y2)2,称为平面内两点间的距离公式，根据该公式，如图，设P(x，y)是圆心坐标为C(a，b)、半径为r的圆上任意一点，则点P适合的条件可表示为√(x−a)2+(y−b)2=r,变形可得 (x-a)²+(y-b)²=r², 我们称其为圆心为C(a，b)，半径为r的圆的标准方程.例如：由圆的标准方程(x-1)²+(y-2)²=25 可得它的圆心为(1,2),半径为5.根据上述材料，结合你所学的知识，完成下列各题.(1)圆心为C(3,4),半径为2的圆的标准方程为 ;(2)若已知⊙O的标准方程为(x-2)²+y²=2²,圆心为C，请判断点A(3,-1)与⊙O的位置关系.18.(12分)已知△ABC内接于⊙O,AB=AC,∠BAC=42°,点D是⊙O上一点.(1)如图①,若BD为⊙O的直径,连接CD,求∠DBC和∠ACD的大小;(2)如图②,若CD∥BA,连接AD,过点D作⊙O的切线,与OC的延长线交于点E，求∠E的大小.19.(12分)如图,在△ABC中,∠ACB=90°,BO为△ABC的角平分线，以点O为圆心，OC为半径作⊙O与线段AC交于点D.(1)求证:AB为⊙O的切线;,AD=2,求BO的长.(2)若tanA=34参考答案考点1 点和圆、直线和圆的位置关系1.D ⊙O的半径为2 cm,线段OA=3cm,OB=2cm，即点A到圆心O的距离大于圆的半径，点B 到圆心O的距离等于圆的半径，∴点A在⊙O外,点B在⊙O上,∴直线AB 与⊙O的位置关系为相交或相切.2.6.5cm或2.5cm 分为两种情况:①当点在圆内时，如图1，∵点到圆上的最小距离PB=4cm,最大距离PA=9cm,∴直径AB=4+9=13(cm),∴半径r=6.5 cm;②当点在圆外时，如图2，∵点到圆上的最小距离PB=4 cm,最大距离PA=9 cm,∴直径AB=9-4=5(cm),∴半径r=2.5cm.3.3cm或5cm ∵直线a⊥b,O为直线b上一动点，∴⊙O与直线a相切时,切点为H,∴OH=1 cm. 当点O在点H的左侧，⊙O与直线a相切时，OP=PH-OH=4-1=3(cm);当点O在点H的右侧，⊙O与直线a相切时，OP=PH+OH=4+1=5(cm);∴⊙O与直线a相切,OP的长为3cm或5cm.考点2 切线的性质与判定1.C ∵BC是⊙O的切线,AB是⊙O的直径,∴AB⊥BC,∴∠ABC=90°,∴∠ACB=90°-∠BAC=90°-35°=55°.2.B 由切线长定理,得PA=PB,∴△BPA 是等腰三角形，故A正确；由圆的对称性可知AB⊥PD，但不一定平分，故B不一定正确；如图，连接OB，OA，由切线的性质，得∠OBP=∠OAP=90°,∴点A,B,P在以OP为直径的圆上，故C正确；∵△BPA是等腰三角形,PD⊥AB,∴PC为△BPA的边AB上的中线,故D正确.3.D 如图,连接OB.∵四边形OABC是菱形.∴OA=AB.∵OA=OB,∴OA=AB=OB,∴∠AOB=60°.∵BD是⊙O的切线,∴∠DBO=90°.∵OB=1,∴BD=√3OB=√3.4.24+6√5如图,连接OE,过点C作CF⊥AD交AD于点F,∵四边形ABCD为平行四边形,∴AB=CD,AD=BC,AD∥BC,∴∠EOD+∠OEC =180°,∵⊙O与BC相切于点E,∴OE⊥BC,∴∠OEC=90°,∴∠EOD=90°,∵CF⊥AD,∴∠CFO=90°,∴四边形OECF为矩形,∴FC=OE,OD=3,∵AD为直径,AD=12,∴FC=OE=OD= 12在Rt△OFC中，由勾股定理得OC²=OF²+FC²=3²+6²=45.∴AB=OC=3√5,∴平行四边形ABCD的周长为12+12+3√5+3√5=24+6√5.5.2√3或2√2连接OB,∵BC是⊙O的切线,∴∠OBC=90°.∵BC=OA,∴OB=BC=2,∴△OBC是等腰直角三角形，∴∠BCO=45°,∴∠ACO≤45°.当△OAC是直角三角形时，①若∠AOC=90°,∴OC=√2OB=2√2,∴AC=√OA2+OC2=√22+(2√2)2=2√3;②若∠OAC=90°,∵BC是⊙O的切线,∴∠CBO=∠OAC=90°.∵BC=OA=OB,∴△OBC是等腰直角三角形，∴OC= 2√2.6.27°∵ PA切⊙O于点A,∴∠OAP=90°.∵∠P=36°, ∴∠AOP=54°. ∴∠B=12∠AOP=27 ∘.7.(1)证明连接OB,如图,∵PA是以AC为直径的⊙O的切线，切点为A,∴∠PAO=90°, ∵OA=OB,AB⊥OP,∴∠POA=∠POB,在△PAO和△PBO中, {AO=BO,∠POA=∠POB,OP=OP,∴△PAO≌△PBO(SAS),∴∠PBO=∠PAO=90°,即OB⊥PB,又∵OB为⊙O的半径,∴PB是⊙O的切线;(2)解设OP与AB交于点D.∵AB⊥OP,AB=6,∴DA=DB=3,∠PDA =∠PDB=90°,∵cos∠PAB=35=DAPA=3PA,∴PA=5,∴PD=√PA2−AD2=√52−32=4,在Rt△APD和Rt△APO中,cos∠APD= PDPA ,cos∠APO=PAPO,8.(1)证明∵∠CAD=∠ABD,∠ABD=∠ACD,∴∠ACD=∠CAD,∴AD=CD;(2)解∵AF是⊙O的切线,∴∠FAB=90°.∵AB是⊙O的直径,∴∠ACB=∠ADB=∠ADF=90°,∴∠ABD+∠BAD=∠BAD+∠FAD=90°. ∴∠ABD=∠FAD.∵∠ABD=∠CAD,∠CAD=∠EAD,∴∠FAD=∠EAD.∵AD=AD,∴△ADF≌△ADE(ASA).∴AF=AE,DF=DE.∵AB=4,BF=5,∴AF =√BF 2−AB 2=3,∴AE=AF=3. ∵S △ABF =12AB ⋅AF =12BF ⋅AD, ∴AD =AB⋅AF BF=4×35=125,∴DE =√AE 2−AD 2=√32−(125)2=95, ∴BE =BF −2DE =75.∵∠AED=∠BEC,∠ADE=∠BCE=90°.∴△BEC ∽△AED. ∴BEAE =BCAD , ∴BC =BE⋅AD AE=2825, ∴sin ∠BAC =BC AB =725.∵∠BDC=∠BAC,∴sin ∠BDC =725.9.证明 (1)∵AB 是⊙O 的直径,∴∠AEB=90°,∴∠EAB+∠EBA=90°. ∵∠CBE=∠BDE,∠BDE=∠EAB,∴∠EAB=∠CBE,∴∠EBA+∠CBE=∠EBA+∠EAB=90°,即∠ABC=90°,∴CB ⊥AB. ∵AB 是⊙O 的直径,∴BC 是⊙O 的切线. (2)∵BD 平分∠ABE,∴∠ABD=∠DBE. ∵∠DAF=∠DBE,∴∠DAF=∠DBA.∵∠ADB=∠FDA,∴△ADF ∽△BDA, ∴ADBD =DFAD ,∴AD ²=DF ·DB. 考点3 三角形的外接圆与内切圆1.C ∵点O 为△ABC 的外心,∠A=40°, ∴∠A =12∠BOC,∴∠BOC =2∠A =80 ∘. 2.C 过点O 作OE ⊥BC 于点E,如图所示:∵∠BAC=120°,AB=AC,∴∠ABC=∠ACB=30°,又 ∵AB̂对应的圆周角为∠ACB 和∠ADB,∴∠ACB=∠ADB=30°, 而BD 为直径,∴∠BAD=90°,在Rt △BAD 中,∠ADB=30°,AD=3, ∴cos30 ∘=ADBD =3BD =√32,∴BD =2√3,∴OB =√3,又∵∠ABD=90°-∠ADB=90°-30°=60°,∠ABC=30°,∴∠OBE=30°. 又∵OE ⊥BC,∴△OBE 为直角三角形. ∴cos ∠OBE =cos30 ∘−BEOB =√3=√32, ∴BE =32.由垂径定理可得BC=2BE= 2×32=3.3.C 如图,∵△ABC是等边三角形.∴△ABC的内切圆和外接圆是同心圆，圆心为O. 设OE=r,AO=R,AD=h,∴h=R+r,故A正确;∵AD⊥BC,∴∠DAC=12∠BAC=12×60°=30°.在Rt△AOE中,∴R=2r,故B正确;∵OD=OE=r,AB=AC=BC=a,∴AE=12AC=12a,∴(12a)2+r2=(2r)2,(12a)2+(12R)2=R².∴r=√36a,R=√33a,故C错误，D正确.4.50°∵∠A=50° ,∴∠BOC=100°.∵OB=OC,∴△OBC为等腰三角形,又∵D为BC 中点，∴OD为BC上的中线，根据等腰三角形三线合一性质可得OD为∠BOC的平分线∴∠BOD=12∠BOC=50∘.5.(2,3) 根据A,B,C三点的坐标建立如图所示的坐标系.根据题意，得AB=√62+32=3√5,AC=√42+82=4√5,BC=√102+52=5√5.∵AB²+AC²=BC².∴∠BAC=90°.设BC的函数表达式为y=kx+b，代入B( -3,3),C(7,-2).得{3=−3k+b,−2=7k+b,解得{k=−12,b=32,∴BC的函数表达式为y=−12x+32.当y=0时,x=3,即G(3,0),∴点A与点G关于BD对称，射线BD是∠ABC的平分线.设点M为三角形的内心，内切圆的半径为r,在BD上找一点M,过点M作ME⊥AB,过点M作MF⊥AC,且ME=MF=r.∵∠BAC=90°,∴四边形MEAF为正方形, S ABC=12AB×AC=12AB×r+12AC×r+12BC×r,解得r=√5,即AE=EM=√5,∴BE=3√5−√5=2√5,∴BM=√BE2+EM2=5,∵B( -3,3),∴M(2,3).∴△ABC内心M的坐标为(2,3).6.1 ∵b+|c−3|+a2−8a=4√b−1−19，∴|c−3|+(a−4)2+(√b−1−2)2= 0,∴c=3,a=4,b=5.∵3²+4²=25=5²,∴c²+a²=b²,∴△ABC是直角三角形,∠ABC=90°.设内切圆的半径为r.根据题意，得S△ABC=12×3×4=12×3×r+12×4×r+12×r×5,∴r=1.(或者r=3+4−52=1)专题检测1.C2.C 如图,∵⊙O的半径为5,点O到直线l 的距离为3,∴CE=2,过点D作AB⊥ OC,垂足为D,交⊙O于A,B两点,且DE=2,∴⊙O上到直线l的距离为2的点为A，B，C，∴⊙O上到直线l的距离为2的点有3个.3.B4.B5.B 如图,连接OA.∵PA,PB是⊙O的切线,A,B是切点,∴∠PBO=∠PAO=90°,∵∠P=70°,∴∠BOA=360°—∠PBO—∠PAO-∠P=110°,∵OA=OB,∴∠ABO=∠BAO=12(180∘−∠BOA)=12(180 ∘−110 ∘)=35 ∘.6.C 两圆内切，圆心距等于半径之差的绝对值,设圆A的半径为R,则AB=R-1,∵AB =4,圆B半径为1,∴R=5,即圆A的半径等于5,∵AB=4,BC=AD=3,由勾股定理可知AC=5,∴AC=5=R,AD=3C在圆上，点D在圆内.7.D 如图,连接OC,设OA交BC于点T.∵AB=AC=2√5,AO平分∠BAC,∴AO⊥BC,BT=TC=4,∴AT=√AC2−CT2=√(2√5)2−42=2.在Rt△OCT中.有r²=(r-2)²+4²,解得r=5.8.D9.D 连接OC、OD、CD,CD交PA于点E,如图,∵PC,PD与⊙O相切,切点分别为C,D,∴OC⊥CP,PC=PD,OP平分∠CPD.∴OP⊥CD,∴CB̂=DB̂,∴∠COB=∠DOB,∵∠CAD=12∠COD,∴∠COB=∠CAD,在Rt△OCP中, OP=√OC2+PC2=√32+42=5,∴sin∠COP=PCOP =45,∴sin∠CAD=45.10.D 连接AQ、PA,如图,∵PQ切⊙A于点Q,∴AQ⊥PQ,∴∠AQP=90°,∴PQ=√AP2−AQ2=√AP2−1,当AP的长度最小时，PQ的长度最小，∵AP⊥x轴时,AP的长度最小,∴AP⊥x轴时,PQ的长度最小,∵A(-3,2),∴此时P点坐标为(-3,0).11.上 12.55°13.55°或125°分两种情况:(1)点A 与点O 在BC 边同侧时,如图1:∵∠BOC=110°,∴∠BAC =110 ∘×12=55 ∘. (2)点A 与点O 在BC 边两侧时,如图2:∵∠BOC=110°,即BĈ所对的圆心角为110°,∴BDC ̂所对的圆心角为：360°—110°=250°. ∴∠BAC =12×250 ∘=125 ∘. 14.4415.130° ∵PA,PB 是⊙O 的切线,A,B 是切点,∴OA ⊥PA,OB ⊥PB,∴∠OAP=∠OBP=90°,∵∠OAP+∠AOB+∠OBP +∠P=360°,∴∠AOB=360°—90°—90°-50°=130°. 16.25π 如图,连接OP 、OA,∵大圆的弦AB 是小圆的切线,∴OP ⊥AB, ∴AP=BP= 12AB =5, 由勾股定理得OA ²-OP ²=AP ²=25, ∴圆环的面积=π×OA ²-π×OP ²=π×(OA ²-OP ²)=25π.17.解 (1)圆心为C(3,4),半径为2的圆的标准方程为(x-3)²+( y-4)²=4.故答案为：(x-3)²+(y-4)²=4. (2)由题意得圆心为C(2.0),∵A (3,−1),∴AC =√(3−2)2+12= √2<2,∴点A 在⊙C 内部.18.解 (1)∵AB=AC,∴∠ABC=∠ACB= 12(180 ∘−∠BAC)=12×(180 ∘−42 ∘)=69 ∘,∵BD 为直径,∴∠BCD=90°,∵∠D=∠BAC=42°,∴∠DBC=90°-∠D=90°-42°=48°; ∴∠ACD=∠ABD=∠ABC-∠DBC=69°-48°=21°; (2)如图,连接OD,∵CD ∥AB,∴∠ACD=∠BAC=42°,∵四边形ABCD 为⊙O 的内接四边形，∴∠B+∠ADC=180°, ∴∠ADC=180°-∠B=180°-69°=111°,∴∠CAD=180°-∠ACD-∠ADC=180°-42°-111°=27°,∴∠COD=2∠CAD=54°, ∵DE 为切线,∴OD ⊥DE,∴∠ODE=90°,∴∠E=90°-∠DOE=90°-54°=36°. 19.(1)证明如图,过点O 作OH ⊥AB 于点H.∵∠ACB=90°,∴OC ⊥BC.∵BO 为△ABC 的角平分线,OH ⊥AB,∴OH=OC,即OH 为⊙O 的半径. ∵OH ⊥AB,∴AB 为⊙O 的切线.(2)解设⊙O 的半径为3x,则OH=OD=OC=3x.在Rt △AOH 中,∵tanA =34, ∴OHAH =34,∴3xAH =34,∴AH=4x, ∴AO =√OH 2+AH 2=√(3x )2+(4x )2=5x,∵AD=2,∴AO=OD+AD=3x+2,∴3x+2=5x,∴x=1,∴OA=3x+2=5,OH=OD=OC=3x=3 . ∴AC=OA+OC=5+3=8.在Rt △ABC 中, ∵tanA =BCAC ,∴BC =AC ⋅tanA =8×34=6, ∴OB =√OC 2+BC 2=√32+62=3√5.。

50：圆与圆的位置关系一、选择题1.（天津3分）已知⊙1O 与⊙2O 的半径分别为3 cm 和4 cm ，若12O O =7 cm ，则⊙1O 与⊙2O 的位置关系是(A) 相交 (B) 相离 (C) 内切 (D) 外切 【答案】D 。

【考点】圆与圆位置关系的判定。

【分析】两圆半径之和3+4=7，等于两圆圆心距12O O =7，根据圆与圆位置关系的判定可知两圆外切。

2．（重庆潼南4分）已知⊙O 1与⊙O 2外切，⊙O 1的半径R=5cm ，⊙O 2的半径r=1cm ，则⊙O 1与⊙O 2的圆心距是A 、1cmB 、4cmC 、5cmD 、6cm【答案】D 。

【考点】圆与圆的位置关系。

【分析】根据两圆的位置关系的性质：相切（两圆圆心距离等于两圆半径之和或两圆半径之差），相离（两圆圆心距离大于两圆半径之和），相交（两圆圆心距离小于两圆半径之和大于两圆半径之差），内含（两圆圆心距离小于两圆半径之差）。

由于两圆外切，故两圆圆心距离等于两圆半径之和；5cm ＋1cm ＝6cm 。

故选D 。

3.（广西贺州3分）已知⊙O 1和⊙O 2的半径分别为2和5，如果两圆的位置关系为外离，那么圆心距O 1O 2的取值范围在数轴上表示正确的是【答案】C 。

【考点】两圆的位置关系，在数轴上表示不等式组的解集。

【分析】根据两圆的位置关系的判定：相切（两圆圆心距离等于两圆半径之和），相离（两圆圆心距离大于两圆半径之和），相交（两圆圆心距离小于两圆半径之和），由已知圆心距O 1O 2的取值范围为大于2＋5＝7。

从而根据在数轴上表示不等式组的解集的方法：把每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示。

故选C。

4..（浙江温州4分）已知线段AB=7cm，现以点A为圆心，2cm为半径画⊙A；再以点B为圆心，3cm为半径画⊙B，则⊙A和⊙B的位置关系A、内含B、相交C、外切D、外离【答案】D。

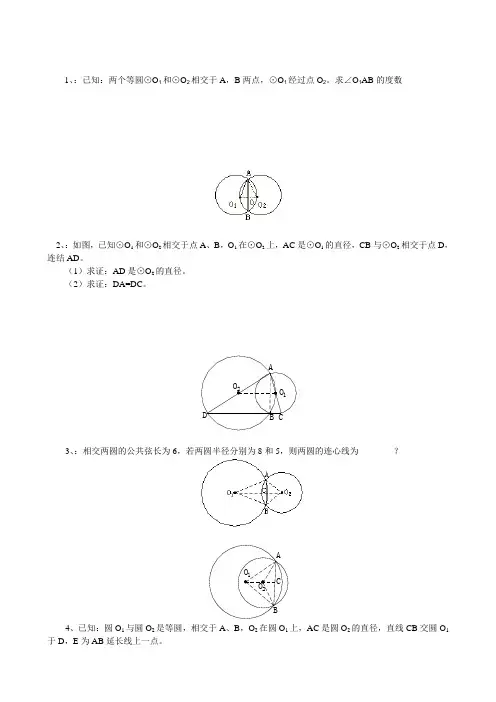
1、：已知：两个等圆⊙O1和⊙O2相交于A，B两点，⊙O1经过点O2。

求∠O1AB的度数2、：如图，已知⊙O1和⊙O2相交于点A、B，O1在⊙O2上，AC是⊙O1的直径，CB与⊙O2相交于点D，连结AD。

（1）求证：AD是⊙O2的直径。

（2）求证：DA=DC。

（1）证明：AD是圆O1的直径；【模拟试题】（答题时间：25分钟）1. 若两圆无公共点，则两圆的位置关系为___________。

2. 若两圆有公共点，则两圆的位置关系为___________。

3. 已知两圆半径为12.4cm 和7.3cm ，则两圆相切时，圆心距等于___________。

4. 已知两圆的半径之比为3：5，若两圆内切时圆心距等于6cm ，则两圆的半径分别为___________；若两圆无公共点，则圆心距d 的取值范围为___________。

5. 若两圆半径为r 和R ，圆心距为d ，且d<R+r ，则两圆位置关系为___________。

6. 若两圆的半径分别是2cm 和4cm ，圆心距是1cm ，则两圆的位置关系是___________。

7. 在△ABC 中，∠C=90°，AC=4cm ，BC=3cm ，圆A 、圆B 、圆C 两两外切，则圆C 的半径是___________。

8. 若两圆直径分别是8+t 和8－t ，圆心距为16，则两圆的位置关系为___________。

9. 若两圆半径分别为R 和r （R>r ），其圆心距为d ，且有Rd 2d r R 222=+-，则两圆的位置关系为___________。

10. 若两圆半径分别为R 和r ，圆心距为d ，且r R d -≥，则两圆位置关系为___________。

11. 已知圆O 1和圆O 2相切，这个图形是___________对称图形，它的对称轴是___________，切点与对称轴的位置关系为___________。

12. 两个半径相等的圆的位置关系有___________种。

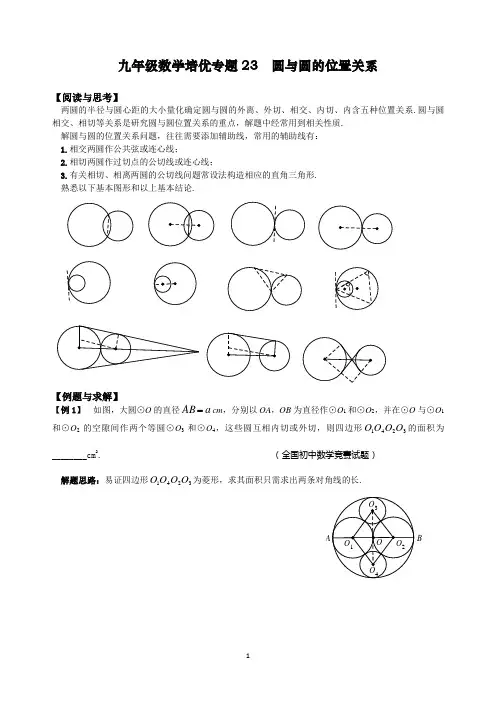
九年级数学培优专题23 圆与圆的位置关系【阅读与思考】两圆的半径与圆心距的大小量化确定圆与圆的外离、外切、相交、内切、内含五种位置关系.圆与圆相交、相切等关系是研究圆与圆位置关系的重点，解题中经常用到相关性质. 解圆与圆的位置关系问题，往往需要添加辅助线，常用的辅助线有： 1.相交两圆作公共弦或连心线；2.相切两圆作过切点的公切线或连心线；3.有关相切、相离两圆的公切线问题常设法构造相应的直角三角形. 熟悉以下基本图形和以上基本结论.【例题与求解】【例1】 如图，大圆⊙O 的直径a AB cm ，分别以OA ，OB 为直径作⊙O 1和⊙O 2，并在⊙O 与⊙O 1和⊙O 2的空隙间作两个等圆⊙O 3和⊙O 4，这些圆互相内切或外切，则四边形3241O O O O 的面积为________cm 2. （全国初中数学竞赛试题） 解题思路：易证四边形3241O O O O 为菱形，求其面积只需求出两条对角线的长.O O 2O 1O 3O 4BA【例2】 如图，圆心为A ，B ，C 的三个圆彼此相切，且均与直线l 相切.若⊙A ，⊙B ， ⊙C 的半径分别为a ，b ，c （b a c <<<0），则a ，b ，c 一定满足的关系式为（ ） A .c a b +=2 B .c a b +=2C .b ac 111+= D .ba c 111+= （天津市竞赛试题）解题思路：从两圆相切位置关系入手，分别探讨两圆半径与分切线的关系，解题的关键是作圆的基本辅助线.lC A 1C 1B 1BA【例3】 如图，已知两圆内切于点P ，大圆的弦AB 切小圆于点C ，PC 的延长线交大圆于点D .求证： （1）∠APD =∠BPD ；（2）CB AC PC PB PA ∙+=∙2. （天津市中考试题）解题思路：对于（1），作出相应辅助线；对于（2），应化简待证式的右边，不妨从AC ·BC =PC ·CD 入手.PBCDA【例4】 如图⊙O 1和⊙O 2相交于点A 及B 处，⊙O 1的圆心落在⊙O 2的圆周上，⊙O 1的弦AC 与⊙O 2交于点D .求证：O 1D ⊥BC .（全俄中学生九年级竞赛试题）解题思路：连接AB ，O 1B ，O 1C ，显然△O 1BC 为等腰三角形，若证O 1D ⊥BC ，只需证明O 1D 平分∠B O 1C .充分运用与圆相关的角.O 1O 2D BCA【例5】 如图，在直角梯形ABCD 中，AD ∥BC ，AB ⊥BC ，AD =1,AB =2，DC =22，点P 在边BC 上运动（与B ，C 不重合）.设PC =x ，四边形ABPD 的面积为y . （1）求y 关于x 的函数关系式，并写出自变量x 的取值范围； （2）若以D 为圆心，21为半径作⊙D ，以P 为圆心，以PC 的长为半径作⊙P ，当x 为何值时，⊙D 与⊙P 相切？并求出这两圆相切时四边形ABPD 的面积. （河南省中考题）解题思路：对于（2），⊙P 与⊙D 既可外切，也可能内切，故需分类讨论，解题的关键是由相切两圆的性质建立关于x 的方程.DCPBA【例6】 如图，ABCD 是边长为a 的正方形，以D 为圆心，DA 为半径的圆弧与以BC 为直径的半圆交于另一点P ，延长AP 交BC 于点N ，求NCBN的值. （全国初中数学联赛试题） 解题思路：AB 为两圆的公切线，BC 为直径，怎样产生比例线段？丰富的知识，不同的视角激活想象，可生成解题策略与方法.N PB A CD【能力与训练】A 级1.如图，⊙A ，⊙B 的圆心A ，B 在直线l 上，两圆的半径都为1cm .开始时圆心距AB ＝4cm ，现⊙A ，⊙B 同时沿直线l 以每秒2cm 的速度相向移动，则当两圆相切时，⊙A 运动的时间为_______秒.（宁波市中考试题）2.如图，O 2是⊙O 1上任意一点，⊙O 1和⊙O 2相交于A ，B 两点，E 为优弧AB 上的一点，EO 2及延长线交⊙O 2于C ，D ，交AB 于F ，且CF ＝1，EC ＝2，那么⊙O 2的半径为_______.（四川省中考试题）（第1题图） （第2题图） （第3题图）3.如图，半圆O 的直径AB ＝4,与半圆O 内切的动圆O 1与AB 切于点M .设⊙O 1的半径为y ，AM 的长为x ，则y 与x 的函数关系是_________________.（要求写出自变量x 的取值范围）（昆明市中考试题）4.已知直径分别为151+和315-的两个圆，它们的圆心距为115-，这两圆的公切线的条数是__________.5.如图，⊙O 1和⊙O 2相交于点A ，B ，且⊙O 2的圆心O 2在圆⊙O 1的圆上，P 是⊙O 2上一点.已知∠A O 1B ＝60°，那么∠APB 的度数是（ ）A .60°B .65°C .70°D .75°（甘肃省中考试题）6.如图，两圆相交于A 、B 两点，过点B 的直线与两圆分别交于C ，D 两点.若⊙O 1半径为5，⊙O 2的半径为2，则AC ：AD 为（ ）A .52:3B .3:52C .1:52D .2:5（第5题图） （第6题图） （第7题图）7.如图，⊙O 1和⊙O 2外切于点T ，它们的半径之比为3:2，AB 是它们的外公切线，A ，B 是切点，ABlBAF CEBAD O 1O 2O 1BOMAO 1O 2PBAO 2DBCAO 1BATO 1O 2＝64，那么⊙O 1和⊙O 2的圆心距是（ ）A .65B .10C .610D .1339208.已知两圆的半径分别为R 和r （r R >），圆心距为d .若关于x 的方程0)(222=-+-d R rx x 有两相等的实数根，那么这两圆的位置关系是（ ）A .外切B .内切C .外离D .外切或内切（连云港市中考试题）9.如图，⊙O 1与⊙O 2相交于A ，B 两点，点O 1在⊙O 2上，点C 为⊙O 1中优弧AB ⌒上任意一点，直线CB 交⊙O 2于D ，连接O 1D .（1）证明：DO 1⊥AC ；（2）若点C 在劣弧AB ⌒上，（1）中的结论是否仍成立？请在图中画出图形，并证明你的结论. （大连市中考试题）DBCA O 1O 2O 1O 2BA图1 图210.如图，已知⊙O 1与⊙O 2外切于点P ，AB 过点P 且分别交⊙O 1和⊙O 2于点A ，B ，BH 切⊙O 2于点B ，交⊙O 1于点C ，H .（1）求证：△BCP ∽△HAP ；（2）若AP :PB ＝3：2，且C 为HB 的中点，求HA :BC .（福州市中考试题）O 1O 2PABCH11.如图，已知⊙B ，⊙C 的半径不等，且外切于点A ，不过点A 的一条公切线切⊙B 于点D ，切⊙C 于点E ，直线AF ⊥DE ，且与BC 的垂直平分线交于点F .求证：BC ＝2AF .（英国数学奥林匹克试题）H F AEDCB12.如图，AB 为半圆的直径，C 是半圆弧上一点.正方形DEFG 的一边DG 在直径AB 上，另一边DE 过△ABC 得内切圆圆心O ，且点E 在半圆弧上.（1）若正方形的顶点F 也在半圆弧上，求半圆的半径与正方形边长的比；（2）若正方形DEFG 的面积为100，且△ABC 的内切圆半径4 r ，求半圆的直径AB .（杭州市中考试题）OCE FDGBAB 级1.相交两圆的半径分别为5cm 和4cm ，公共弦长为6cm ，这两圆的圆心距为_______.2.如图，⊙O 过M 点，⊙M 交⊙O 于A ，延长⊙O 的直径AB 交⊙M 于C .若AB ＝8，BC ＝1，则AM ＝_______.（黑龙江省中考试题）（第2题图） （第3题图） （第4题图）3.已知圆环内直径为a cm ，外直径为b cm ，将50个这样的圆环一个接着一个环套环地连成一条锁链，那么这条锁链拉直后的长度为___________cm .4.如图，已知PQ ＝10，以PQ 为直径的圆与一个以20为半径的圆相切于点P .正方形ABCD 的顶点A ，B 在大圆上，小圆在正方形的外部且与CD 切于点Q .若AB ＝n m +，其中m ，n 为整数，则=+n m ___________.（美国中学生数学邀请赛试题）5.如图，正方形ABCD 的对角线AC ，BD 交于点M ，且分正方形为4个三角形，⊙O 1，⊙O 2，⊙O 3，⊙O 4，分别为△AMB ，△BMC ，△CMD ，△DMA 的内切圆.已知AB ＝1.则⊙O 1，⊙O 2，⊙O 3，⊙O 4所夹的中心（阴影）部分的面积为（ ） A .(4)(322)16π-- B . (322)4π-C .(4)(322)4π-- D . 416π-（太原市竞赛试题）M O 4O 3O 1O 2DC BACDEABO 1O 2DCBAO 1O 2（第5题图） （第6题图） （第7题图）6.如图，⊙O 1与⊙O 2内切于点E ，⊙O 1的弦AB 过⊙O 2的圆心O 2，交⊙O 2于点C ，D .若AC ：CD :BD＝2:4:3，则⊙O 2与⊙O 1的半径之比为（ ）A .2:3B .2:5C .1:3D .1:4QDC B AP7.如图，⊙O 1与⊙O 2外切于点A ，两圆的一条外公切线与⊙O 1相切于点B ，若AB 与两圆的另一条外公切线平行，则⊙O 1与⊙O 2的半径之比为（ ）A .2:5B .1:2C .1:3D .2:3（全国初中数学联赛试题）8.如图，已知⊙O 1与⊙O 2相交于A ，B 两点，过点A 作⊙O 1的切线，交⊙O 2于点C ，过点B 作两圆的割线分别交⊙O 1，⊙O 2于点D ，E ，DE 与AC 相交于点P . （1）求证：PA PE PC PD ∙=∙（2）当AD 与⊙O 2相切且P A ＝6，PC ＝2，PD ＝12时，求AD 的长. （黄冈市中考试题）EP CB DAO 2O 19.如图，已知⊙O 1和⊙O 2外切于A ，BC 是⊙O 1和⊙O 2的公切线，切点为B ，C .连接BA 并延长交⊙O 1于D ，过D 点作CB 的平行线交⊙O 2于E ，F . （1）求证：CD 是⊙O 1的直径；（2）试判断线段BC ，BE ，BF 的大小关系，并证明你的结论. （四川省中考试题）O 1O 2D EFA C B10.如图，两个同心圆的圆心是O ，大圆的半径为13，小圆的半径为5，AD 是大圆的直径，大圆的弦AB ，BE 分别与小圆相切于点C ，F ，AD ，BE 相交于点G ，连接BD . （1）求BD 的长；（2）求2ABE D ∠+∠的度数；（3）求BGAG的值. （淄博市中考试题）G OEFCADB11.如图，点H 为△ABC 的垂心，以AB 为直径的⊙O 1与△BCH 的外接圆⊙O 2相交于点D ，延长AD 交CH于点P.求证：P为CH的中点. （“《数学周报杯”全国初中数学竞赛试题）BDHCPAO1O212.如图，已知AB为半圆O的直径，点P为直径AB上的任意一点，以点A为圆心，AP为半径作⊙A，⊙A与半圆O相交于点C，以点B为圆心，BP为半径作⊙B，⊙B与半圆O相交于点D，且线段CD的中点为M.求证：MP分别与⊙A，⊙B相切. （“《数学周报杯”全国初中数学竞赛试题）MP O BA CD。

直线与圆、圆与圆的位置关系练习A 组一 、选择题图1 图3 图41、（2011甘肃兰州）如图1，AB 是⊙O 的直径，点D 在AB 的延长线上，DC 切⊙O 于点C ，若∠A=25°，则∠D 等于（ ）A ．20°B ．30°C ．40°D ．50°2、（2011四川成都）已知⊙O 的面积为29cm π，若点0到直线l 的距离为cm π，则直线l 与⊙O 的位置关系是（ ）(A)相交 (B)相切 (C)相离 (D)无法确定3、（2011湖北黄冈）如图2，AB 为⊙O 的直径，PD 切⊙O 于点C ，交AB 的延长线于D ，且CO=CD ，则∠PCA=（ ）A ．30°B ．45°C ．60°D ．67.5°4、（2011浙江杭州）在平面直角坐标系xOy 中，以点(-3，4)为圆心，4为半径的圆（ ）A ．与x 轴相交，与y 轴相切B ．与x 轴相离，与y 轴相交C ．与x 轴相切，与y 轴相交D ．与x 轴相切，与5、（2011山东枣庄）如图3，PA 是O ⊙的切线，切点为A ，∠APO=30°，则O ⊙的半径为（）A. 1B.C. 2D. 46、（2009年江西省）如图4，在数轴上，点A 所表示的实数为3，点B 所表示的实数为a , ⊙A 的半径为2.下列说法中，不正确．．．的是（ ） A ．当a ＜5 时，点B 在⊙A 内 B ．当1＜a ＜5 时，点B 在⊙A 内 C ．当a ＜1 时，点B 在⊙A 外 D ．当a ＞5 时，点B 在⊙A 外 7、若两圆的半径分别为5和7，圆心距为2，则这两圆的位置关系是 ( )A ．内含B ．内切C ．相交D ．外切 8、已知两个圆只有一条公切线，那么这两个圆的位置关系是（ ）A. 内切B. 外切C. 相交D. 外离9、已知⊙1O 与⊙2O 的圆心距1O 2O =6cm ，且两圆的半径满足一元二次方程2x -6x+8=0．则两圆的位置关系为()A ．外切B ．内切C ．外离D ．相交10、一个钢管放在V 形架内，右图是其截面图，O 为钢管的圆心．如果钢管的半径为25 cm ，∠MPN ＝60︒，则OP ＝( )A ．50 cmB ．253cmC ．3350cm D ．503cmA B D OCA 图2二 、填空题图6 图7 图811、（2011四川南充市）如图6，PA ，PB 是⊙O 是切线，A ，B 为切点， AC 是⊙O 的直径，若∠BAC=25°，则∠P= _度.12、（2011江苏苏州）如图7，已知AB 是⊙O 的一条直径，延长AB 至C 点，使得AC=3BC ，CD 与⊙O 相切，切点为D.若CD=3，则线段BC 的长度等于__________.13、（2011江苏宿迁）如图8，从⊙O 外一点A 引圆的切线AB ，切点为B ，连接AO 并延长交圆于点C ，连接BC ．若∠A ＝26°，则∠ACB 的度数为 ．14、(2010•泸州)已知⊙0是边长为2的等边△ABC 的内切圆。

圆的中考题归类解析圆的基本性质是初中数学的重点内容之一,在初中数学体系中处于重要地位,在中考中占有较大的分值,是中考的重头戏.题型主要有选择、填空、解答和作图(包括阅读理解和开放探索等).还可与三角形、四边形、相似形、方程、函数等知识点相结合,构成内容丰富、构思新颖的综合性试题而成为中考的压轴题.从2021年各省市的中考试题中所反映出的考点精选几例,解析如下,供同学们参考:考点1 圆的认识例1(2021辽宁沈阳)如图所示,是⊙O 的一条弦，OD AB ⊥，垂足为，交⊙O 于点，点在⊙O 上.（1）若52AOD ∠=，求DEB ∠的度数；（2）若3OC =，5OA =，求的长.分析 由垂径定理可得弧AD=弧BD,根据等弧所对的圆周角与圆心角之间的关系,可得∠DEB;由勾股定理可求得AC 的长,根据垂径定理AC=BC,从而可得AB.解 （1）OD AB ⊥，∴弧AD=弧BD, ∴11522622DEB AOD ∴∠=∠=⨯= （2）OD AB ⊥，∴AC BC ∴=，AOC △为直角三角形，3OC =，5OA =，由勾股定理可得2222534AC OA OC =-=-=,∴28AB AC ∴==.评注 本例着重考查了垂径定理及等弧所对的圆周角与圆心角之间的关系和勾股定理.正确运用垂径定理是解题的关键.考点2 与圆有关的位置关系例2(2021北京)已知：如图，在Rt ABC △中，90C ∠=，点O 在AB 上，以O 为圆心，OA 长为半径的圆与AC AB ，分别交于点D E ，，且CBD A ∠=∠.（1）判断直线BD 与⊙O 的位置关系，并证明你的结论；（2）若:8:5AD AO =，2BC =，求BD 的长.分析 连OD,证∠ODB=900,即OD ⊥BD,得到直线BD 与⊙O相切;连DE,先求得cosA 的值为54,由∠CBD=∠A,则cos ∠CBD =54=BD BC ,又BC=2,则易得BD 的值.解 （1）直线BD 与⊙O 相切.证明：如图，连结OD ,OA OD =，A ADO ∴∠=∠.90C ∠=，90CBD CDB ∴∠+∠=.又CBD A ∠=∠，90ADO CDB ∴∠+∠=.90ODB ∴∠=.∴直线BD 与⊙O 相切.（2）如图，连结DE .AE 是⊙O 的直径， 90ADE ∴∠=.:8:5AD AO =，∴54108cos ===AE AD A 90C ∠=，CBD A ∠=∠，4cos 5BC CBD BD ∴∠==.2BC =，52BD ∴=. 评注 本例考查了切线的判定及直角三角形的边角关系.证得∠ODB=900及cos ∠CBD=54是解题的关键. 考点3 圆中的计算问题例3(2021江苏南通)在一次数学探究性学习活动中，某学习小组要制作一个圆锥体模型，操作规则是：在一块边长为16cm 的正方形纸片上剪出一个扇形和一个圆，使得扇形围成圆锥的侧面时，圆恰好是该圆锥的底面.他们首先设计了如图所示的方案一，发现这种方案不可行，于是他们调整了扇形和圆的半径，设计了如图所示的方案二.（两个方案的图中，圆与正方形相邻两边及扇形的弧均相切.方案一中扇形的弧与正方形的两边相切）（1）请说明方案一不可行的理由；（2）判断方案二是否可行若可行，请确定圆锥的母线长及其底面圆 半径；若不可行，请说明理由.分析 通过计算,得出方案一正方形的对角线AC 的长大于所给正方形的对角线,从而方案一不可行;对于方案二,设圆锥底面圆的半径为r cm ，圆锥的母线长为R cm ，即AF=R,O 2F=r,则O 2C=r 2,扇形弧长218090R R l ππ==,底面圆周长r C π2=,根据2162=++r r R 及22R r ππ=求得R,r. 解（1）理由如下： ∵扇形的弧长ππ81801690=⋅=l ，圆锥底面周长＝2πr ， 根据圆锥底面圆周长应等于侧面扇形弧长,即ππ82=r , ∴圆的半径r 为4cm. 即AE=16cm,O 1E=4cm,241=C O cm,由于所给正方形纸片的对角线长为162cm ，而制作这样的圆锥实际需要正方形纸片的对角线AC 长为164422042++=+(cm)，∵ 2042162+>，∴方案一不可行.（2）方案二可行.求解过程如下：设圆锥底面圆的半径为r cm ，圆锥的母线长为R cm ，则(12)162r R ++=， ① 2π2π4R r =. ② 由①②，可得64232021282352R -==+，162802322352r -==+. 故所求圆锥的母线长为320212823-cm ，底面圆的半径为8023223-cm. 评注 本例主要考查了圆锥的有关计算,解题关键是圆锥侧面展开图的扇形弧长应等于底面圆周长.考点4 圆的综合与创新例4(2021浙江嘉兴) 24.如图，直角坐标系中，已知两点(00)(20)O A ，，，，点B 在第一象限且OAB △为正三角形，OAB △的外接圆交y 轴的正半轴于点C ，过点C 的圆的切线交x 轴于点D .（1）求B C ，两点的坐标；（2）求直线CD 的函数解析式；（3）设E F ，分别是线段AB AD ，上的两个动点，且EF 平分四边形ABCD 的周长.试探究：AEF △的最大面积分析 作BG ⊥OA,由等边△OAB 的边长为2,得OG=1,BG=3,从而B(1,3),连AC,可得∠CAO=300,从而OC=332,则C(0,332);在Rt △OCD 中,求得OD,则点D 坐标可得,再用待定系数法可求得直线CD 的函数解析式;先求得四边形ABCD 的周长,设AE 为t,则AF 可用t 的代数式表示, △AEF 的面积A AF AE S sin 21⋅=是一个关于t 的二次函数,根据二次函数的 极值求得△AEF 面积的最大值. 解（1）(20)A ，，2OA ∴=.作BG OA ⊥于G ，OAB △为正三角形，1OG ∴=，3BG =.(13)B ∴，.连AC ，90AOC ∠=，60ACO ABO ∠=∠=，则∠CAO=300,23tan 303OC OA ∴==.2303C ⎛⎫∴ ⎪ ⎪⎝⎭，. （2）90AOC ∠=，AC ∴是圆的直径， 又CD 是圆的切线，CD AC ∴⊥. 30OCD ∴∠=，2tan 303OD OC ==. 203D ⎛⎫∴- ⎪⎝⎭，. 设直线CD 的函数解析式为(0)y kx b k =+≠，则233203b k b ⎧=⎪⎪⎨⎪=-+⎪⎩，解得3233k b ⎧=⎪⎨=⎪⎩.∴直线CD 的函数解析式为2333y x =+. （3）2AB OA ==，23OD =，423CD OD ==，233BC OC ==， ∴四边形ABCD 的周长2363+. 设AE t =，AEF △的面积为S ，则333AF t =+-，)333(4360sin 210t t AF AE S -+=⋅= 233393733434632S t t t ⎡⎤⎛⎫⎛⎫+⎢⎥=+-=--++ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦.∴当96t +=时，max 3128S =+. 点E F ，分别在线段AB AD ，上，0220323t t ⎧⎪∴⎨++⎪⎩≤≤≤≤，2t ≤≤. 96t += 满足2t ≤≤， AEF ∴△38+. 评注 本例是一道以圆为背景,与等边三角形、四边形、坐标系、一次函数、二次函数等知识点相结合,构成的内容丰富、构思新颖的综合题.同时本例又是一道几何动态题.是近年来中考数学的热点题型.这类试题信息量大，对学生获取信息和处理信息的能力要求较高；解题时需要用运动和变化的眼光去观察和研究问题，并特别关注运动与变化中的不变量、不变关系或特殊关系，动中取静，静中求动.。

中考数学分类（含答案）圆与圆的位置关系一、选择题 1．（2010安徽芜湖）若两圆相切，圆心距是7，其中一圆的半径为10，则另一个圆的半径为__________． 【答案】3或172．（2010甘肃兰州） 已知两圆的半径R 、r 分别为方程0652=+-x x 的两根，两圆的圆心距为1，两圆的位置关系是A ．外离B ．内切C ．相交D ．外切 【答案】B3．（2010山东济宁）已知⊙O 1与⊙O 2相切，⊙O 1的半径为3 cm ，⊙O 2的半径为2 cm ，则O 1O 2的长是A ．1 cmB ．5 cmC ．1 cm 或5 cmD ．0.5cm 或2.5cm【答案】C 4．（2010山东日照）已知两圆的半径分别为3cm ，5 cm ，且其圆心距为7cm ，则这两圆的位置关系是（A ）外切 （B ）内切 （C ）相交 （D ）相离 【答案】C5．（2010四川眉山）⊙O 1的半径为3cm ，⊙O 2的半径为5cm ，圆心距O 1O 2=2cm ，这两圆的位置关系是A ．外切B ．相交C ．内切D ．内含 【答案】C 6．（2010浙江宁波） 两圆的半径分别为3和5，圆心距为7，则两圆的位置关系是 (A)内切 (B)相交 (C)外切 (D)外离 【答案】B 7．（2010浙江绍兴）如图为某机械装置的截面图,相切的两圆⊙O 1, ⊙O 2均与⊙O 的弧AB 相切,且O 1O 2∥l 1( l 1为水 平线)，⊙O 1,⊙O 2的半径均为30 mm,弧AB 的 最低点到l 1的距离为30 mm,公切线l 2与l 1间的 距离为100 mm.则⊙O 的半径为( )A.70 mmB.80 mmC.85 mmD.100 mm【答案】B8．（2010湖南长沙）已知⊙O 1、⊙O 2的半径分别是12r =、24r =，若两圆相交，则圆心距O 1O 2可能取的值是（ ）． A 、2 B 、4 C 、6 D 、8 【答案】B ．9．（2010江苏宿迁）外切两圆的半径分别为2 cm 和3cm ，则两圆的圆心距是A ．1cmB ．2cmC ．3cmD ．5cm【答案】D10．（2010 山东济南）已知两圆的半径分别是3和2，圆心的坐标分别是（0，2）和（0，-4），那么两圆的位置关系是（ ）A.内含B.相交C.相切D.外离 【答案】D 11．（2010江苏无锡）已知两圆内切，它们的半径分别为3和6，则这两圆的圆心距d 的取值满足 （ ） A ．9d > B ． 9d = C ． 39d << D ．3d = 【答案】D12．（2010湖南邵阳）如图（四）在边长为1的小正方形组成的网格中，半径为2的1O 的圆心1O 在格点上，将一个与1O 重合的等圆向右平移2个单位，再向上平移2个单位得到2O ，则2O 与1O 的位置关系是（ ）A ．内切B ．外切C ．相交D ．外离第10题图AB单位：mml 1l 2图（四） 【答案】C13．（2010年上海）已知圆O 1、圆O 2的半径不相等，圆O 1的半径长为3，若圆O 2上的点A 满足AO 1 = 3，则圆O 1与圆O 2的位置关系是（ ）A.相交或相切B.相切或相离C.相交或内含D.相切或内含【答案】A 14．（2010重庆綦江县）两圆的圆心距为7cm ，半径分别为5cm 和2cm ，则两圆的位置关系是（ ）A ．内切B ．外切C ．外离D ．内含 【答案】B 15．（2010山东临沂）已知两圆的半径分别是2㎝和4㎝，圆心距是6㎝，那么这两圆的位置关系是（A ）外离 （B ）外切 （C ）相交 （D ）内切 【答案】B16．（2010福建宁德）如图，在8×4的方格（每个方格的边长为1个单位长）中，⊙A 的半径为1，⊙B 的半径为2，将⊙A 由图示位置向右平移1个单位长后， ⊙A 与静止的⊙B 的位置关系是（ ）．A.内含B.内切C.相交D.外切【答案】D 17．（2010江苏常州）若两圆的半径分别为2和3，圆心距为5，则两圆的位置关系为A.外离B.外切C.相交D.内切 【答案】B第9题图18．（2010 四川成都）已知两圆的半径分别是4和6，圆心距为7，则这两圆的位置关系是（ ）（A ）相交 （B ）外切 （C ）外离 （D ）内含 【答案】A 19．（2010湖南常德）已知⊙O 1的半径为5㎝, ⊙O 2的半径为6㎝,两圆的圆心距O 1 O 2=11㎝,则两圆的位置关系为( ) A ．内切 B ． 外切 C ．相交 D ．外离 【答案】B20．（2010湖北省咸宁）如图，两圆相交于A ，B 两点，小圆经过大圆的圆心O ，点C ，D 分别在两圆上，若100ADB ∠=︒，则ACB ∠的度数为 A ．35︒ B ．40︒ C ．50︒D ．80︒【答案】B 21．（2010江苏扬州）已经⊙O 1、⊙O 2的半径分别为5cm,、8cm ，且他们的圆心距为8cm ，则⊙O 1与⊙O 2的位置关系为（ ）A ．外离B ．相交C ．相切D ．内含 【答案】B22．（2010云南楚雄）已知⊙1O 和⊙2O 的半径分别为2cm 和3cm ，两圆的圆心距为5cm ，则两圆的位置关系是（ ）A ．外切B ．外离C ．相交D ．内切 【答案】A 23．（2010 湖北孝感）有四个命题：①两条直线被第三条直线所截，同旁内角互补；②有两边和其中一边的对角对应相等的两个三角形全等；③菱形既是轴对称图形又是中心对称图形；④两圆的半径分别是3和4，圆心距为d ，若两圆有公共点，则.71<<d 其中正确的命题有（ ） A ．1个 B ．2个 C ．3个 D ．4个 【答案】A24．（2010 广东汕头）已知方程0452=+-x x 的两根分别为⊙1与⊙2的半径，且O 1O 2＝3，那么两圆的位置关系是（ ）A ．相交B ．外切C ．内切D ．相离 全品中考网【答案】C 25．（2010 四川泸州）已知⊙O 1与⊙O 2的半径分别为2和3，两圆相交，则两圆的圆心距m 满足（ ）A ．m =5B ．m =1C ．m ＞5D ．1＜m ＜5【答案】D26．（2010 山东淄博）已知两圆的半径分别为R 和r （R ＞r ），圆心距为d ．如图，若数轴上的点A 表示R －r ，点B 表示R ＋r ，当两圆外离时，表示圆心距d 的点D 所在的位置是（A ）在点B 右侧 （B ）与点B 重合（C ）在点A 和点B 之间 （D ）在点A 左侧 【答案】A 27．（2010 甘肃）已知大圆的半径为5，小圆的半径为3，两圆圆心距为7，则这两圆的位置关系为（ ）A ．外离B ．外切 Ｃ．相交 D ．内含 【答案】C 28．（2010 广西玉林、防城港）在数轴上，点A 所表示的实数是－2，⊙A 的半径为2，⊙B 的半径为1，若⊙B 与⊙A 外切，则在数轴上点B 所表示的实数是： （ ） A ．1 B ．－5 C ．1或 －5D ．―１或―3 【答案】C29．（2010 湖北咸宁）如图，两圆相交于A ，B 两点，小圆经过大圆的圆心O ，点C ，D分别在两圆上，若100ADB ∠=︒，则ACB ∠的度数为A ．35︒B ．40︒C ．50︒D ．80︒【答案】B30．（2010辽宁大连）已知两圆半径分别为4和7，圆心距为3，那么这两个圆的位置关系是（）A.内含B.内切C.相交D.外切【答案】B 31．（2010湖北宜昌）两圆的半径分别为2和1，圆心距为3，则反映这两圆位置关系的为图（ ）。

点和圆、直线和圆的位置关系一、选择题1．如图，P为圆O外一点，OP交圆O于A点，且OA=2AP．甲、乙两人想作一条通过P点且与圆O相切的直线，其作法如下：〔甲〕以P为圆心，OP长为半径画弧，交圆O于B点，那么直线PB即为所求；〔乙〕作OP的中垂线，交圆O于B点，那么直线PB即为所求．对于甲、乙两人的作法，以下判断何者正确？〔〕A．两人皆正确B．两人皆错误C．甲正确，乙错误D．甲错误，乙正确二、解答题2．如图，⊙O是△ACD的外接圆，AB是直径，过点D作直线DE∥AB，过点B作直线BE∥AD，两直线交于点E，假如∠ACD=45°，⊙O的半径是4cm〔1〕请判断DE与⊙O的位置关系，并说明理由；〔2〕求图中阴影局部的面积〔结果用π表示〕．3．如图，四边形ABCD是平行四边形，以对角线BD为直径作⊙O，分别与BC，AD相交于点E，F．〔1〕求证：四边形BEDF为矩形；〔2〕BD2=BE•BC，试判断直线CD与⊙O的位置关系，并说明理由．4．如图，点D是⊙O的直径CA延长线上的一点，点B在⊙O上，且AB=AD=AO．〔1〕求证：BD是⊙O的切线；〔2〕假设点E是劣弧BC上一点，AE与BC相交于点F，且∠ABE=105°，S△BEF=8〔﹣1〕，求△ACF的面积和CF的长．5．如图，在△ABC中，∠C=90°，∠ABC的平分线交AC于点E，过点E作BE的垂线交AB 于点F，⊙O是△BEF的外接圆．〔1〕求证：AC是⊙O的切线．〔2〕过点E作EH⊥AB于点H，求证：CD=HF．6．如图，AB是⊙O的直径，C是⊙O上的一点，过点A作AD⊥CD于点D，交⊙O于点E，且=．〔1〕求证：CD是⊙O的切线；〔2〕假设tan∠CAB=，BC=3，求DE的长．7．如图，在△ABC中，∠ABC=90°，以AB的中点O为圆心，OA为半径的圆交AC于点D，E 是BC的中点，连接DE，OE．〔1〕判断DE与⊙O的位置关系，并说明理由；〔2〕求证：BC2=2CD•OE；〔3〕假设cos∠BAD=，BE=，求OE的长．8．如图，BC是以AB为直径的⊙的切线，且BC=AB，连接OC交⊙O于点D，延长AD交BC 于点E，F为BE上一点，且DF=FB．〔1〕求证：DF是⊙O的切线；〔2〕假设BE=2，求⊙O的半径．9．如图，在△ABO中，OA=OB，C是边AB的中点，以O为圆心的圆过点C．〔1〕求证：AB与⊙O相切；〔2〕假设∠AOB=120°，AB=4，求⊙O的面积．10．如图，⊙O中，点C为的中点，∠ACB=120°，OC的延长线与AD交于点D，且∠D=∠B．〔1〕求证：AD与⊙O相切；〔2〕假设点C到弦AB的间隔为2，求弦AB的长．11．如图，⊙O的直径AB为10cm，弦BC为6cm，D、E分别是∠ACB的平分线与⊙O，AB的交点，P为AB延长线上一点，且PC=PE．〔1〕求AC、AD的长；〔2〕试判断直线PC与⊙O的位置关系，并说明理由．12．如图，在⊙O中，直径AB平分弦CD，AB与CD相交于点E，连接AC、BC，点F是BA延长线上的一点，且∠FCA=∠B．〔1〕求证：CF是⊙O的切线．〔2〕假设AC=4，tan∠ACD=，求⊙O的半径．13．如图，在△ABC中，以BC为直径的⊙O与边AB交于点D，E为的中点，连接CE交AB 于点F，AF=AC．〔1〕求证：直线AC是⊙O的切线；〔2〕假设AB=10，BC=8，求CE的长．14．如图，在△ABC中，以AB为直径的⊙O交AC于点M，弦MN∥BC交AB于点E，且ME=1，AM=2，AE=．〔1〕求证：BC是⊙O的切线；〔2〕求⊙O的半径．15．如图，在Rt△ABC中，∠ACB=90°，以AC为直径作⊙O交AB于点D点，连接CD．〔1〕求证：∠A=∠BCD；〔2〕假设M为线段BC上一点，试问当点M在什么位置时，直线DM与⊙O相切？并说明理由．16．如图，在△ABC中，∠ABC=90°，D是边AC上的一点，连接BD，使∠A=2∠1，E是BC 上的一点，以BE为直径的⊙O经过点D．〔1〕求证：AC是⊙O的切线；〔2〕假设∠A=60°，⊙O的半径为2，求阴影局部的面积．〔结果保存根号和π〕17．如图，⊙O中，FG、AC是直径，AB是弦，FG⊥AB，垂足为点P，过点C的直线交AB的延长线于点D，交GF的延长线于点E，AB=4，⊙O的半径为．〔1〕分别求出线段AP、CB的长；〔2〕假如OE=5，求证：DE是⊙O的切线；〔3〕假如tan∠E=，求DE的长．18．如图，点B、C、D都在半径为6的⊙O上，过点C作AC∥BD交OB的延长线于点A，连接CD，∠CDB=∠OBD=30°．〔1〕求证：AC是⊙O的切线；〔2〕求弦BD的长；〔3〕求图中阴影局部的面积．19．如图，点B、C、D都在⊙O上，过C点作CA∥BD交OD的延长线于点A，连接BC，∠B=∠A=30°，BD=2．〔1〕求证：AC是⊙O的切线；〔2〕求由线段AC、AD与弧CD所围成的阴影局部的面积．〔结果保存π〕20．如图，在△ABC中，以AC为直径作⊙O交BC于点D，交AB于点G，且D是BC中点，DE ⊥AB，垂足为E，交AC的延长线于点F．〔1〕求证：直线EF是⊙O的切线；〔2〕假设CF=5，cos∠A=，求BE的长．21．如图，⊙O的直径CD垂直于弦AB，垂足为E，F为DC延长线上一点，且∠CBF=∠CDB．〔1〕求证：FB为⊙O的切线；〔2〕假设AB=8，CE=2，求sin∠F．22．如图，在△ABC中，∠ABC=90°，以AB为直径的⊙O与AC边交于点D，过点D的直线交BC边于点E，∠BDE=∠A．〔1〕判断直线DE与⊙O的位置关系，并说明理由．〔2〕假设⊙O的半径R=5，tanA=，求线段CD的长．23．如图，在△ABC中，AD是BC边上的中线，以AB为直径的⊙O交BC于点D，过D作MN ⊥AC于点M，交AB的延长线于点N，过点B作BG⊥MN于G．〔1〕求证：△BGD∽△DMA；〔2〕求证：直线MN是⊙O的切线．24．如图，⊙O的直径AC与弦BD相交于点F，点E是DB延长线上的一点，∠EAB=∠ADB．〔1〕求证：EA是⊙O的切线；〔2〕点B是EF的中点，求证：以A、B、C为顶点的三角形与△AEF相似；〔3〕AF=4，CF=2．在〔2〕条件下，求AE的长．25．如图，点A是⊙O上一点，OA⊥AB，且OA=1，AB=，OB交⊙O于点D，作AC⊥OB，垂足为M，并交⊙O于点C，连接BC．〔1〕求证：BC是⊙O的切线；〔2〕过点B作BP⊥OB，交OA的延长线于点P，连接PD，求sin∠BPD的值．26．如下图，△ABC内接于⊙O，AB是⊙O的直径，D是AB延长线上一点，连接DC，且AC=DC，BC=BD．〔1〕求证：DC是⊙O的切线；〔2〕作CD的平行线AE交⊙O于点E，DC=10，求圆心O到AE的间隔．27．如图，BD为⊙O的直径，AB=AC，AD交BC于点E，AE=1，ED=2．〔1〕求证：∠ABC=∠D；〔2〕求AB的长；〔3〕延长DB到F，使得BF=BO，连接FA，试判断直线FA与⊙O的位置关系，并说明理由．28．如图，在Rt△ABC中，∠B=30°，∠ACB=90°，延长CA到O，使AO=AC，以O为圆心，OA长为半径作⊙O交BA延长线于点D，连接CD．〔1〕求证：CD是⊙O的切线；〔2〕假设AB=4，求图中阴影局部的面积．29．如图，△ABC中，∠C=90°，点G是线段AC上的一动点〔点G不与A、C重合〕，以AG 为直径的⊙O交AB于点D，直线EF垂直平分BD，垂足为F，EF交BC于点E，连结DE．〔1〕求证：DE是⊙O的切线；〔2〕假设cosA=，AB=8，AG=2，求BE的长；〔3〕假设cosA=，AB=8，直接写出线段BE的取值范围．30．如图，⊙O是△ABC外接圆，AB是⊙O的直径，弦DE⊥AB于点H，DE与AC相交于点G，DE、BC的延长线交于点F，P是GF的中点，连接PC．〔1〕求证：PC是⊙O的切线；〔2〕假设⊙O的半径是1， =，∠ABC=45°，求OH的长．励志赠言经典语录精选句；挥动**，放飞梦想。

中考复习专题训练与圆有关的位置关系一、选择题1.⊙O1的半径为1cm，⊙O2的半径为4cm，圆心距O1O2=3cm，这两圆的位置关系是( )A. 相交B. 内切C. 外切D. 内含2.⊙O的半径为4，线段OP=4，则点P与⊙O的位置关系是（）A. 点P在⊙O外B. 点P在⊙O内C. 点P在⊙O上D. 不能确定3.两圆外离，作它们的两条内公切线，四个切点构成的四边形是（）A. 矩形B. 等腰梯形C. 矩形或等腰梯形D. 菱形4. 已知线段AB=7cm，现以点A为圆心，2cm为半径画⊙A；再以点B为圆心，3cm为半径画⊙B，则⊙A 和⊙B的位置关系（）A. 内含B. 相交C. 外切D. 外离5.下列四个命题中，真命题是( )A. 相等的圆心角所对的两条弦相等；B. 圆既是中心对称图形也是轴对称图形；C. 平分弦的直径一定垂直于这条弦；D. 相切两圆的圆心距等于这两圆的半径之和.6.在△ABC中，cosB=，∠C=45°，AB=8，以点B为圆心4为半径的⊙B与以点C为圆心的⊙C相离，则⊙C的半径不可能为（）A. 15B. 5C. 6D. 77. 如图，已知⊙O的半径为4，点D是直径AB延长线上一点，DC切⊙O于点C，连接AC，若∠CAB=30°，则BD的长为（）A. 4B. 8C. 4D. 28.下列说法正确的是（）A. 任意三点可以确定一个圆B. 平分弦的直径垂直于弦，并且平分该弦所对的弧C. 同一平面内，点P到⊙O上一点的最小距离为2，最大距离为8，则该圆的半径为5D. 同一平面内，点P到圆心O的距离为5，且圆的半径为10，则过点P且长度为整数的弦共有5条9.如图，AB为⊙O的直径，P为AB延长线上一点，PT切⊙O于T，若PT=6，PB=2，则⊙O的直径为（）A. 8B. 10C. 16D. 1810.如图，在等腰三角形△ABC中，O为底边BC的中点，以O为圆心作半圆与AB，AC相切，切点分别为D，E．过半圆上一点F作半圆的切线，分别交AB，AC于M，N．那么的值等于（）A. B. C. D. 111.如图，⊙O的半径为2，点O到直线L的距离为3，点O是直线L上的一个动点，PQ切⊙O于点Q，则PQ的最小值为（）A. B. C. 3 D. 512.已知如图，PA、PB切⊙O于A、B，MN切⊙O于C，交PB于N；若PA=7.5cm，则△PMN的周长是（）A. 7.5cmB. 10cmC. 15cmD. 12.5cm二、填空题13.已知⊙P在直角坐标平面内，它的半径是5，圆心P（﹣3，4），则坐标原点O与⊙P的位置关系是________14.已知点P在半径为5的⊙O外，如果设OP=x，那么x的取值范围是________．15.如图，已知扇形AOB的半径为6，圆心角为90°，E是半径OA上一点，F是上一点．将扇形AOB沿EF对折，使得折叠后的圆弧恰好与半径OB相切于点G．若OE=4，则O到折痕EF的距离为________．16.如图，在Rt△ABC中，∠C=90°，AC≠BC，点M是边AC上的动点．过点M作MN∥AB交BC于N，现将△MNC沿MN折叠，得到△MNP．若点P在AB上．则以MN为直径的圆与直线AB的位置关系是________．17.如图，在⊙O中，OB为半径，AB是⊙O的切线，OA与⊙O相交于点C，∠A=30°，OA=8，则阴影部分的面积是________．18. 如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是的中点，CE⊥AB于点E，过点D的切线交EC的延长线于点G，连接AD，分别交CE、CB于点P、Q，连接AC，关于下列结论：①∠BAD=∠ABC；②GP=GD；③点P是∠ACQ的外心，其中正确结论是________ （只需填写序号）．19.如图，AE、AD、BC分别切⊙O于E、D、F，若AD=20，则△ABC的周长为 ________20.如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=4 ．若动点D在线段AC上（不与点A、C重合），过点D作DE⊥AC交AB边于点E．点A关于点D的对称点为点F，以FC为半径作⊙C，当DE=________时，⊙C与直线AB相切．21.如图，在△ABC中，BC=4，以点A为圆心，2为半径的⊙A与BC相切于点D，交AB于点E，交AC于点F，点P是⊙A上的一点，且∠EPF=45°，则图中阴影部分的面积为________．三、解答题22.如图，已知PA、PB是⊙O的切线，A、B为切点，∠OAB＝30°．（1）求∠APB的度数；（2）当OA＝3时，求AP的长．23.如图所示，在梯形ABCD中，AD∥BC，AB⊥BC，以AB为直径的⊙O与DC相切于E．已知AB=8，边BC 比AD大6．（1）求边AD、BC的长；（2）在直径AB上是否存在一动点P，使以A、D、P为顶点的三角形与△BCP相似？若存在，求出AP的长；若不存在，请说明理由．24.在⊙O中，AB为直径，C为⊙O上一点．（Ⅰ）如图①，过点C作⊙O的切线，与AB的延长线相交于点P，若∠CAB=32°，求∠P的大小；（Ⅱ）如图②，D为优弧ADC上一点，且DO的延长线经过AC的中点E，连接DC与AB相交于点P，若∠CAB=16°，求∠DPA的大小．25.解答题（1）如图1，已知⊙O的半径是4，△ABC内接于⊙O，AC=4 ．①求∠ABC的度数；②已知AP是⊙O的切线，且AP=4，连接PC．判断直线PC与⊙O的位置关系，并说明理由；（2）如图2，已知▱ABCD的顶点A、B、D在⊙O上，顶点C在⊙O内，延长BC交⊙O于点E，连接DE．求证：DE=DC．参考答案一、选择题B C C D B D C D C B B C二、填空题13.点O在⊙P上14.x＞515.216.相交17.8 ﹣π18.②③19.4020.或21.4﹣π三、解答题22.解：（1）∵在△ABO中，OA=OB，∠OAB=30°，∴∠AOB=180°-2×30°=120°，∵PA、PB是⊙O的切线，∴OA⊥PA，OB⊥PB，即∠OAP=∠OBP=90°，∴在四边形OAPB中，∠APB=360°-120°-90°-90°=60°．（2）如图，连接OP；∵PA、PB是⊙O的切线，∴PO平分∠APB，即∠APO=∠APB=30°，又∵在Rt△OAP中，OA=3，∠APO=30°，∴AP=.23.解：（1）方法1：过D作DF⊥BC于F，在Rt△DFC中，DF=AB=8，FC=BC﹣AD=6，∴DC2=62+82=100，即DC=10．设AD=x，则DE=AD=x，EC=BC=x+6，∴x+（x+6）=10．∴x=2．∴AD=2，BC=2+6=8．方法2：连OD、OE、OC，由切线长定理可知∠DOC=90°，AD=DE，CB=CE，设AD=x，则BC=x+6，由射影定理可得：OE2=DE•EC．即：x（x+6）=16，解得x1=2，x2=﹣8，（舍去）∴AD=2，BC=2+6=8．（2）存在符合条件的P点．设AP=y，则BP=8﹣y，△ADP与△BCP相似，有两种情况：①△ADP∽△BCP时，有即∴y=；②△ADP∽△BPC时，有即∴y=4．故存在符合条件的点P，此时AP=或4．24.解：（Ⅰ）连接OC，如图①，∵PC为切线，∴OC⊥PC，∴∠OCP=90°，∵OA=OC，∴∠OCA=∠CAB=32°，∴∠POC=∠OCA+∠CAB=64°，∴∠P=90°﹣∠POC=90°﹣64°=26°；（Ⅱ）如图②，∵点E为AC的中点，∴OD⊥AC，∴∠OEA=90°，∴∠AOD=∠CAB+∠OEA=16°+90°=106°，∴∠C= ∠AOD=53°，∴∠DPA=∠BAC+∠C=16°+53°=69°25.（1）解：①连结OA、OC，如图1，∵OA=OC=4，AC=4 ，∴OA2+OC2=AC2，∴△OCA为等腰直角三角形，∠AOC=90°，∴∠ABC= ∠AOC=45°；②直线PC与⊙O相切．理由如下：∵AP是⊙O的切线，∴∠OAP=90°，而∠AOC=90°，∴AP∥OC，而AP=OC=4，∴四边形APCO为平行四边形，∵∠AOC=90°，∴四边形AOCP为矩形，∴∠PCO=90°，∴PC⊥OC，∴PC为⊙O的切线（2）证明：∵四边形ABCD为平行四边形，∴AB∥CD，AD∥BC，∴∠B+∠A=180°，∠DCE=∠B，∵∠E+∠A=180°，∴∠E=∠B，∴∠DCE=∠E，∴DC=DE．。

圆与圆的位置关系一、圆与圆的位置关系（由距离判断位置关系）8、如果两圆的半径分别为R和r，圆心距为d，那么R＋r＜d＜R－r（R＞r两圆．4、如果⊙O1的半径是5cm，⊙O2的半径是7cm，且2≤O1O2≤12，则两圆位置关系是．相切、相交．12、两圆的直径分别为8cm和10cm，圆心距为9cm，这两圆的位置关系是．外切．8、如果⊙O1和⊙O2的半径分别是3和8，点O1和O2的坐标分别是（0，3）和（4，0），那么⊙A与⊙B位置关系的是……………………………………………………………（A）（A）内切；（B）相交；（C）外切；（D）外离．8、如果两个圆的半径分别为4cm 和6cm ，那么下列说法中，错误的是……（C）（Ａ）圆心距为2cm时，两圆内切；（Ｂ）圆心距为6cm时，两圆相交；（Ｃ）圆心距为9cm时，两圆外切；（Ｄ）圆心距为11cm时，两圆外离．8、⊙O和⊙O′的半径分别为R和R′，圆心距OO′＝5，R＝3，当0＜R′＜2时，⊙O和⊙O′的位置关系是……………………………………………………………（）（A）内含；（B）外切；（C）相交；（D）外离．（2005年陕西省中考试题）D．5、已知两圆的圆心距是5，两圆的半径是方程x2－7x＋10＝0的两个根，则这两圆的位置关系是．相交．8、相切的两圆半径分别为3cm和2cm，则两圆的圆心距为．1或5．8、两圆的半径都是8cm，圆心距也是8cm，则这两圆位置关系的是…………（B）（A）内切；（B）相交；（C）外切；（D）外离．9、直角坐标系中，两圆的圆心坐标分别是（3，0）和（0，1），它们的半径分别是3和5，则这两个圆的位置关系是．内切．二、圆与圆的位置关系（知位置关系求参数）7、若半径分别为R和r的⊙O1和⊙O2相交，且R＝4cm，O1O2＝10cm，那么r的取值范围是．解：∵相交，∴| 4－r |＜10＜r＋4，∴－10＜（4－r）＜10，且10＜r＋4，∴6＜r＜14．11、已知两圆内切，圆心距为2cm，如果其中一个圆的半径为3cm，那么另一个圆的半径为cm．5或1．（2007年1月普陀卷）14、矩形ABCD中，AB＝5，BC＝12 ．如果分别以A、C为圆心的两圆相切，点D在圆C内，点B在圆C外，那么圆A的半径r的取值范围是．（2003年上海市中考试题）解：∵⊙C的半径R的取值范围是5＜R＜12，R＋r＝13，∴当⊙A与⊙C外切时，1＜r＜8；当⊙A与⊙C内切时，18＜r＜25．∴⊙A的半径r的取值范围是1＜r＜8或18＜r＜25．（图一）AB CD14、半径为d 的两圆外切，半径为2d 的圆与这两个圆都相切，这样的圆有…（ A ）（A ）5个； （B ）4个； （C ）3个； （D ）2个．8、已知：一个三角形的三边长分别为4cm 、5cm 、6cm ．如果以它的顶点为圆心，作三个圆两两相切，求这三个圆的半径． 1.5cm 、2.5cm 、3.5cm ．8、已知：如图一，在等腰Rt △ABC 中，∠C ＝90°，AB ＝4，⊙C 的半径为1，若点P 是AB 边上的一个动点， （与点B 、C 不重合），⊙P 以AP 为半径．当AP 为多长 时，圆P 与圆C 相切． （根据2004年上海市中考试题改编） 解：x 1＝27，x 2＝67．8．已知两个圆有公共点，两圆半径分别为2cm 、3cm ，则这两圆的圆心距d 的取值范围是 ． 1≤d ≤5．18、已知两圆半径分别为1和7，下列各长度的圆心距中，这两圆相交的是（ ）（A ）5； （B ）6； （C ）7； （D ）8 ． C ．12、如图一，在10×6的网格中（每个小正方形的边长均为1个单位长度），⊙A 的半径为1，⊙B 的 半径为2．要使⊙A 与静止的⊙B 内切，那么⊙A 由 图示位置需向右平移 个单位长度．4或6．（图五）C A B · · A B （图一）。

中考总复习：圆的有关概念、性质与圆有关的位置关系—巩固练习（基础）【巩固练习】一、选择题1. 已知⊙1O 与⊙2O 的半径分别为3 cm 和4 cm ，若12O O =7 cm ，则⊙1O 与⊙2O 的位置关系是（ ）A ．相交B ．相离C ．内切D ．外切2．如图，AB 是⊙O 的直径，点C 、D 在⊙O 上 ，∠BOD=110°，AC∥OD，则∠AOC 的度数 （ ）A. 70°B. 60°C. 50°D. 40°3．如图所示，AB 是⊙O 的直径，CD 为弦，CD ⊥AB 于点E ，则下列结论中不成立的是( )A ．∠COE ＝∠DOEB ．CE ＝DEC ．OE ＝BED ．»»BDBC第2题 第3题 第5题 第6题4．（2015•黑龙江）如图，⊙O 的半径是2，AB 是⊙O 的弦，点P 是弦AB 上的动点，且1≤OP≤2，则弦AB 所对的圆周角的度数是（ ）A ．60°B ．120°C ．60°或120°D ．30°或150°5．如图所示，△ABC 内接于圆O ，∠A ＝50°；∠ABC ＝60°，BD 是圆O 的直径，BD 交AC 于点E ，连接DC ，则∠AEB 等于( )A ．70°B ．110°C ．90°D ．120°6．小明不慎把家里的圆形玻璃打碎了，其中四块碎片如图所示，为配成与原来大小一样的圆形玻璃，小明带到商店去的一块玻璃碎片应该是( )A ．第①块B ．第②块C ．第③块D ．第④块二、填空题7．（2015•雁江区模拟）如图，MN 是半径为2的⊙O 的直径，点A 在⊙O 上，∠AMN=30°，B 为弧AN 的中点，P 是直径MN 上一动点，则PA+PB 的最小值为 .8．如图所示，⊙O的直径AC＝8 cm，C为⊙O上一点，∠BAC＝30°，则BC＝________cm．第8题第9题9．两圆有多种位置关系，图中(如图所示)不存在的位置关系是__________．10．如图所示，AB与⊙O相切于点B，AO的延长线交⊙O于点C，连接BC．若∠A＝36°，则∠C＝______．11．如图，直线PA过半圆的圆心O，交半圆于A，B两点，PC切半圆与点C，已知PC=3，PB=1，则该半圆的半径为　．第10题第11题第12题12．如图所示．B是线段AC上的一点，且AB:AC＝2:5．分别以AB、AC为直径画圆，则小圆的面积与大圆的面积之比为________．三、解答题13．已知AB与⊙O相切于点C，OA=OB．OA、OB与⊙O分别交于点D、E.(1) 如图①，若⊙O的直径为8，AB=10，求OA的长(结果保留根号)；(2)如图②，连接CD、CE，若四边形ODCE为菱形．求ODOA的值．14. 如图所示，在Rt△ABC中，∠C＝90°，O为直角边BC上一点，以O为圆心、OC为半径的圆恰好与斜边AB相切于点D，与BC交于另一点E．(1)求证：△AOC≌△AOD；(2)若BE＝1，BD＝3，求⊙O的半径及图中阴影部分的面积S．15．（2015•上城区二模）如图，已知四边形ABCD内接于圆，对角线AC与BD相交于点E，F在AC上，AB=AD，∠BFC=∠BAD=2∠DFC．（1）若∠DFC=40°，求∠CBF的度数；（2）求证：CD⊥DF．l16. 如图，已知∠ABC=90°，AB=BC．直线与以BC为直径的圆O相切于点C．点F是圆O上异于B、Cl的动点，直线BF与相交于点E，过点F作AF的垂线交直线BC与点D．（1）如果BE=15，CE=9，求EF的长；（2）证明：①△CDF∽△BAF；②CD=CE；（3）探求动点F在什么位置时，相应的点D位于线段BC的延长线上，且使CD，请说明你的理由．【答案与解析】一、选择题1.【答案】D；O O=7，根据圆与圆位置关系的判定可知两圆外切.【解析】两圆半径之和3+4=7，等于两圆圆心距122.【答案】D；【解析】由AB是⊙O的直径，点C、D在⊙O上，知OA＝OC，根据等腰三角形等边对等角的性质和三角形内角和定理，得∠AOC＝180°－2∠OAC.由AC∥OD，根据两直线平行，内错角相等的性质，得∠OAC＝∠AOD.由AB是⊙O的直径，∠BOD=110°，根据平角的定义，得∠AOD＝180°－∠BOD=70°.∴∠AOC＝180°－2×70°＝40°.故选D.3.【答案】C；【解析】由垂径定理知A、B、D都正确．4.【答案】C；【解析】作OD⊥AB，如图，∵点P是弦AB上的动点，且1≤OP≤2，∴OD=1，∴∠OAB=30°，∴∠AOB=120°，∴∠AEB=∠AOB=60°，∵∠E+∠F=180°，∴∠F=120°，即弦AB所对的圆周角的度数为60°或120°．故选C．5.【答案】B；【解析】∵∠A=50°，∴∠D=50°，又∵BD是直径，∴∠BCD=90°，∴∠DBC=90°-50°=40°，∠ABD=60°-40°=20°，∴∠BEC=50°+20°=70°，∴∠AEB=180°-70°=110°.6.【答案】B；【解析】因为第②块含有圆周的一部分，可以找到圆心，量出半径.其他块都不行.二、填空题7．【答案】2；【解析】如图，作点B关于MN的对称点B′，连接OA、OB′、AB′，由轴对称确定最短路线问题可知，AB′与M的交点即为所求的使PA+PB的值最小的点，∵∠AMN=30°，∴∠AON=2∠AMN=2×30°=60°，∵B为弧AN的中点，∴∠NOB′=×60°=30°，∴∠AOB′=90°，∴△AOB′是等腰直角三角形，∵⊙O的半径为2，∴AB′=2，即PA+PB的最小值为为2．8．【答案】4；【解析】因为AC为直径，根据直径所对的圆周角为直角，得∠ABC＝90°，则BC＝AC·sin∠BAC＝4(am)．9．【答案】相交；【解析】认真观察、判断可发现每两圆间不存在的位置关系是：相交．10．【答案】27°；【解析】如图，连结OB，由AB与⊙O相切于点B，得∠ABO＝90°，因为∠A＝36°，所以∠AOB＝54°，所以∠C＝27°.11．【答案】4；【解析】连接OC，则由直线PC是圆的切线，得OC⊥PC.设圆的半径为x，则在Rt△OPC中，PC=3，OC= x，OP=1＋x，根据地勾股定理，得OP2=OC2＋PC2，即（1＋x）2= x2＋32，解得x=4.即该半圆的半径为4.12．【答案】4:25；三、解答题13.【答案与解析】(1) 如图①，连接OC ，则OC=4.∵AB 与⊙O 相切于点C ，∴OC⊥AB. ∴在△OAB 中，由OA=OB ，AB=10得1AC AB 52==.∴ 在△RtOAB 中，OA ===.(2)如图②，连接OC ，则OC=OD.∵四边形ODCE 为菱形，∴OD=DC.∴△ODC 为等边三角形.∴∠AOC=60°.∴∠A=30°.∴1OC 1OD 1OC OA 2OA 2OA 2===，，即.14.【答案与解析】解：（1）∵ AB 切⊙O 于D ，∴OD ⊥AB ．在Rt △AOC 和Rt △AOD 中，,.OC OD AO AO =⎧⎨=⎩ ∴Rt △AOC ≌Rt △AOD(HL)．(2)设半径为r ，在Rt △ODB 中，，解得r ＝4．2223(1)r r +=+ 由(1)有AC ＝AD ，∴，2229(3)AC AC +=+ 解得AC ＝12，∴．22111112945482222S AC BC r πππ=-=⨯⨯-⨯=-g 15.【答案与解析】解：（1）∵∠ADB=∠ACB ，∠BAD=∠BFC ，∴∠ABD=∠FBC ，又∵AB=AD ，∴∠ABD=∠ADB ，∴∠CBF=∠BCF ，∵∠BFC=2∠DFC=80°，∴∠CBF==50°；（2）令∠CFD=α，则∠BAD=∠BFC=2α，∵四边形ABCD 是圆的内接四边形，∴∠BAD+∠BCD=180°，即∠BCD=180°﹣2α，又∵AB=AD ，∴∠ACD=∠ACB ，∴∠ACD=∠ACB=90°﹣α，∴∠CFD+∠FCD=α+（90°﹣α）=90°，∴∠CDF=90°，即CD ⊥DF ．16.【答案与解析】解：（1）∵直线与以BC 为直径的圆O 相切于点C ，l ∴∠BCE=90°，又∵BC 为直径，∴∠BFC=∠CFE=90°.∴∠CFE=∠BCE.∵∠FEC=∠CEB，∴△CEF∽△BEC.∴CE EF BE EC =.∵BE=15，CE=9，即：9EF 159=，解得：EF=275.（2）证明：①∵∠FCD+∠FBC=90°，∠ABF+∠FBC=90°，∴∠ABF=∠FCD.同理：∠AFB=∠CFD.∴△CDF∽△BAF.②∵△CDF∽△BAF，∴CF CD BF BA =.又∵△CEF∽△BCF，∴CF CE BF BC =.∴CD CE BA BC=.又∵AB=BC，∴CE=CD.（3）当F 在⊙O 的下半圆上，且»»2BF BC 3=时，相应的点D 位于线段BC 的延长线上，且使CD.理由如下：CE.在Rt△BCE 中，tan∠CBE=CEBC =，∴∠CBE=30°，∴»CF所对圆心角为60°.∴F 在⊙O 的下半圆上，且»»2BF BC 3=.。

圆与圆的位置关系中考题一、题目。

1. 已知两圆的半径分别为3cm和4cm，圆心距为5cm，则这两圆的位置关系是（）A. 内切。

B. 外切。

C. 相交。

D. 相离。

解析：设两圆的半径分别为R和r（R≥slant r），圆心距为d。

当d = R + r时，两圆外切；当d=R r时，两圆内切；当R r< d< R + r时，两圆相交；当d> R + r时，两圆相离。

这里R = 4cm，r=3cm，d = 5cm。

因为R+r=4 + 3=7cm，R r=43 = 1cm，1cm<5cm<7cm，即R r< d< R + r，所以两圆的位置关系是相交，答案选C。

2. 若⊙ O_1与⊙ O_2的半径分别是3和2，圆心距O_1O_2=5，则两圆的位置关系是（）A. 外离。

B. 外切。

C. 相交。

D. 内切。

解析：设⊙ O_1半径R = 3，⊙ O_2半径r = 2，圆心距d=O_1O_2=5。

因为R + r=3+2 = 5，此时d = R + r。

所以两圆的位置关系是外切，答案选B。

3. 已知⊙ A的半径为5，圆心A(3,4)，坐标原点O与⊙ A的位置关系是（）A. 点O在⊙ A内。

B. 点O在⊙ A上。

C. 点O在⊙ A外。

D. 无法确定。

解析：先计算点O(0,0)到点A(3,4)的距离d。

根据两点间距离公式d=√((x_2)-x_{1)^2+(y_2-y_1)^2}，这里x_1=3,y_1=4,x_2 = 0,y_2=0。

d=√((0 3)^2)+(0 4)^{2}=√(9 + 16)=√(25)=5。

因为⊙ A的半径r = 5，此时d=r。

所以点O在⊙ A上，答案选B。

4. 两圆的半径分别为2和3，圆心距为7，则这两圆的位置关系为（）A. 外离。

B. 外切。

C. 相交。

D. 内切。

解析：设两圆半径R = 3，r = 2，圆心距d = 7。

因为R+r=3 + 2=5，而d = 7>5，即d> R + r。

高三数学圆与圆的位置关系试题答案及解析1.已知圆和两点，，若圆上存在点，使得，则的最大值为（）A．B．C．D．【答案】B【解析】由题意知，点P在以原点（0，0）为圆心，以m为半径的圆上，又因为点P在已知圆上，所以只要两圆有交点即可，所以，故选B.【考点】本小题主要考查两圆的位置关系，考查数形结合思想，考查分析问题与解决问题的能力.2.已知圆C的方程为，若以直线上任意一点为圆心，以l为半径的圆与圆C没有公共点，则k的整数值是（）A．l B．0C．1D．2【答案】【解析】由题意知，直线过定点，圆与圆相离.圆心到直线大于，所以，，解得，故的整数值为，选．【考点】圆与圆的位置关系，点到直线的距离公式.3.已知数列，圆，圆，若圆C2平分圆C1的周长，则的所有项的和为.【答案】4024【解析】设圆与圆交于,，则直线的方程为：，化简得：又圆平分圆的周长，则直线过,代入的方程得：, ∴.【考点】圆与圆的位置关系、直线方程、数列求和.4.已知圆C1：(x－2)2＋(y－3)2＝1，圆C2：(x－3)2＋(y－4)2＝9，M，N分别是圆C1，C2上的动点，P为x轴上的动点，则|PM|＋|PN|的最小值为( )A．5－4B．－1 C．6－2D．【答案】A【解析】设P(x,0)，设C1(2,3)关于x轴的对称点为C′1(2，－3)，那么|PC1|＋|PC2|＝|PC′1|＋|PC2|≥|C′1C2|＝＝5而|PM|＝|PC1|－1，|PN|＝|PC2|－3∴|PM|＋|PN|＝|PC1|＋|PC2|－4≥5－4.5.若圆x2＋y2＝4与圆x2＋y2＋2ay－6＝0(a>0)的公共弦的长为2，则a＝________.【答案】1【解析】由得2ay＝2，即y＝，则2＋2＝22，解得a＝1.6.圆(x＋2)2＋y2＝4与圆(x－2)2＋(y－1)2＝9的位置关系为()．A．内切B．相交C．外切D．相离【答案】B【解析】由题意知，两圆的圆心分别为(－2,0)，(2,1)，故两圆的圆心距离为，两圆的半径之差为1，半径之和为5，而1< <5，所以两圆的位置关系为相交．7.若圆x2＋y2＝4与圆x2＋y2＋2ax－6＝0(a＞0)的公共弦的长为2，则a＝________.【答案】1【解析】x2＋y2＋2ax－6＝0(a>0)可知圆心为(－a,0)，半径为，两圆公共弦所在方程为(x2＋y2＋2ax－6)－(x2＋y2)＝－4，即x＝，所以有2－2＝2解得a＝1或－1(舍去)．8.若圆C1：x2＋y2＋2ax＋a2－4＝0(a∈R)与圆C2：x2＋y2－2by＋b2－1＝0(b∈R)外切，则a＋b的最大值为________．【答案】3.【解析】依题意知C1：(x＋a)2＋y2＝4，C2：x2＋(y－b)2＝1，则|C1C2|＝＝2＋1＝3，∴a2＋b2＝9，∴ (θ为参数)，∴a＋b＝3(sin θ＋cos θ)＝3 sin≤3.9.设集合，，若存在实数，使得，则实数的取值范围是___________．【答案】【解析】首先集合实际上是圆上的点的集合，即表示两个圆，说明这两个圆相交或相切（有公共点），由于两圆半径都是1，因此两圆圆心距不大于半径这和2，即，整理成关于的不等式：，据题意此不等式有实解，因此其判别式不大于零，即，解得．【考点】两圆位置关系及不等式有解问题．10.设集合，，若存在实数，使得，则实数的取值范围是___________．【答案】【解析】首先集合实际上是圆上的点的集合，即表示两个圆，说明这两个圆相交或相切（有公共点），由于两圆半径都是1，因此两圆圆心距不大于半径这和2，即，整理成关于的不等式：，据题意此不等式有实解，因此其判别式不大于零，即，解得．【考点】两圆位置关系及不等式有解问题．11.若点和点到直线的距离依次为和，则这样的直线有（）A．条B．条C．条D．条【答案】C【解析】以点为圆心，以为半径长的圆的方程为，以点为圆心，且以为半径的圆的方程为，则直线为两圆的公切线，，即圆与圆外切，因此两圆的公切线有条，即直线有三条，故选C.【考点】1.两圆的位置关系；2.两圆的公切线12.直线l1：y=x、l2:y=x+2与⊙C：的四个交点把⊙C分成的四条弧长相等，则m=（）A．0或1B．0或-1C．-1D．1【答案】B【解析】直线l1：y=x与l2:y=x+2之间的距离为，⊙C：的圆心为（m，m），半径r2=m2+m2，由题意可得解得 m=0或m=-1，故选B.【考点】1.直线与圆的位置关系；2.点到直线的距离.13.已知圆,圆,分别是圆上的动点,为轴上的动点,则的最小值为（）A．B．C．D．【答案】A【解析】如图圆C1关于x轴的对称圆的圆心坐标A（2，-3），半径为1，圆C2的圆心坐标（3，4），半径为3，|PM|+|PN|的最小值为圆A与圆C2的圆心距减去两个圆的半径和，即故选A．【考点】圆与圆的位置关系点评：中档题，利用数形结合思想，将|PM|+|PN|的最小值转化成为圆A与圆C2的圆心距减去两个圆的半径和。

2012年全国中考数学试题分类解析汇编(159套63专题）专题50：圆与圆的位置关系一、选择题1. （2012上海市4分）如果两圆的半径长分别为6和2，圆心距为3，那么这两个圆的位置关系是【】A．外离B．相切C．相交D．内含【答案】D。

【考点】圆与圆的位置关系。

【分析】根据两圆的位置关系的判定：外切（两圆圆心距离等于两圆半径之和），内切（两圆圆心距离等于两圆半径之差），相离（两圆圆心距离大于两圆半径之和），相交（两圆圆心距离小于两圆半径之和大于两圆半径之差），内含（两圆圆心距离小于两圆半径之差）。

因此，∵两个圆的半径分别为6和2，圆心距为3，6﹣2=4，4＞3，即两圆圆心距离小于两圆半径之差，∴这两个圆的位置关系是内含。

故选D。

2. （2012浙江杭州3分）若两圆的半径分别为2cm和6cm，圆心距为4cm，则这两圆的位置关系是【】A．内含B．内切C．外切D．外离【答案】B。

【考点】圆与圆的位置关系。

【分析】根据两圆的位置关系的判定：外切（两圆圆心距离等于两圆半径之和），内切（两圆圆心距离等于两圆半径之差），相离（两圆圆心距离大于两圆半径之和），相交（两圆圆心距离小于两圆半径之和大于两圆半径之差），内含（两圆圆心距离小于两圆半径之差）。

因此，∵两圆的半径分别为2cm和6cm，圆心距为4cm．则d=6﹣2=4。

∴两圆内切。

故选B。

3. （2012浙江宁波3分）如图，用邻边分别为a，b（a＜b）的矩形硬纸板裁出以a为直径的两个半圆，再裁出与矩形的较长边、两个半圆均相切的两个小圆．把半圆作为圆锥形圣诞帽的侧面，小圆恰好能作为底面，从而做成两个圣诞帽（拼接处材料忽略不计），则a与b满足的关系式是【】A ．b=a B ．2C ．2D ．【答案】D 。

【考点】圆锥的计算。

【分析】∵半圆的直径为a ，∴半圆的弧长为a2π。

∵把半圆作为圆锥形圣诞帽的侧面，小圆恰好能作为底面， ∴设小圆的半径为r ，则：2r=a 2ππ，解得：1r=a 4如图小圆的圆心为B ，半圆的圆心为C ，作BA⊥CA 于A 点， 则由勾股定理，得：AC 2+AB 2=BC 2，即：2221a a +b =a+a 24224ππππ⎛⎫⎛⎫⎛⎫- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，整理得：。

圆与圆的位置关系1．圆心距的定义两圆圆心之间的距离叫做圆心距．如图，O1O2的长度就是圆心距；我们把通过两圆圆心的直线叫做连心线，直线O1O2就是两圆的连心线．(1)我们通常用O1O2表示圆心距，实际上圆心距应该是它的长度而不是线段本身；(2)注意圆心距和连心线是不同的，圆心距是线段的长度，连心线是直线；(3)由此可知，任意两个圆的组合图形都是轴对称图形，它们的对称轴就是两圆的连心线．【例1】如图，已知O1与O2的直径都是2 cm，线段AB＝3 cm.求O1和O2的圆心距．分析：根据圆心距的定义，圆心距是连接两圆圆心的线段的长度，所以O1和O2的圆心距等于两圆半径的和再加上线段AB的长．解：∵O1与O2的直径都是2 cm，∴O1A＝O2B＝1 cm.∵O1O2＝O1A＋O2B＋AB＝1＋1＋3＝5(cm)，∴O1和O2的圆心距是5 cm.2．圆与圆的位置关系两个圆的位置关系有且只有7种情况：设两圆的半径分别是r1和r2，圆心距是d，则：(1)当圆心距d＞r1＋r2时，两个圆没有公共点，并且每个圆上的点都在另一个圆的外部，称这两个圆外离．．，如图1.(2)当d＝r1＋r2时，两个圆有唯一的公共点，并且除了这个公共点外，每个圆上的点都在另一个圆的外部，称这两个圆外切．．．．．，如图2，这个公共点叫做切点．(3)当r2－r1＜d＜r1＋r2(设r1≤r2)时，两个圆恰好有两个不同的公共点，称这两个圆相交．．，如图3.(4)当d＝r2－r1(设r1＜r2)时，两个圆有唯一的公共点，并且除了这个公共点外，一个圆上的点都在另一个圆的内部，称这两个圆内切．．．．．，如图4，这个公共点叫做切点．(5)当0＜d＜r2－r1(设r1＜r2)时，两个圆没有公共点，并且一个圆上的点都在另一个圆的内部，称这两个圆内含．．．，如图5.．．但不同心(6)当d＝0且r1≠r2时，两个圆没有公共点，并且一个圆上的点都在另一个圆的内部，两个圆的圆心重合，称这两个圆内含．．．，如图6.．．，简称它们为同心圆．．且同心(7)当d＝0且r1＝r2时，两个圆重合．．．．要判定两圆的位置关系，有两种具体的途径：(1)根据两圆公共点的个数判断①当两圆没有公共点时，两圆的位置关系是外离或内含；②当两圆有且只有一个公共点时，两圆的位置关系是内切或外切；③当两圆有两个公共点时，两圆的位置关系是相交．(2)根据两圆的半径与圆心距的关系判断．【例2－1】已知O1和O2的半径分别为3 cm和2 cm且O1O2＝1 cm，则O1与O2的位置关系为__________．解析：已知O1和O2的半径分别为3 cm和2 cm且O1O2＝1 cm，所以3－2＝1，即r1－r2＝d，因此O1和O2的位置关系为内切．答案：内切【例2－2】两圆圆心都在y轴上，且两圆相交于A，B两点，点A的坐标为(2,1)，则点B的坐标为( )．A．(－2,1) B．(－2，－1)C．(2，－1) D．(0,1)解析：∵圆心都在y轴上的两圆所构成的图形是轴对称图形，且对称轴是y轴，∴它们的交点A，B关于y轴对称．∵点A的坐标为(2,1)，且关于y轴对称的点的纵坐标不变，横坐标互为相反数，∴B点坐标为(－2,1)．答案：A【例2－3】已知A，B相切，圆心距为10 cm，其中A的半径为4 cm，则B的半径为______．解析：两圆相切，有可能两圆外切，也有可能两圆内切，所以B的半径就有两种情况．设B的半径为R.(1)如果两圆外切，那么d＝10＝4＋R，R＝6 cm；(2)如果两圆内切，那么d ＝|R－4|＝10，R＝－6(舍去)或R＝14.答案：6 cm或14 cm【例2－4】如图，O的半径为5 cm，点P是O外一点，OP＝8 cm.求：(1)以P为圆心作P与O外切，小圆P的半径是多少？(2)以P为圆心作P与O内切，大圆P的半径是多少？分析：由小圆P与O外切，可知小圆P与O的半径的和是OP的长，即8 cm，又知O的半径为5 cm，从而求出小圆P的半径；同理，大圆P与O内切，可知大圆P 与O的半径的差是OP的长，即8 cm.也能求出大圆P的半径．解：(1)设P与O外切于点A，则PA＝PO－OA，∴PA＝3 cm.(2)设P与O内切于点B，则PB＝PO＋OB，∴PB＝13 cm.【例2－5】已知：如图，△ABC 中，∠C ＝90°，AC ＝12，BC ＝8，以AC 为直径作O ，以B 为圆心，4为半径作B ．求证：O 与B 相外切． 分析：要证明两圆外切就要分别求两圆的半径和圆心距．本题中圆O 的半径很容易求出，就是线段AC 的一半，即6；圆B 的半径是4，是已知的；根据勾股定理可以求出线段OB 的长．根据d ＝R ＋r ，可以判定两圆外切．证明：连接BO .∵AC 为O 的直径，AC ＝12，∴O 的半径OC ＝12AC ＝6.∵∠C ＝90°且BC ＝8，∴BO ＝OC 2＋BC 2＝62＋82＝10.∵O 的半径R 1＝6，B 的半径R 2＝4， ∴BO ＝R 1＋R 2.∴O 与B 相外切．【例2－6】O 1和O 2交于A ，B 两点，且O 1经过点O 2.若∠AO 1B ＝90°，那么∠AO 2B 的度数是__________．错解：135°(如图1)错因分析：错解只考虑到r 2＜r 1，且O 1，O 2在公共弦AB 两侧时的情形，未考虑到r 2＞r 1，且O 1，O 2在公共弦同侧时的情形(如图2)．如果能联想：“一条弦所对的圆心角为90°，则这弦所对的圆周角为多少度”的问题，并运用分类讨论的思想画出两圆心在公共弦的同侧、两侧两种情况，且r 2＜r 1，或r 2＞r 1，则可避免错误．正解：135°或45°3．如何判定圆与圆的位置关系圆与圆的位置关系是本章中的重点知识，是近几年各地中考试题中的热点问题，也是学好圆这一章的关键，那么圆与圆的位置关系如何判定呢？一方面，可以根据两圆公共点的个数来判定． 圆与圆的位置关系共五种，是由两圆的公共点来定义的．两圆没有公共点——外离或内含；两圆有唯一公共点——外切或内切；两圆有两个公共点——相交．另一方面，可以根据两圆圆心距与半径的数量关系来判定．判定两圆的位置关系，除定义外，既可根据两圆半径与圆心距的关系来判定，又可根据两圆内、外公切线的总条数来判定．若设两圆的半径分别为R，r(R＞r)，圆心距为d，则有：(1)d＞R＋r⇔两圆外离；(2)d＝R＋r⇔两圆外切；(3)d＝R－r⇔两圆内切；(4)R－r＜d＜R＋r⇔两圆相交；(5)d＜R－r⇔两圆内含．【例3－1】若A和B相切，它们的半径分别为8 cm和2 cm，则圆心距AB为( )．A．10 cm B．6 cmC．10 cm或6 cm D．以上答案均不对解析：因为A和B相切，它们的半径分别为8 cm和2 cm，所以，当两圆相外切时，圆心距＝8＋2＝10 cm；当两圆相内切时，圆心距＝8－2＝6 cm.答案：C【例3－2】如图，用半径R＝3 cm，r＝2 cm的钢球测量口小内大的内孔的直径D．测得钢球顶点与孔口平面的距离分别为a＝4 cm，b＝2 cm，则内孔直径D的大小为( )．A．9 cm B．8 cm C．7 cm D．6 cm解析：因为a＋R＝b＋r＋O2H，a＝4，b＝2，R＝3，r＝2，所以O2H＝3.又根据两圆外切，可得O1O2＝R＋r＝3＋2＝5，根据勾股定理可得，O1H2＝O1O22－O2H2，所以O1H＝4.所以D＝R＋O1H＋r＝3＋4＋2＝9(cm)．故选A．答案：A4．利用两圆外切和内切的位置关系解题两圆外切和内切是圆与圆的几种位置关系中，具有“分界线”作用的两种特殊的位置关系，通常把这两种位置关系统称为两圆相切．解答问题时注意结合移动和变化的思想来思考，特别注意不能遗漏掉其中任何一个答案．而且在证明两圆外切或内切时通常要添加辅助线，例如作两圆的连心线或圆心距等．【例4－1】已知O1与O2的半径分别为4和5，则O1与O2内切时，O1O2等于__________．解析：当两圆内切时，d＝R－r，所以当O1与O2内切时，O1O2等于1.答案：1【例4－2】已知O1与O2的半径分别为3和5，O1O2的长是x2－10x＋16＝0的根，则O1与O2的位置关系是( )．A．外离B．外切C．内切 D．外切或内切解析：解方程x2－10x＋16＝0，得x1＝2，x2＝8.当O1O2＝2时，因为R－r＝5－3＝2，所以O1与O2内切，当O1O2＝8时，因为R＋r＝5＋3＝8，所以O1与O2外切．答案：D5．利用两圆相交的位置关系计算定理：两圆相交时，连心线垂直平分两圆的公共弦．定理：两圆相切时，连心线通过切点．当两个圆相交时，由于连心线垂直平分公共弦，可以根据线段的垂直关系求特殊线段的长和角的度数．如果两个圆是等圆，则两圆的两个公共点与两个圆的圆心都组成一个等腰三角形，据此可以求出更多的线段和角．解题时特别需要注意的是：画两圆相交时，往往只画圆心在公共弦两侧的情况，从而漏掉了圆心在公共弦同侧的情况，导致解题不全．在已知两圆半径和公共弦长，求两圆的圆心距时，应分别计算圆心在公共弦同侧和圆心在公共弦两侧时的圆心距的长．【例5】两个同样大小的肥皂泡黏在一起，其剖面如图所示(点O，O′是圆心)，分隔两个肥皂泡的肥皂膜PQ成一条直线，TP，NP分别为两圆的切线，求∠TPN的大小．分析：因为两个圆大小相同，所以半径OP＝O′P＝OO′.又TP，NP分别为两圆的切线，所以PT⊥OP，PN⊥O′P，即∠OPT＝∠O′PN＝90°，所以∠TPN等于360°分别减去∠OPT，∠O′PN，∠OPO′即可．解：∵OP＝OO′＝PO′，∴△PO′O是一个等边三角形．∴∠OPO′＝60°.又∵TP与NP分别为两圆的切线，∴∠TPO＝∠NPO′＝90°.∴∠TPN＝360°－2×90°－60°＝120°.。