3_2动量守恒定律

v ex v ex 2）守恒条件 合外力为零 F = ∑ Fi = 0 ）
Fxex = 0 , F F
ex y
p x = ∑ mi vix = C x p y = ∑ mi viy = C y p z = ∑ mi viz = C z
= 0, = 0,
ex z
4） 动量守恒定律只在惯性参考系中成立 是自 ） 动量守恒定律只在惯性参考系中成立, 惯性参考系中成立 然界最普遍， 然界最普遍，最基本的定律之一 .
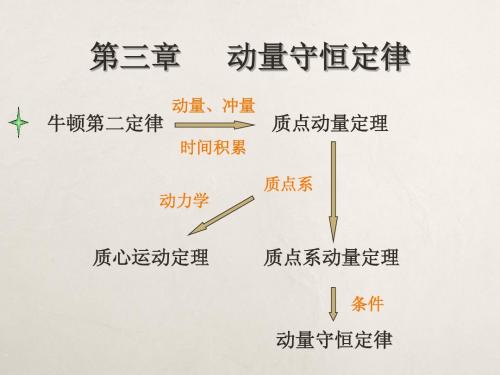
3 – 2 动量守恒定律
第三章动量守恒定律和能量守恒定律
例如在碰撞, 打击, 爆炸等问题中. 认为系统动量守恒 . 例如在碰撞 打击 爆炸等问题中 3）若某一方向合外力为零 则此方向动量守恒 . ） 某一方向合外力为零, 方向动量守恒 方向合外力为零
i v ex v in 当 F << F 时，可 略去外力的作用, 近似地 略去外力的作用
因dm的喷射，火箭总质量M在减少，减少量为−dM， 的喷射，火箭总质量 在减少，减少量为− ， 的喷射 在减少 故有dm = −dM。于是上式变为 故有 。
0 = [(M + dM )(v + dv ) (−dM )(v + dv − u)] Mv + − = Mdv + udM
积分得 0 =
v M
火箭在运行时生成的炽热气体高速向后喷 火箭在运行时生成的炽热气体高速向后喷 使火箭主体获得向前的动量。 射, 使火箭主体获得向前的动量。若将火 箭的总质量M分成两部分 火箭主体质量 箭的总质量 分成两部分, 分成两部分 M−dm ；将被喷射的物质质量 。 − 将被喷射的物质质量dm。 时刻, 尚未被喷出, 在t 时刻 dm尚未被喷出 火箭总质量相 尚未被喷出 对于地面的速度为v，动量为Mv； 对于地面的速度为 ，动量为 ；在t+dt 时刻, 被以相对于火箭的速度(称为喷射 时刻 dm被以相对于火箭的速度 称为喷射 被以相对于火箭的速度 速度) 喷出 喷出, 速度 u喷出 火箭主体则以 v+dv的速度相 的速度相 对于地面运行。 对于地面运行。
5
3 – 2 动量守恒定律
第三章动量守恒定律和能量守恒定律
将火箭主体和喷射物质视为一个系统, 将火箭主体和喷射物质视为一个系统 并忽略作用于 系统的仅有的外力，即火箭所受重力Mg, 那么根据动量 系统的仅有的外力，即火箭所受重力 守恒定律， 方向的分量式应有 守恒定律，在z方向的分量式应有
0 = [ M − dm )v + dv ) (dm )v + dv − u) − Mv ( ( + ( ]
∫ dv
0
+ u∫
dM
M0
M0 = v − u ln M M
6
3 – 2 量守恒定律
第三章动量守恒定律和能量守恒定律
火箭主体在其质量从M 火箭主体在其质量从 0变到 M0 v = u ln M时所达到的速度为 时所达到的速度为 M 火箭的速度决定于喷射速度和质量比 0/M)的自然 火箭的速度决定于喷射速度和质量比(M 的自然 质量比
对数。化学燃烧过程所达到的喷射速度理论值为 5×103m·s-1 , 而实际能达到的只是此值的一半左右 。 × 而实际能达到的只是此值的一半左右。 提高火箭速度的潜力在于提高质量比(M0/M)。 提高火箭速度的潜力在于提高质量比 。 是火箭尚未发射时的质量, 在(M0/M)中, M0是火箭尚未发射时的质量 包括负 中 火箭外壳等结构及全部燃料质量, 是负载及外 载 、 火箭外壳等结构及全部燃料质量 M是负载及外 壳 等 质 量 。 要 使 火 箭 主 体 超 过 第 一 宇 宙 速 度 (7.9 km⋅s−1)，用以发射人造地球卫星 质量比要高达 左 ⋅ ，用以发射人造地球卫星, 质量比要高达55左 右。大质量比困难, 一般采用多级火箭来实现。 大质量比困难 一般采用多级火箭来实现。
水平方向上 动量守恒
mv v' = − cos θ M
3 – 2 动量守恒定律
第三章动量守恒定律和能量守恒定律
运载火箭在运行时, 自身携带的燃料(液态氢 液态氢) 例 2 运载火箭在运行时 自身携带的燃料 液态氢 在氧化剂(液态氧 的作用下急剧燃烧, 液态氧)的作用下急剧燃烧 在氧化剂 液态氧 的作用下急剧燃烧 生成炽热气体并 相对火箭以高速u向后喷射 向后喷射， 相对火箭以高速 向后喷射，致使火箭主体获得向前 的动量。火箭总重量为M0，火箭主体重量为M， 的动量。火箭总重量为 ，火箭主体重量为 ，求火 箭最后能达到的速度。 箭最后能达到的速度。
3 – 2 动量守恒定律 第三章动量守恒定律和能量守恒定律 v v ex t v v 质点系动量定理 I = ∫ ∑ Fi d t = ∑ p i − ∑ p i 0
t0 i i i
动量守恒定律
v ex v ex 若质点系所受的合外力为零 若质点系所受的合外力为零 F = ∑ Fi = 0
则系统的总动量守恒，即 则系统的总动量守恒， 守恒
7
理论值 umt = 5 × 103 m ⋅ s −1
实际值 ump ≈ umt / 2
多级火箭技术
3 – 2 动量守恒定律
第三章动量守恒定律和能量守恒定律
运载火箭技术反映了当代科技水平的综合技术, 运载火箭技术反映了当代科技水平的综合技术, 但其动力学原理仍是动量定理和动量守恒定律。 但其动力学原理仍是动量定理和动量守恒定律。
v p=
∑
v pi
i
保持不变 . 保持不变
v ex 力的瞬时作用规律 F
v iv v v dp ex = , F = 0, P = C dt
1）系统的动量守恒是指系统的总动量不变，系 ）系统的动量守恒是指系统的总动量不变， 总动量不变 统内任一物体的动量是可变的, 各物体的动量必相 统内任一物体的动量是可变的 各物体的动量必相 对于同一惯性参考 同一惯性参考系 对于同一惯性参考系 .
3 – 2 动量守恒定律
第三章动量守恒定律和能量守恒定律
如图所示, 大炮在发射时炮身会发生反冲现象。 例 1 如图所示 大炮在发射时炮身会发生反冲现象。 设炮身的仰角为θ, 炮弹和炮身的质量分别为m和 设炮身的仰角为 炮弹和炮身的质量分别为 和M, 炮 弹在离开炮口时的速率为v, 弹在离开炮口时的速率为 若忽略炮身反冲时与地面的 摩擦力, 求炮身的反冲速率。 摩擦力 求炮身的反冲速率。