三角函数及其应用练习题

三角函数的应用题考点一: 锐角三角函数的定义及性质例1．如图，在矩形ABCD 中，DE ⊥AC 于E ，设∠ADE ＝α，且cos α＝53，AB ＝4，则AD 的长为( ) A ．3 B ．316 C ．320 D ．516例2．直线y=kx-4与y 轴相交所成的锐角的正切值为12，则k 的值为 .1.在Rt △ABC 中,∠C=90°,BC=4,AC=3,则cosA 的值为2.如图，在△ABC 中，∠C=90°，∠B=50°，AB=10，则BC 的长为（ ） ° ° ° D.10cos50°考点二: 特殊角的三角函数值例3．计算：2102452(3.14)π---+-例4．化简2)130(tan - ＝（ ）A 、331- B 、13- C 、133- D 、13-1.计算：2.计算45tan 30cos 60sin -的值是 。

3．已知在△ABC 中，若2sin 1cos 02A B ⎛⎫-+-= ⎪ ⎪⎝⎭，求∠C 的度数。

考点三: 锐角三角函数的关系例6．在△ABC 中，∠C ＝90°，sinA ＝35，则tanA ·cosA 的值是（ ）A 、35B 、45C 、925D 、16251．如果α是锐角，且22sin sin 541α+︒=，那么α的度数是（ ）A ．54°B ．46°C ．36°D ．26°2．已知∠A ＋∠B ＝90°，则下列各式中正确的是（ ）＝sinB ＝cosB ＝cosB ＝tanB[例1]如图，AD∥BC，AC⊥BC，若AD=3，DC=5，且∠B=30°，求AB 的长。

[例2]如图，四边形ABCD中，∠D=90°，AD=3，DC=4，AB=13，BC=12，求sinB。

[例3]如图，在河的对岸有水塔AB，今在C处测得塔顶A的仰角为30°，前进20米后到D处，又测得A的仰角为45°，求塔高AB。

2008年5.若αααcos ,0sin 2tan 则且<=的值是 （ ） A.51 B.-51 C.55 D.-55 9在ABC ∆中，已知AB=2，AC=7，BC=3.则角B 等于 （ ）A.6πB.4πC.3πD.π3216.在ABC∆中，若____________________ABC ,cos 1sin sin 2的形状是则∆+=C B A22.计算下列代数式的值：（8分）()421-02-320cos 617-sin log25.03+++⎪⎭⎫ ⎝⎛ππ20094.下列命题正确的是（ ）A.小于90的角是锐角B.若角α与角β的终边相同，那么αβ=C.若sin sin αβ=，则αβ=D.在ABC 中，若cos cos A B =，则A B =7.函数sin y x =263x ππ⎛⎫≤≤⎪⎝⎭的值域是（ ） A.[]1,1- B. 1,12⎡⎤⎢⎥⎣⎦C. 12⎡⎢⎣⎦D. ⎤⎥⎣⎦19.在ABC 中，已知0tan tan 1A B <⋅<，则ABC 的形状是_________.22.（本小题满分8分)已知4tan 23α=-，(,)42ππα∈，计算下列代数式的值2)41sin 2cos2πααα++-20107.在△ABC 中，已知3,5,7===c b a ，则此三角形的最大角是（ ） A. 3πB.32π C. 6πD. 65π16. 若,21tan =α则________cos 3sin 2cos sin =-+αααα23.已知：.21)t a n (),,2(,5102cos2sin=-∈=-βπππααα求)2tan(βα-的值.（8分）20116、使 成立的一个区间是 （ ）A 、B 、C 、D 、17、函数 的最小正周期 ___________________23知： ， ， ，求： 的值。

x x cos sin ≤]443[ππ，-]22[ππ，-]434[ππ，],0[πT x x x y cos sin 3cos 2+=︒<<︒360270βα＋α2cos ︒<-<︒18090βα54)cos(-=-βα54)cos(=+βα20123、由下列条件决定的角θ中，一定是第二象限的是（ ）.A 0<cos 0>sin θθ且 .B 0<cos •sin θθ.C 0>tan 0>cos θθ且 .D 0>tan •cos θθ13.函数⎪⎭⎫ ⎝⎛-=32s i n 2πx y 的最小正周期是____________. 14.21.已知51=cos -sin αα，且α为第一象限角.求下列各式的值：⑴α2sin ；⑵αtan .（10)2013４．若的值等于（ ）Ａ.０ Ｂ. 13Ｃ.１ Ｄ. 43１４．已知α是2sin cos tan 2,sin cos ααααα-=+则第二象限角，则cos sin cos sin αααα+的值是______． １９．（本小题满分８分）已知3cos 5α=-，()0,a π∈，求下列各式的值： （１）tan α；（２）sin 2cos2.αα+20147.函数cos y x x =+的最小正周期和最大值分别是 A. ,2π B. 2,1πC. 1πD. 2,2π 14.已知1sin cos 5αα+=，且()0,απ∈，则s i n c o s αα-=______19.（本小题满分8分）已知,,,022ππαβπαβ⎛⎫⎛⎫+∈-∈- ⎪ ⎪⎝⎭⎝⎭，且()()312sin ,cos ,513αβαβ+=-=求cos2α的值.20154、已知cos θ.tan θ>0,那么角θ是（ ） A 、第一或第二象限角 B 、第三或第四象限角C 、第一或第三象限角D 、第二或第四象限角 14、=--+)4sin()3cos(45cos 65sinππππ____________ 19、（本小题8分）已知βα,均为锐角，且sin α=55)cos(,53-=+βα，求sin β20163、已知cos α=55，且α为第四象限角，则sin α=（ ） A —51B 51C —552 D 552 15、在△ABC 中，已知a=1,c=2,∠A=30°，则∠C=________19、已知∠A ，∠B ，∠C 是△ABC 的三个内角，且cosA=1715，cosB=53，求sinC 的值20174.cos α＝－513,tan α＞0,则sin α＝( ).A.－513B.1213C.±1213D.51215.将函数f (x )＝sin2x 的图象向右平移π4个单位长度,所得图象经过点(π4,y 0),则y 0的值为 .19.(本小题满分8分)已知tan α＝2. (1)求tan(α＋π4)的值；(2)求sin2αsin 2α＋sin αcos α－cos 2α－1的值.2018一个选择题，倍角公式的运用一个大题，求一个边的长度。

1.6 三角函数模型简单应用1．函数的2cos 3cos 2y x x =-+最小值为（ ） A ．2 B ．0 C ．41- D ．62．2sin 5cos )(+-⋅=x x x x f ，若a f =)2(，则)2(-f 的值为（ ）． A ．－a B ．2＋a C ．2－a D ．4－a3．设A 、B 都是锐角，且cosA ＞sinB 则A+B 的取值是 （ ） A ．⎪⎭⎫⎝⎛ππ,2 B ．()π,0 C ．⎪⎭⎫ ⎝⎛2,0πD ．⎪⎭⎫⎝⎛2,4ππ4．若函数)(x f 是奇函数，且当0<x 时，有x x x f 2sin 3cos )(+=，则当0>x 时，)(x f 的表达式为（ ）A ．x x 2sin 3cos +B ．x x 2sin 3cos +-C ．x x 2sin 3cos -D ．x x 2sin 3cos --5．下列函数中是奇函数的为( )A ．y=xx x x cos cos 22-+B ．y=xx x x cos sin cos sin -+ C ．y=2cosxD ．y=lg(sinx+x 2sin 1+)6．在满足xx4πtan 1πsin +＝0的x 中，在数轴上求离点6最近的那个整数值是 ． 7．已知()3s i n 4fx a x b x =++（其中a 、b 为常数），若()52=f ，则()2f -=__________．8．若︒>30cos cos θ，则锐角θ的取值范围是_________． 9．由函数⎪⎭⎫ ⎝⎛≤≤=6563sin 2ππx x y 与函数y ＝2的图象围成一个封闭图形，这个封闭图形的面积是_________．10．函数1sin(2)2y x θ=+的图象关于y 轴对称的充要条件是11．如图，表示电流强度I 与时间t 的关系式),0,0)(sin(>>+=ωϕωA t A I 在一个周期内的图象.①试根据图象写出)sin(ϕω+=t A I 的解析式 ②为了使)sin(ϕω+=t A I 中t 在任意一段1100秒的时间内I 能同时取最大值|A|和最小值－|A|， 那么正整数ω的最小值为多少？12．讨论函数y=lgcos2x 的的定义域、值域、奇偶性、周期性和单调性等函数的基本性质13．函数2()122cos 2sin f x a a x x =---的最小值为()()g a a R ∈，（1）求g a ()的表达式；（2）若1()2g a =，求a 及此时()f x 的最大值14．已知f(x)是定义在R 上的函数，且1()(2)1()f x f x f x ++=-(1)试证f(x)是周期函数. (2)若f(3)=3-，求f(2005)的值.15．已知函数)0,0)(sin()(πϕωϕω≤≤>+=x x f 是R 上的偶函数，其图象关于点⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛2π0，对称，且在,043πM 上是单调函数，求ϕω和的值．1.6 三角函数模型简单应用1．Ｂ 2．D 3．C 4．B 5．Ｄ 6．1 7．3 8．︒<<︒300θ 9．π34 10．,2k k Z πθπ=+∈11．（1）)3100sin(300ππ+=t I （2）629=ω12．定义域：(kπ-4π,kπ+4π),k ∈Z;值域]0,(-∞；奇偶性：偶函数；周期性：周期函数，且T=π;单调性：在(kπ-4π,kπ] (k ∈Z)上递增，在［kπ,kπ+4π)上递减13．2()122cos 2sin f x a a x x =--- 2122cos 2(1cos )a a x x =----22cos 2cos 12x a x a =---222(cos )12()22aa x a a R =----∈ (1)函数()f x 的最小值为()g a1.122a a <-<-当时即时，cos 1x =-由得 22()2(1)12122a a g a a =-----=2.11222a a -≤≤-≤≤当时即时，cos 2a x =由得 2()122a g a a =---3.122a a >>当时即时，cos 1x =由，22()2(1)1222a a g a a =----得＝14a -综上所述得 21(2)()12(22)214(2)a a g a a a a a <-⎧⎪⎪=---≤≤⎨⎪->⎪⎩－ (2) g a a ()=∴-≤≤1222有 2211243022a a a a -=++=－－得 13()a a ∴=-=-或舍221()2(cos )1222a a a f x x a =-=----将代入 211()2(cos )22f x x =++得cos 1x =当 2()x k k Z π=∈即时得 max ()5f x =14．(1)由1()(2)1()f x f x f x ++=-，故f(x+4)=)2(1)2(1+-++x f x f =1()f x -f(x+8)=f(x+4+4)=1(4)f x -+=f(x)，即8为函数()f x 的周期(2)由 f(x+4) =1()f x -，得f(5) =13(1)3f -= ∴f(2005)=f(5+250×8)=f(5)=33 15． 由f （x ）为偶函数，知|f （0）|=1,结合πϕ≤≤0，可求出2πϕ=．又由图象关于⎪⎭⎫⎝⎛0,43πM 对称，知043=⎪⎭⎫⎝⎛πf ，即043cos =ωπ 又0>ω及()()()2,1,01232,,2,1,0243=+=∴=+=k k k k ωππωπ ． 当k=0,1即32=ω，2时，易验证f （x ）在⎥⎦⎤⎢⎣⎡2,0π上单减；k≥2时，f （x ）在⎥⎦⎤⎢⎣⎡2,0π上不是单调的函数．综上所述22,32πωϕ==或。

初中三角函数应用题10道(1)求步道AC 的长度（结果保留根号）；(2)游客中心Q 在点A 的正东方向，步道AC 与步道BQ 交于点P 小明和爸爸分别从B 处和A 处同时出发去游客中心，小明跑步的速度是每分钟请计算说明爸爸的速度要达到每分钟多少米，他俩可同时到达游客中心．0.1）（参考数据：2 1.414≈，3 1.732≈，6 2.449≈）2．（2023春·重庆沙坪坝·九年级重庆八中校考阶段练习）下图是儿童游乐场里的一个娱乐项目转飞椅的简图，该设施上面有一个大圆盘（圆盘的半径是 3.5OA =米），圆盘离地面的高度1 6.5OO =米，且1OO ⊥地面l ，圆盘的圆周上等间距固定了一些长度相等的绳子，绳子的另一端系着椅子（将椅子看作一个点，比如图中的点B 和1B ），当旋转飞椅静止时绳子是竖直向下的，如图中的线段AB ，绳长为4.8米固定不变．当旋转飞椅启动时，圆盘开始旋转从而带动绳子和飞椅一起旋转，旋转速度越大，飞椅转得越高，当圆盘旋转速度达到最大时，飞椅也旋转到最高点，此时绳子与竖直方向所成的夹角为57α=︒．（参考数据：sin 570.84︒≈，cos570.55︒≈，tan 57 1.54︒≈）(1)求飞椅离地面的最大距离（结果保留一位小数）；(2)根据有关部门要求，必须在娱乐设施周围安装安全围栏，而且任何时候围栏和飞椅的水平距离必须超过2米．已知该旋转飞椅左侧安装有围栏EF ，且EF l ⊥，19.8O E =米，请问圆盘最大旋转速度的设置是否合规？并说明理由．3．（2023春·重庆渝北·九年级校联考阶段练习）如图，某大楼的顶部竖有一块宣传牌AB ，小明在斜坡的坡脚D 处测得宣传牌底部B 的仰角为45︒，沿斜坡DE 向上走到E 处测得宣传牌顶部A 的仰角为31︒，已知斜坡DE 的坡度3:4，10DE =米，22DC =米，求宣传牌AB 的高度．（测角器的高度忽略不计，参考数据：sin 310.52︒≈，cos310.86︒≈，tan 310.6)︒≈。

三角函数的应用专项训练姓名：__________班级：__________评价：__________一、单选题（共8小题）1. 已知α是第四象限角，且3sin2α＝8cosα，则cos等于( )A. －B. －C.D.2. 已知α∈，sinα＝，则tanα等于( )A. －B. 2C.D. －23. 若α∈(0，π)，sin(π－α)＋cosα＝，则sinα－cosα的值为( )A. B. － C. D. －4. 函数f(x)＝(0<x<π)的大致图象是( )A. B. C. D.5. 为了得到函数y＝sin的图象，可以将函数y＝sin的图象( )A. 向右平移个单位长度B. 向右平移个单位长度C. 向左平移个单位长度D. 向左平移个单位长度6. 下列函数中，以为周期且在区间上单调递增的是( )A. f(x)＝|cos 2x|B. f(x)＝|sin 2x|C. f(x)＝cos|x|D. f(x)＝sin|x|7. 已知函数f(x)＝cosωx＋sinωx，ω>0，x∈R.若曲线y＝f(x)与直线y＝1的交点中，相邻交点的距离的最小值为，则y＝f(x)的最小正周期为( )A. B. π C. 2π D. 3π8. 已知函数f(x)＝sin(ωx＋φ)，x＝－为f(x)的零点，x＝为y＝f(x)的图象的对称轴，且f(x)在上单调，则ω的最大值为( )A. 11B. 9C. 7D. 5二、多选题（共5小题）9. 函数f(x)＝A sin(ωx＋φ)(A>0，ω>0,0≤φ≤2π)的部分图象如图所示，则下列说法正确的是( )A. ω＝B. ω＝C. φ＝D. A＝510. 已知函数f(x)＝A sin(ωx＋φ)的部分图象如图所示，则下列说法错误的是( )A. 函数y＝f(x)的图象关于直线x＝－对称B. 函数y＝f(x)的图象关于点对称C. 函数y＝f(x)在上单调递减D. 该图象对应的函数解析式为f(x)＝2sin11. 将曲线y＝sin2x－sin(π－x)sin上每个点的横坐标伸长为原来的2倍(纵坐标不变)，得到g(x)的图象，则下列说法正确的是( )A. g(x)的图象关于直线x＝对称B. g(x)在[0，π]上的值域为C. g(x)的图象关于点对称D. g(x)的图象可由y＝cos x＋的图象向右平移个单位长度得到12. 函数y＝sin的图象向右平移个单位长度后与函数f(x)的图象重合，则下列结论中正确的是( )A. f(x)的一个周期为－2πB. y＝f(x)的图象关于直线x＝－对称C. x＝是f(x)的一个零点D. f(x)在上单调递减13. 对于函数f(x)＝给出下列四个命题，其中为真命题的是( )A. 该函数是以π为最小正周期的周期函数B. 当且仅当x＝π＋kπ(k∈Z)时，该函数取得最小值－1C. 该函数的图象关于直线x＝π＋2kπ(k∈Z)对称D. 当且仅当2kπ<x<＋2kπ(k∈Z)时，0<f(x)≤三、填空题（共4小题）14. y＝tan(2x＋θ)图象的一个对称中心为，若－<θ<，则θ＝________.15. 设函数f(x)＝A sin(ωx＋φ)，A>0，ω>0，－<φ<，x∈R的部分图象如图所示，则A＋ω＋φ＝________.16. 要得到函数y＝sin的图象，只需将函数y＝cos 2x的图象向________平移________个单位长度．17. 在如图所示的矩形ABCD中，点E，P分别在边AB，BC上，以PE为折痕将△PEB翻折为△PEB′，点B′恰好落在边AD上，若sin∠EPB＝，AB＝2，则折痕PE的长为________．四、解答题（共4小题）18. 已知函数f(x)＝2sin·cos－sin(x＋π)．(1)求f(x)的最小正周期；(2)将f(x)的图象向右平移个单位长度，得到函数g(x)的图象，求函数g(x)在区间[0，π]上的最大值和最小值．19. 已知f(x)＝(sin x＋cos x)2－cos2x.(1)求函数f(x)的最小正周期及单调递增区间；(2)若θ∈，f＝，求sin的值．20. 如图为电流强度I与时间t的关系式I＝A sin(ωt＋φ)的图象．(1)试根据图象写出I＝A sin(ωt＋φ)的解析式；(2)为了使I＝A sin(ωx＋φ)中t在任意一段秒的时间内电流强度I能同时取得最大值|A|与最小值－|A|，那么正整数ω的最小值是多少？21. 如图，某城市拟在矩形区域ABCD内修建儿童乐园，已知AB＝200米，BC＝400米，点E，N分别在AD，BC上，梯形DENC为水上乐园；将梯形EABN分成三个活动区域，M在AB上，且点B，E关于MN对称．现需要修建两道栅栏ME，MN将三个活动区域隔开．设∠BNM＝θ，两道栅栏的总长度L(θ)＝ME＋MN.(1)求L(θ)的函数表达式，并求出函数L(θ)的定义域；(2)求L(θ)的最小值及此时θ的值．1. 【答案】A【解析】∵3sin2α＝8cosα，∴sin2α＋2＝1，整理可得9sin4α＋64sin2α－64＝0，解得sin2α＝或sin2α＝－8(舍去)．∵α是第四象限角，∴sinα＝－，∴cos＝cos＝－cos＝sinα＝－.2. 【答案】A【解析】因为α∈，sinα＝，所以cosα＝－1-sin2α＝－＝－，所以tanα＝＝－.3. 【答案】C【解析】由诱导公式得sin(π－α)＋cosα＝sinα＋cosα＝，平方得(sinα＋cosα)2＝1＋2sinαcosα＝，则2sinαcosα＝－<0，所以(sinα－cosα)2＝1－2sinαcosα＝，又因为α∈(0，π)，所以sinα－cosα>0，所以sinα－cosα＝.4. 【答案】B【解析】因为f(x)＝，＝＝＝＝|cos x|，所以，其在(0，π)上的大致图象为B选项中的图象.5. 【答案】B【解析】将函数y＝sin的图象向右平移个单位长度，得y＝sin＝sin 的图象．6. 【答案】A【解析】选项A中，函数f(x)＝|cos 2x|的周期为，当x∈时，2x∈，函数f(x)单调递增，故选项A正确；选项B中，函数f(x)＝|sin 2x|的周期为，当x∈时，2x∈，函数f(x)单调递减，故选项B不正确；选项C中，函数f(x)＝cos|x|＝cos x的周期为2π，故选项C不正确；选项D中，f(x)＝sin|x|＝由正弦函数图象知，在x≥0和x<0时，f(x)均以2π为周期，但在整个定义域上f(x)不是周期函数，故选项D不正确．7. 【答案】D【解析】将函数f(x)＝cosωx＋sinωx，ω>0，x∈R化简，可得f(x)＝sin.曲线y＝f(x)与直线y＝1相交，令f(x)＝1，则ωx＋＝＋2kπ或ωx＋＝＋2kπ，k∈Z.设距离最小的相邻交点的横坐标分别为x1，x2，∴－＝ω(x2－x1)，∴x2－x1＝＝，解得ω＝，∴y＝f(x)的最小正周期T＝＝3π.8. 【答案】B【解析】因为x＝－为f(x)的零点，x＝为f(x)的图象的对称轴，所以－＝＋kT，即＝T＝·，所以ω＝4k＋1(k∈N*)，又因为f(x)在上单调，所以－＝≤＝，即ω≤12，由此得ω的最大值为9.9. 【答案】ACD【解析】由函数的图象可得A＝5，周期T＝＝11－(－1)＝12，∴ω＝.再由“五点法”作图可得×(－1)＋φ＝2kπ，k∈Z，∴φ＝2kπ＋，k∈Z，∵0≤φ≤2π，∴φ＝.故选ACD.10. 【答案】ABC【解析】由函数的图象可得A＝2，由·＝－，得ω＝2.再由最值得2×＋φ＝2kπ＋，k∈Z，又|φ|<，得φ＝，得函数f(x)＝2sin，故选项D正确；当x＝－时，f(x)＝0，不是最值，故选项A错误；当x＝－时，f(x)＝－2，不等于零，故选项B错误；由＋2kπ≤2x＋≤＋2kπ，k∈Z，得＋kπ≤x≤＋kπ，k∈Z，故选项C错误.11. 【答案】ABD【解析】y＝sin2x－sin(π－x)sin＝＋sin x cos x＝sin 2x－cos 2x＋＝sin＋，∴g(x)＝sin＋，对于选项A，当x＝时，x－＝，∴g(x)关于直线x＝对称，故选项A正确；对于选项B，当x∈[0，π]时，x－∈，∴sin∈，∴g(x)∈，故选项B正确；对于选项C，当x＝时，x－＝0，g＝，∴g(x)关于点对称，故选项C错误；对于选项D，y＝cos x＋的图象向右平移个单位长度得到y＝cos＋＝cos ＋＝sin＋＝g(x)的图象，故选项D正确．12. 【答案】ABC【解析】∵函数y＝sin的图象向右平移个单位长度后与函数f(x)的图象重合，∴f(x)＝sin＝sin，∴f(x)的一个周期为－2π，故选项A正确；∵y＝f(x)＝sin，∴y＝f(x)的图象的对称轴方程满足2x－＝kπ＋(k∈Z)，∴当k＝－2时，y＝f(x)的图象关于直线x＝－对称，故选项B正确；由f(x)＝sin＝0，得2x－＝kπ(k∈Z)，得x＝＋(k∈Z)，∴x＝是f(x)的一个零点，故选项C正确；当x∈时，2x－∈，∴f(x)在上单调递增，故选项D错误．13. 【答案】CD【解析】由题意知函数f(x)＝画出f(x)在x∈[0，2π]上的图象，如图所示，由图象知，函数f(x)的最小正周期为2π，故A选项错误；在x＝π＋2kπ(k∈Z)和x＝＋2kπ(k∈Z)时，该函数都取得最小值－1，故B选项错误；由图象知，函数图象关于直线x＝＋2kπ(k∈Z)对称，故C选项正确；在2kπ<x<＋2kπ(k∈Z)时，0<f(x)≤，故D选项正确.14. 【答案】－或【解析】函数y＝tan x图象的对称中心是，其中k∈Z，则令2x＋θ＝，k∈Z，其中x＝，即θ＝－，k∈Z.又－<θ<，所以当k＝1时，θ＝－.当k＝2时，θ＝，所以θ＝－或.15. 【答案】3＋【解析】由图可知A＝2，＝－＝，所以T＝2π，所以ω＝1.再根据f＝2得sin ＝1，所以＋φ＝＋2kπ(k∈Z)，即φ＝＋2kπ(k∈Z)．又因为－<φ<，所以φ＝，因此A＋ω＋φ＝3＋.16. 【答案】左【解析】方法一：y＝sin＝cos＝cos＝cos.因此要得到函数y＝sin的图象，只需将函数y＝cos 2x的图象向左平移个单位长度．方法二：y＝cos 2x＝sin＝－sin＝－sin2，y＝sin＝－sin2.因此要得到函数y＝sin的图象，只需将函数y＝cos 2x的图象向左平移个单位长度．17. 【答案】【解析】根据题意，设BE＝m，由sin∠EPB＝，得PE＝3m，cos∠PEB＝，从而得到cos∠B′EA＝cos(π－2∠PEB)＝－cos 2∠PEB＝1－2cos2∠PEB＝，由翻折特点可得B′E＝BE＝m.又AE＝2－m，在Rt△B′AE中，cos∠B′EA＝＝，解得m＝，所以PE＝3m＝.18. 【答案】解(1)f(x)＝2sin·cos－sin(x＋π)＝cos x＋sin x＝232cosx+12sinx＝2sin，∴f(x)的最小正周期T＝＝2π.(2)由已知得g(x)＝f＝2sin.∵x∈[0，π]，∴x＋∈，∴sin∈，∴g(x)＝2sin∈[－1,2]，∴函数g(x)在区间[0，π]上的最大值为2，最小值为－1.19. 【答案】解(1)f(x)＝(sin x＋cos x)2－cos2x＝(1＋2sin x cos x)－cos2x＝sin 2x－＋＝sin＋.所以函数f(x)的最小正周期T＝＝π.由2kπ－≤2x－≤2kπ＋，k∈Z,得kπ－≤x≤kπ＋，k∈Z，所以函数f(x)的单调递增区间为(k∈Z)．(2)由(1)得f＝sin＋＝sin＋＝cosθ＋＝，所以cosθ＝，因为θ∈，所以sinθ＝－√1−cos2θ1-cos2θ＝－，所以sin 2θ＝2sinθcosθ＝－，cos 2θ＝2cos2θ－1＝－，所以sin＝sin 2θcos－cos 2θsin＝－.20. 【答案】解(1)由题图知，A＝300，T＝－＝，∴ω＝＝100π.∵－＝－，∴φ＝＝，∴I＝300sin(t≥0)．(2)问题等价于T≤，即≤，∴ω≥200π，∴正整数ω的最小值为629.21. 【答案】解(1)在矩形ABCD中，∵B，E关于MN对称，∠BNM＝θ，∴∠AME ＝2θ，∠MEN＝，且BM＝ME.在Rt△AEM中，AM＝ME cos 2θ＝BM cos 2θ.又∵AM＋BM＝200(米)，∴BM cos 2θ＋BM＝200，∴BM＝ME＝＝，∴Rt△EMN中，MN＝＝.∴L(θ)＝ME＋MN＝＋在Rt△BMN中，BN＝MN cosθ＝，∵0<BM<200,0<BN<400，∴函数L(θ)的定义域为.(2)L(θ)＝ME＋MN＝＋＝＝.令t＝sinθ，∵θ∈，∴t∈，令φ(t)＝－t2＋t＝－2＋，当t＝时，φ(t)取最大值，最大值为，此时θ＝，L(θ)取最小值．∴L(θ)的最小值为400 米，此时θ＝.第11页共11页。

高二数学三角函数应用练习题及答案一、选择题1. 下列函数中，不是周期函数的是：A. y = 2sin(x + π)B. y = 3cos(2x)C. y = 4tan(x)D. y = 5cot(3x)答案：C2. 函数y = 2sin(3x)的最小正周期是：A. 2πB. π/3C. π/2D. 2π/3答案：B3. 函数y = 4cos(2x + π/4)的最大值和最小值之差是：A. 4B. 2C. 8D. 6答案：C4. 若点P(x, y)在单位圆上，则函数y = 3sinθ的图象中，点P的坐标满足：A. x^2 + y^2 = 1B. x^2 + y^2 ≦ 1C. x^2 + y^2 ＞ 1D. x^2 + y^2 ＜ 1答案：A5. 已知三角函数f(x) = a sin(bx + c)，其中a > 0，且|a| ≠ 1，下列说法正确的是：A. 当a > 1时，函数f(x)的图象在x轴上有两个非重合的零点；B. 当a < 0时，函数f(x)的图象在x轴上有两个非重合的零点；C. 当|a| < 1时，函数f(x)的图象在x轴上没有零点；D. 当|a| > 1时，函数f(x)的图象在x轴上有两个非重合的零点。

答案：D二、填空题1. 函数y = 2sin(3x)的一个零点是________。

答案：π/62. 完全图f(x) = a sin(bx + c)的一个最大值点是(π/4, 3)，则a的值为________。

答案：33. 函数f(x) = 5cos(x)中，最小正周期的长度为________。

答案：2π4. 函数f(x) = 2tan(2x - π/4)的最值之差为________。

答案：45. 若图像y = sin^2(x + a)与y = cos^2(x + b)重合，则a + b =________。

答案：π/2三、计算题1. 将函数y = 2sin(3x)的图象向左平移3个单位得到图象y = 2sin(3x + k)，求k。

九年级三角函数的应用练习题：1、右图：在甲楼A处测得乙楼顶的仰角为30°，测得乙楼底的俯角为45°，两楼相距60米。

求两楼高度2、右图：在甲楼A处测得乙楼顶的仰角为60°，测得乙楼底的俯角为45°，甲楼高100米。

求乙楼高度和两楼距离3、右图：在甲楼顶测得乙楼顶的仰角为30°，在甲楼底测得乙楼顶的仰角为60°，甲楼的高为50米。

求乙楼高度4、右图：小明在A处测得塔顶仰角为30°，前进100米至B处,测得塔顶仰角为45°。

求塔高5、如图，一飞机从一高炮C的正上方D点2 000 m 经过，沿水平方向飞行，稍后到达B 点，此时仰角45°，一分钟后飞机到达A点，仰角为30°，求飞机从B到A的速度?6、右图：身高1．80米的同学测得旗杆顶的仰角为60°，他与旗杆的距离为5米，求旗杆高7、右图：发射塔AB在山顶上，在距离山100米的C处，测得A、B的仰角为60°和45°求发射塔AB高度8、右图：小明在A处测得塔顶仰角为45°，前进100米至B处,测得塔顶仰角为60°，已知山高50米，求CD9.一轮船以每小时20海里的速度沿正东方向航行，上午8时，该船在A处测得某灯塔位于它的北偏东30º的B处。

上午9时行至C处，测得灯塔恰好在它的正北方向，此时它与灯塔的距离是海里。

（结果保留根号）10.在一次实践活动中，小兵从A 地出发，沿东北方向行进了5 千米到达B 地，然后再沿西北方向行进了5千米到达目的地C 。

（1）A 、C 两地的距离为 千米。

（2）试确定目的地C 在A 地的什么地方？11.如图,某地为响应市政府“形象重于生命”的号召,在甲建筑物上从点A 到点E 挂一长为30米的宣传条幅,在乙建筑物的顶部D 点测得条幅顶端A 点的仰角为40°,测得条幅底端E 的俯角为26°,求甲、乙两建筑物的水平距离BC 的长(精确到0.1米).12.如图,小山上有一座铁塔AB,在D 处测得点A 的仰角为∠ADC=60°,点B 的仰角为∠BDC=45°;在E 处测得A 的仰角为∠E=30°,并测得DE=90米, 求小山高BC 和铁塔高AB(精确到0.1米).13.某民航飞机在大连海域失事,为调查失事原因,决定派海军潜水员打捞飞机上的黑匣子,如图所示,一潜水员在A 处以每小时8海里的速度向正东方向划行,在A 处测得黑匣子B 在北偏东60°的方向,划行半小时后到达C 处,测得黑匣子B 在北偏东30 °的方向,在潜水员继续向东划行多少小时,距离黑匣子B 最近,并求最近距离. BDA CE FF30︒北A 60︒C14.在拓宽工程中, 要伐掉一棵树AB,在地面上事先划定以B 为圆心,半径与AB 等长的圆形危险区,现在某工人站在离B 点3米远的D 处测得树的顶点A 的仰角为60°,树的底部B 点的俯角为30°, 如图所示,问距离B 点8米远的保护物是否在危险区内?B30︒DA60︒C E。

第一章 直角三角形的边角关系1.5 三角函数的应用精选练习一、单选题1．（2022·江苏泰州·九年级期中）一条上山直道的坡度为17∶，沿这条直道上山，则前进100米所上升的高度为（ ）A ．700米B．米C．米D．2．（2022·吉林省第二实验学校九年级阶段练习）某书店拿取高处书籍的登高梯如图位置摆放，登高梯AC 的顶端A 恰好放在书架的第七层的顶端．已知登高梯的长度AC 为3米，登高梯与地面的夹角ACB Ð为72o ，则书架第七层顶端离地面的高度AB 为（ ）A ．3sin 72°米B ．3sin 72o 米C ．3cos 72°米D ．3cos 72o米3．（2022·江苏苏州·九年级期中）如图，小王在高台上的点A 处测得塔底点C 的俯角为α，塔顶点D 的仰角为β，已知塔的水平距离AB a =，则此时塔高CD 的长为（ ）A ．sin sin a a a b +B ．tan tan a a a b +C ．tan tan aa b +D ．tan tan tan tan a a b a b+【答案】B【分析】在Rt △ABD 和Rt ABC △中，利用锐角三角函数求出,BD BC ，即可求解．【详解】解：根据题意得：90ABD ABC Ð=Ð=°，在Rt △ABD 中，tan tan BD AB a b b ==，在Rt ABC △中，tan tan BC AB a a a ==，∴tan tan CD BD BC a a a b =+=+．即此时塔高CD 的长为tan tan a a a b +．故选：B【点睛】本题主要考查了解直角三角形，熟练掌握锐角三角函数是解题的关键．4．（2022·山东济南·模拟预测）小明去爬山，在山脚A 看山顶D 的仰角30CAD Ð=°，小明在坡比为5:12的山坡上走1300米到达B 处，此时小明看山顶的仰角60DBF Ð=°，则山高CD 为（ ）米A ．(600-B ．()250C ．(350+D ．【点睛】本题主要考查了解直角三角形的实际应用，明确题意，准确构造直角三角形是解题的关键．5．（2022·河北石家庄·九年级期中）如图，一块矩形薄木板ABCD 斜靠在墙角MON 处（OM ON ^，点A ，B ，C ，D ，O ，M ，N 在同一平面内），已知AB m =，AD n =，ADO a Ð=，则点B 到ON 的距离等于（ ）A ．cos cos m n a a×+×B ．sin cos m n a a ×+×C ．cos sin m n a a×+×D ．sin sin m n a a×+×过点B 作BH ON ^于H ∴B 到ON 的距离是BH ∵OM ON ^，矩形ABCD ∴BAQ DAO DAO Ð+Ð=Ð∴ADO BAQ a Ð=Ð=，6．（2022·河北·石家庄市第四十二中学九年级期中）如图，沿AB 方向架桥BD ，以桥两端B D 、出发，修公路BC 和DC ，测得150ABC Ð=°，1800BC =m ，105BCD Ð=°，则公路DC 的长为（ ）A ．900mB ．mC ．mD ．1800m【点睛】本题考查解直角三角形和三角形内角和定理，熟练掌握直角三角形边角关系是解题的关键．二、填空题7．（2022·广西贵港·九年级期中）桔棉，亦叫“桔皋”，我国古代井上汲水的工具.它是在井旁架上设一杠杆，杠杆上竹竿一端A 处系绳子，绳子另一端悬绑汲器，竹竿另一端B 处绑石块等重物，用不大的力量即可将灌满水的汲器提起，桔棒的使用体现了我国古代劳动人民的智慧.如图是《天工开物·水利》中的桔棉图，若竹竿A ，B 两处的距离为12m ，当汲器伸到井口时，绳子受重力作用垂直于水平面，此时竹竿AB 与绳子的夹角为53°，则绑重物的B 端与悬绑汲器的绳子之间的距离是_______m.（忽略提水时竹竿产生的形变）（参考数据：sin 530.8cos530.6tan 53 1.3°»°»°»，，）由题意得，在Rt ABC △∴sin BC AB BAC =Ðg ，∵12m AB BAC =Ð=，∴()120.89.6m BC »´=，故答案为：9.6．【点睛】本题考查解直角三角形的应用，熟练掌握解直角三角形相关知识是解题的关键．8．（2022·山东·淄博市张店区第九中学九年级期中）倡导“低碳环保”让“绿色出行”成为一种生活常态．小明买了一辆自行车作为代步工具，各部件的名称如图1所示，图2是该自行车的车架示意图，上管36cm AC =，且上管AC 与立管AB 互相垂直，下管45cm BC =，座管AE 可以伸缩，点A B E ，，在同一条直线上，且75ABD Ð=°．若座管AE 伸长到18cm ，则座垫E 到后下叉BD 的距离为______cm ．（结果精确到1cm ，参考数据sin750.97°»，cos750.26°»，tan75 3.73°»）∵45cm BC =，36cm AC =，∴22245AB BC AC =-=-在Rt FBE V 中，sin EF EB =´故答案为：44．9．（2022·山东济南·九年级期中）如图，太阳光线与地面成30°的角，照射在小木棒AB 上，小木棒在地面上的投影CD 的长是8cm ，则小木棒AB 的长是______cm ．10．（2022·江苏苏州·九年级期中）一艘观光游船从港口A 以北偏东60°的方向出港观光，航行80海里至C 处时发生了侧翻沉船事故．一艘在港口正东方向的海警船接到求救信号，测得事故船在它的北偏东37°方向，马上以40海里每小时的速度前往救援．海警船大约需_____小时到达事故船C 处，(sin 530.8cos530.6°»°»，)【点睛】本题考查了解直角三角形的应用键．三、解答题11．（2022·重庆市万盛经济技术开发区溱州中学九年级期中）隋唐洛阳城国家遗址公园里有一地标性建筑物——明堂天堂．现已成为中外游客到洛阳旅游打卡的网红地、如图，天堂外观5层，内部9层，由建筑主体、台基和宝顶三部分组成．为测量天堂AB （左边较高的建筑物）的高度，几名中学生在天堂旁边明堂的台基E 处测得天堂建筑主体顶端C 处的仰角为22°，往前水平行进14米至F 处，测得天堂顶端点A 的仰角为30°，已知天堂宝顶AC 高188．米，明堂台基EF 距地面DB 的高DE 为10米，请计算天堂AB 的高的值．（结果精确到1米；参考数据：sin 220.37°»，cos 220.93°»，tan 220.40°» 1.73»）12．（2022·江苏苏州·九年级期中）图1是某型号挖掘机，该挖掘机是由基座、主臂和伸展臂构成，图2是其侧面结构示意图（MN 是基座的高，MP 是主臂，PQ 是伸展臂）．已知基座高度MN 为0.5米，主臂MP长为α的范围是：060a °<£°，伸展臂伸展角β的范围是：45135b °££°．(1)如图3，当45a =°时，伸展臂PQ 恰好垂直并接触地面，伸展臂PQ 长为 米；(2)若（1）中PQ 长度不变，求该挖掘机最远能挖掘到距点N 水平正前方多少米的土石．（结果保留根号）∵45a =°，∴PHM V 为等腰直角三角形，∴sin 3PH PM a ==∴45QPH Ð=°，∴sin 45 3.5QH PH PQ ==°=´∴7232MH MPPH =+=+一、填空题1．（2022·陕西汉中·九年级期末）某区域平面示意图如图所示，AB 和BC 是两条互相垂直的公路，800AB =米，甲勘测员在A 处测得点D 位于北偏东45°，乙勘测员在C 处测得点D 位于南偏东60°，300CD =米，则公路BC 的长为___________米．（结果保留根号）的面积为___________米2【分析】延长BA 交CD 于G 点，在Rt EFB D 中，根据锐角三角函数定义求出EF ，在Rt CGA V 中，根据锐角则3CG BF ==（米），由题意得：30EBF Ð=°，在Rt EFB D 中，tan BF EF =在Rt CGA V 中，AG CG =∴1AB CE EF AG =+-=+3．（2022·江苏苏州·九年级期中）如图是某风车示意图，其相同的四个叶片均匀分布，水平地面上的点M 在旋转中心O 的正下方．某一时刻，太阳光线恰好垂直照射叶片OA OB ，，此时各叶片影子在点M 右侧成线段CD ，设太阳光线与地面的夹角为a ，测得2tan 3a ＝，8.5m 13m MC CD ＝，＝，风车转动时，叶片外端离地面的最大高度等于 _____m ．4．（2022·浙江温州·八年级期中）如图1是某小车侧面示意图，图2是该车后备箱开起侧面示意图，具体数据如图所示(单位：cm)且AF BE ∥，60BAF Ð=°，10BD =，箱盖开起过程中，点A ，C ，F 不随箱盖转动，点B ，D ，E 绕点A 沿逆时针方向转动90°，即90BAB ¢Ð=°分别到点B ¢，D ¢，E ¢的位置，气簧活塞杆CD 随之伸长CD ¢已知直线BE B E ¢¢^，CD CB ¢=，那么AB 的长为______cm ，CD ¢的长为______cm ．5．（2022·山东威海·九年级期中）如图，一架水平飞行的无人机在A处测得正前方河岸边C处的俯角为α，a=，无人机沿水平线AF方向继续飞行80米至B处时，被河对岸D处的小明测得其仰角为30°．无tan2MC=米，则河流的宽度CD为人机距地面的垂直高度用AM表示，点M，C，D在同一条直线上，其中100______．\ME AB==，AM BEÐ=，tan由已知可得：BAC a\80Ð==米，ACMME ABAM二、解答题6．（2022·山东东营·九年级期中）如图，台风中心位于点O处，并沿东北方向（北偏东45°），以40千米/小时的速度匀速移动，在距离台风中心50千米的区域内会受到台风的影响，在点O的北偏东15°方向，距离80千米的地方有一城市B，问：B市是否会受到此台风的影响？若受到影响，请求出受到影响的时间；若不受到影响，请说明理由．【点睛】此题考查了解直角三角形的应用—方向角问题以及勾股定理的应用．此题难度适中，注意掌握数形结合思想的应用，能从实际问题中整理出直角三角形是解答本题的关键．7．（2022·江苏苏州·九年级期中）一种拉杆式旅行箱的示意图如图所示，箱体长50cm AB =，拉杆最大伸长距离30cm BC =，（点A 、B 、C 在同一条直线上），在箱体的底端装有一圆形滚轮A e ，A e 与水平地面切于点D ，AE DN ∥，某一时刻，点B 距离水平地面40cm ，点C 距离水平地面61cm ．(1)求圆形滚轮的半径AD 的长；(2)当人的手自然下垂拉旅行箱时，人感觉较为舒服，已知某人的手自然下垂在点C 处且拉杆达到最大延伸距离时，点C 距离水平地面66.6cm ，求此时拉杆箱与水平面AE 所成角CAE Ð的大小（精确到1°，参考数据：sin500.77°»，cos500.64°»，tan50 1.19°»）．【答案】(1)5cmAD =(2)50CAE °Ð=【分析】（1）作BH AF ^于点G ，交DM 于点H ，则ABG ACF ∽V V ，设圆形滚轮的半径AD 的长是cm x ，根据相似三角形的对应边的比相等，即可列方程求得x 的值；（2）根据题意求得CF 的长，在Rt ACF V 中，求得sin CAE Ð，即可求得CAE Ð的度数．【详解】（1）解：设圆形滚轮的半径AD 的长是cm x ，作BH AE ^于点G ，交DM 于点H ，则BG CF ∥，∴ABG ACF ∽V V ，∴BG AB CF AC=，即4050615030x x -=-+，8．（2022·江苏苏州·九年级期中）如图，水坝的横截面是梯形()DC AB ABCD ∥，迎水坡BC 的坡角a 为30°，背水坡AD 的坡度i 为1:1.2，坝项宽 2.5DC =米，坝高5米．求：(1)坝底宽AB 的长（结果保留根号）；(2)在上题中，为了提高堤坝的防洪能力，市防汛指挥部决定加固堤坝，要求坝顶CD 加宽0.5米，背水坡AD 的坡度改为1:1.4，求横截面增加的面积（结果保留根号）。

专题08《三角函数的实际应用》题型一、利用仰角和俯视解决问题【例1】如图为放置在水平桌面上的台灯的平面示意图，灯臂AO长为40cm，与水平面所形成的夹角∠OAM为75°．由光源O射出的边缘光线OC，OB与水平面所形成的夹角∠OCA，∠OBA分别为90°和30°，求该台灯照亮水平面的宽度BC（不考虑其他因素，结果精确到0.1cm．温馨提示：sin75°≈0.97，cos75°≈0.26，）．【变式1-1】小明在楼高AB＝15米的楼顶A处测得一电视塔底部C的俯角为31°，测得塔顶D的仰角为52°，求楼顶A到塔顶D的距离（结果保留整数）．（参考数据：sin31°＝0.52，cos31°＝0.86，tan31°＝0.80，sin52°＝0.79，cos52°＝0.62，tan52°＝1.28）【变式1-2】如图，C地在A地的正东方向，因有大山阻隔，由A地到C地需绕行B地．已知B地位于A地北偏东67°方向，距离A地520km，C地位于B地南偏东30°方向．若打通穿山隧道，建成两地直达高铁，求A地到C地之间高铁线路的长．（结果保留整数）（参考数据：sin67°≈，cos67°≈，tan67°≈，≈1.73）【变式1-3】如图，两幢建筑物AB和CD，AB⊥BD，CD⊥BD，AB＝15m，CD＝20m．AB 和CD之间有一景观池，小双在A点测得池中喷泉处E点的俯角为42°，在C点测得E点的俯角为45°，点B、E、D在同一直线上．求两幢建筑物之间的距离BD．（结果精确到0.1m）【参考数据：sin42°＝0.67，cos42°＝0.74，tan42°＝0.90】【例2】如图，小明想测山高和索道的长度．他在B处仰望山顶A，测得仰角∠B＝31°，再往山的方向（水平方向）前进80m至索道口C处，沿索道方向仰望山顶，测得仰角∠ACE ＝39°．（1）求这座山的高度（小明的身高忽略不计）；（2）求索道AC的长（结果精确到0.1m）．（参考数据：tan31°≈，sin31°≈，tan39°≈，sin39°≈）【变式2-1】为了测量竖直旗杆AB的高度，某综合实践小组在地面D处竖直放置标杆CD，并在地面上水平放置一个平面镜E，使得B，E，D在同一水平线上（如图所示）．该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A（此时∠AEB＝∠FED），在F处测得旗杆顶A 的仰角为45°，平面镜E的俯角为67°，测得FD＝2.4米．求旗杆AB的高度约为多少米？（结果保留整数，参考数据：sin67°≈，cos67°≈，tan67°≈）【变式2-2】如图，为了测量山顶铁塔AE的高，小明在27m高的楼CD底部D测得塔顶A的仰角为45°，在楼顶C测得塔顶A的仰角36°52′．已知山高BE为56m，楼的底部D 与山脚在同一水平线上，求该铁塔的高AE．（参考数据：sin36°52′≈0.60，tan36°52′≈0.75）【变式2-3】某公园的人工湖边上有一座假山，假山顶上有一竖起的建筑物CD，高为10米，数学小组为了测量假山的高度DE，在公园找了一水平地面，在A处测得建筑物点D（即山顶）的仰角为35°，沿水平方向前进20米到达B点，测得建筑物顶部C点的仰角为45°，求假山的高度DE．（结果精确到1米，参考数据：sin35°≈，cos35°≈，tan35°≈）题型二、方位角的应用【例1】钓鱼岛自古以来就是我国的神圣领土，为维护国家主权和海洋权利，我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理．如图，某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A 、B ，B 船在A 船的正东方向，且两船保持20海里的距离，某一时刻两海监船同时测得在A 的东北方向，B 的北偏东15°方向有一我国渔政执法船C ，求此时船C 与船B 的距离是多少．（结果保留根号）【变式1-1】如图，某旅游景区为方便游客，修建了一条东西走向的木栈道AB ，栈道AB 与景区道路CD 平行．在C 处测得栈道一端A 位于北偏西42︒方向，在D 处测得栈道另一端B 位于北偏西32︒方向．已知120CD m =，80BD m =，求木栈道AB 的长度（结果保留整数）．（参考数据：17sin 3232︒≈，17cos3220︒≈，5tan 328︒≈，27sin 4240︒≈，3cos 424︒≈，9tan 42)10︒≈【变式1-2】如图，位于A 处的海上救援中心获悉：在其北偏东68︒方向的B 处有一艘渔船遇险，在原地等待营救．该中心立即把消息告知在其北偏东30︒且距离A 点20海里的C 处救生船，此时，遇险船在救生船的正东方向B 处，现救生船沿着航线CB 前往B 处救援，求救生船到达B 处行驶的距离？（参考数据：sin 680.90︒≈，cos680.36︒≈，tan 68 2.50︒≈，1.7)≈【例2】我国北斗导航装备的不断更新，极大方便人们的出行．某中学从A 地出发，组织学生利用导航到B 、C 两个地区进行研学考察活动，出发时，发现C 地恰好在A 地正北方向，且距离A 地15.3千米．但是导航显示路线应沿北偏东45°方同走到B 地，再沿北偏西37°方向走一段距离才能到达C地，求B，C两地的距离（精确到1千米）．（参考数据sin37°≈0.6，cos37°≈0.8，tan37°≈0.7）【变式2-1】某区域平面示意图如图，点O在河的一侧，AC和BC表示两条互相垂直的公路．甲勘测员在A处测得点O位于北偏东45°，乙勘测员在B处测得点O位于南偏西73.7°，测得AC＝840m，BC＝500m．请求出点O到BC的距离．参考数据：sin73.7°≈，cos73.7°≈，tan73.7°≈【变式2-2】码头A、B位于东西走向的河岸线l上，一游轮在P处测得码头A在其北偏东70°，游轮向东航行10分钟后到达Q处，此时测得码头B在其北偏东35°．已知游轮的速度为30千米/小时，两码头A、B相距2千米．（1）求点P到河岸线l的距离；（2）若该游轮按原速度从点Q驶向码头B，则它至少需要多长时间才能到达码头B？（参考数据：sin35°≈，cos35°≈，tan35°≈，sin70°≈，cos70°≈，tan70°≈）【变式2-3】海岛A 的周围8 n mile 内有暗礁，渔船跟踪鱼群由西向东航行，在点B 处测得海岛A 位于北偏东67︒，航行12n mlie 到达C 点，又测得小岛A 在北偏东45︒方向上．如果渔船不改变航线继续向东航行，那么它有没有触礁的危险？请说明理由．（参考数据：12sin 6713︒≈，5cos 6713︒，12tan 67)5︒≈题型三、综合类【例1】如图，马路的两边CF ，DE 互相平行，线段CD 为人行横道，马路两侧的A ，B 两点分别表示车站和超市．CD 与AB 所在直线互相平行，且都与马路的两边垂直，马路宽20米，A ，B 相距62米，∠A ＝67°，∠B ＝37°．（1）求CD 与AB 之间的距离；（2）某人从车站A 出发，沿折线A →D →C →B 去超市B ．求他沿折线A →D →C →B 到达超市比直接横穿马路多走多少米．（参考数据：sin67°≈，cos67°≈，tan67°≈，sin37°≈，cos37°≈，tan37°≈）【变式1-1】如图，某学校教学楼AB的后面有一建筑物CD，在距离CD正后方28米的观测点P处，以22︒的仰角测得建筑物的顶端C恰好挡住教学楼的顶端A，而在建筑物CD 上距离地面2米高的E处，测的教学楼的顶端A的仰角为45︒，求教学楼AB的高度（结果保留整数，2 tan22)5︒≈．【变式1-2】如图，校园内有两幢高度相同的教学楼AB，CD，大楼的底部B，D在同一平面上，两幢楼之间的距离BD长为24米，小明在点E（B，E，D在一条直线上）处测得教学楼AB顶部的仰角为45°，然后沿EB方向前进8米到达点G处，测得教学楼CD顶部的仰角为30°．已知小明的两个观测点F，H距离地面的高度均为1.6米，求教学楼AB的高度AB长．（精确到0.1米）参考值：≈1.41，≈1.73．【变式1-3】在一次综合实践课上，同学们为教室窗户设计一个遮阳篷，小明同学绘制的设计图如图所示，其中AB表示窗户，且AB＝2米，BCD表示直角遮阳蓬，已知当地一年中正午时刻太阳光与水平线CD的最小夹角∠PDN＝18.6°，最大夹角∠MDN＝64.5°请你根据以上数据，帮助小明同学计算出遮阳篷中CD的长是多少米？（结果精确到0.1）（参考数据：sin18.6°≈0.32，tan18.6°≈0.34，sin64.5°≈0.90，tan64.5°≈2.1）【变式1-4】如图是某斜拉桥引申出的部分平面图，AE，CD是两条拉索，其中拉索CD与水平桥面BE的夹角为72°，其底端与立柱AB底端的距离BD为4米，两条拉索顶端距离AC为2米，若要使拉索AE与水平桥面的夹角为35°，请计算拉索AE的长．（结果精确到0.1米）（参考数据：sin35°≈，cos35°≈，tan35°≈，sin72°≈，cos72°≈，tan72°≈）【变式1-5】2018年2月17日上午10点34分，我国自主研制的第二架C919大型客机在上海浦东国际机场进行首次飞行，这意味着C919大型客机逐步拉开全面试验试飞的新征程．这大大激发了同学们对航空科技的兴趣，如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸，图中AB∥CD，AM∥BN∥ED，AE⊥DE，请根据图中数据，求出线段BE和CD的长．（sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，结果保留小数点后一位）【变式1-6】如图，在一条河流的两岸分别有A，B，C，D四棵景观树，已知AB∥CD，某数学活动小组测得∠DAB＝45°，∠CBE＝73°，AB＝10m，CD＝30m，请计算这条河的宽度．（参考数据：sin73°≈，cos73°≈，tan73°≈）【课堂练习】1、如图所示，小河中学九年级数学活动小组选定测量学校前面小河对岸大树BC的高度，他们在斜坡上D处测得大树顶端B的仰角是30°，朝大树方向下坡走6米到达坡底A处，在A处测得大树顶端B的仰角是48°．若斜坡FA的坡比i＝1：，求大树的高度．（结果保留整数，参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11，≈1.73）2、小明家所在居民楼的对面有一座大厦AB，AB＝80米，为测量这座居民楼与大厦之间的距离，小明从自己家的窗户C处测得大厦顶部A的仰角为37°，大厦底部B的俯角为48°．求小明家所在居民楼与大厦的距离CD的长度．（结果保留整数）（参考数据：）3、若商场为方便消费者购物，准备将原来的阶梯式自动扶梯改造成斜坡式动扶梯，如图所示，已知原阶梯式自动扶梯AB长为10m，扶梯AB的坡度i为1：．改造后的斜坡式动扶梯的坡角∠ACB为15°，请你计算改造后的斜坡式自动扶梯AC的长度．（结果精确到0.1m．参考数据：sin15°≈0.26，cos15°≈0.97，tanl5°≈0.27）4、共享单车为人们的生活带来了极大的便利．如图，一辆单车放在水平的地面上，车把头下方A处与坐垫下方B处在平行于地面的水平线上，A，B之间的距离为49cm，现测得AC，BC与AB的夹角分别为45°，68°．若点C到地面的距离CD为28cm，坐垫中轴E处与点B的距离BE为5cm，求点E到地面的距离．（结果保留一位小数，参考数据：sin68°≈0.93，cos68°≈0.37，tan68°≈2.50）。

初中数学三角函数计算及应用题
三角函数是初中数学中一个重要的概念，它在解决实际问题中有着广泛的应用。

下面我将为你提供一些关于三角函数的计算和应用题。

1. 计算题
(1) 已知sin(30°) = 1/2，那么sin(150°) = _______。

(2) 若tan(45°) = 1，则cos(60°) = _______。

(3) 已知cos(60°) = 1/2，则sin(120°) = _______。

2. 应用题
(1) 一座塔的高度为 h 米，太阳光与水平面的夹角为α，则塔在太阳光下的影子长度为多少？
(2) 在直角三角形中，一个锐角为30°，其对边长为3，求这个直角三角形的斜边长。

(3) 一辆汽车以速度 v 向南行驶，遇到一个障碍物后向西行驶了45°，如果汽车行驶的距离为 d 米，那么它转向后行驶的距离是多少？。

三角函数应用专项练习题(经典)1. 问题描述本文档收集了一些经典的三角函数应用练题，帮助学生强化对三角函数的理解和应用能力。

这些练题包括求解三角函数的值、求解三角函数方程、求解三角函数不等式等。

每个问题都提供了解题思路和详细步骤，供学生参考。

2. 练题2.1 求解三角函数的值2.1.1 题目一已知角A为第一象限角，且sin A = 0.5，求cos A的值。

2.1.2 题目二已知角B为第二象限角，且tan B = -√3，求sin B的值。

2.2 求解三角函数方程2.2.1 题目三解方程sin x = 0.8，在区间[0, 2π]内。

2.2.2 题目四解方程2cos^2 x - 3 = 0，在区间[-π, π]内。

2.3 求解三角函数不等式2.3.1 题目五求解不等式sin x - cos x ≤ 0，在区间[-π/2, π/2]内。

2.3.2 题目六求解不等式tan^2 x - 2tan x + 1 ≥ 0，在区间[-π, π]内。

3. 解答和步骤3.1 求解三角函数的值3.1.1 题目一由sin A = 0.5可知，角A的对边为0.5，斜边假设为1。

根据勾股定理，可以求得角A的邻边为√(1^2 - 0.5^2) = √(1 - 0.25) =√0.75 = √(3/4) = √3/2。

由于角A为第一象限角，邻边为正数。

所以cos A = √3/2。

3.1.2 题目二由tan B = -√3可知，角B的对边为-√3，邻边假设为1。

根据勾股定理，可以求得角B的斜边为√(1^2 + (-√3)^2) = √(1 + 3) = √4 = 2。

由于角B为第二象限角，邻边为负数。

所以sin B = -√3/2。

3.2 求解三角函数方程3.2.1 题目三解方程sin x = 0.8，可以通过求逆函数arcsin来得到解。

使用计算器可以得到arcsin 0.8 ≈ 0.927。

因为arcsin的定义域是[-π/2, π/2]，所以解法中要考虑解在这个区间的情况。

初中三角函数的应用例题1.一座山峰高度为1800米，从山脚测得与山顶的夹角为30°，求山脚到山顶的实际水平距离。

解：设山脚到山顶的水平距离为x，则根据三角函数的定义，有tan30°=1800/x。

将30°转化为弧度制，即tan(π/6)=1800/x，解得x=1800/(tan(π/6)) ≈ 3600米。

所以山脚到山顶的实际水平距离约为3600米。

2.一条船从港口出发，先顺时针航行90°，然后逆时针航行120°，最后顺时针航行150°，求船的最终航向与出发港口到最终位置的直线之间的夹角。

解：根据题意，船的最终航向与出发港口到最终位置的直线之间的夹角等于船的顺时针航行角度减去船的逆时针航行角度，即90°-120°+150°=120°。

所以船的最终航向与出发港口到最终位置的直线之间的夹角为120°。

3.一个轮半径为40厘米的车轮以每秒10米的速度匀速滚动，求车轮的角速度。

解：车轮每滚动一周，车轮上的任意一点都绕轮心旋转360°，所以车轮的角速度是360°/一周所需要的时间。

滚动一周的时间可以通过速度和距离的关系求得，即一周所需时间为2πr/v，其中r为半径，v为速度。

所以车轮的角速度为360°/(2πr/v)=(360°v)/(2πr)。

代入半径r=40厘米和速度v=10米/秒，计算可得车轮的角速度约为(360°×10米/秒)/(2π×40厘米)≈0.90弧度/秒。

4.一架飞机从A地飞往B地，两地相距1200公里。

飞机的地速为400千米/小时，假设直飞过程中风速与飞机速度方向相反，风速为120公里/小时，求飞机的实际航速和方向。

解：设飞机的实际航速为v，飞机速度与风速的夹角为θ。

根据三角函数的定义，有cosθ=(400-120)/v。

专题41 三角函数的应用1.某人的血压满足函数关系式f (t )＝24sin160πt ＋110，其中，f (t )为血压，t 为时间，则此人每分钟心跳的次数是( ) A ．60 B ．70 C ．80 D ．90 【答案】C【解析】∵T ＝2π160π＝180，∴f ＝1T ＝80.2.为了研究钟表与三角函数的关系，建立如图所示的坐标系，设秒针尖位置p (x ，y ).若初始位置为P 0(√32，12)，当秒针从P 0(注此时t ＝0)正常开始走时，那么点P 的纵坐标y与时间t 的函数关系为( )A ．y ＝sin (π30t +π6)B ．y ＝sin (−π60t −π6) C ．y ＝sin (−π30t +π6) D ．y ＝sin (−π30t +π3)【答案】C【解析】由题意，函数的周期为T ＝60，∴ω＝2π60＝π30. 设函数解析式为y ＝sin (−π30t +φ)(因为秒针是顺时针走动)， ∵初始位置为P 0(√32，12)，∴t ＝0时，y ＝12， ∴sin φ＝12， ∴φ可取π6，∴函数解析式为y ＝sin (−π30t +π6). 3.如下图所示为一简谐振动的图象，则下列判断正确的是( )A ．该质点的振动周期为0.7sB ．该质点的振幅为5cmC ．该质点在0.1s 和0.5s 时振动速度最大D ．该质点在0.3s 和0.7s 时的加速度为零 【答案】B【解析】由题中图象可知振幅为5cm ，故选B.4.电流I (A)随时间t (s)变化的关系式是I ＝5sin(100πt ＋π3)，则当t ＝1200时，电流I 为( ) A ．5A B ．52AC ．2AD ．－5A 【答案】B【解析】把t ＝1200代入关系式得I ＝5sin(π2＋π3)＝5sin 56π＝56(A)，故选B.5.若近似认为月球绕地球公转与地球绕太阳公转的轨道在同一平面内，且均为正圆，又知这两种转动同向，如图所示，月相变化的周期为29.5天(如图是相继两次满月时，月、地、日相对位置的示意图).则月球绕地球一周所用的时间T 等于( )A．24.5天B．29.5天C．28.5天D．24天【答案】B【解析】由图知，地球从E1到E2用时29.5天，月球以月、地、日一条线重新回到月、地、日一条线，完成一个周期.6.如下图是一向右传播的绳波在某一时刻绳上各点的位置图，经过1周期后，乙点的位2置将如同()A．甲B．丙C．丁D．戊【答案】C周期，绳波正好从乙点传到【解析】因为绳波从乙点传到戊点正好是一个周期，经过12丁点.又在绳波的传播过程中，绳上各点只是上下振动，即纵坐标在变，横坐标不变，周期，乙点位置将移至它关于x轴的对称点处，即横坐标不变，纵坐标与图所以经过12中的丁点相同.7.如下图，质点P在半径为2的圆周上逆时针运动，其初始位置为P0(√2，－√2)，角速度为1，那么点P到x轴距离d关于时间t的函数图象大致为()A．B．C．D．【答案】C【解析】∵P0(√2，－√2)，∴∠P0Ox＝π4.按逆时针转时间t后得∠POP0＝t，∠POx＝t－π4，此时P点纵坐标为2sin(t－π4)，∴d＝2|sin(t－π4)|.当t＝0时，d＝√2，排除A、D；当t＝π4时，d＝0，排除B.8.如下图，一个大风车的半径为8米，它的最低点离地面2米，风车翼片静止时处于水平位置.风车启动后，按逆时针方向每12分钟旋转一周，则当启动17分钟时，风车翼片的端点P离地面距离为______米；风车翼片的端点离地面距离h(米)与启动时间t(分钟)之间的函数关系式为______.【答案】14h＝8sinπ6t＋10(t≥0)【解析】由题意，T＝12，∴ω＝π6，设f(t)＝A sin(ωt＋φ)＋B(A＞0)，则{A+B=18,−A+B=2,∴A＝8，B＝10，∵当t＝0时，f(t)＝10，∴φ＝0，∴f(t)＝8sinπ6t＋10，当t＝17时，f(17)＝14.9.如下图，一个水轮的半径为4m，水轮圆心O距离水面2m，已知水轮每分钟转动5圈，如果当水轮上点P从水中浮现时(图中点P0)开始计算时间.(1)将点P 距离水面的高度z (m)表示为时间t (s)的函数； (2)点P 第一次到达最高点大约需要多少时间？ 【答案】(1)如下图所示建立直角坐标系，设角φ(−π2<φ<0)是以Ox 为始边，OP 0为终边的角. OP 每秒钟内所转过的角为5×2π60＝π6，则OP 在时间t (s)内所转过的角为π6t .由题意可知水轮逆时针转动，得z ＝4sin (π6t +φ)＋2.当t ＝0时，z ＝0，得sin φ＝－12，即φ＝－π6.故所求的函数关系式为z ＝4sin (π6t −π6)＋2. (2)令z ＝4sin (π6t −π6)＋2＝6，得sin (π6t −π6)＝1，令π6t －π6＝π2，得t ＝4，故点P 第一次到达最高点大约需要4s.10.如下图，游乐场中的摩天轮匀速转动，每转一圈需要12分钟，其中圆心O 距离地面40.5米，半径为40米.如果你从最低处登上摩天轮，那么你与地面的距离将随时间的变化而变化，以你登上摩天轮的时刻开始计时，请解答下列问题：(1)求出你与地面的距离y (米)与时间t (分钟)的函数关系式； (2)当你第4次距离地面60.5米时，用了多长时间？【答案】(1)由已知可设y ＝40.5－40cos ωt ，t ≥0，由周期为12分钟可知，当t ＝6时，摩天轮第1次到达最高点，即此函数第1次取得最大值，所以6ω＝π，即ω＝π6. 所以y ＝40.5－40cos π6t (t ≥0).(2)设转第1圈时，第t 0分钟时距地面60.5米，由60.5＝40.5－40cos π6t 0，得cos π6t 0＝－12，所以π6t 0＝2π3或π6t 0＝4π3，解得t 0＝4或t 0＝8.所以t ＝8(分钟)时，第2次距地面60.5米，故第4次距离地面60.5米时，用了12＋8＝20(分钟).11.下表是芝加哥1951～1981年月平均气温(华氏).以月份为x 轴，x ＝月份－1，以平均气温为y 轴. (1)描出散点图.(2)用正弦曲线去拟合这些数据. (3)这个函数的周期是多少？ (4)估计这个正弦曲线的振幅A .(5)选择下面四个函数模型中哪一个最适合这些数据？ ①yA ＝cos (πx6)； ②y−46A＝cos (πx6)；③y−46−A＝cos (πx6)； ④y−26A＝sin (πx6).【答案】(1)(2)如下图所示.(3)1月份的气温最低为21.4,7月份的气温最高为73.0，根据图知，T2＝7－1＝6，∴T ＝12.(4)2A ＝最高气温－最低气温＝73.0－21.4＝51.6，∴A ＝25.8. (5)∵x ＝月份－1，∴不妨取x ＝2－1＝1，y ＝26.0， 代入①，得yA ＝26.025.8＞1≠cos π6，∴①错误； 代入②，得y−46A ＝26.0−4625.8＜0≠cos π6，∴②错误；同理④错误，∴③最适合这些数据.12.某港口水深y (m)是时间t (0≤t ≤24，单位：h)的函数，记作y ＝f (t )，下面是某日水深的数据.经长期观察，y ＝f (t )的曲线可近似地看成是函数y ＝A sin ωt ＋b 的图象. (1)试根据以上数据，求出函数y ＝f (t )的近似解析式；(2)一般情况下，船舶航行时，船底高出海底的距离为5m 或5m 以上时认为是安全的(船舶依靠时，船底只需不碰海底即可)，某船吃水深度(船底离水面的距离)为6.5m ，如果该船希望在同一天内安全进出港，那么它至多能在港内停留多长时间？(忽略进出港所需的时间)，【答案】(1)由已知数据，描出曲线如图.易知函数y ＝f (t )的周期T ＝12，振幅A ＝3，b ＝10，∴ω＝2πT ＝π6，∴y ＝3sin π6t ＋10. (2)由题意，该船进出港时，水深应不小于5＋6.5＝11.5(m)， 由y ≥11.5，得3sin π6t ＋10≥11.5， ∴sin π6t ≥12.①∵0≤t ≤24，∴0≤π6t ≤4π，② 由①②得π6≤π6t ≤5π6或13π6≤π6≤17π6. 化简得1≤t ≤5或13≤t ≤17.∴该船在1：00至5：00或13：00到17：00能安全进港，故该船可在当日凌晨1时进港，17时离港，它在港内至多停留16小时. 13.已知电流I 与时间t 的关系为I ＝A sin(ωt ＋φ).(1)如图所示的是I ＝A sin(ωt ＋φ)(ω＞0，|φ|＜π2)在一个周期内的图象，根据图中数据求I ＝A sin(ωt ＋φ)的解析式；(2)如果t 在任意一段1150秒的时间内，电流I ＝A sin(ωt ＋φ)都能取得最大值和最小值，那么ω的最小正整数值是多少？【答案】(1)由图知A ＝300，设t 1＝－1900，t 2＝1180， 则周期T ＝2(t 2－t 1)＝2(1180+1900)＝175，∴ω＝2πT ＝150π. 又当t ＝1180时，I ＝0，即sin (150π·1180+φ)＝0， 而|φ|＜π2，∴φ＝π6.故所求的解析式为I ＝300sin (150πt +π6). (2)依题意，周期T ≤1150，即2πω≤1150(ω＞0)，∴ω≥300π＞942，又ω∈N *，故所求最小正整数ω＝943.14.如图表示电流强度I 与时间t 的关系I ＝A sin(ωt ＋φ)在一个周期内的图象.(1)试根据图象写出I ＝A sin(ωt ＋φ)的解析式；(2)为了使I ＝A sin(ωt ＋φ)中l 在任意一段1100秒的时间内电流强度I 能同时取得最大值|A |与最小值－|A |，那么正常整数ω的最小值是多少？ 【答案】(1)由图知，A ＝300. 设t 0＝－1300，t 1＝1150，t 2＝160.∵T ＝t 2－t 0＝160－(－1300)＝150，∴ω＝2πT ＝100π. ∴ω·(－1300)＋φ＝2k π，k ∈Z ，∴φ＝π3＋2k π，k ∈Z ， ∴I ＝300sin(100πt ＋π3). (2)由题意知T ≤1100，即2πω≤1100， ∴ω≥200π，∴最小的正整数ω＝629.。

高中三角函数应用题1. 一架飞机以每小时500公里的速度直线飞行。

从地面上观察，飞机升高的角度为30度。

求飞机升高的速度。

解题思路：飞机升高的速度可以视为飞机在垂直方向上的速度分量，而飞机的速度是以每小时500公里的速度直线飞行，可以视为飞机在水平方向上的速度分量。

根据三角函数的性质，可以得到以下关系式：sin30° = 飞机升高速度 / 飞机速度sin30° = 飞机升高速度 / 500解得：飞机升高速度= 500 * sin30° = 250公里/小时所以飞机升高的速度为250公里/小时。

2. 一辆汽车以匀速行驶，速度为每小时60公里。

从地面上观察，汽车与地面的夹角为45度。

求汽车在水平方向上的速度和垂直方向上的速度。

解题思路：汽车在水平方向上的速度可以视为汽车的速度在水平方向上的分量，而汽车的速度是每小时60公里。

根据三角函数的性质，可以得到以下关系式：cos45° = 汽车在水平方向上的速度 / 60解得：汽车在水平方向上的速度= 60 * cos45° ≈ 42.42公里/小时汽车在垂直方向上的速度可以视为汽车的速度在垂直方向上的分量，根据三角函数的性质，可以得到以下关系式：sin45° = 汽车在垂直方向上的速度 / 60解得：汽车在垂直方向上的速度= 60 * sin45° ≈ 42.42公里/小时所以汽车在水平方向上的速度和垂直方向上的速度都约为42.42公里/小时。

3. 一根高度为20米的杆倾斜，与水平地面的夹角为60度。

从杆的顶端向底部看，底部与杆的夹角为30度。

求杆的实际高度。

解题思路：根据题意可知，底部与杆的夹角为30度，即底部与水平地面的夹角为90度-30度=60度。

所以整个杆与水平地面的夹角为60度+60度=120度。

根据三角函数的性质，可以得到以下关系式：tan120° = 杆的实际高度 / 20解得：杆的实际高度= 20 * tan120° ≈ -34.64米由于角度为120度时的tan值为负数，所以实际高度为-34.64米。

§5.3三角函数的图象、性质及应用根底篇固本夯基【根底集训】考点一三角函数的图象及其变换1.将函数y=sin(x+π6)图象上所有的点向左平移π4个单位长度,再把图象上各点的横坐标扩大到原来的2倍(纵坐标不变),那么所得图象的解析式为()A.y=sin(2x+5π12) B.y=sin(x2+5π12)C.y=sin(x2-π12) D.y=sin(x2+5π24)答案B2.如图是函数f(x)=Asin(ωx+φ)(ω>0,A>0)在区间[-π6,5π6]上的图象,为了得到这个图象,只需将g(x)=Acos ωx的图象()A.向右平移π6个单位长度 B.向右平移π12个单位长度C.向右平移π8个单位长度 D.向左平移π6个单位长度答案B3.将函数f(x)=2sin(4x-π3)的图象向左平移π6个单位,再把所有点的横坐标伸长到原来的2倍,得到函数y=g(x)的图象,那么以下关于函数y=g(x)的说法错误的选项是()A.最小正周期为πB.图象关于直线x=π12对称C.图象关于点(π12,0)对称 D.初相为π3答案C4.将函数f(x)=2sin(2x+φ)(φ<0)的图象向左平移π3个单位长度,得到偶函数g(x)的图象,那么φ的最大值是.答案-π6考点二三角函数的性质及其应用5.函数f(x)=(sin x+cos x)sin x,那么以下说法不正确的为()A.函数f(x)的最小正周期为πB.f(x)在[3π8,7π8]上单调递减C.f(x)的图象关于直线x=-π8对称D.将f(x)的图象向右平移π8个单位长度,再向下平移12个单位长度后会得到一个奇函数的图象答案D6.假设f(x)为偶函数,且在(0,π2)上满足:对任意x1<x2,都有f(x1)-f(x2)x1-x2>0,那么f(x)可以为()A. f(x)=cos(x+5π2) B. f(x)=|sin(π+x)| C. f(x)=-tan x D. f(x)=1-2cos22x答案B7.点P(32,-3√32)是函数y=Asin(ωx+φ)(ω>0)图象上的一个最低点,M,N是与点P相邻的两个最高点,假设∠MPN=60°,那么该函数的最小正周期是()A.3B.4C.5D.6答案D8.向量a=(cos x,0),b=(0,√3sin x),记函数f(x)=(a+b)2+√3sin 2x.(1)求函数f(x)的最小值及取得最小值时x的取值集合;(2)求函数f(x)的单调递增区间.解析(1)f(x)=(a+b)2+√3sin 2x=1+2sin2x+√3sin 2x=√3sin 2x-cos 2x+2=2sin(2x-π6)+2.当且仅当2x-π6=-π2+2kπ(k∈Z),即x=-π6+kπ(k∈Z)时, f(x)min=0,此时x的取值集合为{x|x=-π6+kπ,k∈Z}.(2)由-π2+2kπ≤2x-π6≤π2+2kπ(k∈Z),得-π6+kπ≤x≤π3+kπ(k∈Z),所以函数f(x)的单调递增区间为[-π6+kπ,π3+kπ](k∈Z).综合篇知能转换【综合集训】考法一关于三角函数图象的问题1.(2021课标Ⅱ,3,5分)函数y=Asin(ωx+φ)的局部图象如下列图,那么()A.y=2sin(2x-π6) B.y=2sin(2x-π3)C.y=2sin(x+π6) D.y=2sin(x+π3)答案A2.(2021河北衡水中学3月全国大联考,9)将曲线C1:y=2cos(2x-π6)上的点向右平移π6个单位长度,再将各点横坐标缩短为原来的12,纵坐标不变,得到曲线C2,那么C2的方程为()A.y=2sin 4xB.y=2sin(4x-π3)C.y=2sin xD.y=2sin(x-π3)答案A3.(2021届黑龙江哈师大附中9月月考,7)函数f(x)=sin(ωx+φ)(ω>0,|φ|<π2)的图象如下列图,为了得到g(x)=sin 3x的图象,只需将f(x)的图象()A.向右平移π4个单位长度 B.向左平移π4个单位长度C.向右平移π12个单位长度 D.向左平移π12个单位长度答案C4.(2021广东肇庆二模,14)函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的局部图象如下列图,那么f(-π3)的值是.答案-√62考法二三角函数的单调性问题5.(2021河南郑州一模,8)函数f(x)=sin(ωx+θ)(ω>0,-π2≤θ≤π2)的图象相邻的两个对称中心之间的距离为π2,假设将函数f(x)的图象向左平移π6个单位长度后得到偶函数g(x)的图象,那么函数f(x)的一个单调递减区间为()A.[-π3,π6] B.[π4,7π12]C.[0,π3] D.[π2,5π6]答案B6.(2021广东省际名校联考(二),15)将函数f(x)=1-2√3·cos2x-(sin x-cos x)2的图象向左平移π3个单位,得到函数y=g(x)的图象,假设x∈[-π2,π2],那么函数g(x)的单调递增区间是.答案[-5π12,π12]7.(2021届吉林白城通榆一中第一次月考,20)函数f(x)=2sin(ωx+φ)(ω>0,|φ|<π2)的图象与直线y=2两相邻交点之间的距离为π,且图象关于直线x=π3对称.(1)求y=f(x)的解析式;(2)先将函数f(x)的图象向左平移π6个单位,再将图象上所有点的横坐标伸长到原来的2倍,得到函数g(x)的图象.求g(x)的单调递增区间以及g(x)≥√3的x的取值范围.解析(1)由可得T=π,∴2πω=π,∴ω=2,又f(x)的图象关于直线x=π3对称,∴2×π3+φ=kπ+π2,k∈Z,∴φ=kπ-π6,k∈Z,∵|φ|<π2,∴φ=-π6.∴f(x)=2sin(2x-π6).(2)由(1)可得f(x)=2sin(2x-π6),∴g(x)=2sin(x+π6),由2kπ-π2≤x+π6≤2kπ+π2,k∈Z得2kπ-2π3≤x≤2kπ+π3,k∈Z,∴g(x)的单调递增区间为[2kπ-2π3,2kπ+π3],k∈Z.∵2sin(x+π6)≥√3,∴sin(x+π6)≥√32,∴2kπ+π3≤x+π6≤2kπ+2π3,k∈Z,∴2kπ+π6≤x≤2kπ+π2,k∈Z,∴g(x)≥√3的x的取值范围为{x|2kπ+π6≤x≤2kπ+π2,k∈Z}.考法三三角函数的奇偶性、周期性、对称性的有关问题8.(2021届湖南长沙一中第一次月考,9)将函数f(x)=2sin(2x-π6)-1的图象向左平移π6个单位长度得到函数g(x)的图象,那么以下说法正确的选项是()A.函数g(x)的最小正周期是π2B.函数g(x)的图象关于直线x=-π12对称C.函数g(x)在(π6,π2)上单调递减D.函数g(x)在(0,π6)上的最大值是1 答案C9.(2021河南六市第一次联考,5)函数f(x)=2sinωx+π6(ω>0)的图象与函数g(x)=cos(2x+φ)(|φ|<π2)的图象的对称中心完全相同,那么φ为()A.π6B.-π6C.π3D.-π3答案D10.(2021届四川绵阳南山中学9月月考,18)函数f(x)=cos2ωx+√3sin ωxcosωx(ω>0)的最小正周期为π.(1)求f(23π)的值;(2)求函数f(x)的单调区间及其图象的对称轴方程.解析(1)f(x)=cos2ωx+√3sin ωxcosωx=1+cos2ωx2+√32sin 2ωx=12cos 2ωx+√32sin 2ωx+12=sin(2ωx+π6)+12.∵f(x)的最小正周期为π,ω>0,∴2π2ω=π,∴ω=1.∴f(x)=sin(2x+π6)+12.∴f(23π)=sin(4π3+π6)+12=sin 3π2+12=-1+12=-12.(2)因为y=sin x的单调增区间为[-π2+2kπ,π2+2kπ],k∈Z,单调减区间为[π2+2kπ,3π2+2kπ],k∈Z,所以由-π2+2kπ≤2x+π6≤π2+2kπ,k∈Z,得-π3+kπ≤x≤π6+kπ,k∈Z.由π2+2kπ≤2x+π6≤3π2+2kπ,k∈Z,得π6+kπ≤x≤2π3+kπ,k∈Z.∴f(x)的单调增区间为[-π3+kπ,π6+kπ],k∈Z,单调减区间为[π6+kπ,2π3+kπ],k∈Z.∵y=sin x图象的对称轴为x=kπ+π2,k∈Z,∴2x+π6=π2+kπ,k∈Z.∴f(x)图象的对称轴方程为x=π6+kπ2,k∈Z.考法四三角函数的最值11.(2021山西3月质检,7)将函数f(x)=sin x的图象向右平移π4个单位长度后得到函数y=g(x)的图象,那么函数y=f(x)·g(x)的最大值为()A.2+√24B.2-√24C.1D.12答案 A12.(2021湖北武昌调研,8)函数y=cos 2x+2sin x 的最大值为( ) A.34B.1C.32D.2 答案 C【五年高考】考点一 三角函数的图象及其变换1.(2021课标Ⅰ,9,5分)曲线C 1:y=cos x,C 2:y=sin (2x +2π3),那么下面结论正确的选项是( )A.把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2 B.把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 2 C.把C 1上各点的横坐标缩短到原来的12,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2 D.把C 1上各点的横坐标缩短到原来的12,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 2 答案 D2.(2021天津,6,5分)将函数y=sin (2x +π5)的图象向右平移π10个单位长度,所得图象对应的函数( ) A.在区间[3π4,5π4]上单调递增 B.在区间[3π4,π]上单调递减 C.在区间[5π4,3π2]上单调递增 D.在区间[3π2,2π]上单调递减 答案 A3.(2021北京,7,5分)将函数y=sin (2x -π3)图象上的点P (π4,t)向左平移s(s>0)个单位长度得到点P'.假设P'位于函数y=sin 2x 的图象上,那么( )A.t=12,s 的最小值为π6B.t=√32,s 的最小值为π6C.t=12,s 的最小值为π3D.t=√32,s 的最小值为π3答案 A4.(2021课标Ⅲ,14,5分)函数y=sin x-√3cos x 的图象可由函数y=sin x+√3cos x 的图象至少向右平移 个单位长度得到. 答案23π 5.(2021江苏,9,5分)定义在区间[0,3π]上的函数y=sin 2x 的图象与y=cos x 的图象的交点个数是 . 答案 7考点二 三角函数的性质及其应用6.(2021山东,7,5分)函数f(x)=(√3sin x+cos x)(√3cos x-sin x)的最小正周期是()A.π2B.π C.3π2D.2π答案B7.(2021课标Ⅱ,9,5分)以下函数中,以π2为周期且在区间(π4,π2)单调递增的是()A. f(x)=|cos 2x|B. f(x)=|sin 2x|C. f(x)=cos|x|D. f(x)=sin|x|答案A8.(2021课标Ⅲ,12,5分)设函数f(x)=sin(ωx+π5)(ω>0),f(x)在[0,2π]有且仅有5个零点.下述四个结论:①f(x)在(0,2π)有且仅有3个极大值点②f(x)在(0,2π)有且仅有2个极小值点③f(x)在(0,π10)单调递增④ω的取值范围是[125,29 10)其中所有正确结论的编号是()A.①④B.②③C.①②③D.①③④答案D9.(2021课标Ⅰ,11,5分)关于函数f(x)=sin|x|+|sin x|有下述四个结论:① f(x)是偶函数② f(x)在区间(π2,π)单调递增③ f(x)在[-π,π]有4个零点④ f(x)的最大值为2其中所有正确结论的编号是()A.①②④B.②④C.①④D.①③答案C10.(2021课标Ⅱ,10,5分)假设f(x)=cos x-sin x在[-a,a]是减函数,那么a的最大值是()A.π4B.π2C.3π4D.π答案A11.(2021课标Ⅱ,7,5分)假设将函数y=2sin 2x的图象向左平移π12个单位长度,那么平移后图象的对称轴为()A.x=kπ2-π6(k∈Z) B.x=kπ2+π6(k∈Z)C.x=kπ2-π12(k∈Z) D.x=kπ2+π12(k∈Z)答案B12.(2021课标Ⅰ,8,5分)函数f(x)=cos(ωx+φ)的局部图象如下列图,那么f(x)的单调递减区间为()A.(kπ-14,kπ+34),k ∈ZB.(2π-14,2kπ+34),k ∈Z C.(k -14,k +34),k ∈Z D.(2k -14,2k +34),k ∈Z 答案 D13.(2021课标Ⅰ,12,5分)函数f(x)=sin(ωx+φ)(ω>0,|φ|≤π2),x=-π4为f(x)的零点,x=π4为y=f(x)图象的对称轴,且f(x)在(π18,5π36)单调,那么ω的最大值为( )A.11B.9C.7D.5 答案 B14.(2021天津,7,5分)函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)是奇函数,将y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为g(x).假设g(x)的最小正周期为2π,且g (π4)=√2,那么f (3π8)=( ) A.-2 B.-√2 C.√2 D.2 答案 C15.(2021上海,15,5分)ω∈R ,函数f(x)=(x-6)2·sin(ωx),存在常数a ∈R ,使得f(x+a)为偶函数,那么ω的值可能为( ) A.π2 B.π3 C.π4 D.π5答案 C16.(2021天津,7,5分)设函数f(x)=2sin(ωx+φ),x∈R ,其中ω>0,|φ|<π.假设f (5π8)=2, f (11π8)=0,且f(x)的最小正周期大于2π,那么( )A.ω=23,φ=π12B.ω=23,φ=-11π12 C.ω=13,φ=-11π24D.ω=13,φ=7π24答案 A17.(2021课标Ⅱ,14,5分)函数f(x)=sin 2x+√3cos x-34(x ∈[0,π2])的最大值是 .答案 118.(2021北京,9,5分)函数f(x)=sin 22x 的最小正周期是 . 答案 π219.(2021北京,11,5分)设函数f(x)=cos (ωx -π6)(ω>0).假设f(x)≤f (π4)对任意的实数x 都成立,那么ω的最小值为 . 答案2320.(2021浙江,18,14分)设函数f(x)=sin x,x ∈R . (1)θ∈[0,2π),函数f(x+θ)是偶函数,求θ的值; (2)求函数y=[f (x +π12)]2+[f (x +π4)]2的值域.解析 此题主要考查三角函数及其恒等变换等根底知识,同时考查运算求解能力.考查的数学素养是逻辑推理及数学运算,考查了化归与转化思想.(1)因为f(x+θ)=sin(x+θ)是偶函数,所以,对任意实数x 都有sin(x+θ)=sin(-x+θ),即sin xcos θ+cos xsin θ=-sin xcos θ+cos xsin θ,故2sin xcos θ=0,所以cos θ=0.又θ∈[0,2π),因此θ=π2或3π2.(2)y=[f(x+π12)]2+[f(x+π4)]2=sin2(x+π12)+sin2(x+π4)=1-cos(2x+π6)2+1-cos(2x+π2)2=1-12(√32cos2x-32sin2x)=1-√32cos(2x+π3).因此,函数的值域是[1-√32,1+√32].思路分析(1)根据偶函数的定义,知f(-x+θ)=f(x+θ)恒成立,利用三角恒等变换,得出cos θ=0,从而求出θ的值.(2)将函数解析式化简为y=Asin(ωx+φ)+B或y=Acos(ωx+φ)+B的形式,利用三角函数的性质求值域.21.(2021浙江,18,14分)函数f(x)=sin2x-cos2x-2√3sin xcos x(x∈R).(1)求f(2π3)的值;(2)求f(x)的最小正周期及单调递增区间.解析此题主要考查三角函数的性质及其变换等根底知识,同时考查运算求解能力.(1)由sin2π3=√32,cos2π3=-12,得f(2π3)=(√32)2-(-12)2-2√3×√32×(-12)=2.(2)由cos 2x=cos2x-sin2x与sin 2x=2sin xcos x得f(x)=-cos 2x-√3sin 2x=-2sin(2x+π6).所以f(x)的最小正周期是π.由正弦函数的性质得π2+2kπ≤2x+π6≤3π2+2kπ,k∈Z,解得π6+kπ≤x≤2π3+kπ,k∈Z.所以f(x)的单调递增区间是[π6+kπ,2π3+kπ](k∈Z).教师专用题组考点一三角函数的图象及其变换1.(2021四川,3,5分)为了得到函数y=sin(2x-π3)的图象,只需把函数y=sin 2x的图象上所有的点()A.向左平行移动π3个单位长度B.向右平行移动π3个单位长度C.向左平行移动π6个单位长度D.向右平行移动π6个单位长度答案D2.(2021湖南,9,5分)将函数f(x)=sin 2x的图象向右平移φ(0<φ<π2)个单位后得到函数g(x)的图象.假设对满足|f(x1)-g(x2)|=2的x1,x2,有|x1-x2|min=π3,那么φ=()A.5π12B.π3C.π4D.π6答案D3.(2021安徽,11,5分)假设将函数f(x)=sin(2x+π4)的图象向右平移φ个单位,所得图象关于y轴对称,那么φ的最小正值是.答案3π8考点二三角函数的性质及其应用4.(2021浙江,5,5分)设函数f(x)=sin2x+bsin x+c,那么f(x)的最小正周期()A.与b有关,且与c有关B.与b有关,但与c无关C.与b无关,且与c无关D.与b无关,但与c有关答案B5.(2021陕西,3,5分)如图,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin(π6x+φ)+k,据此函数可知,这段时间水深(单位:m)的最大值为()A.5B.6C.8D.10答案C6.(2021安徽,10,5分)函数f(x)=Asin(ωx+φ)(A,ω,φ均为正的常数)的最小正周期为π,当x=2π3时,函数f(x)取得最小值,那么以下结论正确的选项是()A. f(2)< f(-2)< f(0)B. f(0)< f(2)< f(-2)C. f(-2)< f(0)< f(2)D. f(2)< f(0)< f(-2)答案A7.(2021浙江,11,6分)函数f(x)=sin2x+sin xcos x+1的最小正周期是,单调递减区间是.答案π;[38π+kπ,78π+kπ](k∈Z)8.(2021江苏,16,14分)向量a=(cos x,sin x),b=(3,-√3),x∈[0,π].(1)假设a∥b,求x的值;(2)记f(x)=a·b,求f(x)的最大值和最小值以及对应的x的值.解析(1)因为a=(cos x,sin x),b=(3,-√3),a∥b,所以-√3cos x=3sin x.假设cos x=0,那么sin x=0,与sin2x+cos2x=1矛盾,故cos x≠0.于是tan x=-√33.又x∈[0,π],所以x=5π6.(2)f(x)=a·b=(cos x,sin x)·(3,-√3)=3cos x-√3sin x=2√3cos(x+π6).因为x ∈[0,π],所以x+π6∈[π6,7π6], 从而-1≤cos (x +π6)≤√32.于是,当x+π6=π6,即x=0时, f(x)取到最大值3; 当x+π6=π,即x=5π6时, f(x)取到最小值-2√3.9.(2021北京,15,13分)函数f(x)=√2sin x 2cos x 2-√2sin 2x2.(1)求f(x)的最小正周期;(2)求f(x)在区间[-π,0]上的最小值. 解析 (1)因为f(x)=√22sin x-√22(1-cos x)=sin (x +π4)-√22,所以f(x)的最小正周期为2π. (2)因为-π≤x ≤0,所以-3π4≤x+π4≤π4. 当x+π4=-π2,即x=-3π4时, f(x)取得最小值. 所以f(x)在区间[-π,0]上的最小值为f (-3π4)=-1-√22. 10.(2021天津,15,13分)函数f(x)=sin 2x-sin 2(x -π6),x ∈R . (1)求f(x)的最小正周期;(2)求f(x)在区间[-π3,π4]上的最大值和最小值. 解析 (1)由,有f(x)=1-cos2x 2-1-cos (2x -π3)2=12(12cos2x+√32sin2x)-12cos 2x=√34sin 2x-14cos 2x=12sin (2x -π6).所以, f(x)的最小正周期T=2π2=π.(2)因为f(x)在区间[-π3,-π6]上是减函数,在区间[-π6,π4]上是增函数, f (-π3)=-14, f (-π6)=-12, f (π4)=√34,所以, f(x)在区间[-π3,π4]上的最大值为√34,最小值为-12.11.(2021山东,16,12分)设f(x)=sin xcos x-cos 2(x +π4).(1)求f(x)的单调区间;(2)在锐角△ABC 中,角A,B,C 的对边分别为a,b,c.假设f (A2)=0,a=1,求△ABC 面积的最大值. 解析 (1)由题意知f(x)=sin2x 2-1+cos (2x+π2)2=sin2x 2-1-sin2x 2=sin 2x-12.由-π2+2kπ≤2x ≤π2+2kπ,k∈Z ,可得-π4+kπ≤x ≤π4+kπ,k∈Z ; 由π2+2kπ≤2x ≤3π2+2kπ,k∈Z ,可得π4+kπ≤x ≤3π4+kπ,k∈Z . 所以f(x)的单调递增区间是[-π4+kπ,π4+kπ](k ∈Z ); 单调递减区间是[π4+kπ,3π4+kπ](k ∈Z ). (2)由f (A 2)=sin A-12=0,得sin A=12, 由题意知A 为锐角,所以cos A=√32.由余弦定理a 2=b 2+c 2-2bccos A,可得1+√3bc=b 2+c 2≥2bc,即bc ≤2+√3,且当b=c 时等号成立.因此12bcsin A ≤2+√34. 所以△ABC 面积的最大值为2+√34. 评析 此题考查三角恒等变换,三角函数的图象与性质,以及解三角形等根底知识和根本方法,对运算能力有较高要求.属中等难度题.12.(2021重庆,18,13分)函数f(x)=sin π2-x ·sin x-√3cos 2x.(1)求f(x)的最小正周期和最大值; (2)讨论f(x)在[π6,2π3]上的单调性. 解析 (1)f(x)=sin (π2-x)sin x-√3cos 2x =cos xsin x-√32(1+cos 2x)=12sin 2x-√32cos 2x-√32=sin (2x -π3)-√32,因此f(x)的最小正周期为π,最大值为2-√32. (2)当x ∈[π6,2π3]时,0≤2x-π3≤π,从而当0≤2x-π3≤π2,即π6≤x ≤5π12时, f(x)单调递增,当π2≤2x-π3≤π,即5π12≤x ≤2π3时, f(x)单调递减. 综上可知, f(x)在[π6,5π12]上单调递增,在[5π12,2π3]上单调递减. 【三年模拟】一、单项选择题(每题5分,共45分)1.(2021届四川绵阳南山中学,5)要得到函数y=sin 2x+√3cos 2x(x ∈R )的图象,可将y=2sin 2x 的图象向左平移( ) A.π6个单位 B.π3个单位C.π4个单位 D.π12个单位答案A2.(2021届吉林白城通榆一中第一次月考,8)假设函数f(x)=cos 2ωx(ω>0)在区间[0,π3]上为减函数,在区间[π3,π2]上为增函数,那么ω=()A.3B.2C.32D.23答案C3.(2021届黑龙江大庆一中第一次月考,10)假设函数f(x)=sin(2x+φ)+b对任意实数x,都有f(x+π3)=f(-x), f(2π3)=-1,那么实数b的值为()A.-2或0B.0或1C.±1D.±2答案A4.(2021届黑龙江哈师大附中9月月考,11)函数f(x)=asin x-√3cos x图象的一条对称轴为直线x=5π6,且f(x1)·f(x2)=-4,那么|x1+x2|的最小值为()A.-π3B.0 C.π3D.2π3答案D5.(2021届宁夏银川一中第一次月考,6)函数f(x)=sin(2x+φ)(|φ|<π2)的图象向左平移π6个单位后关于y轴对称,那么函数f(x)在[0,π2]上的最小值为()A.-√32B.-12C.12D.√32答案B6.(2021届广西桂林十八中第一次月考,8)将函数y=sin(2x-π6)的图象向左平移π4个单位,所得函数图象的一条对称轴方程为()A.x=π3B.x=π6C.x=π12D.x=-π12答案C7.(2021届四川邻水实验学校第一次月考,5)函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的局部图象如下列图,将函数f(x)的图象向左平移π6个单位,得到函数g(x)的图象,那么当x∈[0,π]时,不等式g(x)<1的解集为()A.[0,π4] B.[7π12,π]C.[0,π4)∪(7π12,π] D.(π4,7π12)答案C8.(2021届吉林白城通榆一中第一次月考,5)将函数y=sin (x -π3)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移π3个单位,得到的图象对应的解析式是( ) A.y=sin 12x B.y=sin (12x -π2) C.y=sin (12x -π6) D.y=sin (2x -π6) 答案 C9.(2021届河南中原名校第二次质量考评)函数f(x)=sin (2x -π3),假设方程f(x)=13在(0,π)的根为x 1,x 2(x 1<x 2),那么sin(x 1-x 2)=( ) A.-2√23B.-√32C.-12D.-13答案 A二、多项选择题(每题5分,共15分)10.(改编题)函数f(x)=12cos x ·sin (x +π3),那么以下结论中错误的选项是( ) A. f(x)既是奇函数又是周期函数 B. f(x)的图象关于直线x=π12对称 C. f(x)的最大值为1D. f(x)在区间[0,π4]上单调递减 答案 ACD11.(改编题)以下选项正确的选项是( ) A.存在实数x,使sin x+cos x=π3B.假设α,β是锐角△ABC 的内角,那么sin α>cos βC.函数y=sin (23x -7π2)是偶函数 D.函数y=sin 2x 的图象向右平移π4个单位,得到y=sin (2x +π4)的图象 答案 ABC12.(改编题)函数f(x)=sin xsin (x +π3)-14的定义域为[m,n](m<n),值域为[-12,14],那么n-m 的值不可能是( ) A.5π12B.7π12C.3π4D.11π12 答案 CD三、填空题(每题5分,共15分)13.(2021届四川绵阳南山中学月考,15)函数y=Msin(ωx+φ)(M>0,ω>0,0<φ<π)的图象关于直线x=13对称.该函数的局部图象如下列图,AC=BC=√22,C=90°,那么f (12)的值为 .答案√3414.(2021届四川邻水实验学校第一次月考,15)将函数f(x)=cos x-√3sin x(x ∈R )的图象向左平移α(α>0)个单位长度后,所得到的图象关于原点对称,那么α的最小值是 . 答案π615.(2021届宁夏银川一中第一次月考,15)假设函数y=cos(x+φ)(-π≤φ≤π)的图象向左平移π3个单位后,与函数y=sin (x +π6)的图象重合,那么φ= . 答案 -2π3四、解答题(共45分)16.(2021届吉林白城通榆一中第一次月考,19)函数f(x)=Asin (ωx +π6)(A>0,ω>0)的局部图象如下列图. (1)求A,ω的值及f(x)的单调增区间; (2)求f(x)在区间[-π6,π4]上的最大值和最小值.解析 (1)由题图可得A=1,最小正周期T=2(2π3-π6)=π,∴ω=2πT=2. ∴f(x)=sin (2x +π6).由-π2+2kπ≤2x+π6≤π2+2kπ,k∈Z , 得-π3+kπ≤x ≤π6+kπ,k∈Z ,∴函数f(x)的单调递增区间为[-π3+kπ,π6+kπ],k ∈Z . (2)∵-π6≤x ≤π4,∴-π6≤2x+π6≤2π3,∴-12≤sin (2x +π6)≤1,∴函数f(x)在区间[-π6,π4]上的最大值为1,最小值为-12.17.(2021届宁夏银川一中第一次月考,17)函数f(x)=sin 2ωx+√3sin ωx·sin (ωx +π2)-1(ω>0)图象的相邻两条对称轴之间的距离为π2. (1)求ω的值;(2)当x ∈[-π12,π2]时,求函数f(x)的值域.解析 (1)f(x)=1-cos2ωx2+√3sin ωxcos ωx -1 =√32sin 2ωx -12cos 2ωx -12=sin (2ωx -π6)-12.由题意得函数f(x)的最小正周期为π, ∴2π2ω=π,解得ω=1,∴f(x)=sin (2x -π6). (2)∵x∈[-π12,π2],∴2x -π6∈[-π3,5π6],根据正弦函数的图象可得当2x-π6=π2,即x=π3时, f(x)=sin (2x -π6)取最大值1,当2x-π6=-π3,即x=-π12时, f(x)=sin (2x -π6)取最小值-√32,∴-12-√32≤sin (2x -π6)-12≤12,即当x ∈[-π12,π2]时,f(x)的值域为[-1+√32,12].18.(2021届黑龙江哈尔滨六中第一次调研,20)将函数y=sin x 的图象上所有点的横坐标缩短到原来的12(纵坐标不变),再将所得的图象向左平移π6个单位长度后得到函数f(x)的图象. (1)写出函数f(x)的解析式; (2)假设对任意x ∈[-π6,π12], f 2(x)-mf(x)-1≤0恒成立,求实数m 的取值范围;(3)求实数a 和正整数n,使F(x)=f(x)-a 在[0,nπ]上恰有2 019个零点.解析 (1)把函数y=sin x 的图象上所有点的横坐标缩短到原来的12(纵坐标不变)得y=sin 2x,再将所得的图象向左平移π6个单位得f(x)=sin (2x +π3)的图象, ∴f(x)=sin (2x +π3). (2)∵x∈[-π6,π12],∴2x+π3∈[0,π2]. ∴f(x)∈[0,1].令t=f(x),t ∈[0,1].那么g(t)=t 2-mt-1≤0恒成立,故有g(0)=-1≤0且g(1)=-m ≤0,∴m≥0.(3)∵F(x)=f(x)-a 在[0,nπ]上恰有2 019个零点,故f(x)的图象和直线y=a 在[0,nπ]上恰有2 019个交点. ①当a>1或a<-1时, f(x)的图象与直线y=a 在[0,nπ]上无交点.②当a=1或a=-1时, f(x)的图象与直线y=a 在[0,nπ]上恰有2 019个交点,那么n=2 019. ③当-1<a<√32或√32<a<1时, f(x)的图象和直线y=a 在[0,π]上恰有2个零点.∴f(x)的图象和直线y=a 在[0,nπ]上有偶数个交点,不会有2 019个交点. ④当a=√32时, f(x)的图象与直线y=a 在[0,π]上有3个交点.此时n=1 009才能使f(x)的图象和直线y=a 在[0,nπ]上有2 019个交点. 综上所述,当a=1或a=-1时,n=2 019,当a=√32时,n=1 009,符合题意.。

选择题: 1. 轮船航行到C 处测得小岛A的方向为北偏西27°，那么从A 观测此时C•处的方向为（ ）A ．南偏东27°B ．东偏西27°C ．南偏东73°D ．东偏西73°2. 在Rt △ABC 中，∠C=90°，BC=a ，AC=b ，且3a=4b ，则∠A 的度数是（ ）A ．°B ．°C ．53°13′D ．53°48′3. 如果坡角的余弦值为31010，那么坡度为（ ） A ．1：10 B ．3：10 C ．1：3 D ．3：14. 若等腰△ABC 的底边BC 上高为2，cotB=12，则△ABC 的周长为（ ） A ．2+5 B ．1+25 C ．2+25 D ．4+55. 每周一学校都要举行庄严的升国旗仪式，让我们体会到了国旗的神圣，某同学产生了用所学知识测量旗杆高度的想法，在地面距杆脚5米远的地方，•他用测倾器测得杆顶的仰角为α，且tan α=3，则杆高（不计测倾器高度）为（ ）A ．10mB ．12mC ．15mD ．20m6. 如图1所示，在锐角△ABC 中，BE ⊥AC ，∠ADE=∠C ，记△ADE 的面积为S 1，△ABC 的面积为S 2，则12S S =（ ） A ．sin 2A B ．cos 2A C ．tan 2A D ．cot 2A(1) (2) (3)7. 已知楼房AB 高50m ，•如图2所示，•电视收视塔塔基距楼房房基的水平距离BD•为50m ，塔高DC 为15033m ，则下列结论正确的是（ ） A ．由楼顶望塔顶仰角为60° B ．由楼顶望塔顶俯角为60°C ．由楼顶望塔顶仰角为30°D ．由楼顶望塔基俯角为30°8. 一树的上段CB 被风折断，树梢着地，树顶着地处B 与树根A 相距6m ，则原来的树高是（ ）（折断后树梢与地面成30°角）。

三角函数练习题一、选择题1. 已知角α的终边经过点P(3, 4)，则sinα的值为（）A. 3/5B. 4/5C. 4/5D. 3/52. 若cosθ = 1/2，且θ为第三象限角，则sinθ的值为（）A. √3/2B. √3/2C. 1/2D. 1/23. 已知tanα = 2，求cos2α的值为（）A. 1/5B. 3/5C. 3/5D. 1/54. 若sin^2α + cos^2α = 1，则下列等式成立的是（）A. sinα = cosαB. sinα= tanαC. cosα = cotαD. tanα = cotα二、填空题1. 已知sinα = 1/2，且α为第一象限角，则cosα = ______。

2. 若tanθ = √3，且θ为第四象限角，则sinθ = ______。

3. 已知cosβ = √2/2，且β为第二象限角，则tanβ =______。

4. 若sin^2α + cos^2α = 1，则sinαcosα = ______。

三、解答题1. 已知sinα = 3/5，求cosα的值。

2. 已知tanθ = 4/3，求sinθ和cosθ的值。

3. 已知cosβ = 1/2，求sinβ和tanβ的值。

4. 已知sin^2α + cos^2α = 1，证明：(1 cosα)/(1 + cosα) = sin^2α/(1 + cosα)。

5. 已知tanθ = √3，求sin2θ和cos2θ的值。

6. 已知sinα + cosα = 1，求sinα和cosα的值。

四、应用题1. 在直角三角形ABC中，∠C为直角，∠A的度数为30°，BC边长为6cm，求AB和AC的长度。

2. 一个物体从A点出发，沿直线向正北方向移动了100米后到达B点，然后转向正东方向移动了150米到达C点。

求物体从A点到C点的直线距离。

3. 在平面直角坐标系中，点P的坐标为(3, 4)，求点P到原点O的距离及点P与x轴的夹角。

三角函数与三角恒等式的应用练习题及解析练习题1：已知正弦函数sin(x)的定义域为[-π/2, π/2]，求使得sin(x) = 1/2的解集。

解析：根据正弦函数的性质，sin(x) = 1/2的解集是{x | x = π/6 + 2kπ （k为整数）}。

练习题2：已知余弦函数cos(x)的定义域为[0, π]，求使得cos(x) = -1/2的解集。

解析：根据余弦函数的性质，cos(x) = -1/2的解集是{x | x = 2π/3 + 2kπ （k为整数）}。

练习题3：已知正切函数tan(x)的定义域为(-π/2, π/2)，求使得tan(x) = 0的解集。

解析：根据正切函数的性质，tan(x) = 0的解集是{x | x = kπ （k为整数）}。

练习题4：已知正弦函数sin(x)的定义域为[-π/2, π/2]，求使得sin(x) = cos(x)的解集。

解析：利用三角恒等式sin^2(x) + cos^2(x) = 1，可得sin(x) = cos(x)的解集为{x | x = π/4 + kπ （k为整数）}。

练习题5：已知正弦函数sin(x)的定义域为[-π/2, π/2]，求使得sin^2(x) = 3/4的解集。

解析：利用三角恒等式sin^2(x) + cos^2(x) = 1，可得cos^2(x) = 1 - sin^2(x) = 1 - 3/4 = 1/4。

由于余弦函数的定义域也为[-π/2, π/2]，所以cos(x) = ±1/2。

因此，sin(x) = ±√(3/4) = ±√3/2。

根据正弦函数和余弦函数的定义域，求解sin^2(x) = 3/4，得解集为{x | x = π/3 + 2kπ （k为整数）, x = -π/3 + 2kπ （k为整数）}。

练习题6：已知正弦函数sin(x)的定义域为[-π/2, π/2]，求使得tan(x) = sin(x)的解集。

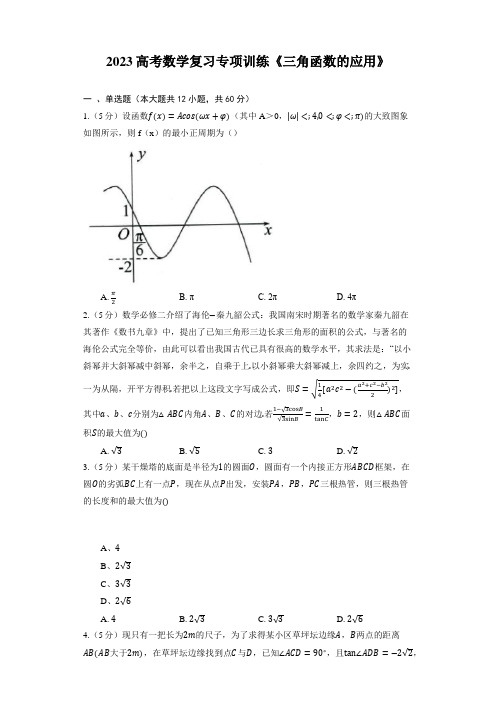
2023高考数学复习专项训练《三角函数的应用》一、单选题（本大题共12小题，共60分）1.（5分）设函数f(x)=Acos(ωx+φ)（其中A＞0，|ω|<;4,0<;φ<;π)的大致图象如图所示，则f（x）的最小正周期为（）A. π2B. πC. 2πD. 4π2.（5分）数学必修二介绍了海伦−秦九韶公式：我国南宋时期著名的数学家秦九韶在其著作《数书九章》中，提出了已知三角形三边长求三角形的面积的公式，与著名的海伦公式完全等价，由此可以看出我国古代已具有很高的数学水平，其求法是：“以小斜幂并大斜幂减中斜幂，余半之，自乘于上.以小斜幂乘大斜幂减上，余四约之，为实.一为从隔，开平方得积.若把以上这段文字写成公式，即S=√14[a2c2−(a2+c2−b22)2]，其中a、b、c分别为△ABC内角A、B、C的对边.若√3cosB√3sinB =1tanC，b=2，则△ABC面积S的最大值为()A. √3B. √5C. 3D. √23.（5分）某干燥塔的底面是半径为1的圆面O，圆面有一个内接正方形ABCD框架，在圆O的劣弧BC上有一点P，现在从点P出发，安装PA，PB，PC三根热管，则三根热管的长度和的最大值为()A、4B、2√3C、3√3D、2√6A. 4B. 2√3C. 3√3D. 2√64.（5分）现只有一把长为2m的尺子，为了求得某小区草坪坛边缘A，B两点的距离AB(AB大于2m)，在草坪坛边缘找到点C与D，已知∠ACD=90∘，且tan∠ADB=−2√2，测得AC=1.2m，CD=0.9m，BD=1m，则AB=()A. √373m B. √5m C. √172m D. 3√22m5.（5分）已知函数f（x）=Asin（ωx+φ）（A>;0,ω>;0,|φ|<;π2)在一个周期内的图象如图所示.若方程f（x）=m在区间[0，π]上有两个不同的实数解x1,x2，则x1+x2的值为（)A. π3B. 23π或43π C. 43π D. π3或43π6.（5分）设y=f(t)是某港口水的深度y(米)关于时间t(时)的函数，其中0⩽t⩽24.下表是该港口某一天从0时至24时记录的时间t与水深y的关系：经长期观观察，函数y=f(t)的图象可以近似地看成函数y=k+Asin(ωt+φ)的图象.在下面的函数中，最能近似表示表中数据间对应关系的函数是()A、y=12+3sinπ6t,t∈[0,24]B、y=12+3sin(π6t+π),t∈[0,24]C、y=12+3sinπ12t,t∈[0,24]D、y=12+3sin(π12t+π2),t∈[0,24]A. y=12+3sinπ6t,t∈[0,24]B. y=12+3sin(π6t+π),t∈[0,24]C. y=12+3sinπ12t,t∈[0,24]D. y=12+3sin(π12t+π2),t∈[0,24]7.（5分）泰山于1987年12月12日被列为世界文化与自然双重遗产，泰山及其周边坐落着许多古塔.某兴趣小组为了测量某古塔的高度，如图所示，在地面上一点A处测得塔顶B的仰角为60∘，在塔底C处测得A处的俯角为45∘.已知山岭高CD为256米，则塔高BC为()A. 256(√2−1)米B. 256(√3−1)米C. 256(√6−1)米D. 256(2√3−1)米8.（5分）为迎接校运动会的到来，学校决定在半径为20√2m，圆心角为π的扇形空地4OPQ内部修建一平行四边形观赛场地ABCD，如图所示，则观赛场地面积的最大值为( )A. 200m2B. 400(2−√2)m2C. 400(√3−1)m2D. 400(√2−1)m29.（5分）如图所示，单摆从某点开始来回摆动，离开平衡位置O的距离s（cm）和时)，那么单摆摆动一个周期所需的时间为间t（s）的函数关系式为s=6sin(2πt+π6（）A. 2πsB. πsC. 0.5sD. 1s10.（5分）小明在学完《解直角三角形》一章后，利用测角仪和校园旗杆的拉绳测量校园旗杆的高度，如图，旗杆PA的高度与拉绳PB的长度相等，小明先将PB拉到PB′的位置，测得∠PB′C=α(B′C为水平线)，测角仪B′D的高度为1米，则旗杆PA的高度为()A. 11+sin α米 B. 11−cos α米 C. 11−sin α米D. 11+cos α米11.（5分）瀑布是庐山的一大奇观，为了测量某个瀑布的实际高度，某同学设计了如下测量方案：有一段水平山道，且山道与瀑布不在同一平面内，瀑布底端与山道在同一平面内，可粗略认为瀑布与该水平山道所在平面垂直，在水平山道上A 点位置测得瀑布顶端仰角的正切值为32，沿山道继续走20m ，抵达B 点位置测得瀑布顶端的仰角为π3.已知该同学沿山道行进的方向与他第一次望向瀑布底端的方向所成角为π3，则该瀑布的高度约为()A. 60mB. 90mC. 108mD. 120m12.（5分）设y =f(t)是某港口水的深度y （米）关于时间t （时）的函数，其中0⩽t ⩽24，表格中是该港口某一天从0时至24时记录的时间t 与水深y 的关系：经长期观察，函数y =f(t)的图象可以近似地看成函数y =k +Asin(ωt +φ)的图象.下面的函数中，最能近似表示表中数据间对应关系的函数是（ ）A. y =12+3sin π6t,t ∈[0，24] B. y =12+3sin(π6t +π2)，t ∈[0，24] C. y =12+3sin π12t,t ∈[0,24] D. y =12+3sin(π12t +π2)，t ∈[0,24] 二 、填空题（本大题共5小题，共25分）13.（5分）振动量函数y =√2sin(ωx +φ)(ω>;0)的初相和频率分别为-π和32，则它的运动周期为_______________，相位是_______________.14.（5分）如图，在平面直角坐标系中，点P 以每秒π2的角速度从点A 出发，沿半径为2的上半圆逆时针移动到B ，再以每秒π3的角速度从点B 沿半径为1的下半圆逆时针移动到坐标原点O，则上述过程中动点P的纵坐标y关于时间t的函数表达式为__________.15.（5分）函数f(x)=sin(ωx+φ)(其中ω>;0,|φ|<;π2)的图象如图所示，则函数f(x)=sin(ωx+φ)的最小正周期为_______________；为了得到g(x)=sinωx的图象，只需把y=f(x)的图象上所有的点向右平移_______________个单位长度.16.（5分）已知海湾内海浪的高度y(米)是时间t(0⩽t⩽24，单位：小时)的函数，记作y=f(t).某日各时刻记录的浪高数据如下表：经长期观测，y=f(t)可近似地看成是函数y=Acosωt+b.根据以上数据，可得函数y=Acosωt+b的表达式为__________.17.（5分）一个匀速旋转的摩天轮每12分钟转一周，最低点距地面2米，最高点距地面18米，P是摩天轮轮周上一定点，从P在最低点时开始计时，则16分钟后P点距地面的高度是____．三、解答题（本大题共6小题，共72分）18.（12分）某地为发展旅游业，在旅游手册中给出了当地一年每个月的月平均气温表，根据图中提供的数据，试用y=Asin(ωt+φ)+b近似地拟合出月平均气温y(单位：℃)与时间t(单位：月)的函数关系，并求出其周期和振幅，以及气温达到最大值和最小值的时间.(答案不唯一)19.（12分）某地种植大棚蔬菜，已知大棚内一天的温度(单位：℃)随时间t(单位：ℎ)的变化近似满足函数关系：f(t)=12−3sin(π12t+π3)，t∈[0,24).(1)求实验室这一天的最大温差；(2)若某种蔬菜的生长要求温度不高于10.5℃，若种植这种蔬菜，则在哪段时间大棚需要降温？20.（12分）如图，有一块以点O为圆心的半圆形空地，要在这块空地上划出一个内接矩形ABCD开辟为绿地，使其一边AD落在半圆的直径上，另两点B，C落在半圆的圆周上.已知半圆的半径长为20m.(1)如何选择关于点O对称的点A，D的位置，可以使矩形ABCD的面积最大，最大值是多少?(2)沿着AB，BC，CD修一条步行小路从A到D，如何选择A，D位置，使步行小路的距离最远?21.（12分）健康成年人的收缩压和舒张压一般为120～140mmHg和60～90mmHg.心脏跳动时，血压在增加或减小.血压的最大值、最小值分别称为收缩压和舒张压，血压计上的读数就是收缩压和舒张压，读数120/80mmHg为标准值.记某人的血压满足函数式p(t)=25sin160πt+115，其中p(t)为血压(mmHg)，t为时间(min)，试回答下列问题：(1)求函数p(t)的周期;(2)求此人每分钟心跳的次数;(3)求出此人的血压在血压计上的读数，并与正常值比较.22.（12分）如果α为小于360°的正角，且这个角的7倍角的终边与这个角的终边重合，则这样的角α是否存在?23.（12分）某港口的水深y（米）是时间t（0≤t≤24，单位：小时）的函数，下面是每天时间与水深的关系表：（A＞0，ω＞0）.（1）根据以上数据，求出y=f（t）的解析式；（2）若船舶航行时，水深至少要11.5米才是安全的，则船舶在一天中有几个小时可以安全进出该港？答案和解析1.【答案】C;【解析】略2.【答案】A;【解析】此题主要考查正弦定理在解三角形中的应用，两角和与差公式，考查二次函数求最值问题，考查转化思想，属于较难题．先利用两角和的正弦公式、三角形的内角和、诱导公式化简已知条件可得sinC=√3sinA，由正弦定理可得c=√3a代入面积公式结合二次函数的性质即可求解.解：因为√3cosB√3sinB =1tanC=cosCsinC，所以sinC=√3sinCcosB+√3cosCsinB=√3sin(B+C)=√3sinA，由正弦定理可得：c=√3a，代入面积公式可得：S=√14[a2⋅3a2−(a2+3a2−222)2]=√14[3a4−(2a2−2)2]=√14(−a4+8a2−4)=√14[−(a2−4)2+12]=√−14(a2−4)2+3，所以当a=2时，−14(a2−4)2+3取得最大值3，所以△ABC面积S的最大值为√3，故选：A.3.【答案】null;【解析】此题主要考查三角函数的实际应用，属于基础题.求出|PA|+|PB|+|PC|=2√3sin(θ+φ)，利用三角函数的性质即可求解.解：如图，设∠PAC=θ，θ∈[0,π4]，可得|PA|+|PB|+|PC|=2[cosθ+sin(π4−θ)+sinθ]=(2+√2)cosθ+(2−√2)sinθ=2√3sin(θ+φ)，其中tanφ=3+2√2，φ∈(π4,π2 )，所以(|PA|+|PB|+|PC|)max=2√3，由的范围可以取到最大值.故选B.4.【答案】C;【解析】此题主要考查解三角形的实际应用，考查数学运算的核心素养与应用意识，属于中档题.由题意可得AD=1.5m，利用tan∠ADB，求出cos∠ADB，进一步进行求解即可.解：因为∠ACD=90∘，AC=1.2m，CD=0.9m，所以AD=√AC2+CD2=1.5m.因为tan∠ADB=−2√2，所以cos∠ADB=−13，所以AB=√1.52+12−2×1.5×1×(−13)=√172m.5.【答案】D;【解析】略6.【答案】null;【解析】此题主要考查由y=Asin(ωx+φ)的部分图象确定其解析式以及应用，通过对实际问题的分析，转化为解决三角函数问题，属基础题.通过排除法进行求解，由y=f(t)可以近似看成y=k+Asin(ωx+φ)的图象，故可以把已知数据代入y=k+Asin(ωx+φ)中，分别按照周期和函数值排除，即可求出答案．解：排除法：∵y=f(t)可以近似看成y=k+Asin(ωx+φ)的图象，∴由T=12可排除C、D，将(3,15)代入，排除B.故选A.7.【答案】B;此题主要考查了三角形的边角关系应用问题，也考查了数形结合思想和运算求解能力，属于基础题．根据题意结合图形，利用三角形的边角关系，即可求出塔高BC 的值．解：如图所示，在Rt △ACD 中，∠CAD =45°，CD =256， 所以AD =256，在Rt △ABD 中，∠BAD =60°， 所以BD =ADtan∠BAD =256√3， 所以BC =BD −CD =256√3−256， 即塔高BC 为256(√3−1)米． 故选：B.8.【答案】D;【解析】如图所示，连接OC ，设∠COA =θ，作DF ⊥OP ，CE ⊥OP ，垂足分别为F ，E ．根据平面几何知识可知，AB =CD =EF ，DF =OF =CE ，∴CE =20√2sinθ，EF =OE −OF =20√2cosθ−20√2sinθ．故四边形ABCD 的面积S 等于四边形DFEC 的面积，即有S =20√2sinθ×20√2(cosθ−sinθ)=400(sin2θ+cos2θ−1)=400√2sin(2θ+π4)−400，其中θ∈(0,π4)．所以当sin(2θ+π4)=1，即θ=π8时，S max =400(√2−1)，即观赛场地面积的最大值为400(√2−1)m 2．故选D ．9.【答案】D;10.【答案】C; 【解析】此题主要考查三角函数在实际生活中的应用. 由题设可得PA −1=PAsinα，即可得结果. 解：由题设，PC =PB′sinα=PAsinα，而PC =PA −1，所以PA −1=PAsinα，可得PA =11−sinα米.故选：C11.【答案】A; 【解析】此题主要考查解三角形的应用，根据题意作出示意图是解答该题的关键，考查空间立体感、学科素养和运算能力，属于中档题．作出示意图，过点B 作BC ⊥OA 于C ，结合三角函数和勾股定理，转化为平面几何中的简单计算，即可得解．解：根据题意作出如下示意图，其中tanα=32，β=θ=π3，AB =20m ，过点B 作BC ⊥OA 于C ， 设OH =3x ，则OA =OH tanα=2x ，OB =OH tanβ=√3x ，在Rt △ABC 中，因为AB =20，θ=π3，所以AC =AB ×cos π3=10，BC =AB ×sin π3=10√3，所以OC =OA −AC =2x −10，在Rt △OBC 中，由勾股定理知，(2x −10)2+(10√3)2=(√3x)2， 化简得x 2−40x +400=0，解得x =20， 所以瀑布的高度OH =3x =60m.故答案选：A.12.【答案】A;【解析】略13.【答案】23;3πx−π; 【解析】略14.【答案】f(t)={2sinπt2,0<t⩽2sin[π3(t−2)+π],2<t⩽5;【解析】此题主要考查利用三角函数的定义解决实际问题，在做题过程中点的坐标与角度之间的关系，属于综合题.解：由三角函数的定义可得：当动点P在半径为2的上半圆上运动时，t∈(0,2],终边OP对应的角度为π2t，所以P点坐标为(2cosπ2t,2sinπ2t)，当动点P在半径为1的下半圆上运动时，t∈(2,5],终边OP对应的角度为π3(t−2)+π，所以P点坐标为(cos[π3(t−2)+π],sin[π3(t−2)+π])，综上：动点P的纵坐标y关于时间t的函数表达式为y={2sinπ2t,t∈(0,2]sin[π3(t−2)+π],t∈(2,5]15.【答案】π;π6+kπ,k∈Z;【解析】略16.【答案】y=12cosπ6t+1;【解析】此题主要考查了三角函数模型的应用的相关知识，试题难度一般. 解题时先计算出周期和振幅，然后求解解析式即可.解：由表中数据，知周期T=12，∴ω=2πT =2π12=π6，由t=0，y=1.5，得A+b=1.5；由t=3，y=1.0，得b=1.0，∴A=0.5，b=1，∴y=12cosπ6t+1.17.【答案】14;【解析】解：设P 与地面高度与时间t 的关系，f （t ）=Asin （ωt+φ）+B （A ＞0，ω＞0，φ∈[0，2π）），由题意可知：A=8，B=10，T=12，所以ω=，又因为f （0）=2，故ϕ=-πt所以f （16）=8sin(π- ． 故答案为：14．18.【答案】解：根据图象可知，当t =1时，y 有最小值15;当t =8时，y 有最大值27. ∴{−A +b =15ω+φ=−π28ω+φ=π2A +b =27解得{A =6b =21ω=π7φ=−9π14， ∴y =6sin(π7t −9π14)+21，周期T =2πω=2ππ7=14，振幅A =6.气温在1月份时达到最低， 在8月份时达到最高.;【解析】此题主要考查由y =Asin(ωt +φ)的部分图象确定其解析式，属于中档题． 当t =8月份时平均气温达到最大值25℃，当t =1月份时，平均气温达到最小值15℃，列出方程组，结合周期与振幅，从而可得函数解析式．19.【答案】解：(1)由题意，函数f(t)=12−3sin(π12t +π3)，t ∈[0,24), 根据正弦型函数的性质可得−1⩽sin(π12t +π3)⩽1，所以f(t)max=15,f(t)min=9，可得f(t)max−f(t)min=6，则实验室这一天的最大温差为6℃.(2)由题意，令f(t)>10.5，即12−3sin(π12t+π3)>10.5，即sin(π12t+π3)<12，因为t∈[0,24),可得π12t+π3∈[π3,7π3),所以5π6<π12t+π3<13π6，解得6<t<22，即在6时至22时这段时间内大棚需要降温.;【解析】此题主要考查了函数y=Asin(ωx+φ)的图象与性质，三角函数模型的应用，属于中档题.(1)根据正弦型函数的性质可得−1⩽sin(π12t+π3)⩽1，求得f(t)max=15,f(t)min=9，进而求得这一天的最大温差；(2)根据题意，令f(t)>10.5，得到sin(π12t+π3)<12，利用正弦型函数的性质，求得t的范围即可求解.20.【答案】解(1)连接OB，如图所示，设∠AOB=θ，则AB=OBsinθ=20sinθ，OA=OBcosθ=20cosθ，且θ∈(0,π2).因为A，D关于点O对称，所以AD=2OA=40cosθ.设矩形ABCD的面积为S，则S=AD·AB=40cosθ·20sinθ=400sin2θ.因为θ∈(0,π2)，所以2θ∈(0,π)，所以当sin2θ=1，即θ=π4时，S max=400(m2).此时AO=DO=10√2(m).故当A，D距离圆心O为10√2m时，矩形ABCD的面积最大，其最大面积是400m2.(2)由(1)知AB=20sinθ，AD=40cosθ，所以AB+BC+CD=40sinθ+40cosθ=40√2sin(θ+π4)，又θ∈(0,π2)，所以θ+π4∈(π4,3π4)，当θ+π4=π2，即θ=π4时，(AB+BC+CD)max=40√2(m)，此时AO=DO=10√2(m)，即当A，D距离圆心O为10√2m时，步行小路的距离最远.;【解析】此题主要考查三角函数在实际生活中的应用，考查正弦函数的最值，是中档题21.【答案】解(1)T =2π|ω|=2π160π =180(min).(2)f =1T=80. 即此人每分钟心跳的次数为80.(3)p(t)max =115+25=140(mmHg)，p(t)min =115−25=90(mmHg)， 即收缩压为140mmHg ，舒张压为90mmHg.此人的血压在血压计上的读数为140/90mmHg ，在正常值范围内.;【解析】此题主要考查三角函数在实际生活中的应用，考查正弦函数的周期与频率之间的关系以及求正弦函数的的值域相关问题，属于一般题.22.【答案】解：由题意，有7α=k·360°＋α(k ∈Z)，即α=k·60°． 又由于0°＜α＜360°，即0°＜k·60°＜360°(k ∈Z)，则k 取1，2，3，4，5，所以α的值可取60°，120°，180°240°，300°．; 【解析】略.23.【答案】【解析】（1）由题表中数据可得：水深的最大值为13，最小值为7，所以{A +B =13,−A +B =7B =13+72=10,A =13−72=3,且相隔12小时达到一次最大值，说明周期为12，因此T=2πω=12,ω=π6,故f(t)=3sin π6t +10(0≤t ≤24)（2）要想船舶安全，必须f （t ）≥11.5，即3sin π6t +10≥11.5， 所以sin π6t ≥12，所以2kπ+π6≤π6t ≤5π6+2kπ,k ∈Z ，解得12k+1≤t≤5+12k ，k ∈Z ，当k=0时，1≤t≤5；当k=1时，13≤t≤17.故船舶能安全进出该港的时间段为1：00至5：00，13：00至17：00，共8个小时.; 【解析】略。