人教版小学五年级下册数学概念和公式
- 格式:doc
- 大小:24.00 KB
- 文档页数:2

第一单元小数乘法1、小数乘整数(P2、3):意义——求几个相同加数的和的简便运算.如:1.5×3表示1.5的3倍是多少或3个1.5的和的简便运算.计算方法:先把小数扩大成整数;按整数乘法的法则算出积;再看因数中一共有几位小数,就从积的右边起数出几位点上小数点.2、小数乘小数(P4、5):意义——就是求这个数的几分之几是多少.如:1.5×0.8就是求1.5的十分之八是多少.1.5×1.8就是求1.5的1.8倍是多少.计算方法:先把小数扩大成整数;按整数乘法的法则算出积;再看因数中一共有几位小数,就从积的右边起数出几位点上小数点.注意:计算结果中,小数部分末尾的0要去掉,把小数化简;小数部分位数不够时,要用0占位.p 3、规律(1)(P9):一个数(0除外)乘大于1的数,积比原来的数大;一个数(0除外)乘小于1的数,积比原来的数小.4、求近似数的方法一般有三种:(P10)⑴四舍五入法;⑵进一法;⑶去尾法5、计算钱数,保留两位小数,表示计算到分.保留一位小数,表示计算到角.6、(P11)小数四则运算顺序跟整数是一样的.7、运算定律和性质:加法:加法交换律:a+b=b+a 加法结合律:(a+b)+c=a+(b+c)减法:减法性质:a-b-c=a-(b+c) a-(b-c)=a-b+c乘法:乘法交换律:a×b=b×a乘法结合律:(a×b)×c=a×(b×c)乘法分配律:(a+b)×c=a×c+b×c【(a-b)×c=a×c-b×c】除法:除法性质:a÷b÷c=a÷(b×c)第二单元小数除法8、小数除法的意义:已知两个因数的积与其中的一个因数,求另一个因数的运算.如:0.6÷0.3表示已知两个因数的积0.6与其中的一个因数0.3,求另一个因数的运算.9、小数除以整数的计算方法(P16):小数除以整数,按整数除法的方法去除.,商的小数点要和被除数的小数点对齐.整数部分不够除,商0,点上小数点.如果有余数,要添0再除.10、(P21)除数是小数的除法的计算方法:先将除数和被除数扩大相同的倍数,使除数变成整数,再按“除数是整数的小数除法”的法则进行计算.注意:如果被除数的位数不够,在被除数的末尾用0补足.11、(P23)在实际应用中,小数除法所得的商也可以根据需要用“四舍五入”法保留一定的小数位数,求出商的近似数.12、(P24、25)除法中的变化规律:①商不变性质:被除数和除数同时扩大或缩小相同的倍数(0除外),商不变.②除数不变,被除数扩大,商随着扩大.③被除数不变,除数缩小,商扩大.13、(P28)循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数.循环节:一个循环小数的小数部分,依次不断重复出现的数字.如6.3232……的循环节是32.14、小数部分的位数是有限的小数,叫做有限小数.小数部分的位数是无限的小数,叫做无限小数.第三单元观察物体15、从不同的角度观察物体,看到的形状可能是不同的;观察长方体或正方体时,从固定位置最多能看到三个面.第四单元简易方程16、(P45)在含有字母的式子里,字母中间的乘号可以记作“•”,也可以省略不写.加号、减号除号以及数与数之间的乘号不能省略.17、a×a可以写作a•a或a ,a 读作a的平方. 2a表示a+a18、方程:含有未知数的等式称为方程.使方程左右两边相等的未知数的值,叫做方程的解.求方程的解的过程叫做解方程.19、解方程原理:天平平衡.等式左右两边同时加、减、乘、除相同的数(0除外),等式依然成立.20、10个数量关系式:加法:和=加数+加数一个加数=和-两一个加数减法:差=被减数-减数被减数=差+减数减数=被减数-差乘法:积=因数×因数一个因数=积÷另一个因数除法:商=被除数÷除数被除数=商×除数除数=被除数÷商21、所有的方程都是等式,但等式不一定都是等式.22、方程的检验过程:方程左边=……23、方程的解是一个数;解方程式一个计算过程.=方程右边所以,X=…是方程的解.第五单元多边形的面积23、公式:长方形:周长=(长+宽)×2——【长=周长÷2-宽;宽=周长÷2-长】字母公式:C=(a+b)×2面积=长×宽字母公式:S=ab正方形:周长=边长×4 字母公式:C=4a面积=边长×边长字母公式:S=a平行四边形的面积=底×高字母公式:S=ah三角形的面积=底×高÷2 ——【底=面积×2÷高;高=面积×2÷底】字母公式:S=ah÷2梯形的面积=(上底+下底)×高÷2 字母公式:S=(a+b)h÷2【上底=面积×2÷高-下底,下底=面积×2÷高-上底;高=面积×2÷(上底+下底)】24、平行四边形面积公式推导:剪拼、平移25、三角形面积公式推导:旋转平行四边形可以转化成一个长方形;两个完全一样的三角形可以拼成一个平行四边形,长方形的长相当于平行四边形的底;平行四边形的底相当于三角形的底;长方形的宽相当于平行四边形的高;平行四边形的高相当于三角形的高;长方形的面积等于平行四边形的面积,平行四边形的面积等于三角形面积的2倍,因为长方形面积=长×宽,所以平行四边形面积=底×高.因为平行四边形面积=底×高,所以三角形面积=底×高÷226、梯形面积公式推导:旋转27、三角形、梯形的第二种推导方法老师已讲,自己看书两个完全一样的梯形可以拼成一个平行四边形, 知道就行.平行四边形的底相当于梯形的上下底之和;平行四边形的高相当于梯形的高;平行四边形面积等于梯形面积的2倍,因为平行四边形面积=底×高,所以梯形面积=(上底+下底)×高÷228、等底等高的平行四边形面积相等;等底等高的三角形面积相等;等底等高的平行四边形面积是三角形面积的2倍.29、长方形框架拉成平行四边形,周长不变,面积变小.30、组合图形:转化成已学的简单图形,通过加、减进行计算.第六单元统计与可能性31、平均数=总数量÷总份数32、中位数的优点是不受偏大或偏小数据的影响,用它代表全体数据的一般水平更合适. 第七单元数学广角33、数不仅可以用来表示数量和顺序,还可以用来编码.34、邮政编码:由6位组成,前2位表示省(直辖市、自治区)0 5 4 0 0 1前3位表示邮区前4位表示县(市)最后2位表示投递局35、身份证码:18位1 3 0 52 1 1 9 7 8 03 0 1 0 0 1 9河北省邢台市邢台县出生日期顺序码校验码倒数第二位的数字用来表示性别,单数表示男,双数表示女.。

五年级上册数学公式小结第一单元:小数的乘法一个因数乘另一个因数,两个因数的小数位数之和有几位,积就有几位。
例如:3.45×6.29=21.7005但是如果乘得的积小数末尾是零,零就可以省略不写。
例如:3.65×6.72=24.528第二单元:小数的除法一个数(零除外)除以小于一的数,商比被除数大。
一个数(零除外)除以大于一的数,商比被除数小。
例如:30÷0.5=6030÷5= 6两数相除,除数是小数,被除数也是小数,除数将小数点向右移成整数,移了几位,被除数也就向右移动几位,相互抵消。
例如:2.36÷0.02=236÷2小数部分的位数是无限小数,叫做无限小数。
例如:0.232323……就是一个无限小数。
第四单元:简易方程1. 功效×时间=工作总量工作总量÷功效= 时间工作总量÷时间= 功效例如:王师傅一小时加工8个零件,他工作一天加工多少个零件?解:设王师傅工作一天加工x 个零件功效×时间=工作总量X=24×8X=192答:王师傅工作一天加工192个零件。
2.路程=时间×速度用字母表示为:s=vt例如:小明和小红家相距560米,学校在两家的中央,小明和小红在校门口分手,七分钟后他们同时到家,小明平均每分钟走45米,问小红平均每分钟走多少米?解:设小红平均每分钟走x米.路程=时间×速度560=(x+45)×7560÷7=x+45X=35答:小红平均每分钟走35米。
等式不变的规律:方程两边同时加上或减去相同的数,左右两边仍然相等。
方程两边同时乘或除以相同的数(零除外),左右两边仍然相等。
第五单元多边形的面积1千米=1000米1米=10分米1分米=10厘米1厘米=10毫米100公顷=1平方千米1平方千米=1000000平方米1平方米=100平方分米1公顷=10000平方米平行四边形的面积=底×高用字母表示为:s=ah 正方形的面积=边长×边长用字母表示为:s=a的平方长方形的面积=长×宽用字母表示为:s=ab 三角形的面积=(底×高)÷2用字母表示为:s=(a×h) ÷2梯形的面积=(上底+下底)×高÷2用字母表示为:s=(a+b)h÷2一个长方形木条拉成平行四边形,周长不变,面积改变。

人教版小学五年级数学上下册公式大全,可下载!五年级上册数学公式小结第一单元:小数的乘法一个因数乘另一个因数,两个因数的小数位数之和有几位,积就有几位。
例如:3.45×6.29=21.7005但是如果乘得的积小数末尾是零,零就可以省略不写。
例如:3.65×6.72=24.528第二单元:小数的除法一个数(零除外)除以小于一的数,商比被除数大。
一个数(零除外)除以大于一的数,商比被除数小。
例如:30÷0.5=60 30÷5= 6两数相除,除数是小数,被除数也是小数,除数将小数点向右移成整数,移了几位,被除数也就向右移动几位,相互抵消。
例如:2.36÷0.02=236÷2小数部分的位数是无限小数,叫做无限小数。
例如:0.232323……就是一个无限小数。
第四单元:简易方程1. 功效×时间=工作总量工作总量÷功效=时间工作总量÷时间=功效例如:王师傅一小时加工8个零件,他工作一天加工多少个零件?解:设王师傅工作一天加工x 个零件功效×时间=工作总量X=24×8X=192答:王师傅工作一天加工192个零件。
2.路程=时间×速度用字母表示为:s=vt例如:小明和小红家相距560米,学校在两家的中央,小明和小红在校门口分手,七分钟后他们同时到家,小明平均每分钟走45米,问小红平均每分钟走多少米?解:设小红平均每分钟走x米.路程=时间×速度560=(x+45)×7560÷7=x+45X=35答:小红平均每分钟走35米。
等式不变的规律:方程两边同时加上或减去相同的数,左右两边仍然相等。
方程两边同时乘或除以相同的数(零除外),左右两边仍然相等。
第五单元多边形的面积1千米=1000米1米=10分米1分米=10厘米1厘米=10毫米100公顷=1平方千米1平方千米=1000000平方米1平方米=100平方分米1公顷=10000平方米平行四边形的面积=底×高用字母表示为:s=ah正方形的面积=边长×边长用字母表示为:s=a的平方长方形的面积=长×宽用字母表示为:s=ab三角形的面积=(底×高)÷2 用字母表示为:s=(a×h) ÷2梯形的面积=(上底+下底)×高÷2 用字母表示为:s=(a+b)h÷2一个长方形木条拉成平行四边形,周长不变,面积改变。

第一单元:小数乘法1、小数乘整数的意义与整数乘法的意义相同,就是求几个相同加数的和的简便运算。
如:1.2×5表示5个1.2是多少。
2、一个数乘纯小数的意义就是求这个数的十分之几、百分几、千分之几……是多少。
如:1.2×0.5表示求1.2的十分之五是多少。
3、小数乘法的计算方法:计算小数乘法,先按整数乘法算出积,再看因数中一共有几位小数,就从积的右边起数出几位,点上小数点。
乘得的积的小数位数不够,要在前面用0补足,再点上小数点。
4、一个数(0除外)乘1,积等于原来的数。
一个数(0除外)乘大于1的数,积比原来的数大。
一个数(0除外)乘小于1的数,积比原来的数小。
5、整数乘法的交换律、结合律和分配率,对于小数乘法也适用。
第二单元:小数除法1、小数除法的意义与整数除法的意义相同,是已知两个因数的积与其中一个因数,求另一个因数的运算。
如:2.4÷1.6表示已知两个因数的积是2.4与其中一个因数是1.6,求另一个因数是多少。
2、小数除以整数,按整数除法的方法去除,商的小数点要和被除数的小数点对齐。
如果除到末尾仍有余数,要添0再继续除。
3、被除数比除数大的,商大于1。
被除数比除数小的,商小于1。
4、计算除数是小数的除法,先移动除数的小数点,使它变成整数,除数的小数点向右移动几位,被除数的小数点也向右移动几位,数位不够的要添0补足。
再按照除数是整数的小数除法进行计算。
5、一个数(0除外)除以1,商等于原来的数。
一个数(0除外)除以大于1的数,商比原来的数小。
一个数(0除外)除以小于1的数,商比原来的数大。
6、A除以B=A÷B;A除B=B÷A;A去除B=B÷A;A被B除=A÷B。
7、一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。
8、小数部分的位数是有限的小数,叫做有限小数。
小数部分是无限的小数叫做无限小数。

第三单元常用公式一:长方体和正方体的棱长总和:长方体的棱长总和:1:2:字母表示:正方体的棱长总和:1:2:字母表示:正方体的棱长总和= 正方体的棱长=二:长方体和正方体的表面积:(平方米·平方厘米·平方分米·平方毫米)长方体的表面积=1:2:长方体的表面积=1:2:正方体的表面积=正方体一个面的面积=三:长方体和正方体的体积长方体的体积=1:正方体的体积=长方体或正方体底面的面积叫做底面积。
长方体或正方体的体积 =底面积×高一个正方体的棱长扩大a倍 棱长总和扩大a倍 表面积扩大a×a倍 体积扩大a× a× a倍。
四计算不规则物体的体积可以用排水法。
水中物体的体积 不规则物体的体积 =容器的底面积×水面上升 或下降 的高度。
水面上升 或下降 的高度=水中物体的体积不规则物体的体积 ÷容器的底面积五容积(容器所能容纳物体的体积叫做它们的容积。
)升或毫升长方体和正方体的容积计算方法 跟体积的计算方法相同。
但是容积要从容器里面量出长、宽、高。
物体的容积一般都小于物体的体积。
只是为了计算方便 我们把厚度忽略不计。
1. 一个长方体纸箱,长和宽都是3 dm,高是4 dm,做这样的一个纸箱需要纸板( ) dm 2,它的容积是( ) dm32.把一个长5 dm,宽4 dm,高3 dm的长方体截成一个最大的正方体,这个正方体的体积是()。
3.一个长20m,宽10m,深2m的水池,这个水池的占地面积是()4.一个正方体的表面积是96cm2,它的一个面的面积是(),它的体积是()。
5.一个正方体的底面积25平方分米,它的表面积是()平方分米,它的体积是()立方分米6.一个长方体的棱长总和是36厘米,从一个顶点出发的三条棱的和是()厘米7.一个正方体纸盒的表面积是5.1平方分米,它的占地面积是()平方分米8.一根长方体木料长3米,现在把这根木料锯成4段后,表面积比原来增加了48平方分米,原来这个长方体木料的体积是()立方分米。

人教版数学五年级下册:全册知识点归纳五年级上册知识点概念总结1.小数乘整数的意义:求几个相同加数和的简便运算;一个数乘纯小数的意义是求这个数的十分之几、百分之几、千分之几……是多少。
2.小数乘法法则先按照整数乘法的计算法则算出积,再看因数中共有几位小数,就从积的右边起数出几位,点上小数点;如果位数不够,就用“0”补足。
3.小数除法小数除法的意义与整数除法的意义相同,就是已知两个因数的积与其中一个因数,求另一个因数的运算。
4.除数是整数的小数除法计算法则先按照整数除法的法则去除,商的小数点要和被除数的小数点对齐;如果除到被除数的末尾仍有余数,就在余数后面添“0”,再继续除。
5.除数是小数的除法计算法则先移动除数的小数点,使它变成整数,除数的小数点也向右移动几位(位数不够的补“0”),然后按照除数是整数的除法法则进行计算。
6.积的近似数:四舍五入是一种精确度的计数保留法,与其他方法本质相同。
但特殊之处在于,采用四舍五入,能使被保留部分的与实际值差值不超过最后一位数量级的二分之一:假如0~9等概率出现的话,对大量的被保留数据,这种保留法的误差总和是最小的。
7.数的互化(1)小数化成分数原来有几位小数,就在1的后面写几个零作分母,把原来的小数去掉小数点作分子,能约分的要约分。
(2)分数化成小数用分母去除分子。
能除尽的就化成有限小数,有的不能除尽,不能化成有限小数的,一般保留三位小数。
(3)化有限小数一个最简分数,如果分母中除了2和5以外,不含有其他的质因数,这个分数就能化成有限小数;如果分母中含有2和5 以外的质因数,这个分数就不能化成有限小数。
(4)小数化成百分数只要把小数点向右移动两位,同时在后面添上百分号。
(5)百分数化成小数把百分数化成小数,只要把百分号去掉,同时把小数点向左移动两位。
(6)分数化成百分数通常先把分数化成小数(除不尽时,通常保留三位小数),再把小数化成百分数。
(7)百分数化成小数先把百分数改写成分数,能约分的要约成最简分数。

第五单元多边形的面积第一单元:小数的乘法1千米=1000米1米=10分米一个因数乘另一个因数,两个因数的小数位数之和有几1分米=10厘米1厘米=10毫米位,100公顷=1平方千米1平方千米=1000000平方积就有几位。
米例如:3.45×6.29=21.70051平方米=100平方分米1公顷=10000平方米但是如果乘得的积小数末尾是零,零就可以省略不写。
平行四边形的面积=底×高用字母表示为:s=ah 例如:3.65×6.72=24.528正方形的面积=边长×边长用字母表示为:s=a 第二单元:小数的除法的平方一个数(零除外)除以小于一的数,商比被除数大。
长方形的面积=长×宽用字母表示为:s=ab 一个数(零除外)除以大于一的数,商比被除数小。
三角形的面积=(底×高)÷2例如:30÷0.5=6030÷5= 6用字母表示为:s=(a ×h)÷2两数相除,除数是小数,被除数也是小数,梯形的面积=(上底+下底)×高÷2用字母表示为:s=(a+b)h ÷2除数将小数点向右移成整数,移了几位,一个长方形木条拉成平行四边形,周长不变,面积改变。
五年级数学下册概念公式被除数也就向右移动几位,相互抵消。
例如:2.36÷0.02=236÷2一、旋转、平移小数部分的位数是无限小数,叫做无限小数。
时针旋转1小时是30度例如:0.232323……就是一个无限小数。
第四单元:简易方程二、因数与倍数1.功效×时间=工作总量工作总量÷功效=时间1、如果a×b=c(a、b、c 都是不为0的整数),工作总量÷时间=功效那么a、b 就是c 得因数,c 就是a、b 的倍数。
例如:王师傅一小时加工8个零件,他工作一天加工多2、一个数的因数个数是有限的,其中最小的因少个零件?数是1,最大的因数是它本身。

五年级数学下册知识点归纳总结一、图形的变换图形变换的基本方式是平移、对称和旋转。
1、轴对称:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴。
(1)学过的轴对称平面图形:长(正)方形、圆形、等腰三角形、等边三角形、等腰梯形……等腰三角形有1条对称轴,等边三角形有3条对称轴,长方形有2条对称轴,正方形有4条对称轴,等腰梯形有1条对称轴,任意梯形和平行四边形不是轴对称图形。
(2)圆有无数条对称轴。
(3)对称点到对称轴的距离相等。
(4)轴对称图形的特征和性质:①对应点到对称轴的距离相等;②对应点的连线与对称轴垂直;③对称轴两边的图形大小、形状完全相同。
3、对称图形包括轴对称图形和中心对称图形。
平行四边形(除棱形)属于中心对称图形。
2、旋转:在平面内,一个图形绕着一个顶点旋转一定的角度得到另一个图形的变化较做旋转,定点O叫做旋转中心,旋转的角度叫做旋转角,原图形上的一点旋转后成为的另一点成为对应点。
(1)生活中的旋转:电风扇、车轮、纸风车(2)旋转三要素;旋转中心、旋转角度和旋转方向。
(3)长方形绕中点旋转180度与原来重合,正方形绕中点旋转90度与原来重合。
等边三角形绕中点旋转120度与原来重合。
旋转的性质:(1)图形的旋转是图形上的每一点在平面上绕某个固定点旋转固定角度的位置移动;(2)其中对应点到旋转中心的距离相等;(3)旋转前后图形的大小和形状没有改变;(4)两组对应点非别与旋转中心的连线所成的角相等,都等于旋转角;(5)旋转中心是唯一不动的点。
3、对称和旋转的画法:旋转要注意:顺时针、逆时针、度数二、因数和倍数1、整除:被除数、除数和商都是自然数,并且没有余数。
整数与自然数的关系:整数包括自然数。
2、因数、倍数:大数能被小数整除时,大数是小数的倍数,小数是大数的因数。
例:12是6的倍数,6是12的因数。
(1)数a能被b整除,那么a就是b的倍数,b就是a的因数。

人教版五年级数学下册知识点梳理概念与公式第一单元《观察物体三》1、不同角度观察一个物体,看到的面都是两个或三个相邻的面。
2、不可能一次看到长方体或正方体相对的面。
第二单元因数和倍数一、因数和倍数。
在整数除法中,如果商是整数而没有余数,我们就说被除数是除数的倍数,除数是被除数的余数.又如整数a能被b整除(a÷b=c),那么a就是b的倍数,b就是a 的因数。
因数和倍数是相互依存的,不能单独存在。
因数:一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身。
一个数的因数的求法:成对地按顺序找,或用除法找。
倍数:一个数的倍数的个数是无限的,最小的倍数是它本身。
一个数的倍数的求法:依次乘自然数。
二、自然数按能不能被2整除分为:奇数偶数奇数:不是2的倍数的数叫做奇数。
偶数:是2的倍数的数叫做偶数。
最小的奇数是1,最小的偶数是0。
2、3、5倍数的特征:个位上是0,2,4,6,8的数都是2的倍数。
个位上是0或5的数,是5的倍数。
一个数各位上的数的和是3的倍数,这个数就是3的倍数。
如果一个数同时是2和5的倍数,那它的个位上的数字一定是0。
同时是2、3、5的倍数,个位上是0并且各位上的数的和是3的倍数,这个数就同时是2、3、5的倍数。
最大的两位数是90,最小的两位数是30,最小的三位数是120。
三、自然数按因数的个数来分:质数、合数、1.质数:一个数,如果只有1和它本身两个因数,这样的数叫做质数(或素数)。
如2,3,5,7,11,13,17,19……都是质数。
合数:一个数,如果除了1和它本身还有别的因数,这样的数叫做合数。
如4,6,8,9,10,12,14,15,16,18,20,22,26,49……都是合数。
合数至少有三个因数,1、它本身、别的因数1:只有1个因数。
“1”既不是质数,也不是合数。
最小的质数是2,最小的合数是4。
20以内的质数:有8个(2、3、5、7、11、13、17、19)(1)所有的奇数都是质数。
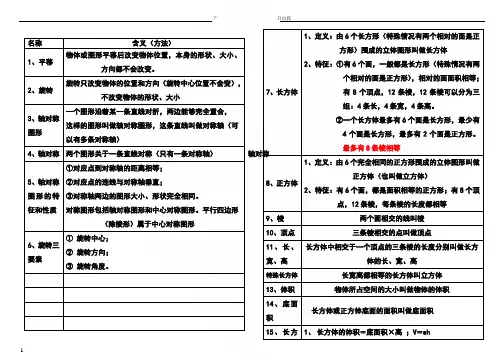
名称含义(方法)1、平移物体或图形平移后改变物体位置,本身的形状、大小、方向都不会改变。
2、旋转旋转只改变物体的位置和方向(旋转中心位置不会变),不改变物体的形状、大小3、轴对称图形一个图形沿着某一条直线对折,两边能够完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴(可以有多条对称轴)4、轴对称两个图形关于一条直线对称(只有一条对称轴)轴对称5、轴对称图形的特征和性质①对应点到对称轴的距离相等;②对应点的连线与对称轴垂直;③对称轴两边的图形大小、形状完全相同。
对称图形包括轴对称图形和中心对称图形。
平行四边形(除棱形)属于中心对称图形6、旋转三要素①旋转中心;②旋转方向;③旋转角度。
7、长方体1、定义:由6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形叫做长方体2、特征:①有6个面,一般都是长方形(特殊情况有两个相对的面是正方形),相对的面面积相等;有8个顶点,12条棱,12条棱可以分为三组:4条长,4条宽,4条高。
②一个长方体最多有6个面是长方形,最少有4个面是长方形,最多有2个面是正方形。
最多有8条棱相等8、正方体1、定义:由6个完全相同的正方形围成的立体图形叫做正方体(也叫做立方体)2、特征:有6个面,都是面积相等的正方形;有8个顶点,12条棱,每条棱的长度都相等9、棱两个面相交的线叫棱10、顶点三条棱相交的点叫做顶点11、长、宽、高长方体中相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高特殊长方体长宽高都相等的长方体叫立方体13、体积物体所占空间的大小叫做物体的体积14、底面积长方体或正方体底面的面积叫做底面积15、长方1、长方体的体积=底面积×高;V=sh1体的体积长方体的体积底面积=体积÷高;s=V÷h高=体积÷底面积;h==V÷s2、长方体的体积=长×宽×高;V=abh长=体积÷宽÷高(或长=体积÷(宽×高)) a=V÷b÷h或V÷﹙bh﹚宽=体积÷长÷高(或宽=体积÷(长×高)) b=V÷a÷h或V÷﹙ah﹚高=体积÷长÷宽(或高=体积÷(长×宽)) h=V÷a÷b或V÷﹙ab﹚16、立方体的体积正方体的体积=棱长×棱长×棱长=棱长³V = a×a×a=a³=sh17、通用体积公式正(长)方体的体积=底面积×高=sh18、表面积定义长(正)方体6个面的总面积叫作它的表面积前或后面的面积=长×高;左或右面的面积=宽×高;上或下面的面积=长×宽19、长方体表面积1、长方体表面积=长×宽×2+长×高×2+宽×高×2= 2(长×宽+长×高+宽×高)S表= 2ab+2ah+2b h= 2(ab+ah+bh)2、有一组对面是正方形的长方体:表面积=正方形边长×高×4+正方形边长²×2S表=2 a ²+4ah长方体表面积3、5个面的面积如粉刷教室、鱼缸等S=(长×高+宽×高)×2+长×宽4个面面积如:通风管、流水管等S=(长×宽+长×高)×220、生活实际油箱、罐头盒等都是6个面;游泳池、鱼缸等都只有5个面;水管、烟囱、通风管等都只有4个面。
(完整版)⼈教版⼩学五年级下册数学概念和公式五年级下册总复习基本概念和公式2、因数和倍数:如:5×6=30,我们就可以说5和6是30的因数,30是5和6 的倍数。
①⼀个数的因数个数是有限的。
⼀个数最⼩的因数是1,最⼤的因数是它本⾝,②⼀个数的倍数的个数是⽆限的。
⼀个数最⼩的倍数是它本⾝,没有最⼤的倍数,3、公因数:两个或⼏个数的共同有的因数叫公因数,最⼤的那个叫最⼤公因数。
公倍数:两个或⼏个数的共同有的倍数叫公倍数,最⼩的那个叫最⼩公倍数。
4、2的倍数特征:个位上是0、2、4、6、8的数都是2的倍数。
5的倍数特征:个位上是0或5的数都是5的倍数。
3的倍数特征:各个数位上的数的和是3的倍数,这个数就是3的倍数。
5、偶数:是2的倍数的数叫偶数。
“0”也是偶数。
奇数:不是2的倍数的数叫奇数。
6、质数:⼀个⾃然数,只有1和它本⾝两个因数的数叫质数,或叫素数。
合数:⼀个⾃然数,除了1和它本⾝还有别的因数的数叫合数。
1既不是质数也不是合数,最⼩的质数是2,最⼩的合数是4。
100以内的质数表:2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,7、把单位“1”平均分成若⼲份,表⽰其中⼀份或⼏份的数叫分数。
如:73表⽰把单位“1”平均分成(7)份,表⽰其中(3)份的数,73的分数单位是(71),有(3)这样的分数单位。
把3⽶长的绳⼦平均分成5份,每份占全长的(51),每段长(53)⽶。
8、1⽶的53等于3⽶的(51) 9、分数与除法的关系: BA =(A )÷(B),分数的分⼦相单于被除数,分数线相单于除号,分母相单于除数,分数值相单于商。
10、真分数:分⼦(⼩于)分母的数叫真分数。
假分数:分⼦(⼤于)或者(等于)分母的分数叫假分数。
最简分数:分⼦和分母只有公因数(1)的分数叫最简分数。
11、分数的基本性质:分数的分⼦和分母同时(乘上)或(除以)相同的数(0除外),分数的⼤⼩不变,这叫做分数的基本性质。
人教版小学生五年级数学知识点总结(8篇)还在苦恼没有小学五年级的知识点总结吗?在日常的学习中,是不是听到知识点,就立刻清醒了?知识点就是掌握某个问题/知识的学习要点。
下面是小编给大家整理的人教版小学生五年级数学知识点总结,仅供参考希望能帮助到大家。
人教版小学生五年级数学知识点总结篇11、长方形周长=(长+宽)×2 字母公式:C=(a+b)×2长方形面积=长×宽字母公式:S=ab2、正方形周长=边长×4 字母公式:C=4a正方形面积=边长×边长字母公式:S=a23、平行四边形的面积=底×高字母公式: S=ah4、三角形的面积=底×高÷2 字母公式: S=ah÷2(三角形的'底=面积×2÷高; 三角形的高=面积×2÷底)5、梯形的面积=(上底+下底)×高÷2 字母公式: S=(a+b)h÷2(上底=面积×2÷高-下底,下底=面积×2÷高-上底;高=面积×2÷(上底+下底) )注明:求三角形的底或高和梯形的上下底或高时,可根据公式列方程求解。
这样容易列出方程,也好理解。
6、三角形面积公式推导:平行四边形可以转化成一个长方形;两个完全一样的三角形可以拼成一个平行四边形,长方形的长相当于平行四边形的底;长方形的宽相当于平行四边形的高;因为长方形面积=长×宽,所以平行四边形面积=底×高,长方形的面积等于平行四边形的面积。
平行四边形的底相当于三角形的底;平行四边形的高相当于三角形的高;平行四边形的面积等于等底等高三角形面积的2倍。
7、两个完全一样的梯形可以拼成一个平行四边形。
平行四边形的底相当于梯形的上下底之和;平行四边形的高相当于梯形的高;平行四边形面积等于梯形面积的2倍,因为平行四边形面积=底×高,所以梯形面积=(上底+下底)×高÷28、等底等高的平行四边形面积相等;等底等高的三角形面积相等;等底等高的平行四边形面积是三角形面积的2倍。
人教版小学五年级数学上下册公式大全五年级上册数学公式小结第一单元:小数的乘法小数相乘时,积的小数位数等于两个因数的小数位数之和。
例如,3.45×6.29=21.7005.如果乘得的积小数末尾是零,则可以省略不写。
例如,3.65×6.72=24.528.第二单元:小数的除法当一个数(零除外)除以小于一的数时,商比被除数大。
当一个数(零除外)除以大于一的数时,商比被除数小。
两数相除时,如果除数是小数,被除数也是小数,除数将小数点向右移成整数,移了几位,被除数也就向右移动几位,相互抵消。
例如,2.36÷0.02=236÷2.小数部分的位数是无限小数,叫做无限小数。
例如,0.……就是一个无限小数。
第四单元:简易方程根据功效、时间和工作总量之间的关系,可以列出以下方程:功效×时间=工作总量工作总量÷功效=时间工作总量÷时间=功效例如,XXX一小时加工8个零件,他工作一天加工多少个零件?解:设王师傅工作一天加工x个零件,根据功效、时间和工作总量之间的关系,可以列出方程:功效×8= x,解得x=24×8=192.答案为:XXX工作一天加工192个零件。
根据路程、时间和速度之间的关系,可以列出以下方程:路程=时间×速度,用字母表示为s=vt。
例如,XXX和XXX家相距560米,学校在两家的中央,XXX和XXX在校门口分手,七分钟后他们同时到家,XXX 平均每分钟走45米,问小红平均每分钟走多少米?解:设小红平均每分钟走x米,根据路程、时间和速度之间的关系,可以列出方程:560=(x+45)×7,解得x=35.答案为:小红平均每分钟走35米。
等式不变的规律:方程两边同时加上或减去相同的数,左右两边仍然相等。
方程两边同时乘或除以相同的数(零除外),左右两边仍然相等。
第五单元:多边形的面积在计算多边形的面积时,需要注意以下单位换算关系:1千米=1000米1米=10分米1分米=10厘米1厘米=10毫米100公顷=1平方千米1平方千米=xxxxxxx平方米1平方米=100平方分米1公顷=平方米不同形状的多边形的面积计算公式如下:平行四边形的面积=底×高,用字母表示为s=ah。
五年级数学下册概念公式一、旋转、平移时针旋转1小时是30度二、因数与倍数1、如果a×b=c(a、b、c都是不为0的整数),那么a、b就是c得因数,c就是a、b的倍数。
2、一个数的因数个数是有限的,其中最小的因数是1,最大的因数是它本身。
一个数的倍数是无限的,其中最小的倍数是它本身,没有最大倍数。
3、奇数与偶数:自然数中,是2的倍数的数叫做偶数(0也是偶数),不是2的倍数的数叫做奇数。
偶数:个位是0,2,4,6,8的数。
奇数:个位不是0,2,4,6,8的数。
4、倍数特征:2的倍数的特征:各位是0,2,4,6,8。
3(或9)的倍数的特征:各个数位上的数之和是3(或9)的倍数。
5的倍数的特征:各位是0,5。
5、质数与合数:质数:一个数,如果只有1和它本身两个约数,这样的数叫做质数(或素数)。
合数:一个数,如果除了1和它本身还有别的约数,这样的数叫做合数。
1不是质数,也不是合数。
1既不是质数也不是合数。
6、奇数与偶数的运算规律偶数+偶数=偶数奇数+奇数=奇数奇数+偶数=奇数偶数-偶数=偶数奇数-奇数=奇数奇数-偶数=奇数偶数个偶数相加是偶数,奇数个奇数相加是奇数。
偶数×偶数=偶数奇数×奇数=奇数奇数×偶数=偶数7、质因数:如果一个质数是某个数的因数,那么这个质数就是这个数的质因数。
8、分解质因数:把一个合数用质因数相成的方式表示出来叫做分解质因数。
9、100以内的质数表:2、 3、 5、 7、 11、 13、17、1923、29、31、 37、 41、 43、47、5359、61、67、71、 73、 79、83、89、97三、长方体的认识、表面积、体积和容积1. 长方体有6个面,一般都是长方形(特殊情况有两个相对的面是正方形),相对的面面积相等;有8个顶点,12条棱,12条棱可以分为三组:4条长,4条宽,4条高。
2. 正方体有6个面,都是面积相等的正方形;有8个顶点,12条棱,每条棱的长度都相等。
小学五年级数学公式1. 速度×时间=路程;路程÷速度=时间;路程÷时间=速度2. 单价×数量=总价;总价÷单价=数量;总价÷数量=单价3.工作效率×工作时间=工作总量工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率4. 加数+加数=和,和-一个加数=另一个加数5.被减数-减数=差;被减数-差=减数;差+减数=被减数6. 因数×因数=积;积÷一个因数=另一个因数被除数÷除数=商;被除数÷商=除数;商×除数=被除数小学数学图形计算公式1 、正方形:C周长 S面积 a边长周长=边长×4 C=4a;面积=边长×边长 S=a×a2 、正方体:V:体积 a:棱长表面积=棱长×棱长×6 S表=a×a×6体积=棱长×棱长×棱长 V=a×a×a3 、长方形: C周长 S面积 a边长周长=(长+宽)×2 C=2(a+b);面积=长×宽 S=ab 重量单位换算1吨=1000 千克;1千克=1000克;1千克=1公斤人民币单位换算1元=10角;1角=10分;1元=100分时间单位换算1世纪=100年 1年=12月大月(31天)有:1\3\5\7\8\10\12月小月(30天)的有:4\6\9\11月平年2月28天, 闰年2月29天平年全年365天, 闰年全年366天1日=24小时 1时=60分1分=60秒 1时=3600秒小学数学几何形体周长面积体积计算公式1、长方形的周长=(长+宽)×2 C=(a+b)×22、正方形的周长=边长×4 C=4a3、长方形的面积=长×宽 S=ab4、正方形的面积=边长×边长 S=a.a= a5、三角形的面积=底×高÷2 S=ah÷26、平行四边形的面积=底×高 S=ah和差问题的公式(和+差)÷2=大数;(和-差)÷2=小数和倍问题和÷(倍数-1)=小数;小数×倍数=大数(或者和-小数=大数)差倍问题差÷(倍数-1)=小数;小数×倍数=大数(或小数+差=大数)相遇问题相遇路程=速度和×相遇时间相遇时间=相遇路程÷速度和速度和=相遇路程÷相遇时间长度单位换算1千米=1000米 1米=10分米1分米=10厘米 1米=100厘米1厘米=10毫米面积单位换算1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米小学数学定义定理公式(二)一、算术方面1.加法交换律:两数相加交换加数的位置,和不变.2.加法结合律:三个数相加,先把前两个数相加,或先把后两个数相加,再同第三个数相加,和不变.3.乘法交换律:两数相乘,交换因数的位置,积不变.4.乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相乘,再和第三个数相乘,它们的积不变.5.乘法分配律:两个数的和同一个数相乘,可以把两个加数分别同这个数相乘,再把两个积相加,结果不变.如:(2+4)×5=2×5+4×5.6.除法的性质:在除法里,被除数和除数同时扩大(或缩小)相同的倍数,商不变.0除以任何不是0的数都得0.7.等式:等号左边的数值与等号右边的数值相等的式子叫做等式.等式的基本性质:等式两边同时乘以(或除以)一个相同的数,等式仍然成立.8.方程式:含有未知数的等式叫方程式.1/ 1。
总复习;基本概念和公式
1、 因数和倍数:如:5×6=30,我们就可以说5和6是30的因数,30是5和6 的倍数。
①一个数最小的因数是1,最大的因数是它本身,因数的个数是有限的。
②一个数最小的倍数是它本身,没有最大的倍数,倍数的个数是无限的。
2、 公因数:两个或几个数的共同有的因数叫公因数,最大的那个叫最大公因数。
公倍数;两个或几个数的共同有的倍数叫公倍数,最小的那个叫最小公倍数。
3、2的倍数特征:个位上是0、2、
4、6、8的数都是2的倍数。
5的倍数特征:个位上是0或5的数都是5的倍数。
3的倍数特征:各个数位上的数的和是3的倍数,这个数就是3的倍数。
4、偶数:是2的倍数的数叫偶数。
奇数:不是2的倍数的数叫奇数。
5、质数:只有1和它本身两个因数的数叫质数,或叫素数。
合数:除了1和它本身还有别的因数的数叫合数。
︴1不是质数也不是合数,最小的质数是2,最小的合数是4.
︴100以内的质数表:
6、73表示把单位“1”平均分成( ),其中的( )份就是它的73
,它的分数单位是( ),有( )这样的分数单位。
把3米长的绳子平均分成5份,每份占全长的( ),每段长( )米。
7、1米的5
3等于3米的( ) 8、分数与除法的关系:B
A =( )÷( ) 9、真分数:分子( )分母的数叫真分数。
假分数:分子( )或者( )分母的分数叫假分数。
最简分数:分子和分母只有公因数( )的分数叫最简分数。
10、分数的基本性质:分数的分子和分母同时( )或( )相同的数(0
除外),分数的大小不变,这叫做分数的基本性质。
11、约分:把一个分数化成和它相等,但分子和分母都比较小的分数叫约分。
通分:把异分母分数分别化成和原来分数相等的同分母分数叫通分。
12、分数加减法:同分母分数加减:分母不变,分子相加减。
异分母分数加减:先通分变同分母,再分子相加减。
13、总棱长:长方体总棱长=(长+宽+高)×4
正方体总棱长=棱长×12
14、总面积:6个面的:长方体=(长×宽+长×高+宽×高)×2
(或长×宽×2+长×高×2+宽×高×2)
正方体=棱长×棱长×6
5个面的:长方体=长×宽+长×高×2+宽×高×2
正方体=棱长×棱长×5
4个面的:长方体=长×高×2+宽×高×2
正方体=棱长×棱长×4
15、体积和容积:长方体=长×宽×高
正方体=棱长×棱长×棱长
16、单位进率:
面积:1平方米=()平方分米体积:1立方米=()立方分米 1平方分米=()平方厘米 1立方分米=()立方厘米容积:1升(1L)=()立方分米
1毫升(1ml)=()立方厘米
1升=()毫升
()分()分()分()分()分
17、打电话:1人→ 2人→ 4人→()人→()人→()人
18、找次品:2 - 3个物品:测()次
4 - 9个物品:测()次
10 - 27个物品:测()次。