
对傅里叶分析的认识与应用
摘要:通过对傅里叶级数的学习与了解,我对傅里叶技级数的发现,推理与认识进行了归纳总结与演绎,并且在解决实际问题上进行了一些工作。 关键词:傅里叶级数;热传导方程;傅里叶分析
1. 引言
傅里叶级数通常指将一个周期为一的函数
2()
ikx e f x π-表示为:
11
sin 2cos 2n n n n n i
a A kx B kx ππ∞
∞
==++∑∑的形式的变换,当然周期也可以是2π,
2,l ∞什么的,都可以作此展开,而傅里叶级数中,中也有其完美的美学意义与历史价值,《死海古卷》里有句古话:“一个波动包含无数频率。”成分这也是对傅立叶级数的最好评价。更不用说用完美的正弦曲线绘制世界所给人带来的那种惊叹,周期运动,是宇宙中最常见的巧合。 2. 理论
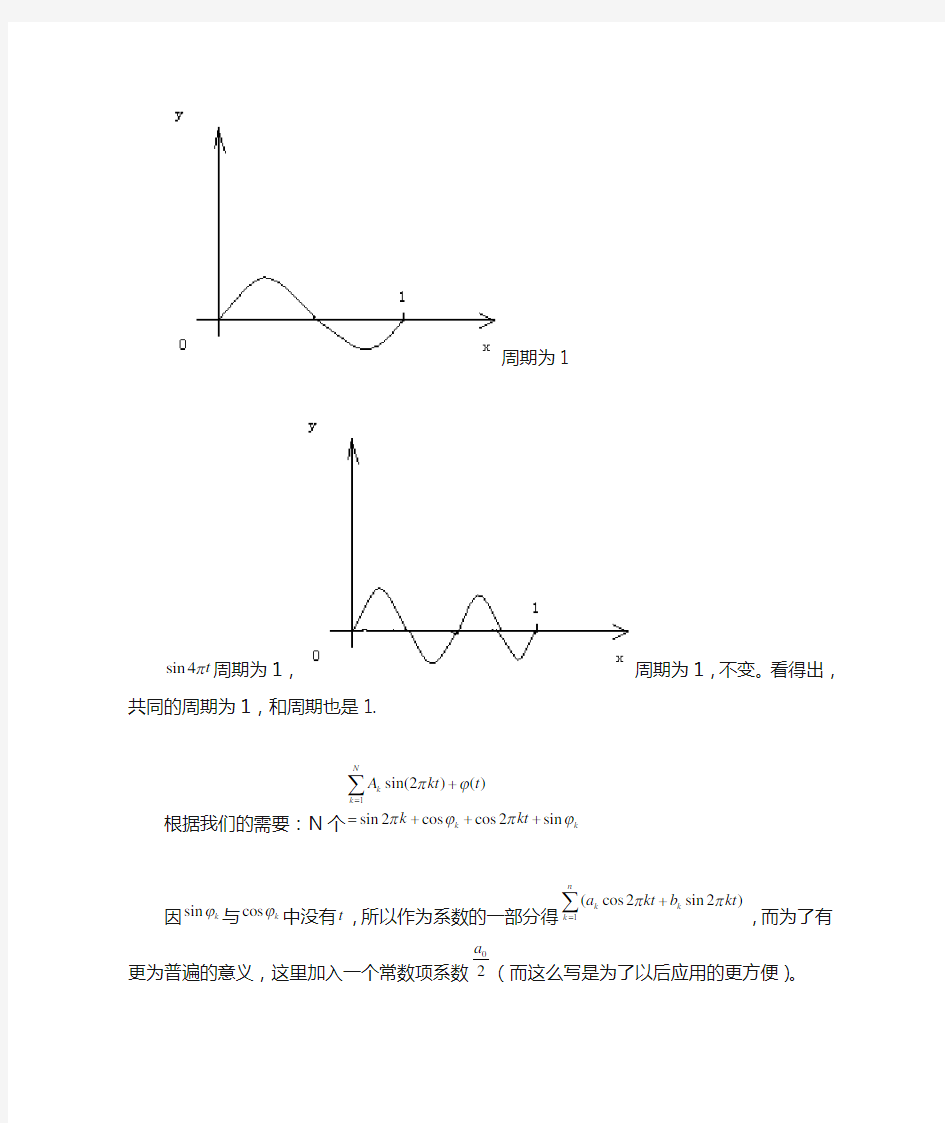
对于傅立叶级数的得出,我会通过自身认识进行展出,对于sin 2t π
周期为1
sin 4t π周期为1,周期为1,不
变。看得出,共同的周期为1,和周期也是1.
根据我们的需要:N 个1sin(2)()
sin 2cos cos 2sin N
k k k k
A kt t k kt π?π?π?=+=+++∑
因sin k ?与cos k ?中没有t ,所以作为系数的一部分得1(cos 2sin 2)n
k k k a kt b kt ππ=+∑,
而为了有更为普遍的意义,这里加入一个常数项系数0
2
a (而这么写是为了以后应用的更方便)。
01
(cos 2sin 2)2n
k k k a a kt b kt ππ=++∑ (1) 0
2
a 更像是交流电路中的直流分量。 一个函数用sin x 与cos x 表征,那么其实就是函数在sin x 与cos x 上的一种投影。就像()f x 在x 上的投影为()f x ,一条函数的曲线在空间中可以向任意一些坐标进行投影(只有这些坐标之间正交才有意义)而在傅里叶分析中,()f x 在
sin 2kt π与cos 2kt π所形成的无限维希尔伯特空间上进行n 次投影就得出了傅里
叶级数的各项系数。
2.1我们要证明这是一个合格的正交坐标系: 傅里叶级数将可能具有的系数:1,sin 2,cos 2kx kx ππ 分别取:
1,sin 2kx π 1
sin 20kxdx π=?
1,cos 2kx π 1
cos 20kxdx π=?
sin 2,cos 2kx kx ππ 1
sin 2cos 20kx kxdx ππ=?
由此可以证明所有基底相互正交。
2.2证明所求系数为()f x 在基底上的投影长度。
在1上 1
00()a f x dx =?
在sin 2kx π上 1
()sin 2n a f x kxdx π=?
在cos 2kx π上 1
()cos 2n b f x kxdx π=?
在2ikx
e
π上 1
20
()ikx n c f x e dx π=?
从上式得出,系数便是一种希尔伯特空间的投影取值。 对于2ikx e π2cos 2sin 2ikx e kx i kx πππ=+
22cos 22ikx ikx e e kx πππ-+= 22sin 22ikx ikx
e e kx i
πππ-+=
则(1)式变为:222201()222ikx ikx ikx ikx
n k k k a e e e e a b i
ππππ--=++++∑
2201()222n ikx ikx k k k k k a a ib a ib e e ππ-=-+=++∑ 2201
()2n
ikx ikx k k k a c e c e ππ--==++∑ 因为对称性原理k k c c *
-=
201
2n
ikx k k a c e π==+∑ 而对于其中一项系数m c 列出22()n
ikx
ikx m k k m
c e f x c e ππ≠=-∑-
同除得2ikx
e
π----
22()1
()n
imx
i k m x m k k c e
f x c e ππ--==-∑
积分:1
1
122()0
()n
ikx i k m x m k m
c dt f x e dx e dx ππ-≠=-∑
?
??
其
中,
10
1
2(
)
1
1()02()
2()
i k m x i k m x
i k m x
e dx e
e
e i k m i k m πππππ---=
=
-=--?
1
20
()imx m c e f x dx π=?
2.3总结:给一个()f x ,如果写出()f x =21
n
ikx k k c e π=∑
1
20
()ikx k c e f x dx π=?
而01
1
()n n n n f x a a b ∞∞
===++∑∑是在cos x 与sin x 为基底的态函数,此时不考虑cos x 与
sin x 同时为x 的函
数
两图中,()f x 不
发生变化,只有坐标发生了变化。
(,)(cos ,sin )f x y f x x →这里事实上就是傅里叶变换的过程
二.对原方程的认识
这个图很不陌生,可以用振动方程的
定解条件来解:002
2
121(,)sin sin cos n F
n x n x n t
u x t T n
l l l πππωπ
∞
==∑ 我们可以化简为:1
(,)sin
cos
n n n x n t
u x t B l l
ππ∞
==∑ 当0t =时,1
(,)sin
n n n x
u x t B l
π∞
==∑是图中折线的傅里叶级数00()sin L n x B u x dx
l π=?看得出,没有余弦分量,是奇函数,居然推出(0,
)x l ∈-时因为如图:
则当长为2l 的弦被
以图中的方式拉开,弦的方程与l 时并没有不同之处只是取值范围发生了延拓。
如果在[]0,1内可积,可以想象为点乘,由()1
0,()()f g f t g t dt =?当()f t 与()
g t 正交时,(),0f g = f 的模为f ()()()2
1
2
.f f f f t dt ==?
而勾股定理为
()2
2
2
f g f g +=+所以只有当(),0f g =勾股定理成立。
3.应用:
这里例举一个一维例子
圆环的初始温度为()f x
设:周期为1,即21r π=则(1)()f x f x += 令(,)u x t 为温度在x 与t 上的分布(t 为时间)
(,)u x t 就变成了周期函数:(1,)(,)u x t u x t +=
利用我们在数理方程上所学习的方程式:t xx u au = a = 因为u 为周期函数 2(,)()ikt
k
k u x t c t e
π∞
-=-∞
=∑
带入方程得:
22()2(0)k k c t k c π=-
由1
20()iky f e f y dy π-=? f 为傅里叶变换。
()2(,)ikx
k k u x t c t e π∞
=∞
=∑ t 在k c 中
()2ikx k k c t e π∞
=∞
=∑ 求出()k c t 即可(,)u x t
求k c
()'2ikt
t k
k u c t e
π∞
-=-∞
=
∑ 22()(2)n
ikx xx k k
u c t ik e ππ=∑
222()(4)n
ikx xx k k
u c t k e ππ=-∑
代入方程 :t xx u au =
2ikx
k
k c e
π∞
=∞
∑=2224()n
ikx k k
a k c t e ππ-∑
对应系数:'
22()4()k k c t a k c t π=- 为一阶线性微分方程
解得:2()(0)ikt k k c t c e π-=
引入初始条件()f x ()f x 2(0)n
ikx xx k k u c e π=∑ (0)()k c f k =
2222(,)()k t ikx
k u x t f k e
e ππ∞
-=-∞
=
∑
3. 小结
本文以课本知识为主,叙述了傅里叶级数的意义,虽然没有太多学术价值,但是在创作论文的过程中,笔者学到了,注意到了很多重要的意义,对于培养数学思维与兴趣产生了帮助,更对物理物理的学习产生了巨大帮助。
参考文献:
[1]梁昆淼.数学物理方法.高等教育出版社. [M].2010.1.第四版.
TO THE FOURIER SERIES
UNDERSTANDING AND APPLICATION
Abstract: By all semester’s learning and deliberate of the Fourier series. I had
summary and conclusion about the discovery and application .
Key words: Fourier series; Fourier Analysis; equation of heat conduction
傅里叶(Fourier )级数的指数形式与傅里叶变换 专题摘要:根据欧拉(Euler )公式,将傅里叶级数三角表示转化为指数表示,进而得到傅里叶积分定理,在此基础上给出傅里叶变换的定义和数学表达式。 在通信与信息系统、交通信息与控制工程、信号与信息处理等学科中,都需要对各种信号与系统进行分析。通过对描述实际对象数学模型的数学分析、求解,对所得结果给以物理解释、赋予其物理意义,是解决实际问题的关键。这种数学分析方法主要针对确定性信号的时域和频域分析,线性时不变系统的描述以及信号通过线性时不变系统的时域分析与变换域分析。所有这些分析方法都离不开傅里叶变换、拉普拉斯变换和离散时间系统的z 变换。而傅里叶变换的理论基础是傅里叶积分定理。傅里叶积分定理的数学表达式就是傅里叶级数的指数形式。 不但傅里叶变换依赖于傅里叶级数,就是纯数学分支的调和分析也来源于函数的傅里叶级数。因此,傅里叶级数无论在理论研究还是在实际应用中都占有非常重要的地位。我们承认满足狄里克莱(Dirichlet )条件下傅里叶级数的收敛性结果,不去讨论和深究傅里叶展式的唯一性问题。 傅里叶级数的指数形式 一个以T 为周期的函数)(t f ,在]2 ,2[T T 上满足狄里克莱条件:1o
)(t f 连续或只有有限个第一类间断点;2o 只有有限个极值点。那么)(t f 在]2 ,2[T T - 上就可以展成傅里叶级数。在连续点处 ∑∞ =++=1 )sin cos (2)(n n n t n b t n a a t f ωω, (1) 其中 T πω2= , ),2,1,0(,cos )(2 22Λ==?-n dt t n t f T a T T n ω, (2) ),3,2,1(,sin )(2 22 Λ==?-n dt t n t f T b T T n ω, (3) 根据欧拉(Euler )公式:θθθsin cos j e j +=,(1)式化为 ∑∞=--?? ????-+++=10222)(n t jn t jn n t jn t jn n j e e b e e a a t f ωωωω ∑∞=-?? ? ???++-+=10222n t jn n n t jn n n e jb a e jb a a ωω, (4) 若令 dt t f T c T T ?-=22 0)(1 Λ,3,2,1,)(1 ]sin )[cos (1 sin )(1cos )(1222 2222 22==-=-=-=????-----n dt e t f T dt t n j t n t f T dt t n t f T j dt t n t f T jb a c T T t jn T T T T T T n n n ωωωωω Λ,3,2,1,)(1 22 ==?--n dt e t f T c T T t jn n ω 综合n n c c c -,,0,可合并成一个式子 Λ,2,1,0,)(1 22 ±±==?--n dt e t f T c T T t jn n ω, (5)
傅里叶变换在信号处理中的应用 傅里叶变换在物理学、电子类学科、数论、组合数学、信号处理、
概率论、统计学、密码学、声学、光学、海洋学、结构动力学等领域都有着广泛的应用(例如在信号处理中,傅里叶变换的典型用途是将信号分解成幅值谱——显示与频率对应的幅值大小)。 尽管最初傅立叶分析是作为热过程的解析分析的工具,但是其思想方法仍然具有典型的还原论和分析主义的特征。"任意"的函数通过一定的分解,都能够表示为正弦函数的线性组合的形式,而正弦函数在物理上是被充分研究而相对简单的函数类,这一想法跟化学上的原子论想法何其相似!奇妙的是,现代数学发现傅立叶变换具有非常好的性质,使得它如此的好用和有用,让人不得不感叹造物的神奇: 1.傅立叶变换是线性算子,若赋予适当的范数,它还是酉算子; 2.傅立叶变换的逆变换容易求出,而且形式与正变换非常类似; 3.正弦基函数是微分运算的本征函数,从而使得线性微分方程的求解可以转化为常系数的代数方程的求解.在线性时不变的物理系统内,频率是个不变的性质,从而系统对于复杂激励的响应可以通过组合其对不同频率正弦信号的响应来获取; 4.著名的卷积定理指出:傅立叶变换可以化复杂的卷积运算为简单的乘积运算,从而提供了计算卷积的一种简单手段; 5.离散形式的傅立叶变换可以利用数字计算机快速的算出(其算法称为快速傅立叶变换算法(FFT)). 正是由于上述的良好性质,傅里叶变换在物理学、数论、组合数学、信号处理、概率、统计、密码学、声学、光学等领域都有着广泛的应用。
有関傅立叶变换的FPGA实现 傅立叶变换是数字信号处理中的基本操作,广泛应用于表述及分析离散时域信号领域。但由于其运算量与变换点数N的平方成正比关系,因此,在N较大时,直接应用DFT算法进行谱变换是不切合实际的。然而,快速傅立叶变换技术的出现使情况发生了根本性的变化。本文主要描述了采用FPGA来实现2k/4k/8k点FFT的设计方法。 离散傅里叶变换的应用 DFT在诸多多领域中有着重要应用,下面仅是颉取的几个例子。需要指出的是,所有DFT的实际应用都依赖于计算离散傅里叶变换及其逆变换的快速算法,即快速傅里叶变换(快速傅里叶变换(即FFT)是计算离散傅里叶变换及其逆变换的快速算法。)。 1.频谱分析 DFT是连续傅里叶变换的近似。因此可以对连续信号x(t)均匀采样并截断以得到有限长的离散序列,对这一序列作离散傅里叶变换,可以分析连续信号x(t)频谱的性质。前面还提到DFT应用于频谱分析需要注意的两个问题:即采样可能导致信号混叠和截断信号引起的频谱泄漏。可以通过选择适当的采样频率(见奈奎斯特频率)消减混叠。选择适当的序列长度并加窗可以抑制频谱泄漏。 2.数据压缩 由于人类感官的分辨能力存在极限,因此很多有损压缩算法利用
傅里叶分析之掐死教程(完整版)更新于2014.06.06 Heinrich · 6 个月前 作者:韩昊知乎:Heinrich 微博:@花生油工人知乎专栏:与时间无关的故事 谨以此文献给大连海事大学的吴楠老师,柳晓鸣老师,王新年老师以及张晶泊老师。 转载的同学请保留上面这句话,谢谢。如果还能保留文章来源就更感激不尽了。 我保证这篇文章和你以前看过的所有文章都不同,这是12年还在果壳的时候写的,但是当时没有来得及写完就出国了……于是拖了两年,嗯,我是拖延症患者…… 这篇文章的核心思想就是: 要让读者在不看任何数学公式的情况下理解傅里叶分析。 傅里叶分析不仅仅是一个数学工具,更是一种可以彻底颠覆一个人以前世界观的思维模式。但不幸的是,傅里叶分析的公式看起来太复杂了,所以很多大一新生
上来就懵圈并从此对它深恶痛绝。老实说,这么有意思的东西居然成了大学里的杀手课程,不得不归咎于编教材的人实在是太严肃了。(您把教材写得好玩一点会死吗?会死吗?)所以我一直想写一个有意思的文章来解释傅里叶分析,有可能的话高中生都能看懂的那种。所以,不管读到这里的您从事何种工作,我保证您都能看懂,并且一定将体会到通过傅里叶分析看到世界另一个样子时的快感。至于对于已经有一定基础的朋友,也希望不要看到会的地方就急忙往后翻,仔细读一定会有新的发现。 ——————————————以上是定场诗—————————————— 下面进入正题: 抱歉,还是要啰嗦一句:其实学习本来就不是易事,我写这篇文章的初衷也是希望大家学习起来更加轻松,充满乐趣。但是千万!千万不要把这篇文章收藏起来,或是存下地址,心里想着:以后有时间再看。这样的例子太多了,也许几年后你都没有再打开这个页面。无论如何,耐下心,读下去。这篇文章要比读课本要轻松、开心得多…… p.s.本文无论是cos还是sin,都统一用“正弦波”(Sine Wave)一词来代表简谐波。 一、什么是频域 从我们出生,我们看到的世界都以时间贯穿,股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法我们称其为时域分析。而我们也想当然的认为,世间万物都在随着时间不停的改变,并且永远不会静止下来。但如果我告诉你,用另一种方法来观察世界的话,你会发现世界是永恒不变的,你会不会觉得我疯了?我没有疯,这个静止的世界就叫做频域。 先举一个公式上并非很恰当,但意义上再贴切不过的例子: 在你的理解中,一段音乐是什么呢?
毕业论文 题目:傅里叶级数及其应用作者:姜广辉 指导教师:李博 职称:讲师 院系:理学院数学系 专业:数学与应用数学 班级:10级1班 日期: 2014年5月
傅里叶级数及其应用 摘要:傅里叶级数是数学分析中的一个重要概念,具有较好的几何和代数性质,伴随着科技的进步与发展,涉及了许多数学命题的讨论和应用,傅里叶级数的相关知识已经成为从事科学研究和工程设计等科技人员必备的数学基础.通过对傅里叶、拉格朗日、狄利克雷、黎曼等人在傅里叶级数方面的贡献,介绍了傅里叶级数起源和发展历程.同时文章以在图案设计和铁路客运量预测上的应用说明了傅里叶级数的价值.在图案设计设计方面,运用MATLAB软件,编写傅里叶级数的程序语言,通过自定义函数、编写画图函数程序、对图形多余部分处理、图形线条加粗等步骤,进而得到傅里叶级数的图形.通过对最基本的傅里叶级数的图形的组合、排列可以构成丰富的图案.在铁路客运量预测方面,基于傅里叶级数预测模型,以我国2004—2009年铁路客运量为数据基础,通过将时间序列划分为趋势性和季节性部分,分别采用最小二乘法和傅里叶级数预测法对两者进行拟合,应用MATLAB软件,求出预测模型,并进行预测.通过对预测结果的误差分析,表明:采用傅里叶级数预测法预测我国铁路客运量的效果较好.因此傅里叶级数在一定程度上受到了很多数学家的欢迎. 关键词:傅里叶级数;收敛性;MATLAB软件;图案设计;预测模型
Fourier series and its applications Abstract:Fourier series is a mathematical analysis of an important concept,and has good geometry and algebraic properties,along with the progress and development of technology,involving a lot of discussion and application of mathematical propositions,Fourier series of relevant knowledge has become a mathematical foundation for scientific research and engineering design and other technical personnel necessary. Through Fourier,Lagrange,Dirichlet, Riemann,who contribute in terms of Fourier series,Fourier series introduces the origin and development process,while the article in the graphic design and rail application passenger traffic forecast illustrates the value of the Fourier series. In the design of graphic design,the use of MATLAB software program written in the language of Fourier series,via a custom function,the preparation process of drawing functions,the excess part of the graphics processing,graphics,bold lines and other steps,then get the Fourier series pattern by the combination of the basic pattern of the Fourier series,the arrangement may constitute a rich patterns. Railway passenger traffic forecast,prediction model based on Fourier series to the railway passenger traffic volume of 2004-2009 data base,by the time series into trend and seasonal part,respectively,using the least squares method and fourier Fourier series prediction method for both fitting using MATLAB software,find the prediction model and predict the outcome of the prediction error by analysis showed that:Fourier series prediction method to predict the effect of China's railway passenger volume better. So to some extent,the Fourier series has been welcomed by many mathematicians. Keywords:Fourier series;convergence;MATLAB software;graphic design;prediction model
傅里叶变换在信号处理中的应用 姓名董柱班级电气工程及其自动化学号1109141013 摘要: 傅里叶变换是一种特殊的积分变换。通过傅里叶变换把信号的从时域变换到频域研究,采用频域法较之经典时域的方法有很多突出的优点,虽然傅里叶分析不是信息科学与技术领域中唯一的变换域方法,但是不得不承认,在此领域中,傅里叶变换分析始终有着广泛的应用,通过傅里叶变换实现信号的滤波,调制,抽样是傅里叶变换在信号处理中最主要的作用。通过对信号的调制可以将信号的低频成分调制到高频,实现频谱搬移,减少马间串扰,提高抗噪声新能,有利于信号的远距离传输,另外,对信号采样可以使连续信号离散化,有利于用计算机对信号进行处理,总之,傅里叶变换在信号处理中有着非常重要的作用。傅里叶变换是学习其他频域变换的基础。 关键词: 傅里叶变换,时域,频域,信号处理,信息科学与技术,滤波,调制,抽样。 一傅里叶变换 1.定义 f(t)是t的函数,如果t满足狄里赫莱条件:具有有限个间断点;具有有限个极值点;绝对可积。则有下图①式成立。称为积分运算f(t)的傅立叶变换, ②式的积分运算叫做F(ω)的傅立叶逆变换。F(ω)叫做f(t)的像函数,f(t)叫做 F(ω)的像原函数。F(ω)是f(t)的像。f(t)是F(ω)原像。 ① 傅里叶变换 傅里叶逆变换 2.分类 连续傅立叶变换:一般情况下,若“傅立叶变换”一词的前面未加任何限定语,则指的是“连续傅立叶变换”。“连续傅立叶变换”将平方可积的函数f(t) 表示成复指数函数的积分或级数形式。 f(t) = \mathcal^[F(ω)] = \frac{\sqrt{2π}} \int\limits_{-\infty}^\infty F(ω)e^{iωt}\,dω.
实验二傅里叶分析及应用 姓名学号班级 一、实验目的 (一)掌握使用Matlab进行周期信号傅里叶级数展开和频谱分析 1、学会使用Matlab分析傅里叶级数展开,深入理解傅里叶级数的物理含义 2、学会使用Matlab分析周期信号的频谱特性 (二)掌握使用Matlab求解信号的傅里叶变换并分析傅里叶变换的性质 1、学会运用Matlab求连续时间信号的傅里叶变换 2、学会运用Matlab求连续时间信号的频谱图 3、学会运用Matlab分析连续时间信号的傅里叶变换的性质 (三)掌握使用Matlab完成信号抽样并验证抽样定理 1、学会运用MATLAB完成信号抽样以及对抽样信号的频谱进行分析 2、学会运用MATLAB改变抽样时间间隔,观察抽样后信号的频谱变化 3、学会运用MATLAB对抽样后的信号进行重建 二、实验条件 需要一台PC机和一定的matlab编程能力 三、实验内容 2、分别利用Matlab符号运算求解法和数值计算法求下图所示信号的FT,并画出其频谱图(包括幅度谱和相位谱)[注:图中时间单位为:毫秒(ms)]。
符号运算法: Ft= sym('t*(Heaviside(t+2)-Heaviside(t+1))+Heaviside(t+1)-Heaviside(t-1)+(-t)*(Heavi side(t-1)-Heaviside(t-2))'); Fw = fourier(Ft); ezplot(abs(Fw)),grid on; phase = atan(imag(Fw)/real(Fw)); ezplot(phase);grid on; title('|F|'); title('phase'); 3、试用Matlab 命令求ω ωωj 54 -j 310)F(j ++= 的傅里叶反变换,并绘出其时域信号图。
河北联合大学 本科毕业设计(论文) 题目傅里叶变换在信号与系统中的应用 院系理学院 专业班级07数学一班 学生姓名刘帅 学生学号200710050113 指导教师佟玉霞 2011年5月24日
题目傅里叶变换在信号与系统中的应用 专业数学与应用数学姓名刘帅学号200710050113 主要内容、基本要求、主要参考资料等 主要内容 傅里叶变换是一种重要的变换,且在与通信相关的信号与系统中有着广泛的应用。本文主要研究傅里叶变换的基本原理;其次,掌握其在滤波,调制、解调,抽样等方面中的应用。分析了信号在通信系统中的处理方法,通过傅里叶变换推导出信号调制解调的原理,由此引出对频分复用通信系统的组成原理的介绍。 基本要求 通过傅里叶变换实现一个高通滤波,低通滤波,带通滤波。用傅里叶变换推导出信号调制解调的原理。通过抽样实现连续信号离散化,简化计算。另外利用调制的原理推导出通信系统中的时分复用和频分复用。 参考资料 [1]《信号与系统理论、方法和应用》徐守时著中国科技大学出版社 2006年3月修订二版 [2]《信号与系统》第二版上、下册郑君里、应启珩、杨为理著高等教育出版社 [3]《通信系统》第四版 Simon Haykin 著宋铁成、徐平平、徐智勇等译沈 连丰审校电子工业出版社 [4]《信号与系统—连续与离散》第四版 Rodger E.Ziemer 等著肖志涛等译 腾建辅审校电子工业出版社 [5]《现代通信原理》陶亚雄主编电子工业出版社 [6]《信号与系统》乐正友著清华大学出版社 [7]《信号与线性系统》阎鸿森、王新风、田惠生编西安交通大学出版社 [8]《信号与线性系统》张卫钢主编郑晶、徐琨、徐建民副主编西安电 子科技大学出版社 [9] https://www.doczj.com/doc/f39739355.html,/view/191871.htm//百度百科傅里叶变换 [10]《通信原理》第六版樊昌信曹丽娜编著国防工业出版社 [11]A.V.Oppenheim,A.S.Willsky with S.H.Nawab.Siganals and systems(Second edition).Prentice-Hall,1997.中译:刘树棠。信号与系统。西安交通工业大学出版社 完成期限 指导教师 专业负责人
M A T L A B实验二傅里叶 分析及应用 Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】
实验二傅里叶分析及应用 一、实验目的 (一)掌握使用Matlab进行周期信号傅里叶级数展开和频谱分析 1、学会使用Matlab分析傅里叶级数展开,深入理解傅里叶级数的物理含义 2、学会使用Matlab分析周期信号的频谱特性 (二)掌握使用Matlab求解信号的傅里叶变换并分析傅里叶变换的性质 1、学会运用Matlab求连续时间信号的傅里叶变换 2、学会运用Matlab求连续时间信号的频谱图 3、学会运用Matlab分析连续时间信号的傅里叶变换的性质 (三)掌握使用Matlab完成信号抽样并验证抽样定理 1、学会运用MATLAB完成信号抽样以及对抽样信号的频谱进行分析 2、学会运用MATLAB改变抽样时间间隔,观察抽样后信号的频谱变化 3、学会运用MATLAB对抽样后的信号进行重建 二、实验条件 Win7系统,MATLAB R2015a 三、实验内容 1、分别利用Matlab符号运算求解法和数值计算法求下图所示信号的FT,并画出其频谱图(包括幅度谱和相位谱)[注:图中时间单位为:毫秒(ms)]。
符号运算法
t (20 π ex p(-3 t) heaviside(t) - 8 π ex p(-5 t) heaviside(t))/(2 π) 数值运算法 2、试用Matlab 命令求ω ωωj 54 -j 310)F(j ++=的傅里叶反变换,并绘出其时域信 号图。 两个单边指数脉冲的叠加 3、已知门函数自身卷积为三角波信号,试用Matlab 命令验证FT 的时域卷积定理 。
傅里叶变换在MATLZB里的应用 摘要:在现代数学中,傅里叶变换是一种非常重要的变换,且在数字信号处理中有着广泛的应用。本文首先介绍了傅里叶变换的基本概念、性质及发展情况;其次,详细介绍了分离变数法及积分变换法在解数学物理方程中的应用。傅立叶变换将原来难以处理的时域信号转换成了易于分析的频域信号,再利用傅立叶反变换将这些频域信号转换成时域信号。应用MATLAB实现信号的谱分析和对信号消噪。 关键词:傅里叶变换;MA TLAB软件;信号消噪 Abstract: In modern mathematics,Fourier transform is a transform is very important ,And has been widely used in digital signal processing.This paper first introduces the basic concepts, properties and development situation of Fourier transform ;Secondly, introduces in detail the method of separation of variables and integral transform method in solving equations in Mathematical Physics.Fourier transformation makes the original time domain signal whose analysis is difficult easy, by transforming it into frequency domain signal that can be transformed into time domain signal by inverse transformation of Fourier. Using Mat lab realizes signal spectral analysis and signal denoising. Key word: Fourier transformation, software of mat lab ,signal denoising 1、傅里叶变换的提出及发展 在自然科学和工程技术中为了把较复杂的运算转化为较简单的运算,人们常常采用所谓变换的方法来达到目的"例如在初等数学中,数量的乘积和商可以通过对数变换化为较简单的加法和减法运算。在工程数学里积分变换能够将分析运算(如微分,积分)转化为代数运算,正是积分变换这一特性,使得它在微分方程和其它方程的求解中成为重要方法之一。 1804年,法国科学家J-.B.-J.傅里叶由于当时工业上处理金属的需要,开始从事热流动的研究"他在题为<<热的解析理论>>一文中,发展了热流动方程,并且指出如何求解"在求解过程中,他提出了任意周期函数都可以用三角级数来表示的想法。他的这种
1.前言 1.1背景 利用变换可简化运算,比如对数变换,极坐标变换等。 类似的,变换也存在于工程,技术领域,它就是积分变换。 积分变换的使用,可以使求解微分方程的过程得到简化, 比如乘积可以转化为卷积。什么是积分变换呢?即为利用 含参变量积分,把一个属于A函数类的函数转化属于B函 数类的一个函数。傅里叶变换和拉普拉斯变换是两种重要 积分变换。分析信号的一种方法是傅立叶变换,傅里叶变换能 够分析信号的成分,也能够利用成分合成信号。可以当做信号 的成分的波形有很多,例如锯齿波,正弦波,方波等等。傅立 叶变换是利用正弦波来作为信号的成分。 拉普拉斯变换最早由法国数学家天文学家 Pierre Simon Laplace (拉普拉斯)(1749-1827)在他的与概率论相关科学研究 中引入,在他的一些基本的关于拉普拉斯变换的结果写在 他的著名作品《概率分析理论》之中。即使在19世纪初, 拉普拉斯变换已经发现,但是关于拉普拉斯变换的相关研 究却一直没什么太大进展,直至一个英国数学家,物理学 家,同时也是一位电气工程师的Oliver Heaviside奥利 弗·亥维赛(1850-1925)在电学相关问题之中引入了算 子运算,而且得到了不少方法与结果,对于解决现实问题 很有好处,这才引起了数学家对算子理论的严格化的兴 趣。之后才创立了现代算子理论。算子理论最初的理论依 据就是拉普拉斯变换的相关理论,拉普拉斯变换相关理论 的继续发展也是得益于算理理论的更进一步发展。这篇文 章就是针对傅里叶变换和拉普拉斯变换的相关定义,相关 性质,以及相关应用做一下简要讨论,并且分析傅里叶变 换和拉普拉斯变换的区别与联系。 1.2预备知识
快速傅里叶变换的原理及其应用 摘要 快速傅氏变换(FFT),是离散傅氏变换的快速算法,它是根据离散傅氏变换的奇、偶、虚、实等特性,对离散傅立叶变换的算法进行改进获得的。它对傅氏变换的理论并没有新的发现,但是对于在计算机系统或者说数字系统中应用离散傅立叶变换,可以说是进了一大步。傅里叶变换的理论与方法在“数理方程”、“线性系统分析”、“信号处理、仿真”等很多学科领域都有着广泛应用,由于计算机只能处理有限长度的离散的序列,所以真正在计算机上运算的是一种离散傅里叶变换. 虽然傅里叶运算在各方面计算中有着重要的作用,但是它的计算过于复杂,大量的计算对于系统的运算负担过于庞大,使得一些对于耗电量少,运算速度慢的系统对其敬而远之,然而,快速傅里叶变换的产生,使得傅里叶变换大为简化,在不牺牲耗电量的条件下提高了系统的运算速度,增强了系统的综合能力,提高了运算速度,因此快速傅里叶变换在生产和生活中都有着非常重要的作用,对于学习掌握都有着非常大的意义。 关键词快速傅氏变换;快速算法;简化;广泛应用
Abstract Fast Fourier Transform (FFT), is a discrete fast Fourier transform algorithm, which is based on the Discrete Fourier Transform of odd and even, false, false, and other characteristics of the Discrete Fourier Transform algorithms improvements obtained. Its Fourier transform theory has not found a new, but in the computer system or the application of digital systems Discrete Fourier Transform can be said to be a big step into. Fourier transform theory and methods in the "mathematical equation" and "linear systems analysis" and "signal processing, simulation," and many other areas have a wide range of applications, as the computer can only handle a limited length of the sequence of discrete, so true On the computer's operation is a discrete Fourier transform. Fourier Although all aspects of computing in the calculation has an important role, but its calculation was too complicated, a lot of computing system for calculating the burden is too large for some Less power consumption, the slow speed of operation of its system at arm's length, however, have the fast Fourier transform, Fourier transform greatly simplifying the making, not in power at the expense of the conditions to increase the speed of computing systems, and enhance the system The comprehensive ability to improve the speed of operation, the Fast Fourier Transform in the production and life have a very important role in learning to master all have great significance. Key words Fast Fourier Transform; fast algorithm; simplified; widely used
傅立叶变换在图像处理中有非常非常的作用。因为不仅傅立叶分析涉及图像处理的很多方面,傅立叶的改进算法, 比如离散余弦变换,gabor与小波在图像处理中也有重要的分量。 印象中,傅立叶变换在图像处理以下几个话题都有重要作用: 1.图像增强与图像去噪 绝大部分噪音都是图像的高频分量,通过低通滤波器来滤除高频——噪声; 边缘也是图像的高频分量,可以通过添加高频分量来增强原始图像的边缘; 2.图像分割之边缘检测 提取图像高频分量 3.图像特征提取: 形状特征:傅里叶描述子 纹理特征:直接通过傅里叶系数来计算纹理特征 其他特征:将提取的特征值进行傅里叶变换来使特征具有平移、伸缩、旋转不变性 4.图像压缩 可以直接通过傅里叶系数来压缩数据;常用的离散余弦变换是傅立叶变换的实变换; 傅立叶变换 傅里叶变换是将时域信号分解为不同频率的正弦信号或余弦函数叠加之和。连续情况下要求原始信号在一个周期内满足绝对可积条件。离散情况下,傅里叶变换一定存在。冈萨雷斯版<图像处理>里面的解释非常形象:一个恰当的比喻是将傅里叶变换比作一个玻璃棱镜。棱镜是可以将光分解为不同颜色的物理仪器,每个成分的颜色由波长(或频率)来决定。傅里叶变换可以看作是数学上的棱镜,将函数基于频率分解为不同的成分。当我们考虑光时,讨论它的光谱或频率谱。同样,傅立叶变换使我们能通过频率成分来分析一个函数。 傅立叶变换有很多优良的性质。比如线性,对称性(可以用在计算信号的傅里叶变换里面); 时移性:函数在时域中的时移,对应于其在频率域中附加产生的相移,而幅度频谱则保持不变; 频移性:函数在时域中乘以e^jwt,可以使整个频谱搬移w。这个也叫调制定理,通讯里面信号的频分复用需要用到这个特性(将不同的信号调制到不同的频段上同时传输); 卷积定理:时域卷积等于频域乘积;时域乘积等于频域卷积(附加一个系数)。(图像处理里面这个是个重点) 信号在频率域的表现 在频域中,频率越大说明原始信号变化速度越快;频率越小说明原始信号越平缓。当频率为0时,表示直流信号,没有变化。因此,频率的大小反应了信号的变化
傅里叶级数 本文意在阐述傅里叶级数是什么,如何通过数学推导得出,以及傅里叶级数代表的物理含义。 1.完备正交函数集 要讨论傅里叶级数首先得讨论正交函数集。如果n个函数 φ1t,φ2t,…,φn t构成一个函数集,若这些函数在区间t1,t2上满足 φi tφj t t2 t1dt= 0 ,i≠j K i ,i=j(1) 如果是复数集,那么正交条件是 φi tφj?t t2 t1dt= 0 ,i≠j K i ,i=j(2) φj?t为函数φj t的共轭复函数。 有这个定义,我们可以证明出一些函数集是完备正交函数集。比如三角函数集和复指数函数集在一个周期内是完备正交函数集。 先证明三角函数集: 设φn t=cos nωt,φm t=cos mωt,把φn t,φm t代入(1)得 φi tφj t t0+T t0dt=cos nωt cos mωt dt t0+T t0 当n≠m时 =1 2 cos n+mωt+cos n?mωt t0+T t0 dt =1 2sin n+mωt (n+m)ω +sin n?mωt (n?m)ωt t0+T =0 (n,m=1,2,3,…,n≠m) 当n=m时 =1 2 cos2nωt t0+T t0 dt =T 2 再证两个都是正弦的情况 设φn t=sin nωt,φm t=sin mωt,把φn t,φm t代入(1)得 φi tφj t t0+T t0dt=sin nωt sin mωt dt t0+T t0 当n≠m时
=1 2 cos n+mωt?cos n?mωt t0+T t0 dt =1 2sin n+mωt (n+m)ω ?sin n?mωt (n?m)ωt t0+T =0 (n,m=1,2,3,…,n≠m) 当n=m时 =1 2 cos2nωt t0+T t0 dt =T 2 最后证明两个是不同名的三角函数的情况 设φn t=cos nωt,φm t=sin mωt,把φn t,φm t代入(1)得 φi tφj t t0+T t0dt=cos nωt sin mωt dt t0+T t0 =1 2 sin n+mωt?sin n?mωt t0+T t0 dt =1 2 ?cos n+mωt (n+m)ω +cos n?mωt (n?m)ωt t0+T =0 (n,m为任意整数) 因为两个三角函数相乘只有以上三种情况:两个皆为余弦函数相乘;两个皆为正弦函数相乘;一个为正弦函数,另一个为余弦函数相乘;三种情况皆满足正交函数集的定义,所以三角函数集为正交函数集。至于三角函数集的完备性可以从n,m的取值为任意整数可以得出,三角函数集是完备正交函数集。证毕。 由于三角函数集是完备正交函数集,而根据欧拉公式,我们容易联想到复指数函数集是否也是完备正交函数集呢。 接着是复指数函数集的证明 设φn t=?jnωt,φm t=?jmωt,则φj?t=??jmωt把φn t,φj?t代入(2)得 φi tφj?t t0+T t0dt=?jnωt t0+T t0 ??jmωt dt =?j(n?m)ωt t0+T t0 dt 当n≠m时,根据欧拉公式 =cos n?mωt+j sin?(n?m)ωt t0+T t0 dt =sin n?mωt n?mω?j cos?(n?m)ωt n?mωt t0+T =0 (n,m=1,2,3,…,n≠m)
图像傅里叶变换 冈萨雷斯版<图像处理>里面的解释非常形象:一个恰当的比喻是将傅里叶变换比作一个玻璃棱镜。棱镜是可以将光分解为不同颜色的物理仪器,每个成分的颜色由波长(或频率)来决定。傅里叶变换可以看作是数学上的棱镜,将函数基于频率分解为不同的成分。当我们考虑光时,讨论它的光谱或频率谱。同样, 傅立叶变换使我们能通过频率成分来分析一个函数。 Fourier theory讲的就是:任何信号(如图像信号)都可以表示成一系列正弦信号的叠加,在图像领域就是将图像brightness variation 作为正弦变量。比如下图的正弦模式可在单傅里叶中由三个分量编码:频率f、幅值A、相位γ这 三个value可以描述正弦图像中的所有信息。1.frequency frequency在空间域上可由亮度调节,例如左图的frequency比右图的frequency 低…… 2.幅值magnitude(amplitude)sin函数的幅值用于描述对比度,或者说是图像中最明和最暗的峰值之间的差。(一个负幅值表示一个对比逆转,即明暗交换。) 3.相位表示相对于原始波形,这个波形的偏移量(左or右)。=================================================================一个傅里叶变换编码是一系列正弦曲线的编码,他们的频率从0开始(即没有调整,相位为0,平均亮度处),到尼奎斯特频率(即数字图像中可被编码的最高频率,它和像素大小、resolution有关)。傅里叶变换同时将图像中所有频率进行编码:一个只包含一个频率f1的信号在频谱上横坐标f为f1的点处绘制一个单峰值,峰值高度等于对应的振幅amplitude,或者正弦曲线信号的高度。如下图所示。
傅里叶分析应用于热传导问题 (物理系 郭素梅 指导教师 陆立柱) 〔摘要〕 傅里叶分析是一种重要的数学工具,本文综述了用傅里叶分析解决细杆的热传导问题,并进行了讨论。傅里叶分析包括傅里叶级数和傅里叶积分,用傅里叶级数法解决有界细杆的热传导问题,用含参数的傅里叶变换法解决无界细杆的热传导问题,比其它方法更系统,体现出一种数学与物理对应的美感。 〔关键词〕 傅里叶级数 傅里叶积分 傅里叶变换 细杆的热传导问题 引言 1822年,傅里叶在研究热传导问题时,创造了傅里叶分析,随着时代的进步,这一数学工具被广泛地应用于信号分析、匹配滤波、图象处理等方面,掌握这种具有广泛用途和发展前景的工具是十分必要的.热传导是历来研究的热点,尤其是随着计算机电子设备的高集成化发展,机器内发热部件和集成电路元件的发热量随之增加,传统的强制冷方式已不能达到理想效果,因此,热传导设计成了重要问题。万变不离其宗,为了更好地掌握傅里叶分析,为了更好地掌握热传导问题,本文就一维热传导问题对傅里叶分析作了全面详尽的论述。 1. 傅里叶分析 1.1 傅里叶级数 傅里叶级数在应用上有以下优点[1] :能表示不连续的函数、周期函数,能对任意函数作调 和分析。 若函数()f x 以2l 为周期,即 (2)()f x l f x +=[2] (1.1.1) 则可取三角函数族 1, cos x l π,cos 2x l π, … cos n x l π ,… sin x l π,sin 2x l π, … sin n x l π , … (1.1.2) 作为基本函数族,将()f x 展开为级数 [3] ()f x =0a + 1 (n n a ∞ =∑cos n x l π+n b cos n x l π) (1.1.3) 可以证明,函数族(1.1.2)是正交完备的[4] 。根据三角函数族的正交性,可求得(1.1.3)中的展 开系数为
实验二傅里叶分析及应用 一、实验目的 (一)掌握使用Matlab进行周期信号傅里叶级数展开和频谱分析 1、学会使用Matlab分析傅里叶级数展开,深入理解傅里叶级数的物理含义 2、学会使用Matlab分析周期信号的频谱特性 (二)掌握使用Matlab求解信号的傅里叶变换并分析傅里叶变换的性质 1、学会运用Matlab求连续时间信号的傅里叶变换 2、学会运用Matlab求连续时间信号的频谱图 3、学会运用Matlab分析连续时间信号的傅里叶变换的性质 (三)掌握使用Matlab完成信号抽样并验证抽样定理 1、学会运用MATLAB完成信号抽样以及对抽样信号的频谱进行分析 2、学会运用MATLAB改变抽样时间间隔,观察抽样后信号的频谱变化 3、学会运用MATLAB对抽样后的信号进行重建 二、实验条件 安装winXP系统的电脑一台、matlab 7.0软件 三、实验内容 1、已知周期三角信号如下图所示[注:图中时间单位为:毫秒(ms)]: (1)试求出该信号的傅里叶级数[自己求或参见课本P112或P394],利用Matlab编程实现其各次谐波[如1、3、5、13、49]的叠加,并验证其收敛性;
解: 命令文件: clear all;close all;clc; t=-10:0.01:10; omega=pi; y=abs(sawtooth(pi*0.5*t,0.5)); plot(t,y),grid on; axis([-10,10,0,3]); n_max=[1,3,5,13,49]; N=length(n_max); for k=1:N n=1:2:n_max(k); b=4./((pi*n).^2); x=b*cos(omega*n'*t); figure; plot(t,y); hold on; x=x+1/2; plot(t,x); hold off; axis([-10,10,0,3]); title(['最大谐波数=',num2str(n_max(k))]); end 图像:
周期信号的傅里叶级数分析 连续时间LTI 系统的时域分析: 以冲激函数为基本信号 系统零状态响应为输入信号与系统冲激响应之卷积 傅立叶分析 以正弦函数或复指数函数作为基本信号 系统零状态响应可表示为一组不同频率的正弦函数或复指数函数信号响应的加权和或积分; 周期信号: 定义在区间 (,)-∞∞ ,每隔一定时间 T ,按相同 规律重复变化的信号,如图所示 。它可表示为 f (t )=f ( t +m T ) 其中 m 为正整数, T 称为信号的周期,周期的倒数称为频率。 t ()t f 1 1 -T 2 /T 0 周期信号的特点: (1) 它是一个无穷无尽变化的信号,从理论上也是无始无终的,时 间范围为(,)-∞∞ (2) 如果将周期信号第一个周期内的函数写成 ,则周期信 号 ()f t 可以写成
0()() n f t f t nT ∞ =-∞ = -∑ (3)周期信号在任意一个周期内的积分保持不变,即有 ()()()a T b T T a b f t dt f t dt f t dt ++= =? ? ? 1. 三角形式的傅立叶级数 周期信号 f t () ,周期为1T ,角频率 11122T f π πω= = 该信号可以展开为下式三角形式的傅立叶级数。 []∑∞ =++ =++++++++=1 1 1 011121211110)sin()cos(...)sin()cos(... )2sin()2cos()sin()cos()(n n n n n t n b t n a a t n b t n a t b t a t b t a a t f ωωωωωωωω 式中各正、余弦函数的系数 n n b a , 称为傅立叶系数,函数通过它可以完全表示。 傅立叶系数公式如下