遗传算法(大作业)

人工智能试验陈述学号：姓名：试验名称：遗传算法试验日期： 2016.1.5【试验名称】遗传算法【试验目标】控制遗传算法的基起源基础理,熟习遗传算法的运行机制,学会用遗传算法来求解问题.【试验道理】遗传算法（Genetic Algorithm）是模仿达尔文生物进化论的天然选择和遗传学机理的生物进化进程的盘算模子,是一种经由过程模仿天然进化进程搜刮最优解的办法.遗传算法是从代表问题可能潜在的解集的一个种群开端的,而一个种群则由经由基因编码的必定命目标个别构成.每个个别现实上是染色体带有特点的实体.在一开端须要实现从表示型到基因型的映射即编码工作.因为模仿基因编码的工作很庞杂,我们往往进行简化,如二进制编码,初代种群产生之后,按照适者生计和优越劣汰的道理,逐代演变产生出越来越好的近似解,在每一代,依据问题域中个别的顺应度大小选择个别,并借助于天然遗传学的遗传算子进行组合交叉和变异,产生出代表新的解集的种群.这个进程将导致种群像天然进化一样的后生代种群比前代加倍顺应于情况,末代种群中的最优个别经由解码,可以作为问题近似最优解.遗传算法程度流程图为：【试验内容】标题：已知f(x)=x*sin(x)+1,xÎ[0,2p],求f(x)的最大值和最小值.数据构造：struct poptype{double gene[length];//染色体double realnumber;//对应的实数xdouble fitness;//顺应度double rfitness;//相对顺应度double cfitness;//累计顺应度};struct poptype population[popsize+1];//最后一位存放max/minstruct poptype newpopulation[popsize+1];//染色体编码：[0,2]x π∈,变量长度为 2 π,取小数点后6位,因为2262322*102;π<<是以,染色体由23位字节的二进制矢量暗示,则X 与二进制串（<b 22 b 21…… b 0>）2之间的映射如下：()22222102010bb ......b 2'i i i b x =⎛⎫=•= ⎪⎝⎭∑;232'21x x π=- 顺应度函数： 因为请求f(x)的最值,所以顺应度函数即可为f(x).但为了确保在轮赌法选择过中,每个个别都有被选中的可能性,是以须要将所有顺应度调剂为大于0的值.是以,设计求最大值的顺应度函数如下：将最小问题转化为求-f(x)的最大值,同理,设计最小值的顺应度函数如下：种群大小：本试验默以为50,再进行种群初始化.试验参数：重要有迭代数,交叉概率,变异概率这三个参数.一般交叉概率在0.6-0.9规模内,变异概率在0.01-0.1规模内.可以经由过程手动输入进行调试.重要代码如下：void initialize()//种群初始化{srand(time(NULL));int i,j;for(i=0;i<popsize;i++)for(j=0;j<23;j++)population[i].gene[j]=rand()%2;void transform()//染色体转化为实数x{int i,j;for(i=0;i<=popsize+1;i++){population[i].realnumber=0;for(j=0;j<23;j++)population[i].realnumber+=population[i].gene[j]*pow(2 ,j);population[i].realnumber=population[i].realnumber*2*p i/(pow(2,23)-1);}}void cal_fitness()//盘算顺应度{int i;for(i=0;i<popsize;i++)population[i].fitness=population[i].realnumber*sin(po pulation[i].realnumber)+6;}void select()//选择操纵{int mem,i,j,k;double sum=0;double p;for (mem=0;mem<popsize;mem++)sum+=population[mem].fitness;for (mem=0;mem<popsize; mem++)population[mem].rfitness=population[mem].fitness/sum;population[0].cfitness=population[0].rfitness;for (mem=1;mem<popsize;mem++)population[mem].cfitness=population[mem-1].cfitness+population[mem].rfitness;for (i=0;i<popsize;i++){ //轮赌法选择机制p=rand()%1000/1000.0;if (p<population[0].cfitness)newpopulation[i]=population[0];else{for (j=0;j<popsize;j++)if(p>=population[j].cfitness&&p<population[j+1].cfitness)newpopulation[i]=population[j+1];}}for (i=0;i<popsize;i++)//复制给下一代population[i]=newpopulation[i];}void cross()//交叉操纵{int i, mem, one;int first = 0;double x;for(mem=0;mem<popsize;mem++){x = rand()%1000/1000.0;if (x<pcross){++first;if (first%2==0)Xover(one,mem);//个别间染色体进行交叉函数else one=mem;}}}void mutate()//变异操纵{int i, j,t;double x;for (i=0;i<popsize;i++)for(j=0;j<length;j++){x=rand()%1000/1000.0;if (x<pvariation){if(population[i].gene[j])population[i].gene[j]=0; else population[i].gene[j]=1;}}}void cal_max()//盘算最大值{int i;double max,sum=0;int max_m;max=population[0].fitness;for(i=0;i<popsize-1;i++){if(population[i].fitness>population[i+1].fitness)if(population[i].fitness>=max){max=population[i].fitness;max_m=i;}else if(population[i+1].fitness>=max){max=population[i+1].fitness;max_m=i + 1;}}if(max>population[popsize].fitness){iteration=0;for (i=0;i<length;i++)population[popsize].gene[i]=population[max_m].gene[i]; population[popsize].fitness=population[max_m].fitness; }for (i=0;i<length;i++)sum=population[popsize].gene[i]-population[max_m].gene[i];if(sum==0)iteration++;transform();printf("%f,%f,%f,%f\n",population[popsize].fitness,po pulation[popsize+1].fitness,population[popsize].realnumbe r,population[popsize+1].realnumber);}【试验成果】。

遗传算法经典实例遗传算法是一种从若干可能的解决方案中自动搜索最优解的算法，它可以用来解决各种复杂的优化问题，是进化计算的一种。

它的基本过程是：对初始种群的每个个体都估计一个适应度值，并从中选择出最优的个体来作为新一代的父本，从而实现进化的自然演化，经过几代的迭代最终得到最优的解。

在许多复杂的优化问题中，遗传算法能产生比其它方法更优的解。

下面，我们将列出几个典型的遗传算法经典实例，以供参考。

1.包问题背包问题可以分解为：在一定的物品中选择出最优的物品组合需求，在有限的背包中装入最大价值的物品组合。

针对这个问题，我们可以使用遗传算法来求解。

具体而言，首先，需要构建一个描述染色体的数据结构，以及每个染色体的适应度评估函数。

染色体的基本单元是每个物品，使用0-1二进制编码表示该物品是否被选取。

然后，需要构建一个初始种群，可以使用随机生成的方式，也可以使用经典进化方法中的锦标赛选择、轮盘赌选择或者较优概率选择等方法生成。

最后，使用遗传算法的基本方法进行迭代，直至得出最优解。

2.着色问题图着色问题是一个比较复杂的问题，它涉及到一个无向图的节点和边的颜色的分配。

其目的是为了使相邻的节点具有不同的颜色，从而尽可能减少图上边的总数。

此问题中每种可能的颜色可以看作一个个体。

染色体中每个基因对应一条边，基因编码可以表示边上节点的着色颜色。

求解这个问题，我们可以生成一个初始群体，通过计算它们的适应度量，然后使用遗传算法的基本方法进行迭代，直至收敛于最优解。

3.舍尔旅行商问题费舍尔旅行商问题是一个求解最短旅行路径的问题，它可以分解为：从起点到终点访问给定的一组城市中的每一个城市，并且回到起点的一个最短旅行路径的搜索问题。

用遗传算法求解费舍尔旅行商问题，通常每个个体的染色体结构是一个由城市位置索引构成的序列，每个索引对应一个城市，表示在旅行路径中的一个节点，那么该路径的适应度就是城市之间的距离和，通过构建一个初始种群，然后结合遗传算法中的进化方法，如变异、交叉等进行迭代，最终得出最优解。

遗传算法excel
遗传算法是一种模拟自然选择和遗传机制的优化算法，它可以
用于解决复杂的优化问题。

在Excel中，可以使用VBA（Visual Basic for Applications）编程语言来实现遗传算法。

下面我将从
几个方面来介绍在Excel中实现遗传算法的基本步骤和方法。

1. 设计遗传算法的基本流程：
遗传算法的基本流程包括初始化种群、选择、交叉、变异和
适应度评估等步骤。

在Excel中，可以使用VBA编写代码来实现这
些步骤。

首先，需要定义个体的编码方式，然后随机生成初始种群。

接着进行选择操作，选择适应度高的个体作为父代，然后进行交叉
和变异操作生成新的个体，最后进行适应度评估，更新种群。

2. 编写VBA代码实现遗传算法：
在Excel中，可以使用VBA编辑器编写代码来实现遗传算法。

首先需要打开Excel，按下Alt + F11组合键打开VBA编辑器，然
后在模块中编写遗传算法的相关代码，包括种群的初始化、选择、
交叉、变异等操作，以及适应度函数的编写。

通过VBA代码，可以
实现遗传算法的各个步骤，并在Excel中进行运行和调试。

3. 应用范围：
在Excel中实现遗传算法可以用于解决各种优化问题，比如旅行商问题、工程优化、资源分配等。

通过编写VBA代码，可以将遗传算法应用到实际的数据分析和决策问题中，帮助优化问题的求解。

总的来说，在Excel中实现遗传算法需要使用VBA编程语言，通过编写相应的代码来实现遗传算法的各个步骤，从而解决各种复杂的优化问题。

希望以上介绍能够对你有所帮助。

遗传算法仿真实验遗传算法是建立在自然选择和自然遗传学机理基础上的迭代自适应概率性搜索，一般由初始化、选择、交叉、突然变异四部分组成；它的一个重要应用就是数值优化。

一、实验目的：1、了解用于数值优化的遗传算法的原理2、用 matlab 语言编程实现遗传算法二．实验任务：计算以下一元函数的最大值并按上例所示画出适应度函数图：1、f(x)=x^2+4x+6 ，x∈[1,5] 要求解精确到 6 位小数2、f(x)=xsin(10πx)+2，x∈[-1,2] 要求解精确到 6 位小数三．实验过程1）f(x)=x^2+4x+6 ，x∈[1,5]接下来用 matlab 语言编程实现该遗传算法：function [Max_Value,x]=one(umin,umax)%运行参数Size=80;G=100;CodeL=22;E=round(rand(Size,CodeL));%产生 80 个离散点的二进制编码解码%主程序for k=1:1:Gtime(k)=k;for s=1:1:Sizem=E(s,:);y=0;for i=1:1:CodeLy=y+m(i)*2^(i-1);endx=(umax-umin)*y/4194303+umin;F(s)= myfunction_one (x); %调用 my function _ one 函数产生每个离散点的适应度endJi=1./F;%注意这里是点乘BestJ(k)=min(Ji);%每步最优的目标函数fi=F;%定义适应度函数[Oderfi,Indexfi]=sort(fi);%将 80 个个体的适应度从小到大排序Bestfi=Oderfi(Size);BestS=E(Indexfi(Size),:);bfi(k)=Bestfi;%每步最优的适应度fi_sum=sum(fi);fi_Size=(Oderfi/fi_sum)*Size;fi_S=floor(fi_Size);kk=1;for i=1:1:Size %选择并复制个体for j=1:1:fi_S(i)TempE(kk,:)=E(Indexfi(i),:);kk=kk+1;endendpc=0.25;n=ceil(22*rand);%随机产生交叉的位for i=1:2:(Size-1)temp=rand;if pc>temp %满足交叉条件for j=n:1:22TempE(i,j)=E(i+1,j);TempE(i+1,j)=E(i,j);endendendTempE(Size,:)=BestS;E=TempE;pm=0.01for i=1:1:Sizefor j=1:1:CodeLtemp=rand;if pm>tempif TempE(i,j)==0TempE(i,j)=1;elseTempE(i,j)=0;endendendendTempE(Size,:)=BestS;E=TempE;end%满足变异条件Max_Value=Bestfi %输出最大值BestS %输出最大值对应的离散点的二进制编码x %输出取最大值是 x 的值figure(1); %画出迭代 100 步的适应度变化图和目标函数图plot(time,BestJ);xlabel('Times');ylabel('Best J');figure(2);plot(time,bfi);xlabel('times');ylabel('Best F');%以下是计算适应度函数的程序：function t=myfunction_one(x)t=x^2+4x+6;将程序保存为.m文件，在命令窗口输入：one(1,5)回车，运行程序，得到结果如下：Max_V alue =51.0000x =5.0000即函数在x=5.0000，处得到最大值51.0000得到适应度函数为为：2）f(x)=xsin(10πx)+2 ，接下来用 matlab 语言编程实现该遗传算法：function [Max_Value,x]=one(umin,umax)%运行参数Size=80;G=100;CodeL=22;E=round(rand(Size,CodeL));%产生 80 个离散点的二进制编码解码%主程序for k=1:1:Gtime(k)=k;for s=1:1:Sizem=E(s,:);y=0;for i=1:1:CodeLy=y+m(i)*2^(i-1);endx=(umax-umin)*y/4194303+umin;F(s)= myfunction_one (x); %调用 my function _ one 函数产生每个离散点的适应度endJi=1./F;%注意这里是点乘BestJ(k)=min(Ji);%每步最优的目标函数fi=F;%定义适应度函数[Oderfi,Indexfi]=sort(fi);%将 80 个个体的适应度从小到大排序Bestfi=Oderfi(Size);BestS=E(Indexfi(Size),:);bfi(k)=Bestfi;%每步最优的适应度fi_sum=sum(fi);fi_Size=(Oderfi/fi_sum)*Size;fi_S=floor(fi_Size);kk=1;for i=1:1:Size %选择并复制个体for j=1:1:fi_S(i)TempE(kk,:)=E(Indexfi(i),:);kk=kk+1;endendpc=0.25;n=ceil(22*rand);%随机产生交叉的位for i=1:2:(Size-1)temp=rand;if pc>temp %满足交叉条件for j=n:1:22TempE(i,j)=E(i+1,j);TempE(i+1,j)=E(i,j);endendendTempE(Size,:)=BestS;E=TempE;pm=0.01for i=1:1:Sizefor j=1:1:CodeLtemp=rand;if pm>tempif TempE(i,j)==0TempE(i,j)=1;elseTempE(i,j)=0;endendendendTempE(Size,:)=BestS;E=TempE;end%满足变异条件Max_Value=Bestfi %输出最大值BestS %输出最大值对应的离散点的二进制编码x %输出取最大值是 x 的值figure(1); %画出迭代 100 步的适应度变化图和目标函数图plot(time,BestJ);xlabel('Times');ylabel('Best J');figure(2);plot(time,bfi);xlabel('times');ylabel('Best F');%以下是计算适应度函数的程序：function t=myfunction_one(x)t=x*sin(10*pi*x)+2;将程序保存为.m文件，在命令窗口输入：one(-1,2)回车，运行程序，得到结果如下：Max_V alue =3.8503x =1.8506即函数在x= 2.0000 处得到最大值18.0000得到适应度函数为：。

用遗传算法求解TSP问题遗传算法（Genetic Algorithm——GA），是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型，它是由美国Michigan大学的J。

Holland教授于1975年首先提出的。

J.Holland 教授和它的研究小组围绕遗传算法进行研究的宗旨有两个：抽取和解释自然系统的自适应过程以及设计具有自然系统机理的人工系统。

遗传算法的大致过程是这样的:将每个可能的解看作是群体中的一个个体或染色体，并将每个个体编码成字符串的形式，根据预定的目标函数对每个个体进行评价,即给出一个适应度值。

开始时,总是随机的产生一些个体，根据这些个体的适应度，利用遗传算子-—选择（Selection）、交叉（Crossover)、变异（Mutation)对它们重新组合，得到一群新的个体.这一群新的个体由于继承了上一代的一些优良特性，明显优于上一代，以逐步向着更优解的方向进化.遗传算法主要的特点在于：简单、通用、鲁棒性强。

经过二十多年的发展，遗传算法已经在旅行商问题、生产调度、函数优化、机器学习等领域得到成功的应用。

遗传算法是一类可用于复杂系统优化的具有鲁棒性的搜索算法，与传统的优化算法相比,主要有以下特点：1、遗传算法以决策变量的编码作为运算对象.传统的优化算法往往直接决策变量的实际植本身,而遗传算法处理决策变量的某种编码形式，使得我们可以借鉴生物学中的染色体和基因的概念，可以模仿自然界生物的遗传和进化机理，也使得我们能够方便的应用遗传操作算子.2、遗传算法直接以适应度作为搜索信息，无需导数等其它辅助信息。

3、遗传算法使用多个点的搜索信息,具有隐含并行性。

4、遗传算法使用概率搜索技术，而非确定性规则。

遗传算法是基于生物学的,理解或编程都不太难。

下面是遗传算法的一般算法步骤:1、创建一个随机的初始状态初始种群是从解中随机选择出来的，将这些解比喻为染色体或基因，该种群被称为第一代，这和符号人工智能系统的情况不一样;在那里,问题的初始状态已经给定了。

遗传算法学习--多⽬标优化中的遗传算法在⼯程运⽤中，经常是多准则和对⽬标的进⾏择优设计。

解决含多⽬标和多约束的优化问题称为：多⽬标优化问题。

经常，这些⽬标之间都是相互冲突的。

如投资中的本⾦最少，收益最好，风险最⼩~~多⽬标优化问题的⼀般数学模型可描述为：Pareto最优解（Pareto Optimal Solution）使⽤遗传算法进⾏求解Pareto最优解：权重系数变换法：并列选择法：基本思想：将种群全体按⼦⽬标函数的数⽬等分为⼦群体，对每⼀个⼦群体分配⼀个⽬标函数，进⾏择优选择，各⾃选择出适应度⾼的个体组成⼀个新的⼦群体，然后将所有这些⼦群体合并成⼀个完整的群体，在这个群体⾥进⾏交叉变异操作，⽣成下⼀代完整群体，如此循环，最终⽣成Pareto最优解。

如下图：排列选择法：基于Pareto最优个体的前提上，对群体中的各个个体进⾏排序，依据排序进⾏选择，从⽽使拍在前⾯的Pareto最优个体将有更⼤的可能性进⼊下⼀代群体中。

共享函数法：利⽤⼩⽣境遗传算法的技术。

算法对相同个体或类似个体是数⽬加⼀限制，以便能够产⽣出种类较多的不同的最优解。

对于⼀个个体X,在它的附近还存在有多少种、多⼤程度相似的个体，是可以度量的，这种度量值称为⼩⽣境数。

计算⽅法：s(d)为共享函数，它是个体之间距离d的单调递减函数。

d(X,Y)为个体X,Y之间的海明距离。

在计算出⼩⽣境数后，可以是⼩⽣境数较⼩的个体能够有更多的机会被选中，遗传到下⼀代群体中，即相似程度较⼩的个体能够有更多的机会被遗传到下⼀代群体中。

解决了多⽬标最优化问题中，使解能够尽可能的分散在整个Pareto最优解集合内，⽽不是集中在其Pareto最优解集合内的某⼀个较⼩的区域上的问题。

混合法：1. 并列选择过程：按所求多⽬标优化问题的⼦⽬标函数的个数，将整个群体均分为⼀些⼦群体，各个⼦⽬标函数在相应的⼦群体中产⽣其下⼀代⼦群体。

2. 保留Pareto最优个体过程：对于⼦群体中的Pareto最优个体，不让其参与个体的交叉和变异运算，⽽是直接保留到下⼀代⼦群体中。

遗传算法优化svm参数遗传算法是一种基于自然选择和进化理论的优化算法，适用于求解复杂的非线性优化问题。

由于支持向量机（SupportVector Machine，SVM）在机器学习中被广泛应用于分类和回归问题，因此使用遗传算法来优化SVM的参数是一个常见的研究方向。

SVM是一种二分类模型，通过在特征空间中寻找最佳的超平面对数据进行分类。

根据问题的不同，SVM具有多个参数需要进行调优，包括C（正则化常数）和核函数中的参数等。

使用遗传算法来优化这些参数可以通过以下步骤实现：1. 确定问题的适应度函数：在遗传算法中，适应度函数用于评估每个个体的性能。

对于SVM参数优化问题，可以选择采用交叉验证准确率或分类精度作为适应度函数。

2. 初始化种群：在遗传算法中，初始化种群是一个重要的步骤。

对于SVM参数优化问题，可以随机生成一组初始参数作为种群的起始点。

3. 选择操作：选择操作是根据适应度函数的结果选择优秀的个体。

常用的选择算法有轮盘赌选择和锦标赛选择等。

4. 交叉操作：交叉操作是从选择的个体中随机选择两个或多个个体，通过某种方式进行交叉生成新的个体。

在SVM参数优化问题中，可以选择单点交叉、多点交叉或均匀交叉等策略。

5. 变异操作：变异操作是为了确保种群具有一定的多样性，防止算法陷入局部最优解。

在SVM参数优化中，可以通过改变个体的某个或多个参数的值来进行变异。

6. 评价和重复：每次进行选择、交叉和变异操作后，都需要对生成的新个体进行评价并计算适应度值。

重复上述步骤直到满足终止条件为止，比如达到最大迭代次数或适应度达到某个阈值。

在进行SVM参数优化时，有几个问题需要考虑：1. 参数范围：对于每个参数，需要明确其可能的取值范围。

例如，正则化常数C通常取值为0到无穷大之间的正实数。

2. 交叉验证：在SVM参数优化中，使用交叉验证是常见的一种方式。

通过将数据集划分为训练集和验证集，可以评估不同参数组合的性能。

常用的交叉验证方法有k折交叉验证和留一验证等。

遗传算法求函数极值遗传算法是一种基于模拟生物进化过程的优化算法，它通过模拟生物的进化过程中的遗传、交叉和变异等操作，对问题的解空间进行，并到满足最优条件的解。

它被广泛应用于求解各种复杂问题，包括函数极值问题。

在使用遗传算法求函数极值的过程中，首先需要明确问题的目标函数。

目标函数是一个将自变量映射到一个实数值的函数，它描述了问题的优化目标。

例如，我们可以考虑一个简单的目标函数f(x)，其中x表示自变量，f(x)表示因变量。

遗传算法的基本流程如下：1.初始化种群：随机生成一组初始解，也就是种群。

种群中的每个个体都是一个可能的问题解，而个体中的染色体则表示了问题解的具体数值。

2.适应度评估：对于种群中的每个个体，通过计算目标函数的值，评估每个个体的适应度。

适应度越高的个体，越有可能成为下一代个体的基因。

3.选择操作：根据个体的适应度，选择一些个体作为下一代遗传操作的基因。

4.交叉操作：从选择出的个体中随机选择一对个体，进行交叉操作。

交叉操作通过交换两个个体的染色体信息，产生新的个体。

5.变异操作：对交叉操作生成的新个体进行变异操作。

变异操作通过改变个体染色体中的部分基因，引入新的解，以增加问题解的多样性。

6.新种群产生：基于交叉和变异操作，生成新的种群。

7.终止条件判断：如果满足终止条件（例如达到最大迭代次数、找到了满足要求的解等），则停止算法；否则，返回第2步。

通过以上步骤的循环迭代，遗传算法可以到问题的最优解，即函数的极值。

由于遗传算法充分利用了进化算法的生物特点，具有全局能力和自适应优化能力，因此在函数极值求解中得到了广泛的应用。

遗传算法的关键在于如何进行适应度评估、选择操作、交叉操作和变异操作。

适应度评估是指根据目标函数计算个体的适应度值，一般情况下适应度越高的个体越有可能成为下一代的基因。

选择操作可以采用轮盘赌选择、最优选择等方式，根据个体的适应度选择一定数量的个体进行交叉和变异。

交叉操作通过交换染色体信息，产生新的个体；变异操作通过改变个体染色体中的部分基因，引入新的解。

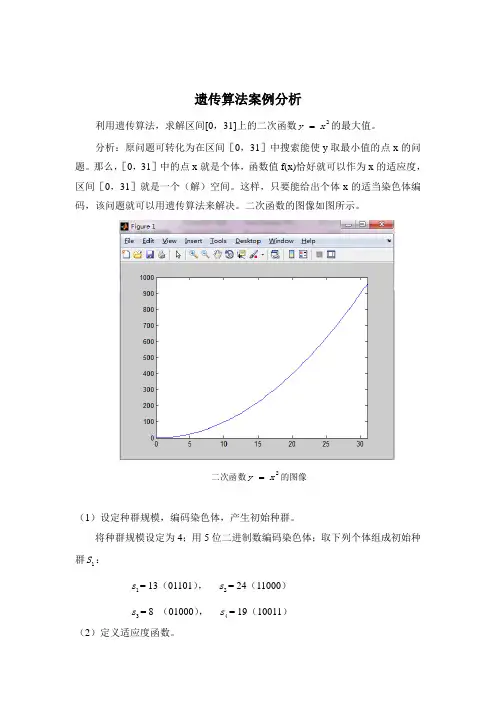
遗传算法案例分析利用遗传算法，求解区间[0，31]上的二次函数2y x =的最大值。

分析：原问题可转化为在区间［0，31］中搜索能使y 取最小值的点x 的问题。

那么，［0，31］中的点x 就是个体，函数值f(x)恰好就可以作为x 的适应度，区间［0，31］就是一个（解）空间。

这样，只要能给出个体x 的适当染色体编码，该问题就可以用遗传算法来解决。

二次函数的图像如图所示。

二次函数2y x =的图像（1）设定种群规模，编码染色体，产生初始种群。

将种群规模设定为4；用5位二进制数编码染色体；取下列个体组成初始种群1S ：1s = 13（01101）， 2s = 24（11000）3s = 8 （01000）， 4s = 19（10011）（2）定义适应度函数。

取适应度函数：f (x ) = 2x 。

（3）计算各代种群中的各个体的适应度，并对其染色体进行遗传操作，直到适应度最高的个体（即31（11111））出现为止。

首先计算种群S 1中各个体的适应度()1f s 。

容易求得， f (s 1) = f (13) = 132= 169 f (s 2) = f (24) = 242= 576 f (s 3) = f (8) = 82= 64 f (s 4) = f (19) = 192= 361 再计算种群1S 中各个体的选择概率。

选择概率的计算公式为∑==N j j i i x f x f x P 1)()()(由此求得， P (s 1) = P (13) = 0.14 P (s 2) = P (24) = 0.49 P (s 3) = P (8) = 0.06 P (s 4) = P (19) = 0.31 用赌轮选择法可得，赌轮选择法示意图设从区间［0，1］中产生4个随机数如下：r 1 = 0.450126，r2= 0.110347r 3 = 0.572496，r4= 0.98503表1 第一代选中次数表染色体适应度选择概率积累概率选中次数s1=01101 169 0.14 0.14 1s2=11000 576 0.49 0.63 2s3=01000 64 0.06 0.69 0s4=10011 361 0.31 1 1 于是，经复制得群体：s 1’ =11000（24），s2’ =01101（13）s 3’ =11000（24），s4’ =10011（19）设交叉率pc =100%，即S1中的全体染色体都参加交叉运算。