1. 在一个金属板加工车间内,要从尺寸为48分米?96分米的大块矩形金属板上切割下小块
的金属板。此车间接到订单要求生产8块大小为36分米?50分米的矩形金属板,13块大小为24分米?36分米的矩形金属板,以及15块大小为18分米?30分米的矩形金属板。这些金属板都需要从现有的大金属板上切割下来。为了生产出满足订单要求的金属板,最少可以使用多少块大金属板? 列出该问题的线性规划模型。
2. 某县级市正在研究引进公交系统以减轻市内自驾车引起的烟尘污染。这项研究的目标是
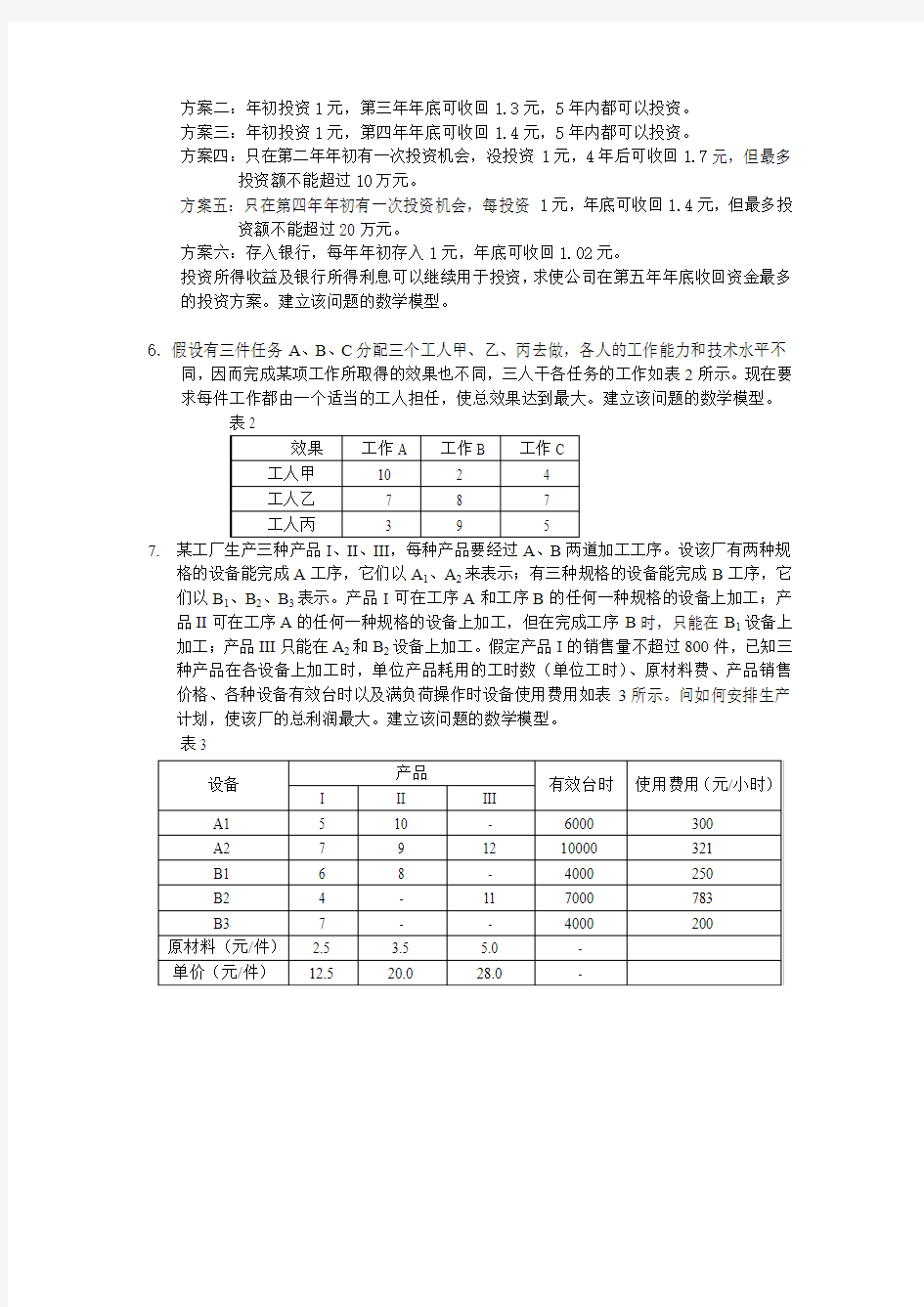
寻求满足运输所需要的最少公交车数。在收集了必要的信息之后,市政工程师注意到,每天所需的最少公交车数随一天中的时间不同而变化,而且所需的最少公交车数在若干连续的4小时间隔内可以近似看成一个常数。图1描述了工程师的发现,为了完成公交车所需的日常维护,每辆公交车一天只能连续运行8小时,问该市至少需要多少量公交车?列出该问题的线性规划模型。
0:00
4:008:0012:0016:0020:0024:00
48124
8
10
7
12
4
图1
3. 某银行正在制订一项总额可达6000万元的贷款策略,表1提供了各类贷款的相关数据。
表1
贷款类型 利率 坏账比率 个人 0.140 0.10 汽车 0.130 0.07 住房 0.120 0.03 农业 0.125 0.05 商业
0.100
0.02
其中,坏账不可收回且不产生利息收入。
为了与其它金融机构竞争,要求银行把至少40%的资金分配给农业和商业贷款。为扶持当地的住房产业,住房贷款至少要等于个人、汽车和住房贷款总额的50%。银行还有一项明确的政策,不允许坏账的总比例超过全部贷款的4%。试寻求一种最佳贷款策略,使得银行的净收益达到最大。建立此问题的线性规划模型。
4.某种产品在未来4个季度的需求量分别是300,400,450,250件,每件的价格在第1季度以20元开始,其随后的每个季度增加2元。供应商在任一季度最多可以提供产品400件。尽管我们可以利用前面季度的低价优势,但它会导致每季度每件3.5元的储存成本,另外,从一个季度到下一季度的最大件数不能超过100件,试为该产品建立一个最优的采购计划以满足需求且使总成本最低。建立该问题的线性规划模型。
5. 某公司有30万元可用于投资,投资方案有下列几种:
方案一:年初投资1元,第二年年底收回1.2元,5年内都可投资,但投资额不能超过
15万。
方案二:年初投资1元,第三年年底可收回1.3元,5年内都可以投资。
方案三:年初投资1元,第四年年底可收回1.4元,5年内都可以投资。
方案四:只在第二年年初有一次投资机会,没投资1元,4年后可收回1.7元,但最多投资额不能超过10万元。
方案五:只在第四年年初有一次投资机会,每投资1元,年底可收回1.4元,但最多投资额不能超过20万元。
方案六:存入银行,每年年初存入1元,年底可收回1.02元。
投资所得收益及银行所得利息可以继续用于投资,求使公司在第五年年底收回资金最多的投资方案。建立该问题的数学模型。
6.假设有三件任务A、B、C分配三个工人甲、乙、丙去做,各人的工作能力和技术水平不同,因而完成某项工作所取得的效果也不同,三人干各任务的工作如表2所示。现在要求每件工作都由一个适当的工人担任,使总效果达到最大。建立该问题的数学模型。
表2
7.某工厂生产三种产品I、II、III,每种产品要经过A、B两道加工工序。设该厂有两种规
格的设备能完成A工序,它们以A1、A2来表示;有三种规格的设备能完成B工序,它们以B1、B2、B3表示。产品I可在工序A和工序B的任何一种规格的设备上加工;产品II可在工序A的任何一种规格的设备上加工,但在完成工序B时,只能在B1设备上加工;产品III只能在A2和B2设备上加工。假定产品I的销售量不超过800件,已知三种产品在各设备上加工时,单位产品耗用的工时数(单位工时)、原材料费、产品销售价格、各种设备有效台时以及满负荷操作时设备使用费用如表3所示。问如何安排生产计划,使该厂的总利润最大。建立该问题的数学模型。
表3
附录2 线性规划案例 Appendix 2 Projects of Linear Programming 案例1 食油生产问题(1) 食油厂精炼两种类型的原料油——硬质油和软质油,并将精制油混合得到一种食油产品。硬质原料油来自两个产地:产地1和产地2,而软质原料油来自另外三个产地:产地3,产地4和产地5。据预测,这5种原料油的价格从一至六月分别为: 产品油售价为200元/吨。 硬质油和软质油需要由不同的生产线来精炼。硬质油生产线的每月最大处理能力为200吨,软质油生产线最大处理能力为250吨/月。五种原料油都备有贮罐,每个贮罐的容量均为1000吨,每吨原料油每月的存贮费用为5元。而各种精制油以及产品无油罐可存贮。精炼的加工费用可略去不计。产品的销售没有任何问题。 产品食油的硬度有一定的技术要求,它取决于各种原料油的硬度以及混合比例。产品食油的硬度与各种成份的硬度以及所占比例成线性关系。根据技术要求,产品食油的硬度必须不小于3.0而不大于6.0。各种原料油的硬度如下表(精制过程不会影响硬度):
假设在一月初,每种原料油都有500吨存贮而要求在六月底仍保持这样的贮备。 问题1:根据表1预测的原料油价格,编制逐月各种原料油采购量、耗用量及库存量计划,使本年内的利润最大。 问题2:考虑原料油价格上涨对利润的影响。据市场预测分析,如果二月份硬质原料油价格比表1中的数字上涨X%,则软质油在二月份的价格将比表1中的数字上涨2X%,相应地,三月份,硬质原料油将上涨2X%,软质原料油将上涨4X%,依此类推至六月份。试分析X从1到20的各情况下,利润将如何变化? 案例2 食油生产问题(2) 在案例1中,附加以下条件,求解新的问题: 1.每一个月所用的原料油不多于三种。 2.如果在某一个月用一种原料油,那么这种油不能少于20吨。 3.如果在一个月中用了硬质油1或硬质油2,则在这个月中就必须用软质油5。案例3 机械产品生产计划问题 机械加工厂生产7种产品(产品1到产品7)。该厂有以下设备:四台磨床、两台立式钻床、三台水平钻床、一台镗床和一台刨床。每种产品的利润(元/件,在这里,利润定义为销售价格与原料成本之差)以及生产单位产品需要的各种设备的工时(小时)如下表。表中的短划表示这种产品不需要相应的设备加工。
第五章线性规划在管理中的应用 某企业停止了生产一些已经不再获利的产品,这样就产生了一部分剩余生产力。管理层考虑将这些剩余生产力用于新产品Ⅰ、Ⅱ、Ⅲ的生产。可用的机器设备是限制新产品产量的主要因素,具体数据如下表: 司的利润最大化。 1、判别问题的线性规划数学模型类型。 2、描述该问题要作出决策的目标、决策的限制条件以及决策的总绩效测度。 3、建立该问题的线性规划数学模型。 4、用线性规划求解模型进行求解。 5、对求得的结果进行灵敏度分析(分别对最优解、最优值、相差值、松驰/剩余量、对偶价格、目标函数变量系数和常数项的变化范围进行详细分析)。 6、若销售部门表示,新产品Ⅰ、Ⅱ生产多少就能销售多少,而产品Ⅲ最少销售18件,请重新完成本题的1-5。 解: 1、本问题是资源分配型的线性规划数学模型。 2、该问题的决策目标是公司总的利润最大化,总利润为: + + 决策的限制条件: 8x1+ 4x2+ 6x3≤500 铣床限制条件 4x1+ 3x2≤350 车床限制条件 3x1+ x3≤150 磨床限制条件 即总绩效测试(目标函数)为: max z= + + 3、本问题的线性规划数学模型 max z= + + S.T.8x1+ 4x2+ 6x3≤500 4x1+ 3x2≤350 3x1+ x3≤150 x1≥0、x2≥0、x3≥0 4、用Excel线性规划求解模板求解结果:最优解(50,25,0),最优值:30元。 5、灵敏度分析
目标函数最优值为: 30 变量最优解相差值 x1 50 0 x2 25 0 x3 0 .083 约束松弛/剩余变量对偶价格 1 0 .05 2 75 0 3 0 .033 目标函数系数范围: 变量下限当前值上限 x1 .4 .5 无上限 x2 .1 .2 .25 x3 无下限.25 .333 常数项数范围: 约束下限当前值上限 1 400 500 600 2 275 350 无上限 3 150 (1)最优生产方案: 新产品Ⅰ生产50件、新产品Ⅱ生产25件、新产品Ⅲ不安排。最大利润值为30元。 (2)x3 的相差值是意味着,目前新产品Ⅲ不安排生产,是因为新产品Ⅲ的利润太低,若要使新产品Ⅲ值得生产,需要将当前新产品Ⅲ利润元/件,提高到元/件。 (3)三个约束的松弛/剩余变量0,75,0,表明铣床和磨床的可用工时已经用完,而车床的可用工时还剩余75个工时; 三个对偶价格,0,表明三种机床每增加一个工时可使公司增加的总利润额。 (4)目标函数系数范围 表明新产品Ⅰ的利润在元/件以上,新产品Ⅱ的利润在到之间,新产品Ⅲ的利润在以下,上述的最佳方案不变。 (5)常数项范围 表明铣床的可用条件在400到600工时之间、车铣床的可用条件在275工时以上、磨铣床的可用条件在到工时之间。各自每增加一个工时对总利润的贡献元,0元,元不变。 6、若产品Ⅲ最少销售18件,修改后的的数学模型是: max z= + + S.T.8x1+ 4x2+ 6x3≤500 4x1+ 3x2≤350 3x1+ x3≤150 x3≥18 x1≥0、x2≥0、x3≥0 这是一个混合型的线性规划问题。 代入求解模板得结果如下: 最优解(44,10,18),最优值:元。 灵敏度报告: 目标函数最优值为: 变量最优解相差值 x1 44 0 x2 10 0 x3 18 0 约束松弛/剩余变量对偶价格
线性规划应用案例
市场营销应用 案例一:媒体选择 在媒体选择中应用线性规划的目的在于帮助市场营销经理将固定的广告预算分配到各种广告媒体上,可能的媒体包括报纸、杂志、电台、电视和直接邮件。在这些媒体中应用线性规划,目的是要使宣传范围、频率和质量最大化。对于应用中的约束条件通常源于对公司政策、合同要求及媒体的可用性。在下面的应用中,我们将介绍如何应用线性规划这一工具来建立模型进而解决媒体选择问题。 REL发展公司正在私人湖边开发一个环湖社区。湖边地带和住宅的主要市场是距离开发区100英里以内的所有中上收入的家庭。REL公司已经聘请BP&J 来设计宣传活动。 考虑到可能的广告媒体和要覆盖的市场,BP&J建议将第一个月的广告局限于5种媒体。在第一个月末,BP&J将依据本月的结果再次评估它的广告策略。BP&J已经收集到了关于受众数量、广告单价、各种媒体一定周期内可用的最大次数以及评定5种媒体各自宣传质量的数据。质量评定是通过宣传质量单位来衡量的。宣传质量单位是一种用于衡量在各个媒体中一次广告的相对价值的标准,它建立于BP&J在广告业中的经验,将众多因素考虑在内,如受众层次(年龄、收入和受众受教育的程度)、呈现的形象和广告的质量。表4-1列出了收集到的这些信息。 表4-1 REL发展公司可选的广告媒体
REL发展公司提供给BP&J第一个月广告活动的预算是30000美元。而且,REL公司对BP&J如何分配这些资金设置了如下限制:至少要使用10次电视广告,达到的受众至少要有50000人,并且电视广告的费用不得超过18000美元。应当推荐何种广告媒体选择计划呢? 案例二:市场调查 公司开展市场营销调查以了解消费者个性特点、态度以及偏好。专门提供此种信息的市场营销调查公司,经常为客户机构开展实际调查。市场营销调查公司提供的典型服务包括涉及计划、开展市场调查、分析收集数据、提供总结报告和对客户提出意见。在调查设计阶段,应当对调查对象的数量和类型设定目标或限额。市场营销调查公司的目标是以最小的成本满足客户要求。 市场调查公司(MSI)专门评定消费者对新的产品、服务和广告活动的反映。一个客户公司要求MSI帮助确定消费者对一种近期推出的家具产品的反应。在与客户会面的过程中,MSI统一开展个人入户调查,以从有儿童的家庭和无儿童的家庭获得回答。而且MSI还同意同时开展日间和晚间调查。尤其是,客户的合同要求依据以下限制条款进行1000个访问: ●至少访问400个有儿童的家庭; ●至少访问400个无儿童的家庭; ●晚间访问的家庭数量必须不少于日间访问的家庭数量; ●至少40%有儿童的家庭必须在晚间访问; ●至少60%无儿童的家庭必须在晚间访问。 因为访问有儿童的家庭需要额外的访问时间,而且晚间访问者要比日间访问者获得更多收入,所以成本因访问的类型不同而不同。基于以往的调查研究,预计的访问费用如下表所示: 以最小总访问成本满足合同要求的家庭——时间访问计划是什么样的
第五章线性规划在管理中的应用 5.1 某企业停止了生产一些已经不再获利的产品,这样就产生了一部分剩余生产力。管理层考虑将这些剩余生产力用于新产品Ⅰ、Ⅱ、Ⅲ的生产。可用的机器设备是限制新产品产量的主要因素,具体数据如下表: 量,使得公司的利润最大化。 1、判别问题的线性规划数学模型类型。 2、描述该问题要作出决策的目标、决策的限制条件以及决策的总绩效测度。 3、建立该问题的线性规划数学模型。 4、用线性规划求解模型进行求解。 5、对求得的结果进行灵敏度分析(分别对最优解、最优值、相差值、松驰/剩余量、对偶价格、目标函数变量系数和常数项的变化范围进行详细分析)。 6、若销售部门表示,新产品Ⅰ、Ⅱ生产多少就能销售多少,而产品Ⅲ最少销售18件,请重新完成本题的1-5。 解: 1、本问题是资源分配型的线性规划数学模型。 2、该问题的决策目标是公司总的利润最大化,总利润为: 0.5x1+ 0.2x2+ 0.25x3 决策的限制条件: 8x1+ 4x2+ 6x3≤500 铣床限制条件 4x1+ 3x2≤350 车床限制条件 3x1+ x3≤150 磨床限制条件 即总绩效测试(目标函数)为: max z= 0.5x1+ 0.2x2+ 0.25x3 3、本问题的线性规划数学模型 max z= 0.5x1+ 0.2x2+ 0.25x3 S.T.8x1+ 4x2+ 6x3≤500 4x1+ 3x2≤350 3x1+ x3≤150 x1≥0、x2≥0、x3≥0 4、用Excel线性规划求解模板求解结果:最优解(50,25,0),最优值:30元。 5、灵敏度分析
目标函数最优值为 : 30 变量最优解相差值 x1 50 0 x2 25 0 x3 0 .083 约束松弛/剩余变量对偶价格 1 0 .05 2 75 0 3 0 .033 目标函数系数范围 : 变量下限当前值上限 x1 .4 .5 无上限 x2 .1 .2 .25 x3 无下限 .25 .333 常数项数范围 : 约束下限当前值上限 1 400 500 600 2 275 350 无上限 3 37.5 150 187.5 (1)最优生产方案: 新产品Ⅰ生产50件、新产品Ⅱ生产25件、新产品Ⅲ不安排。最大利润值为30元。 (2)x3 的相差值是0.083意味着,目前新产品Ⅲ不安排生产,是因为新产品Ⅲ的利润太低,若要使新产品Ⅲ值得生产,需要将当前新产品Ⅲ利润0.25元/件,提高到0.333元/件。 (3)三个约束的松弛/剩余变量0,75,0,表明铣床和磨床的可用工时已经用完,而车床的可用工时还剩余75个工时; 三个对偶价格0.05,0,0.033表明三种机床每增加一个工时可使公司增加的总利润额。 (4)目标函数系数范围 表明新产品Ⅰ的利润在0.4元/件以上,新产品Ⅱ的利润在0.1到0.25之间,新产品Ⅲ的利润在0.333以下,上述的最佳方案不变。 (5)常数项范围 表明铣床的可用条件在400到600工时之间、车铣床的可用条件在275工时以上、磨铣床的可用条件在37.5到187.5工时之间。各自每增加一个工时对总利润的贡献0.05元,0元,0.033元不变。 6、若产品Ⅲ最少销售18件,修改后的的数学模型是: max z= 0.5x1+ 0.2x2+ 0.25x3 S.T.8x1+ 4x2+ 6x3≤500 4x1+ 3x2≤350 3x1+ x3≤150 x3≥18 x1≥0、x2≥0、x3≥0 这是一个混合型的线性规划问题。 代入求解模板得结果如下: 最优解(44,10,18),最优值:28.5元。 灵敏度报告: 目标函数最优值为 : 28.5 变量最优解相差值 x1 44 0 x2 10 0
实例matlab-非线性规划-作业
现代设计方法-工程优化理论、方法与设计 姓名 学号 班级 研 问题 : 某厂向用户提供发动机,合同规定,第一、二、三季度末分别交货40台、60台、80台。每季度的生产费用为 (元),其中x 是该季生产的台数。若交货后有剩余,可用于下季度交货,但需支付存储费,每台每季度c 元。已知工厂每季度最大生产能力为100台,第一季度开始时无存货,设a=50、b=0.2、c=4,问工厂应如何安排生产计划,才能既满足合同又使总费用最低。讨论a 、b 、c 变化对计划的影响,并作出合理的解释。 问题的分析和假设: 问题分析:本题是一个有约束条件的二次规划问题。决策变量是工厂每季度生产的台数,目标函数是总费用(包括生产费用和存储费)。约束条件是生产合同,生产能力的限制。在这些条件下需要如何安排生产计划,才能既满足合同又使总费用最低。 问题假设: 1、工厂最大生产能力不会发生变化; 2、合同不会发生变更; 3、第一季度开始时工厂无存货; 4、生产总量达到180台时,不在进行生产; 5、工厂生产处的发动机质量有保证,不考虑退货等因素; 6、不考虑产品运输费用是否有厂家承担等和生产无关的因素。 符号规定: x1——第一季度生产的台数; x2——第二季度生产的台数; 180-x1-x2——第三季度生产的台数; y1——第一季度总费用; y2——第二季度总费用; y3——第三季度总费用; y ——总费用(包括生产费用和存储费)。 ()2bx ax x f +=
建模: 1、第一、二、三季度末分别交货40台、60台、80台; 2、每季度的生产费用为 (元); 3、每季度生产数量满足40 ≤x1≤100,0≤x2≤100,100≤x1+x2 ≤180; 4、要求总费用最低,这是一个目标规划模型。 目标函数: y1 2111x b x a Z ?+?= y2()4012222-?+?+?=x c x b x a Z y3()()()10018018021221213 -+?+--?+--?=x x c x x b x x a Z y x x x x x x Z Z Z Z 68644.04.04.0149201 212221321--+++=++= 40≤x1≤100 0≤x2≤100 100≤x1+x2≤180 ()2 bx ax x f +=
2.某市柴油机厂年度产品生产计划的优化研究 1)问题的提出 某市柴油机厂是我国生产中小功率柴油机的重点骨干企业之一,主要产品有2105柴油机、 X2105柴油机、X4105柴油机、X4110柴油机、X6105柴油机、X6110柴油机,产品市场占 有率大,覆盖面广,广泛用于农业机械、工程机械、林业机械、船舶、发电机组等。在同行 业中占有一定的优势。但另一方面,也确实存在管理方法陈旧、管理手段落后的实际问题, 尤其是随着经济体制改革的深入,以前在计划经济体制下生存的国营企业越来越不适应市场 经济的要求。为改变这种不利局面,厂领导决定实行科学管理,其中努力提高企业编制产品 生产计划的科学性是一个重要的目标。 2)生产现状及资料分析 柴油机的主要生产过程为原材料经过锻造、铸造或下料,再进行热处理、机加工工序,进入 总装,最后试车、装箱、入成品库。该厂将毛坯生产工艺,即锻造、铸造或下料过程渐渐向 外扩散,形成专业化生产,以达到规模效益,故该厂柴油机生产过程主要可以分三大类:热 处理、机加工、总装。与产品生产有关的数据资料如下: 每种产品的单位产值如下表: 序号产品型号及产品名称单位产值(元) 1 2105柴油机5400 2 X2105柴油机6500 3 X4105柴油机12000 4 X4110柴油机14000 5 X6105柴油机18500 6 X6110柴油机20000 每件产品所需的热处理、机加工、总装工时及全厂能提供的三种总工时如下表:序号产品型号及产品名称热处理(工时) 机加工(工时) 总装(工时) 1 2105柴油机10.58 14.58 17.08 2 X2105柴油机11.0 3 7.05 150 3 X4105柴油机20.11 23.96 29.37 4 X4110柴油机32.26 27.7 33.38 5 X6105柴油机37.68 29.3 6 55.1 6 X6110柴油机40.84 40.43 53.5 全年提供总工时120000 95000 180000 产品原材料主要是生铁、焦碳、废钢、钢材四大类资源,供应科根据历年的统计资 料及当年的原材料市场情况,给出了各种原材料的最大供应量如下表: 原材料名称生铁(吨) 焦碳(吨) 废钢(吨) 钢材(吨) 最大供应量1562 951 530 350 单位产品原材料消耗情况如下表: 序号产品型号及名称生铁(吨) 焦碳(吨) 废钢(吨) 钢材(吨) 1 2105柴油机0.18 0.11 0.06 0.04 2 X2105柴油机0.19 0.12 0.06 0.04 3 X4105柴油机0.35 0.22 0.12 0.08 4 X4110柴油机0.36 0.23 0.13 0.09 5 X6105柴油机0.54 0.33 0.18 0.12
线性规划 线性规划是处理线性目标函数和线性约束的一种较为成熟的方法,目前已经广泛应用于军事、经济、工业、农业、教育、商业和社会科学等许多方面。 8.2.1 基本数学原理 线性规划问题的标准形式是: ????? ??????≥=+++=+++=++++++=0,,,min 21221122222121112 121112211n m n mn m m n n n n n n x x x b x a x a x a b x a x a x a b x a x a x a x c x c x c z 或 ???? ?????=≥===∑∑==n j x m i b x a x c z j n j i j ij n j j j ,,2,1,0,,2,1,min 1 1 写成矩阵形式为: ?? ???≥==O X b AX CX z min 线性规划的标准形式要求使目标函数最小化,约束条件取等式,变量b 非负。不符合这几个条件的线性模型可以转化成标准形式。 MATLAB 采用投影法求解线性规划问题,该方法是单纯形法的变种。 8.2.2 有关函数介绍 在MATLAB 工具箱中,可用linprog 函数求解线性规划问题。 linprog 函数的调用格式如下: ●x=linprog(f,A,b):求解问题minf'*x ,约束条件为A*x<=b 。 ●x=linprog(f,A,b,Aeq,beq):求解上面的问题,但增加等式约束,即Aeq*x=beq 。若没有不等式约束,则令A=[ ],b=[ ]。 ●x=linprog(f,A,b,Aeq,beq,lb,ub):定义设计x 的下界lb 和上界ub ,使得x 始终在该范围内。若没有等式约束,令Aeq=[ ],beq=[ ]。 ●x=linprog(f,A,b,Aeq,beq,lb,ub,x0):设置初值为x0。该选项只适用于中型问题,默认时大型算法将忽略初值。 ●x=linprog(f,A,b,Aeq,beq,lb,ub,x0,options):用options 指定的优化参数进行最小化。 ●[x,fval]=linprog(…):返回解x 处的目标函数值fval 。 ●[x,lambda,exitflag]=linprog(…):返回exitflag 值,描述函数计算的退出条件。 ●[x,lambda,exitflag,output]=linprog(…):返回包含优化信息的输出参数output 。 ●[x,fval,exitflag,output,lambda]=linprog(…):将解x 处的拉格朗日乘子返回到lambda 参数中。
线性规划作业 (数学规划作业一) 1、用两种编程方式求解下列问题 2、将下述问题化成标准线性规划问题 3、奶制品的生产销售计划 一奶制品加工厂用牛奶生产A 1、A 2两种奶制品,1桶牛奶可以在甲类生产设备上用12h 加工成3kg A 1种奶制品,或在在乙类生产设备上用8h 加工成4kg A 2种奶制品.若A 1、A 2两种奶制品全部能售出,且甲种奶制品售价24元/kg, 乙种奶制品售价16元/kg 。现在工厂每天能得到50桶牛奶,每天正式工人总的劳动时间为480h,且甲类生产设备每天至多加工100kg 甲种奶制品, 乙类生产设备每天加工乙种奶制品没有限制.为了增加工厂的获利,开发了奶制品的深加工技术,用2h 和3元加工费,可将1kg A 1加工成0.8kg 高级奶制品B 1;也可将1kg A 2加工成0.75kg 高级奶制品B 2,B 1与B 2售价分别为44元与32元,试为该工厂制订一个生产计划,使每天获利最大.并进一步讨论以下3 个问题: (1)、若用30元买一桶牛奶,投资3元可以增加1h 劳动时间,是否投资?若每天投资150元,可获利多少? (2)、每kg 高级奶制品B 1与B 2的获利经常有10%的波动,对制订生产销售计划有影响?若B 2的获利下降10%,计划是否变化? (3)、若工厂已签订了每天销售10kg A 1的合同并且必须满足,该合同对工厂的获利有什么影响? 4、供水问题 某市从A 、B 、C 三个水库向甲、乙、丙、丁四个生活区供应自来水,C 不能向丁区供水. 四个生活区每天的基本生活用水分别为30,70,10,10(单位103 t ),并且每天申请了额外 的用水量分别为50,70,20,40(单位103t );三个水库每天最多只能供应50,60,50(单位103 t ). 由于地理位置不同,向各区送水所需的引水管理费不同(表1),其他管理费每单位(103 t)450 元,但向各区都统一收取每单位(103 t)900元.问怎样制定供水方案,才能使获利最大? 为了增加供水量,拟对水库进行改造,使各水库的最大供水量增加1倍,问怎样制定供水方案,才能使获利最大? 表1 引水管理费(元/103 t) ??? ??-≤+---≤-+--≤+--2 1432143214321321 32..x x x x x x x x x x x x t s 4 321432min x x x x z +++=) ,,,{min(max 1 1 21 1i m i im i m i i i m i i x x a x a x a i ∑∑∑=== ???=≥=+++m i x x x x t s i m ,,2,1,01.21
线性规划的应用 线性规划是运筹学中一个重要分支,它是研究线性约束条件下线性目标函数的极值问题的数学理论和方法。广泛应用于军事作战、经济分析、经营管理和工程技术等方面。如:经济管理、交通运输、工农业生为合理地利用有限的人力、物力、财力等资源作出的最优决策,提供科学的依据。 线性规划作为运筹学的一个研究较早、发展较快、应用广泛、方法较成熟的重要分支,它在日常生活中的典型应用主要有:1合理利用线材问题:如何下料使用材最少 2配料问题:在原料供应量的限制下如何获取最大利润 3投资问题:从投资项目中选取方案,使投资回报最大 4产品生产计划:合理利用人力、物力、财力等,使获利最大 5劳动力安排:用最少的劳动力来满足工作的需要 6运输问题:如何制定调动方案,使总运费最小 其实,也就是说,线性规划在运筹学中的研究对象主要是在有一定的人力、财力、资源条件下,如何合理安排使用,效益最高和在某项任务确定后,如何安排人、财、物,使之最省。 例如: 某公司现有三条生产线来生产两种新产品,其主要数据如表1.1所示。请问如何生产可以让公司每周利润最大?
表1 产品组合问题的数据表 此问题是在生产线可利用时间受到限制的情形下寻求每周利润最大化的产品组合问题。 在建立产品组合模型的过程中,以下问题需要得到回答: (1)要做出什么决策? (2)做出的决策会有哪些条件限制? (3)这些决策的全部评价标准是什么? (1)变量的确定 要做出的决策是两种新产品的生产水平,记x1为每周生产产品甲的产量,x2为每周生产产品乙的产量。一般情况下,在实际问题中常常称为变量(决策变量)。 (2)约束条件 求目标函数极值时的某些限制称为约束条件。如两种产品在相应生产线上每周生产时间不能超过每条生产线的可得时间,对于生产线一,有x1≤4,类似地,其它生产线也有不等式约束。 (3)目标函数 对这些决策的评价标准是这两种产品的总利润,即目标函数是要求每周的生产利润(可记为z,以百元为计量单位)为最大 这样,可以把产品组合问题抽象地归结为一个数学模型: max z = 3x1+5x2 s.t. x1 ≤4 2x2 ≤12 3x1+ 2x2 ≤18 x1≥0,x2 ≥0
高考考点:《不等关系、线性规划与基本不等式》的案例分析 一、高考要求 1.不等关系 了解现实世界和日常生活中的不等关系,了解不等式组的实际背景。 2.一元二次不等式 (1)会从实际背景中抽象出一元二次不等式模型。 (2)通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的联系。 (3)会解一元二次不等式,对给定的一元二次不等式,会设计求解的程序框图。 3.二元一次不等式组与简单的线性规划问题 (1)会从实际情境中抽象出二元二次不等式组。 (2)了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组。 (3)会从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决。 4.基本不等式: (1)了解基本不等式的证明过程。 (2)会用基本不等式解决简单的最大(小)值问题。 二、规律分析
【规律总结】 全面分析这六年来的试题,可以看出,山东卷全面落实考纲对这一部分的规定,考查不等式的解法、线性规划和基本不等式的应用,每年的考查形式稍有变化,但总体上考点不变。具体来说,有这样的规律: (1)文科几乎每年涉及一元二次不等式的解法。理科涉及绝对值不等式的解法较多,一般与集合、函数的定义域求解结合较多,以选择题为主。 (2)几乎每年都考查线性规划问题,并且基本上都是以填空题和选择题的形式出现,只有2010年在填空题中考查了基本不等式,分析发现2010年以前山东高考是填空题的形式进行考查,2011年之后,则改为以选择题的形式考查。 (2)从2011年开始,山东高考考查线性规划的比重和难度在逐渐增加,2011年只是考查求线性规划的最大值问题,2012年的高考既考查求最大值又增加了求最小值,这两年都设计一个小题,2013则是设计了两个小题,并且与解析几何相结合,难度教以往有所增加。2014年将线性规划问题文科放在了第10,理科在9,难度再次增大。
姓名:刘巧林班级:建工系工程管理1班学号:1101021041 2、某公司在5年内考虑下列投资,已知: 项目A:可以从第1年到第4年的年初投资,并于次年年末收回本利115%; 项目B:在第3年的年初投资,到第5年年末收回本利125%,但规定投资额不能超过4万元; 项目C:在第2年年初投资,到第5年年末收回本利135%,但投资额不能超过3万元 项目D:可以在每年年初购买债券,年底归还,利息0,06,但规定第3年与第4年不能同时购买债券; 公司有资金100 万元,问如何投资,才能使第5年年末拥有的资金最多?请建立线性规划模型。 解:a、1)确定决策变量:连续投资问题 设Xij(i=1-5) j=(1、2、3、4) 2)约束条件: 第一年:项目A、D可以在当年投资,并可以收回成本。X11+X14=100第二年:本年末才能收到上一年D的投资。项目A、C、D可以在当年投资项目C在第5年年末可以收回成本 X21+X23+X24=1.06X14 第三年:本金:第一年A项目的本利+第二年D项目的本利。项目A、B、D可以在当年投资。但是项目D需要对比在第三年和第四年哪年的投资所得的资金更多。 X31+X32+X34=1.15X11+1.06X24 第四年:本金:第二年A项目的本利+第三年的D项目本利。项目啊A可以投资 X41=1.15X21+1.06X34 第五年:本金:第三年的A项目的本利。项目D可以投资。 X54=1.15X31 同时B、C有限制X32≤4 X23≤3 目标函数及其模型:Max z=1.15X41+1.25X32+1.35X23+1.06X54= S.t X11+X14=100 X21+X23+X24=1.06X14 X31+X32+X34=1.15X11+1.06X24 X41=1.15X21+1.06X34 X54=1.15X31 X32≤4 X23≤3
实验报告 课程名称:运筹学导论 实验名称:线性规划问题实例分析专业名称:信息管理与信息系统 指导教师:刘珊 团队成员:邓欣(20112111 蒋青青(20114298 吴婷婷(20112124 邱子群(20112102 熊游(20112110 余文媛(20112125 日期:2013-10-25 成绩:___________
1.案例描述 南部联盟农场是由以色列三个农场组成的联合组织。该组织做出了一个关于农场农作物的种植计划,如下: 每一个农场的农业产出受限于两个量,即可使用的灌溉土地量和用于灌溉的水量。数据见下表: 适合本地区种植的农作物包括糖用甜菜、棉花和高粱。这三种作物的差异在于它们每亩的期望净收益和水的消耗量不同。另外农业部门已经制定了南部联盟农场作物总亩数的最大配额,见下表: 作物的任何组合可以在任何农场种植,技术部门的任务是找出一个种植方案使南部联盟农场的净收益最大化。 2.建立模型 决策变量为Xi(i=1,2,……,9,表示每个农场每种作物的种植量。 MAX Z=1000(X1+X2+X3+750(X4+X5+X6+250(X7+X8+X9 约束条件: (1)每一个农场使用的土地 X1+X4+X7≤400
X2+X5+X8≤600 X3+X6+X9≤300 (2每一个农场的水量分布 3X1+2X4+X7≤600 3X2+2X5+X8≤800 3X3+2X6+X9≤375 (3每一种作物的总种植量 X1+X2+X3≤600 X4+X5+X6≤500 X7+X8+X9≤325 非负约束Xi≥0 , i=1,2, (9) 3.计算机求解过程 步骤1.生成表格 步骤2.输入数据
案例:连续投资的优化问题 一、题目: 某企业在今后五年内考虑对下列项目投资,已知:,从第一年到第四年每年年初需要投资,并于次年末收回本利115%。项目A,但规定最大投资额不超B,第三年年初需要投资,到第五年末能收回本利125%项目40万元。过,但规定最大投资额不超,第二年年初需要投资,到第五年末能收回本利140%项目C 30万元。过6%。项目D,五年内每年年初可购买公债,于当年末归还,并加利息问它应如何确定给这些项目的每年投100万元,该企业5年内可用于投资的资金总额为资使得到第五年末获得的投资本利总额为最大? 二、建立上述问题的数学模型的投资额,它们都是待定的年初给项目A,B,C,D, X (i=1.2.3.4.5)为第i设X,X , X iDiB1AiC每年年初均可投资,年末收回本利,固每年的投资额应该等于手中拥未知量。由于项目D 有的资金额。建立该问题的线性规划模型如下: +1.06X+1.40X+1.25XMax Z=1.15X5D 2C4A3B X+X=1000000 (1) 1D1A X+X+X=1.06X (2) 1D2C2A2D X+X+X=1.15X+1.06X (3) 3A 3B 3D 1A 2D s.t. X+X=1.15X+1.06X(4) 3D 4A 4D 2A X=1.15X+1.06X (5)5D 3A4D X<=400000 (6) 3B X<=300000 (7) 2C X , X , X, X>=0 i=1,2,3,4,5 iD1AiCiB 经过整理后如下: Max Z=1.15X+1.40X+1.25X+1.06X5D 2C4A3B X+X=1000000 1D1A-1.06X+ X+X+X =0 2D2A2C1D-1.15X-1.06X+ X+X+X=0 3D3A1A3B2D s.t. -1.15X-1.06X +X+X=0 4D3D4A2A-1.15X-1.06X+ X=0 5D4D3A X<=400000 3B X<=300000 2C i=1,2,3,4,5 , X , X, X>=0 X iDiBiC1A 求解过程以及相应的结果三、Excel中进行布局并输入相应的公式)在Excel1 (
8.2 线性规划 线性规划是处理线性目标函数和线性约束的一种较为成熟的方法,目前已经广泛应用于军事、经济、工业、农业、教育、商业和社会科学等许多方面。 8.2.1 基本数学原理 线性规划问题的标准形式是: ????? ??????≥=+++=+++=++++++=0,,,min 21221122222121112 121112211n m n mn m m n n n n n n x x x b x a x a x a b x a x a x a b x a x a x a x c x c x c z ΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛ 或 ???? ?????=≥===∑∑==n j x m i b x a x c z j n j i j ij n j j j ,,2,1,0,,2,1,min 1 1ΛΛ 写成矩阵形式为: ?? ???≥==O X b AX CX z min 线性规划的标准形式要求使目标函数最小化,约束条件取等式,变量b 非负。不符合这几个条件的线性模型可以转化成标准形式。 MATLAB 采用投影法求解线性规划问题,该方法是单纯形法的变种。 8.2.2 有关函数介绍 在MATLAB 工具箱中,可用linprog 函数求解线性规划问题。 linprog 函数的调用格式如下: ●x=linprog(f,A,b):求解问题minf'*x ,约束条件为A*x<=b 。 ●x=linprog(f,A,b,Aeq,beq):求解上面的问题,但增加等式约束,即Aeq*x=beq 。若没有不等式约束,则令A=[ ],b=[ ]。 ●x=linprog(f,A,b,Aeq,beq,lb,ub):定义设计x 的下界lb 和上界ub ,使得x 始终在该范围内。若没有等式约束,令Aeq=[ ],beq=[ ]。 ●x=linprog(f,A,b,Aeq,beq,lb,ub,x0):设置初值为x0。该选项只适用于中型问题,默认时大型算法将忽略初值。 ●x=linprog(f,A,b,Aeq,beq,lb,ub,x0,options):用options 指定的优化参数进行最小化。 ●[x,fval]=linprog(…):返回解x 处的目标函数值fval 。 ●[x,lambda,exitflag]=linpro g(…):返回exitflag 值,描述函数计算的退出条件。 ●[x,lambda,exitflag,output]=linprog(…):返回包含优化信息的输出参数output 。 ●[x,fval,exitflag,output,lambda]=linprog(…):将解x 处的拉格朗日乘子返回到
市场营销应用 案例一:媒体选择 在媒体选择中应用线性规划的目的在于帮助市场营销经理将固定的广告预算分配到各种广告媒体上,可能的媒体包括报纸、杂志、电台、电视和直接邮件。在这些媒体中应用线性规划,目的是要使宣传范围、频率和质量最大化。对于应用中的约束条件通常源于对公司政策、合同要求及媒体的可用性。在下面的应用中,我们将介绍如何应用线性规划这一工具来建立模型进而解决媒体选择问题。 REL发展公司正在私人湖边开发一个环湖社区。湖边地带和住宅的主要市场是距离开发区100英里以内的所有中上收入的家庭。REL公司已经聘请BP&J 来设计宣传活动。 考虑到可能的广告媒体和要覆盖的市场,BP&J建议将第一个月的广告局限于5种媒体。在第一个月末,BP&J将依据本月的结果再次评估它的广告策略。BP&J已经收集到了关于受众数量、广告单价、各种媒体一定周期内可用的最大次数以及评定5种媒体各自宣传质量的数据。质量评定是通过宣传质量单位来衡量的。宣传质量单位是一种用于衡量在各个媒体中一次广告的相对价值的标准,它建立于BP&J在广告业中的经验,将众多因素考虑在内,如受众层次(年龄、收入和受众受教育的程度)、呈现的形象和广告的质量。表4-1列出了收集到的这些信息。 表4-1 REL发展公司可选的广告媒体
REL发展公司提供给BP&J第一个月广告活动的预算是30000美元。而且,REL公司对BP&J如何分配这些资金设置了如下限制:至少要使用10次电视广告,达到的受众至少要有50000人,并且电视广告的费用不得超过18000美元。应当推荐何种广告媒体选择计划呢? 案例二:市场调查 公司开展市场营销调查以了解消费者个性特点、态度以及偏好。专门提供此种信息的市场营销调查公司,经常为客户机构开展实际调查。市场营销调查公司提供的典型服务包括涉及计划、开展市场调查、分析收集数据、提供总结报告和对客户提出意见。在调查设计阶段,应当对调查对象的数量和类型设定目标或限额。市场营销调查公司的目标是以最小的成本满足客户要求。 市场调查公司(MSI)专门评定消费者对新的产品、服务和广告活动的反映。一个客户公司要求MSI帮助确定消费者对一种近期推出的家具产品的反应。在与客户会面的过程中,MSI统一开展个人入户调查,以从有儿童的家庭和无儿童的家庭获得回答。而且MSI还同意同时开展日间和晚间调查。尤其是,客户的合同要求依据以下限制条款进行1000个访问: ●至少访问400个有儿童的家庭; ●至少访问400个无儿童的家庭; ●晚间访问的家庭数量必须不少于日间访问的家庭数量; ●至少40%有儿童的家庭必须在晚间访问; ●至少60%无儿童的家庭必须在晚间访问。 因为访问有儿童的家庭需要额外的访问时间,而且晚间访问者要比日间访问者获得更多收入,所以成本因访问的类型不同而不同。基于以往的调查研究,预计的访问费用如下表所示: 以最小总访问成本满足合同要求的家庭——时间访问计划是什么样的呢?
1.人力资源分配问题 设司机和乘务人员分别在各时间段开始时上班,并连续工作8小时,问该公交线路应怎样安排司机和乘务人员,既能满足工作需要,又使配备司机和乘务人员的人数最少? 解:设x i 表示第i班次时开始上班的司机和乘务人员数, 这样我们建立如下的数学模型。 目标函数:Min x1 + x2 + x3 + x4 + x5 + x6 约束条件:s.t. x1 + x6 ≥60 x1 + x2 ≥70 x2 + x3 ≥60 x3 + x4 ≥50 x4 + x5 ≥20 x5 + x6 ≥30 x1,x2,x3,x4,x5,x6 ≥0 运用lingo求解: Objective value: 150.0000 ariable Value Reduced Cost X1 60.00000 0.000000 X2 10.00000 0.000000 X3 50.00000 0.000000 X4 0.000000 0.000000 X5 30.00000 0.000000 X6 0.000000 0.000000 例2.一家中型的百货商场,它对售货员的需求经过统计分析如下表所示。为了保证售货人员充分休息,售货人员每周工作5天,休息两天,并要求休息的两天是连续的。问应该如何安排售货人员的作息,既满足工作需要,又使配备的售货人员的人数最少?
解:设x i ( i = 1,2,…,7)表示星期一至日开始休息的人数,这样我们建立如下的数学模型。 目标函数:Min x1 + x2 + x3 + x4 + x5 + x6 + x7 约束条件:s.t. x1 + x2 + x3 + x4 + x5 ≥28 x2 + x3 + x4 + x5 + x6 ≥15 x3 + x4 + x5 + x6 + x7 ≥24 x4 + x5 + x6 + x7 + x1 ≥25 x5 + x6 + x7 + x1 + x2 ≥19 x6 + x7 + x1 + x2 + x3 ≥31 x7 + x1 + x2 + x3 + x4 ≥28 x1,x2,x3,x4,x5,x6,x7 ≥0 lingo求解 Objective value: 36.00000 Variable Value Reduced Cost X1 12.00000 0.000000 X2 0.000000 0.3333333 X3 11.00000 0.000000 X4 5.000000 0.000000 X5 0.000000 0.000000 X6 8.000000 0.000000 X7 0.000000 0.000000 例3. 某储蓄所每天的营业时间为上午9:00到下午17:00,根据经验,每天不同时间段所需要 储蓄所可以雇佣全时和半时两类服务员。全时服务员每天报酬为100元,从上午9:00到下午17:00工作,但中午12:00到下午14:00之间必须安排1小时的午餐时间;储蓄所每天可以雇佣不超过3名的半时服务员,每个半时服务员必须连续工作4小时,报酬为40元。问: 1) 储蓄所应该如何雇佣全时和半时两类服务员? 2) 如果不能雇佣半时服务员,每天至少增加多少经费? 3) 如果雇佣半时服务员的数量没有限制,每天可以减少多少经费? 解:设x1, x2分别表示12~13,13~14进行午餐的全时服务人员, y1,y2,y3,y4,y5分别表示9~10,10~11,11~12,12~13,13~14开始工作的半时服务人员,则问题1的模型如下所示: min=100*x1+100*x2+40*y1+40*y2+40*y3+40*y4+40*y5; x1+x2+y1>4; x1+x2+y1+y2>3; x1+x2+y1+y2+y3>4; x2+y1+y2+y3+y4>6; x1+y2+y3+y4+y5>5; x1+x2+y3+y4+y5>6; x1+x2+y4+y5>8; x1+x2+y5>8; y1+y2+y3+y4+y5<3;
基础训练 1.若变量x ,y 满足约束条件,则目标函数z =x -2y 的最大值为 A .-9 B .0 C .9 D .15 2.已知满足,则的最小值是 A .1 B .2 C .5 D 3.已知、满足,且的最大值是最小值的倍,则 的值是 A B C D . 4.在中,三个顶点分别为A (2,4), B (-1,2) ,C (1,0),点P (x ,y )在的内部及其边界上运动,则y -x 的取值范围为 A .[1,3] B .[-3,1] C .[-1,3] D .[-3,-1] 5.已知变量满足约束条件 A .1 B . C D .0 6.设,其中实数满足,若的最大值为6,则的最小值为 A . B . C . D .0 23y x x ≥-??≤? ,x y 250 300x y x x y -+≥?? -≥??+≥? y x z +=2x y 2y x x y x a ≥?? +≤??≥? 2z x y =+4a 4ABC △ABC △,x y 50,210,10, x y x y x +-≤??-+≤??-≥? 4z x y =+,x y 2000x y x y y k +≥?? -≤??≤≤? z z 3-2-1-
7.已知实数满足且数列为等差数列,则实数的最大值是_______________. 8.已知实数满足 _______________. 9.已知x,y满足条件,求: (1)4x?3y的最大值; (2)x2+y2的最大值; (3 ,x y 2, 1 , 2 , x y x y x +≤ ? ?? ≥ ? ? ≥ ?? 4,,2 x z y z y x, 0, , 260, x y x x y > ? ? ≥ ? ?+-≤ ? 75230 7110 4100 x y x y x y --≤ ? ? +-≤ ? ?++≥ ?