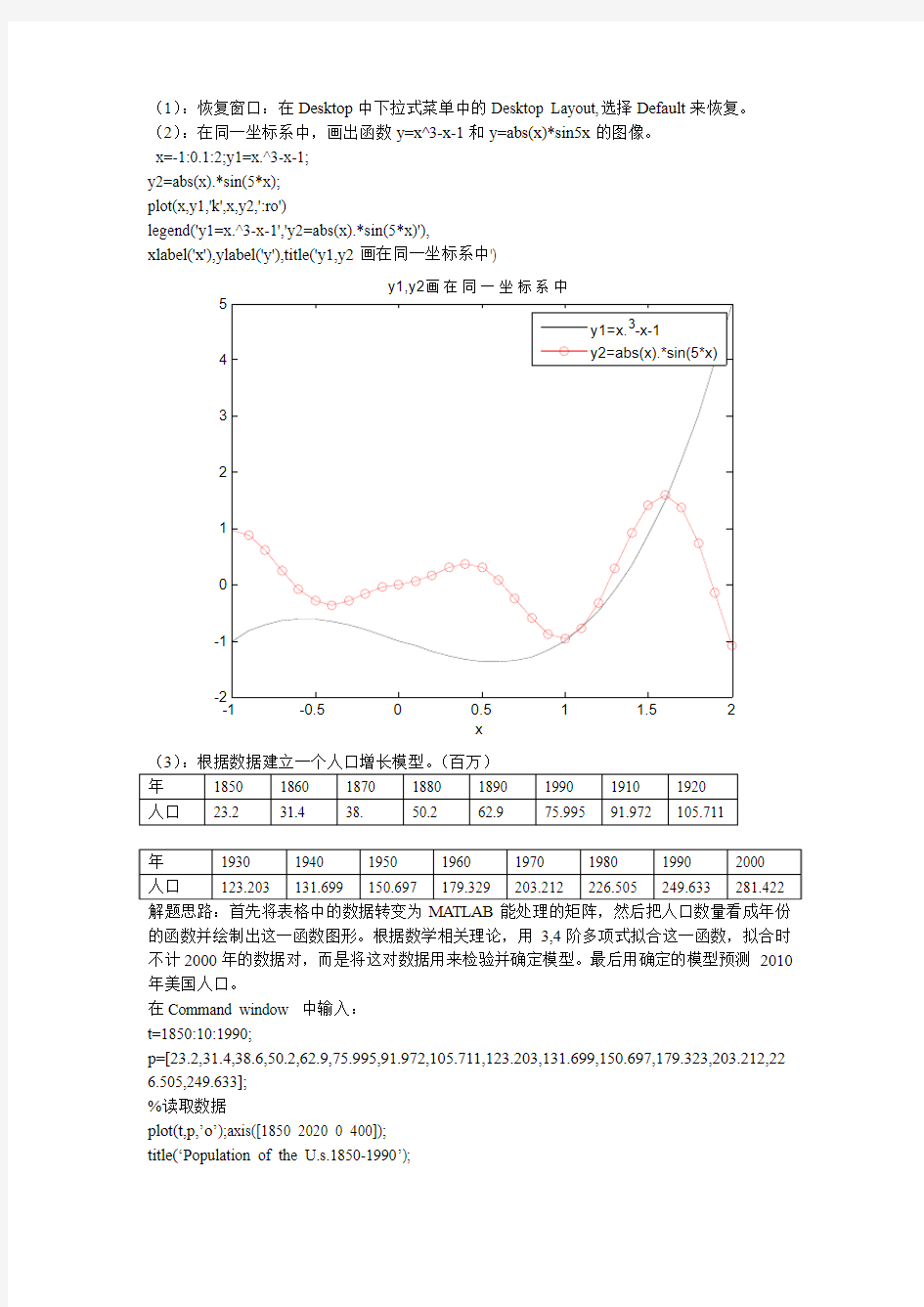
(1):恢复窗口:在Desktop 中下拉式菜单中的Desktop Layout,选择Default 来恢复。 (2):在同一坐标系中,画出函数y=x^3-x-1和y=abs(x)*sin5x 的图像。 x=-1:0.1:2;y1=x.^3-x-1; y2=abs(x).*sin(5*x); plot(x,y1,'k',x,y2,':ro')
legend('y1=x.^3-x-1','y2=abs(x).*sin(5*x)'),
xlabel('x'),ylabel('y'),title('y1,y2画在同一坐标系中')
-1
-0.50
0.51 1.52
x
y
y1,y2画在同一坐标系中
(3):根据数据建立一个人口增长模型。(百万)
的函数并绘制出这一函数图形。根据数学相关理论,用3,4阶多项式拟合这一函数,拟合时不计2000年的数据对,而是将这对数据用来检验并确定模型。最后用确定的模型预测2010年美国人口。
在Command window 中输入: t=1850:10:1990;
p=[23.2,31.4,38.6,50.2,62.9,75.995,91.972,105.711,123.203,131.699,150.697,179.323,203.212,226.505,249.633]; %读取数据
plot(t,p,’o ’);axis([1850 2020 0 400]); title(‘Population of the U.s.1850-1990’);
ylabel(‘Millions ’);%绘制出数据的函数图形并加以修饰
f1=polyfit(t,p,3);f2=polyfit(t,p,4);%对数据做3,4阶多项式拟合,结果分别为f1和f2 v=[polyval(f1,2000),polyval(f2,2000)];%计算当t=2000时多项式f1,f2的值 abs(v-251.422) %计算两个模型与2000年人口数的绝对误差。
186018801900192019401960198020002020
Population of the U.s.1850-1990
M i l l i o n s
ans =
28.9561 30.8937
由计算结果可以确定3阶多项式可作为此问题的数学模型,因此进一步进行预测: V1=polyval(f1,2010)
V1 =
311.6136
即由3阶多项式拟合可预测到2010年美国人口将达到311.6148百万人。
(4):研究捕食者与被捕食者(Lotka-V oltrra )模型的相互作用系数α和β的影响。 X’1=x1- x1x2 α X’2=x2+x1x2β
X1(0)=x2(0)=1,0<=t<=10
建立M 文件,再调用微分方程求解器ode45求出数值解。
function dx=lotka(t,x) global alpha beita
dx=[x(1)-alpha*x(1)*x(2);-x(2)+beita*x(1)*x(2)];
第二步:调用ode45命令求数值解。在Command Window 中输入下面的命令。 global alpha beita
alpha=0.1;beita=0.2;
[t,x]=ode45('lotka',[0,10],[1,1]);%求模型的数值解 plot(t,x(:,1),'k',t,x(:,2),':k')%画模型的图像解 title('alpha=0.1;beita=0.2,Lotka-V oltrra'), xlabel('t'),ylabel('x1,x2'), legend('x1’,'x2'),
1
2
3
4
56
7
8
9
10
0100200300400500600
700800900
1000alpha=0.1;beita=0.2,Lotka-Voltrra
t
x 1,x 2
第二章
MATLAB 的变量是以字母开头,由字母,数字,下划线组成。同一字母的大小写表示不同的变量。
常见的变量有四种:数值变量(double )字符变量(char )符号变量(sym )结构变量(struct )。MATLAB 存储变量时用图标和文字来注明变量的类型。例如输入:
x1=1/3 x2=’1/3’ x3=sym(‘1/3’) x4.x=1/3
可以在workspace 中看到它们各自不同的图标和变量类型的文字解释。它们分别是double 型,char 型,sym 型,struct 型变量。
下面主要讨论数值型变量的有关问题。
在MA TLAB 中,不用事先定义变量的特性(实数或复数),也不用事先定义变量的维数。一旦某个变量被赋值,则该变量连同其值将被存放于Workspace 中,直到该变量被清除或被重新赋值。例如在Command Window 中输入A=5+4i,b=5-4*i,c=8都将是有效的。如想观察A 的值,可在Comamnd Window 中输入变量名,然后再按回车键。如果再输一次A=5,观察A 时就不是先前的5+4i 了。
在MATLAB 中,有些字符被自动赋值,可称之为固有变量。还有些字符已被MA TLAB 定义为函数名或M 文件名。因此,在定义变量名时,要尽量回避固有变量名,函数名和M
文件名。下面这些字符是常见的固有变量。在定义时变量时,一定不要将它们重新赋值。
i or j: 虚数单位,即根下负1
pi:圆周率
eps:机器误差:ξ =2^-52=2.2204*10^-16
realmin :最小正实数:2^-1022=2.2251*10^-308
realmax :最大正实数:(2- ε)⊥1023=1.7977*10^308
Inf :无穷大
NaN:非数
ans:当前答案
(2):MATLAB默认的数据显示格式是short格式,可以通过键入format V来改变显示格式。其中V为所需的显示格式。MA TLAB提供的显示格式有:
short 5位固定点格式,如:3.1416
long 15位双精度固定点格式如:3.14159265358979
short e 5位浮点格式,如:3.1416e+000
long e 15位双精度7位单精度浮点格式,如:3.141592653589793e+000
short eng 5位工程格式,如:3.1416e+000
long eng 16位工程格式,如:3.14159265358979e+000
(3):特殊含义的符号
[] 中括号,用于生成矩阵
()圆括号,函数参数的引入符号以及运算次序规则符号
,逗号,在句尾表示换行,并显示结果;在矩阵中则是元素分隔符
;分号,在句尾表示换行,不显示结果;在矩阵中表示换行
‘单引号,是一运算符,表示矩阵转置运算
:冒号,是一运算符,可生成一等差序列并表示成向量
%百分号,从它起直到它所在的行尾,其间所有的命令,计算机均不执行,即%是一个注释符
@函数句柄
“引号
.点。小数点。在算术运算符前表示点对点运算;在变量中加点,表示该变量为结构变量···续行符
第三章矩阵的操作
3.1
生成矩阵的三种基本方法:直接输入,由外部文件下载输入,利用MA TLAB的函数来生成。
直接输入的两种方法:方式一:在Command Window中直接输入
例如:A=[1 -1 0;1/2 3 1/3;0 10 1] 回车即可
A =
1.0000 -1.0000 0
0.5000 3.0000 0.3333
0 10.0000 1.0000
方式二:矩阵编辑器输入。
首先在Command Window中输入B=1;接着在Workspace中双击B的图标,调出数组编辑器(Array Editor)在表格中输入相应的元素,关闭数组编辑器,则Wordspace中存放的就是所需的矩阵B,以后就可以直接调用。
矩阵也可以由外部数据文件导入。
先将其拷贝下来并粘贴到Excel或记事本中,然后保存为B.csv或B.txt文件。例如,假设已将B.txt存放于C:\matlab\work中只需在MA TLAB的File菜单下选Import Data,然后选中B并打开,根据提示选Next和Finish.当Workspace中出现了B的标记后。说明已成功输入了B。
当然还可以通过编写程序来得到某个矩阵。
键入0:10
ans =
0 1 2 3 4 5 6 7 8 9 10
键入hilb(3)得到Hilbert矩阵
ans =
1.0000 0.5000 0.3333
0.5000 0.3333 0.2500
0.3333 0.2500 0.2000
键入rand(3,2),可得到3*2的矩阵:
rand(3,2)
ans =
0.9501 0.4860
0.2311 0.8913
0.6068 0.7621
这样的命令很多,可以通过键入命令help elmat查看。
zeros(m,n) m*n零矩阵
ones(m,n) 元素全为1的m*n矩阵
eye(m,n) m*n辨识矩阵,主对角元素全为1,其余元素全为0;若m=n则eye(m)为m 阶单位阵
rand(m,n) m*n随机矩阵,其中元素服从离散均匀分布
randn(m,n) m*n随机矩阵,其中元素服从离散正态分布
hadamard(n) n阶Hadamard矩阵
hankel(n) n阶Hankel矩阵
hilb(n) n阶Hilb矩阵
invhilb(n) n阶Hilbert逆矩阵
magic(n) n阶幻方矩阵
pascal(n) n阶pascal矩阵
下面介绍函数命令linspace和运算符号——冒号。
它们都可以用来生成行向量(特殊矩阵)
linspace(x1,x2) 以x1为起点,以x2为终点等距生成100个数据的行向量
linspace(x1,x2,N) 以x1为起点,以x2为终点等距生成N个数据的行向量
x1:x2 生成以x1为起点,以x2为终点,步长为1的行向量,要求x2>x1
x1:t:x2生成以x1为起点,以x2为终点,步长为t的行向量(可以有t<0)
3.2
矩阵结构的变换
diag(v)
若v为矩阵(不一定是方阵),则diag(v)生成以v的主对角元素为元素的列向量。而daig(v,k)生成以v的第k条对角线元素为元素的列向量。K=0表示主对角线,k>0表示主对角线的上方,k<0表示主对角线的下方。
若v为n维向量,则diag(v)生成以v为主对角元素的n阶方阵,而diag(v,k)生成n+\k\阶方阵,且v为此方阵的第k条对角线元素。
blkdiag
主对角元素为子矩阵的对角矩阵。
例如输入:A=[1,2;3,4];B=[5,6];
blkdiag(A,B)
ans =
1 2 0 0
3 4 0 0
0 0 5 6
tril
提取下三角矩阵。调用规则(A,k)。其中A为矩阵,k=0表示提取A的主对角线及其下方的元素而成的下三角矩阵,切可缺省;k>0表示提取A的主对角线上方第k条对角线及其下方的元素而成的下三角矩阵;k<0表示提取A的主对角线下方第k条对角线及其下方的元素而成的下三角矩阵。例如:
A=[1,2,3,4;11,2,5,6;22,33,3,7]
tril(A)
A =
1 2 3 4
11 2 5 6
22 33 3 7
ans =
1 0 0 0
11 2 0 0
22 33 3 0
>> tril(A,2)
ans =
1 2 3 0
11 2 5 6
22 33 3 7
>> tril(A,-2)
ans =
0 0 0 0
0 0 0 0
22 0 0 0
triu
提取上三角矩阵,调用格式triu(A,k),规则与tril的规则相同。
在线性代数中常常会交换矩阵的两行或两列,划去矩阵的某行或某列,提取矩阵的某个子矩阵等这样的一些操作。实现方法:
设有m*n矩阵A其第i行第j列表示为A(i,j).(矩阵的标识)
从中取出第二行第三列的元素,
A=[1 2 3 4;5 6 7 8;9 10 11 12];
A(2,3)
ans =
7
把7改为其他元素:
>> A(2,3)=0;
A
A =
1 2 3 4
5 6 0 8
9 10 11 12
矩阵的标识A(i,j)中,i或j不仅可以是正整数,还可以是冒号或向量。例如,A(i,:) 表示A的第i行元素。而A(i,[2,3])表示A的第i行,第2,3列的元素。利用矩阵的标识命令可以完成从矩阵A中提取子矩阵,划去矩阵的行或列及交换矩阵的行或列。
A(2,:)
ans =
5 6 0 8
>> A([1,2],[2,3])
ans =
2 3
6 0
划去A的第2行
>> B=A([1,3],:)
B =
1 2 3 4
9 10 11 12
第1列和第2列交换,第3列和第4列交换
>> D=A(:,[2 1 4 3])
D =
2 1 4 3
6 5 8 0
10 9 12 11
还可以用空矩阵划去某行或某列的操作。
空矩阵的表达式[]键入X=[]
X =
[]
它表示矩阵不含有任何元素,是一个空矩阵。空矩阵不是0,也不是不存在。A=(m,:)=[]表示删除A的第m行元素
A=(:,n)=[] 表示删除A的第n列元素
A=[1 2 3 4 5 6;7 8 9 10 11 12;13 14 15 16 17 18];
A(:,[2,5])=[]
A =
1 3 4 6
7 9 10 12
13 15 16 18
MATLAB可以将若干个子矩阵拼装成一个大矩阵。
a11=[1 2];a12=3;a13=[4 5 6];
a21=[7 8;13 14];a22=[9;15];a23=[10 11 12;16 17 18];
A=[a11 a12 a13;a21 a22 a23] A =
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
A.*B 的运算规则是;矩阵A ,B 以及运算结果都是同阶矩阵,且A.*B 是A,B 的对应元素相乘。
已知x=0,1,2,3,4.5,5.5,6.5求y=x^2+3x 所对应的值。 x=[0,1,2,3,4.5,5.5,6.5]; y=x.*(x+3) y =
Columns 1 through 6
0 4.0000 10.0000 18.0000 33.7500 46.7500
Column 7
61.7500
-10
-8-6-4-20246810
-20020406080100120
140
x=-10:1:10;
y=x.*(x+3);
plot(x,y,'k')
x1=0:3;x2=4.5:6.5;x=[x1 x2];
y=x.*(x+3);
plot(x,y,'k')
>> y
y =
Columns 1 through 6
0 4.0000 10.0000 18.0000 33.7500 46.7500
Column 7
61.7500
矩阵的除法运算(省略)
MATLAB的命令函数
5.1基本函数
可以在Command Window中输入help elfun命令查到所有的基本函数(标量函数)。定义域和值域都是复数集。只有函数realpow(.)和reallog(.)realsqrt()的定义域才与数学中相应函数的定义域相同。
例如:sqrt(2)
ans =
1.4142
>> sqrt(i)
ans =
0.7071 + 0.7071i
>> realsqrt(i)
??? Error using ==> realsqrt
Realsqrt produced complex result.
这些函数的输入参数可以是矩阵。
例如:x=[1 2;3 4];
y=sqrt(x)
y =
1.0000 1.4142
1.7321
2.0000
(2)
x=1:7;
y=sin(x)
y =
0.8415 0.9093 0.1411 -0.7568 -0.9589 -0.2794 0.6570
>> y=x.*sin(x)
y =
0.8415 1.8186 0.4234 -3.0272 -4.7946 -1.6765 4.5989
5.2
数据分析函数(Data Analysis)
在Comamand Window中输入help datafun查到所有的数据分析函数。
一般来说,数据分析函数的输入量应是列向量(数据分析函数又被称为向量函数)。如果是行向量,数据分析函数同样可以计算。如果输入矩阵,则数据分析函数按列向量计算。
max([1 4 3 2]) 输入的是行向量
ans =
4
x =
1 6 9
2 4 3
3 2 10
>> x=[1 6 9;2 4 3;3 2 10];
max(x)
ans =
3 6 10(按列向量)
5.3 矩阵函数(Matrix Functions)
所谓矩阵函数是指函数命令的输入变量为矩阵。可以在Command Window窗口中键入help matfun命令查到所有的矩阵函数。用help+函数名的方法,可以对其中任一函数的功能作进一步的了解。
关于矩阵分析的命令:
norm(X) 求矩阵或向量的范数,对于矩阵X而言是X的最大奇异值,也就是X的
2范数
norm(X,2) 与norm(X)相同
norm(X,1) X的1范数
norm(X,inf) X的无穷范数
rank(A) 求矩阵A的秩
det(A) 求方阵A的行列式
trace(A) 矩阵A主对角元素之和
rref(A) 对矩阵A进行初等变换,变换成阶梯型矩阵
A=[1 2 3 4;5 10 15 20;6 7 8 9];
rref(A)
ans =
1 0 -1 -2
0 1 2 3
0 0 0 0
2;关于解线性方程组的命令(Linear Equations)
/和\ 线性方程组的求解命令
inv(A) 求方阵A的逆
cond(A) 求A的条件数
chol(A) 求正订方阵A的Cholesky分解
lu(A) 求A的LU分解,调用格式一般为[L,U]=lu(X),其中U是上三角矩阵,L 是一个下三角矩阵且满足X=L*U,允许X不是方阵。
pinv(A) 求矩阵A的伪逆
a=[10 2 3;2 3 4;3 4 8];
chol(a)
ans =
3.1623 0.6325 0.9487
0 1.6125 2.1086
0 0 1.6291
A=[10 -7 0;-3 2 6;5 -1 5];
[L,U]=lu(A)
L =
1.0000 0 0
-0.3000 -0.0400 1.0000
0.5000 1.0000 0
U =
10.0000 -7.0000 0
0 2.5000 5.0000
0 0 6.2000
5.3 求特征值和奇异数的命令
eig(A) 求A的特征值和特征向量。调用格式一般为E=eig(A)或[V,D]=eig(A).E是方阵A的特征值构成的向量,D是以A的特征值为主对角线元素的对角矩阵,V是与特征值相对应的特征向量所构成的满秩矩阵,且满足A*V=V*D
svd(A) 求A的奇异值分解,调用格式一般为:[U,S,V]=svd(X),其中S 是一个维数与X相同的对角矩阵,且对角线元素非负递减,U和V是酒矩阵,且满足X=U*S*V’ploy(A)
求矩阵的特征多项式和以1,-1,0为根的多项式。
e=poly([0 1;0 2])
e =
该矩阵的多项式为e=x^-2x
1 -
2 0
>> c=poly([1 -1 0])
c =
1 0 -1 0
多项式为c=x^3-x
6.1平面曲线的绘制
在x-y坐标面上绘制函数图形的主要命令是plot。其调用格式是plot(x,y),其中x是向量,y是与x同维的向量。
x=-pi:0.01:pi;
y=x.*sin(x);
plot(x,y)
-4
-3
-2
-1
1
2
3
4
00.20.40.60.811.21.41.61.8
2
Plot 的调用格式还可以是plot(x1,y1,x2,y2,x3,y3``````),用于同一坐标系下绘制多条函数曲线。其中一组(xi,yi )表示一组函数。
x1=-3:0.05:3;x2=-2.9:0.02:2.9; y1=sin(x1.^2);y2=exp(-x2.^2); plot(x1,y1,x2,y2)
-3
-2
-1
1
2
3
-1-0.8-0.6-0.4-0.200.20.40.60.8
1
1:曲线的修饰
设S 使修饰变量,用plot(x,y,s)或plot(x1,y1,S1,x2,y2,s2…….)可以对曲线y 的线型和颜色进行修饰。S 是一个单引号括起来的字符。字符可以是下表的任意一种颜色和(多个)线型字符的组合。
2,3,4,6,8,10,15,25,30)
2:坐标轴的控制
命令axis 被用来控制坐标轴的范围。常用格式为: axis([xmin xmax,ymin,ymax]) 指定x,y 的取值范围 axis equal 使x,y 轴的单位长度相等 axis aquare 使坐标面为正方形 3:图形标注,说明,网格 (1):图形标注命令
title(‘S ’) 题头标注,S 为说明文的字符 xlabel(‘S ’) X 轴标注,S 为说明文的字符 ylabel(‘S ’) Y 轴标注,S 为说明文的字符
3:图形说明命令
legend(‘S1’,’S2’,’Sn’,pos) 线性说明,Si为说明文字符。Pos为整数,用来指定标注的位置
pos=-1 坐标系范围外右边
pos=0 坐标系范围内,并尽可能少的遮挡曲线
pos=1 坐标系范围内右上角,是默认值
pos=2 坐标系范围内左上角
pos=3 坐标系范围内左下角
pos=4 坐标系范围内右下角
(3)网格命令
grid on 在坐标面上画网格
grid off 在坐标面上去除网格
grid 在两者之间切换
x1=-3:0.05:3;x2=-2.9:0.02:2.9;
y1=sin(x1.^2);y2=exp(-x2.^2);
plot(x1,y1,x2,y2)
x=-pi:0.01:pi;
x=-pi:0.01:pi;
x=-pi:0.01:pi;
y1=sin(x);y2=cos(x);y3=sin(x)-cos(x);
plot(x,y1,'r',x,y2,'k',x,y3,'g','linewidth',2)
axis equal
grid
legend('y=sin(x)','y=cos(x)','y=sin(x)-cos(x)',0)
xlabel('自变量');ylabel('函数');title('图形修饰练习');
-3
-2
-1
01
2
3
-2-1.5-1-0.500.5
11.52自变量
函数
图形修饰练习
6-1 试验目的计算特征值,实现算法 试验容:随机产生一个10阶整数矩阵,各数均在-5和5之间。 (1) 用MATLAB 函数“eig ”求矩阵全部特征值。 (2) 用幂法求A 的主特征值及对应的特征向量。 (3) 用基本QR 算法求全部特征值(可用MATLAB 函数“qr ”实现矩阵的QR 分解)。 原理 幂法:设矩阵A 的特征值为12n ||>||||λλλ≥???≥并设A 有完全的特征向量系12,,,n χχχ???(它们线性无关),则对任意一个非零向量0n V R ∈所构造的向量序列1k k V AV -=有11()lim ()k j k k j V V λ→∞ -=, 其中()k j V 表示向量的第j 个分量。 为避免逐次迭代向量k V 不为零的分量变得很大(1||1λ>时)或很小(1||1λ<时),将每一步的k V 按其模最大的元素进行归一化。具体过程如下: 选择初始向量0V ,令1max(),,,1k k k k k k k V m V U V AU k m +===≥,当k 充分大时1111,max()max() k k U V χλχ+≈ ≈。 QR 法求全部特征值: 111 11222 111 ,1,2,3,k k k k k A A Q R R Q A Q R k R Q A Q R +++==????==??=???? ??????==?? 由于此题的矩阵是10阶的,上述算法计算时间过长,考虑采用改进算法——移位加速。迭 代格式如下: 1 k k k k k k k k A q I Q R A R Q q I +-=?? =+? 计算k A 右下角的二阶矩阵() () 1,1 1,() (),1 ,k k n n n n k k n n n n a a a a ----?? ? ??? 的特征值()()1,k k n n λλ-,当()()1,k k n n λλ-为实数时,选k q 为()()1,k k n n λλ-中最接近(),k n n a 的。 程序
%求四阶线性方程组的MA TLAB程序 clear Ab=[0.001 2 1 5 1; 3 - 4 0.1 -2 2; 2 -1 2 0.01 3; 1.1 6 2.3 9 4];%增广矩阵 num=[1 2 3 4];%未知量x的对应序号 for i=1:3 A=abs(Ab(i:4,i:4));%系数矩阵取绝对值 [r,c]=find(A==max(A(:))); r=r+i-1;%最大值对应行号 c=c+i-1;%最大值对应列号 q=Ab(r,:),Ab(r,:)=Ab(i,:),Ab(i,:)=q;%行变换 w=Ab(:,c),Ab(:,c)=Ab(:,i),Ab(:,i)=w;%列变换 n=num(i),num(i)=num(c),num(c)=n;%列变换引起未知量x次序变化for j=i:3 Ab(j+1,:)=-Ab(j+1,i)*Ab(i,:)/Ab(i,i)+Ab(j+1,:);%消去过程 end end %最后得到系数矩阵为上三角矩阵 %回代算法求解上三角形方程组 x(4)=Ab(4,5)/Ab(4,4); x(3)=(Ab(3,5)-Ab(3,4)*x(4))/Ab(3,3); x(2)=(Ab(2,5)-Ab(2,3)*x(3)-Ab(2,4)*x(4))/Ab(2,2); x(1)=(Ab(1,5)-Ab(1,2)*x(2)-Ab(1,3)*x(3)-Ab(1,4)*x(4))/Ab(1,1); for s=1:4 fprintf('未知量x%g =%g\n',num(s),x(s)) end %验证如下 %A=[0.001 2 1 5 1; 3 -4 0.1 -2 2;2 -1 2 0.01 3; 1.1 6 2.3 9 4]; %b=[1 2 3 4]'; %x=A\b; %x1= 1.0308 %x2= 0.3144 %x3= 0.6267 %x4= -0.0513
第一章插值方法 1.1Lagrange插值 1.2逐步插值 1.3分段三次Hermite插值 1.4分段三次样条插值 第二章数值积分 2.1 Simpson公式 2.2 变步长梯形法 2.3 Romberg加速算法 2.4 三点Gauss公式 第三章常微分方程德差分方法 3.1 改进的Euler方法 3.2 四阶Runge-Kutta方法 3.3 二阶Adams预报校正系统 3.4 改进的四阶Adams预报校正系统 第四章方程求根 4.1 二分法 4.2 开方法 4.3 Newton下山法 4.4 快速弦截法 第五章线性方程组的迭代法 5.1 Jacobi迭代 5.2 Gauss-Seidel迭代 5.3 超松弛迭代 5.4 对称超松弛迭代 第六章线性方程组的直接法 6.1 追赶法 6.2 Cholesky方法 6.3 矩阵分解方法 6.4 Gauss列主元消去法
第一章插值方法 1.1Lagrange插值 计算Lagrange插值多项式在x=x0处的值. MATLAB文件:(文件名:Lagrange_eval.m)function [y0,N]= Lagrange_eval(X,Y,x0) %X,Y是已知插值点坐标 %x0是插值点 %y0是Lagrange插值多项式在x0处的值 %N是Lagrange插值函数的权系数 m=length(X); N=zeros(m,1); y0=0; for i=1:m N(i)=1; for j=1:m if j~=i; N(i)=N(i)*(x0-X(j))/(X(i)-X(j)); end end y0=y0+Y(i)*N(i); end 用法》X=[…];Y=[…]; 》x0= ; 》[y0,N]= Lagrange_eval(X,Y,x0) 1.2逐步插值 计算逐步插值多项式在x=x0处的值. MATLAB文件:(文件名:Neville_eval.m)function y0=Neville_eval(X,Y,x0) %X,Y是已知插值点坐标 %x0是插值点 %y0是Neville逐步插值多项式在x0处的值 m=length(X); P=zeros(m,1); P1=zeros(m,1); P=Y; for i=1:m P1=P; k=1; for j=i+1:m k=k+1;
常用计算方法 1.超越方程的求解 一超越方程为 x (2ln x – 3) -100 = 0 求超越方程的解。 [算法]方法一:用迭代算法。将方程改为 01002ln()3 x x =- 其中x 0是一个初始值,由此计算终值x 。取最大误差为e = 10-4,当| x - x 0| > e 时,就用x 的值换成x 0的值,重新进行计算;否则| x - x 0| < e 为止。 [程序]P1_1abs.m 如下。 %超越方程的迭代算法 clear %清除变量 x0=30; %初始值 xx=[]; %空向量 while 1 %无限循环 x=100/(2*log(x0)-3); %迭代运算 xx=[xx,x]; %连接结果 if length(xx)>1000,break ,end %如果项数太多则退出循环(暗示发散) if abs(x0-x)<1e-4,break ,end %当精度足够高时退出循环 x0=x; %替换初值 end %结束循环 figure %创建图形窗口 plot(xx,'.-','LineWidth',2,'MarkerSize',12)%画迭代线'.-'表示每个点用.来表示,再用线连接 grid on %加网格 fs=16; %字体大小 title('超越方程的迭代折线','fontsize',fs)%标题 xlabel('\itn','fontsize',fs) %x 标签 ylabel('\itx','fontsize',fs) %y 标签 text(length(xx),xx(end),num2str(xx(end)),'fontsize',fs)%显示结果 [图示]用下标作为自变量画迭代的折线。如P0_20_1图所示,当最大误差为10-4时,需要迭代19次才能达到精度,超越方程的解为27.539。 [算法]方法二:用求零函数和求解函数。将方程改为函数 100()2ln()3f x x x =-- MATLAB 求零函数为fzero ,fzero 函数的格式之一是 x = fzero(f,x0) 其中,f 表示求解的函数文件,x0是估计值。fzero 函数的格式之二是 x = fzero(f,[x1,x2])
1、Newdon迭代法求解非线性方程 function [x k t]=NewdonToEquation(f,df,x0,eps) %牛顿迭代法解线性方程 %[x k t]=NewdonToEquation(f,df,x0,eps) %x:近似解 %k:迭代次数 %t:运算时间 %f:原函数,定义为内联函数 ?:函数的倒数,定义为内联函数 %x0:初始值 %eps:误差限 % %应用举例: %f=inline('x^3+4*x^2-10'); ?=inline('3*x^2+8*x'); %x=NewdonToEquation(f,df,1,0.5e-6) %[x k]=NewdonToEquation(f,df,1,0.5e-6) %[x k t]=NewdonToEquation(f,df,1,0.5e-6) %函数的最后一个参数也可以不写。默认情况下,eps=0.5e-6 %[x k t]=NewdonToEquation(f,df,1) if nargin==3 eps="0".5e-6; end tic; k=0; while 1 x="x0-f"(x0)./df(x0); k="k"+1; if abs(x-x0) < eps || k >30 break; end x0=x; end t=toc; if k >= 30 disp('迭代次数太多。'); x="0"; t="0"; end
2、Newdon迭代法求解非线性方程组 function y="NewdonF"(x) %牛顿迭代法解非线性方程组的测试函数 %定义是必须定义为列向量 y(1,1)=x(1).^2-10*x(1)+x(2).^2+8; y(2,1)=x(1).*x(2).^2+x(1)-10*x(2)+8; return; function y="NewdonDF"(x) %牛顿迭代法解非线性方程组的测试函数的导数 y(1,1)=2*x(1)-10; y(1,2)=2*x(2); y(2,1)=x(2).^+1; y(2,2)=2*x(1).*x(2)-10; return; 以上两个函数仅供下面程序的测试 function [x k t]=NewdonToEquations(f,df,x0,eps) %牛顿迭代法解非线性方程组 %[x k t]=NewdonToEquations(f,df,x0,eps) %x:近似解 %k:迭代次数 %t:运算时间 %f:方程组(事先定义) ?:方程组的导数(事先定义) %x0:初始值 %eps:误差限 % %说明:由于虚参f和df的类型都是函数,使用前需要事先在当前目录下采用函数M文件定义% 另外在使用此函数求解非线性方程组时,需要在函数名前加符号“@”,如下所示 % %应用举例: %x0=[0,0];eps=0.5e-6; %x=NewdonToEquations(@NewdonF,@NewdonDF,x0,eps) %[x k]=NewdonToEquations(@NewdonF,@NewdonDF,x0,eps) %[x k t]=NewdonToEquations(@NewdonF,@NewdonDF,x0,eps) %函数的最后一个参数也可以不写。默认情况下,eps=0.5e-6 %[x k t]=NewdonToEquations(@NewdonF,@NewdonDF,x0,eps)
第8章 常微分方程初值问题数值解法 8.1 引言 8.2 欧拉方法 8.3 龙格-库塔方法 8.4 单步法的收敛性与稳定性 8.5 线性多步法
8.1 引 言 考虑一阶常微分方程的初值问题 00(,),[,],(). y f x y x a b y x y '=∈=(1.1) (1.2) 如果存在实数 ,使得 121212(,)(,).,R f x y f x y L y y y y -≤-?∈(1.3) 则称 关于 满足李普希茨(Lipschitz )条件, 称为 的李普希茨常数(简称Lips.常数). 0>L f y L f (参阅教材386页)
计算方法及MATLAB 实现 所谓数值解法,就是寻求解 在一系列离散节点 )(x y <<<<<+121n n x x x x 上的近似值 . ,,,,,121+n n y y y y 相邻两个节点的间距 称为步长. n n n x x h -=+1 如不特别说明,总是假定 为定数, ),2,1( ==i h h i 这时节点为 . ) ,2,1,0(0 =+=i nh x x n 初值问题(1.1),(1.2)的数值解法的基本特点是采取 “步进式”. 即求解过程顺着节点排列的次序一步一步地向前推进. 00(,),[,], (). y f x y x a b y x y '=∈=
描述这类算法,只要给出用已知信息 ,,,21--n n n y y y 计算 的递推公式. 1+n y 一类是计算 时只用到前一点的值 ,称为单步法. 1+n y n y 另一类是用到 前面 点的值 , 1+n y k 11,,,+--k n n n y y y 称为 步法. k 其次,要研究公式的局部截断误差和阶,数值解 与 精确解 的误差估计及收敛性,还有递推公式的计算 稳定性等问题. n y )(n x y 首先对方程 离散化,建立求数值解的递推 公式. ),(y x f y ='
用MATLAB实现结构可靠度计算 口徐华…朝泽刚‘u刘勇‘21 。 (【l】中国地质大学(武汉工程学院湖北?武汉430074; 12】河海大学土木工程学院江苏?南京210098 摘要:Matlab提供了各种矩阵的运算和操作,其中包含结构可靠度计算中常用的各种数值计算方法工具箱,本文从基本原理和相关算例分析两方面,阐述利用Matlab,编制了计算结构可靠度Matlab程.序,使得Matlab-语言在可靠度计算中得到应用。 关键词:结构可靠度Matlab软件最优化法 中图分类号:TP39文献标识码:A文章编号:1007-3973(200902-095-Ol 1结构可靠度的计算方法 当川概率描述结构的可靠性时,计算结构可靠度就是计算结构在规定时问内、规定条件F结构能够完成预定功能的概率。 从简单到复杂或精确稃度的不同,先后提出的可靠度计算方法有一次二阶矩方法、二次二阶矩方法、蒙特卡洛方法以及其他方法。一次■阶矩方法又分为。I-心点法和验算点法,其中验算点法足H前可靠度分析最常川的方法。 2最优化方法计算可靠度指标数学模型 由结构111n个任意分布的独立随机变量一,x:…以表示的结构极限状态方程为:Z=g(■.托…t=0,采用R-F将非正念变量当罱正态化,得到等效正态分布的均值o:和标准差虹及可靠度指标B,由可靠度指标B的几何意义知。o;辟
开始时验算点未知,把6看成极限状态曲面上点P(■,爿:---37,的函数,通过优化求解,找到B最小值。求解可靠皮指标aJ以归结为以下约束优化模型: rain睁喜t华,2 s.,.Z=g(工i,x2’,…,工:=0 如极限状态方栉巾某个变最(X。可用其他变量表示,则上述模型jfIJ‘转化为无约束优化模型: 。。B!:手f生丛r+阻:坚:坠:盐尘}二剐 t∞oY?’【叫,J 3用MATLAB实现结构可靠度计算 3.1Matlab简介 Matlab是++种功能强、效率高、便.丁.进行科学和工程计算的交互式软件包,汇集了人量数学、统计、科学和工程所需的函数,MATI.AB具有编程简甲直观、用户界mf友善、开放性强等特点。将MATLAB用于蒙特卡罗法的一个显著优点是它拥有功能强大的随机数发生器指令。 3.2算例 3.2.I例:已知非线形极限状态方程z=g(t r'H=567f r-0.5H2=0’f、r服从正态分布。IIf=0.6,o r=0.0786;la|_ 2.18,o r_0.0654;H服从对数正态分布。u H= 3218,O。 =0.984。f、r、H相互独立,求可靠度指标B及验算点(,,r’,H‘。 解:先将H当量正念化:h=ln H服从正态分布,且 ,‘-““了:等专虿’=,。49?口二-、『五ir面_。。3
《计算方法》实验报告 指导教师: 学院: 班级: 团队成员:
一、题目 例2.7应用Newton 迭代法求方程210x x --=在1x =附近的数值解 k x ,并使其满足8110k k x x ---< 原理: 在方程()0f x =解的隔离区间[],a b 上选取合适的迭代初值0x ,过曲线()y f x =的点()() 00x f x ,引切线 ()()()1000:'l y f x f x x x =+- 其与x 轴相交于点:()() 0100 'f x x x f x =-,进一步,过曲线()y f x =的 点()()11x f x , 引切线 ()()()2111: 'l y f x f x x x =+- 其与x 轴相交于点:() () 1211 'f x x x f x =- 如此循环往复,可得一列逼近方程()0f x =精确解*x 的点 01k x x x ,,,,,其一般表达式为: ()() 111 'k k k k f x x x f x ---=- 该公式所表述的求解方法称为Newton 迭代法或切线法。
程序: function y=f(x)%定义原函数 y=x^3-x-1; end function y1=f1(x0)%求导函数在x0点的值 syms x; t=diff(f(x),x); y1=subs(t,x,x0); end function newton_iteration(x0,tol)%输入初始迭代点x0及精度tol x1=x0-f(x0)/f1(x0);k=1;%调用f函数和f1函数 while abs(x1-x0)>=tol x0=x1;x1=x0-f(x0)/f1(x0);k=k+1; end fprintf('满足精度要求的数值为x(%d)=%1.16g\n',k,x1); fprintf('迭代次数为k=%d\n',k); end 结果:
作者:夏云木子 1、 >> syms re(x) re(y) re(z) >> input('计算相对误差:'),re(x)=10/1991,re(y)=0.0001/1.991,re(y)=0.0000001/0.0001991 所以可知re(y)最小,即y精度最高 2、 >> format short,A=sqrt(2) >> format short e,B=sqrt(2) >> format short g,C=sqrt(2)
>> format long,D=sqrt(2) >> format long e,E=sqrt(2) >> format long g,F=sqrt(2) >> format bank,H=sqrt(2) >> format hex,I=sqrt(2) >> format +,J=sqrt(2) >> format,K=sqrt(2)
3、 >> syms A >> A=[sqrt(3) exp(7);sin(5) log(4)];vpa(pi*A,6) 4、1/6251-1/6252=1/6251*6252 5、(1)1/(1+3x)-(1-x)/(1+x)=x*(3*x-1)/[(1+3*x)*(1+x)] (2) sqrt(x+1/x)-sqrt(x-1/x)=2/x/[sqrt(x-1/x)+sqrt(x+1/x)] (3) log10(x1)-log(x2)=log10(x1/x2) (4) [1-cos(2*x)]/x =x^2/factorial(2)-x^4/factorial(4)+x^6/factorial(6)-…
function [x0,k]=bisect1(fun1,a,b,ep) if nargin<4 ep=1e-5; end fa=feval(fun1,a); fb=feval(fun1,b); if fa*fb>0 x0=[fa,fb]; k=0; return; end k=1; while abs(b-a)/2>ep x=(a+b)/2; fx=feval(fun1,x); if fx*fa<0 b=x; fb=fx; else a=x; fa=fx;
end end x0=(a+b)/2; >> fun1=inline('x^3-x-1'); >> [x0,k]=bisect1(fun1,1.3,1.4,1e-4) x0 = 1.3247 k = 7 >> 简单迭代法 function [x0,k]=iterate1(fun1,x0,ep,N) if nargin<4 N=500; end if nargin<3 ep=1e-5; end x=x0; x0=x+2*ep;
while abs(x-x0)>ep & k
计算方法作业(作者:夏云木子) 1、help linspace type linspace 2、a1=[5 12 47;13 41 2;9 6 71];a2=[12 9;6 15;7 21];B=a1*a2, C=a1(:,1:2).*a2, D=a1.^2,
E=a1(:).^2 3、a1=[5 12 47;13 41 2;9 6 71];a2=[12 9;6 15;7 21];a1(4:5,1:3)=a2.';a1([4 5],:)=a1([5 4],:);b1=a1
c1=b1(4,1),c2=b1(5,3),D=b1(3:4,:)*a2 4、a1=[5 12 47;13 41 2;9 6 71]; E=eye(3,3); S = a1 + 5*a1' - E, S1=a1^3-rot90(a1)^2+6*E 5、a1=[5 12 47;13 41 2;9 6 71];s=5;A=s-a1,B=s*a1,C=s.*a1,D=s./a1,E=a1./s
6、c=[1 2 3 4;5 6 7 8;9 10 11 12;13 14 15 16];A=c^-4,B=(c^3)^-1,C=(3*c+5*c^-1)/5
7、a=[1 i 3;9i 2-i 8;7 4 8+i];A=a.' 8、abc=[-2.57 8.87;-0.57 3.2-5.5i];m1=sign(abc),m2=round(abc),m3=floor(abc) Sign为符号函数,round表示四舍五入取整,floor表示舍去小数部分取整
9、x=[1 4 3 2 0 8 10 5]';y=[8 0 0 4 2 1 9 11]';A=dot(x,y) 10、a=[3.82 5.71 9.62];b=[7.31 6.42 2.48];A=dot(a,b),B=cross(a,b) 11、P=[5 7 8 0 1];Pf=poly(P);Px=poly2str(Pf,'x') 12、P=[3 0 9 60 0 -90];K1=polyval(P,45),K2=polyval(P,-123),K3=polyval(P,579) 13、P1=[13 55 0 -17 9];P2=[63 0 26 -85 0 105];PP=conv(P1,P2);P1P2=poly2str(PP,'x'),[Q,r]=deconv(P2,P1)
信息系统分析与设计作业 层次分析法确定绩效评价权重在matlab中的实现 小组成员:孙高茹、王靖、李春梅、郭荣1 程序简要概述 编写程序一步实现评价指标特征值lam、特征向量w以及一致性比率CR的求解。 具体的操作步骤是:首先构造评价指标,用专家评定法对指标两两打分,构建比较矩阵,继而运用编写程序实现层次分析法在MATLAB中的应用。 通过编写MATLAB程序一步实现问题求解,可以简化权重计算方法与步骤,减少工作量,从而提高人力资源管理中绩效考核的科学化电算化。 2 程序在matlab中实现的具体步骤 function [w,lam,CR] = ccfx(A) %A为成对比较矩阵,返回值w为近似特征向量 % lam为近似最大特征值λmax,CR为一致性比率 n=length(A(:,1)); a=sum(A); B=A %用B代替A做计算 for j=1:n %将A的列向量归一化 B(:,j)=B(:,j)./a(j); end s=B(:,1); for j=2:n s=s+B(:,j); end c=sum(s);%计算近似最大特征值λmax w=s./c; d=A*w lam=1/n*sum((d./w)); CI=(lam-n)/(n-1);%一致性指标 RI=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45,1.49,1.51];%RI为随机一致
性指标 CR=CI/RI(n);%求一致性比率 if CR>0.1 disp('没有通过一致性检验'); else disp('通过一致性检验'); end end 3 案例应用 我们拟构建公司员工绩效评价分析权重,完整操作步骤如下: 3.1构建的评价指标体系 我们将影响员工绩效评定的指标因素分为:打卡、业绩、创新、态度与品德。 3.2专家打分,构建两两比较矩阵 A = 1.0000 0.5000 3.0000 4.0000 2.0000 1.0000 5.0000 3.0000 0.3333 0.2000 1.0000 2.0000 0.2500 0.3333 0.5000 1.0000 3.3在MATLAB中运用编写好的程序实现 直接在MATLAB命令窗口中输入 [w,lam,CR]=ccfx(A) 继而直接得出 d = 1.3035 2.0000 0.5145 0.3926 w = 0.3102 0.4691 0.1242 0.0966 lam =4.1687
功率谱密度的三种matlab 实现方法 一:实验目的: (1)掌握三种算法的概念、应用及特点; (2)了解谱估计在信号分析中的作用; (3) 能够利用burg 法对信号作谱估计,对信号的特点加以分析。 二;实验内容: (1)简单说明三种方法的原理。 (2)用三种方法编写程序,在matlab 中实现。 (3)将计算结果表示成图形的形式,给出三种情况的功率谱图。 (4)比较三种方法的特性。 (5)写出自己的心得体会。 三:实验原理: 1.周期图法: 周期图法又称直接法。它是从随机信号x(n)中截取N 长的一段,把它视为能量有限x(n)真实功率谱)(jw x e S 的估计)(jw x e S 的抽样. 认为随机序列是广义平稳且各态遍历的,可以用其一个样本x(n)中的一段)(n x N 来估计该随机序列的功率谱。这当然必然带来误差。由于对)(n x N 采用DFT ,就默认)(n x N 在时域是周期的,以及)(k x N 在频域是周期的。这种方法把随机序列样本x(n)看成是截得一段)(n x N 的周期延拓,这也就是周期图法这个名字的来历。
2.相关法(间接法): 这种方法以相关函数为媒介来计算功率谱,所以又叫间接法。这种方法的具体步骤是: 第一步:从无限长随机序列x(n)中截取长度N 的有限长序列列 )(n x N 第二步:由N 长序列)(n x N 求(2M-1)点的自相关函数)(m R x ∧ 序列。 )()(1)(1 m n x n x N m R N n N N x += ∑-=∧ (2-1) 这里,m=-(M-1)…,-1,0,1…,M-1,M N ,)(m R x 是双边序列,但是由自相关函数的偶对称性式,只要求出m=0,。。。,M-1的傅里叶变换,另一半也就知道了。 第三步:由相关函数的傅式变换求功率谱。即 jwm M M m X jw x e m R e S ----=∧∧ ∑= )()(1) 1( 以上过程中经历了两次截断,一次是将x(n)截成N 长,称为加数据窗,一次是将x(n)截成(2M-1)长,称为加延迟窗。因此所得的功率谱仅是近似值,也叫谱估计,式中的)(jw x e S 代表估值。一般取M< 基本代数部分 如何用matlab求阶乘 factorial(n)求n的阶乘 如何用matlab配方 没有发现matlab有这一命令,不过我们可以调用maple的命令,调用方法如下: 首先加载maple中的student函数库,加载方法为:maple(‘with(student)’) 然后运行maple中的配方命令,格式为: maple(’completesquare(f)’)把f配方,其中f为代数表达式或代数方程maple(’completesquare(f,x)’)把f按指定的变量x配方,其中f同上maple(’completesquare(f,{x,y,...})’)把f按指定的变量x,y,...配方 maple(’completesquare(f,[x,y,...])’)把f按指定的变量x,y,...配方, 如何用matlab进行多项式运算 (1)合并同类项 syms 表达式中包含的变量 collect(表达式,指定的变量) (2)因式分解 syms 表达式中包含的变量factor(表达式) (3)展开 syms 表达式中包含的变量 expand(表达式) (4)化简 syms 表达式中包含的变量simplify(表达式) (5)变量替换 syms 表达式和代换式中包含的所有变量subs(表达式,要替换的变量或式子,代换式)我们也可在matlab中调用maple的命令进行多项式的运算,如下: 如何在matlab中调用maple 方法1: maple(’maplestatement’) 其中maplestatement 是完整的maple语句,由一条或几条命令组成,必须符合maple 的语法 方法2: maple(‘function’,arg1, arg2,…) 其中function为maple中的函数名称,arg1, arg2,…是函数function所用的参数。 如何用matlab进行分式运算 发现matlab只有一条处理分式问题的命令,其使用格式如下: [n,d]=numden(f)把符号表达式f化简为有理形式,其中分子和分母的系数为整数且分子分母不含公约项,返回结果n为分子,d为分母。注意:f必须为符号表达式 数值计算方法 实 验 报 告 实验序号:实验二 实验名称:追赶法算法设计及MATLAB实现 实验人: 专业年级: 教学班: 学号: 实验时间: 实验二追赶法算法设计及MATLAB实现 一、实验目的 1.初步掌握算法设计规则; 2.初步掌握MATLAB程序设计规则. 二、实验内容 1.构造利用追赶法求解三对角线性方程组的算法; 2.在MATLAB环境下编写追赶法的程序(函数); 3.自由选择若干个三对角线性方程组求解。 三、实验步骤 1.追赶法算法: 算法名称:thomas 输入参数:向量a,b,c,f 输出参数:输出解信息x 算法的自然语言: Step1:u 1=b 1 ,y 1 =b 1 ; Step2:对于i=2,3,….n; Step2.1:当u 1-i ≠,否则转step5 l i =a i /u 1-i ; u i =b i -l i *c 1-i ; y i =f i -l i *y 1-i ; Step3:当u n ≠时,x n =y n /u n ,否则转step5 Step4:对于:i=n-1,n-2,…..,2,1,转step6 x i =(y i -c i *x 1+i )/u i Step5:无解信息,转step7 Step6:输出x Step7:关机 2.MATLAB程序 function [x,L,U]=thomas(a,b,c,f) n=length(b); % 对A进行分解 u(1)=b(1); for i=2:n if(u(i-1)~=0) l(i-1)=a(i-1)/u(i-1); u(i)=b(i)-l(i-1)*c(i-1); else break; end end L=eye(n)+diag(l,-1); U=diag(u)+diag(c,1); x=zeros(n,1); y=x; % 求解Ly=b y(1)=f(1); for i=2:n y(i)=f(i)-l(i-1)*y(i-1); end % 求解Ux=y if(u(n)~=0) x(n)=y(n)/u(n); end for i=n-1:-1:1 x(i)=(y(i)-c(i)*x(i+1))/u(i); 用递推公式计算定积分 实验目的: 1.充分理解不稳定的计算方法会造成误差的积累,在计算过程中会导致误差的迅速增加,从而使结果产生较大的误差。 2.在选择数值计算公式来进行近似计算时,应学会选用那些在计算过程中不会导致误差迅速增长的计算公式。 3.理解不稳定的计算公式造成误差积累的来源及具体过程; 4.掌握简单的matlab语言进行数值计算的方法。 实验题目: 对n=0,1,2,…,20,计算定积分: 实验原理: 由于y(n)== – 在计算时有两种迭代方法,如下: 方法一: y(n)=– 5*y(n-1),n=1,2,3, (20) 取y(0)== ln6-ln5 ≈0.182322 方法二: 利用递推公式:y(n-1)=-*y(n),n=20,19, (1) 而且,由= * ≤≤*= 可取:y(20)≈*()≈0.008730. 实验内容: 对算法一,程序代码如下: function [y,n]=funa() syms k n t; t=0.182322; n=0; y=zeros(1,20); y(1)=t; for k=2:20 y(k)=1/k-5*y(k-1); n=n+1; end y(1:6) y(7:11) 对算法二,程序代码如下: %计算定积分; %n--表示迭代次数; %y用来存储结果; function [y,n]=f(); syms k y_20; y=zeros(21,1); n=1; y_20=(1/105+1/126)/2; y(21)=y_20; for k=21:-1:2 y(k-1)=1/(5*(k-1))-y(k)/5; n=n+1; end 实验结果: 由于计算过程中,前11个数字太小,后9个数字比较大,造成前面几个数字只显示0.0000的现象,所以先输出前6个,再输出7—11个,这样就能全部显示出来了。 算法一结果: [y,n]=funa %先显示一y(1)—y(6) ans = 0.1823 -0.4116 2.3914 -11.7069 58.7346 07级电信(2)班 刘坤洋 24 实验一 利用MATLAB 实现信号DFT 的计算 一、实验目的: 1、熟悉利用MATLAB 计算信号DFT 的方法 2、掌握利用MATLAB 实现由DFT 计算线性卷积的方法 二、实验设备:电脑、matlab 软件 三、实验内容: 1、练习用matlab 中提供的内部函数用于计算DFT (1) fft(x),fft(x,N),ifft(x),ifft(x,N)的含义及用法 (2) 在进行DFT 时选取合适的时域样本点数N 请举例,并编程实现 题目: 源程序: >> N=30; %数据的长度 >>L=512; %DFT 的点数 >>f1=100; f2=120; >>fs=600; %抽样频率 >>T=1/fs; %抽样间隔 >>ws=2*pi*fs; >>t=(0:N-1)*T; >>f=cos(4*pi*f1*t)+cos(4*pi*f2*t); >>F=fftshift(fft(f,L)); >>w=(-ws/2+(0:L-1)*ws/L)/(2*pi); >>hd=plot(w,abs(F)); >>ylabel('幅度谱') >> xlabel('频率/Hz') 的频谱 分析利用)π4cos()π4cos()(DFT 21t f t f t x +=Hz 600,Hz 120,Hz 10021===s f f f >> title('my picture') 结果图 : (3) 在对信号进行DFT 时选择hamming 窗增加频率分辨率 请举例,并编程实现 题目: 源程序:>> N=50; %数据的长度 >>L=512; %DFT 的点数 >>f1=100;f2=150; >>fs=600; %抽样频率 >>T=1/fs; %抽样间隔 >>ws=2*pi*fs; >>t=(0:N-1)*T; >>f=cos(4*pi*f1*t)+0、15*cos(4*pi*f2*t); 的频谱分析利用)π4cos(15.0)π4cos()(DFT 21t f t f t x +=Hz 600,Hz 150,Hz 10021===s f f f 实验一:有限差分法研究静电场边值问题 实验报告人:年级和班级:学号: 1. 实验用软件工具: Matlab 2. 实验原理:电磁场课本P36-38 1)差分方程 2)差分方程组的解 简单迭代法 高斯-赛德尔迭代法 逐次超松弛法 3. 实验步骤: 1)简单迭代法 程序: hx=41;hy=21; v1=zeros(hy,hx); v1(hy,:)=zeros(1,hx); v1(1,:)=ones(1,hx)*100; v1(:,1)=zeros(hy,1); v1(:,hx)=zeros(hy,1); v1 v2=v1;maxt=1;t=0; k=0; while(maxt>1e-5) k=k+1; maxt=0; for i=2:hy-1 for j=2:hx-1 v2(i,j)=(v1(i,j+1)+v1(i+1,j)+v1(i-1,j)+v1(i,j-1))/4; t=abs(v2(i,j)-v1(i,j)); if(t>maxt) maxt=t;end end end v1=v2; end v2 k clf subplot(1,2,1),mesh(v2) axis([0,41,0,21,0,100]) subplot(1,2,2),contour(v2,15) hold on axis([-1,42,-1,25]) plot([1,1,hx,hx,1],[1,hy+1,hy+1,1,1],'r') text(hx/2,0.3,'0V','fontsize',11); text(hx/2-0.5,hy+0.5,'100V','fontsize',11); text(-0.5,hy/2,'0V','fontsize',11); text(hx+0.3,hy/2,'0V','fontsize',11); hold off 当W=1e-5, 迭代次数:1401次 2)高斯-赛德尔迭代法 程序: hx=41;hy=21; v1=ones(hy,hx); v1(hy,:)=zeros(1,hx); v1(1,:)=ones(1,hx)*100; v1(:,1)=zeros(hy,1); v1(:,hx)=zeros(hy,1); v2=v1;maxt=1;t=0; k=0; while(maxt>1e-5) k=k+1; maxt=0; for i=2:hy-1 for j=2:hx-1 v2(i,j)=(v1(i,j+1)+v1(i+1,j)+v2(i-1,j)+v2(i,j-1))/4; t=abs(v2(i,j)-v1(i,j)); if(t>maxt) maxt=t;end end end v1=v2; end v2 k clf subplot(1,2,1),mesh(v2) axis([0,41,0,21,0,100]) subplot(1,2,2),contour(v2,15) hold on axis([-1,42,-1,25]) plot([1,1,hx,hx,1],[1,hy+1,hy+1,1,1],'r') text(hx/2,0.3,'0V','fontsize',11); text(hx/2-0.5,hy+0.5,'100V','fontsize',11); text(-0.5,hy/2,'0V','fontsize',11); text(hx+0.3,hy/2,'0V','fontsize',11); hold off Southeast University 计算方法实验报告 学生院系: 学生姓名: 学生学号: 实验一 一、实验题目:插值法p245 二、程序设计 P245_main.m x=[0.3 0.42 0.5 0.58 0.66 0.72]; y=[1.04403 1.08462 1.11803 1.15603 1.19817 1.23223]; P245(x,y,0.46); P245(x,y,0.55); P245(x,y,0.6); P245.m function newtint( x,y,xhat ) n=length(y); c=y(:); for j=2:n for i=n:-1:j c(i)=(c(i)-c(i-1))/(x(i)-x(i-j+1)); end end yhat=c(n); for i=n-1:-1:1 yhat=yhat*(xhat-x(i))+c(i); end fprintf('N(%f)= %f' ,xhat,yhat) disp('/n' ) end 三、程序运行结果 N(0.460000)= 1.100724/n N(0.550000)= 1.141271/n N(0.600000)= 1.166194/n 2 实验二 一、实验题目:舍入误差与数值稳定性p217_4 二、程序设计 n=input('输入N=\n'); y1=0; y2=0; digits(40); format long; y=0.5*(1.5-1/n-1/(n+1)); for j=2:n y1=y1+1/(j*j-1); end fprintf('%s y1=%g\n','从小到大计算结果',y1); if floor(log10(abs(y1-y)))-log10(abs(y1-y))matlab计算
实验2追赶法算法设计及MATLAB实现
用递推公式计算定积分matlab版
利用MATLAB实现信号DFT的计算
matlab实现有限差分法计算电场强度(最新)
东南大学计算方法实验报告matlab版