当前位置：文档之家› 指数分布

指数分布

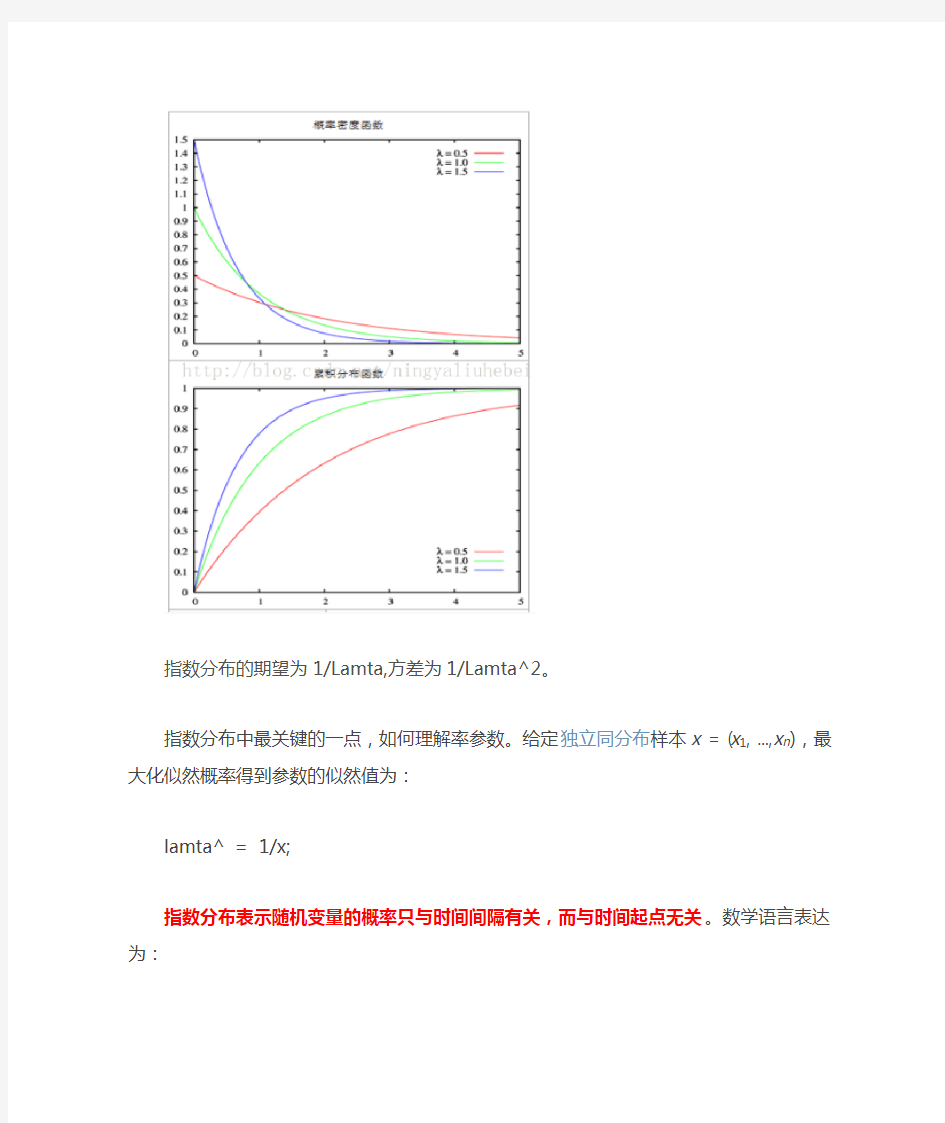
指数分布是连续型随机变量，指数分布具有无记忆性，指数分布是特殊的gamma分布。

指数分布（Exponential distribution）是一种连续概率分布。指数分布可以用来表示独立随机事件发生的时间间隔，比如旅客进机场的时间间隔、中文维基百科新条目出现的时间间隔等等。

指数分布的定义形式：

λ就表示平均每单位时间发生该事件的次数，是指数函数的分布参数；f(x:λ) = λe^(-λx),表示在该时刻发生时间的概率。比如放射性衰变就遵循这一分布，这里的半衰期就对应1/λ.

指数分布的期望为1/Lamta,方差为1/Lamta^2。

指数分布中最关键的一点，如何理解率参数。给定独立同分布样本x= (x1, ...,x n)，最大化似然概率得到参数的似然值为：

lamta^ = 1/x;

指数分布表示随机变量的概率只与时间间隔有关，而与时间起点无关。数学语言表达为：

p(T>s+t | T >t ) = p(T>s) for all s,t >= 0

指数分布常用来描述“寿命”类随机变量的分布，例如家电使用寿命，动植物寿命，电话问题里的通话时间等等。“寿命”类分布的方差非常大，以致于

已经使用的时间是可以忽略不计的。

例如有一种电池标称可以充放电500次（平均寿命），但实际上，很多充放电次数数倍于500次的电池仍然在正常使用，也用很多电池没有使用几次

就坏了——这是正常的，不是厂方欺骗你，是因为方差太大的缘故。随机取一节电池，求它还能继续使用300次的概率，我们认为与这节电池是否使用过与曾经使用过多少次是没有关系的。

有人戏称服从指数分布的随机变量是“永远年轻的”，一个60岁的老人与一个刚出生的婴儿，他们能够再活十年的概率是相等的，你相信吗？——如果人的寿命确实是服从指数分布的话，回答是肯定的。

贴一道题加深理解

标准正态分布表

标准正态分布表集团文件发布号：（9816-UATWW-MWUB-WUNN-INNUL-DQQTY-

标准正态分布表

4432198653 1.80.964 1 0.964 8 0.965 6 0.966 4 0.967 2 0.967 8 0.968 6 0.969 3 0.970 0.970 6 1.90.971 3 0.971 9 0.972 6 0.973 2 0.973 8 0.974 4 0.975 0.975 6 0.976 2 0.976 7 20.977 2 0.977 8 0.978 3 0.978 8 0.979 3 0.979 8 0.980 3 0.980 8 0.981 2 0.981 7 2.10.982 1 0.982 6 0.983 0.983 4 0.983 8 0.984 2 0.984 6 0.985 0.985 4 0.985 7 2.20.986 1 0.986 4 0.986 8 0.987 1 0.987 4 0.987 8 0.988 1 0.988 4 0.988 7 0.989 2.30.989 3 0.989 6 0.989 8 0.990 1 0.990 4 0.990 6 0.990 9 0.991 1 0.991 3 0.991 6 2.40.991 8 0.992 0.992 2 0.992 5 0.992 7 0.992 9 0.993 1 0.993 2 0.993 4 0.993 6 2.50.993 8 0.994 0.994 1 0.994 3 0.994 5 0.994 6 0.994 8 0.994 9 0.995 1 0.995 2 2.60.995 3 0.995 5 0.995 6 0.995 7 0.995 9 0.996 0.996 1 0.996 2 0.996 3 0.996 4 2.70.996 5 0.996 6 0.996 7 0.996 8 0.996 9 0.997 0.997 1 0.997 2 0.997 3 0.997 4 2.80.997 4 0.997 5 0.997 6 0.997 7 0.997 7 0.997 8 0.997 9 0.997 9 0.998 0.998 1 2.90.998 1 0.998 2 0.998 2 0.998 3 0.998 4 0.998 4 0.998 5 0.998 5 0.998 6 0.998 6 x00.10.20.30.40.50.60.70.80.9 30.998 7 0.999 0.999 3 0.999 5 0.999 7 0.999 8 0.999 8 0.999 9 0.999 9 1.000 正态分布概率表 Φ（ u ） =

t分布和标准规定正态分布

数理统计实验 t分布与标准正态分布院（系）: 班级: 成员:

成员: 成员: 指导老师: 日期:

目录 t分布与标准正态分布的关系 (1) 一、实验目的 (1) 二、实验原理 (1) 三、实验内容及步骤 (1) 四、实验器材 (6) 五、实验结果分析 (6) 六、实验结论 (6)

t分布与标准正态分布的关系一、实验目的正态分布是统计中一种很重要的理论分布，是许多统计方法的理论基础。正态分布有两个参数，μ和σ，决定了正态分布的本质。为了应用和计算方便，常将一般的正态变量X通过μ变换[(X-μ)/σ]转化成标准正态变量μ，以使原来各种形态的正态分布都转换为μ=0，σ=1的标准正态分布，亦称μ分布。对于标准正态分布来说，μ是数据整体的平均值，σ是整体的标准差。但实际操作过程中，人们往往难以获得μ和σ。因此人们只能通过样本对这两个参数做出估计，用样本平均值和样本标准差代替整体的平均值和标准差，从而得出了t分布。另外从图像的层面说，正态分布的位置和形态只与μ和σ有关，而t分布不只与样本平均值和样本标准差有关，还与自由度相关。通过实验了解t分布与标准正态分布之间的关系。二、实验原理运用EXCEL软件验证t分布与标准正态分布的关系，绘制相应的统计图表进行分析。三、实验内容及步骤 1.打开Excel文件，将“t分布与标准正态分布N（0，1）”合并并居中，黑体，20字号，红色；

2.选中文件,选项,自定义功能区,加载开发工具.在开发工具中插入滚动条,调节滚动条大小； 3.设置A2单元格格式,数字自定义区”!n=#,##0;[红色]￥-#,##0”.然后左对齐,设置为红色；

Gamma分布与指数分布

Gamma分布与指数分布 "Gamma 分布gamma distribution; form of gamma distribution;" 在学术文献中的解释 1、在地震序列的有序性、地震发生率的齐次性、计数特征具有独立增量和平稳增量情况下,可以导出地震发生i 次时间的概率密度为Gamma 密度函数(亦称为Gamma分布) r (称为伽马函数，它是用一个积分式定义的，不是初等函数。伽马函数有性质： r(x+i)=x , (r) (0)=1, r (1/2)=，▽对证整数n,有r (n+1)=n伽马分布里面r ( a ,(分布函数已经了解)。a ,个指代何种意义的参数？比如在化工里面有这样一个问题，说反应器管道的长度L服从r ( a分布，那么a，是和管道形状和尺度相关的参数。a，是两个分布调整参量，该分布的期望二C+(a /也就是说a /调整期望；分布的方差二a / (3，由此并不需要单独定义二者，应该共同对分布起作用！伽马函数r(z)的定义域是，C-{-n,n=0,1,2,...}其中C为复数域，Re (z) >0 时，常见的积分是收敛，也就是说r(z)可用常见的积分定义。如 1 种常见的积分： r (z)二/ {0

指数分布如果随机变量X 的概率密度为公式 P (X>0二入乘以(e的一入X次方)；p(x<0)=0 则称X遵从指数分布(参数为为。在概率论和统计学中，指数分布( Exponentialdistribution )是一种连续概率分布。指数分布可以用来表示独立随机事件发生的时间间隔，比如旅客进机场的时间间隔、中文维基百科新条目出现的时间间隔等等。许多电子产品的寿命分布一般服从指数分布。有的系统的寿命分布也可用指数分布来近似。它在可靠性研究中是最常用的一种分布形式。指数分布是伽玛分布和威布尔分布的特殊情况，产品的失效是偶然失效时，其寿命服从指数分布。指数分布可以看作当威布尔分布中的形状系数等于 1 的特殊分布，指数分布的失效率是与时间t 无关的常数，所以分布函数简单。

指数分布

指数分布设连续型随机变量X 的密度函数为0 ()00x e x f x x λλ-?≥=?为常数。其分布函数为0 10 ()()00x x e x F x f t dt x λ-?-≥==? >，我们有 (|)()x P X s t X t e P X s λ->+>==>，如果X 解释为寿命，这表明如果已知X 的寿命大于t 年，则它再活s 年的概率与年龄t 无关，这是指数分布的重要特征。因此指数分布为“永远年青”的分布。例：某型号计算机，无故障工作的时间X （单位h ）服从参数为1 100 的指数分布，求它无故障工作50—100h 的概率是多少？它的运转时间少于100h 的概率是多少？解由题设X 的密度函数为1100 10 ()100 00x e x f x x -?≥? =??===在内无冲击于是X 的分布函数为()1()1,0t F t R t e t λ-=-=->

标准正态分布表

标准正态分布表 x 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0 0.500 0 0.504 0 0.508 0 0.512 0 0.516 0 0.519 9 0.523 9 0.527 9 0.531 9 0.535 9 0.1 0.539 8 0.543 8 0.547 8 0.551 7 0.555 7 0.559 6 0.563 6 0.567 5 0.571 4 0.575 3 0.2 0.579 3 0.583 2 0.587 1 0.591 0 0.594 8 0.598 7 0.602 6 0.606 4 0.610 3 0.614 1 0.3 0.617 9 0.621 7 0.625 5 0.629 3 0.633 1 0.636 8 0.640 4 0.644 3 0.648 0 0.651 7 0.4 0.655 4 0.659 1 0.662 8 0.666 4 0.670 0 0.673 6 0.677 2 0.680 8 0.684 4 0.687 9 0.5 0.691 5 0.695 0 0.698 5 0.701 9 0.705 4 0.708 8 0.712 3 0.715 7 0.719 0 0.722 4 0.6 0.725 7 0.729 1 0.732 4 0.735 7 0.738 9 0.742 2 0.745 4 0.748 6 0.751 7 0.754 9 0.7 0.758 0 0.761 1 0.764 2 0.767 3 0.770 3 0.773 4 0.776 4 0.779 4 0.782 3 0.785 2 0.8 0.788 1 0.791 0 0.793 9 0.796 7 0.799 5 0.802 3 0.805 1 0.807 8 0.810 6 0.813 3 0.9 0.815 9 0.818 6 0.821 2 0.823 8 0.826 4 0.828 9 0.835 5 0.834 0 0.836 5 0.838 9 1 0.841 3 0.843 8 0.846 1 0.848 5 0.850 8 0.853 1 0.855 4 0.857 7 0.859 9 0.86 2 1 1.1 0.864 3 0.866 5 0.868 6 0.870 8 0.872 9 0.87 4 9 0.877 0 0.879 0 0.881 0 0.883 0 1.2 0.884 9 0.886 9 0.888 8 0.890 7 0.892 5 0.894 4 0.89 6 2 0.898 0 0.899 7 0.901 5 1.3 0.903 2 0.904 9 0.906 6 0.90 8 2 0.90 9 9 0.911 5 0.913 1 0.914 7 0.916 2 0.917 7 1.4 0.919 2 0.920 7 0.922 2 0.923 6 0.925 1 0.926 5 0.927 9 0.929 2 0.930 6 0.931 9 1.5 0.933 2 0.934 5 0.935 7 0.937 0 0.938 2 0.939 4 0.940 6 0.941 8 0.943 0 0.944 1 1.6 0.945 2 0.946 3 0.947 4 0.948 4 0.949 5 0.950 5 0.951 5 0.952 5 0.953 5 0.953 5 1.7 0.955 4 0.956 4 0.957 3 0.958 2 0.959 1 0.959 9 0.960 8 0.961 6 0.962 5 0.963 3 1.8 0.964 1 0.964 8 0.965 6 0.966 4 0.967 2 0.967 8 0.968 6 0.969 3 0.970 0 0.970 6 1.9 0.971 3 0.971 9 0.972 6 0.973 2 0.973 8 0.974 4 0.975 0 0.975 6 0.976 2 0.976 7 2 0.977 2 0.977 8 0.978 3 0.978 8 0.979 3 0.979 8 0.980 3 0.980 8 0.981 2 0.981 7 2.1 0.982 1 0.982 6 0.983 0 0.983 4 0.983 8 0.984 2 0.984 6 0.98 5 0 0.985 4 0.985 7 2.2 0.98 6 1 0.986 4 0.986 8 0.98 7 1 0.987 4 0.987 8 0.988 1 0.988 4 0.988 7 0.98 9 0 2.3 0.989 3 0.989 6 0.989 8 0.990 1 0.990 4 0.990 6 0.990 9 0.991 1 0.991 3 0.991 6 2.4 0.991 8 0.992 0 0.992 2 0.992 5 0.992 7 0.992 9 0.993 1 0.993 2 0.993 4 0.993 6 2.5 0.993 8 0.994 0 0.994 1 0.994 3 0.994 5 0.994 6 0.994 8 0.994 9 0.995 1 0.995 2 2.6 0.995 3 0.995 5 0.995 6 0.995 7 0.995 9 0.996 0 0.996 1 0.996 2 0.996 3 0.996 4 2.7 0.996 5 0.996 6 0.996 7 0.996 8 0.996 9 0.997 0 0.997 1 0.997 2 0.997 3 0.997 4 2.8 0.997 4 0.997 5 0.997 6 0.997 7 0.997 7 0.997 8 0.997 9 0.997 9 0.998 0 0.998 1 2.9 0.998 1 0.998 2 0.998 2 0.998 3 0.998 4 0.998 4 0.998 5 0.998 5 0.998 6 0.998 6 x 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 3 0.998 7 0.999 0 0.999 3 0.999 5 0.999 7 0.999 8 0.999 8 0.999 9 0.999 9 1.000 0

正态分布、指数分布、对数正态分布和威布尔分布函数及其在工程分析中的应用.

正态分布、指数分布、对数正态分布和威布尔分布函数及其在工程分析中的应用 071330225 张洋洋

目录正态分布函数 (3) 正态分布应用领域 (4) 正态分布案例分析 (5) 指数分布函数 (5) 指数分布的应用领域 (6) 指数分布案例分析 (7) 对数正态分布函数 (7) 对数正态分布的应用领域 (9) 对数正态分布案例分析 (9) 威布尔分布函数 (10) 威布尔分布的应用领域 (16) 威布尔分布案例分析 (16) 附录 (18) 参考文献 (21)

正态分布函数【1】 0.20 0.15 0.10 0.05 105510 正态分布概率密度函数f（t）蓝线：μ=-1 σ=2 红线：μ=1 σ=2 棕线：μ=-1 σ=3 绿线：μ=1 σ=3 均数μ决定正态曲线的中心位置；标准差σ决定正态曲线的陡峭或扁平程度。σ越小，曲线越陡峭；σ越大，曲线越扁平。 1.0 0.8 0.6 0.4 0.2 105510 正态分布函数F（t）蓝线：μ=-1 σ=2 红线：μ=1 σ=2 棕线：μ=-1 σ=3 均数μ改变，图像会进行平移，标准差σ改变，图形陡峭度发生变化。σ越小，图像越陡。

1.0 0.8 0.6 0.4 0.2 105510 正态分布可靠度函数R（t）蓝线：μ=-1 σ=2 红线：μ=1 σ=2 棕线：μ=-1 σ=3 均数μ改变，图像会进行平移，标准差σ改变，图形陡峭度发生变化。σ越小，图像越陡。 2.5 2.0 1.5 1.0 0.5 105510 正态分布失效率函数λ（t）蓝线：μ=-1 σ=2 红线：μ=1 σ=2 棕线：μ=-1 σ=3 均数μ改变，图像会进行平移，标准差σ改变，图形陡峭度发生变化。σ越小，图像越陡。正态分布应用领域【1】正态分布是一种最常见的连续型随机变量的分布,它在概率论和数理统计中无论在理论研究还是实际应用上都占有头等重要的地位,这是因为它在误差理论、无线电噪声理论、自动控制、产品检验、质量控制、质量管理等领域都有广泛应用.数理统计中许多重要问题的解决都是以正态分布为基础的.某些医学现象，如同质群体的身高、红细胞数、血红蛋白量、胆固醇等，以及实验中的随机误差，呈现为正态或近似正态分布；有些资料虽为偏态分布，但经数据变换后可成为正态或近似正态分布，故可按正态分布规律处理。

正态分布讲解(含标准表)

2．4正态分布复习引入：总体密度曲线:样本容量越大，所分组数越多，各组的频率就越接近于总体在相应各组取值的概率．设想样本容量无限增大，分组的组距无限缩小，那么频率分布直方图就会无限接近于一条光滑曲线,这条曲线叫做总体密度曲线．总体密度曲线 b 单位 O 频率/组距 a 它反映了总体在各个范围内取值的概率．根据这条曲线，可求出总体在区间(a，b)内取值的概率等于总体密度曲线，直线x=a，x=b及x轴所围图形的面积．观察总体密度曲线的形状，它具有“两头低，中间高，左右对称”的特征，具有这种特征的总体密度曲线一般可用下面函数的图象来表示或近似表示： 2 2 () 2 , 1 (),(,) 2 x x e x μ σ μσ ? πσ - - =∈-∞+∞ 式中的实数μ、)0 (> σ σ是参数，分别表示总体的平均数与标准差，, ()x μσ ? 的图象为正态分布密度曲线,简称正态曲线．讲解新课：

一般地，如果对于任何实数a b <，随机变量X 满足 ,()()b a P a X B x dx μσ?<≤=?, 则称 X 的分布为正态分布（normal distribution ) ．正态分布完全由参数μ和σ确定，因此正态分布常记作),(2 σ μN ．如果随机变量 X 服从正态分布，则记为X ～),(2σμN . 经验表明，一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和，它就服从或近似服从正态分布．例如，高尔顿板试验中，小球在下落过程中要与众多小木块发生碰撞，每次碰撞的结果使得小球随机地向左或向右下落，因此小球第1次与高尔顿板底部接触时的坐标 X 是众多随机碰撞的结果，所以它近似服从正态分布．在现实生活中，很多随机变量都服从或近似地服从正态分布．例如长度测量误差；某一地区同年龄人群的身高、体重、肺活量等；一定条件下生长的小麦的株高、穗长、单位面积产量等；正常生产条件下各种产品的质量指标（如零件的尺寸、纤维的纤度、电容器的电容量、电子管的使用寿命等）；某地每年七月份的平均气温、平均湿度、降雨量等；一般都服从正态分布．因此，正态分布广泛存在于自然现象、生产和生活实际之中．正态分布在概率和统计中占有重要的地位．说明:1参数μ是反映随机变量取值的平均水平的特征数，可以用样本均值去佑计；σ是衡量随机变量总体波动大小的特征数，可以用样本标准差去估计． 2.早在 1733 年，法国数学家棣莫弗就用n ！的近似公式得到了正态分布．之后，德国数学家高斯在研究测量误差时从另一个角度导出了它，并研究了它的性质，因此，人们也称正态分布为高斯分布． 2．正态分布),(2 σ μN ）是由均值μ和标准差σ唯一决定的分布通过固定其中一个值，讨论均值与标准差对于正态曲线的影响

数学分布(泊松分布、二项分布、正态分布、均匀分布、指数分布) 生存分析贝叶斯概率公式全概率公式讲解

数学期望：随机变量最基本的数学特征之一。它反映随机变量平均取值的大小。又称期望或均值。它是简单算术平均的一种推广。例如某城市有10万个家庭，没有孩子的家庭有1000个，有一个孩子的家庭有9万个，有两个孩子的家庭有6000个，有3个孩子的家庭有3000个，则此城市中任一个家庭中孩子的数目是一个随机变量，记为X，它可取值0，1，2，3，其中取0的概率为0.01，取1的概率为0.9，取2的概率为0.06，取3的概率为0.03，它的数学期望为0×0.01＋1×0.9＋2×0.06＋3×0.03等于1.11，即此城市一个家庭平均有小孩1.11个，用数学式子表示为：E(X)=1.11。也就是说，我们用数学的方法分析了这个概率性的问题，对于每一个家庭，最有可能它家的孩子为1.11个。可以简单的理解为求一个概率性事件的平均状况。各种数学分布的方差是： 1、一个完全符合分布的样本 2、这个样本的方差概率密度的概念是：某种事物发生的概率占总概率(1)的比例,越大就说明密度越大。比如某地某次考试的成绩近似服从均值为80的正态分布，即平均分是80分，由正态分布的图形知x=80时的函数值最大，即随机变量在80附近取值最密集，也即考试成绩在80分左右的人最多。下图为概率密度函数图(F(x)应为f(x)，表示概率密度)：

离散型分布：二项分布、泊松分布连续型分布：指数分布、正态分布、X 2分布、t 分布、F 分布抽样分布只与自由度，即样本含量（抽样样本含量）有关二项分布（binomial distribution ）：例子抛硬币 1、重复试验（n 个相同试验，每次试验两种结果，每种结果概率恒定————伯努利试验） 2、抽样分布

指数族和几何分布

指数族和几何分布关于指数族和广义线性模型的相关知识，详情请点击。以φ为参数的指数分布为： ,...2,1)1();(1=-=-y y p y ，φφφ （1）证明指数分布是指数族分布。 ) 1log ))1exp((log()log )1log()1exp(()1();(1φφφφφφ φφ-+?-=+--=-=-y y y p y 于是， )1log()1log()(, )() 1(),1(log 1)(η ηφφ ηφφηe e a y y T e y b -=--==-=?-==，（2）使用具有几何反应变量的广义线性模型，执行回归，可得典型反应函数为： η φ ηηηe y E y T E g -====11 1] ;[] );([)( （3）给定一组训练集},...,2,1);,{()()(m i y x i i =，令一个样本的log 似然性为);|()()(θi i x y p ，下面我们求解随机梯度上升的更新规则。先写出

)1log(11 log 1log ))1log )1g(log(exp(lo );|(log )()() ()()()()()()()()()()()(-+=--=--=---==--i T i T i T i T x i i T x i i T x x i i T i i i e y x e y x e e y x y x y p l θθθθθθθφφφθθ， )(θl 关于j θ求导，得到 ) ( )()()()()( )()())1(1 ()1() 1()()()()()(i j x i x i j i i j x i j x i i j j x e y e x y x e x e y x l i T i T i T i T θθθθθ---- =--?+=??-- 所以梯度上升更新规则为 )()()11(:)(i j x i j j x e y i T θαθθ-- +=。

几种常见的分布

一、常见数据类型数据可大致分为离散我们先来看一看平时遇到的数据。在正式的解释分布之前，型数据和连续型数据。离散型数据结果只当你掷骰子的时候，离散型数据顾名思义就是只取几个特定的值。例如：。1,2,3,4,5,6，不会出现类似1.5,2.5有连续型数据这个范围可以是有限的或者是连续型数据可以取任意值。在一个给定的范围内，等 54kg,54.4kg,54.33333kg无穷的。例如：一个人的体重或者身高，可以取值等都没有问题。下面就开始介绍分布的类型。二、分布类型）Bernoulli Distribution伯努利分布（首先从最简单的分布开始，伯努利分布实际上是一个听起来最容易理解的分布。。代表0failure1代表success及伯努利分布一次实验有两个可能的结果，比如pX表示失，一个取值为1并代表成功，成功概率为0随机变量pX一个取值为pq1?或者说1?p。败，失败概率为q(0,1)∈xp(1?p)，我们(0,1)x这里，概率分布函数为px(1?p)1?x，其中∈xx1?也可以写成如下形式：x=0x=1pP(x)={1?p x=1 ，，，x=0p，P(x)={1?p，但是这俩概率加和应该0.5成功和失败的概率没必要相同，也就是没必要都是，比如可以是下面的图：为 1. p(failure)=0.85p(success)=0.15p(failure)这个图就是p(success)=0.15，，

=0.85。服从伯努利下面说一下随机变量的期望，一个分布的期望就是这个分布的均值。X X分布的随机变量的期望值就是： p)=p?(1?E(X)=1?p+0?(1?p)=pE(X)=1?p+0服从伯努利分布的随机变量的方差是：p)(1?=p?p=pV(X)=E(X)?[E(X)] V(X)=E(X2)?[E(X)]2=p?p2=p(1?p)222明天今天会不会去健身，还有许多伯努利分布的例子，比如说明天是否会下雨，乒乓球比赛是不是会赢。）均匀分布（Uniform Distribution而任何一个结果出现的概率中的任何一个，1到6当你掷骰子的时候，结果出现与伯努利分布不都是相同的，这就是均匀分布最原始的雏形。你可能看出来了，n n个出现的结果的概率都是相同的。同的是，这X X为均匀分布是指密度函数如下：一个随机变量<∞≤b?f(x)=1ba?∞(a+b)2V(X)= Variance->V(X)=(b?a)21212?a)(b2b=0a=0，所以对于标准