高三一轮复习资料知识点详解

高三地理一轮复习的知识点分析（经典版）编制人：__________________审核人：__________________审批人：__________________编制单位：__________________编制时间：____年____月____日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的经典范文，如演讲稿、总结报告、合同协议、方案大全、工作计划、学习计划、条据书信、致辞讲话、教学资料、作文大全、其他范文等等，想了解不同范文格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, this shop provides you with various types of classic sample essays, such as speech drafts, summary reports, contract agreements, project plans, work plans, study plans, letter letters, speeches, teaching materials, essays, other sample essays, etc. Want to know the format and writing of different sample essays, so stay tuned!高三地理一轮复习的知识点分析在学习上，注重理论联系实际，关注社会热点，培养应用能力，如让学生掌握地理学科广泛应用和社会价值性，运用地理知识和技能，去解释一些自然现象，解决一些实际的社会问题。

高中数学一轮总复习数与代数知识点详解在高中数学的学习中，数与代数是一个重要的知识点，涉及到了数的运算、代数式的化简、方程等内容。

本文将详细解析高中数学一轮总复习中数与代数的知识点。

一、数的运算1.整数运算在整数运算中，我们需要掌握整数的加法、减法、乘法和除法。

整数的加法和减法运算按照正负数的规则进行，乘法和除法运算需要注意正负数相乘的规则。

2.分数运算分数是整数除法的结果，我们需要了解分数的加法、减法、乘法和除法运算的规则，同时也需要掌握化简分数的方法。

3.小数运算小数运算包括加法、减法、乘法和除法，需要特别注意小数的位数对齐，以及运算结果的精确度。

4.百分数运算百分数是将分数表示的百分数转化为小数表示的百分数。

百分数运算包括百分数的加法、减法、乘法和除法，需要注意将百分数转化为小数进行运算。

二、代数式的化简1.代数式的基本概念代数式由常数、变量和运算符号组成，涉及到代数式的基本概念，比如多项式、单项式、系数、字母等。

2.代数式的合并同类项合并同类项是化简代数式的基本方法之一，需要将具有相同字母的项合并为一个项，并按照系数的大小进行排序。

3.代数式的提公因式提公因式也是化简代数式的常用方法，通过找出各项的公因式并提取出来，可以简化代数式的复杂度。

4.代数式的分解因式分解因式是将代数式因式分解的过程，需要掌握一些常用的因式分解公式，比如平方差公式、完全平方公式等。

5.代数式的乘法公式代数式的乘法公式包括平方公式、差积公式、和差积公式等，通过运用这些公式可以简化代数式的乘法运算。

三、方程1.一元一次方程一元一次方程是一个未知数的一次方程，我们需要掌握解一元一次方程的基本方法，包括化简方程、移项、合并同类项、解得未知数等。

2.一元二次方程一元二次方程是一个未知数的二次方程，我们需要掌握解一元二次方程的基本方法，包括配方法、因式分解法、求根公式等。

3.二元一次方程组二元一次方程组是两个未知数的一次方程组，我们需要掌握解二元一次方程组的基本方法，包括代入法、消元法等。

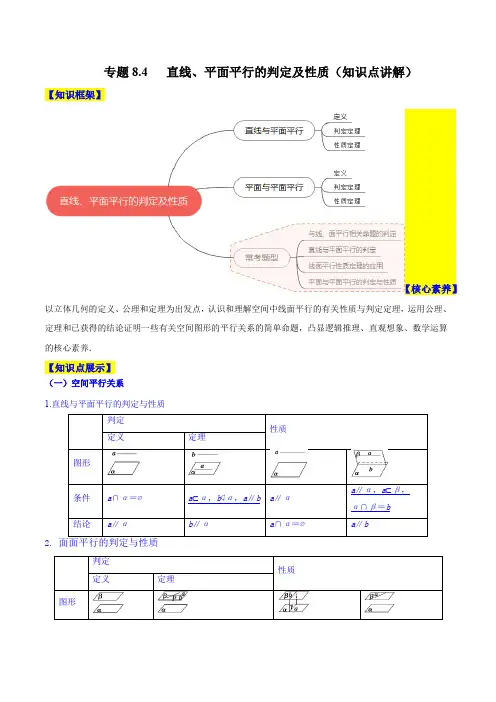
专题8.4 直线、平面平行的判定及性质（知识点讲解）【知识框架】【核心素养】以立体几何的定义、公理和定理为出发点，认识和理解空间中线面平行的有关性质与判定定理，运用公理、定理和已获得的结论证明一些有关空间图形的平行关系的简单命题，凸显逻辑推理、直观想象、数学运算的核心素养．【知识点展示】（一）空间平行关系1.直线与平面平行的判定与性质a∥α，a⊂β，2.利用线面平行的定义，一般用反证法；利用线面平行的判定定理(a ⊄α，b ⊂α，a ∥b ⇒a ∥α)，其关键是在平面内找(或作)一条直线与已知直线平行，证明时注意用符号语言的叙述；)利用面面平行的性质定理(α∥β，a ⊂α⇒a ∥β)； 利用面面平行的性质(α∥β，a ⊄β，a ∥α⇒a ∥β)． （二）平行关系中的三个重要结论(1)垂直于同一条直线的两个平面平行，即若a ⊥α，a ⊥β，则α∥β. (2)垂直于同一个平面的两条直线平行，即若a ⊥α，b ⊥α，则a ∥b. (3)平行于同一个平面的两个平面平行，即若α∥β，β∥γ，则α∥γ.【常考题型剖析】题型一：与线、面平行相关命题的判定例1. （2023·全国·高三专题练习）已知m ，n 为两条不同的直线，α，β为两个不同的平面，则下列结论中正确的是（ ） A ．若m //α，m //n ，则n //α B ．若m //α，n //α，则m //n C ．若m //α，n ⊂α，则m //nD ．若m //α，m ⊂β，αβ＝n ，则m //n例2.（2022·上海静安·二模）在下列判断两个平面α与β平行的4个命题中，真命题的个数是（ ）. （1）α、β都垂直于平面r ，那么α∥β. （2）α、β都平行于平面r ，那么α∥β. （3）α、β都垂直于直线l ，那么α∥β.（4）如果l 、m 是两条异面直线，且l ∥α，m ∥α，l ∥β，m ∥β，那么α∥β A ．0B ．1C ．2D ．3例3．（四川·高考真题（文））下列命题正确的是（ ） A ．若两条直线和同一个平面所成的角相等，则这两条直线平行 B ．若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行 C ．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D ．若两个平面都垂直于第三个平面，则这两个平面平行例4. （2022·云南师大附中模拟预测（理））若α，β是两个不同平面，m ，n 是两条不同直线，则下列4个推断中正确的是（ ）A ．m α∥，m β∥，n ⊂α，n m n β⊂⇒∥B ．m α⊂，n β⊂，m n αβ⇒∥∥C ．m α∥，n α∥，m β⊂，n βαβ⊂⇒∥D ．m α⊂，n β⊂，m n αβ⇒∥∥ 【方法技巧】直线、平面间平行的判定方法(1)关注是否符合判定定理与性质定理，并注意定理中易忽视的条件． (2)结合题意构造或绘制图形，结合图形作出判断． (3)利用实物进行空间想象，比较判断．(4)熟记一些常见结论，如垂直于同一条直线的两个平面平行等． 题型二：直线与平面平行的判定例5.（2023·全国·高三专题练习）在直三棱柱111ABC A B C -中，D 、E 、F 、M 、N 分别是BC 、11B C 、1AA 、1CC 、1A C 的中点，给出下列四个判断：①//EF 平面1ADB ；②//EM 平面1ADB ； ③//EN 平面1ADB ； ④1//A M 平面1ADB ， 错误的序号为___________.例6.【多选题】（2017·全国·高考真题（文））如图，在下列四个正方体中，A ，B 为正方体的两个顶点，M ，N ，Q 为所在棱的中点，则在这四个正方体中，直线AB 与平面MNQ 平行的是（ ）A．B．C．D．例7.（2023·全国·高三专题练习）如图，AB是圆O的直径，点C是圆O上异于,A B的点，直线PC 平面ABC，,E F分别是PA，PC的中点.记平面BEF与平面ABC的交线为l，求证：直线l//平面PAC【总结提升】证明直线与平面平行的方法(1)线面平行的定义：一条直线与一个平面无公共点(不相交)．(2)线面平行的判定定理：关键是找到平面内与已知直线平行的直线．常利用三角形的中位线、平行四边形的对边、成比例线段出现平行线或过已知直线作一平面找其交线．注意内外平行三条件，缺一不可．题型三：线面平行性质定理的应用例8.（福建·高考真题（文））如图，在正方体ABCD-A1B1C1D1中，AB＝2，点E为AD的中点，点F在CD 上．若EF∥平面AB1C，则线段EF的长度等于________．例9.(2019·全国卷Ⅰ改编)如图，直四棱柱ABCD ­A 1B 1C 1D 1的底面是菱形，AA 1＝4，AB ＝2，∠BAD ＝60°，E ，M ，N 分别是BC ，BB 1，A 1D 的中点．证明：MN ∥平面C 1DE .例10.如图，在直四棱柱ABCD ­A 1B 1C 1D 1中，E 为线段AD 上的任意一点(不包括A ，D 两点)，平面CEC 1∩平面BB 1D ＝FG .证明：FG ∥平面AA 1B 1B ．【总结提升】 1.思路方法：(1)通过线面平行可得到线线平行，其中一条线应是两平面的交线，要树立这种应用意识． (2)利用线面平行性质必须先找出交线． 2.易错提醒（1）在推证线面平行时，一定要强调直线不在平面内，否则，会出现错误.（2）线面平行关系证明的难点在于辅助面和辅助线的添加，在添加辅助线、辅助面时一定要以某一性质定理为依据，绝不能主观臆断.（3）解题中注意符号语言的规范应用. 题型四：平面与平面平行的判定与性质例11.（2023·全国·高三专题练习）已知长方体1111ABCD A B C D -中，4AB AD ==，12AA =，E ，F 分别为棱11A B 和11A D 的中点，M 为长方体表面上任意一点．若BM ∥平面AEF ，则BM 的最大值为（ ）A．B ．C ．D ．6例12.（2020·全国·高三专题练习（文））如图，平面//α平面β，PAB △所在的平面与α，β分别交于CD 和AB ，若2PC =，3CA =，1CD =，则AB =______．例13.（2023·全国·高三专题练习）如图，在正方体1111ABCD A B C D -中，E ，F分别为棱11,DD CC 的中点.求证：平面1//AEC 平面BDF例14.（陕西·高考真题（文））如图,四棱柱ABCD －A 1B 1C 1D 1的底面ABCD 是正方形, O 为底面中心, A 1O∥平面ABCD, 12AB AA ==.（1）证明: 平面A 1BD // 平面CD 1B 1;（2）求三棱柱ABD －A 1B 1D 1的体积.【规律方法】 1.证明面面平行的常用方法 (1)利用面面平行的定义．(2)利用面面平行的判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行． (3)利用“垂直于同一条直线的两个平面平行”．(4)利用“如果两个平面同时平行于第三个平面，那么这两个平面平行”． (5)利用“线线平行”“线面平行”“面面平行”的相互转化．2.面面平行的应用(1)两平面平行，构造与之相交的第三个平面，可得交线平行．(2)两平面平行，其中一个平面内的任意一条直线与另一个平面平行，可用于证明线面平行．3.三种平行关系之间的转化其中线面平行是核心，线线平行是基础，要注意它们之间的灵活转化．专题8.4 直线、平面平行的判定及性质（知识点讲解）【知识框架】【核心素养】以立体几何的定义、公理和定理为出发点，认识和理解空间中线面平行的有关性质与判定定理，运用公理、定理和已获得的结论证明一些有关空间图形的平行关系的简单命题，凸显逻辑推理、直观想象、数学运算的核心素养．【知识点展示】（一）空间平行关系1.直线与平面平行的判定与性质a∥α，a⊂β，2.利用线面平行的定义，一般用反证法；利用线面平行的判定定理(a ⊄α，b ⊂α，a ∥b ⇒a ∥α)，其关键是在平面内找(或作)一条直线与已知直线平行，证明时注意用符号语言的叙述；)利用面面平行的性质定理(α∥β，a ⊂α⇒a ∥β)； 利用面面平行的性质(α∥β，a ⊄β，a ∥α⇒a ∥β)． （二）平行关系中的三个重要结论(1)垂直于同一条直线的两个平面平行，即若a ⊥α，a ⊥β，则α∥β. (2)垂直于同一个平面的两条直线平行，即若a ⊥α，b ⊥α，则a ∥b. (3)平行于同一个平面的两个平面平行，即若α∥β，β∥γ，则α∥γ.【常考题型剖析】题型一：与线、面平行相关命题的判定例1. （2023·全国·高三专题练习）已知m ，n 为两条不同的直线，α，β为两个不同的平面，则下列结论中正确的是（ ） A ．若m //α，m //n ，则n //α B ．若m //α，n //α，则m //n C ．若m //α，n ⊂α，则m //n D ．若m //α，m ⊂β，αβ＝n ，则m //n【答案】D 【解析】 【分析】举例说明判断A ，B ，C ；利用线面平行的性质判断D 作答. 【详解】如图，长方体1111ABCD A B C D -中，平面1111D C B A 视为平面α，对于A ，直线AB 视为m ，直线11A B 视为n ，满足m //α，m //n ，而n ⊂α，A 不正确；对于B，直线AB视为m，直线BC视为n，满足m//α，n//α，而m与n相交，B不正确；A D视为n，满足m//α，n⊂α，显然m与n是异面直线，C不正确；对于C，直线AB视为m，直线11对于D，由直线与平面平行的性质定理知，D正确.故选：D例2.（2022·上海静安·二模）在下列判断两个平面α与β平行的4个命题中，真命题的个数是（）.（1）α、β都垂直于平面r，那么α∥β.（2）α、β都平行于平面r，那么α∥β.（3）α、β都垂直于直线l，那么α∥β.（4）如果l、m是两条异面直线，且l∥α，m∥α，l∥β，m∥β，那么α∥βA．0B．1C．2D．3【答案】D【解析】【分析】由面面平行的判定定理及其相关结论分析可得结果.【详解】由面面平行的判定定理分析可知（1）错，（2），（3），（4）正确.故选：D例3．（四川·高考真题（文））下列命题正确的是（）A．若两条直线和同一个平面所成的角相等，则这两条直线平行B．若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D．若两个平面都垂直于第三个平面，则这两个平面平行【答案】C【解析】【详解】若两条直线和同一平面所成角相等，这两条直线可能平行，也可能为异面直线，也可能相交，所以A错；一个平面不在同一条直线的三点到另一个平面的距离相等，则这两个平面平行，故B错；若两个平面垂直同一个平面两平面可以平行，也可以垂直；故D错；故选项C正确.例4. （2022·云南师大附中模拟预测（理））若α，β是两个不同平面，m ，n 是两条不同直线，则下列4个推断中正确的是（ ）A ．m α∥，m β∥，n ⊂α，n m n β⊂⇒∥B ．m α⊂，n β⊂，m n αβ⇒∥∥C ．m α∥，n α∥，m β⊂，n βαβ⊂⇒∥D ．m α⊂，n β⊂，m n αβ⇒∥∥【答案】A【解析】【分析】利用线面，面面位置关系逐项分析即得.【详解】对于A ，如图，n ⊂α，n n βαβ⊂⇒⋂=，结合m α，m β，可知m n ∥，故A 正确；对于B ，如图，m ，n 可能异面，故B 错误；对于C ，如图，α，β可能相交，故C 错误；对于D ，如图，αβ，可能相交，故D 错误.故选：A ．【方法技巧】直线、平面间平行的判定方法(1)关注是否符合判定定理与性质定理，并注意定理中易忽视的条件．(2)结合题意构造或绘制图形，结合图形作出判断．(3)利用实物进行空间想象，比较判断．(4)熟记一些常见结论，如垂直于同一条直线的两个平面平行等．题型二：直线与平面平行的判定例5.（2023·全国·高三专题练习）在直三棱柱111ABC A B C -中，D 、E 、F 、M 、N 分别是BC 、11B C 、1AA 、1CC 、1A C 的中点，给出下列四个判断：①//EF 平面1ADB ；②//EM 平面1ADB ；③//EN 平面1ADB ；④1//A M 平面1ADB ，错误的序号为___________.【答案】①②④【解析】【分析】连接DE 、1A E 、CE 、EF 、EM 、EN 、1A M 、FM ，证明出平面1//A CE 平面1AD B ，利用面面平行的性质结合假设法可判断①②③④的正误.【详解】连接DE 、1A E 、CE 、EF 、EM 、EN 、1A M 、FM ，在三棱柱111ABC A B C -中，因为11//BB CC 且11BB CC =，所以，四边形11BB C C 为平行四边形，则11//BC B C 且11BC B C =，D 、E 分别为BC 、11B C 的中点，则1//CD B E 且1CD B E =，故四边形1CDB E 为平行四边形，则1//CE B D ，CE ⊄平面1ADB ，1B D ⊂平面1ADB ，故//CE 平面1ADB ，同理可证四边形1BB ED 为平行四边形，则11////DE BB AA ，11DE BB AA ==，则四边形1AA ED 为平行四边形，所以，1//A E AD ，1A E ⊄平面1ADB ，AD ⊂平面1ADB ，则1//A E 平面1ADB ，1CE A E E =，故平面1//A CE 平面1AD B ，EN ⊂平面1A CE ，则//EN 平面1ADB ，③对；对于①，若//EF 平面1ADB ，EF EN E =，则平面//EFN 平面1ADB ，因为过点E 且与平面1ADB 平行的平面只有一个，矛盾，故①错，同理可知，②④均错.故答案为：①②④.例6.【多选题】（2017·全国·高考真题（文））如图，在下列四个正方体中，A ，B 为正方体的两个顶点，M ，N ，Q 为所在棱的中点，则在这四个正方体中，直线AB 与平面MNQ 平行的是（ ）A ．B ．C ．D ．【答案】BCD【解析】【分析】利用线面平行判定定理逐项判断可得答案．【详解】对于选项A，OQ∥AB，OQ与平面MNQ是相交的位置关系，故AB和平面MNQ不平行，故A错误；对于选项B，由于AB∥CD∥MQ，结合线面平行判定定理可知AB∥平面MNQ，故B正确；对于选项C，由于AB∥CD∥MQ，结合线面平行判定定理可知AB∥平面MNQ：故C正确；对于选项D，由于AB∥CD∥NQ，结合线面平行判定定理可知AB∥平面MNQ：故D正确；故选：BCD例7.（2023·全国·高三专题练习）如图，AB 是圆O 的直径，点C 是圆O 上异于,A B 的点，直线PC ⊥平面ABC ，,E F 分别是PA ，PC 的中点.记平面BEF 与平面ABC 的交线为l ，求证：直线l //平面PAC【答案】证明见解析【解析】【分析】先通过//EF AC 可得出//EF 平面ABC ，再利用线面平行的性质即可证明.【详解】因为,E F 分别是,PA PC 的中点，所以//EF AC ，又因为AC ⊂平面ABC ，EF ⊄平面ABC ，所以//EF 平面ABC ，又EF ⊂平面BEF ，平面BEF 与平面ABC 的交线为l ，所以//EF l ，而l ⊄平面PAC ，EF ⊂平面PAC ，所以//l 平面P AC .【总结提升】证明直线与平面平行的方法(1)线面平行的定义：一条直线与一个平面无公共点(不相交)．(2)线面平行的判定定理：关键是找到平面内与已知直线平行的直线．常利用三角形的中位线、平行四边形的对边、成比例线段出现平行线或过已知直线作一平面找其交线．注意内外平行三条件，缺一不可． 题型三：线面平行性质定理的应用例8.（福建·高考真题（文））如图，在正方体ABCD -A 1B 1C 1D 1中，AB ＝2，点E 为AD 的中点，点F 在CD 上．若EF ∥平面AB 1C ，则线段EF 的长度等于________．【解析】【分析】根据直线与平面平行的性质定理可得//EF AC ,再根据E 为AD 的中点可得F 为CD 的中点,从而根据三角形的中位线可得.【详解】如图:因为//EF 平面1AB C ,EF ⊂平面DABC ,且平面1A C B 平面ABCD AC =,所以//EF AC ,又因为E 为AD 的中点,所以F 为CD 的中点, 所以12EF AC =,因为正方体的棱长为2.所以AC =所以EF =故答案为.例9.(2019·全国卷Ⅰ改编)如图，直四棱柱ABCD ­A 1B 1C 1D 1的底面是菱形，AA 1＝4，AB ＝2，∠BAD ＝60°，E ，M，N分别是BC，BB1，A1D的中点．证明：MN∥平面C1DE.【答案】见解析【解析】证明:连接B1C，ME.因为M，E分别为BB1，BC的中点，所以ME∥B1C，且ME＝12B1C．又因为N为A1D的中点，所以ND＝12A1D．由题设知A1B1//=DC，可得B1C//=A1D，故ME//=ND，因此四边形MNDE为平行四边形，所以MN∥ED．又MN⊄平面C1DE，ED⊂平面C1DE，所以MN∥平面C1DE.例10.如图，在直四棱柱ABCD­A1B1C1D1中，E为线段AD上的任意一点(不包括A，D两点)，平面CEC1∩平面BB1D＝FG.证明：FG∥平面AA1B1B．【答案】见解析【解析】证明：在直四棱柱ABCD­A1B1C1D1中，BB1∥CC1，BB1⊂平面BB1D，CC1⊄平面BB1D，所以CC1∥平面BB1D．又CC1⊂平面CEC1，平面CEC1∩平面BB1D＝FG，所以CC1∥FG.因为BB1∥CC1，所以BB1∥FG.而BB1⊂平面AA1B1B，FG⊄平面AA1B1B，所以FG∥平面AA1B1B．【总结提升】1.思路方法：(1)通过线面平行可得到线线平行，其中一条线应是两平面的交线，要树立这种应用意识．(2)利用线面平行性质必须先找出交线．（1）在推证线面平行时，一定要强调直线不在平面内，否则，会出现错误.（2）线面平行关系证明的难点在于辅助面和辅助线的添加，在添加辅助线、辅助面时一定要以某一性质定理为依据，绝不能主观臆断.（3）解题中注意符号语言的规范应用.题型四：平面与平面平行的判定与性质例11.（2023·全国·高三专题练习）已知长方体1111ABCD A B C D -中，4AB AD ==，12AA =，E ，F 分别为棱11A B 和11A D 的中点，M 为长方体表面上任意一点．若BM ∥平面AEF ，则BM 的最大值为（ ）A．B ．C ．D ．6【答案】C【解析】【分析】由面面平行的性质结合题意可确定点M 所在的平面，再由平面几何的性质即可确定BM 的值为最大值时的位置，即可求解【详解】如图所示，取G ，H 分别为棱11B C 和11D C 的中点，连接11,,,BG DH BD B D ,由题意易知1111,BF B D GH B D ∥∥，所以BF GH ∥；又易知AF BG ∥，故可以证明平面BGHD ∥平面AEF ；又BM ∥平面AEF ，由面面平行的性质可知M ∈平面BGHD ，所以由题意可知M 在等腰梯形BGHD 四条边上运动，过点H 作HQ BD ⊥，交BD 于点Q ，由题意可知BD GH DH BG DQ ====所以HQ BQ BD DQ =-=所以BH又BD BH ==，所以故当M 与D 点重合时，BM 的值为最大值，此时BM BD ==例12.（2020·全国·高三专题练习（文））如图，平面//α平面β，PAB △所在的平面与α，β分别交于CD 和AB ，若2PC =，3CA =，1CD =，则AB =______． 【答案】52【解析】【分析】根据面面平行的性质，证得//CD AB ，结合CD PC AB PA =，即可求解. 【详解】由题意，平面//α平面β，PAB △所在的平面与α，β分别交于CD 和AB ， 根据面面平行的性质，可得//CD AB ，所以CD PC AB PA =， 因为2PC =，3CA =，1CD =，所以15522CD PA AB PC ⋅⨯===.故答案为：52. 例13.（2023·全国·高三专题练习）如图，在正方体1111ABCD A B C D -中，E ，F 分别为棱11,DD CC 的中点.求证：平面1//AEC 平面BDF【答案】证明见解析【解析】【分析】根据1//DF EC ，可证明1//EC 平面BDF ；又//BF AE ，可得//AE 平面BDF .进而根据线面平行证明面面平行.【详解】证明：在正方体1111ABCD A B C D -中，E ，F 分别为棱11,DD CC 的中点， 所以11111,22DE DD C F CC ==. 因为11CC DD =，且11//CC DD ，所以1DE C F =，且1//DE C F ，所以四边形1DEC F 是平行四边形，所以1//DF EC 又DF ⊂平面BDF ，1EC ⊄平面BDF ，所以1//EC 平面BDF .同理，//BF AE ，又BF ⊂平面BDF ，AE ⊄平面BDF ， 所以//AE 平面BDF .又1AE EC E ⋂=，1,AE EC ⊂平面1AEC ，所以平面1//AEC 平面BDF 例14.（陕西·高考真题（文））如图,四棱柱ABCD －A 1B 1C 1D 1的底面ABCD 是正方形, O 为底面中心, A 1O∥平面ABCD, 1AB AA =（1）证明: 平面A 1BD // 平面CD 1B 1;（2）求三棱柱ABD －A 1B 1D 1的体积.【答案】（1）证明见解析；（2）1.【解析】【详解】试题分析：（1）要证明1A C ⊥平面11BB D D ，只要证明1A C 垂直于平面11BB D D 内的两条相交直线即可，由已知可证出1A C ⊥BD ，取11B D 的中点为1E ，通过证明四边形11A OCE 为正方形可证1A C ⊥1E O ．由线面垂直的判定定理问题得证；（2）由已知1A O 是三棱柱ABD ﹣A 1B 1D 1的高，由此能求出三棱柱ABD ﹣A 1B 1D 1的体积 试题解析：（Ⅰ）∵四棱柱ABCD ﹣A 1B 1C 1D 1的底面ABCD 是正方形，O 为底面中心，A 1O ⊥平面ABCD ，AB=AA 1=，由棱柱的性质可得BB 1和DD 1平行且相等，故四边形BB 1D 1D 为平行四边形，故有BD 和B 1D 1平行且相等．而BD 不在平面CB 1D 1内，而B 1D 1在平面CB 1D 1内，∴BD ∥平面CB 1D 1．同理可证，A 1BCD 1为平行四边形，A 1B ∥平面CB 1D 1．而BD 和A 1B 是平面A 1BD 内的两条相交直线，故有平面A 1BD ∥平面CD 1B 1 ．（Ⅱ）由题意可得A 1O 为三棱柱ABD ﹣A 1B 1D 1的高．三角形A 1AO 中，由勾股定理可得A 1O===1，∴三棱柱ABD ﹣A 1B 1D 1的体积V=S △ABD •A 1O=•A 1O=×1=1．【规律方法】1.证明面面平行的常用方法 (1)利用面面平行的定义．(2)利用面面平行的判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行．(3)利用“垂直于同一条直线的两个平面平行”．(4)利用“如果两个平面同时平行于第三个平面，那么这两个平面平行”．(5)利用“线线平行”“线面平行”“面面平行”的相互转化．2.面面平行的应用(1)两平面平行，构造与之相交的第三个平面，可得交线平行．(2)两平面平行，其中一个平面内的任意一条直线与另一个平面平行，可用于证明线面平行．3.三种平行关系之间的转化其中线面平行是核心，线线平行是基础，要注意它们之间的灵活转化．。

高三数学第一轮复习知识点总结高三数学第一轮复习知识点总结第一：高考数学中有函数、数列、三角函数、平面向量、不等式、立体几何等九大章节。

主要是考函数和导数，这是我们整个高中阶段里最核心的板块，在这个板块里，重点考察两个方面：第一个函数的性质，包括函数的单调性、奇偶性;第二是函数的解答题，重点考察的是二次函数和高次函数，分函数和它的一些分布问题，但是这个分布重点还包含两个分析就是二次方程的分布的问题，这是第一个板块。

第二：平面向量和三角函数。

重点考察三个方面：一个是划减与求值，第一，重点掌握公式，重点掌握五组基本公式。

第二，是三角函数的图像和性质，这里重点掌握正弦函数和余弦函数的性质，第三，正弦定理和余弦定理来解三角形。

难度比较小。

第三：数列。

数列这个板块，重点考两个方面：一个通项;一个是求和。

第四：空间向量和立体几何。

在里面重点考察两个方面：一个是证明;一个是计算。

第五：概率和统计。

这一板块主要是属于数学应用问题的范畴，当然应该掌握下面几个方面，第一……等可能的概率，第二………事件，第三是独立事件，还有独立重复事件发生的概率。

第六：解析几何。

这是我们比较头疼的问题，是整个试卷里难度比较大，计算量最高的题，当然这一类题，我总结下面五类常考的题型，包括第一类所讲的直线和曲线的位置关系，这是考试最多的内容。

考生应该掌握它的通法，第二类我们所讲的动点问题，第三类是弦长问题，第四类是对称问题，这也是2008年高考已经考过的一点，第五类重点问题，这类题时往往觉得有思路，但是没有答案，当然这里我相等的是，这道题尽管计算量很大，但是造成计算量大的原因，往往有这个原因，我们所选方法不是很恰当，因此，在这一章里我们要掌握比较好的算法，来提高我们做题的准确度，这是我们所讲的第六大板块。

第七：押轴题。

考生在备考复习时，应该重点不等式计算的方法，虽然说难度比较大，我建议考生，采取分部得分整个试卷不要留空白。

这是高考所考的七大板块核心的考点。

知识点总结1 集合与简易逻辑一、集合(一)元素与集合1.集合的含义某些指定对象的部分或全体构成一个集合．构成集合的元素除了常见的数、点等数学对象外，还可以是其他对象．2.集合元素的特征(1)确定性：集合中的元素必须是确定的，任何一个对象都能明确判断出它是否为该集合中的元素．(2)互异性：集合中任何两个元素都是互不相同的，即相同元素在同一个集合中不能重复出现．(3)无序性：集合与其组成元素的顺序无关．3.元素与集合的关系元素与集合之间的关系包括属于(记作a A ∈)和不属于(记作a A ∉)两种．4.集合的常用表示法集合的常用表示法有列举法、描述法、图示法(韦恩图)．5.常用数集的表示 数集 自然数集 正整数集 整数集 有理数集 实数集符号 NN ∗或N + Z Q R (二)集合间的基本关系1.集合A 为集合B 的子集 ，记作A B ⊆（或B A ⊇），读作“A 包含于B ”（或“B 包含A ”）.(2)真子集：若A B ⊆，且存在b B ∈，但b A ∉，则集合A 是集合B 的真子集，记作AB （或B A ⊃≠）. 读作“A 真包含于B ”或“B 真包含A ”.(3)相等：对于两个集合A 与B ，如果A B ⊆，同时B A ⊆，那么集合A 与B 相等，记作A =B ．(4)空集：把不含任何元素的集合叫做空集，记作∅；(三)集合的基本运算(1)交集：由所有属于集合A 且属于集合B 的元素组成的集合，叫做A 与B 的交集，记作A B ⋂， 即{}|A B x x A x B ⋂=∈∈且．(2) 并集：由所有属于集合A 或属于集合B 的元素组成的集合，叫做A 与B 的并集，记作A B ⋃，(3) 即{}|A B x x A x B ⋃=∈∈或．(3)补集：对于一个集合A ，由全集U 中不属于集合A 的所有元素组成的集合称为集合A 相对于全集U 的补集，简称为集合A 的补集，记作U C A ，即{|,}U C A x x U x A =∈∉且．(四)集合的运算性质(1)集合的运算性质：①交换律：A ∪B ＝B ∪A ；A ∩B ＝B ∩A ；②结合律：(A ∪B )∪C ＝A ∪(B ∪C )；(A ∩B )∩C ＝A ∩(B ∩C )；③分配律：(A ∩B )∪C ＝(A ∪C )∩(B ∪C )；(A ∪B )∩C ＝(A ∩C )∪(B ∩C )；【集合常用结论】1.子集个数：含有n个元素的有限集合M，其子集个数为2n；其真子集个数为2n－1；其非空子集个数为2n－1；其非空真子集个数为2n－2.2. 是任何集合的子集，是任何非空集合的真子集.3.∁U(A∪B)＝(∁U A)∩(∁U B)；∁U(A∩B)＝(∁U A)∪(∁U B)；4.A∪B＝A⇔B⊆A；A∩B＝B⇔B⊆A.5.集合运算中的常用方法若已知的集合是不等式的解集，用数轴求解；若已知的集合是点集，用数形结合法求解；若已知的集合是抽象集合，用Venn图求解.二、简易逻辑(一).全称命题、特称(存在性)命题及其否定(1)全称命题p：∀x∈M，p(x)，其否定为特称(存在性)命题：¬p：∃x0∈M，¬p(x0).(2)特称(存在性)命题p：∃x0∈M，p(x0)，其否定为全称命题：¬p：∀x∈M，¬p(x).(二).充分条件与必要条件的判定方法(1)定义法：若p⇒q，则p是q的充分条件(或q是p的必要条件)；若p⇒q，且q⇏p，则p是q的充分不必要条件(或q是p的必要不充分条件).(2)集合法：利用集合间的包含关系。

高三数学一轮复习知识点详细高三是整个中学生活的关键时期，对于将要面临高考的学生们来说，备考是最重要的任务之一。

而高考数学作为一门重要的科目，需要一轮复习提高自己的数学水平和应试能力。

本文将详细介绍高三数学一轮复习的知识点。

一、代数与函数在代数与函数中，我们需要重点复习的知识点有：1. 分式方程：包括分式的乘除与分式的方程与不等式；2. 二次函数：掌握二次函数的定义、性质以及相关的图像变换；3. 复杂函数的运算：包括函数的合并、分解、复合与反函数；4. 分式与整式的混合运算：理解分式与整式的加减及乘法与整式的除法运算；5. 二元一次方程组：熟悉二元一次方程组的解法；6. 等差数列与等比数列：掌握等差数列与等比数列的性质，并进行相关题目的解答；7. 幂指函数：理解幂函数与指数函数的图像变换与性质。

二、空间与几何在空间与几何中，我们需要重点复习的知识点有：1. 空间向量：包括向量的定义、加法、数量积与向量的共线与垂直关系；2. 圆锥曲线：掌握圆、椭圆、抛物线和双曲线的定义、相关性质与图像变换；3. 球与球面上的直线与平面：认识球与球面上直线与平面的性质、夹角、交点等；4. 空间几何体的体积与表面积：熟悉各种几何体的体积与表面积计算；5. 空间几何体的相交关系：包括平行与垂直关系、位似关系等。

三、数与统计在数与统计中，我们需要重点复习的知识点有：1. 随机事件与概率：理解随机事件的定义与基本性质，掌握概率的计算方法与相关公式；2. 二项式定理：掌握二项式展开的方法与应用；3. 组合数学与排列组合：了解排列组合计算的基本方法与公式，掌握应用技巧；4. 数据的整理与分析：学会收集数据、整理数据、制作统计图与分析统计结果。

四、解析几何在解析几何中，我们需要重点复习的知识点有：1. 平面直角坐标系与向量：理解平面直角坐标系的性质，掌握向量的加法、减法、数量积与向量的共线关系；2. 平面图形的方程：熟悉直线、圆、抛物线、双曲线及椭圆图形的方程；3. 几何变换：掌握平移、旋转、对称与放缩等几何变换的基本概念与性质。

高三数学一轮知识点总结归纳高三数学是学生们备战高考的关键时期，对于数学知识点的总结归纳是非常重要的。

本文将对高三数学一轮知识点进行全面梳理，帮助同学们更好地复习与巩固学习内容。

一、函数与方程1. 函数的性质与图像a. 定义域、值域与奇偶性b. 函数的增减性与最值c. 函数的周期性与对称性d. 常见函数的图像与性质总结2. 一次函数与二次函数a. 一次函数的定义与性质b. 一次函数的图像与常见问题c. 二次函数的定义与性质d. 二次函数的图像与常见问题3. 指数与对数函数a. 指数函数的定义与性质b. 指数函数的图像与常见问题c. 对数函数的定义与性质d. 对数函数的图像与常见问题4. 幂函数与反比例函数a. 幂函数的定义与性质b. 幂函数的图像与常见问题c. 反比例函数的定义与性质d. 反比例函数的图像与常见问题二、三角函数1. 基本概念与性质a. 弧度制与角度制的转换b. 正弦、余弦、正切函数的定义与性质c. 正弦、余弦、正切函数的图像与常见问题2. 三角函数的基本关系a. 三角函数的周期性与对称性b. 三角函数的和差化积与积化和差c. 三角函数的倍角与半角公式3. 解三角函数方程a. 解简单的三角方程b. 解复杂的三角方程c. 解三角方程组与实际问题应用三、数列与数列的表示方法1. 基本概念与通项公式a. 数列的定义与性质b. 等差数列的通项公式与性质c. 等比数列的通项公式与性质2. 数列求和问题a. 等差数列求和与常见问题b. 等比数列求和与常见问题c. 常用数列求和公式总结3. 递推数列与特殊数列a. 递推数列的定义与常见问题b. 斐波那契数列与常见问题c. 等差数列与等比数列的特殊性质四、空间几何与向量1. 点、直线与平面a. 点的定义与性质b. 直线的定义与性质c. 平面的定义与性质2. 空间图形的方程a. 点、直线的位置关系与方程b. 直线与平面的位置关系与方程c. 平面与平面的位置关系与方程3. 向量的基本概念与运算a. 向量的定义与性质b. 向量的加减法与数量积c. 向量的数量积与向量积4. 空间几何的应用a. 点到直线的距离与投影b. 直线与平面之间的夹角与距离c. 空间图形的体积与表面积计算通过以上的知识点总结归纳，我们可以更好地复习数学知识，加深对各个知识点的理解，并且在解题过程中能够迅速找到思路，提高解题效率。

高三语文复习一轮学问点总结高三语文复习一轮学问点：基础学问①字音辨析题要落实三个内容：形近字的读音，多音字的读音，简单误读字的读音等。

由于广东高考中所涉及的注音都是生活中常用的，因此备考中不必纠缠生僻字音。

字形辨析题虽然考试卷中没有出现，但是在（高考（作文））评分中却加大了对错别字的扣分标准，规定每一个错别字就扣一分，所以平常也应留意规范用字。

②（成语）俗语的复习的立足点是要正确理解成语俗语的整体意义，不要望文生义，同时要留意语境的组合与搭配状况及感情色调运用等。

该学问点的复习无捷径可言，平常对成语俗语多加积累了，考试就简单过关。

③病句的复习肯定要依据《考纲》上规定的六种类型来进行。

依据近几年的高考试卷分析，可知有关病句常考到十三种题型，第一轮复习要求对六类病句十三种题型，有一个全面的清晰的相识，最好各记一两个例句。

高三语文复习一轮学问点：古代诗文的复习①文言文的复习———留意课本文言文的考查，无论是实词、虚词、文句理解，还是语段翻译，各个学问点的考核无一不是源自课本，可见，文言文复习首先要复习好课本。

②诗歌鉴赏的复习对于诗歌的鉴赏，同学们普遍感到难度较大。

复习时肯定要处理好三个问题：一是阅读古诗词，要先解决语言的转换问题，扫除解读赏析中的障碍，然后做其他的题目。

因此，首轮复习时积累肯定量的古诗词就显得尤为必要了。

二是要全面了解高考试题的命制类型和出题设问的角度等，做到心中有数。

三是要形成清晰的答题思路和答题模式。

高三语文复习一轮学问点：现代文阅读复习现代文阅读分为两种，一种是科技类，包括自然科学与社会科学;一种是文学作品，以小说、（散文）为主。

科技文阅读，因为它的科学性、学问性和逻辑性比较突出，复习备考要训练整体把握材料的实力。

同时，答题时要能很快找到相对应的阅读区间。

文学作品，虽然不同作品表现的思想内容、艺术效果不同，但其解读（方法）大同小异，这就要求我们了解一些常规的解读方法。

例如，整体把握，以文解文;读懂题目要求，明确答题角度。

一轮复习高三知识点高三学生在备战高考时，需要进行全面而系统的复习。

一轮复习是为了巩固和回顾高三学年所学的全部知识点，并提高学习效率和成绩。

本文将以中文语文、数学、英语和物理为例，介绍高三知识点的一轮复习方法和注意事项。

1. 中文语文一轮复习中，中文语文的重点在于阅读理解、写作和应用题的训练。

学生可以通过阅读各种文学作品和实景材料，提高自己的阅读理解能力。

同时，要注重写作训练，如议论文、说明文和应用文等。

此外，还可以通过做模拟题和历年高考题，熟悉考试题型和解题思路。

2. 数学高三数学的一轮复习主要包括基础知识巩固、解题方法总结和难点突破。

学生需要重点复习数学公式、函数、方程、不等式等基础知识，并掌握各类题型的解题方法。

此外，还要注重做一些难度较高的试题，提高自己的解题能力。

3. 英语英语一轮复习主要包括听力、阅读、写作和翻译的训练。

学生可以通过听录音、看英文电影和做听力练习，提高自己的听力水平。

同时，要多读英文书籍和文章，拓宽阅读面，提高阅读理解能力。

此外，还要注重写作和翻译的训练，多做一些模拟题和真题。

4. 物理物理的一轮复习主要包括基本概念的回顾、公式的记忆和解题技巧的掌握。

学生需要重点理解和记忆各个物理概念，并熟练运用物理公式进行计算。

同时，要总结归纳解题方法和技巧，以便在考试中能够快速准确地解题。

总结：高三知识点的一轮复习需要注重整体规划和有针对性的练习。

学生需要坚持每天的复习计划，分配好时间，并结合自己的学习特点和重点进行复习。

此外，还可以利用各种辅助材料和资源，如习题集、辅导书和互联网资源等，提高复习效果。

最后，要保持积极的心态和信心，相信自己的能力，努力取得优异的成绩。

高三数学一轮知识点总结大全高三是所有考生的关键时刻，是为了应对高考而付出努力的最后一年。

数学作为高考必考科目之一，具有重要的分数和排名权重。

为了帮助高三学生更好地备考，下面将对高三数学一轮知识点进行全面总结。

一、函数与方程1. 函数的定义：函数是一种特殊的关系，对于定义域内的每个自变量都有唯一对应的因变量。

2. 函数的性质：奇偶性、周期性、增减性、单调性等。

3. 方程与不等式的解：通过求解方程或者不等式，求取未知数的取值范围。

二、数列与递推关系1. 等差数列：一种常见的数列，其中任意两个相邻项之间的差值为常数。

2. 等比数列：一种常见的数列，其中任意两个相邻项之间的比值为常数。

3. 递推关系：通过已知项和递推关系式，求解数列中任意一项的值。

三、平面几何1. 直线与曲线：通过方程或者性质，判断直线与曲线的关系。

2. 圆与其相关概念：弦、弧、切线、切点等。

3. 三角形与多边形：根据性质和定理，解决三角形和多边形相关的问题。

四、空间几何1. 空间中的直线与平面：通过方向向量和点的坐标等信息，求解直线与平面的关系。

2. 空间中的角与距离：根据空间几何相关定理，求解角的大小和点的距离。

3. 空间中的曲线与曲面：通过方程和性质，求解曲线和曲面的特性。

五、立体几何1. 立体的体积和表面积：求解各种形状的体积和表面积，例如（球、圆柱、锥、棱柱、棱锥等）。

2. 空间向量：矢量的定义、性质、运算等。

3. 空间解析几何：点、直线、平面的坐标和性质。

六、概率与统计1. 随机事件：基本概念、性质和运算。

2. 概率计算：频率、概率、事件间的关系和计算方法。

3. 排列组合与分布：排列、组合、二项分布、正态分布等。

七、数学证明与推理1. 数学证明的基本方法：直接证明法、反证法、数学归纳法等。

2. 数学运算与性质：算术运算、整除性质、同余关系等。

3. 数学推理与连续性：数学推理的过程和方法，连续性的概念和性质。

八、复数与数域1. 复数的定义与运算：复数的基本运算、共轭、模长等。

第一章 集合与常用逻辑用语1.1集合的概念知识点1.元素和集合的概念元素：一般地，我们把研究对象统称为元素集合：把一些元素组成的总体叫做集合（简称为集）。

集合通常用大写的字母表示，如A B C 、、、……；元素通常用小写的字母表示，如a b c d 、、、……。

知识点2.集合中元素的特性（1）确定性：给定一个集合，它的元素必须是确定的。

设A 是一个给定的集合，x 是某一具体的对象，则x 或者是A 的元素，或者不是A 的元素，二者必居其一，不能模棱两可．（2）互异性： 给定一个集合，它的任意两个元素是互不相同的。

也就是说集合中的元素是不重复出现的。

集合中相同的元素只能算是一个。

（3）无序性：集合中的元素是不分先后顺序的．知识点3.元素与集合的关系一般地，如果a 是集合A 的元素，就说a 属于A ，记作a A ∈；如果a 不是集合的元素，就说a 不属于A ，记作A a ∉。

特别注意：（1）集合和元素是两个不同的概念，它们之间是个体与整体的关系，并且这种关系是相对的；（2）元素与集合之间不存在大小与相等的关系，只存在属于或不属于的关系。

如2与{}3，只能是{}23∉，不能写成{}23≠。

知识点4.集合的第一种表示方法自然语言和常用数集及记法上面举的例子：中国的直辖市组成的集合。

还比如：地球上的四大洋组成的集合；小于10的所有自然数组成的集合等等我们是可以用自然语言表示一个集合。

数学中有一些常用数集，就是自然语言表示的， 这些常用数集及记法如下： （1）全体非负整数组成的集合称为非负整数集（或自然数集），记作N 。

（2）所有正整数组成的集合称为正整数集，记作*N 或+N 。

（3）全体整数组成的集合称为整数集，记作Z 。

（4）全体有理数数组成的集合称为有理数集，记作Q 。

（5）全体实数组成的集合称为实数集，记作R 。

知识点5.集合的表示方法 （1）自然语言 （2）列举法列举法概念：像这样把集合中的元素一一列举出来，并用大括号括起来表示集合的方法叫做列举法。

高三数学第一轮复习知识点高三数学第一轮复习集合知识点一、集合有关概念1、集合的含义：某些指定的对象集在一起就成为一个集合，其中每一个对象叫元素。

2、集合的中元素的三个特性：1.元素的确定性;2.元素的互异性;3.元素的无序性说明：(1)对于一个给定的集合，集合中的元素是确定的，任何一个对象或者是或者不是这个给定的集合的元素。

(2)任何一个给定的集合中，任何两个元素都是不同的对象，相同的对象归入一个集合时，仅算一个元素。

(3)集合中的元素是平等的，没有先后顺序，因此判定两个集合是否一样，仅需比较它们的元素是否一样，不需考查排列顺序是否一样。

(4)集合元素的三个特性使集合本身具有了确定性和整体性。

3、集合的表示：{}如{我校的篮球队员}，{太平洋,大西洋,印度洋,北冰洋}1.用拉丁字母表示集合：A={我校的篮球队员},B={1,2,3,4,5}2.集合的表示方法：列举法与描述法。

注意啊：常用数集及其记法：非负整数集(即自然数集)记作：N正整数集N*或N+整数集Z有理数集Q实数集R关于属于的概念集合的元素通常用小写的拉丁字母表示，如：a是集合A的元素，就说a属于集合A记作aA，相反，a不属于集合A记作a?A 列举法：把集合中的元素一一列举出来，然后用一个大括号括上。

描述法：将集合中的元素的公共属性描述出来，写在大括号内表示集合的方法。

用确定的条件表示某些对象是否属于这个集合的方法。

①语言描述法：例：{不是直角三角形的三角形}②数学式子描述法：例：不等式x-32的解集是{x?R|x-32}或{x|x-32}4、集合的分类：1.有限集含有有限个元素的集合2.无限集含有无限个元素的集合3.空集不含任何元素的集合例：{x|x2=-5｝二、集合间的基本关系1.包含关系子集注意：有两种可能(1)A是B的`一部分，;(2)A与B是同一集合。

反之:集合A不包含于集合B,或集合B不包含集合A,记作AB或BA2.相等关系(55，且55，则5=5)实例：设A={x|x2-1=0}B={-1,1}元素相同结论：对于两个集合A与B，如果集合A的任何一个元素都是集合B的元素，同时,集合B的任何一个元素都是集合A的元素，我们就说集合A等于集合B，即：A=B三、集合的运算1.交集的定义：一般地，由所有属于A且属于B的元素所组成的集合,叫做A,B的交集.记作AB(读作A交B)，即AB={x|xA，且xB}.2、并集的定义：一般地，由所有属于集合A或属于集合B的元素所组成的集合，叫做A,B的并集。

高三语文一轮复习的知识点归纳整理高三语文一轮复习的知识点归纳1一、文言实词1.通假字(1)北冥有鱼(通"溟"，大海)(2)小知不及大知(通"智"，智慧)(3)此小大之辩也(通"辨"，区别)(4)旬有五日而后反(通"又";通"返"，往返)(5)而徵一国(通"耐"，能)(6)御六气之辩(通"变"，变化)2.古今异义(1)腹犹果然古义：食饱之状今义：副词，表示事实与所说或所料相符(2)众人匹之古义：一般人今义：多数人，大家(3)虽然，犹有未树也。

古义：虽然这样今义：转折连词(4)穷发之北古义：毛，草木今义：头发(5)小年不及大年古义：寿命长的今义：丰收年;春节3.一词多义(1辩此小大之辩也(通"辨"，区别)而御六气之不辩(通"变"，变化)(2)知之二虫又何知(动词，知道)小知不及大知(名词，智慧)(3)名北冥有鱼，其名为鲲(名词，名称)圣人无名(名词，声名)(4)息去以六月息者也(名词，气息，这里指风)生物之以息相吹也(名词，气息)4.词类活用(1)名词用作动词。

而后乃今将图南(往南飞)/奚以之九万里而南为(往南飞)(2)使动用法。

德合一君(使……满意)/彼于致福者(使……到来)/而徵一国者(使……信任)二、文言虚词1.之(1)助词，的。

鹏之背，不知其几千里也/其翼若垂天之云(助词，的)(2)助词，主谓之间取消句子独立性。

鹏之徙于南冥也/生物之以息相吹也/且夫水之积也不厚(3)代词，它。

而莫之夭阏者(4)代词，他。

且举世誉之而不加劝(指宋荣子)众人匹之，不亦悲乎(指彭祖)(5)代词，这些。

之二虫又何知(6)动词，到，往。

奚以之九万里而南为2.而(1)连词，表修饰。

怒而飞/抟扶摇而上者九万里/决起而飞(2)连词，表转折。

而宋荣子犹然笑之/且举世誉之而不加劝/而彭祖乃今以久特闻(3)连词，表并列。

高三物理一轮知识点总结归纳【高三物理一轮知识点总结归纳】高三物理是整个高中物理学习的最后一个阶段，通过一轮的知识点总结归纳，可以更好地巩固和复习所学的物理知识，为高考做好准备。

本文将对高三物理的知识点进行分类和总结，帮助同学们温故知新，查漏补缺。

一、力学部分1. 力的平衡和合成力力的平衡条件、力的合成与分解2. 运动学基础运动的描述、位移与位移矢量、速度与速度矢量、加速度与加速度矢量3. 牛顿运动定律牛顿第一定律、牛顿第二定律、牛顿第三定律、力的合成与分解4. 运动学定律物体匀速圆周运动的运动学定律5. 动能与功率动能的定义、动能定理、功的定义、功率的定义6. 万有引力万有引力定律、重力、地球上自由落体运动7. 斜抛运动斜抛运动的特点、斜抛运动的基本公式、斜抛运动的轨迹二、热学部分1. 热力学基础温度与热平衡、热学温标、热量与焦耳2. 理想气体状态方程法则、气体的等温过程、绝热过程、多次与少次气体的状态方程3. 理想气体的定压定容过程定压过程的一般变化规律、定容过程的一般变化规律4. 等量热与等压热等量热的计算、等压热的计算5. 理想气体的等温过程理想气体等温过程的一般变化规律、理想气体等温过程的图像、理想气体等温线的特点和图像三、光学部分1. 光的折射与全反射光的折射定律、全反射的条件与现象2. 光的干涉与衍射光的干涉现象与应用、衍射现象与应用3. 光的波动性光的直线传播、光的反射、光的折射四、电学部分1. 电流与电阻电流的基本概念、电阻的基本概念、欧姆定律、电阻与导线的长度、材料、截面积之间的关系2. 平衡态电路串联电路、并联电路、电阻定律、电功与电能、电功率与电耗3. 电源及其内部电阻电源的种类及特点、电源的电动势、电源的内阻、电源失效条件4. 静电场静电场的基本概念、静电场的性质、静电势的基本概念和计算五、原子物理与核物理部分1. 粒子与电磁场电子的性质、质子和负电子的荷质比、质子的性质、粒子的运动2. 原子核的结构原子核的组成、原子核的尺寸、原子核的质量与质子数关系、同位素与同位素的应用3. 活动粒子的辐射现象反衰变与衰变、粒子的发射与吸收以上是高三物理一轮知识点的简要总结和归纳，希望对同学们的复习有所帮助。

高三数学第一轮复习知识点高三学生在备战期末考试时，数学科目无疑是他们必须重点复习的科目之一。

为了帮助同学们更好地复习，下面将罗列出高三数学第一轮复习的重点知识点。

希望同学们能够认真学习并熟练掌握这些知识点，为期末考试打下坚实的基础。

1. 数列与数列的表示方法数列是指按一定顺序排列的一组数，包括等差数列、等比数列、递推数列等。

同学们在复习数列时，要了解数列的概念、性质以及应用。

掌握数列的各种表示方法，并能够准确地求解数列中的各个元素。

2. 函数及其表示函数是描述两个变量之间关系的一种工具，包括线性函数、二次函数、指数函数、对数函数等。

同学们需要熟悉函数的概念、图像、性质以及函数的运算法则。

在复习过程中，要能够准确地表示函数，并能够根据函数的性质进行函数的运算与分析。

3. 三角函数三角函数是描述角度之间关系的一种工具，包括正弦函数、余弦函数、正切函数等。

同学们在复习三角函数时，需要掌握三角函数的定义、性质以及相关的基本公式。

熟练使用三角函数解决各种与角度、三角恒等式相关的问题。

4. 平面向量平面向量是描述平面上有大小和方向的量，包括向量的定义、向量的运算、向量的数量积等。

同学们需要了解向量在平面几何中的应用，并能够准确地进行向量的运算与分析。

5. 概率统计概率统计是一种研究随机事件发生的可能性以及收集、整理和分析数据的方法和工具。

同学们需要了解概率与统计的基本概念、概率与统计的基本原理，并能够应用概率统计解决实际问题。

以上就是高三数学第一轮复习的知识点，同学们在复习过程中，要注重理解与记忆，多做相关的练习题，加深对知识点的理解和应用能力。

同时，要保持良好的复习习惯，制定合理的学习计划，合理分配时间，提高学习效率。

相信通过努力与坚持，同学们一定能够在期末考试中取得优异的成绩。

加油！。

第一轮复习知识——原始社会时期（中华文明的起源）（通史）【时空坐标】旧石器时代新石器时代（能人、立人、智人）距今170万年距今约110—115万年前距今约70—20万年距今1万年约7000—5000年前（元谋人）（蓝田人）（北京人）（进入新石器时代）（仰韶文化、大汶文化、河姆渡文化）传说时代约5000年前三皇五帝公元前2070年（龙山文化、红山文化、良渚文化）夏朝建立【阶段特征】（约300万或170万年前～前2070年）中华文明多元起源，奠定了中华民族多元一体的发展基础。

(1)政治上：原始社会组织经历了原始人群、母系氏族社会和父系氏族社会三个阶段。

新石器时代晚期阶级分化明显，出现了权贵阶层，开始向早期国家过渡。

原始社会晚期盛行禅让制。

(2)经济上：经历了旧石器时代、新石器时代。

原始农业出现，旧石器晚期生产力十分低下，以刀耕火种为耕作方式，共同劳动，成果共享。

新石器晚期，贫富分化出现，私有制产生。

(3)文化上：原始宗教和图腾崇拜出现，原始艺术产生。

新石器时代形成了各具特色的地域文化。

【具体知识点】一、旧石器时代——中华先民的出现（1）概念：指以打制方法制作石器的时代。

（2）代表性文化遗址：距今约170万年的元谋人；距今约110万年的蓝田人和距今约70万至20万年的北京人。

（3）遗址分布特点：沿河分布、满天星斗、本土化发展。

（4）生产工具：能以打制方法制作简单工具，如打制石器；山顶洞人制作骨针。

（5）生产方式：渔猎、采集、驯化动物。

（6）生活方式：群居、迁徙、已经学会用火。

（7）居住环境：穴居、巢居、半穴居。

（8）社会形态：原始人群和母系氏族。

（9）交通状况：足迹路的形成。

二、新石器时代——中华文明的诞生（1）概念：是指以磨制方法制作石器的时代。

早期晚期时间距今约7 000至5 000年前距今约5 000年到前2070年代表仰韶文化大汶口文化河姆渡文化龙山文化红山文化良渚文化分布黄河中游黄河下游长江下游黄河流域辽河上游长江下游特征手工业：典型器物是彩绘陶器农业：以粟为主要栽培作物分为早、中、晚3期。

高三数学第一轮复习-知识点高中数学一轮复习知识点第一章-集合考试内容：集合、子集、补集、交集、并集．逻辑联结词．四种命题．充分条件和必要条件．考试要求：（1）理解集合、子集、补集、交集、并集的概念；了解空集和全集的意义；了解属于、包含、相等关系的意义；掌握有关的术语和符号，并会用它们正确表示一些简单的集合．（2）理解逻辑联结词“或”、“且”、“非”的含义理解四种命题及其相互关系；掌握充分条件、必要条件及充要条件的意义．§01.集合与简易逻辑知识要点一、知识结构:本章知识主要分为集合、简单不等式的解法（集合化简）、简易逻辑三部分：二、知识回顾：（一）集合1.基本概念：集合、元素；有限集、无限集；空集、全集；符号的使用.2.集合的表示法：列举法、描述法、图形表示法.集合元素的特征：确定性、互异性、无序性.集合的性质：①任何一个集合是它本身的子集，记为AA；②空集是任何集合的子集，记为A；③空集是任何非空集合的真子集；如果AB，同时BA，那么A=B.如果AB，BC，那么AC.[注]：①Z={整数}（√）②已知集合S中A的补集是一个有限集，则集合A也是有限集.（某）（例：S=N；A=N，则CA={0}）③空集的补集是全集.④若集合A=集合B，则CBA=，CAB=CS（CAB）=D（注：CAB=）.3.①{（某，y）|某y=0，某∈R，y∈R}：坐标轴上的点集.②{（某，y）|某y＜0，某∈R，y∈R：二、四象限的点集.第1页共73页③{（某，y）|某y＞0，某∈R，y∈R}：一、三象限的点集.[注]：①对方程组解的集合应是点集.例：某y3解的集合{(2，1)}.2某3y12②点集与数集的交集是.（例：A={(某，y)|y=某+1}B={y|y=某+1}则A∩B=）4.①n个元素的子集有2个.②n个元素的真子集有2－1个.③n个元素的非空真子n集有2－2个.5.⑴①一个命题的否命题为真，它的逆命题一定为真.否命题逆命题.②一个命题为真，则它的逆否命题一定为真.原命题逆否命题.例：①若ab5，则a2或b3应是真命题.解：逆否：a=2且b=3，则a+b=5，成立，所以此命题为真.②某1且y2，某y3.解：逆否：某+y=3某1且y2nn某=1或y=2.某y3,故某y3是某1且y2的既不是充分，又不是必要条件.⑵小范围推出大范围；大范围推不出小范围.3.例：若某5，某5或某2.4.集合运算：交、并、补.交：AB{某|某A,且某B}并：AB{某|某A或某B}补：CUA{某U,且某A}5.主要性质和运算律（1）包含关系：AA,A,AU,CUAU,AB,BCAC;ABA,ABB;ABA,ABB.（2）等价关系：ABA（3）集合的运算律：交换律：ABBA;ABBA.BAABBCBUUA结合律:(AB)CA(BC);(AB)CA(BC)分配律:.A(BC)(AB)(AC);A(BC)(AB)(AC)0-1律：A,AA,UAA,UAU等幂律：AAA,AAA.求补律：A∩CUA=φA∪CUA=UCUU=φCUφ=U反演律：CU(A∩B)=(CUA)∪(CUB)CU(A∪B)=(CUA)∩(CUB)6.有限集的元素个数第2页共73页定义：有限集A的元素的个数叫做集合A的基数，记为card(A)规定card(φ)=0.基本公式：(1)card(AB)card(A)card(B)card(AB)(2)card(ABC)card(A)card(B)c ard(C)card(AB)card(BC)card(Ccard(ABC)A)(3)card(UA)=card(U)-card(A)(二)含绝对值不等式、一元二次不等式的解法及延伸1.整式不等式的解法根轴法（零点分段法）①将不等式化为a0(某-某1)(某-某2)…(某-某m)>0(<0)形式，并将各因式某的系数化“+”；(为了统一方便)②求根，并在数轴上表示出来；③由右上方穿线，经过数轴上表示各根的点（为什么？）；④若不等式（某的系数化“+”后）是“>0”,则找“线”在某轴上方的区间；若不等式是“<0”,则找“线”在某轴下方的区间.某1某2某3某m-3-某m-2某m-1+-某m+某（自右向左正负相间）则不等式a0某a1某nn1a2某n2an0(0)(a00)的解可以根据各区间的符号确定.2特例①一元一次不等式a某>b解的讨论；②一元二次不等式a某+b 某+c>0(a>0)解的讨论.000二次函数ya某2b某c（a0）的图象一元二次方程有两相异实根有两相等实根无实根a某2b某c0a0的根a某2b某c0(a0)的解集a某2b某c0(a0)的解集某1,某2(某1某2)b某1某22a某某某或某某12b某某2aR某某1某某2第3页共73页2.分式不等式的解法（1）标准化：移项通分化为f(某)f(某)f(某)f(某)>0(或<0)；≥0(或≤0)的形式，g(某)g(某)g(某)g(某)（2）转化为整式不等式（组）3.含绝对值不等式的解法f(某)f(某)f(某)g(某)00f(某)g(某)0;0g(某)0g(某)g(某)（1）公式法：a某bc,与a某bc(c0)型的不等式的解法.（2）定义法：用“零点分区间法”分类讨论.（3）几何法：根据绝对值的几何意义用数形结合思想方法解题.4.一元二次方程根的分布2一元二次方程a某+b某+c=0(a≠0)（1）根的“零分布”：根据判别式和韦达定理分析列式解之.（2）根的“非零分布”：作二次函数图象，用数形结合思想分析列式解之.（三）简易逻辑1、命题的定义：可以判断真假的语句叫做命题。