
圆锥曲线压轴题提升练(解析)
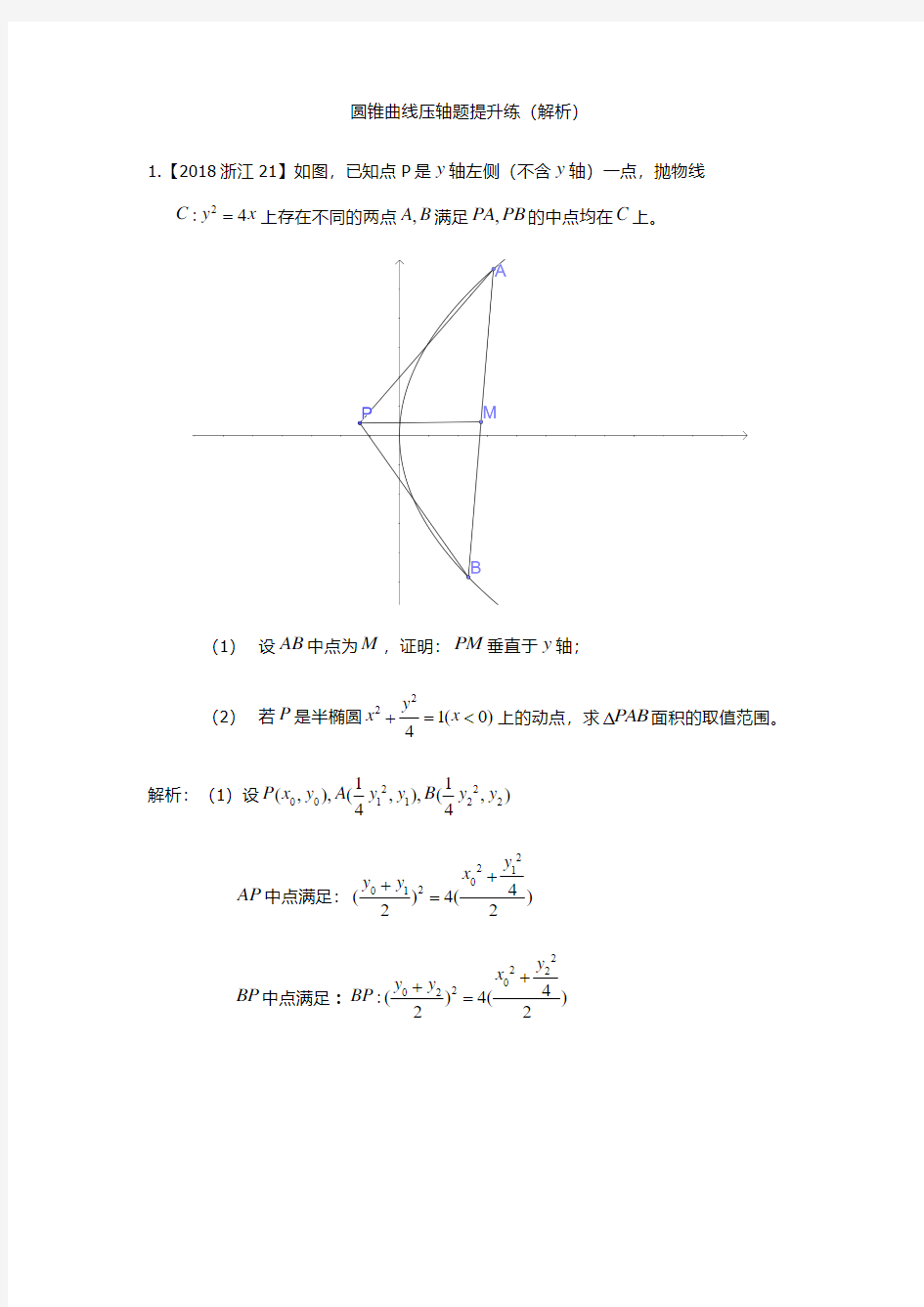
1.【2018浙江21】如图,已知点P 是y 轴左侧(不含y 轴)一点,抛物线
2:4C y x =上存在不同的两点,A B 满足,PA PB 的中点均在C 上。
(1) 设AB 中点为M ,证明:PM 垂直于y 轴;
(2) 若P 是半椭圆2
2
1(0)4
y x x +=<上的动点,求PAB ?面积的取值范围。 解析:(1)设2200112211(,),(,),(,)44
P x y A y y B y y
AP 中点满足:2
2
102014(
)4()22
y x y y ++= BP 中点满足:2
2
202024:(
)4()22
y x y y BP ++=
所以12,y y 是方程2
2
0204()4()22
y x y y ++=即22000
280y y y x y -+-=的两个根,所以
12
02
y y y +=,故PM 垂直于y 轴。 (2)由(1)可知212012002,8y y y y y x y +=?=-
所以222
1200013||()384
PM y y x y x =+-=
-
,12||y y -=
因此,3
2212001||||4)24
PAB
S PM y y y x ?=?-=- 因为2
2
0001(0)4
y x x +=<,所以2200004444[4,5]y x x x -=--+∈ 因此,PAB ?
面积的取值范围是 1. 距离型问题
2.【2018全国3 理20】已知斜率为k 的直线l 与椭圆22
:
143
x y C +=交于,A B 两点,线段AB 的中点为(1,)(0)M m m >
(1)证明:12
k <-
; (2)设F 为C 的右焦点,P 为C 上一点且0FP FA FB ++=,证明:,,FP FA FB 为等差数列,并求出该数列的公差。
解析:(1)由中点弦公式22OM
b k k a ?=-,解得34k m
=-
又因为点M 在椭圆内,故302
m <<
,故1
2k <-
(2)由题意知2,2FA FB FM FP FM +==-,故(1,2)P m -
因为点P 在椭圆上,代入可得3,14m k =
=-,即3
||2
FP = 根据第二定义可知,1211||2,||222
FA x FB x =-
=- 121
||||4()2
FA FB x x +=-+
联立22
212121114371402,4287
4
x y x x x x x x y x ?+=???-+=?+==?
?=-+?? 即121
||||4()32
FA FB x x +=-
+= 故满足2||||||FP FA FB =+,所以,,FP FA FB 为等差数列
设其公差为d ,因为,A B 的位置不确定,则有
1212||||||||2d FA FB x x =±-=±-=
代入得2,1428
d d =±
=± 3.【2018全国3 文20】已知斜率为k 的直线l 与椭圆22
:
143
x y C +=交于,A B 两点,线段AB 的中点为(1,)(0)M m m >
(1)证明:12
k <-
; (2)设F 为C 的右焦点,P 为C 上一点且0FP FA FB ++=,证明
2||||||FP FA FB =+。
解析:(1)设1122(,),(,)A x y B x y ,则
222211221,14343
x y x y +=+=,因为2121y y k x x -=- 两式相减可得:
1212
043
x x y y k +++= 又因为
1212
1,22
x x y y m ++==即12122,2x x y y m +=+=代入上式得 34k m =-
,又因为点M 在椭圆内,故302
m <<,故12k <-
(2)(1,0)F ,设33(,)P x y ,
3311220(1,)(1,)(1,)0FP FA FB x y x y x y ++=?-+-+-=即
3123123()1,()2x x x y y y m =-+==-+=- 因为点P 在椭圆上,代入得
3
4
m =
,所以33(1,),||22P FP -=
因为1||(22x FA x ==-
,同理得2||22
x FB =- 故121
||||4()32
FA FB x x +=-
+= 所以2||||||FP FA FB =+
注意:文理科题目相同,但是给出的解题思路是不同的。
4.【2018天津 理19】设椭圆22
221x y a b
+=的左焦点为F ,上顶点为B .已知椭圆的离心
率为
3
,点A 的坐标为(,0)b ,且||||FB AB ?= (1)求椭圆的方程;
(2)设直线:(0)l y kx k =>与椭圆在第一象限的交点为P ,且l 与直线AB 交于点
Q ,若
||sin ||4
AQ AOQ PQ =∠(O 为原点),求k 的值。
解析:(1)由题意知:
222
2
2259
c a b e a a -===,解得23a b =,又因为||,||FB a AB ==
由||||FB AB ?=知6ab =,解得3,2a b ==
故椭圆方程为22
194
x y += (2)设1122(,),(,)P x y P x y
,则12
2||,||sin y y PQ AQ AOQ
-=
=∠
21212||5
59||4
y AQ AOQ y y PQ y y =∠?=?=- (得到一个等量关系,然后用k 分别表示出12,y y )
联立22212,2
1194y kx
y kx k y y x y y x k =?=???=?=??=-+++=???
181k k =
+,解得12k =或11
28
k = 5.【2018江苏 18】如图,在平面直角坐标系xoy 中,椭圆C
过点1
)2
,焦点
12(F F ,圆O 的直径为12F F 。
(1)求椭圆C 及圆O 的方程;
(2)设直线l 与圆O 相切于第一象限内的点P
(i )设直线l 与椭圆C 有且只有一个公共点,求点P 的坐标; (ii )直线l 与椭圆C 交于,A B 两点.若OAB ?
,求直线l 的方程。
解析:(1)设椭圆方程为22221x y a b +=
,其中c =
1
)2
在椭圆上,故
222
2223114413
a a b
b a b ??+==?????=???-=?
,所以椭圆C 的方程为2214x y += 又因为圆O 的直径为12F F ,故圆的方程为223x y += (2)(i )本题有两种解法:
法一:椭圆和圆有公切线时求点P 的坐标,可先设公切线方程为y kx b =+ 然后根据直线分别与圆和椭圆相切求出,k b 的值,再求出点P 的坐
标,这个方法很容易想到,但是需要两次计算相切时的条件。
法二:题目中让求点P 的坐标,不如一开始就设出点P 的坐标,利用点P 的
坐标表示出切线方程,然后直线与椭圆联立,0?=即可求出点P 的坐标。这里我们选用第二种方法:
设直线与圆的切点00(,)P x y ,则满足22003x y +=,故直线l 的方程为: 0000
()x y y x x y -=-
-即0003x y x y y =-+
联立022*********
23(4)24364014
x y x y y x y x x x y x y ?
=-+??
?+-+-=??+=?? (1)
因为直线l 与椭圆有且只有一个交点,故0?=,即 222222000000(24)4(4)(364)48(2)0x x y y y x ?=--+-=-=
因为点P 位于第一象限,即000,0x y >>
,故001x y == 所以点P
的坐标为
(ii )分析:第二问由于OAB ?的高即为圆的半径,故由面积可以得出弦长
AB 的值,根据弦长再求出直线方程,最容易想到的就是设出直线方程
y kx b =+,根据直线与圆相切可得2233b k =+,然后直线与椭圆联立,根据
韦达定理写出弦长公式,将k 或b 转化成一个,求出即可,但是计算过程很麻烦,下面给出同一个方法的两种不同解法:
解析:设直线方程为y kx b =+,1122(,),(,)A x y B x y ,根据直线与圆相切得
2233b k =+
222
22
(14)844014y kx b k x kbx b x y =+???+++-=?+=?? 2121222
844
,1414kb b x x x x k k -+=-=++
||7
AB ===
将2
2
33b k =+
=
注意此处,根据韦达定理得出的两根和与积的形式本来很复杂,如果利用上式还需要进行平方,再将b 转化为k 的形式计算起来相当复杂,因此我们要想办法避开平方,因此不如直接根据直线与椭圆联立的方程解出两根,再利用弦长公式,就可以避开平方的出现,解法也会简单一些。
2
2
2
1,228(14)84402(14)
kb k x kbx b x k -+++-=?=
+
122
2||4141
x x k k -==++
122
|||417
AB x x k =-==+解得22
5,18k b ==
所以k b ==
y =+
5.定值问题
6.【2018全国1 理】设椭圆2
2:12
x C y +=的右焦点为F ,过F 的直线l 与C 交于,A B 两点,点M 的坐标为(2,0)
(1)当l 与x 轴垂直时,求直线AM 的方程; (2)设O 为坐标原点,证明:OMA OMB ∠=∠
分析:第二问两角度相等如何证明?解析几何中常出现的量无非是距离长度,斜率,
面积,周长,如果你想到了证明两个角余弦值相等,那么恭喜你,你想到了长度,但是长度不容易求得,本题目M 点在x 轴上且角度均从O 点出发,,A B 两点一个在x 轴上方一个在下方,因此可以考虑两条直线关于x 轴对称,而对称又反应了斜率互为相反数的关系,因此本题目虽是证明题的形式出现,但本质上是求定值问题,即120k k +=
解析:(1)由题意知(1,0)F ,当l 与x 轴垂直时,:1l x =,此时(1,2
A ±
,所以直
线AM 的方程为2)y x =- (2)设直线,AM BM 的斜率分别为12,k k
当直线l 斜率不存在时,此时直线,AM BM 的倾斜角互补,则OMA OMB ∠=∠
当直线l 斜率存在时,设1122:(1),(,),(,)l y k x A x y B x y =-
联立2
222221(21)42202(1)x y k x k x k y k x ?+=??+-+-=??=-?
22121222422
,2121
k k x x x x k k -+==++
所以1212121212121212(1)(1)[23()4]
2222(2)(2)
y y k x k x k x x x x k k x x x x x x ---+++=
+=+=------ (注意,此处为什么不需要整理分母部分,因为证明分式为零,只需要证明分子为零即可)
所以222
212122(22)12[4]21210(2)(2)
k k k k k k k x x --++++=
=-- 所以直线,AM BM 的倾斜角互补,则OMA OMB ∠=∠
7.【2018全国1 文20】设抛物线2:2C y x =,点(2,0),(2,0)A B -,过点A 的直线l 与C 交于,M N 两点
(1)当l 与x 轴垂直时,求直线BM 的方程; (2)证明:ABM ABN ∠=∠
解析:(1)当l 与x 轴垂直时,:2l x =,此时(2,2)B ±,直线BM 的方程为
1
(2)2
y x =±+
(2)具体过程可以参考32题,在上题中是分情况讨论直线斜率不存在与存在的情况,其实无需讨论斜率是否存在,可以直接将直线方程设为2x my =+ 设:2l x my =+,直线,BM BN 的斜率分别为12,k k 联立212122
2
2402,42x my y my y y m y y y x
=+??--=?+==-?
=?
所以12121212121224()
022(4)(4)
y y my y y y k k x x my my +++=
+==++++ 所以直线,AM BM 的倾斜角互补,则OMA OMB ∠=∠
8.【2018全国3 理16】已知点(1,1)M -和抛物线2:4C y x =,过C 的焦点且斜率为
k 的直线与抛物线交于,A B 两点,若90ABM ?∠=,则k =________.
解析:用到结论:在抛物线中以焦点弦为直径的圆与准线相切 所以1N M y y ==,设0(,1)N x ,根据焦点弦斜率公式可得
000
12
2AB ON AB AB p k k k k x x x ?=
??=?= 9.【2018北京 理 19】已知抛物线2:2C y px =经过点(1,2)P ,过点(0,1)Q 的直线l 与
抛物线C 有两个不同的交点,A B ,且直线PA 交y 轴于M ,直线PB 交y 轴于
N .
(1)求直线l 的斜率的取值范围;
(2)设O 为原点,,QM QO QN QO λμ==,求证:
1
1
λ
μ
+
为定值。
解析:(1)因为抛物线经过(1,2)P ,则2p =,抛物线方程为24y x =
由题意可知直线l 的斜率存在且不为0,设直线l 的方程为1(0)y kx k =+≠
由2224(24)101
y x
k x k x y kx ?=?+-+=?
=+? 22(24)410k k ?=--??>解得0k <或01k <<
又,PA PB 与y 轴相交,故直线l 不过点(1,2)-,故3k ≠-【最容易遗漏的地方】
所以直线l 斜率的取值范围是(,3)(3,0)(0,1)-∞-?-?
(2)第二问考察有关向量系数的定值问题,很显然需要将,λμ用,A B 两点的坐标表示出来然后在利用直线与抛物线联立即可,实际运算起来发现,λμ和
,M N 两点的纵坐标有关系,所以需要建立,A B 和,M N 坐标的关系,此时就需
要根据,A B 两点坐标大胆写出,PA PB 的直线方程,求出,M N 两点坐标即可,不要想什么便捷方法,怎么问怎么想就可以。
设1122(,),(,)A x y B x y ,由2224(24)101
y x
k x k x y kx ?=?+-+=?
=+? 121222
421
,k x x x x k k
-+=
= 直线PA 的方程为112
2(1)1
y y x x --=
--,令0x =得点M 的纵坐标为1111212211
M y kx y x x -+-+=+=+--,同理得N 点的纵坐标为
221
21N kx y x -+=
+-,由,QM QO QN QO λμ==得1,1M N y y λμ=-=- 所以
1212
111
1
11
11(1)(1)M N x x y y k x k x λ
μ
--+
=
+=+----
221212122
2242()112111
k x x x x k k k x x k k -+-+=?=?=-- 故
1
1
λ
μ
+
为定值。
10.【2018北京文 20】已知椭圆
22
22
:1(0)
x y
M a b
a b
+=>>
的离心率为
3
,焦距为,斜率为k的直线l与椭圆M有两个不同的交点,A B
(1)求椭圆M的方程;
(2)若1
k=,求||
AB的最大值;
(3)设(2,0)
P-,直线PA与椭圆M的另一个交点为C,直线PB与椭圆M的另一个交点为D,若,C D和点71
(,)
42
Q-共线,求k
解析:(1
)由题意知
2
21
3
2
c
a x
y
a
c
c
?
?=
=
??
??+=
??
=
?
??
=
?
(2)设
1122
:,(,),(,)
l y x m A x y B x y
=+
联立22
2
2
46330
1
3
y x m
x mx m
x
y
=+
?
?
?++-=
?
+=
??
2
1212
333
,
24
m m
x x x x
-
+=-=
令22
(6)44(33)0
m m
?=-??->,则24
m<
||
AB==
故当0
m=时,||
AB最大。
(3)题目给出共线,则用向量共线即可,但是需要知道,C D 两点的坐标,因此大胆设出,PA PB 的方程,求出,C D 的坐标(坐标与,A B 坐标产生关联之后即可)
设11223344(,),(,),(,),(,)A x y B x y C x y D x y ,又(2,0)P -,所以可设
1
112
PA y k k x ==
+,直线PA 的方程为:1(2)y k x =+ 12222
21112
(2)(13)12123013
y k x k x k x k x y =+???+++-=?+=?? 则2113211213k x x k +=-+即2
1312
1
1213k x x k =--+,又1112y k x =+,代入得13171247
x x x --=+
【注意此处也可以不转化,直接将3x 转化为11,x y 的形式,但是不如一开始就转化简单】 故1
3147
y y x =
+,1111712(
,)4747x y C x x --++,同理可得2222712(,)4747x y D x x --++ 故33447171(,),(,)4444
QC x y QD x y =+-=+-
因为,,Q C D 三点共线,所以34437171()()()()04444
x y x y +--+-= 将,C D 坐标代入化简可得
12
12
1y y x x -=-,即1k =
11.【2018天津文 19】椭圆22
221(0)x y a b a b
+=>>的右顶点为A ,上顶点为B 。已知
,||AB =(1)求椭圆的方程;
(2)设直线:(0)l y kx k =<与椭圆交于,P Q 两点,l 与直线AB 交于点M ,且点
,P M 均在第四象限,若BPM ?的面积是BPQ ?面积的2倍,求k 的值。
解析:(1)22
194
x y += (2)设1122(,),(,)P x y M x y
212||2||||4||5BPM BPQ S S PM PQ PM OQ x x ??=?=?=?=【需要的等量关
系】,接下来用k 表示出12,x x 即可
2623233y kx
x k y x =???=?+=-+??
,2
2119
4y kx x x y =???=?+=??
所以
632k =+89k =-或1
2k =- 当89k =-
时,120,0x x ><不符合题意,当1
2
k =-时,120,0x x >>符合题意,所以1
2
k =-
2. 极坐标与参数方程问题
12.【2018全国1 选做22】在直角坐标系xoy 中,曲线1C 的方程为1:||2C y k x =+,以坐标原点为极点,x 轴正半轴为极轴建立坐标系,曲线2C 的极坐标方程为
22cos 30ρρθ+-=
(1)求2C 的直角坐标方程;
(2)若1C 与2C 有且仅有三个公共点,求1C 的方程。 解析:(1)22230x y x ++-=
(2)||2y k x =+恒过(0,2)点,当0k ≥时不符合题意
当0k <时,2,0
()2,0
kx x f x kx x +≥?=?
-+
当0x <时,2y kx =-+与2C 恒有两个交点,所以只需当0x ≥时,2y kx =+与
2C 只有一个交点即可,联立
22
22
2(1)(42)10230y kx k x k x x y x =+??++++=?++-=?
令0?=解得4
3
k =-
所以1C 的方程为4
||23
y x =-
+ 13.【2018全国2 选修22】在直角坐标系xoy 中,曲线C 的参数方程为
2cos ()4sin x y θθθ=??=?为参数,直线l 的参数方程为1cos (t )2sin x t y t α
α=+??
=+?
为参数 (1)求C 和l 的直角坐标方程;
(2)若曲线C 截直线l 所得线段的中点坐标为(1,2),求l 的斜率。
解析:(1)曲线C 的直角坐标方程为
22
1416
x y += 当cos 0α≠时,l 的直角坐标方程为tan 2tan y x αα=?+- 当cos 0α=时,l 的直角坐标方程为1x =
(2)考察中点弦问题,因此可以利用中点弦求斜率公式,设中点坐标为
(1,2)M ,则2
2242OM
a k k k k b
?=-?=-?=-
常规做法如下:
将l 的参数方程代入C 的直角坐标方程,整理得关于t 的方程 22(13cos )4(2cos sin )80t t ααα+++-=
因为曲线C 截直线l 所得线段的中点(1,2)在C 内,故上式有两个解,设为
12,t t ,则120t t +=
又因为1224(2cos sin )
13cos t t ααα
++=-
+,故2cos sin 0αα+=
所以直线l 的斜率tan 2k α==-
【此处用到了直线的参数方程的两个用法之一】
14.【2018 全国3 选做22】在平面直角坐标系xoy 中,O 的参数方程为
cos ()sin x y θ
θθ
=??
=?为参数
,过点(0,且倾斜角为α的直线l 与O 交于,A B 两点 (1)求α的取值范围;
(2)求AB 中点P 的轨迹的参数方程。 解析:(1)当斜率不存在时,此时2
π
α=
符合要求
当斜率存在时,若要满足直线与圆相切只需要保证圆心到直线的距离小于半径
即可。
设直线:l y kx =
1(,1)(1,)d k =
根据正切函数图像可知3(,)(,
)42
24
ππππ
α∈?
综上可知3(,
)4
4
ππ
α∈
(2)可以用直线的普通方程来做,但是如果那样题目就失去意义了。既然是
中点,就应该想到直线的参数方程应用中关于中点的用法。、
设直线l
的参数方程为cos (t )sin x t y t α
α
=???=??是参数(3(,)44ππα∈)
将直线的参数方程代入221x y +=
得2
sin 10t α-+=
设P 点对应 的参数为P t
,故12
2
P t t t α+=
=
所以2cos 3((,))44P P x y αα
ππαα
?=?∈?
=??
所以点P
的轨迹方程为2sin 23((,))2
44P
P
x y αππαα
?=?∈??=?
3. 探究性问题
15.【2018 上海 20】设常数2t >,在平面直角坐标系xoy 中,已知点(2,0)F ,直线
:l x t =,曲线28(0,0)y x x t y Γ=≤≤≥:,l 与x 轴交于点A ,与Γ交于点B ,,P Q
分别是曲线Γ与线段AB 上的动点。 (1)用t 表示点B 到点F 的距离;
(2)设3t =,||2FQ =,线段OQ 的中点在直线FP 上,求AQP ?的面积; (3)设8t =,是否存在以,FP FQ 为邻边的矩形FPEQ ,使得点E 在Γ上?若存在求出点P 的坐标,若不存在说明理由。
解析:(1)点F 是抛物线的焦点,所以||22B BF x t =+=+ (2)从中点入手即可
因为||1,||2AF FQ ==
,所以||AQ =
Q ,则OQ 中点坐标为
3(,)22
,所以:2)PF y x =-,联立
2
2
2)23201206()38y x x x x x y x
?=-??-+=?==?=??或舍
所以1()2AQP Q P S AQ x x ?=
?-=
(3)
若存在这样的点E ,则E 点坐标符合抛物线方程,若能求出坐标且符合范围要求,则E 点存在。求E 点坐标时可以利用向量的平行四边形法则:FP FQ FE +=,因此需要求出,P Q 坐标,另外,P Q 两点为动点,但是,P Q 两点可以通过垂直产生关联,求出一个,另外一个就知道了
解析:假设存在这样的E 点,设2(,)8y P y ,则2816PF y
k y =-,所以2168QF y k y -=
216:(2)8y QF y x y -=
-,所以2
483(8,)4y Q y
- 根据FP FQ FE +=可得22
48(6,
)84y y E y
++,点E 在抛物线上,
22248()8(6)48y y y +=+,解得216,855
y y ==<,所以存在这样的E 点。
一、选择题 1. 圆锥曲线经典练习题及解答 大足二中 欧国绪 直线I 经过椭圆的一个顶点和一个焦点,若椭圆中心到 1 l 的距离为其短轴长的丄,则该椭圆 4 的离心率为 1 (A ) ( B ) 3 (C ) I (D ) 2. 设F 为抛物线 c : y 2=4x 的焦点, 曲线 k y= ( k>0)与C 交于点P , PF 丄x 轴,则k= x (B )1 3 (C)— 2 (D )2 3?双曲线 2 x C : T a 2 y_ 1(a 0,b 0)的离心率为2,焦点到渐近线的距离为 '、3,贝U C 的 焦距等于 A. 2 B. 2、2 C.4 D. 4?已知椭圆 C : 0)的左右焦点为 F i ,F 2,离心率为 丄3,过F 2的直线l 3 交C 与A 、 B 两点, 若厶AF i B 的周长为4、、3,则 C 的方程为() 2 A. x_ 3 B. 2 x 2彳 xr y 1 C. 2 x 12 D. 2 x 12 5. y 2 b 2 线的一个焦点在直线 2 A.— 5 6.已知 已知双曲线 2 x ~2 a 1( a 0, b 0)的一条渐近线平行于直线 I : y 2x 10,双曲 2 B — 20 2 为抛物线y 2 ' 1 20 F l 上, 2 y 5 则双曲线的方程为( 也 1 100 A , B 在该抛物线上且位于x 轴的两侧, c 3x 2 1 C.— 25 占 八、、 的焦点, uu uuu OA OB A 、2 (其中O 为坐标原点),则 - 1^/2 8 7.抛物线 =X 2的准线方程是 4 (A) y (B) 2 (C) ) D M 辽 .100 25 ABO 与 AFO 面积之和的最小值是( ) x 1 (D)
高中数学圆锥曲线压轴题集锦2 一.解答题(共60小题) 1.如图,F1(﹣c,0),F2(c,0)分别是双曲线C:=1(a,b>0)的左,右焦点,过点F2作x轴的垂线交双曲线的上半部分于点P,过点F1作直线PF1的垂线交直线l:x=﹣ 于点Q. (1)若点P的坐标为(4,6),求双曲线C的方程及点P处的切线方程; (2)证明:直线PQ与双曲线C只有一个交点; (3)若过l:x=﹣上任一点M作双曲线C:=1(a,b>0)的两条切线,切点分别为T1,T2,问:直线T1T2是否过定点,若过定点,请求出该定点;否则,请说明理由. 2.已知曲线C1:+=1(a>b>0,x≥0)和曲线C2:x2+y2=r2(x≥0)都过点A(0,﹣1),且曲线C1所在的圆锥曲线的离心率为 (1)求曲线C1,C2的方程 (2)设点B,C分别在曲线C1,C2上,k1,k2分别为直线AB,AC的斜率,当k2=4k1时, ①直线BC是否经过定点?请说明理由 ②设E(0,1),求||?||的最大值.
3.已知B(﹣1,0),C(1,0),P是平面上一动点,且满足||?||=?. (1)求点P(x,y)的轨迹C对应的方程. (2)如果点A(m,2)在曲线C上,过点A作曲线C的两条弦AD和AE,且AD⊥AE,问直线DE是否过定点?若过定点,求出该定点坐标;若不过定点,请说明理由. 4.已知F1、F2为椭圆C:的左,右焦点,M为椭圆上的动点,且? 的最大值为1,最小值为﹣2. (1)求椭圆C的方程; (2)过点作不与y轴垂直的直线l交该椭圆于M,N两点,A为椭圆的左顶点.试判断∠MAN是否为直角,并说明理由. 5.已知F1,F2分别是椭圆的左、右焦点F1,F2关于直线x+y﹣2=0的对称点是圆C的一条直径的两个端点. (Ⅰ)求圆C的方程; (Ⅱ)设过点F2的直线l被椭圆E和圆C所截得的弦长分别为a,b.当ab最大时,求直线l 的方程. 6.过抛物线E:x2=2py(p>0)的焦点F作斜率率分别为k1,k2的两条不同直线l1,l2,且k1+k2=2.l1与E交于点A,B,l2与E交于C,D,以AB,CD为直径的圆M,圆N(M,N为圆心)的公共弦所在直线记为l. (Ⅰ)若k1>0,k2>0,证明:; (Ⅱ)若点M到直线l的距离的最小值为,求抛物线E的方程. 7.如图,椭圆C:经过点P(1,),离心率e=,直线l的方程为x=4. (1)求椭圆C的方程; (2)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记PA,
圆锥曲线的综合问题 【考纲要求】 1.考查圆锥曲线中的弦长问题、直线与圆锥曲线方程的联立、根与系数的关系、整体代入 和设而不求的思想. 2.高考对圆锥曲线的综合考查主要是在解答题中进行,考查函数、方程、不等式、平面向 量等在解决问题中的综合运用. 【复习指导】 本讲复习时,应从“数”与“形”两个方面把握直线与圆锥曲线的位置关系.会判断已知直线与曲线的位置关系(或交点个数),会求直线与曲线相交的弦长、中点、最值、定值、点的轨迹、参数问题及相关的不等式与等式的证明问题. 【基础梳理】 1.直线与圆锥曲线的位置关系 判断直线l 与圆锥曲线C 的位置关系时,通常将直线l 的方程Ax +By +C =0(A 、B 不同时 为0)代入圆锥曲线C 的方程F (x ,y )=0,消去y (也可以消去x )得到一个关于变量x (或 变量y )的一元方程. 即?? ?==++0 ),(0y x F c By Ax ,消去y 后得02 =++c bx ax (1)当0≠a 时,设方程02 =++c bx ax 的判别式为Δ,则Δ>0?直线与圆锥曲线C 相交;Δ=0?直线与圆锥曲线C 相切;Δ<0?直线与圆锥曲线C 无公共点. (2)当0=a ,0≠b 时,即得一个一次方程,则直线l 与圆锥曲线C 相交,且只有一个交点, 此时,若C 为双曲线,则直线l 与双曲线的渐近线的位置关系是平行;若C 为抛物线, 则直线l 与抛物线的对称轴的位置关系是平行. 2.圆锥曲线的弦长 (1)定义:直线与圆锥曲线相交有两个交点时,这条直线上以这两个交点为端点的线段叫做 圆锥曲线的弦(就是连接圆锥曲线上任意两点所得的线段),线段的长就是弦长. (2)圆锥曲线的弦长的计算 设斜率为k (k ≠0)的直线l 与圆锥曲线C 相交于A ,B 两点,A (x 1,y 1),B (x 2,y 2),则|AB | =1+k 2 |x 1-x 2|=]4))[(1(212212x x x x k -++=a k ? ? +2 1=1+1 k 2·|y 1-y 2|. (抛物线的焦点弦长|AB |=x 1+x 2+p =2p sin 2 θ ,θ为弦AB 所在直线的倾斜角). 3、一种方法 点差法:在求解圆锥曲线并且题目中交代直线与圆锥曲线相交和被截的线段的中点坐标时,设出直线和圆锥曲线的两个交点坐标,代入圆锥曲线的方程并作差,从而求出直线的斜率,
专题3、圆锥曲线与垂心问题 从近几年圆锥曲线的命题风格看,既注重知识又注重能力,既突出圆锥曲线的本质特征。而现在圆锥曲线中面积、弦长、最值等几乎成为研究的常规问题。“四心”问题进入圆锥曲线,让我们更是耳目一新。因此在高考数学复习中,通过让学生研究三角形的“四心”与圆锥曲线的结合问题,快速提高学生的数学解题能力,增强学生的信心,备战高考. 三角形的垂心:三角形三条高线的交点 (1)、H 是ABC ?的垂心0HA BC HB AC HC AB ??=?=?=。 (2)、垂心到三角形一顶点距离为此三角形外心到此顶点对边距离得2倍。 经典例题: 例1.(2020·浙江高三)记椭圆C :2 2 21x y +=的左右焦点为1F ,2F ,过2F 的直线l 交椭圆于A ,B ,A , B 处的切线交于点P ,设12F F P 的垂心为H ,则PH 的最小值是( ) A B C D 例2.(2020.江苏省高三期中)已知12,F F 是双曲线22221(0,0)x y a b a b -=>>的左?右焦点,过点2F 且垂直于 实轴的直线与双曲线的两条渐近线分别相交于A ,B 两点,则坐标原点O 可能为1ABF ?的( ) A .垂心 B .内心 C .外心 D .重心 例3、(山东高考理)平面直角坐标系xoy 中,双曲线C 1:22 221(0,0)x y a b a b -=>>的渐近线与抛物线 22:2C x py =()0p >交于点O ,A ,B ,若OAB ?的垂心为C 2的焦点,则C 1的离心率为 . 例4、(2020年福建省高三联考16题)已知:椭圆22 184 x y +=的右焦点为,F M 为上顶点,O 为坐标原点, 直线l 交椭圆于,P Q 两点,当F 为PQM ?的垂心时,则PQM ?的面积为 . 例5、已知点()1,0Q 在椭圆C :2 2 12 y x +=上, 过点()0P m , 作直线交椭圆C 于点,,A B ABQ ?的垂心
高考圆锥曲线压轴题型汇总
————————————————————————————————作者:————————————————————————————————日期:
高考圆锥曲线压轴题型总结 直线与圆锥曲线相交,一般采取设而不求,利用韦达定理,在这里我将这个问题分成了三种类型,其中第一种类型的变式比较多。而方程思想,函数思想在这里也用得多,两种思想可以提供简单的思路,简单的说就是只需考虑未知数个数和条件个数,。使用韦达定理时需注意成立的条件。 题型4有关定点,定值问题。将与之无关的参数提取出来,再对其系数进行处理。 (湖北卷)设A 、B 是椭圆 λ=+223y x 上的两点,点N (1,3)是线段AB 的中点,线段AB 的垂直平分线与椭圆相交于C 、D 两点. (Ⅰ)确定λ的取值范围,并求直线AB 的方程; (Ⅱ)试判断是否存在这样的λ,使得A 、B 、C 、D 四点在同一个圆上?并说明理由. (I )解法1:依题意,可设直线AB 的方程为 λ=++-=2 23,3)1(y x x k y 代入,整理得 .0)3()3(2)3(222=--+--+λk x k k x k ① 设是方程则212211,),,(),,(x x y x B y x A ①的两个不同的根, 0])3(3)3([422>--+=?∴k k λ ② ) 3,1(.3) 3(2221N k k k x x 由且+-= +是线段AB 的中点,得 .3)3(,1222 1+=-∴=+k k k x x 解得k=-1,代入②得,λ>12,即λ的取值范围是(12,+∞). 于是,直线AB 的方程为.04),1(3=-+--=-y x x y 即 解法2:设则有),,(),,(2211y x B y x A .0))(())((33, 3212121212 2222121=+-++-??????=+=+y y y y x x x x y x y x λλ 依题意, . ) (3,2 12121y y x x k x x AB ++- =∴≠ . 04),1(3). ,12(.12313,)3,1(.1,6,2,)3,1(222121=-+--=-+∞∴=+?>-==+=+∴y x x y AB N k y y x x AB N AB 即的方程为直线的取值范围是在椭圆内又由从而的中点是λλΘ
(北师大版)高二数学《圆锥曲线》基础测试试题 一、选择题 1.已知椭圆 116 252 2=+y x 上的一点P 到椭圆一个焦点的距离为3,则P 到另一焦点距离为 ( ) A .2 B .3 C .5 D .7 2. 椭圆32x 2+16 y 2 =1的焦距等于( )。 A .4 B 。8 C 。16 D 。123 3.若椭圆的对称轴为坐标轴,长轴长与短轴长的和为18,焦距为6,则椭圆的方程为 ( ) A . 116922=+y x B .1162522=+y x C .1162522=+y x 或125 162 2=+y x D .以上都不对 4.动点P 到点)0,1(M 及点)0,3(N 的距离之差为2,则点P 的轨迹是 ( ) A .双曲线 B .双曲线的一支 C .两条射线 D .一条射线 5.设双曲线的半焦距为c ,两条准线间的距离为d ,且d c =,那么双曲线的离心率e 等于 ( ) A .2 B .3 C .2 D .3 6.抛物线x y 102=的焦点到准线的距离是 ( ) A .25 B .5 C .2 15 D .10 7. 抛物线y 2=8x 的准线方程是( )。 (A )x =-2 (B )x =2 (C )x =-4 (D )y =-2 8.已知抛物线的焦点是F (0,4),则此抛物线的标准方程是( ) (A )x 2=16y (B )x 2=8y (C )y 2=16x (D )y 2=8x 9.经过(1,2)点的抛物线的标准方程是( ) (A )y 2=4x (B )x 2= 21y (C ) y 2=4x 或x 2=2 1 y (D ) y 2=4x 或x 2=4y 10.若抛物线28y x =上一点P 到其焦点的距离为9,则点P 的坐标为 ( ) A .(7, B .(14, C .(7,± D .(7,-±
数学高考圆锥曲线压轴题经典预测 一、圆锥曲线中的定值问题 y2 = b2 (Ⅰ)求椭圆C的方程; (Ⅱ)如图,A,B,D是椭圆C的顶点,P是椭圆C上除顶点外的任意点,直线DP交x轴于点N直线AD交BP于点M,设BP的斜率为k,MN的斜率为m,证明2m-k为定值. y2 = b2
二、圆锥曲线中的最值问题 y2 = b2 (Ⅰ)求椭圆C的方程; (Ⅱ)过原点的直线与椭圆C交于A,B两点(A,B不是椭圆C的顶点).点D 在椭圆C上,且A D⊥AB,直线BD与x轴、y轴分别交于M,N两点. (i)设直线BD,AM的斜率分别为k1,k2,证明存在常数λ使得k1=λk2,并求出λ的值; (ii)求△OMN面积的最大值. ★★已知抛物线C:y2=2px(p>0)的焦点为F,A为C上异于原点的任意一点,过点A的直线l交C于另一点B,交x轴的正半轴于点D,且有|FA|=|FD|.当点A的横坐标为3时,△ADF为正三角形. (Ⅰ)求C的方程; (Ⅱ)若直线l1∥l,且l1和C有且只有一个公共点E, (ⅰ)证明直线AE过定点,并求出定点坐标;
(Ⅰ)求C1、C2的方程; (Ⅱ)过F1作C1的不垂直于y轴的弦AB,M为AB的中点,当直线OM与C2交于P,Q两点时,求四边形APBQ面积的最小值. 三、圆锥曲线与过定点(定直线)问题
四、圆锥曲线与求参数 ★★在平面直角坐标系xOy中,已知椭圆C的中心在原点O,焦点在x轴 (Ⅰ)求椭圆C的方程; 的中点,射线OE交椭圆C与点P,设OP→=tOE→,求实数t的值. 五、存在性问题 y2 = b2
②问直线l上是否存在点P,使得直线OA、OB、OC、OD的斜率k OA、k OB、k OC、k OD满足k OA+k OB+k OC+k OD=0?若存在,求出所有满足条件的点P的坐标;若不存在,说明理由. 六、轨迹方程
1. 平面上一点向二次曲线作切线得两切点,连结两切点的线段我们称切点弦.设过抛物线 22x py =外一点00(,)P x y 的任一直线与抛物线的两个交点为C 、D ,与抛物线切点弦AB 的交点为Q 。 (1)求证:抛物线切点弦的方程为00()x x p y y =+; (2)求证:112|||| PC PD PQ +=. 2. 已知定点F (1,0),动点P 在y 轴上运动,过点P 作PM 交x 轴于点M ,并延长MP 到点N ,且.||||,0PN PM PF PM ==? (1)动点N 的轨迹方程; (2)线l 与动点N 的轨迹交于A ,B 两点,若304||64,4≤≤-=?AB OB OA 且,求直线l 的斜率k 的取值范围. 3. 如图,椭圆13 4: 2 21=+y x C 的左右顶点分别为A 、B ,P 为双曲线134:222=-y x C 右支上(x 轴上方)一点,连AP 交C 1于C ,连PB 并延长交C 1于D ,且△ACD 与△PCD 的面积 相等,求直线PD 的斜率及直线CD 的倾斜角. 4. 已知点(2,0),(2,0)M N -,动点P 满足条件||||PM PN -=记动点P 的轨迹为W . (Ⅰ)求W 的方程;
(Ⅱ)若,A B 是W 上的不同两点,O 是坐标原点,求OA OB ?的最小值. 5. 已知曲线C 的方程为:kx 2+(4-k )y 2=k +1,(k ∈R) (Ⅰ)若曲线C 是椭圆,求k 的取值范围; (Ⅱ)若曲线C 是双曲线,且有一条渐近线的倾斜角是60°,求此双曲线的方程; (Ⅲ)满足(Ⅱ)的双曲线上是否存在两点P ,Q 关于直线l :y=x -1对称,若存在,求出过P ,Q 的直线方程;若不存在,说明理由。 6. 如图(21)图,M (-2,0)和N (2,0)是平面上的两点,动点P 满足: 6.PM PN += (1)求点P 的轨迹方程; (2)若2 ·1cos PM PN MPN -∠=,求点P 的坐标. 7. 已知F 为椭圆22221x y a b +=(0)a b >>的右焦点,直线l 过点F 且与双曲线 12 2 2=-b y a x 的两条渐进线12,l l 分别交于点,M N ,与椭圆交于点,A B . (I )若3 MON π∠= ,双曲线的焦距为4。求椭圆方程。 (II )若0OM MN ?=(O 为坐标原点),1 3 FA AN =,求椭圆的离心率e 。
) 圆锥曲线 一、填空题 1、对于曲线C ∶1 42 2-+-k y k x =1,给出下面四个命题: ①由线C 不可能表示椭圆; ②当1<k <4时,曲线C 表示椭圆; ③若曲线C 表示双曲线,则k <1或k >4; ④若曲线C 表示焦点在x 轴上的椭圆,则1<k <2 5 其中所有正确命题的序号为_____________. ? 2、已知椭圆)0(122 22>>=+b a b y a x 的两个焦点分别为21,F F ,点P 在椭圆上,且满 足021=?PF PF ,2tan 21=∠F PF ,则该椭圆的离心率为 3.若0>m ,点?? ? ??25,m P 在双曲线15422=-y x 上,则点P 到该双曲线左焦点的距离为 . 4、已知圆22:6480C x y x y +--+=.以圆C 与坐标轴的交点分别作为双曲线的一个焦点和顶点,则适合上述条件的双曲线的标准方程为 . 5、已知点P 是抛物线24y x =上的动点,点P 在y 轴上的射影是M ,点A 的坐标是 (4,a ),则当||a >4时,||||PA PM +的最小值是 . 6. 在ABC 中,7 ,cos 18 AB BC B ==- .若以A ,B 为焦点的椭圆经过点C ,则该椭圆的离心率e = . 7.已知ABC ?的顶点B ()-3,0、C ()3,0,E 、F 分别为AB 、AC 的中点,AB 和AC 边上的中线交于G ,且5|GF |+|GE |=,则点G 的轨迹方程为 8.离心率3 5 = e ,一条准线为x =3的椭圆的标准方程是 .
9.抛物线)0(42<=a ax y 的焦点坐标是_____________; 10将抛物线)0()3(42≠-=+a y a x 按向量v =(4,-3)平移后所得抛物线的焦点坐标为 . ^ 11、抛物线)0(12 <=m x m y 的焦点坐标是 . 12.已知F 1、F 2是椭圆2 2 22)10(a y a x -+=1(5<a <10=的两个焦点,B 是短轴的一个端 点,则△F 1BF 2的面积的最大值是 13.设O 是坐标原点,F 是抛物线)0(22>=p px y 的焦点,A 是抛物线上的一点, 与x 轴正向的夹角为60°,则||为 . 14.在ABC △中,AB BC =,7 cos 18 B =-.若以A B ,为焦点的椭圆经过点 C ,则该椭圆的离心率e = . 二.解答题 15、已知动点P 与平面上两定点(A B 连线的斜率的积为定值1 2 -. . (Ⅰ)试求动点P 的轨迹方程C. (Ⅱ)设直线1:+=kx y l 与曲线C 交于M 、N 两点,当|MN |=3 2 4时,求直线l 的方程.
一、圆锥曲线中的定值问题 y2 b2= (Ⅰ)求椭圆C的方程; (Ⅱ)如图,A,B,D是椭圆C的顶点,P是椭圆C上除顶点外的任意点,直线DP交x轴于点N直线AD交BP于点M,设BP的斜率为k,MN的斜率 为m,证明2m-k为定值. y2 b2= 线l的方程为x=4. (Ⅰ)求椭圆C的方程; (Ⅱ)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记PA,PB,PM的斜率分别为k1,k2,k3.问:是否存在常数λ,使得k1+k2=λk3?若存在,求λ的值;若不存在,说明理由. y2 b2= 过F1且垂直于x轴的直线被椭圆C截得的线段长为1. (Ⅰ)求椭圆C的方程; (Ⅱ)点P是椭圆C上除长轴端点外的任一点,连接PF1,PF2,设∠F1PF2的角平分线PM交C的长轴于点M(m,0),求m的取值范围; (Ⅲ)在(2)的条件下,过点P作斜率为k的直线l,使得l与椭圆C有且只有一个公共点,设直线PF1,PF2的斜率分别为k1,k2,若k≠0,试证 y2=1(a>0)的右焦点为F,点A,B分别在 C的两条渐近线AF⊥x轴,AB⊥OB,BF∥OA(O为坐标原点). (Ⅰ)求双曲线C的方程;
|NF| 定值,并求此定值. 二、圆锥曲线中的最值问题 y2 b2= (Ⅰ)求椭圆C的方程; (Ⅱ)过原点的直线与椭圆C交于A,B两点(A,B不是椭圆C的顶点).点D在椭圆C上,且A D⊥AB,直线BD与x轴、y轴分别交于M,N两点.(i)设直线BD,AM的斜率分别为k1,k2,证明存在常数λ使得k1=λk2,并求出λ的值; (ii)求△OMN面积的最大值. ★★已知抛物线C:y2=2px(p>0)的焦点为F,A为C上异于原点的任意一点,过点A的直线l交C于另一点B,交x轴的正半轴于点D,且有|FA|=|FD|.当点A的横坐标为3时,△ADF为正三角形. (Ⅰ)求C的方程; (Ⅱ)若直线l1∥l,且l1和C有且只有一个公共点E, (ⅰ)证明直线AE过定点,并求出定点坐标; (ⅱ)△ABE的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由. y2 b2=1(a>b>0)的左、右焦 y2 b2=1的左、右焦点分 (Ⅰ)求C1、C2的方程; (Ⅱ)过F1作C1的不垂直于y轴的弦AB,M为A B的中点,当直线OM与C2交于P,Q两点时,求四边形AP B Q面积的最小值.
圆锥曲线60道题 一.解答题(共60小题) 1.在平面直角坐标系中,已知椭圆C:+y2=1 (a>0,a≠1)的两个焦点分别是F1,F2, 直线l:y=kx+m(k,m∈R)与椭圆交于A,B两点. (1)若M为椭圆短轴上的一个顶点,且△MF1F2是直角三角形,求a的值; (2)若k=1,且△OAB是以O为直角顶点的直角三角形,求a与m满足的关系; (3)若a=2,且k OA?k OB=﹣,求证:△OAB的面积为定值. 2.已知椭圆(a>b>0)的左、右焦点分别为F1、F2,设点A(0,b),在△AF1F2中,,周长为. (1)求椭圆Γ的方程; (2)设不经过点A的直线l与椭圆Γ相交于B、C两点,若直线AB与AC的斜率之和为﹣1,求证:直线l过定点,并求出该定点的坐标; (3)记第(2)问所求的定点为E,点P为椭圆Γ上的一个动点,试根据△AEP面积S的不同取值范围,讨论△AEP存在的个数,并说明理由. 3.已知椭圆C1:=1(a>b>0)的左、右焦点分别为F1、F2,其中F2也是抛物线C2: y2=4x的焦点,M是C1与C2在第一象限的交点,且|MF2|=. (Ⅰ)求椭圆C1的方程; (Ⅱ)已知菱形ABCD的顶点A、C在椭圆C1上,顶点B,D在直线7x﹣7y+1=0上,求直线AC的方程. 4.已知F1(﹣2,0),F2(2,0),点P满足|PF1|﹣|PF2|=2,记点P的轨迹为E. (1)求轨迹E的方程;
(2)若直线l过点F2且与轨迹E交于P、Q两点. (i)无论直线l绕点F2怎样转动,在x轴上总存在定点M(m,0),使MP⊥MQ恒成立,求实数m的值. (ii)在(i)的条件下,求△MPQ面积的最小值. 5.在平面直角坐标平面中,△ABC的两个顶点为B(0,﹣1),C(0,1),平面内两点P、Q 同时满足: ①++=;②||=||=||;③∥. (1)求顶点A的轨迹E的方程; (2)过点F(,0)作两条互相垂直的直线l1,l2,直线l1,l2与点A的轨迹E的相交弦分别为A1B1,A2B2,设弦A1B1,A2B2的中点分别为M,N. (ⅰ)求四边形A1A2B1B2的面积S的最小值; (ⅱ)试问:直线MN是否恒过一个定点?若过定点,请求出该定点,若不过定点,请说明理由. 6.在平面直角坐标系xOy中,椭圆E:=1(a>b>0)的离心率为,焦距为2.(Ⅰ)求椭圆E的方程. (Ⅱ)如图,动直线l:y=k1x﹣交椭圆E于A,B两点,C是椭圆E上的一点,直线OC的 斜率为k2,且k1k2=,M是线段OC延长线上一点,且|MC|:|AB|=2:3,⊙M的半径为|MC|,OS,OT是⊙M的两条切线,切点分别为S,T,求∠SOT的最大值,并求取得最大值时直线l的斜率. 7.已知椭圆的中心在原点,焦点在x轴上,F1、F2分别为左、右焦点,椭圆的一个顶点与两焦点构成等边三角形,且||=2.
圆锥曲线综合练习 一、 选择题: 1.已知椭圆221102 x y m m +=--的长轴在y 轴上,若焦距为4,则m 等于( ) A .4 B .5 C .7 D .8 2.直线220x y -+=经过椭圆22 221(0)x y a b a b +=>>的一个焦点和一个顶点,则该椭圆的离心率为( ) A B .12 C .2 3 3.设双曲线22 219 x y a -=(0)a >的渐近线方程为320x y ±=,则a 的值为( ) A .4 B .3 C .2 D .1 4.若m 是2和8的等比中项,则圆锥曲线2 2 1y x m +=的离心率是( ) A B C D 5.已知双曲线22 221(00)x y a b a b -=>>,,过其右焦点且垂直于实轴的直线与双曲线交于M N , 两点,O 为坐标原点.若OM ON ⊥,则双曲线的离心率为( ) A B 6.已知点12F F ,是椭圆2 2 22x y +=的两个焦点,点P 是该椭圆上的一个动点,那么12||PF PF +u u u r u u u u r 的最小值是( ) A .0 B .1 C .2 D .7.双曲线221259 x y -=上的点到一个焦点的距离为12,则到另一个焦点的距离为( ) A .22或2 B .7 C .22 D .2 8.P 为双曲线22 1916 x y -=的右支上一点,M N ,分别是圆22(5)4x y ++=和22(5)1x y -+= 上的点, 则||||PM PN -的最大值为( ) A .6 B .7 C .8 D .9 9.已知点(8)P a ,在抛物线24y px =上,且P 到焦点的距离为10,则焦点到准线的距离为( ) A .2 B .4 C .8 D .16 10.在正ABC △中,D AB E AC ∈∈,,向量12DE BC =u u u r u u u r ,则以B C ,为焦点,且过D E ,的双曲线离心率为( ) A B 1 C 1 D 1 11.两个正数a b ,的等差中项是92,一个等比中项是a b >,则抛物线2b y x a =-的焦点坐标是( ) A .5(0)16- , B .2(0)5-, C .1(0)5-, D .1 (0)5 , 12.已知12A A ,分别为椭圆22 22:1(0)x y C a b a b +=>>的左右顶点,椭圆C 上异于12A A ,的点P
第五章压轴题秒杀 很多朋友留言说想掌握秒杀的最后一层。关于秒杀法的最难掌握的一层,便是对于高考数学压轴题的把握。压轴题,各省的难度不一致,但毫无疑问,尤其是理科的,会难倒很多很多很多人。 不过,压轴题并不是那般神秘难解,相反,出题人很怕很怕全省没多少做出来的,明白么?他很怕。那种思想,在群里面我也说过,在这里就不多啰嗦了。 想领悟、把握压轴题的思路,给大家推荐几道题目。 全是数学压轴题,且是理科(09的除山东的外我都没做过,所以不在推荐范围内)。 08全国一,08全国二,07江西,08山东,07全国一 一年过去了,很多题目都忘了,但这几道题,做过之后,虽然一年过去了,可脉络依然清晰。都是一些可以秒杀的典型压轴题,望冲击清华北大的同学细细研究。 记住,压轴题是出题人在微笑着和你对话。 具体的题目的“精”,以及怎么发挥和压榨一道经典题目的最大价值,会在以后的视频里面讲解的很清楚。 不过,我还是要说一下数列压轴题这块大家应该会什么(难度以及要求依次增高)\ 1:通项公式的求法(不甚解的去看一下以前的教案,或者问老师,这里必考。尤其推荐我押题的第一道数列解答题。) 2.:裂项相消(各种形式的都要会)、迭加、迭乘、错位相减求和(这几个是最基本和简单的数列考察方式,一般会在第二问考) 3:数学归纳法、不等式缩放 基本所有题目都是这几个的组合了,要做到每一类在脑中都至少有一道经典题想对应才行哦。 开始解答题了哦,先来一道最简单的。貌似北京的大多挺简单的。 这道题意义在什么呢?对于这道题在高考中出现的可能性我不做解释,只能说不大。意义在于,提醒大家四个字,必须必须必须谨记的四个字:分类讨论!!!!!!! 下面07年山东高考的这道导数题,对分类讨论的考察尤为经典,很具参考性,类似的题目在08、09、10年高考题中见了很多。 (22)(本小题满分14分) 设函数f(x)=x2+b ln(x+1),其中b≠0. (Ⅰ)当b> 时,判断函数f(x)在定义域上的单调性; (Ⅱ)求函数f(x)的极值点; (Ⅲ)证明对任意的正整数n,不等式ln( )都成立. 这道题我觉得重点在于前两问,最后一问..有点鸡肋了~ 这道题,太明显了对吧?
1. 已知点100(,)P x y 为双曲线 22 22 1(8x y b b b -=为正常数)上任一点,2F 为双曲线的右焦点,过1P 作右准线的垂线,垂足为A ,连接2F A 并延长交y 轴于点2P . (1)求线段12P P 的中点P 的轨迹E 的方程; (2)设轨迹E 与x 轴交于B ,D 两点,在E 上任取一点Q 111()(0)x y y ≠,,直线QB ,QD 分别交于y 轴于M ,N 两点.求证:以MN 2. 如图,已知圆G :2 2 2 (2)x y r -+=是椭圆2 216 x y +=1的内接ABC △的内切圆,其中A 为椭圆的左顶点. (1)求圆G 的半径r ; (2)过点M (0,1)作圆G 的两条切线交椭圆于E ,F 两点,证明:直线EF 与圆G 相切. x
3. 设点00(,)P x y 在直线(01)x m y m m =≠±<<,上,过点P 作双曲线22 1x y -=的两条切线,PA PB ,切点为,A B ,定点10M m ?? ??? ,. (1)过点A 作直线0x y -=的垂线,垂足为N ,试求AMN △的垂心G 所在的曲线方 程; (2)求证:A M B 、、三点共线. 4. 作斜率为1 3 的直线l 与椭圆22:1364x y C +=交于,A B 两点(如图所示), 且P 在直线l 的左上方. (1)证明:PAB ? 的内切圆的圆心在一条定直线上; (2)若60o APB ∠=,求PAB ?的面积. A x y O P B
5. 如图,椭圆22122:1(0)x y C a b a b +=>>的离心率为32,x 轴被曲线2 2:C y x b =-截得 的线段长等于1C 的长半轴长.(1)求1C ,2C 的方程;(2)设2C 与y 轴的焦点为M ,过坐标原点O 的直线l 与2C 相交于点A,B ,直线MA,MB 分别与1C 相交与,D E . ①证明:MD ME ⊥; ②记MAB ?,MDE ?的面积分别是1S ,2S .问:是否存在直线l ,使得121732 S S =?请说明理由. 6. 已知抛物线2 :4C y x =的焦点为F ,过点(1,0)K -的直线l 与C 相交于A 、B 两点,点A 关于x 轴的对称点为D . (1)证明:点F 在直线BD 上; (2)设8 9 FA FB =,求BDK ?的内切圆M 的方程 .
圆锥曲线综合测试题 一、选择题 1.如果22 2=+ky x 表示焦点在y 轴上的椭圆,那么实数k 的取值范围是( ) A .()+∞,0 B .()2,0 C .()+∞,1 D .()1,0 2.以椭圆116 252 2=+y x 的顶点为顶点,离心率为2的双曲线方程( ) A .1481622=-y x B .127922=-y x C .1481622=-y x 或127 92 2=-y x D .以上都不对 3.过双曲线的一个焦点2F 作垂直于实轴的弦PQ ,1F 是另一焦点,若∠21π= Q PF ,则双曲线的 离心率e 等于( ) A .12- B .2 C .12+ D .22+ 4.21,F F 是椭圆17 92 2=+y x 的两个焦点,A 为椭圆上一点,且∠02145=F AF ,则Δ12AF F 的面积为( ) A .7 B .47 C .2 7 D .257 5.以坐标轴为对称轴,以原点为顶点且过圆096222=++-+y x y x 的圆心的抛物线的方程() A .23x y =或23x y -= B .23x y = C .x y 92-=或23x y = D .23x y -=或x y 92= 6.设AB 为过抛物线)0(22>=p px y 的焦点的弦,则AB 的最小值为( ) A .2 p B .p C .p 2 D .无法确定 7.若抛物线x y =2上一点P 到准线的距离等于它到顶点的距离,则点P 的坐标为( ) A .1 (,)44± B .1(,84± C .1(,44 D .1(,84 8.椭圆124 492 2=+y x 上一点P 与椭圆的两个焦点1F 、2F 的连线互相垂直,则△21F PF 的面积为 A .20 B .22 C .28 D .24 9.若点A 的坐标为(3,2),F 是抛物线x y 22 =的焦点,点M 在抛物线上移动时,使MA MF +取得最小值的M 的坐标为( )
数学高考圆锥曲线压轴 题 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN
数学高考圆锥曲线压轴题经典预测一、圆锥曲线中的定值问题 ★★椭圆C:x2 a2+ y2 b2=1(a>b>0)的离心率e= 3 2,a+b=3. (Ⅰ)求椭圆C的方程; (Ⅱ)如图,A,B,D是椭圆C的顶点,P是椭圆C上除顶点外的任意点,直线DP交x轴于点N直线AD交BP于点M,设BP的斜率为k,MN的斜率为m,证明2m-k为定值. ★★如图,椭圆C:x2 a2+ y2 b2=1(a>b>0)经过点P(1, 3 2),离心率e= 1 2,直 线l的方程为x=4. (Ⅰ)求椭圆C的方程; (Ⅱ)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记PA,PB,PM的斜率分别为k1,k2,k3.问:是否存在常数λ,使得k1+k2=λk3若存在,求λ的值;若不存在,说明理由. ★★椭圆C:x2 a2+ y2 b2=1(a>b>0)的左右焦点分别是F1,F2,离心率为 3 2,过 F1且垂直于x轴的直线被椭圆C截得的线段长为1. (Ⅰ)求椭圆C的方程; (Ⅱ)点P是椭圆C上除长轴端点外的任一点,连接PF1,PF2,设∠F1PF2的角平分线PM交C的长轴于点M(m,0),求m的取值范围; (Ⅲ)在(2)的条件下,过点P作斜率为k的直线l,使得l与椭圆C有且只 有一个公共点,设直线PF1,PF2的斜率分别为k1,k2,若k≠0,试证明 1 kk1+ 1 kk2 为定值,并求出这个定值. - 2 -
二、圆锥曲线中的最值问题 +y2 b2=1( a>b>0)的离心率为 (Ⅰ)求椭圆C的方程; (Ⅱ)过原点的直线与椭圆C交于A,B两点(A,B不是椭圆C的顶点).点D在椭圆C上,且A D⊥AB,直线BD与x轴、y轴分别交于M,N两点.(i)设直线BD,AM的斜率分别为k1,k2,证明存在常数λ使得k1=λk2,并求出λ的值; (ii)求△OMN面积的最大值. - 3 -
数学高考圆锥曲线压轴题 Revised by Hanlin on 10 January 2021
数学高考圆锥曲线压轴题经典预测一、圆锥曲线中的定值问题 ★★椭圆C:x2 a2 + y2 b2 =1(a>b>0)的离心率e= 3 2 ,a+b=3. (Ⅰ)求椭圆C的方程; (Ⅱ)如图,A,B,D是椭圆C的顶点,P是椭圆C上除顶点外的任意点,直线DP交x轴于点N直线AD交BP于点M,设BP的斜率为k,MN的斜率为m,证明2m-k为定值. ★★如图,椭圆C:x2 a2 + y2 b2 =1(a>b>0)经过点P(1, 3 2 ),离心率e= 1 2 ,直 线l的方程为x=4. (Ⅰ)求椭圆C的方程; (Ⅱ)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记PA,PB,PM的斜率分别为k1,k2,k3.问:是否存在常数λ,使得k1+k2=λk3若存在,求λ的值;若不存在,说明理由. ★★椭圆C:x2 a2 + y2 b2 =1(a>b>0)的左右焦点分别是F1,F2,离心率为 3 2 , 过F1且垂直于x轴的直线被椭圆C截得的线段长为1. (Ⅰ)求椭圆C的方程; (Ⅱ)点P是椭圆C上除长轴端点外的任一点,连接PF1,PF2,设∠F1PF2的角平分线PM交C的长轴于点M(m,0),求m的取值范围;
(Ⅲ)在(2)的条件下,过点P作斜率为k的直线l,使得l与椭圆C有且 二、圆锥曲线中的最值问题 y2 = b2 (Ⅰ)求椭圆C的方程; (Ⅱ)过原点的直线与椭圆C交于A,B两点(A,B不是椭圆C的顶点).点D 在椭圆C上,且A D⊥AB,直线BD与x轴、y轴分别交于M,N两点. (i)设直线BD,AM的斜率分别为k1,k2,证明存在常数λ使得k1=λk2,并求出λ的值; (ii)求△OMN面积的最大值. ★★已知抛物线C:y2=2px(p>0)的焦点为F,A为C上异于原点的任意一点,过点A的直线l交C于另一点B,交x轴的正半轴于点D,且有|FA|= |FD|.当点A的横坐标为3时,△ADF为正三角形. (Ⅰ)求C的方程; (Ⅱ)若直线l1∥l,且l1和C有且只有一个公共点E, (ⅰ)证明直线AE过定点,并求出定点坐标; (ⅱ)△ABE的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
经典例题精析 类型一:求曲线的标准方程 1. 求中心在原点,一个焦点为且被直线截得的弦AB的中点横 坐标为的椭圆标准方程. 思路点拨:先确定椭圆标准方程的焦点的位置(定位),选择相应的标准方程,再利用待定系数法确定、(定量). 解析: 方法一:因为有焦点为, 所以设椭圆方程为,, 由,消去得, 所以 解得 故椭圆标准方程为 方法二:设椭圆方程,,, 因为弦AB中点,所以, 由得,(点差法) 所以 又
故椭圆标准方程为. 举一反三: 【变式】已知椭圆在x轴上的一个焦点与短轴两端点连线互相垂直, 且该焦点与长轴上较近的端点的距离为.求该椭圆的标准方程. 【答案】依题意设椭圆标准方程为(), 并有,解之得,, ∴椭圆标准方程为 2.根据下列条件,求双曲线的标准方程. (1)与双曲线有共同的渐近线,且过点; (2)与双曲线有公共焦点,且过点 解析: (1)解法一:设双曲线的方程为 由题意,得,解得, 所以双曲线的方程为 解法二:设所求双曲线方程为(),
将点代入得, 所以双曲线方程为即 (2)解法一:设双曲线方程为-=1 由题意易求 又双曲线过点,∴ 又∵,∴, 故所求双曲线的方程为. 解法二:设双曲线方程为, 将点代入得, 所以双曲线方程为. 总结升华:先根据已知条件确定双曲线标准方程的焦点的位置(定位),选择相应的标准方程,再利用待定系数法确定、.在第(1)小题中首先设出共渐近线的双曲线系方程. 然后代点坐标求得方法简便.第(2)小题实轴、虚轴没有唯一给出.故应答两个标准方程. (1)求双曲线的方程,关键是求、,在解题过程中应熟悉各元素(、、、及 准线)之间的 关系,并注意方程思想的应用. (2)若已知双曲线的渐近线方程,可设双曲线方程为 (). 举一反三: 【变式】求中心在原点,对称轴在坐标轴上且分别满足下列条件的双曲线的标准方程. (1)一渐近线方程为,且双曲线过点.
专题01曲线和方程 训练篇 B 1.已知A ,B 为双曲线E 的左,右顶点,点M 在E 上,?ABM 为等腰三角形,且顶角为120,则E 的离心率为 A.5 B.2 C.3 D.2 分析 要求e ,不一定要清楚a 和c ,可以求出a ,c 之间的关系,在转化为e 的方程或等式. 解1 设双曲线方程为22 221(0,0)x y a b a b -=>>. 如图所示,||||AB BM =,120ABM ∠=,过点M 作MN x ⊥轴,垂足为N ,在△BMN 中,由于|BM |=|AB |=2a ,则||BN a =, ||3MN a =,故点M 的坐标为(2,3)M a a ,代入双曲线方程得 2 2 2 2 a b c a ==-,即2 2 2c a =,所以2e =. 解2 如图所示,不妨设点M 在第一象限,则直线AM 的方程 3:()AM l y x a =+,直线BM 的方程:3()BM l y x a =-,联立解得23x a y a =???=??,所以点 M 的坐标为(2,3)M a a ,以下同解1. 2.双曲线22 221(0,0)x y a b a b -=>>的渐近线为正方形OABC 的边OA ,OC 所在的直线, 点B 为该双曲线的焦点.若正方形OABC 的边长为2,则a =_______________. 解 不妨令B 为双曲线的右焦点,A 在第一象限,则双曲线如图所示. 因为OABC 为正方形,2=OA ,所以22==c OB , π 4 ∠= AOB . 因为直线OA 是渐近线,方程为= b y x a ,所以tan 1=∠=b AOB a . 又222 8+==a b c ,所以2=a . 3.以抛物线C 的顶点为圆心的圆交C 于A 、B 两点,交C 的准线于D 、E 两点.已知|AB |= 42,|DE|=25,则C 的焦点到准线的距离为 (A)2 (B)4 (C)6 (D)8 解 因为抛物线焦点到准线的距离为p ,所以只要求出p ,因D 在圆上,A 既在圆上,又在抛物线上,从而可以得到三个方程,不妨设抛物线为22y px =()0p >,设圆的方程为 222x y r +=,作出示意图如图所示. O C B A y x F A -1 B 1M N x y -2-4-3234O 1 234 -1 -2-3-4