实习题1
1用两种不容的顺序计算
644834.11000
1
2
≈∑=-n n
,分析误差的变化
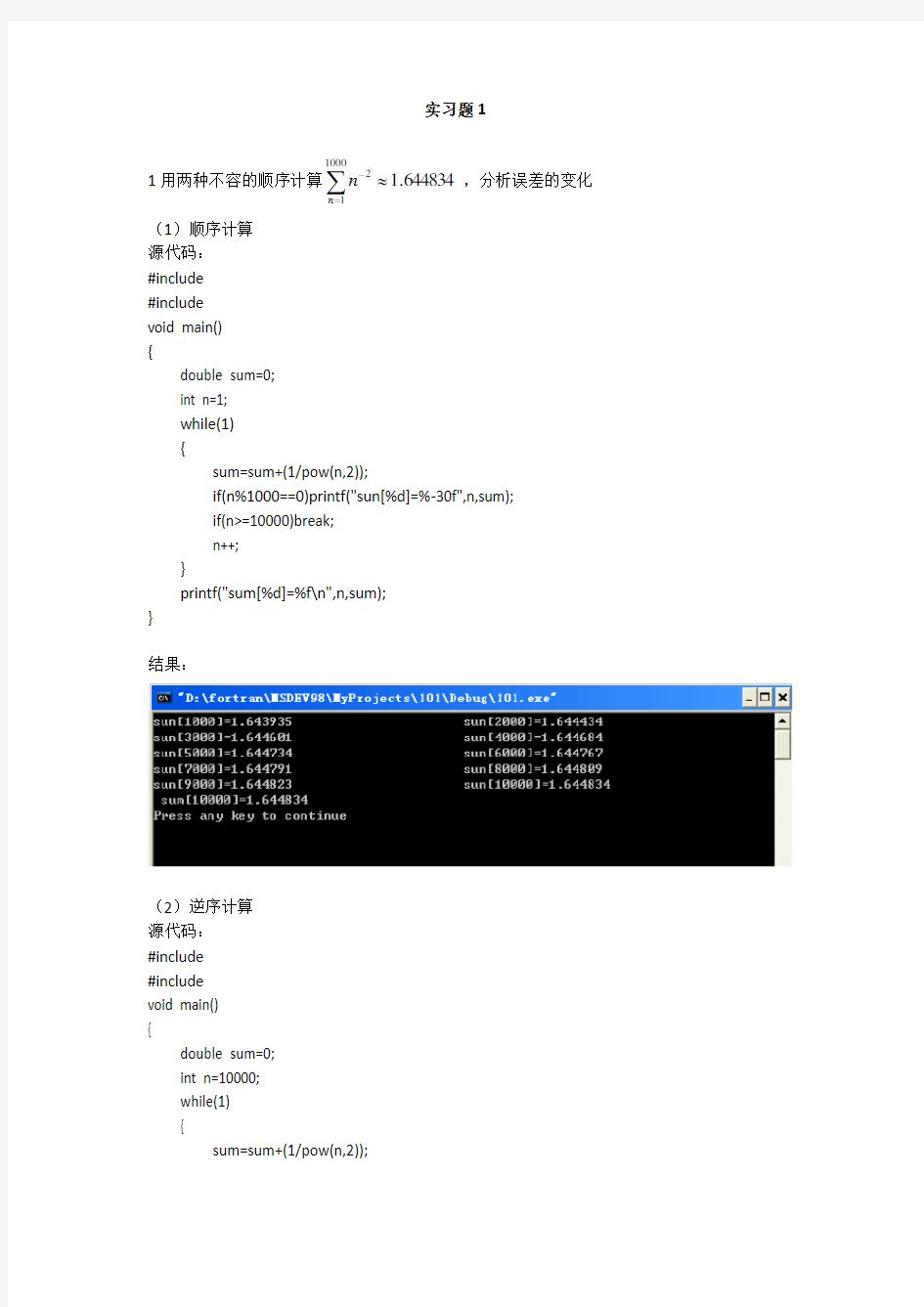
(1)顺序计算 源代码:
#include
结果:
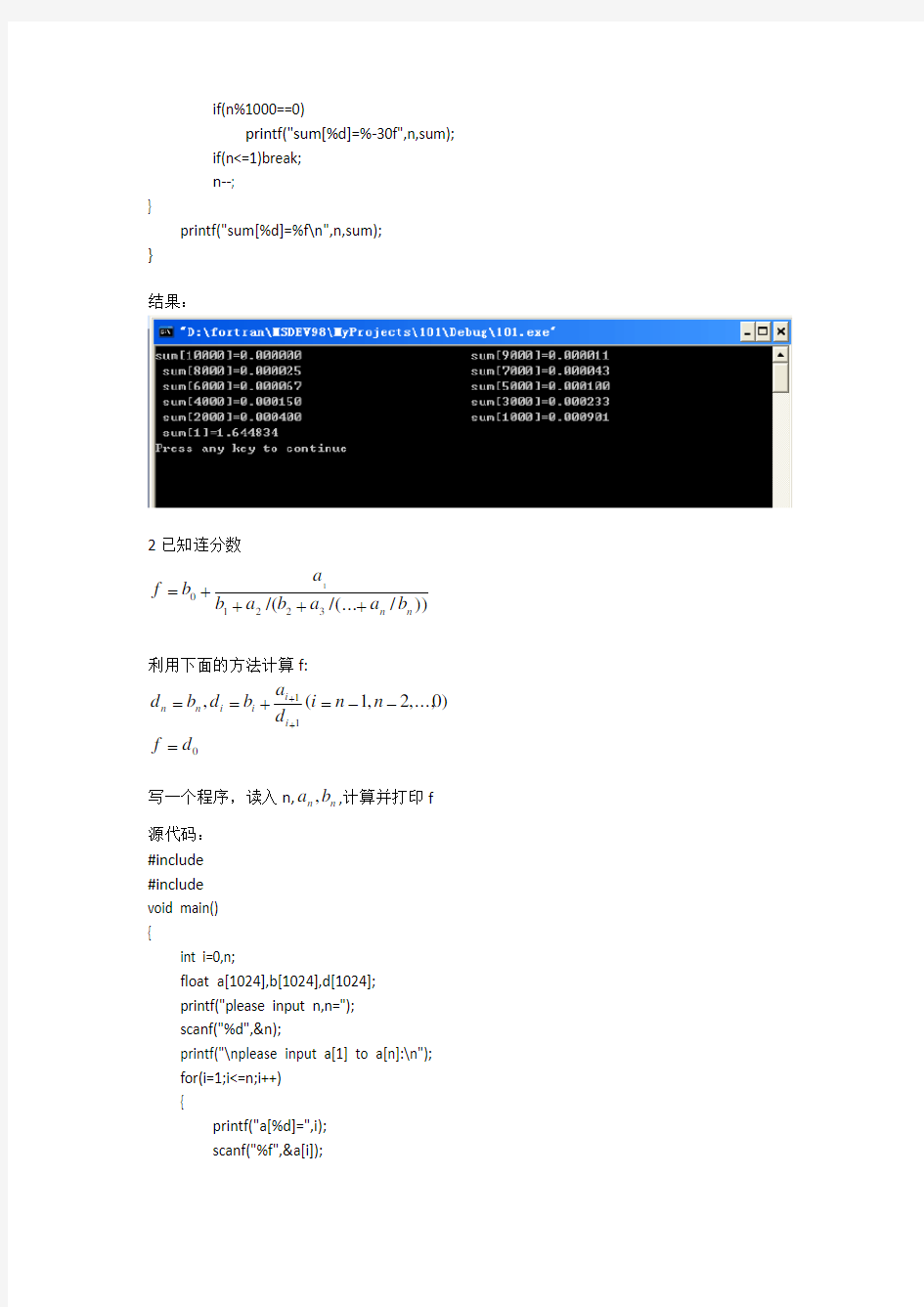
(2)逆序计算 源代码:
#include
if(n%1000==0) printf("sum[%d]=%-30f",n,sum); if(n<=1)break; n--;
} printf("sum[%d]=%f\n",n,sum);
}
结果:
2已知连分数
))//(.../(322101
n n b a a b a b a b f ++++
=
利用下面的方法计算f:
1
1
)0,...,2,1(,d f n n i d a b d b d i i i i n n =--=+==++
写一个程序,读入n,n n b a ,,计算并打印f 源代码:
#include
} printf("\nplease input b[0] to b[n]:\n"); for(i=0;i<=n;i++) { printf("b[%d]=",i); scanf("%f",&b[i]); } d[n]=b[n]; for(i=n-1;i>=0;i--) d[i]=b[i]+a[i+1]/d[i+1]; printf("\nf=%f\n",d[0]); } 结果:
3给出一个有效的算法和一个无效的算法计算积分
?=+=10
)10,...1,0(14n dx x x y n n
源代码:
#include
while(1) { y_1=1.0/(4*n)+y_0/(-4.0); printf("y[%d]=%-20f",n,y_1); if(n>=10) break; y_0=y_1; n++; if(n%3==0) printf("\n"); }
printf("\n 无效算法的输出结果:\n"); printf("y[10]=%-20f",y_2); while(1) { y_3=1.0/n-4.0*y_2; printf("y[%d]=%-20f",m-1,y_3); if(m<=1) break; y_2=y_3; m--; if(m%2==0) printf("\n"); }
}
结果:
4设∑
=-=
N
j N j S 2
21
1
,已知其精确值为
)11123(21+--N N (1)编制按从小到大顺序计算N S 的程序 (2)编制按从小达到的顺序计算N S 的程序
(3)按两种顺序分别计算30000100001000,,S S S ,并指出有效位数
源代码:
#include
\nSN[1000]=%f\nSN[10000]=%f\nSN[30000]=%f\n",SN[1000],SN[10000],SN[30000]); SN[2]=(3.0/2-1.0/2.0-1/3.0)/2.0; for(N=3;N<=30000;N++) SN[N]=SN[N-1]+1.0/(N*N-1); printf("从小到大顺序计算:
\nSN[1000]=%f\nSN[10000]=%f\nSN[30000]=%f\n",SN[1000],SN[10000],SN[30000]); } 结果:
实习题2
1.用牛顿法求下列方程的根
2=-x e x
01=-x xe 02lg =-+x x
源代码:
#include
typedef float (*p)(float ); float ff1(float x) { return x*x-exp(x); }
float ff2(float x) { return x*exp(x)-1; }
float ff3(float x) { return log(x)+x-2; }
float answer(float(*p)(float)) { int k=2; float m=1,n=-1,x2,a,b,c; if (p==ff3)n=2; printf("x[0] = %.4f, x[1] = %.4f, ",m,n); while (1) { if (fabs(m-n)<1e-4) break; a=p(n)*(n-m); b=p(n)-p(m); c=a/b; x2=n-c; m = n; n = x2; printf("x[%d] = %.4f, ",k,x2); k++; if (k%3==0) printf("\n"); }
if (k%3!=0) printf("\n");
printf("iteration times: %d, roots: %.4f\n ",k-2,n);
return 0;
}
main()
{
printf("x*x-exp(x),\n");
answer(ff1);
printf("x*exp(x)-1,\n");
answer(ff2);
printf("lg(x)+x-2,\n");
answer(ff3);
return 0;
}
结果:
2.编写一个割线法的程序,求解上述各方程
源代码:
#include
#include
float gexian(float,float);
float f(float);
main()
{
int i,j;
float x1=2.2;
float x2=2,x3;
scanf("%d",&i);
if(i==1)
printf("%f",x1); else if(i==2) printf("%f",x2); else { for(j=3;j<=i;j++) { x3=gexian(x1,x2); x1=x2; x2=x3; } printf("%f",gexian(x1,x2)); } }
float f(float x) { return (x*x-exp(x)); }
float gexian(float x1,float x2) { return (x2-(f(x2)/(f(x2)-f(x1)))*(x2-x1)); }
结果:
实习题3
1用列主元消去法解下列方程组;
???????=++=-++--=+--=--+4
3443233312)1(421432143214321x x x x x x x x x x x x x x x ???????=++--=++-=-+--=-+-4
341220332282)2(4321
3
2143214321x x x x x x x x x x x x x x x
源程序:
#include
#include
void ColPivot(float*,int,float[]);
void ColPivot(float*c,int n,float x[])
{
int i,j,t,k;
float p;
for(i=0;i<=n-2;i++)
{
k=i;
for(j=i+1;j<=n-1;j++)
if(fabs(*(c+j*(n+1)+i))>(fabs(*(c+k*(n+1)+i))))
k=j;
if(k!=i)
for(j=i;j<=n;j++)
{
p=*(c+i*(n+1)+j);
*(c+i*(n+1)+j)=*(c+k*(n+1)+j);
*(c+k*(n+1)+j)=p;
}
for(j=i+1;j<=n-1;j++)
{
p=(*(c+j*(n+1)+i))/(*(c+i*(n+1)+i));
for(t=i;t<=n;t++)
*(c+j*(n+1)+t)-=p*(*(c+i*(n+1)+t));
}
}
for(i=n-1;i>=0;i--)
{
for(j=n-1;j>=i+1;j--)
(*(c+i*(n+1)+n))-=x[j]*(*(c+i*(n+1)+j));
x[i]=*(c+i*(n+1)+n)/(*(c+i*(n+1)+i));
}
}
void main()
{
int i;
float x[4];
float c[4][5]={1,1,0,3,4,2,1,-1,1,1,3,-1,-1,3,-3,-1,2,3,-1,4};
ColPivot(c[0],4,x);
for(i=0;i<=3;i++)
printf("x[%d]=%f\n",i,x[i]);
}
结果:
第(1)题
第(2)题
2、
源代码:
#include
void main()
{
float x[4];
int i;
float a[4][5]={48,-24,0,-12,4,-24,24,12,12,4,0,6,20,2,-2,-6,6,2,16,-2};
void DirectLU(float*,int,float[]);
DirectLU(a[0],4,x);
for(i=0;i<=3;i++)
printf("x[%d]=%f\n",i,x[i]);
}
void DirectLU(float*u,int n,float x[])
{
int i,r,k;
for(r=0;r<=n-1;r++)
{
for(i=r;r<=n;i++)
for(k=0;k<=r-1;k++)
*(u+r*(n+1)+i)-=*(u+r*(n+1)+k)*(*(u+k*(n+1)+i));
for(i=r+1;i<=n-1;i++)
{
for(k=0;k<=r-1;k++)
*(u+i*(n+1)+r)-=*(u+i*(n+1)+k)*(*(u+k*(n+1)+r));
*(u+i*(n+1)+r)/=*(u+r*(n+1)+r);
}
}
for(i=n-1;i>=0;i--)
{
for(r=n-1;r>=i+1;r--)
*(u+i*(n+1)+n)-=*(u+i*(n+1)+r)*x[r];
x[i]=*(u+i*(n+1)+n)/(*(u+i*(n+1)+i));
}
}
实习题4
1、
源代码:
#include
float Lagrange(float x[],float y[],float xx,int n) //n为(n+1)次插值;{
int i,j;
float *a,yy=0;
a=new float[n];
for(i=0;i<=n-1;i++)
{
a[i]=y[i];
for(j=0;j<=n-1;j++)
if(j!=i)a[i]*=(xx-x[j])/(x[i]-x[j]);
yy+=a[i];
}
delete a;
return yy;
}
void main()
{
float x[5]={-3.0,-1.0,1.0,2.0,3.0};
float y[5]={1.0,1.5,2.0,2.0,1.0};
float xx1=-2,xx2=0,xx3=2.75,yy1,yy2,yy3;
yy1=Lagrange(x,y,xx1,3);
yy2=Lagrange(x,y,xx2,3);
yy3=Lagrange(x,y,xx3,3);
printf("x1=%-20f,y1=%f\n",xx1,yy1);
printf("x2=%-20f,y2=%f\n",xx2,yy2);
printf("x3=%-20f,y3=%f\n",xx3,yy3);
}
结果:
2、
源代码:
#include
float Lagrange(float x[],float y[],float xx,int n) //n为(n+1)次插值;{
int i,j;
float *a,yy=0;
a=new float[n];
for(i=0;i<=n-1;i++)
{
a[i]=y[i];
for(j=0;j<=n-1;j++)
if(j!=i)a[i]*=(xx-x[j])/(x[i]-x[j]);
yy+=a[i];
}
delete a;
return yy;
}
void main()
{
float x[6]={0.30,0.42,0.50,0.58,0.66,0.72};
float y[6]={1.04403,1.08462,1.11803,1.15603,1.19817,1.23223};
float xx1=0.46,xx2=0.55,xx3=0.60,yy1,yy2,yy3;
yy1=Lagrange(x,y,xx1,6);
yy2=Lagrange(x,y,xx2,6);
yy3=Lagrange(x,y,xx3,6);
printf("x1=%-20f,y1=%f\n",xx1,yy1);
printf("x2=%-20f,y2=%f\n",xx2,yy2);
printf("x3=%-20f,y3=%f\n",xx3,yy3);
}
结果:
源代码:
#include
#define N 3
void Difference(float y[],float f[4][4],int n)
{
int k,i;
f[0][0]=y[0];f[1][0]=y[1];f[2][0]=y[2];f[3][0]=y[3];
for(k=1;k<=n;k++)
for(i=0;i<=(N-k);i++)
f[i][k]=f[i+1][k-1]-f[i][k-1];
return;
}
void main()
{
int i,k=1;
float a,b=1,m=21.4,t=1.4,f[4][4]={0};
float x[5]={20,21,22,23,24};
float y[5]={1.30103,1.32222,1.34242,1.36173,1.38021};
Difference(y,f,N);
a=f[0][0];
for(i=1;i<=N;i++)
{
k=k*i;
b=b*(t-i+1);
a=a+b*f[0][i]/k;
}
printf("x(k)\n");
for (i=0;i<=4;i++)
printf( "%-20f",x[i]);
printf("\ny(k)\n");
for (i=0;i<=4;i++)
printf("%-20f",y[i]);
for(k=1;k<=3;k++)
{
printf("\nF(%d)\n ",k);
for(i=0;i<=(3-k);i++)
{
printf("%-20f",f[i][k]);
}
}
printf ("\n");
printf("f(%f)=%-20f",m,a);
printf ("\n");
结果:
实习题5
2、
源代码:
#include
#include
void main()
{
int i,n;
float a[2];
float x[15]={1,1.5,2,2.5,3,3.5,4,4.5,5,5.5,6,6.5,7,7.5,8},z[15];
float
y[15]={33.4,79.50,122.65,159.05,189.15,214.15,238.65,252.50,267.55,280.50,296.65,301.40,310 .40,318.15,325.15};
for(n=0;n<=14;n++) //增加了数组z;
{
z[n]=log(y[n]/x[n]);
}
void Approx(float[],float[],int,int,float[]);
Approx(x,z,15,1,a); //变成一次拟合;
//for(i=0;i<=1;i++)
//printf("a[%d]=%f\n",i,a[i]);
printf("a=exp(a[0])=%f\n",exp(a[0]));
printf("b=-a[1]=%f\n",-a[1]); }
void Approx(float x[],float y[],int m,int n,float a[])
{
int i,j,t;
float *c=new float[(n+1)*(n+2)];
float power(int,float);
void ColPivot(float *,int,float[]);
for(i=0;i<=n;i++)
{
for(j=0;j<=n;j++)
{
*(c+i*(n+2)+j)=0;
for(t=0;t<=m-1;t++)
*(c+i*(n+2)+j)+=power(i+j,x[t]);
}
*(c+i*(n+2)+n+1)=0;
for(j=0;j<=m-1;j++)
*(c+i*(n+2)+n+1)+=y[j]*power(i,x[j]);
}
ColPivot(c,n+1,a);
delete c;
}
void ColPivot(float *c,int n,float x[])
{
int i,j,t,k;
float p;
for(i=0;i<=n-2;i++)
{
k=i;
for(j=i+1;j<=n-1;j++)
if(fabs(*(c+j*(n+1)+i))>(fabs(*(c+k*(n+1)+i))))
k=j;
if(k!=i)
for(j=i;j<=n;j++)
{
p=*(c+i*(n+1)+j);
*(c+i*(n+1)+j)=*(c+k*(n+1)+j);
*(c+k*(n+1)+j)=p;
}
for(j=i+1;j<=n-1;j++)
{
p=(*(c+j*(n+1)+i))/(*(c+i*(n+1)+i));
for(t=i;t<=n;t++)*(c+j*(n+1)+t)-=p*(*(c+i*(n+1)+t));
}
}
for(i=n-1;i>=0;i--)
{
for(j=n-1;j>=i+1;j--)
(*(c+i*(n+1)+n))-=x[j]*(*(c+i*(n+1)+j));
x[i]=*(c+i*(n+1)+n)/(*(c+i*(n+1)+i));
}
float power(int i,float v)
{
float a=1;
while(i--)a*=v;
return a;
}
结果:
实习题6
1、
源代码:
(1)
#include
#include
float Cotes(float(*f)(float),float a,float b,int n)
{
int k;
float c,c1=0,c2,c3,c4;
float h=(b-a)/n;
c2=(*f)(a+h/4);
c3=(*f)(a+h/2);
c4=(*f)(a+3*h/4);
for(k=1;k<=n-1;k++)
{
c1+=(*f)(a+k*h);
c2+=(*f)(a+k*h+h/4);
c3+=(*f)(a+k*h+h/2);
c4+=(*f)(a+k*h+3*h/4);
}
c=h/90*(7*((*f)(a)+(*f)(b))+14*c1+32*c2+12*c3+32*c4);
return c;
}
float f(float x)
{
return 1/sqrt(1+x*x*x);
}
void main()
int i,n=4;
float c;
for(i=0;i<=4;i++)
{
c=Cotes(f,0,1,n);
printf("C(%d)=%f\n",n,c);
n*=2;
}
}
(2)
#include
#include
float Cotes(float(*f)(float),float a,float b,int n)
{
int k;
float c,c1=0,c2,c3,c4;
float h=(b-a)/n;
c2=(*f)(a+h/4);
c3=(*f)(a+h/2);
c4=(*f)(a+3*h/4);
for(k=1;k<=n-1;k++)
{
c1+=(*f)(a+k*h);
c2+=(*f)(a+k*h+h/4);
c3+=(*f)(a+k*h+h/2);
c4+=(*f)(a+k*h+3*h/4);
}
c=h/90*(7*((*f)(a)+(*f)(b))+14*c1+32*c2+12*c3+32*c4);
return c;
}
float f(float x)
{ // return 1/sqrt(1+x*x*x);
if (x==0)
return 1;
else return sin(x)/x;
}
void main()
{
int i,n=4;
float c;
for(i=0;i<=4;i++)
{
// c=Cotes(f,0,1,n);
c=Cotes(f,0,5,n);
printf("C(%d)=%f\n",n,c);
n*=2;
}
}
结果:
(1)
(2)
实习题7 一、改进欧拉法
1、
#include
#include
double Adams (
double (*f)(double x, double y),
double x0,
double y0,
double h,
int N
) {
for(int n=0; n double x1=x0+h; double yp=y0+h*f(x0,y0); double y1=y0+h*f(x1,yp); y1=(yp+y1)/2.0; printf("ty=%f\n",y1); x0=x1; y0=y1; } } int main(void) { double f(double x, double y); double x0=0,y0=0; double x,y,step; long i; step=0.1; Adams(f,x0,y0,0.1,10); } double f(double x, double y) { double r; r=x*x+y*y; return(r); } 2、 int main(void) { double f(double x, double y); double x0=0,y0=0; double x,y,step; step=0.1; Adams(f,x0,y0,0.1,10); } double f(double x, double y) { double r; r=1/(1+y*y); return(r); } 3、 int main(void) { double f(double x, double y); double x0=0,y0=1; double x,y,step; long i; step=0.1; Adams(f,x0,y0,0.1,10); } double f(double x, double y) { double r; r=y-2*x/y; 2017数值计算方法上机实习报告 学院: 专业: 班级: 姓名: 学号: 数值计算方法上机实习题 1. 设?+=1 05dx x x I n n , (1) 由递推公式n I I n n 1 51+ -=-,从0=0.1823I ,1824.00=I 出发,计算20I ; (2) 20=0I ,20=10000I , 用n I I n n 51 5111+-=--,计算0I ; (3) 分析结果的可靠性及产生此现象的原因(重点分析原因)。 解:(1)分别令I 0的近似值为0.1823、0.1824,MATLAB 程序如下: I=0.1823; %题中的已知数据 for n=1:20; I=(-5)*I+1/n; %由递推公式所得 end fprintf('I20=%f\n',I) M=0.1824; %与I 的计算结果形成对比 for i=1:20; M=(-5)*M+1/i; %由递推公式所得 end fprintf('M20=%f\n',M) %% 输出结果 I20=-2055816073.851284 M20=7480927090.212283 (2)分别令I 20的近似值为0、10000,MATLAB 程序如下: I=0; %赋予I20的初始值 for n=0:19; I=(-1/5)*I+1/(5*(20-n)); %由递推公式所得 end fprintf('I0=%f\n',I) M=10000; for i=0:19; M=(-1/5)*M+1/(5*(20-i));%由递推公式所得 end fprintf('M0=%f\n',M) %% 输出结果 I0=0.182322 M0=0.182322 (3)分析: 由输出结果可看出第一种算法为不稳定算法,第二种算法为稳定算法。 由于误差 * 000I I e -= 02211*1*11*555)(5)15(15e e e I I n I n I I I e n n n n n n n n n n ===-=+--+ -=-=------ 数值分析上机实验报告 选题:曲线拟合的最小二乘法 指导老师: 专业: 学号: 姓名: 课题八曲线拟合的最小二乘法 一、问题提出 从随机的数据中找出其规律性,给出其近似表达式的问题,在生产实践和科学实验中大量存在,通常利用数据的最小二乘法求得拟合曲线。 在某冶炼过程中,根据统计数据的含碳量与时间关系,试求含碳量y 与时间t 的拟合曲线。 二、要求 1、用最小二乘法进行曲线拟合; 2、近似解析表达式为()33221t a t a t a t ++=?; 3、打印出拟合函数()t ?,并打印出()j t ?与()j t y 的误差,12,,2,1 =j ; 4、另外选取一个近似表达式,尝试拟合效果的比较; 5、*绘制出曲线拟合图*。 三、目的和意义 1、掌握曲线拟合的最小二乘法; 2、最小二乘法亦可用于解超定线代数方程组; 3、探索拟合函数的选择与拟合精度间的关系。 四、计算公式 对于给定的测量数据(x i ,f i )(i=1,2,…,n ),设函数分布为 ∑==m j j j x a x y 0)()(? 特别的,取)(x j ?为多项式 j j x x =)(? (j=0, 1,…,m ) 则根据最小二乘法原理,可以构造泛函 ∑∑==-=n i m j i j j i m x a f a a a H 1 10))((),,,(? 令 0=??k a H (k=0, 1,…,m ) 则可以得到法方程 ???? ??????? ?=????????????????????????),(),(),(),(),(),(),(),(),(),(),(),(1010101111000100m m m m m m m m f f f a a a ????????????????????? 求该解方程组,则可以得到解m a a a ,,,10 ,因此可得到数据的最小二乘解 ∑=≈m j j j x a x f 0)()(? 曲线拟合:实际工作中,变量间未必都有线性关系,如服药后血药浓度与时间的关系;疾病疗效与疗程长短的关系;毒物剂量与致死率的关系等常呈曲线关系。曲线拟合是指选择适当的曲线类型来拟合观测数据,并用拟合的曲线方程分析两变量间的关系。 五、结构程序设计 在程序结构方面主要是按照顺序结构进行设计,在进行曲线的拟合时,为了进行比较,在程序设计中,直接调用了最小二乘法的拟合函数polyfit ,并且依次调用了plot 、figure 、hold on 函数进行图象的绘制,最后调用了一个绝对值函数abs 用于计算拟合函数与原有数据的误差,进行拟合效果的比较。 实验报告 课程名称: 计算方法 指导老师: 太英 成绩: 实验名称: 第三次上机作业 实验类型: matlab 同组学生: 一、实验目的和要求(必填) 二、实验容和原理(必填) 三、主要仪器设备(必填) 四、操作方法和实验步骤 五、实验数据记录和处理 六、实验结果与分析(必填) 七、讨论、心得 一、实验目的 用龙贝格算法计算积分I =∫ssss s ss 01 ,要求误差不超过ε=12 ×105 二、实验原理 龙贝格算法是由递推算法得来的。由梯形公式得出辛普森公式得出柯特斯公式最后得到龙贝格公式。设将求积区间[a ,b]分为n 个等分,则一共有n+1个等分点,k x a kh =+,0,1,b a h k n -= =,n 。这里用n T 表示复化梯形法求得的积分 值,其下标n 表示等分数。 先考察下一个字段[1,k k x x +],其中点()112 1 2 k k k x x x ++= +,在该子段上二分前后两个积分值 ()()112 k k h T f x f x += +???? ()()21124k k k h T f x f x f x ++? ??? =+ +?? ??????? 显然有下列关系 2112122k h T T f x +? ?=+ ??? 将关系式关于k 从0到n-1累加求和,即可得递推公式1 210 2122n n n k k h T T f x -+=?? =+ ??? ∑ 需要强调指出的是,上式中的b a h n -= 代表二分前的步长,而12 12k x a k h +? ?=++ ??? 根据梯形法的误差公式,积分值n T 的截断误差大致与2h 成正比,因此步长减半后误差将减至四分之一,即有 211 14 n n T T -≈- 将上式移项整理,知 221 1()3 n n n T T T -≈- 按上式,积分值2n T 的误差大致等于21 ()3 n n T T -,如果用这个误差值作为2n T 的 一种补偿,可以期望,所得的()222141 333 n n n n n T T T T T T =+ -=-应当是更好的结果。 组合得到的近似值T 直接验证,用梯形二分前后的两个积分值n T 和2n T 按式组合, 结果得到辛普森法的积分值241 33 n n n S T T =- 再考察辛普森法。其截断误差与4h 成正比。因此,若将步长折半,则误差相应的减至十六分之一。既有 21 16n n I S I S -≈- 由此得 21611515 n n I S S ≈ - 不难验证,上式右端的值其实就等于n C ,就是说,用辛普森法二分前后的两个积分值n S 和2n S ,在按上式再做线性组合,结果得到柯特斯法的积分值n C ,既有 2161 1515n n n C S S ≈ - 重复同样的手续,依据斯科特法的误差公式可进一步导出龙贝格公式 2641 6363 n n n R C C ≈ - 在步长二分的过程中运用公式加工三次,就能将粗糙的积分值n T 逐步加工成精度较高的龙贝格n R ,或者说,将收敛缓慢的梯形值序列n T 加工成熟练迅速的龙贝 格 值序列n R ,这种加速方法称龙贝格算法。 三、实验过程 1.流程图 第一章 一、题目 设∑ =-= N N j S 2 j 2 1 1,其精确值为)11 123(21+--N N 。 1) 编制按从大到小的顺序1 1 13112122 2-+??+-+-=N S N ,计算S N 的通用程序。 2) 编制按从小到大的顺序1 21 1)1(111222-+ ??+--+-= N N S N ,计算S N 的通用程序。 3) 按两种顺序分别计算64210,10,10S S S ,并指出有效位数。(编制程序时用单精度) 4) 通过本次上机题,你明白了什么? 二、通用程序 N=input('Please Input an N (N>1):'); AccurateValue=single((0-1/(N+1)-1/N+3/2)/2); Sn1=single(0); for a=2:N; Sn1=Sn1+1/(a^2-1); end Sn2=single(0); for a=2:N; Sn2=Sn2+1/((N-a+2)^2-1); end fprintf('The value of Sn (N=%d)\n',N); fprintf('Accurate Calculation %f\n',AccurateValue); fprintf('Caculate from large to small %f\n',Sn1); fprintf('Caculate from small to large %f\n',Sn2); disp('____________________________________________________') 三、结果 从结果可以看出有效位数是6位。 感想:可以得出,算法对误差的传播有一定的影响,在计算时选一种好的算法可以使结果更为精确。从以上的结果可以看到从大到小的顺序导致大数吃小数的现象,容易产生较大的误差,求和运算从小数到大数所得到的结果才比较准确。 2.用下列方法求方程e^x+10x-2=0的近似根,要求误差不超过5*10的负4次方,并比较计算量 (1)二分法 (局部,大图不太看得清,故后面两小题都用局部截图) (2)迭代法 (3)牛顿法 顺序消元法 #include for(k=p+1;k 数值分析与实验课程设计 班级: 姓名: 学号: 08级应用数学《数值分析与实验(实践)》任务书 一、设计目的 通过《数值分析与实验(实践)》实践环节,掌握本门课程的众多数值解法和原理,并通过编写C语言或matlab程序,掌握各种基本算法在计算机中的具体表达方法,并逐一了解它们的优劣、稳定性以及收敛性。在熟练掌握C语言或matlab语言编程的基础上,编写算法和稳定性均佳、通用性强、可读性好,输入输出方便的程序,以解决实际中的一些科学计算问题。 二、设计教学内容 1、数值方法的稳定性; 2、利用牛顿法和割线法程序求出非线性方程的解,并比较它们之间的优 劣; 3、高斯消去法和列主元高斯消去法求解线性方程组; 雅克比法和高斯-赛德尔迭代法解方程组; 4、利用Lagrange插值多项式求未知点的近似值; 5、利用所给数据进行数据的多项式和可转化成多项式形式的函数拟合; 6、编写复化辛卜生公式和龙贝格算法,通过实际计算体会各种方法的精确 度; 7、利用改进Euler方法和四阶Runge-Kutta方法求解初值问题的微分方程 组; 8、利用幂法求矩阵按模最大的特征值及对应特征向量; ( 8个中选取1个) 三、设计时间 2011—2012学年第1学期:第16周共计一周 教师签名: 2011年12月12日 前言 数值计算方法是一种利用计算机解决数学问题的数值近似解方法,特别是无法用人工过计算器计算的数学问题。数值计算方法常用于矩阵高次代数方程矩阵特征值与特征向量的数值解法,插值法,线性方程组迭代法,函数逼近,数值积分与微分,常微分方程初值问题数值解等。 作为数学与计算机之间的一条通道,数值计算的应用范围已十分广泛,作为用计算机解决实际问题的纽带,数值算法在求解线性方程组,曲线拟合、数值积分、数值微分,迭代方法、插值法、拟合法、最小二乘法等应用广泛。 数值计算方法是和计算机紧密相连的,现代计算机的出现为大规模的数值计算创造了条件,集中而系统的研究适用于计算机的数值方法是十分必要的。数值计算方法是在数值计算实践和理论分析的基础上发展起来的。 通过数值计算方法与实验将有助于我们理解和掌握数值计算方法基本理论和相关软件的掌握,熟练求解一些数学模和运算,并提高我们的编程能力来解决实际问题。 计算方法实验报告 班级: 学号: 姓名: 成绩: 1 舍入误差及稳定性 一、实验目的 (1)通过上机编程,复习巩固以前所学程序设计语言及上机操作指令; (2)通过上机计算,了解舍入误差所引起的数值不稳定性 二、实验内容 1、用两种不同的顺序计算10000 21n n -=∑,分析其误差的变化 2、已知连分数() 1 01223//(.../)n n a f b b a b a a b =+ +++,利用下面的算法计算f : 1 1 ,i n n i i i a d b d b d ++==+ (1,2,...,0 i n n =-- 0f d = 写一程序,读入011,,,...,,,...,,n n n b b b a a 计算并打印f 3、给出一个有效的算法和一个无效的算法计算积分 1 041 n n x y dx x =+? (0,1,...,1 n = 4、设2 2 11N N j S j == -∑ ,已知其精确值为1311221N N ?? -- ?+?? (1)编制按从大到小的顺序计算N S 的程序 (2)编制按从小到大的顺序计算N S 的程序 (3)按两种顺序分别计算10001000030000,,,S S S 并指出有效位数 三、实验步骤、程序设计、实验结果及分析 1、用两种不同的顺序计算10000 2 1n n -=∑,分析其误差的变化 (1)实验步骤: 分别从1~10000和从10000~1两种顺序进行计算,应包含的头文件有stdio.h 和math.h (2)程序设计: a.顺序计算 #include 数值计算方法I 上机实验考试题(两题任选一题) 1.小型火箭初始质量为900千克,其中包括600千克燃料。火箭竖直向上发射时燃料以15千克/秒的速率燃烧掉,由此产生30000牛顿的恒定推力.当燃料用尽时引擎关闭。设火箭上升的整个过程中,空气阻力与速度平方成正比,比例系数为0.4(千克/米).重力加速度取9.8米/秒2. A. 建立火箭升空过程的数学模型(微分方程); B. 求引擎关闭瞬间火箭的高度、速度、加速度,及火箭到达最高点的时间和高度. 2.小型火箭初始质量为1200千克,其中包括900千克燃料。火箭竖直向上发射时燃料以15千克/秒的速率燃烧掉,由此产生40000牛顿的恒定推力.当燃料用尽时引擎关闭。设火箭上升的整个过程中,空气阻力与速度平方成正比,比例系数记作k ,火箭升空过程的数学模型为 0)0(,0,01222==≤≤-+?? ? ??-==t dt dx x t t mg T dt dx k dt x d m 其中)(t x 为火箭在时刻t 的高度,m =1200-15t 为火箭在时刻t 的质量,T (=30000牛顿)为推力,g (=9.8米/秒2)为重力加速度, t 1 (=900/15=60秒)为引擎关闭时刻. 今测得一组数据如下(t ~时间(秒),x ~高度(米),v ~速度(米/秒)): 现有两种估计比例系数k 的方法: 1.用每一个数据(t,x,v )计算一个k 的估计值(共11个),再用它们来估计k 。 2.用这组数据拟合一个k . 请你分别用这两种方法给出k 的估计值,对方法进行评价,并且回答,能否认为空气阻力系数k=0.5(说明理由). 《数值计算方法》上机实验报告华北电力大学 实验名称数值il?算方法》上机实验课程名称数值计算方法专业班级:电力实08学生姓名:李超然学号:200801001008 成绩: 指导教师:郝育黔老师实验日期:2010年04月华北电力大学实验报告数值计算方法上机实验报吿一. 各算法的算法原理及计算机程序框图1、牛顿法求解非线性方程 *对于非线性方程,若已知根的一个近似值,将在处展开成一阶 xxfx ()0, fx ()xkk 泰勒公式 "f 0 / 2 八八,fxfxfxxxxx 0 0 0 0 0 kkkk2! 忽略高次项,有 ,fxfxfxxx 0 ()()(),,, kkk 右端是直线方程,用这个直线方程来近似非线性方程。将非线性方程的 **根代入,即fx ()0, X ,* fxfxxx 0 0 0 0, ,, kkk fx 0 fx 0 0, 解出 fX 0 *k XX,, k' fx 0 k 水将右端取为,则是比更接近于的近似值,即xxxxk, Ik, Ik fx ()k 八XX, Ikk* fx()k 这就是牛顿迭代公式。 ,2,计算机程序框图:,见, ,3,输入变量、输出变量说明: X输入变量:迭代初值,迭代精度,迭代最大次数,\0 输出变量:当前迭代次数,当前迭代值xkl ,4,具体算例及求解结果: 2/16 华北电力大学实验报吿 开始 读入 l>k /fx()0?,0 fx 0 Oxx,,01* fx ()0 XX,,,?10 kk, ,1,kN, ?xx, 10 输出迭代输出X输出奇异标志1失败标志 ,3,输入变量、输出变量说明: 结束 例:导出计算的牛顿迭代公式,并il ?算。(课本P39例2-16) 115cc (0), 求解结果: 10. 750000 10.723837 10. 723805 10. 723805 2、列主元素消去法求解线性方程组,1,算法原理: 高斯消去法是利用现行方程组初等变换中的一种变换,即用一个不为零的数乘 -个 方程后加只另一个方程,使方程组变成同解的上三角方程组,然后再自下而上 对上三角 3/16 华北电力大学实验报告方程组求解。 列选主元是当高斯消元到第步时,从列的以下(包括)的各元素中选出绝 aakkkkkk 对值最大的,然后通过行交换将其交换到的位置上。交换系数矩阵中的 两行(包括常ekk 数项),只相当于两个方程的位置交换了,因此,列选主元不影响求解的结 ,2,计算机程序框图:,见下页, 输入变量:系数矩阵元素,常向量元素baiji 输出变量:解向量元素bbb,,12n 东南大学计算方法与实习实验报告 学院:电子科学与工程学院 学号:06A12528 姓名:陈毓锋 指导老师:李元庆 实习题1 4、设S N=Σ (1)编制按从大到小的顺序计算S N的程序; (2)编制按从小到大的顺序计算S N的程序; (3)按两种顺序分别计算S1000,S10000,S30000,并指出有效位数。 解析:从大到小时,将S N分解成S N-1=S N-,在计算时根据想要得到的值取合适的最大的值作为首项;同理从小到大时,将S N=S N-1+ ,则取S2=1/3。则所得式子即为该算法的通项公式。 (1)从大到小算法的C++程序如下: /*从大到小的算法*/ #include 计算方法 一、填空题 1.假定x ≤1,用泰勒多项式?+??+++=! !212n x x x e n x ,计算e x 的值,若要求截断误差不超过0.005,则n=_5___ 2. 解 方 程 03432 3=-+x - x x 的牛顿迭代公式 )463/()343(121121311+--+--=------k k k k k k k x x x x x x x 3.一阶常微分方程初值问题 ?????= ='y x y y x f y 0 0)() ,(,其改进的欧拉方法格式为)],(),([21 1 1 y x y x y y i i i i i i f f h +++++= 4.解三对角线方程组的计算方法称为追赶法或回代法 5. 数值求解初值问题的四阶龙格——库塔公式的局部截断误差为o(h 5 ) 6.在ALGOL 中,简单算术表达式y x 3 + 的写法为x+y ↑3 7.循环语句分为离散型循环,步长型循环,当型循环. 8.函数)(x f 在[a,b]上的一次(线性)插值函数= )(x l )()(b f a b a x a f b a b x --+-- 9.在实际进行插值时插值时,将插值范围分为若干段,然后在每个分段上使用低阶插值————如线性插值和抛物插值,这就是所谓分段插值法 10、数值计算中,误差主要来源于模型误差、观测误差、截断误差和舍入误差。 11、电子计算机的结构大体上可分为输入设备 、 存储器、运算器、控制器、 输出设备 五个主要部分。 12、算式2 cos sin 2x x x +在ALGOL 中写为))2cos()(sin(2↑+↑x x x 。 13、ALGOL 算法语言的基本符号分为 字母 、 数字 、 逻辑值、 定义符四大 实习题1 1用两种不容的顺序计算644834.11000 12≈∑=-n n ,分析误差的变化 (1)顺序计算 源代码: #include if(n%1000==0) printf("sum[%d]=%-30f",n,sum); if(n<=1)break; n--; } printf("sum[%d]=%f\n",n,sum); } 结果: 2已知连分数 )) / /(... /( 3 2 2 1 1 n n b a a b a b a b f + + + + = 利用下面的方法计算f: 1 1)0 ,..., 2 ,1 ( , d f n n i d a b d b d i i i i n n = - - = + = = + + 写一个程序,读入n, n n b a,,计算并打印f 源代码: #include 数值计算方法上机实习题 1. 设?+=1 05dx x x I n n , (1) 由递推公式n I I n n 1 51+ -=-,从I 0=0.1824, 0=0.1823I 出发,计算20I ; (2) 20=0I ,20=10000I , 用n I I n n 51 5111+- =--,计算0I ; (3) 分析结果的可靠性及产生此现象的原因(重点分析原因)。 答:第一个算法可得出 e 0=|I 0?I 0 ?| e n =|I n ?I n ?|=5n |e 0| 易知第一个算法每一步计算都把误差放大了5倍,n 次计算后更是放大了5n 倍,可靠性低。 第二个算法可得出 e n =|I n ?I n ?| e 0=(15 )n |e n | 可以看出第二个算法每一步计算就把误差缩小5倍,n 次后缩小了5n 倍,可靠性高。 2. 求方程0210=-+x e x 的近似根,要求41105-+?<-k k x x ,并比较计算量。 (1) 在[0,1]上用二分法; 计算根与步数程序: fplot(@(x) exp(x)+10*x-2,[0,1]); grid on; syms x; f=exp(x)+10*x-2; [root,n]=EFF3(f,0,1); fprintf('root=%6.8f ,n=%d \n',root,n); 计算结果显示: root=0.09057617 ,n=11 (2) 取初值00=x ,并用迭代10 21 x k e x -=+; (3) 加速迭代的结果; (4) 取初值00 x ,并用牛顿迭代法; 实验报告一 题目:非线性方程求解 摘要:非线性方程的解析解通常很难给出,因此线性方程的数值解法就尤为重要。本实验采用两种常见的求解方法二分法和Newton法及改进的Newton法。 前言:(目的和意义) 掌握二分法与Newton法的基本原理和应用。 数学原理: 对于一个非线性方程的数值解法很多。在此介绍两种最常见的方法:二分法和Newton法。 对于二分法,其数学实质就是说对于给定的待求解的方程f(x),其在[a,b]上连续,f(a)f(b)<0,且f(x)在[a,b]内仅有一个实根x*,取区间中点c,若,则c恰为其根,否则根据f(a)f(c)<0是否成立判断根在区间[a,c]和[c,b]中的哪一个,从而得出新区间,仍称为[a,b]。重复运行计算,直至满足精度为止。这就是二分法的计算思想。 Newton法通常预先要给出一个猜测初值x0,然后根据其迭代公式 产生逼近解x*的迭代数列{x k},这就是Newton法的思想。当x0接近x*时收敛很快,但是当x0选择不好时,可能会发散,因此初值的选取很重要。另外,若将该迭代公式改进为 其中r为要求的方程的根的重数,这就是改进的Newton法,当求解已知重数的方程的根时,在同种条件下其收敛速度要比Newton法快的多。 程序设计: 本实验采用Matlab的M文件编写。其中待求解的方程写成function的方式,如下 function y=f(x); y=-x*x-sin(x); 写成如上形式即可,下面给出主程序。 二分法源程序: clear %%%给定求解区间 b=1.5; a=0; %%%误差 R=1; k=0;%迭代次数初值 while (R>5e-6) ; c=(a+b)/2; if f12(a)*f12(c)>0; a=c; else b=c; end R=b-a;%求出误差 k=k+1; end x=c%给出解 Newton法及改进的Newton法源程序:clear %%%% 输入函数 f=input('请输入需要求解函数>>','s') %%%求解f(x)的导数 df=diff(f); 实验报告方程求根——二分法 班级:学号:姓名:百事尢可乐一、目的和要求 1)通过对二分法的编程练习,掌握方程求根的二分法的算法; 2)通过对二分法的上机运算,进一步体会二分法的特点。 二、实习内容 1)二分法的编程实现。 2)进行有根区间和误差限的比较和讨论。 三、算法 流程图: 1)准备:计算f(x)在有根区间[a, b]端点处的值f(a), f(b)。 2)二分:计算f(x)在区间中点c= 2b a 处的函数值f(c)。3)判断 ?若f(c)与f(a)异号,则根位于区间[a, c]内,以c代替b; ?若f(c)与f(a)同号,则根位于区间[c, b]内,以c代替a; 四、实验步骤 1)完成二分法的程序设计及录入; 2)完成程序的编译和链接,并进行修改; 3)用书上的例子对程序进行验证,并进行修改; 4)对比估算次数与实际二分次数; 5)输入不同的区间初值a, b,查看二分次数的变化;6)输入不同的误差限,查看二分次数的变化; 7)完成实验报告。 五、实验结果 1.经编译、链接及例子验证结果正确的源程序: #include 1. 设?+=1 05dx x x I n n , (1) 由递推公式n I I n n 1 51+-=-,从0I 的几个近似值出发,计算20I ; 解:易得:0I =ln6-ln5=0.1823, 程序为: I=0.182; for n=1:20 I=(-5)*I+1/n; end I 输出结果为:20I = -3.0666e+010 (2) 粗糙估计20I ,用n I I n n 51 5111+- =--,计算0I ; 因为 0095.05 6 0079.01020 201 020 ≈<<≈??dx x I dx x 所以取0087.0)0095.00079.0(2 1 20=+= I 程序为:I=0.0087; for n=1:20 I=(-1/5)*I+1/(5*n); end I 0I = 0.0083 (3) 分析结果的可靠性及产生此现象的原因(重点分析原因)。 首先分析两种递推式的误差;设第一递推式中开始时的误差为000I I E '-=,递推过程的舍入误差不计。并记n n n I I E '-=,则有01)5(5E E E n n n -==-=-Λ。因为=20E 20020)5(I E >>-,所此递推式不可靠。而在第二种递推式中n n E E E )5 1(5110-==-=Λ,误差在缩小, 所以此递推式是可靠的。出现以上运行结果的主要原因是在构造递推式过程中,考虑误差是否得到控制, 即算法是否数值稳定。 2. 求方程0210=-+x e x 的近似根,要求4 1105-+?<-k k x x ,并比较计算量。 (1) 在[0,1]上用二分法; 程序:a=0;b=1.0; while abs(b-a)>5*1e-4 c=(b+a)/2; 计算方法与实习实验报告 学院:电气工程学院 指导老师:李翠平 班级:160093 姓名:黄芃菲 学号:16009330 实习题一 实验1 拉格朗日插值法 一、方法原理 n次拉格朗日插值多项式为:L n(x)=y0l0(x)+y1l1(x)+y2l2(x)+…+y n l n(x) n=1时,称为线性插值,L1(x)=y0(x-x1)/(x0-x1)+ y1(x-x0)/(x1-x0)=y0+(y1-x0)(x-x0)/(x1-x0) n=2时,称为二次插值或抛物线插值,精度相对高些 L2(x)=y0(x-x1)(x-x2)/(x0-x1)/(x0-x2)+y1(x-x0)(x-x2)/(x1-x0)/(x1-x2)+y2(x-x0)(x-x1)/(x2-x0)/(x2-x1) 二、主要思路 使用线性方程组求系数构造插值公式相对复杂,可改用构造方法来插值。 对节点x i(i=0,1,…,n)中任一点x k(0<=k<=n)作一n 次多项式l k(x k),使它在该点上取值为1,而在其余点x i(i=0,1,…,k-1,k+1,…,n)上为0,则插值多项式为L n(x)=y0l0(x)+y1l1(x)+y2l2(x)+…+y n l n(x) 上式表明:n 个点x i(i=0,1,…,k-1,k+1,…,n)都是l k(x)的零点。可求得l k 三.计算方法及过程:1.输入节点的个数n 2.输入各个节点的横纵坐标 3.输入插值点 4.调用函数,返回z 函数语句与形参说明 程序源代码如下: 形参与函数类型参数意义 int n 节点的个数 double x[n](double *x)存放n个节点的值 double y[n](double *y)存放n个节点相对应的函数值 double p 指定插值点的值 double fun() 函数返回一个双精度实型函数值,即插值点p 处的近似函数值 #include 第一次&第二次上机作业 上机作业: 1.在Matlab上执行:>> 5.1-5-0.1和>> 1.5-1-0.5 给出执行结果,并简要分析一下产生现象的原因。 解:执行结果如下: 在Matlab中,小数值很难用二进制进行描述。由于计算精度的影响,相近两数相减会出现误差。 2.(课本181页第一题) 解:(1)n=0时,积分得I0=ln6-ln5,编写如下图代码 从以上代码显示的结果可以看出,I 20的近似值为0.7465 (2)I I =∫I I 5+I 10dx,可得∫I I 610dx ≤∫I I 5+I 10dx ≤∫I I 510dx,得 16(I +1)≤I I ≤15(I +1),则有1126≤I 20≤1105, 取I 20=1 105 ,以此逆序估算I 0。代码段及结果如下图所示 (3)从I20估计的过程更为可靠。首先根据积分得表达式是可知,被积函数随着n的增大,其所围面积应当是逐步减小的,即积分值应是随着n的递增二单调减小的,(1)中输出的值不满足这一条件,(2)满足。设I I表示I I的近似值,I I-I I=(?5)I(I0?I0)(根据递推公式可以导出此式),可以看出,随着n的增大,误差也在增大,所以顺序估计时,算法不稳定性逐渐增大,逆序估计情况则刚好相反,误差不断减小,算法逐渐趋于稳定。 2.(课本181页第二题) (1)上机代码如图所示 求得近似根为0.09058 (2)上机代码如图所示 得近似根为0.09064; (3)牛顿法上机代码如下 计算所得近似解为0.09091 第三次上机作业上机作业181页第四题 线性方程组为 [1.13483.8326 0.53011.7875 1.16513.4017 2.53301.5435 3.4129 4.9317 1.23714.9998 8.76431.3142 10.67210.0147 ][ I1 I2 I3 I4 ]=[ 9.5342 6.3941 18.4231 16.9237 ] (1)顺序消元法 A=[1.1348,3.8326,1.1651,3.4017;0.5301,1.7875,2.5330,1.5435; 3.4129, 4.9317,8.7643,1.3142;1.2371,4.9998,10.6721,0.0147]; b=[9.5342;6.3941;18.4231;16.9237]; 上机代码(函数部分)如下 function [b] = gaus( A,b )%用b返回方程组的解 B=[A,b]; n=length(b); RA=rank(A); RB=rank(B); 数值分析上机题(matlab版)(东南大学) 数值分析上机报告 第一章 一、题目 精确值为)1 1 123(21+--N N 。 1) 编制按从大到小的顺序 1 1 131121222-+??+-+-= N S N ,计算S N 的通用程序。 2) 编制按从小到大的顺序 1 21 1)1(111222-+??+--+-= N N S N ,计算S N 的通用程序。 3) 按两种顺序分别计算6 42 10,10, 10S S S ,并指出有效位 数。(编制程序时用单精度) 4) 通过本次上机题,你明白了什么? 二、通用程序 clear N=input('Please Input an N (N>1):'); AccurateValue=single((0-1/(N+1)-1/N+3/2)/2); Sn1=single(0); for a=2:N; Sn1=Sn1+1/(a^2-1); end Sn2=single(0); for a=2:N; Sn2=Sn2+1/((N-a+2)^2-1); end fprintf('The value of Sn using different algorithms (N=%d)\n',N); disp('____________________________________________________') fprintf('Accurate Calculation %f\n',AccurateValue); fprintf('Caculate from large to small %f\n',Sn1); fprintf('Caculate from small to large %f\n',Sn2);最新上海电力学院数值计算方法上机实习题
数值分析上机作业
计算方法第三次上机实习报告
数值分析上机题目详解
计算方法上机题答案
数值分析与实验复化辛卜生公式 龙贝格算法
计算方法上机实习题大作业(实验报告).
数值计算方法I上机实验考试题
《数值计算方法》上机实验报告
东南大学计算方法与实习上机实验一
计算方法试题库讲解
计算方法与实习上机题答案
数值计算方法上机实习题
(完整版)哈工大-数值分析上机实验报告
计算方法与实习 方程求根(二分法)
(完整版)数值计算方法上机实习题答案
东南大学计算方法实验报告
计算方法上机作业集合
数值分析上机题(matlab版)(东南大学)