安徽省铜陵市第五中学2015届高三10月月考数学文试题

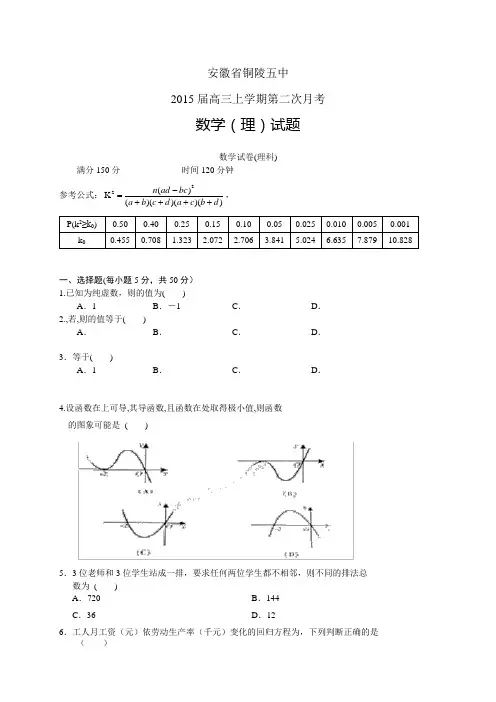
安徽省铜陵五中2015届高三上学期第二次月考数学（理）试题数学试卷(理科)满分150分时间120分钟参考公式：22()K()()()()n ad bca b c d a c b d-=++++，一、选择题(每小题5分，共50分）1.已知为纯虚数，则的值为( )A．1 B．－1 C．D．2.,若,则的值等于( )A．B．C．D．3．等于( )A．1 B．C．D．4.设函数在上可导,其导函数,且函数在处取得极小值,则函数的图象可能是( )5．3位老师和3位学生站成一排，要求任何两位学生都不相邻，则不同的排法总数为( )A．720B．144C．36D．126．工人月工资（元）依劳动生产率（千元）变化的回归方程为，下列判断正确的是（ ）A ．劳动生产率为1000元时，工资为150元B ．劳动生产率提高1000元时，工资提高150元C ．劳动生产率提高1000元时，工资提高90元D ．劳动生产率为1000元时，工资为90元7.在15个村庄中有7个村庄交通不方便，现从中任意选10个村庄，用X 表示这10个村庄中交通不方便的村庄数，下列概率中等于C 74C 86C 1510的是( )A ．P (X ＝2)B ．P (X ≤2)C ．P (X ＝4)D ．P (X ≤4)8.若，则等于( )A ．B ．C ．D ．9.在吸烟与患肺病这两个分类变量的计算中，下列说法正确的是（ ）A.若K 2的观测值为k=6.635,我们有99%的把握认为吸烟与患肺病有关系，那么在100个吸 烟的人中必有99人患有肺病;B.从独立性检验可知有99%的把握认为吸烟与患肺病有关系时，我们说某人吸烟，那么他 有99%的可能患有肺病;C.若从统计量中求出有95% 的把握认为吸烟与患肺病有关系，是指有5% 的可能性使得推判 出现错误;D.以上三种说法都不正确.10.设某批产品合格率为34，不合格率为14，现对该产品进行测试，设第ξ次首次测到正品，则P (ξ＝3)等于( )A ．C 32(14)2×(34)B ．C 32(34)2×(14)C ．(14)2×(34)D ．(34)2×(14)二、填空题（每小题5分，共25分）11．从5名学生中任选4名分别参加数学、物理、化学、生物四科竞赛，且每科竞赛只有1人参加，若甲不参加生物竞赛，则不同的选择方案共有________种． 12.函数在（1，1）处的切线方程是________. 13.设离散型随机变量X 的分布列为则P (1≤X ≤3)＝________.14．已知连续型随机变量x 的分布函数为：⎪⎩⎪⎨⎧≤<≤<=21 a 1x 0ax 0)(x x f 其他 则_____________．15.若(x －a )8＝a 0＋a 1x ＋a 2x 2＋…＋a 8x 8，且a 5＝56，则a 0＋a 1＋a 2＋…＋a 8＝________.三、解答题（共75分，解答应写出必要的文字说明，证明过程或演算步骤）16.（1）若“身高大于175厘米”的为“高个”，“身高小于等于175厘米”的为“非高个”；“脚长大于42码”的为“大脚”，“脚长小于等于42码”的为“非大脚”，请根据上表数据完成下面的2×2列联表。

铜陵五中2014-2015学年度高三第一学期第二次月考数学试卷〔文科〕一、选择题〔每一小题5分，共50分〕1、设集合U={1，2，3，4}，A=｛1，2｝，B={2，4}，如此B)(A ⋂U C 等于〔 〕A.{1，3，4}B.{1，4}C.{2}D.{3}2、函数()xx x f -21)1ln(+-=的定义域为〔 〕 A.〔1，2〕 B.[1，2〕 C.(1，2] D.[1，2]3、函数)12(+x f 的定义域是[0,1]，如此函数)11(-x f 的定义域为〔 〕 A.〔0，1] B.[-1，0〕 C.[34，2] D.[1，3] 4、设R x ∈，如此“03-2>x x 〞是“4>x 〞的( ) A.充分而不必要条件 B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件5、命题P:01,2≥++∈∀ax ax R x 为真命题，如此实数a 的取值范围是〔 〕A.〔0，4]B. 〔∞-，4〕 ⋃ 〔4，∞+〕C.〔∞-，0] ⋃ [4，∞+〕D. [0，4]6、曲线3x y =在点〔b a ,〕处的切线与直线013=++y x 垂直，如此a 的值是〔 〕A.-1B.1±C.1D.3± 7、函数()x x f x f sin cos 4/+⎪⎭⎫ ⎝⎛=π ，如此⎪⎭⎫ ⎝⎛4πf 的值为〔 〕 A.1-2 B.12-+ C.1 D.08、函数a ax x y +=2-3在〔0，1〕内有极小值，如此实数a 的取值范围是〔 〕A.〔0，3〕B.〔0，23〕 C. 〔0，∞+〕 D. 〔∞-，-3〕9、 πθπ<<2,53-2sin =⎪⎭⎫ ⎝⎛+θπ，如此)-tan(θπ的值为〔 〕 A.43 B. 34- C. 43- D. 34 10、在三角形ABC 中，假设1tan tan tan tan ++=B A B A ，如此C cos 的值是〔 〕 A.32- B.22 C. 21 D.21-二、填空题〔每一小题5分，共25分〕11、定义在R 上的奇函数()x f ，假设0>x 时，()()3-x 2x x f =，如此()=1-f12、命题R x x p ∈∀21: ，()()()()0--1212≥x x x f x f ，如此p ⌝是 13、函数x x y cos 2+=在[2,0π ]上取得最大值时，x 的值为 14、不等式0ln ≤+-c x xx 对任意0>x 恒成立，如此c 的取值范围为 15、函数()1-22x e x f =，假设12cos =⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+θπf ，如此θ的值为 三、解答题16、〔12分〕函数()()()1,0)1log(1log ≠>--+=a a x x x f a〔1〕求()x f 的定义域；〔2〕判断()x f 的奇偶性，并给出证明；〔3〕当1>a 时，求使()0>x f 的x 的取值范围。

2014-2015学年安徽省铜陵五中高三（上）10月月考数学试卷（理科）一、选择题：（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知复数z1=m﹣2i，z2=3+4i若为实数，则实数m的值为（）A． B． C．﹣ D．﹣2．设随机变量ξ～N（0，1），若P（ξ＞1）=p，则P（﹣1＜ξ＜0）=（）A．+p B． 1﹣p C． 1﹣2p D．﹣p3．已知t＞0，若（2x﹣2）dx=8，则t=（）A． 1 B．﹣2 C．﹣2或4 D． 44．的展开式中常数项为（）A． B． C． D． 1055．将直线2x﹣y+λ=0沿x轴向左平移一个单位，所得直线与曲线C：（θ为参数）相切，则实数λ的值为（）A．﹣7或3 B．﹣2或8 C． 0或10 D． 1或116．设三次函数f（x）的导函数f′（x），函数y=xf′（x）的图形的一部分如图所示，则（）A． f（x）的极大值为f（），极小值为f（﹣）B． f（x）的极大值为f（0），极小值为f（﹣3）C． f（x）的极大值为f（3），极小值为f（﹣3）D． f（x）的极大值为f（3），极小值为f（0）7．已知f（x）为定义在（﹣∞，+∞）上的可导函数，且f（x）＜f′（x）对于x∈R恒成立，则（）A． f（2）＞e2f（0），f（2010）＞e2010f（0） B． f（2）＜e2f（0），f（2010）＞e2010f （0）C． f（2）＞e2f（0），f（2010）＜e2010f（0） D． f（2）＜e2f（0），f（2010）＜e2010f （0）8．体育老师把9个相同的足球放入编号为1，2，3的三个箱子中，要求每个箱子放球的个数不少于其编号，则不同的放球方法有（）A． 8种 B． 10种 C． 12种 D． 16种9．抛掷两枚骰子，当至少有一枚5点或一枚6点出现时，就说这次实验成功，则在30次实验中成功次数X的期望是（）A． B． C． D． 1010．对大于或等于2的自然数 m的n 次方幂有如下分解方式：22=1+3，32=1+3+5，42=1+3+5+7；23=3+5，33=7+9+11，43=13+15+17+19．根据上述分解规律，若n2=1+3+5+…+19，m3（m∈N*）的分解中最小的数是21，则m+n的值为（）A． 15 B． 16 C． 17 D． 18二、填空题（本大题共5小题，每小题5分，共25分．把答案填在题中横线上）．11．若不等式|x+1|+|x﹣3|≥|m﹣1|恒成立，则m的取值范围为．12．（选修4﹣4：坐标系与参数方程）在极坐标系中，曲线C1：ρ=4上有3个不同的点到曲线的距离等于2，则m= ．13．x10=a0+a1（x﹣1）+a2（x﹣1）2+…+a10（x﹣1）10，则a7的值为．14．已知x＞0，y＞0，若9x2+y2＞（m2+5m）xy恒成立，则实数m的取值范围是．15．给出下列5种说法：①在频率分布直方图中，众数左边和右边的直方图的面积相等；②标准差越小，样本数据的波动也越小③回归直线过样本点的中心（，）；④在回归分析中对于相关系数r，通常，当|r|大于0，75时，认为两个变量存在着很强的线性相关关糸．⑤极点与直角坐标系的原点重合，极轴与x轴非负半轴重合，曲线C的极坐标方程为ρ=2sinθ，直线l的参数方程为（t为参数），直线l与曲线C交于A、B，则线段AB的长等于；其中说法正确的是（请将正确说法的序号写在横线上）．三、解答题：本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤．16．（12分）（2014秋•狮子山区校级月考）设a为实数，函数f（x）=x2e﹣x+2a，x∈R．（Ⅰ）求f（x）的极值；（Ⅱ）当x＞0时，恒有ae x＞x2，求a的取值范围．17．（12分）（2014秋•狮子山区校级月考）已知：x＞0，y＞0，x≠y，且x+y=x2+y2+xy，求证：1＜x+y＜．18．（12分）（2014•北京模拟）在一次对某班42名学生参加课外篮球、排球兴趣小组（每人参加且只参加一个兴趣小组）情况调查中，经统计得到如下2×2列联表：（单位：人）篮球排球总计男同学 16 6 22女同学 8 12 20总计 24 18 42（Ⅰ）据此判断是否有95%的把握认为参加“篮球小组”或“排球小组”与性别有关？（Ⅱ）在统计结果中，如果不考虑性别因素，按分层抽样的方法从两个兴趣小组中随机抽取7名同学进行座谈．已知甲、乙、丙三人都参加“排球小组”．①求在甲被抽中的条件下，乙丙也都被抽中的概率；②设乙、丙两人中被抽中的人数为X，求X的分布列及数学期望E（X）．下面临界值表供参考：P（K2≥k0） 0.15 0.10 0.05 0.025 0.010 0.005 0.001k0 2.072 2.706 3.841 5.024 6.635 7.879 10.828参考公式：K2=．19．（12分）（2015春•南阳校级月考）用数学归纳法证明：1+++…+＜2﹣（n≥2）20．（13分）（2014秋•狮子山区校级月考）袋中装有35个球，每个球上都标有1到35的一个号码，设号码为n的球重克，这些球等可能地从袋中被取出．（1）如果任取1球，试求其重量大于号码数的概率；（2）如果不放回任意取出2球，试求它们重量相等的概率；（3）如果取出一球，当它的重量大于号码数，则放回，搅拌均匀后重取；当它的重量小于号码数时，则停止取球．按照以上规则，最多取球3次，设停止之前取球次数为ξ，求Eξ．21．（14分）（2014•宝鸡三模）设函数f（x）=x2+bln（x+1），其中b≠0．（1）若b=﹣12，求f（x）在[1，3]的最小值；（2）如果f（x）在定义域内既有极大值又有极小值，求实数b的取值范围；（3）是否存在最小的正整数N，使得当n≥N时，不等式恒成立．2014-2015学年安徽省铜陵五中高三（上）10月月考数学试卷（理科）参考答案与试题解析一、选择题：（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知复数z1=m﹣2i，z2=3+4i若为实数，则实数m的值为（）A． B． C．﹣ D．﹣考点：复数代数形式的乘除运算．专题：数系的扩充和复数．分析：若为实数，则设=b，利用待定系数法进行求解即可．解答：解：∵z1=m﹣2i，z2=3+4i，∴若为实数，则设=b，则z1=bz2，即m﹣2i=3b+4bi，即，解得b=﹣，m=﹣，故选：D点评：本题主要考查复数的基本运算，根式复数的四则运算法则，利用待定系数法是解决本题的关键．2．设随机变量ξ～N（0，1），若P（ξ＞1）=p，则P（﹣1＜ξ＜0）=（）A．+p B． 1﹣p C． 1﹣2p D．﹣p考点：正态分布曲线的特点及曲线所表示的意义．专题：计算题．分析：根据随机变量ξ～N（0，1），正态曲线关于x=0对称，得到对称区间对应的概率相等，根据大于1的概率得到小于﹣1的概率，根据对称轴一侧的区间的概率是，得到结果．解答：解：∵随机变量ξ～N（0，1），∴正态曲线关于x=0对称，∵P（ξ＞1）=p，∴P（ξ＜﹣1）=p，∴P（﹣1＜ξ＜0）=﹣p，故选D．点评：本题考查正态分布曲线的特点及曲线所表示的意义，考查正态曲线的对称性的应用，考查关于对称轴对称的区间上的概率相等，本题是一个基础题，题目中所处的字母p可以变式为实数．3．已知t＞0，若（2x﹣2）dx=8，则t=（）A． 1 B．﹣2 C．﹣2或4 D． 4考点：微积分基本定理．专题：导数的综合应用．分析：利用微积分基本定理即可得出．解答：解：∵（x2﹣2x）′=2x﹣2，∴若（2x﹣2）dx==t2﹣2t=8，又t＞0，解得t=4．故选：D．点评：本题考查了微积分基本定理，属于基础题．4．的展开式中常数项为（）A． B． C． D． 105考点：二项式定理的应用．专题：计算题．分析：在的展开式通项公式中，令x的幂指数等于零，求出r的值，即可求得展开式中常数项．解答：解：的展开式通项公式为T r+1==，令=0，r=4．故展开式中常数项为=，故选B．点评：本题主要考查二项式定理，二项展开式的通项公式，求展开式中某项的系数，属于中档题．5．将直线2x﹣y+λ=0沿x轴向左平移一个单位，所得直线与曲线C：（θ为参数）相切，则实数λ的值为（）A．﹣7或3 B．﹣2或8 C． 0或10 D． 1或11考点：参数方程化成普通方程．专题：直线与圆；坐标系和参数方程．分析：先求出平移后所得直线l的方程，把曲线C的方程化为普通方程，求出圆心和半径，再根据圆心到直线l的距离等于半径可得实数λ的值．解答：解：将直线2x﹣y+λ=0沿x轴向左平移一个单位，所得直线l的方程为2（x+1）﹣y+λ=0，即 2x﹣y+2+λ=0．曲线C：（θ为参数）即（x+1）2+（y﹣2）2=5，表示以C（﹣1，2）为圆心，半径等于的圆．再根据圆心到直线l的距离等于半径可得=，可得λ=3 或λ=﹣7，故选：A．点评：本题主要考查把参数方程化为普通方程的方法，点到直线的距离公式、直线和圆的位置关系，属于基础题．6．设三次函数f（x）的导函数f′（x），函数y=xf′（x）的图形的一部分如图所示，则（）A． f（x）的极大值为f（），极小值为f（﹣）B． f（x）的极大值为f（0），极小值为f（﹣3）C． f（x）的极大值为f（3），极小值为f（﹣3）D． f（x）的极大值为f（3），极小值为f（0）考点：利用导数研究函数的极值；导数的运算．专题：数形结合；导数的综合应用．分析：观察图象知，x＜﹣3时，f′（x）＜0．﹣3＜x＜0时，f′（x）＞0．由此知极小值为f（﹣3）．0＜x＜3时，yf′（x）＞0．x＞3时，f′（x）＜0．由此知极大值为f（3）．解答：解：观察图象知，x＜﹣3时，y=x•f′（x）＞0，∴f′（x）＜0，f（x）递减；当﹣3＜x＜0时，y=x•f′（x）＜0，∴f′（x）＞0，f（x）递增．由此知f（x）的极小值为f（﹣3）；当0＜x＜3时，y=x•f′（x）＞0，∴f′（x）＞0，f（x）递增，当x＞3时，y=x•f′（x）＜0，∴f′（x）＜0，f（x）递减．由此知f（x）的极大值为f（3）．故选：C．点评：本题考查函数的极值的性质和应用，解题时要仔细观察图象，注意数形结合思想的合理运用．7．已知f（x）为定义在（﹣∞，+∞）上的可导函数，且f（x）＜f′（x）对于x∈R恒成立，则（）A． f（2）＞e2f（0），f（2010）＞e2010f（0） B． f（2）＜e2f（0），f（2010）＞e2010f （0）C． f（2）＞e2f（0），f（2010）＜e2010f（0） D． f（2）＜e2f（0），f（2010）＜e2010f （0）考点：利用导数研究函数的单调性．专题：压轴题．分析：先转化为函数y=的导数形式，再判断增减性，从而得到答案．解答：解：∵f（x）＜f'（x）从而 f'（x）﹣f（x）＞0 从而＞0从而＞0 从而函数y=单调递增，故 x=2时函数的值大于x=0时函数的值，即所以f（2）＞e2f（0）．同理f（2010）＞e2010f（0）；故选A．点评：本题主要考查函数的单调性与其导函数的正负情况之间的关系，即导函数大于0时原函数单调递增，当导函数小于0时原函数单调递减．8．体育老师把9个相同的足球放入编号为1，2，3的三个箱子中，要求每个箱子放球的个数不少于其编号，则不同的放球方法有（）A． 8种 B． 10种 C． 12种 D． 16种考点：计数原理的应用．专题：计算题．分析：首先在三个箱子中放入要求的个数，下面是一个分类计数问题，可以在每一个箱子中放一个，有1种结果，可以把球分成两份，这两份在三个位置排列，有A32种结果，可以把三个球都放到一个箱子中，有3种结果，相加得到结果．解答：解：首先在三个箱子中放入要求的个数，这样剩下三个足球，这三个足球可以随意放置，下面是一个分类计数问题，第一种方法，可以在每一个箱子中放一个，有1种结果，第二种方法，可以把球分成两份，1和2，这两份在三个位置排列，有A32=6种结果第三种方法，可以把三个球都放到一个箱子中，有3种结果，综上可知共有1+6+3=10种结果，故选B．点评：本题考查分类计数问题，在解题时注意首先要满足条件中的要求，再注意余下的元素所有可能符合的条件，注意做到不重不漏．9．抛掷两枚骰子，当至少有一枚5点或一枚6点出现时，就说这次实验成功，则在30次实验中成功次数X的期望是（）A． B． C． D． 10考点：离散型随机变量的期望与方差．专题：计算题．分析：由题意知试验中的事件是相互独立的，事件发生的概率是相同的，得到成功次数ξ服从二项分布，根据二项分布的期望公式得到结果．解答：解：∵成功次数ξ服从二项分布，每次试验成功的概率为1﹣=，∴在30次试验中，成功次数ξ的期望为×30=．故选C点评：二项分布要满足的条件：每次试验中，事件发生的概率是相同的，各次试验中的事件是相互独立的，每次试验只要两种结果，要么发生要么不发生，随机变量是这n次独立重复试验中事件发生的次数．10．对大于或等于2的自然数 m的n 次方幂有如下分解方式：22=1+3，32=1+3+5，42=1+3+5+7；23=3+5，33=7+9+11，43=13+15+17+19．根据上述分解规律，若n2=1+3+5+…+19，m3（m∈N*）的分解中最小的数是21，则m+n的值为（）A． 15 B． 16 C． 17 D． 18考点：归纳推理．专题：等差数列与等比数列；推理和证明．分析：根据等差数列的通项公式以及数列的求和公式即可求出m，n的值，进而得到答案．解答：解：依题意得 n2=1+3+5+…+19==100，∴n=10．∵m3（m∈N*）的分解中最小的数是21，∴m3=21m+=m2+20m，即m2﹣m﹣20=0，∴（m﹣5）（m+4）=0，∴m=5或m=﹣4．又 m∈N*，∴m=5，∴m+n=15．故选：A点评：归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质；（2）从已知的相同性质中推出一个明确表达的一般性命题（猜想）．二、填空题（本大题共5小题，每小题5分，共25分．把答案填在题中横线上）．11．若不等式|x+1|+|x﹣3|≥|m﹣1|恒成立，则m的取值范围为m∈[﹣3，5] ．考点：绝对值不等式的解法．专题：转化思想．分析：根据绝对值的意义|x+1|+|x﹣3|表示数轴上的x对应点到3和﹣1对应点的距离之和，它的最小值等于4，可得答案．解答：解：|x+1|+|x﹣3|表示数轴上的x对应点到﹣1和3对应点的距离之和，它的最小值等于4，由不等式|x+1|+|x﹣3|≥|m﹣1|恒成立知，|m﹣1|≤4，m∈[﹣3，5]故答案为m∈[﹣3，5]．点评：本题考查绝对值的意义，绝对值不等式的解法，求出|x+1|+|x﹣3|的最小值，是解题的关键．12．（选修4﹣4：坐标系与参数方程）在极坐标系中，曲线C1：ρ=4上有3个不同的点到曲线的距离等于2，则m= ±2．考点：简单曲线的极坐标方程．专题：坐标系和参数方程．分析：把极坐标方程化为直角坐标方程，再根据弦心距等于半径的一半，求得m的值．解答：解：曲线C1：ρ=4即 x2+y2=16，表示以原点为圆心、半径等于4的圆，曲线即x+y﹣m=0，即 x+y﹣m=0，由题意可得，弦心距等于半径的一半，即=2，求得m=±2，故答案为：±2．点评：本题主要考查把极坐标方程化为直角坐标方程的方法，点到直线的距离公式的应用，属于基础题．13．x10=a0+a1（x﹣1）+a2（x﹣1）2+…+a10（x﹣1）10，则a7的值为120 ．考点：二项式系数的性质．专题：二项式定理．分析：把x10转化为[（x﹣1）+1]10，利用二项式定理的通项公式，求出a8的值．解答：解：因为x10=[（x﹣1）+1]10=a0+a1（x﹣1）+a2（x﹣1）2+…+a10（x﹣1）10，所以a7=C103=120故答案为：120．点评：本题考查二项式定理展开式中系数的求法，二项式特定项的求法，考查计算能力．14．已知x＞0，y＞0，若9x2+y2＞（m2+5m）xy恒成立，则实数m的取值范围是﹣6＜m＜1 ．考点：函数恒成立问题．专题：计算题．分析：由题意9x2+y2＞（m2+5m）xy两边除以xy，然后利用均值不等式进行求解；解答：解：∵x＞0，y＞0，若9x2+y2＞（m2+5m）xy恒成立，∴＞m2+5m，只要求出的最小值即可，∵=+≥2=6，∴m2+5m＜6，解得﹣6＜m＜1，故答案为：﹣6＜m＜1．点评：此题看似函数的恒成立问题，其实质还是考查均值不等式的应用，是一道基础题；15．给出下列5种说法：①在频率分布直方图中，众数左边和右边的直方图的面积相等；②标准差越小，样本数据的波动也越小③回归直线过样本点的中心（，）；④在回归分析中对于相关系数r，通常，当|r|大于0，75时，认为两个变量存在着很强的线性相关关糸．⑤极点与直角坐标系的原点重合，极轴与x轴非负半轴重合，曲线C的极坐标方程为ρ=2sinθ，直线l的参数方程为（t为参数），直线l与曲线C交于A、B，则线段AB的长等于；其中说法正确的是②③④⑤（请将正确说法的序号写在横线上）．考点：命题的真假判断与应用．专题：简易逻辑．分析：①对众数理解不到位，应该是“中位数”左右两边面积相等；②标准差反映的是样本数据的离散程度，因此应该标准差越小，波动越小；③根据回归直线的性质可知，所有回归直线都过样本点的中心，即过（）；④线性回归相关系数r，一看正负，二看绝对值，绝对值以0.75为界，大于则有很强的相关性，否则认为弱相关；⑤先化成直角坐标系下的方程，然后再进一步求直线与圆的相交弦的弦长．解答：解：对于①：众数指的是出现频率最高的数，未必是中间的数，因此①不对；对于②：标准差是方差的算术平方根，因此也反映了样本数据的离散程度，因此标准差越小，则数据越集中，波动越小，故②正确；对于③：样本点的中心是（），所有回归直线都经过样本点的中心，故③正确；对于④：线性回归相关系数r，一看正负，决定是正相关还是负相关；二看绝对值，绝对值以0.75为界，大于0.75则有很强的相关性，否则认为弱相关；对于⑤：ρ=2sinθ的方程为x2+（y﹣1）2=1，参数方程为（t为参数）的方程为，则圆心到直线的距离为．则半径是1，所以弦长为，故⑤正确．故答案为：②③④⑤．②③④⑤点评：此类问题一般难度不大，主要是考查基础知识为主，因此解决问题必须把概念理解到位，方法掌握到位才能解决问题．三、解答题：本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤．16．（12分）（2014秋•狮子山区校级月考）设a为实数，函数f（x）=x2e﹣x+2a，x∈R．（Ⅰ）求f（x）的极值；（Ⅱ）当x＞0时，恒有ae x＞x2，求a的取值范围．考点：导数在最大值、最小值问题中的应用；利用导数研究函数的极值．专题：综合题；导数的综合应用．分析：（Ⅰ）求导数，确定函数的单调性，即可求f（x）的极值；（Ⅱ）当x＞0时，恒有ae x＞x2，分离参数，求最值，即可求a的取值范围．解答：解：（Ⅰ）由题意知f（x）的定义域为R，f′（x）=e﹣x（2x﹣x2），令f′（x）=0⇒x=0或2，列表如下：x （﹣∞，0） 0 （0，2） 2 （2，+∞）f′（x）﹣ 0 + 0 ﹣f（x）减极小值增极大值减由上表可知f（x）极小值=f（0）=2a；．…（6分）（Ⅱ）由ae x＞x2，∴3a＞x2e﹣x+2a，∀x∈（0，+∞）令f（x）=x2e﹣x+2a，由（Ⅰ）可知：当x∈（0，+∞）时，x=2时，f（x）min=f（2）=，所以…（12分）点评：本题考查导数知识的运用，考查函数的极值与最值，正确运用分离参数求最值是关键．17．（12分）（2014秋•狮子山区校级月考）已知：x＞0，y＞0，x≠y，且x+y=x2+y2+xy，求证：1＜x+y＜．考点：不等式的证明．专题：不等式．分析：根据条件便可得到xy=（x+y）2﹣（x+y），而由基本不等式便可得到，解该关于x+y的不等式即可得出要证的结论．解答：证：由已知得：x+y=（x+y）2﹣xy；即xy=（x+y）2﹣（x+y）；∵x＞0，y＞0，x≠y；∴；即；∴；解得；∴结论成立．点评：考查完全平方式及基本不等式的运用，注意基本不等式中等号“=”成立的条件，学习本题解一元二次不等式的方法．18．（12分）（2014•北京模拟）在一次对某班42名学生参加课外篮球、排球兴趣小组（每人参加且只参加一个兴趣小组）情况调查中，经统计得到如下2×2列联表：（单位：人）篮球排球总计男同学 16 6 22女同学 8 12 20总计 24 18 42（Ⅰ）据此判断是否有95%的把握认为参加“篮球小组”或“排球小组”与性别有关？（Ⅱ）在统计结果中，如果不考虑性别因素，按分层抽样的方法从两个兴趣小组中随机抽取7名同学进行座谈．已知甲、乙、丙三人都参加“排球小组”．①求在甲被抽中的条件下，乙丙也都被抽中的概率；②设乙、丙两人中被抽中的人数为X，求X的分布列及数学期望E（X）．下面临界值表供参考：P（K2≥k0） 0.15 0.10 0.05 0.025 0.010 0.005 0.001k0 2.072 2.706 3.841 5.024 6.635 7.879 10.828参考公式：K2=．考点：独立性检验的应用．专题：综合题；概率与统计．分析：（Ⅰ）由表中数据得K2的观测值，与临界值比较，即可得出结论；（Ⅱ）①方法一：令事件B为“甲被抽到”；事件A为“乙丙被抽到”，则P（B|A）=；方法二：令事件C为“在甲被抽到的条件下，乙丙也被抽到”，则P（C）=；②由题知X的可能值为0，1，2，求出相应的概率，可得X的分布列及数学期望E（X）．解答：解：（Ⅰ）由表中数据得K2的观测值k==≈4.582＞3.841．…2分所以，据此统计有95%的把握认为参加“篮球小组”或“排球小组”与性别有关．…4分（Ⅱ）①由题可知在“排球小组”的18位同学中，要选取3位同学．方法一：令事件B为“甲被抽到”；事件A为“乙丙被抽到”，则P（A∩B）=，P（A）=．所以P（B|A）====．…7分方法二：令事件C为“在甲被抽到的条件下，乙丙也被抽到”，则P（C）===．②由题知X的可能值为0，1，2．依题意P（X=0）==；P（X=1）==；P（X=2）==．从而X的分布列为X 0 1 2P…10分于是E（X）=0×+1×+2×==．…12分．点评：考查分类变量的独立性检验，条件概率，随机变量的分布列、数学期望等，中等题．19．（12分）（2015春•南阳校级月考）用数学归纳法证明：1+++…+＜2﹣（n≥2）考点：数学归纳法．专题：点列、递归数列与数学归纳法．分析：原题要求利用数学归纳法证明数列不等式，首先验证n=2时不等式成立，然后假设n=k时不等式成立，然后利用归纳假设证明n=k+1时不等式成立，最后下结论．解答：证明：①当n=2时，原不等式左边=，右边=，左边＜右边，不等式成立；②假设当n=k时，原不等式成立，即1+++…+＜2﹣成立，则当n=k+1时，1+++…++＜2﹣+===．即n=k+1时原不等式也成立．综上，对于任意n（n∈N*且n≥2）原不等式成立．点评：本题考查利用数学归纳法证明数列不等式，利用归纳法证明与自然数有关的命题，关键是用上归纳假设，是中档题．20．（13分）（2014秋•狮子山区校级月考）袋中装有35个球，每个球上都标有1到35的一个号码，设号码为n的球重克，这些球等可能地从袋中被取出．（1）如果任取1球，试求其重量大于号码数的概率；（2）如果不放回任意取出2球，试求它们重量相等的概率；（3）如果取出一球，当它的重量大于号码数，则放回，搅拌均匀后重取；当它的重量小于号码数时，则停止取球．按照以上规则，最多取球3次，设停止之前取球次数为ξ，求Eξ．考点：离散型随机变量的期望与方差；等可能事件的概率．专题：计算题；概率与统计．分析：（1）利用重量大于号码数，建立不等式，确定n的可能取值，从而可求概率；（2）利用它们重量相等，建立等式，确定n的可能取值，从而可求概率；（3）确定ξ的可能取值，求得相应的概率，从而可求Eξ．解答：解：（1）由＞n，可得n2﹣12n+30＞0，…（1分）∴n＞6+或n＜6﹣，由于n∈N*，所以n可取1，2，3，9，10，11，12，13，…，35共30个数，…（3分）故，…（4分）（2）因为是不放回任意取出2球，故这是编号不相同的两个球，设它们的编号分别为n1和n2，由5n1+15=﹣5n2+15，得，…（5分）因为n1≠n2，所以n1+n2=10，从而满足条件的球有（1，9），（2，8），（3，7），（4，6）…（7分）故概率为…（8分）（3）ξ的可能取值为1，2，3，则，P（ξ=2）=；P（ξ=3）=；∴Eξ=1×．…（12分）点评：本题考查概率的计算，考查离散型随机变量的期望，考查学生的计算能力，属于中档题．21．（14分）（2014•宝鸡三模）设函数f（x）=x2+bln（x+1），其中b≠0．（1）若b=﹣12，求f（x）在[1，3]的最小值；（2）如果f（x）在定义域内既有极大值又有极小值，求实数b的取值范围；（3）是否存在最小的正整数N，使得当n≥N时，不等式恒成立．考点：一元二次方程的根的分布与系数的关系；函数恒成立问题；函数在某点取得极值的条件；利用导数求闭区间上函数的最值．专题：综合题；压轴题．分析：（1）当b=﹣12时，由得x=2，可判断出当x∈[1，2）时，f（x）单调递减；当x∈（2，3]时，f（x）单调递增，故f（x）在[1，3]的最小值在x=2时取得．（2）要使f（x）在定义域内既有极大值又有极小值，即f（x）在定义域内与X轴有三个不同的交点，即使在（﹣1，+∞）有两个不等实根，即2x2+2x+b=0在（﹣1，+∞）有两个不等实根，可以利用一元二次函数根的分布可得，解之即可求b的范围．（3）先构造函数h（x）=x3﹣x2+ln（x+1），然后研究h（x）在[0，+∞）上的单调性，求出函数h（x）的最小值，从而得到ln（x+1）＞x2﹣x3，最后令，即可证得结论．解答：解：（1）由题意知，f（x）的定义域为（﹣1，+∞），b=﹣12时，由，得x=2（x=﹣3舍去），当x∈[1，2）时，f′（x）＜0，当x∈（2，3]时，f′（x）＞0，所以当x∈[1，2）时，f（x）单调递减；当x∈（2，3]时，f（x）单调递增，所以f（x）min=f（2）=4﹣12ln3（2）由题意在（﹣1，+∞）有两个不等实根，即2x2+2x+b=0在（﹣1，+∞）有两个不等实根，设g（x）=2x2+2x+b，则，解之得；（3）对于函数f（x）=x2﹣ln（x+1），令函数h（x）=x3﹣f（x）=x3﹣x2+ln（x+1）则，∴当x∈[0，+∞）时，h′（x）＞0所以函数h（x）在[0，+∞）上单调递增，又h（0）=0，∴x∈（0，+∞）时，恒有h（x）＞h（0）=0即x2＜x3+ln（x+1）恒成立．取，则有恒成立．显然，存在最小的正整数N=1，使得当n≥N时，不等式恒成立点评：本题以函数为载体，考查函数的最值，考查函数的单调性．第一问判断f（x）在定义域的单调性即可求出最小值．第二问将f（x）在定义域内既有极大值又有极小值问题转化为f（x）在定义域内与X轴有三个不同的交点是解题的关键，第三问的关键是构造新函数，利用导数证明不等式．。

铜陵市第五中学2015届高三上学期第二次月考数学（文科）试题一、选择题（每小题5分，共50分）1、设集合U={1，2，3，4}，A=｛1，2｝，B={2，4}，则B)(A ⋂U C 等于（ ）A.{1，3，4}B.{1，4}C.{2}D.{3} 2、函数()xx x f -21)1ln(+-=的定义域为（ ） A.（1，2） B.[1，2） C.(1，2] D.[1，2] 3、已知函数)12(+x f 的定义域是[0,1]，则函数)11(-x f 的定义域为（ ） A.（0，1] B.[-1，0） C.[34，2] D.[1，3]4、设R x ∈，则“03-2> x x ”是“4>x ”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件 5、命题P:01,2≥++∈∀ax ax R x 为真命题，则实数a 的取值范围是（ ）A.（0，4]B. （∞-，4） ⋃ （4，∞+）C.（∞-，0] ⋃ [4，∞+）D. [0，4]6、已知曲线3x y =在点（b a ,）处的切线与直线013=++y x 垂直，则a 的值是（ ）A.-1B.1±C.1D.3± 7、已知函数()x x f x f sin cos 4/+⎪⎭⎫⎝⎛=π ，则⎪⎭⎫⎝⎛4πf 的值为（ ） A.1-2 B. 12-+ C.1 D.0 8、函数a ax x y +=2-3在（0，1）内有极小值，则实数a 的取值范围是（ ）A.（0，3）B.（0，23） C. （0，∞+） D. （∞-，-3） 9、已知πθπ<<2,53-2sin =⎪⎭⎫⎝⎛+θπ，则)-tan(θπ的值为（ ） A.43 B. 34- C. 43- D. 34 10、在三角形ABC 中，若1tan tan tan tan ++=B A B A ，则C cos 的值是（ ）A.32-B. 22C. 21D. 21-二、填空题（每小题5分，共25分）11、定义在R 上的奇函数()x f ，若0>x 时，()()3-x 2x x f =，则()=1-f 12、已知命题R x x p ∈∀21: ，()()()()0--1212≥x x x f x f ，则p ⌝是13、函数x x y cos 2+=在[2,0π]上取得最大值时，x 的值为14、不等式0ln ≤+-c x xx对任意0>x 恒成立，则c 的取值范围为 15、已知函数()1-22x e x f =，若12cos =⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛+θπf ，则θ的值为 三、解答题16、（12分）已知函数()()()1,0)1log(1log ≠>--+=a a x x x f a （1）求()x f 的定义域；（2）判断()x f 的奇偶性，并给出证明；（3）当1>a 时，求使()0>x f 的x 的取值范围。

高三10月月考试题高 三 数 学 2014.10注意事项：1．本试卷共4页．满分160分，考试时间120分钟．2．请将填空题的答案和解答题的解题过程写在答题卡的规定区域，在本试卷上答题无效． 3．答题前，务必将自己的姓名、学校、考试号写在答题卡的指定位置．一、填空题：本大题共14小题，每小题5分，共计70分，请把答案直接填写在答题卡相．．．．应位置．．．上． 1．已知集合{|},{|12},()R A x x a B x x A C B R =<=<<=且，则实数a 的取值范围是▲ ．2．命题“若a 2+b 2=0，则a=0且b=0”的逆否命题是 ▲ ． 3．已知函数3()2log cos x f x x x =++,则()=f x ' ▲ ． 4的值域是[0,)+∞，则实数m 的取值范围是▲ ．5．已知定义域为R 的函数)(x f为奇函数.且满足)()2(x f x f -=+，当[]1,0∈x 时，12)(-=x x f ，则6．若sinx 3)(+=x x f ，则满足不等式0)3()12(>-+-m f m f 的m 的取值范围为 ▲ ．7．已知函数3()y f x x =+为偶函数，且(10)10,f =若函数()()4g x f x =+，则(10)g -=▲ ．89．已知函数f(x)＝x 2－3x ＋m ，g(x)＝2x 2－4x ，若f(x)≥g(x)恰在x ∈[－1，2]上成立，则实数m 的值为 ▲ ．10．一个人喝了少量酒后,血液中的酒精含量迅速上升到0.3mg/mL,在停止喝酒后,血液中的酒精含量以每小时25%的速度减少,为了保障交通安全,某地根据《道路交通安全法》规定:驾驶员血液中的酒精含量不得超过0.09 mg/mL,那么,一个喝了少量酒后的驾驶员,至少经过 ▲ 小时,才能开车(精确到1小时). 11．已知函数123()=+1234x x x x f xx x x x +++++++++，则5522f f ⎛⎛-+- ⎝⎝＝ ▲ ． 12．()f x 的定义域为实数集R 对于任意的x R ∈都有(1)(1)f x f x +=-.若在区间[1,3]-上函数()()g x f x mx m =--恰有四个不同的零点，则实数m 的取值范围是 ▲ ．13．设函数f(x)＝ax 2＋bx ＋c(a<0)的定义域为D ，若所有点(s ，f(t))(s 、t ∈D )构成一个正方形区域，则a 的值为 ▲ ．14．定义在),0(+∞上的函数)(x f 满足：①当[)3,1∈x 时②)(3)3(x f x f =.设关于x 的函数a x f x F -=)()(的零点从小到大依次为*12,,,,()n x x x n N ∈.若(1,3)a ∈，则=++++-n n x x x x 21221 ▲ ．（用n 表示） 二、解答题：本大题共6小题，共计90分．解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题卡的指定区域内． 15．（本小题满分14分）设命题p ：实数x 满足22430x ax a -+<,其中0a >,命题q ：实数x 满足2260,280.x x x x ⎧--≤⎪⎨+->⎪⎩.(1)若1a =且p q ∧为真,求实数x 的取值范围;(2)若p ⌝是q ⌝的充分不必要条件,求实数a 的取值范围.16．（本小题满分14分）已知四边形ABCD 是矩形，AB =，BC ，将△ABC 沿着对角线AC 折起来得到1AB C ∆，且顶点B 1在平面AB=CD 上射影O 恰落在边AD 上，如图所示．（1）求证：AB 1⊥平面B 1CD ；（2）求三棱锥B 1﹣ABC 的体积1B -ABC V ．17．（本小题满分14分）过去的2013年，我国多地区遭遇了雾霾天气，引起口罩热销．某品牌口罩原来每只成本为6元，售价为8元，月销售5万只．(1) 据市场调查，若售价每提高0.5元，月销售量将相应减少0.2万只，要使月总利润不低于原来的月总利润(月总利润＝月销售总收入－月总成本)，该口罩每只售价最多为多少元？(2) 为提高月总利润，厂家决定下月进行营销策略改革，计划每只售价x(x ≥9)元，并投入265(x －9)万元作为营销策略改革费用．据市场调查，每只售价每提高0.5元，月销售量将相应减少0.2（x －8）2万只．则当每只售价x 为多少时，下月的月总利润最大？并求出下月最大总利润．18．（本小题满分16分）（1）若函数)(x f 在2=x 时取得极值，求实数a 的值；（2）若0)(≥x f 对任意),1[+∞∈x 恒成立，求实数a 的取值范围．19．（本小题满分16分）已知函数()()()2log 41,xf x kx k =++∈R 是偶函数.（1）求k 的值；（2）设函数()24log 23x g x a a ⎛⎫=⋅- ⎪⎝⎭，其中0.a >若函数()f x 与()g x 的图象有且只有一个交点，求a 的取值范围.20．（本小题满分16分）已知函数()ln f x ax x x =+的图象在点x e =（e 为自然对数的底数）处的切线的斜率为3．（1）求实数a 的值；（2）若2()f x kx ≤对任意0x >成立，求实数k 的取值范围； （3）当1n m >>*(,)m n N ∈时，证明：参考答案1．2≥a 【解析】通过数轴分析得：2≥a . 考点：集合的交并补 2．若0a ≠或0b ≠,则220a b +≠【解析】试题分析：原命题：若p 则q .逆否命题为：若q ⌝则p ⌝.注意“且”否之后变“或”. 考点：命题的逆否命题. 3． 4．[][)0,19,+∞【解析】试题分析：由题意得：函数1)3(2+-+=x m mx y 的值域包含[0,)+∞，当0=m 时，),,0[13+∞⊃∈+-=R x y 满足题意；当0≠m 时，要满足值域包含[0,)+∞，需使得.0,0≥∆>m 即9≥m 或10≤<m ，综合得：实数m 的取值范围是[][)0,19,+∞.考点：函数值域5【解析】解：因为定义域为R 的函数)(x f 为奇函数.且满足)()2(x f x f-=+，周期为4，当[]1,0∈x 时，12)(-=x x f ，则21(lo2=-6．m>-2 【解析】 试题分析：因为sinx3)(+=x x f 的定义域为R 关于原点对称切满足()()f x f x -=-,所以函数()f x 为奇函数,又因为'()3cosx>0f x =+,所以函数f(x)在R 上单调递增.则(21)(3)0(21)(3)f m f m f m f m -+->⇒->--(21)(3)213f m f m m m ⇒->-⇒->-⇒m>-2,故填m>-2.考点：奇偶性 单调性 不等式 7．2014 【解析】试题分析：由函数3()y f x x =+为偶函数，且(10)10,f =得2010)10(10)10()10()10(33=-⇒+=-+-f f f从而2014420104)10()10(=+=+-=-f g ，故应填入2014．考点：函数的奇偶性． 8．3 【解析】考点：对数运算． 9．2【解析】由题意，x 2－3x ＋m ≥2x 2－4x ，即x 2－x －m ≤0的解集是[－1，2]，所以m ＝2. 10．5【解析】设x 小时后,该驾驶员血液中的酒精含量不超过0.09mg/mL,则有0.3·()x≤0.09,即()x≤0.3,估算或取对数计算得至少5小时后,可以开车. 11．答案：8解析：因为f(x)＝xx ＋1＋x ＋1x ＋2＋x ＋2x ＋3＋x ＋3x ＋4＝4－⎝⎛⎭⎫1x ＋1＋1x ＋2＋1x ＋3＋1x ＋4.设g(x)＝1x ＋1＋1x ＋2＋1x ＋3＋1x ＋4， 则g(－5－x)＝－⎝⎛⎭⎫1x ＋4＋1x ＋3＋1x ＋2＋1x ＋1，所以g(x)＋g(－5－x)＝0，从而f(x)＋f(－5－x)＝8， 故f ⎝⎛⎭⎫－52＋2＋f ⎝⎛⎭⎫－52－2＝8.12【解析】试题分析：因为对任意的x R ∈都有(1)(1)f x f x +=-，所以函数()f x 的周期为2. 由在区间[1,3]-上函数()()g x f x mx m=--恰有四个不同的零点，即函数()f x mx m=+在[1,3]-上有四个不同的零点.即函数()y f x =与函数()h x mx m =+在[1,3]-有四个不同的交点.所以0(3)1h <≤.解得考点：1.分段函数的性质.2.函数的周期性.3.函数的等价变换. 13．答案：－4 解析：|x 1－x 2|＝f max (x)，b 2－4aca 2＝4ac －b 24a，|a|＝2－a ，∴ a ＝－4. 14．6(31)n - 【解析】试题分析：由①当[)3,1∈x 时，可画出()f x 在[)1,3上的图象，根据②)(3)3(x f x f =，只要将()f x 在[)1,3上的图象沿x 轴伸长到原来的3倍，再沿y轴伸长到原来的3倍即可得到()f x 在[)3,9上的图象，以此类推，可得到在[)[)9,27,27,81上的图象，关于x 的函数ax f x F -=)()(的零点，可看成函数()y f x =与y a=图象交点的横坐标，由函数()y f x =图象的对称性可知：,如图，所以就有)()212126136636363313n n n x x ---+++=+⨯+⨯++⨯==-122126(31)n n n x x x x -++++=-考点：函数图象与性质及等比数列求和.15．解析：由22430x ax a -+<得(3)()0x a x a --<,又0a >,所以3a x a <<, 当1a =时,1<3x <,即p 为真时实数x 的取值范围是1<3x <.由2260280x x x x ⎧--≤⎪⎨+->⎪⎩,得23x <≤,即q 为真时实数x 的取值范围是23x <≤.若p q ∧为真,则p 真且q 真,所以实数x 的取值范围是23x <<.(Ⅱ)p ⌝是q ⌝的充分不必要条件,即p ⌝⇒q ⌝,且q ⌝⇒/p⌝,设A={|}x p ⌝,B={|}x q ⌝,则AB ,又A={|}x p ⌝={|3}x x a x a ≤≥或,B={|}x q ⌝={23x x ≤>或}, 则0<2a ≤,且33a >所以实数a 的取值范围是12a <≤. 16．解析：（1）1B O ⊥Q 平面ABCD ，CD ⊂平面ABCD ， ∴1B O CD ⊥，又CD ⊥AD ，AD I 1B O =O ∴CD ⊥平面1AB D ，又1AB ⊂平面1AB D∴1AB CD ⊥，又11AB B C ⊥，且1B C CD C =I1AB ∴⊥平面1B CD（2）由于1AB ⊥平面1B CD ，1B D ⊂平面ABCD ，所以11AB B D ⊥ 在1Rt AB D ∆中，17．解：(1) 设每只售价为x 元，则月销售量为⎝⎛⎭⎫5－x －80.5×0.2万只，由已知得⎝⎛⎭⎫5－x －80.5×0.2(x －6)≥(8－6)×5，(3分)∴ 25x 2－535x ＋2965≤0，即2x 2－53x ＋296≤0，(4分) 解得8≤x ≤372，(5分)即每只售价最多为18.5元．(6分)(2) 下月的月总利润y ＝⎣⎢⎡⎦⎥⎤5－x －80.5×0.2（x －8）2·(x －6)－265(x －9)(9分) ＝2.4－0.4x x －8－15x ＋234－1505＝－0.4（x －8）－0.8x －8－15x ＋845＝－⎣⎢⎡⎦⎥⎤45（x －8）＋x －85＋745，(10分) ∵ x ≥9，∴45（x －8）＋x －85≥2425＝45，(12分) 当且仅当45（x －8）＝x －85，即x ＝10，y min ＝14，(13分)答：当x ＝10时，下月的月总利润最大，且最大利润为14万元．(14分) 18．（1，依题意有：0)2('=f ，即此时：函数)(x f 在)2,1(上单调递减，在),2(+∞上单调递增，满足在2=x 时取得极值分（2）依题意：0)(≥x f 对任意),1[+∞∈x 恒成立等价转化为0)(min ≥x f 在),1[+∞∈x 恒成立 6分令)('=x f 得：1,1221=-=x a x 8分当112≤-a 即1≤a 时，函数0)('≥x f 在),1[+∞恒成立，则)(x f 在),1[+∞单调递增，于是022)1()(min ≥-==a f x f ，解得：1≤a ，此时：1≤a 10分②当112>-a 即1>a 时，函数)(x f 在]12,1[-a 单调递减，在),12[+∞-a 单调递增，于是022)1()12()(min <-=<-=a f a f x f ，不合题意，此时：Φ∈a综上所述：实数a 的取值范围是1≤a 12分. 说明：本题采用参数分离法或者先用必要条件)1(≥f 缩小参数范围也可以.考点：1.函数的极值与导数；2.函数的最值与导数；3.分类讨论的思想. 19．解：（1）∵2()log (41)()x f x kx k =++∈R 是偶函数，∴2()log (41)()x f x kx f x --=+-=对任意x R ∈，恒成立 2分 即：22log (41)2log (41)x x x kx kx +--=++恒成立，∴1k =- 5分（2）由于0a >，所以24()log (2)3xg x a a =⋅-定义域为24(log ,)3+∞， 也就是满足423x>7分 ∵函数()f x 与()g x 的图象有且只有一个交点， ∴方程224log (41)log (2)3xxx a a +-=⋅-在24(log ,)3+∞上只有一解即：方程414223x xxa a +=⋅-在24(log ,)3+∞上只有一解 9分 令2,x t =则43t >，因而等价于关于t 的方程 24(1)103a t at ---=（*）在4(,)3+∞上只有一解 10分①当1a =时，解得34(,)43t =-∉+∞，不合题意； 11分 当01a <<时，记24()(1)13h t a t at =---，其图象的对称轴203(1)a t a =<- ∴函数24()(1)13h t a t at =---在(0,)+∞上递减，而(0)1h =- ∴方程（*）在4(,)3+∞无解 13分②当1a >时，记24()(1)13h t a t at =---，其图象的对称轴203(1)a t a =>- 所以，只需4()03h <，即1616(1)1099a a ---<，此恒成立 ∴此时a 的范围为1a > 15分 综上所述，所求a 的取值范围为1a > 16分 19．20．解析：（1）∵()ln f x ax x x =+，∴'()ln 1f x a x =++， 1分 又∵()f x 的图象在点x e =处的切线的斜率为3，∴'()3f e =，即ln 13a e ++=，∴1a =； 2分 （2） 由（1）知，()ln f x x x x=+，∴2()f x kx ≤对任意0x >成立对任意0x >成立， 4分，则问题转化为求()g x 的最大值，，解得1x =， 5分 当01x <<时，'()0g x >，∴()g x 在(0,1)上是增函数；当1x >时，'()0g x <，∴()g x 在(1,)+∞上是减函数． 6分 故()g x 在1x =处取得最大值(1)1g =，∴1k≥即为所求； 8分（3分 由（2）知，1ln (0)x x x ≥+>，∴'()0h x ≥， 10分 ∴()h x 是(1,)+∞上的增函数，∵1n m >>，∴()()h n h m >，即分∴ln ln ln ln mn n n n mn m m m ->-， 12分 即ln ln ln ln mn n m m mn m n n +>+，ln ln ln ln mnm mn nnm m n +>+，ln()ln()n m m n mn nm >， 13分∴()()n mm nmn nm >，∴ 14分。

高三月考试卷一、选择题（每小题5分，共50分）1、已知集合A={}，函数的值域为B ，则为（ ）A.（1，2]B.[1,2]C.[0,1]D.(1,)2、已知函数是R 上的单调增函数且为奇函数，则的值为（ ）A.恒为正数B.恒为负数C.恒为0D.可正可负3、已知函数，则函数的定义域是（ ）A. B.C.｛且｝D. ｛或｝4、下列命题中，说法错误的是（ ）A ．“若，则”的否命题是：“若，则”B ．“”的否定是：“”C ．“是真命题”是“是真命题”的充分不必要条件D ．若“，则函数是偶函数”的的逆命题是真命题5、()()()等于则可导在设xx x f x x f x x f x 3lim ,0000--+→（ ）A ．B ．C ．D ．6、函数的图象如图1所示，则的图象可能是（ ）7、为得到函数的图象，只需将函数的图像（ ）A ．向左平移个长度单位B ．向右平移个长度单位C ．向左平移个长度单位D ．向右平移个长度单位8、函数图像的对称轴方程可能是 （ ）A ．B ．C ．D ．9、函数),2||,0,0()sin(R x A B x A y ∈<>>++=πϕωϕω的部分图象如图所示，则函数表达式为：（ ）A ．1)63sin(2+-=ππx y B ．1)36sin(2+-=ππx y C ．1)63sin(2-+=ππx y D ．1)36sin(2++=ππx y10、若△的内角，满足6sin 4sin 3sin A B C ==，则 （ ）A ．B ．C ．D ．二、填空题（每小题5分，共25分）11、曲线21x y xe x =++在点（0,1）处的切线方程为12、命题：的否定是13、函数f (x )＝3sin x +sin(π2+x )的最大值是 14、在中，角所对的边分.若，则15、对于下列命题：① 在中，若，则为等腰三角形；② 在中，角的对边分别为，若，则有两组解；③ 设，，，则；④ 将函数的图像向左平移个单位，得到函数的图像. 其中正确命题的编号是 .（写出所有正确结论的编号）三、解答题16、（13分）定义在R 上的奇函数有最小正周期4，且时，.（Ⅰ）求在[-2,2]上的解析式；（Ⅱ）判断在(0,2)上的单调性，并给予证明；（III ）当为何值时，关于方程在[-2,2]上有实数解？17、（12分）已知命题，；命题，使得。

安徽省铜陵市第五中学2015届高三上学期第一次月考数学（理）试题一、选择题：(本大题共10小题，每小题5分，共50分,在每小题给出的四个选项中，只有一项是符合题目要求的)1.在复平面内，复数（是虚数单位）对应的点位于（）A.第一象限B.第二象限C.第三象限D.第四象限2. 有一段“三段论”推理是这样的：对于可导函数，如果，那么是函数的极值点，因为函数在处的导数值，所以，是函数的极值点.以上推理中（）A大前提错误B小前提错误C推理形式错误D结论正确3. 已知直线是的切线，则的值为（）A . B. C. D.4.曲线3πcos02y x x⎛⎫= ⎪⎝⎭≤≤与轴以及直线所围图形的面积为（）A．B．C．D．5．设是函数的导函数，将和的图象画在同一个直角坐标系中，不可能正确的是（）6.平面几何中，有边长为的正三角形内任一点到三边距离之和为定值，类比上述命题，棱长为的正四面体内任一点到四个面的距离之和为（）．A. B．C．D．7.的展开式中含x的正整数指数幂的项数共有( )项。

A. 0B. 2C. 4D. 68.直线的倾斜角为,曲线在处的切线的倾斜角为,则的值是( )A. B. C. D.9.将4个颜色互不相同的球全部放入编号为1和2的两个盒子里，使得放入每个盒子里的球的个数不小于该盒子的编号，则不同的放球方法有（）A．10种B．20种C．36种D．52种10．若函数在内有极小值，则（）A. B. C. D.二、填空题(本大题共5小题，每小题5分，共25分．把答案填在题中横线上)．11.定义运算，则符合条件的复数为12.若点在内，则有结论 0OBC OAC OAB S OA S OB S OC ∆∆∆⋅+⋅+⋅=，把命题类比推广到空间，若点在四面体内，则有结论： 13．已知函数53123-++=ax x x y ,若函数在总是单调函数，则的取值范围 14.记者要为5名志愿者和他们帮助的2位老人拍照，要求排成一排，2位老人相邻但不排在两端，不同的排法共有 种.15.如果（为实常数）的展开式中所有项的系数和为0，则展开式中含项的系数为 .三、解答题：本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤．16. （本小题12分）已知复数22(815)(918)z m m m m i =-++-+在复平面内表示的点为A ，实数 m 取什么值时，（1）z 为实数？z 为纯虚数？（2）A 位于第三象限？17. （本小题12分）用分析法证明： 已知,求证18. （本小题12分）已知函数）（）（023≠++=a cx bx ax x f 是定义在R 上的奇函数，且时，函数取极值1．（1）求的值；（2）若对任意的，均有成立，求s 的最小值；19. (本小题12分)已知函数321(),3f x x ax bx =++且 （1）试用含的代数式表示； （2）讨论的单调区间.20.（本小题13分）已知数列的前项和． （1）计算，，，；（2）猜想的表达式，并用数学归纳法证明你的结论．21.（本小题14分）已知函数，（）.（Ⅰ）若有最值，求实数的取值范围；（Ⅱ）当时，若存在、，使得曲线在与处的切线互相平行，求证：.参考答案一．选择题二、填空题11. 12.若点O 在四面体ABCD 内，则有+++= 13. 14.960 15.-5 三、解答题16.解：（1）当＝0即m ＝3或m ＝6时，z 为实数； …………3分 当，即m ＝5时，z 为纯虚数.………………………6分（2）当即即3<m<5时，对应点在第三象限. …………12分17 :要证，只需证22)()(b a b a -<-即，只需证，即证 显然成立，因此成立18.解：(1)函数）（）（023≠++=a cx bx ax x f 是定义在R 上的奇函数,），（）（x f x f -=-∴即对于恒成立，. ,时，函数取极值1. ∴,解得: ．故……………………………………………6分 (2),)1)(1(232323)(2+-=-='x x x x f , 时,上是减函数, ……………8分故上最小值为＝－1，最大值为,因此当时,12min ()()2Max f x f x f x f x -≤-=（）（）．12min ()()Max f x f x s f x f x s -≤⇔-≤（）（），故s 的最小值为2 ………12分19.依题意,得()1120f a b '-=-+=,-------------------2分 故.------------------------4分 由得()()321213f x x ax a x =++-, 故()()()2221121f x x ax a x x a '=++-=++-, 令,则或,---------------------6分 ① 当时, ,当变化时,与的变化如下表:由此得,函数的单调增区间为(,)和(,),单调减区间为(,). ② 当时,.此时恒成立,且仅在处,故函数的单调增区间为.③ 当时, ,同理可得函数的单调增区间为和,单调减区间为.---------9分综上:当时,函数的单调增区间为(,)和(,),单调减区间为(,);当时,函数的单调增区间为; 当时,函数的单调增区间为和,单调减区间为…………………12分 20解：（1）依题设可得，，，；------------------4分 （2）猜想：．证明：①当时，猜想显然成立． ②假设时，猜想成立，即．那么，当时，，即111(1)k k k S a k a +++=-+． 又，所以111(1)1k k ka k a k +++=-++， 从而111(1)(2)(1)[(1)1]k a k k k k +==+++++．即时，猜想也成立．故由①和②，可知猜想成立．…………………13分21解析：（Ⅰ） 22211)(x ax x x x a x f -+=+-='，由知，①当时，，在上递增，无最值；②当时，的两根均非正，因此，在上递增，无最值；③当时，有一正根，在上递减，在上递增；此时，有最小值； 所以，实数的范围为. …………8分 （Ⅱ）证明：依题意：1)11(111121222121=+⇒+-=+-x x a x x a x x a ， 由于，且，则有22121212121)2()(22x x x x x x x x x x a +<⋅≤+⇒≥+⋅=22121)2()(2x x x x +<+∴. …………14分。

铜陵市第五中学2014-2015学年高三理科月考试卷满分150分 时间120分钟选择题：(本大题共10小题，每小题5分，共50分,在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知复数i z i m z 43,221+=-=若21z z 为实数，则实数m 的值为( )A ．83B ．32C ．83-D ． 32-2．设随机变量ξ服从正态分布N(0,1)，若P(ξ>1)= p ，则P(-1<ξ<0)= ( ) A ．p+21 B ．p -1 C ．p-21D ．p 21-3. 已知0>t ，若8)22(0=-⎰tdx x ，则t = ( ) A.1 B.-2 C.-2或4 D.44．(x ＋12x )8的展开式中常数项为( )A ．3516B ．358C ．354D ．1055． 将直线x y x 沿02=+-λ轴向左平移一个单位，所得直线与曲线C ：⎪⎩⎪⎨⎧+=+-=θθsin 52cos 51y x （θ为参数）相切，则实数λ的值为（ ）A.7或—3B. —2或8C.0或10D.1或116. 设三次函数)(x f 的导函数为)(x f '，函数(y x f x '=⋅）A ．()f x 的极大值为(3)f ，极小值为(3)f -B ．)(x f 的极大值为)3(f ，极小值为)3(-fC ．)(x f 的极大值为)3(-f ，极小值为)3(fD ．)(x f 的极大值为)3(-f ，极小值为)3(f7.已知)(x f 为定义在),(+∞-∞上的可导函数,且)()(x f x f '<对于R x ∈恒成立,则( )A ． )0()2(2f e f ⋅>, )0()2010(2010f e f ⋅< B ． )0()2(2f e f ⋅<,)0()2010(2010f e f ⋅>C ． )0()2(2f e f ⋅>, )0()2010(2010f e f ⋅> D ． )0()2(2f e f ⋅<,)0()2010(2010f e f ⋅< 8.将9个相同的小球放入编号为1，2，3的三个箱子里，要求每个箱子放球的个数不小于其编号数，则不同的放球方法共有（ ）A. 8种B. 10种C. 12种D. 16种9.抛掷两枚骰子，当至少有一枚5点或一枚6点出现时，就说这次试验成功，则30次试验中成功次数的均值为（ ）A. 10B. 20C. 350D. 34010．对大于或等于2的自然数 m 的n 次方幂有如下分解方式：22＝1＋3,32＝1＋3＋5,42＝1＋3＋5＋7；23＝3＋5,33＝7＋9＋11,43＝13＋15＋17＋19.根据上述分解规律，若n2＝1＋3＋5＋…＋19, m3(m ∈N*)的分解中最小的数是21，则m ＋n 的值为( )．A. 15B. 16C. 17D. 18二、填空题(本大题共5小题，每小题5分，共25分．把答案填在题中横线上)． 11. 若不等式131x x m ++-≥-恒成立，则m 的取值范围是 ．12.在极坐标系中，曲线1:4C ρ=上有3个不同的点到曲线2:sin()4C mπρθ+=的距离等于2，则m = .13.的值为，则71010221010)1(.......)1()1(a x a x a x a a x -++-+-+= ． 14. 已知0,0x y >>，若2229(5)x y m m x y +>+恒成立，则实数m 的取值范围是 ．15．给出下列5种说法：①在频率分布直方图中，众数左边和右边的直方图的面积相等；②标准差越小，样本数据的波动也越小；③回归直线过样本点的中心(),x y ；④在回归分析中对于相关系数r ，通常,当r大于0,75时,认为两个变量存在着很强的线性相关关糸. ⑤极点与直角坐标系的原点重合，极轴与x 轴非负半轴重合，曲线C 的极坐标方程为，直线l 的参数方程为(t 为参数）,直线l 与曲线C 交于A 、B,则 线段AB 的长等于；其中说法正确的是_________（请将正确说法的序号写在横线上）.三、解答题：本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤．16（本小题满分12分）设a 为实数，函数2()2,xf x x e a x R -=+∈。

铜陵市第五中学2014-2015学年高三理科月考试卷满分150分 时间120分钟选择题：(本大题共10小题，每小题5分，共50分,在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知复数i z i m z 43,221+=-=若21z z 为实数，则实数m 的值为( )A ．83B ．32C ．83-D ． 32-2．设随机变量ξ服从正态分布N(0,1)，若P(ξ>1)= p ，则P(-1<ξ<0)= ( ) A ．p+21 B ．p -1 C ．p-21D ．p 21-3. 已知0>t ，若8)22(0=-⎰tdx x ，则t = ( ) A.1 B.-2 C.-2或4 D.44．(x ＋12x )8的展开式中常数项为( )A ．3516B ．358C ．354D ．1055． 将直线x y x 沿02=+-λ轴向左平移一个单位，所得直线与曲线C ：⎪⎩⎪⎨⎧+=+-=θθsin 52cos 51y x （θ为参数）相切，则实数λ的值为（ ）A.7或—3B. —2或8C.0或10D.1或116. 设三次函数)(x f 的导函数为)(x f '，函数(y x f x '=⋅）A ．()f x 的极大值为(3)f ，极小值为(3)f -B ．)(x f 的极大值为)3(f ，极小值为)3(-fC ．)(x f 的极大值为)3(-f ，极小值为)3(fD ．)(x f 的极大值为)3(-f ，极小值为)3(f7.已知)(x f 为定义在),(+∞-∞上的可导函数,且)()(x f x f '<对于R x ∈恒成立,则( )A ． )0()2(2f e f ⋅>, )0()2010(2010f e f ⋅< B ． )0()2(2f e f ⋅<,)0()2010(2010f e f ⋅>C ． )0()2(2f e f ⋅>, )0()2010(2010f e f ⋅> D ． )0()2(2f e f ⋅<,)0()2010(2010f e f ⋅< 8.将9个相同的小球放入编号为1，2，3的三个箱子里，要求每个箱子放球的个数不小于其编号数，则不同的放球方法共有（ ）A. 8种B. 10种C. 12种D. 16种9.抛掷两枚骰子，当至少有一枚5点或一枚6点出现时，就说这次试验成功，则30次试验中成功次数的均值为（ ）A. 10B. 20C. 350D. 34010．对大于或等于2的自然数 m 的n 次方幂有如下分解方式：22＝1＋3,32＝1＋3＋5,42＝1＋3＋5＋7；23＝3＋5,33＝7＋9＋11,43＝13＋15＋17＋19.根据上述分解规律，若n2＝1＋3＋5＋…＋19, m3(m ∈N*)的分解中最小的数是21，则m ＋n 的值为( )．A. 15B. 16C. 17D. 18二、填空题(本大题共5小题，每小题5分，共25分．把答案填在题中横线上)． 11. 若不等式131x x m ++-≥-恒成立，则m 的取值范围是 ．12.在极坐标系中，曲线1:4C ρ=上有3个不同的点到曲线2:sin()4C mπρθ+=的距离等于2，则m = .13.的值为，则71010221010)1(.......)1()1(a x a x a x a a x -++-+-+= ． 14. 已知0,0x y >>，若2229(5)x y m m x y +>+恒成立，则实数m 的取值范围是 ．15．给出下列5种说法：①在频率分布直方图中，众数左边和右边的直方图的面积相等；②标准差越小，样本数据的波动也越小；③回归直线过样本点的中心(),x y ；④在回归分析中对于相关系数r ，通常,当r大于0,75时,认为两个变量存在着很强的线性相关关糸. ⑤极点与直角坐标系的原点重合，极轴与x 轴非负半轴重合，曲线C 的极坐标方程为，直线l 的参数方程为(t 为参数）,直线l 与曲线C 交于A 、B,则 线段AB 的长等于；其中说法正确的是_________（请将正确说法的序号写在横线上）.三、解答题：本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤．16（本小题满分12分）设a 为实数，函数2()2,xf x x e a x R -=+∈。

铜陵五中2014-2015学年度高三第一学期第二次月考数学试卷(理科)满分150分时间120分钟参考公式：22()K()()()()n ad bca b c d a c b d-=++++，一、选择题(每小题5分，共50分）1.已知为纯虚数，则的值为( )A．1 B．－1 C．D．2.,若,则的值等于( )A．B．C．D．3．等于( )A．1 B．C．D．4.设函数在上可导,其导函数,且函数在处取得极小值,则函数的图象可能是( )5．3位老师和3位学生站成一排，要求任何两位学生都不相邻，则不同的排法总数为 ( )A．720B．144C．36D．126．工人月工资（元）依劳动生产率（千元）变化的回归方程为，下列判断正确的是（）A．劳动生产率为1000元时，工资为150元B．劳动生产率提高1000元时，工资提高150元C．劳动生产率提高1000元时，工资提高90元D．劳动生产率为1000元时，工资为90元7.在15个村庄中有7个村庄交通不方便，现从中任意选10个村庄，用X 表示这10个村庄中交通不方便的村庄数，下列概率中等于C 74C 86C 1510的是( )A ．P (X ＝2)B ．P (X ≤2)C ．P (X ＝4)D ．P (X ≤4)8.若，则等于( )A ．B ．C ．D ．9.在吸烟与患肺病这两个分类变量的计算中，下列说法正确的是（ ）A.若K 2的观测值为k=6.635,我们有99%的把握认为吸烟与患肺病有关系，那么在100个吸 烟的人中必有99人患有肺病;B.从独立性检验可知有99%的把握认为吸烟与患肺病有关系时，我们说某人吸烟，那么他 有99%的可能患有肺病;C.若从统计量中求出有95% 的把握认为吸烟与患肺病有关系，是指有5% 的可能性使得推判 出现错误;D.以上三种说法都不正确.10.设某批产品合格率为34，不合格率为14，现对该产品进行测试，设第ξ次首次测到正品，则P (ξ＝3)等于( )A ．C 32(14)2×(34)B ．C 32(34)2×(14)C ．(14)2×(34)D ．(34)2×(14)二、填空题（每小题5分，共25分）11．从5名学生中任选4名分别参加数学、物理、化学、生物四科竞赛，且每科竞赛只有1人参加，若甲不参加生物竞赛，则不同的选择方案共有________种． 12.函数在（1，1）处的切线方程是________. 13.设离散型随机变量X 的分布列为则P (1≤X ≤3)＝________.14．已知连续型随机变量x 的分布函数为：⎪⎩⎪⎨⎧≤<≤<=21 a 1x 0ax 0)(x x f 其他 则_____________．15.若(x －a )8＝a 0＋a 1x ＋a 2x 2＋…＋a 8x 8，且a 5＝56，则a 0＋a 1＋a 2＋…＋a 8＝________.三、解答题（共75分，解答应写出必要的文字说明，证明过程或演算步骤）长大于42码”的为“大脚”，“脚长小于等于42码”的为“非大脚”，请根据上表数据完成下面的2×2列联表。

安徽省铜陵市第五中学2015届高三上学期第一次月考数学（文）试题一、选择题：1、已知集合M={0,1,3},N={X|X=3a,a ∈M}，则MUN 等于A 、{0}B 、{0,3}C 、{1，3，9}D 、{0，1，3，9}2、已知函数ƒ（X ）为奇函数且当X>0时，ƒ（X ）=X 2+ 则ƒ（-1）=A 、-2B 、0C 、1D 、23、X>2是X 2-3X+2>0成立的A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、非充要条件4、命题“对任意X ∈R ，都有X 2≥0”的否定为：A 、对任何X ∈R ，都有X 2＜0B 、不存在X ∈R ，都有X 2＜0C 、存在X 0∈R ，使X 02≥0D 、存在X 0∈R ，使X 02＜05、幂函数ƒ（X ）的图像过点（1/2， ）则log 4ƒ(2)值 A 、1/4 B 、-1/4 C 、2 D 、-26、函数+（X ）= 则满足ƒ（X ）≤2的X 范围A 、[-1，2]B 、[0，2]C 、[1，+∞]D 、[-1，+∞]7、下列函数中，在区间（0，+∞）上为增函数的是 A 、y=lg(X+2) B 、y=-√X+1 C 、y=(1/2)X D 、y=X+8、没a=0.50.5,b=0.30.5，c=log 0.30.2，则A 、c ＜b ＜aB 、b ＜a ＜cC 、c ＜a ＜bD 、a ＜c ＜b9、已知函数ƒ（X ）是定义在R 上的奇函数，且周期为2，若当X ∈[0，1]时ƒ（X ）=2X -1，则ƒ（log 6）值A 、-B 、-5C 、-D 、-6 10、下列为其命题是：A 、]X 0∈R e Xo ≤0B 、V X ∈R ，2X ＞X 2C 、a+b=0的充要条件是a/b=-1D 、a ＞1,b ＞1是ab ＞1的充分条件。

二、填空：1、A={X|2≤X≤6} B={X|2a≤X≤a+3}，若B ⊆A ，则实数a 范围2、ƒ（X ）=√X+2 +lg （2-X ）定义域3、若命题“V X ∈R ，X 2+2tx+1＞0”的否定是真命题，则a 范围4、设偶函数ƒ（X ）对任意X ∈R ，都有ƒ（X+3）=- ，且当X ∈[-3，-2]时，ƒ（X ）=4X ，则ƒ（107.5）=5、ƒ（X ）= 若ƒ (X)在R 上单调递增，则a 范围三、解答题：1、设条件P ：2X 2-3X+1≤0，条件q:X 2-(2a+1)X+a(a+1) ≤0，若¬P 是¬q 的必要不充分条件，求实数a 范围：2、设函数ƒ（X ）是R 上的奇函数，当X≥0时ƒ（X ）=X 2+4X①求ƒ（X ）表达式②证明：ƒ（X ）在区间（0，+∞）上是增函数X 2+1，X ≤1 1-log 2X ,X ＞1 1 x 5/2 √2 2 1 f(x)3、已知函数ƒ（X）=√log2(X-1)的定义域为A，ƒ（X）=（1/2）X（-1≤X≤0）的值域为B，①求A∩B②若C={X|a≤X≤2a-1}且C⊆B，求a范围：4、函数ƒ（X）=X2+ （X≠0，a∈R）（1）判断ƒ（X）奇偶性（2）若ƒ（X）在区间[2，+∞]上是增函数，求a范围。

安徽省铜陵市第五中学2015届高三数学10月月考试题文选择题（每小题5分，共50分）1、已知集合A={-2≤xxx}，函数)(2)(Axxxf∈-=的值域为B，则BA)(⋂RC为（）A.（1，2] B.[1,2] C.[0,1] D.(1,∞+)2、已知函数()x f是R上的单调增函数且为奇函数，则()1f的值为（）A.恒为正数B.恒为负数C.恒为0D.可正可负3、已知函数()11+=xxf，则函数())(x f f的定义域是（）A.{}1-≠x xB.{}2-≠x xC.｛1-≠xx且2-≠x｝ D. ｛1-≠xx或2-≠x｝4、下列命题中，说法错误的是（）A．“若p，则q”的否命题是：“若p⌝，则q⌝”B．“2-,22>>∀xxx”的否定是：“02-,22≤≤∃xxx”C．“qp∧是真命题”是“qp∨是真命题”的充分不必要条件D．若“0=b，则函数()cbxaxxf++=2是偶函数”的的逆命题是真命题5、()()()等于则可导在设xxxfxxfxxfx3lim,0--+→（）A．()2xf'B．()xf'C．()3xf'D．()4xf'6、函数()y f x=的图象如图1所示，则()y f x'=的图象可能是（）7、为得到函数πcos3y x⎛⎫=+⎪⎝⎭的图象，只需将函数siny x=的图像（）A．向左平移π6个长度单位B．向右平移π6个长度单位C ．向左平移5π6个长度单位D ．向右平移5π6个长度单位8、函数sin(2)3y x π=+图像的对称轴方程可能是 （ ） A ．6x π=-B ．12x π=-C ．6x π=D ．12x π=9、函数),2||,0,0()sin(R x A B x A y ∈<>>++=πϕωϕω的部分图象如图所示，则函数表达式为：（ ）A ．1)63sin(2+-=ππx yB ．1)36sin(2+-=ππx yC ．1)63sin(2-+=ππx yD ．1)36sin(2++=ππx y10、若△ABC 的内角，,,A B C 满足6sin 4sin 3sin A B C ==，则cos B = （ ）A ．15B ．34C ．315D ．1116填空题（每小题5分，共25分）11、曲线21xy xe x =++在点（0,1）处的切线方程为 12、命题：01,2=+-∈∃x x R x 的否定是 13、函数f(x)＝3sin x +sin(π2+x)的最大值是14、在ABC ∆中，角,,A B C 所对的边分,,a b c .若cos sin a A b B =，则2sin cos cos A A B += 15、对于下列命题：① 在ABC ∆中，若B A 2sin 2sin =，则ABC ∆为等腰三角形；② 在ABC ∆中，角C B A ,,的对边分别为c b a ,,，若6,10,4π===A b a ，则ABC ∆有两组解；③ 设32014sinπ=a ，32014cos π=b ，32014tan π=c ，则c b a <<；④ 将函数)43sin(π+=x y 的图像向左平移个6π单位，得到函数)43cos(π+=x y 的图像. 其中正确命题的编号是 .（写出所有正确结论的编号）解答题16、（13分）定义在R 上的奇函数()x f 有最小正周期4，且()2,0∈x 时，()133+=xxx f . （Ⅰ）求()x f 在[-2,2]上的解析式；（Ⅱ）判断()x f 在(0,2)上的单调性，并给予证明；（III ）当λ为何值时，关于方程()λ=x f 在[-2,2]上有实数解？17、（12分）已知命题[]2,1:∈∀x p ，02≥-a x ；命题Rx q ∈∃0:，使得()011020<+-+x a x 。

安徽省铜陵市数学高三文数10月月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分）(2018高二上·浙江月考) 若集合，，那么A .B .C .D .2. （2分）若复数z满足iz＝2＋4i，则在复平面内z对应的点的坐标是（）A . （2，4）B . （2，－4）C . （4，－2）D . （4，2）3. （2分） (2016高一下·安徽期中) 已知向量，均为单位向量，它们的夹角为60°，则|2 ﹣3 |等于（）A . 1B .C .D .4. （2分）已知，则“”是“”的（）A . 充分不必要条件B . 必要不充分条件C . 充要条件D . 既不充分也不必要条件5. （2分） (2017高二上·阳高月考) 已知两条直线若，则（）A . 5B . 4C . 3D . 26. （2分） (2016高一下·临川期中) 一个等比数列{an}的前n项和为48，前2n项和为60，则前3n项和为（）A . 63B . 108C . 75D . 837. （2分）设sinα+sinβ=，则sinα-cos2β的最大值为（）A .B .C . -8. （2分） (2019高一上·邗江期中) 函数的图象大致是（）A .B .C .D .9. （2分）(2017·武汉模拟) 已知函数，若将f（x）的图象向左平移个单位后所得函数的图象关于原点对称，则φ=（）A .B .D .10. （2分）设直线与轴的交点为P，点P把圆的直径分为两段，则其长度之比为（）A . 或B . 或C . 或D . 或11. （2分）长方体的三个相邻面的面积分别是2，3，6，这个长方体的顶点都在同一个球面上，则这个球的表面积为（）A .B .C .D .12. （2分） (2016高二下·广东期中) 设f（x）=x•cosx﹣sinx，则（）A . f（﹣3）+f（2）＞0B . f（﹣3）+f（2）＜0C . f（﹣3）+f（2）=0D . f（﹣3）﹣f（2）＜0二、填空题 (共4题；共4分)13. （1分）(2017·武邑模拟) 已知实数u，v，x，y满足u2+v2=1，，则z=ux+vy的最大值是________．14. （1分）(2012·全国卷理) 三棱柱ABC﹣A1B1C1中，底面边长和侧棱长都相等，∠BAA1=∠CAA1=60°，则异面直线AB1与BC1所成角的余弦值为________15. （1分）已知过定点P（﹣1，0）的直线l：（其中t为参数）与圆x2+y2﹣2x﹣4y+4=0交于M，N两点，则MN的中点坐标为________．16. （1分） (2018高二上·长安期末) 若函数在上存在递增区间，则的取值范围是________．三、解答题 (共6题；共50分)17. （10分） (2018高二上·通辽月考) 已知△ABC中，角A，B，C的对边分别为a，b，c，cos A＝，sin B＝ cos C．（1）求tan C的值；（2）若a＝，求△ABC的面积．18. （5分） (2016高一下·临川期中) 已知a1=2，点（an ， an+1）在函数f（x）=x2+2x的图象上，其中n=1，2，3，…．（1）求a3，a4的值；（2）证明数列{lg（1+an）}是等比数列，并求数列{an}的通项公式；（3）记bn= + ，求数列{bn}的前n项和Sn．19. （10分）求y= 值域．20. （10分）(2017·襄阳模拟) 如图，在直角梯形SABC中，∠B=∠C= ，D为边SC上的点，且AD⊥SC，现将△SAD沿AD折起到达PAD的位置（折起后点S记为P），并使得PA⊥AB．（1）求证：PD⊥平面ABCD；（2）已知PD=AD，PD+AD+DC=6，G是AD的中点，当线段PB取得最小值时，则在平面PBC上是否存在点F，使得FG⊥平面PBC？若存在，确定点F的位置，若不存在，请说明理由．21. （10分） (2020高三上·海淀期末) 已知函数 .（Ⅰ）求曲线在点处的切线方程；（Ⅱ）若函数有极小值，求证：的极小值小于 .22. （5分） (2016·江苏) 如图，在平面直角坐标系xOy中，已知以M为圆心的圆M：x2+y2﹣12x﹣14y+60=0及其上一点A（2，4）．（1）设圆N与x轴相切，与圆M外切，且圆心N在直线x=6上，求圆N的标准方程；（2）设平行于OA的直线l与圆M相交于B、C两点，且BC=OA,求直线l的方程；（3）设点T（t,0）满足：存在圆M上的两点P和Q,使得 ,求实数t的取值范围。

2014-2015学年安徽省铜陵五中高三（上）10月月考数学试卷（文科）一、选择题（每小题5分，共50分）1．已知集合A={x|x2﹣x≤0}，函数f（x）=2﹣x（x∈A）的值域为B，则（∁R A）∩B为（） A．（1，2] B． C． D．（1，+∞）2．已知函数f（x）是R上的单调增函数且为奇函数，则f（1）的值（） A．恒为正数 B．恒为负数 C．恒为0 D．可正可负3．已知函数，则函数f的定义域是（）A． {x|x≠﹣1} B． {x|x≠﹣2} C． {x|x≠﹣1且x≠﹣2} D． {x|x≠﹣1或x≠﹣2}4．下列命题中，说法错误的是（）A．“若p，则q”的否命题是：“若￢p，则￢q”B．“∀x＞2，x2﹣2x＞0”的否定是：“∃x≤2，x2﹣2x≤0”C．“p∧q是真命题”是“p∨q是真命题”的充分不必要条件D．“若b=0，则函数f（x）=ax2+bx+c是偶函数”的逆命题是真命题5．设f（x）在x0可导，则等于（）A． 2f'（x0） B． f'（x0） C． 3f'（x0） D． 4f'（x0）6．函数y=f（x）的图象如图所示，则y=f′（x）的图象可能是（）A． B． C． D．7．为得到函数的图象，只需将函数y=sinx的图象（） A．向左平移个长度单位 B．向右平移个长度单位C．向左平移个长度单位 D．向右平移个长度单位8．函数y=sin（2x+）图象的对称轴方程可能是（）A． x=﹣ B． x=﹣ C． x= D． x=9．数y=Asin（ωx+φ）+B（A＞0，φ＞0，|φ|＜，x∈R）的部分图象如图所示，则函数的表达式为（）A． B．C． D．10．若△ABC的内角A，B，C满足6sinA=4sinB=3sinC，则cosB=（）A． B． C． D．二、填空题（每小题5分，共25分）11．曲线y=xe x+2x+1在点（0，1）处的切线方程为．12．命题：∃x∈R，x2﹣x+1=0的否定是．13．函数的最大值是．14．△ABC中，角A，B，C所对的边分别为a，b，c，若acosA=bsinB，则sinAcosA+cos2B= ．15．对于下列命题：①在△ABC中，若sin2A=sin2B，则△ABC为等腰三角形；②在△ABC中，角A，B，C的对边分别为a，b，c，若a=4，b=10，A=，则△ABC有两组解；③设a=sin，b=cos，c=tan，则a＜b＜c；④将函数y=sin（3x+）的图象向左平移个单位，得到函数y=cos（3x+）的图象．其中正确命题的编号是．（写出所有正确结论的编号）三、解答题16．定义在R上的奇函数f（x）满足f（x）=f（x+4），且x∈（0，2]时，f（x）=．（1）求f（x）在上的解析式；（2）判断f（x）在上的单调性，并给予证明；（3）当λ为何值时，关于方程f（x）=λ在上有实数解？17．已知命题P：“对任意x∈，x2﹣a≥0”，命题q：“存在x∈R，x2+（a﹣1）x+1＜0”若“p 或q”为真，“p且q”为假命题，求实数a的取值范围．18．已知函数f（x）=x3+（1﹣a） x2﹣a（a+2）x+b（a，b∈R）．（Ⅰ）若函数f（x）的图象过原点，且在原点处的切线斜率是﹣3，求a，b的值；（Ⅱ）若函数f（x）在区间（﹣1，1）上不单调，求a的取值范围．19．已知函数，g（x）=sinx•cosx．（Ⅰ）求函数y=f（x）图象的对称轴方程；（Ⅱ）求函数h（x）=f（x）+g（x）的值域．20．已知函数f（x）=（1）求f（x）的定义域和值域；（2）若曲线f（x）在点P（x0，f（x0））（﹣＜x0＜）处的切线平行直线y=x，求在点P处的切线方程．21．已知函数f（x）=2sin（ωx+φ）（0＜φ＜π，ω＞0）为偶函数，且函数y=f（x）图象的两相邻对称轴间的距离为π．（1）求函数y=f（x）的解析式；（2）已知△ABC中角 A、B、C所对的边分别是a、b、c，且f（A+）=，c=2a，求sinC的值．2014-2015学年安徽省铜陵五中高三（上）10月月考数学试卷（文科）参考答案与试题解析一、选择题（每小题5分，共50分）1．已知集合A={x|x2﹣x≤0}，函数f（x）=2﹣x（x∈A）的值域为B，则（∁R A）∩B为（） A．（1，2] B． C． D．（1，+∞）考点：交、并、补集的混合运算．专题：函数的性质及应用．分析：利用集合的交、并、补集的混合运算法则直接求解．解答：解：∵集合A={x|x2﹣x≤0}，函数f（x）=2﹣x（x∈A）的值域为B，∴A={x|0≤x≤1}，B={x|1≤x≤2}，∴（∁R A）∩B={x|x＜0或x＞1}∩{x|1≤x≤2}={x|1＜x≤2}=（1，2]．故选：A．点评：本题考查集合的交、并、补集的混合运算，是基础题，解题时要认真审题，注意不等式的合理运用．2．已知函数f（x）是R上的单调增函数且为奇函数，则f（1）的值（） A．恒为正数 B．恒为负数 C．恒为0 D．可正可负考点：奇偶性与单调性的综合．专题：计算题．分析：根据奇函数的定义，我们易求了f（0）的值，然后根据函数f（x）是R上的单调增函数，我们即可判断出f（1）的值的符号．解答：解：∵函数f（x）是R上的奇函数∴f（0）=0，又∵f（x）在R上递增，∴f（1）＞f（0）=0，故选A．点评：本题考查的知识点是函数奇偶性与单调性的综合应用，其中根据奇函数的定义，判断出f（0）=0，是解答本题的关键．3．已知函数，则函数f的定义域是（）A． {x|x≠﹣1} B． {x|x≠﹣2} C． {x|x≠﹣1且x≠﹣2} D． {x|x≠﹣1或x≠﹣2}考点：函数的定义域及其求法．专题：计算题．分析：定义域是自变量x的取值范围所组成的集合，所以，我们要求出 f中x的取值范围．通过求出f的表达式来解决问题．解答：解：由函数，得f=，∴综合得x≠﹣1且x≠﹣2故选C．点评：复合函数的定义域是经常被考查的，所以要理解其解题时要注意的问题：综合考虑各个式子有意义．4．下列命题中，说法错误的是（）A．“若p，则q”的否命题是：“若￢p，则￢q”B．“∀x＞2，x2﹣2x＞0”的否定是：“∃x≤2，x2﹣2x≤0”C．“p∧q是真命题”是“p∨q是真命题”的充分不必要条件D．“若b=0，则函数f（x）=ax2+bx+c是偶函数”的逆命题是真命题考点：命题的真假判断与应用．专题：简易逻辑．分析：根据四种命题，全称命题的否定，充要条件的定义，偶函数的定义，逐一判断四个结论的正误，可得答案．解答：解：“若p，则q”的否命题是：“若￢p，则￢q”，故A正确；“∀x＞2，x2﹣2x＞0”的否定是：“∃x＞2，x2﹣2x≤0”，故B错误；“p∧q是真命题”⇔“p，q均为真命题”，“p∨q是真命题”⇔“p，q中存在真命题”，故“p∧q是真命题”是“p∨q是真命题”的充分不必要条件，即C正确；“若b=0，则函数f（x）=ax2+bx+c是偶函数”的逆命题为“若f（x）=ax2+bx+c是偶函数，则b=0”为真命题，故D正确．故选：B点评：本题以命题的真假判断为载体考查了四种命题，全称命题的否定，充要条件的定义，偶函数的定义等知识点，难度不大，属于基础题．5．设f（x）在x0可导，则等于（） A． 2f'（x0） B． f'（x0） C． 3f'（x0） D． 4f'（x0）考点：极限及其运算．专题：计算题．分析：由函数在某点的导数的定义可得 f′（x0）=，而要求的式子可化为+3，由此得出结论．解答：解：∵f（x）在x0可导，∴f′（x0）=．∴==+=f′（x0）+3=f′（x0）+3f′（x0）=4f′（x0），故选D．点评：本题考查极限及其运算，求解的关键有二，一是熟练掌握导数的定义，二是导数极限定义式的格式记忆准确，如此才能想到改变分子上两个函数式的顺序得出正确答案．此也是本题的一个易错点，极易出错，解决的办法就是对定义掌握准确，属于基础题．6．函数y=f（x）的图象如图所示，则y=f′（x）的图象可能是（）A． B． C． D．考点：函数的图象；导数的运算．专题：导数的概念及应用．分析：先看定义域，然后先依据原函数的单调性，判断导函数的符号，还无法辨别的再根据原函数增减的快慢判断导函数的绝对值的大小．解答：解：依据原函数图象可看出①当x＜0时，函数y=f（x）递增，所以此时f′（x）＞0，y=f′（x）的图象在x轴上方；②当x＞0时，函数y=f（x）递减，所以f′（x）＜0，y=f′（x）的图象在x轴下方．故选D点评：判断原函数与导函数图象之间的关系，主要是依据三点：在定义域内的某区间上①原函数递增，则导函数为正，图象在x轴上方；原函数递减，则导函数为负，图象在x轴下方；②极值点处的导数为零；③原函数增或减得越快（慢），则导函数的绝对值越大（小）．7．为得到函数的图象，只需将函数y=sinx的图象（） A．向左平移个长度单位 B．向右平移个长度单位C．向左平移个长度单位 D．向右平移个长度单位考点：函数y=Asin（ωx+φ）的图象变换．专题：计算题．分析：利用诱导公式将y=cos（x+）转化为y=sin（x+），利用平移知识解决即可．解答：解：∵y=cos（x+）=cos（﹣x﹣）=sin=sin（x+），∴要得到y=sin（x+）的图象，只需将函数y=sinx的图象向左平移个长度单位，故选C．点评：本题考查函数y=Asin（ωx+φ）的图象变换，将y=cos（x+）转化为y=sin（x+）是关键，考查理解与转化的能力，属于中档题．8．函数y=sin（2x+）图象的对称轴方程可能是（）A． x=﹣ B． x=﹣ C． x= D． x=考点：函数y=Asin（ωx+φ）的图象变换．分析：令2x+=求出x的值，然后根据k的不同取值对选项进行验证即可．解答：解：令2x+=，∴x=（k∈Z）当k=0时为D选项，故选D．点评：本题主要考查正弦函数对称轴的求法．属基础题．9．数y=Asin（ωx+φ）+B（A＞0，φ＞0，|φ|＜，x∈R）的部分图象如图所示，则函数的表达式为（）A． B．C． D．考点：由y=Asin（ωx+φ）的部分图象确定其解析式．专题：计算题．分析：通过函数的表达式的形式结合图象，求出B，A，求出函数的周期，得到ω，函数经过（2，3）以及φ的范围求出φ的值，得到选项．解答：解：由题意可知A=2，B=1，T==6，ω==，因为函数经过（2，3）所以3=2sin（×2+φ）+1，|φ|＜，φ=﹣，所以函数的表达式为；故选A．点评：本题考查三角函数的解析式的求法，函数图象的应用，注意周期的求法以及φ的求法是本题的关键，考查计算能力．10．若△ABC的内角A，B，C满足6sinA=4sinB=3sinC，则cosB=（）A． B． C． D．考点：三角函数的恒等变换及化简求值．专题：三角函数的图像与性质．分析：由题意利用正弦定理，推出a，b，c的关系，然后利用余弦定理求出cosB的值．解答：解：△ABC的内角A，B，C满足6sinA=4sinB=3sinC，所以6a=4b=3c，不妨令a=2，b=3，c=4，所以由余弦定理：b2=a2+c2﹣2accosB，所以cosB=，故选D．点评：本题是基础题，考查正弦定理，余弦定理的应用，考查计算能力，常考题型．二、填空题（每小题5分，共25分）11．曲线y=xe x+2x+1在点（0，1）处的切线方程为y=3x+1 ．考点：导数的几何意义．专题：计算题．分析：根据导数的几何意义求出函数y在x=0处的导数，从而求出切线的斜率，再用点斜式写出切线方程，化成斜截式即可；解答：解：y′=e x+x•e x+2，y′|x=0=3，∴切线方程为y﹣1=3（x﹣0），∴y=3x+1．故答案为：y=3x+1点评：本题考查了导数的几何意义，同时考查了导数的运算法则，本题属于基础题．12．命题：∃x∈R，x2﹣x+1=0的否定是∀x∈R，x2﹣x+1≠0 ．考点：特称命题；命题的否定．专题：计算题．分析：利用特称命题的否定是全称命题，写出结果即可．解答：解：因为特称命题的否定是全称命题，所以∃x∈R，x2﹣x+1=0的否定是：∀x∈R，x2﹣x+1≠0．故答案为：∀x∈R，x2﹣x+1≠0．点评：本题考查特称命题与全称命题的否定关系，考查基本知识的应用．13．函数的最大值是2 ．考点：三角函数的最值；运用诱导公式化简求值．专题：计算题．分析：先根据两角和与差的正弦公式进行化简，再由正弦函数的性质即可得到其最大值．解答：解：由．故答案为：2点评：本题主要考查两角和与差的正弦公式和正弦函数的性质﹣﹣最值．考查考生对正弦函数的性质的掌握和应用．三角函数式高考的一个必考点，重点在对于基础知识的考查．14．△ABC中，角A，B，C所对的边分别为a，b，c，若acosA=bsinB，则sinAcosA+cos2B= 1 ．考点：正弦定理；三角函数的化简求值．专题：计算题．分析：利用正弦定理化简已知的等式，得到sinAcosA=sin2B，代入所求的式子中，利用同角三角函数间的基本关系化简，即可求出所求式子的值．解答：解：∵acosA=bsinB，由正弦定理得：sinAcosA=sinBsinB=sin2B，则sinAcosA+cos2B=sin2B+cos2B=1．故答案为：1点评：此题考查了正弦定理，以及同角三角函数间的基本关系，熟练掌握正弦定理是解本题的关键．15．对于下列命题：①在△ABC中，若sin2A=sin2B，则△ABC为等腰三角形；②在△ABC中，角A，B，C的对边分别为a，b，c，若a=4，b=10，A=，则△ABC有两组解；③设a=sin，b=cos，c=tan，则a＜b＜c；④将函数y=sin（3x+）的图象向左平移个单位，得到函数y=cos（3x+）的图象．其中正确命题的编号是③，④．（写出所有正确结论的编号）考点：命题的真假判断与应用．分析：①运用三角函数的等价转换，②运用三角形正余弦定理，③考察的是三角函数的周期，④是函数图象的平移，向左平移n个单位，则自变量要加上n，向右平移n个单位，则变成自变量减去n解答：解：①：由题意可知，A=B满足条件，但是我们有sin（π﹣2A）=sin2A，∴存在π﹣2A=2B，∴2A+2B=π时，即A+B=90°时，也满足条件，∴故①错．②：知道两边和一个相对应的夹角，可以运用正弦定理，得：，∴sinB=＞1，∴此时△ABC无解，即画不出这样的图形．故②错；③：∵sinx、cosx是周期函数，且周期为2π，tanx也为周期函数，周期为π，∴sin=sin=﹣，cos=cos=﹣，tan=tan=∴a＜b＜c，故③正确；④：由函数图象左移个单位可知，函数变为 y=sin=sin=cos（3x+）∴故④正确．故答案为：③④．点评：三角函数等价转换，对称性，周期性，单调性，以及函数的平移和正余弦定理是常考点三、解答题16．定义在R上的奇函数f（x）满足f（x）=f（x+4），且x∈（0，2]时，f（x）=．（1）求f（x）在上的解析式；（2）判断f（x）在上的单调性，并给予证明；（3）当λ为何值时，关于方程f（x）=λ在上有实数解？考点：奇偶性与单调性的综合．专题：函数的性质及应用．分析：（1）由条件可得函数的周期为4，设x∈，根据f（﹣x）===﹣f（x），求得f（x）=．再根据奇函数的定义可得f（0）=0，从而求得可得，f（x）在上的解析式．（2）根据f（0）=0，当x∈（0，2]时，由于f（x）=1﹣＞0，且f（x）随着x的增大而增大，可得f（x）在上是增函数．再利用函数的单调性的定义进行证明．（3）由题意可得，本题即求函数λ=f（x）在上的值域，再利用函数的单调性求得函数f（x）在上的值域．解答：解：（1）∵奇函数f（x）满足f（x）=f（x+4），故函数的周期为4．由于x∈（0，2]时，f（x）=，设x∈，故 f（﹣x）===﹣f（x），∴f（x）=．再根据奇函数的定义可得f（0）=0，可得，f（x）在上的解析式为f（x）=．（2）在上，f（0）=0，当x∈（0，2]时，由于f（x）==1﹣＞0，且f（x）随着x的增大而增大，故f（x）在上是增函数．证明：设0≤x1＜x2≤2，则由f（x1）﹣f（x2）=﹣=＜0，可得f（x1）＜f（x2），故f（x）在上是增函数．（3）由题意可得，本题即求函数λ=f（x）在上的值域．利用函数的单调性求得函数f（x）在上的值域为 {λ|y=0，或＜λ≤，或﹣≤λ＜﹣}，故λ的范围为：{λ|y=0，或＜λ≤，或﹣≤λ＜﹣}．点评：本题主要考查函数的周期性、单调性和奇偶性的应用，求函数的解析式和函数的值域，体现了转化的数学思想，属于基础题．17．已知命题P：“对任意x∈，x2﹣a≥0”，命题q：“存在x∈R，x2+（a﹣1）x+1＜0”若“p 或q”为真，“p且q”为假命题，求实数a的取值范围．考点：复合命题的真假．专题：简易逻辑．分析：根据二次函数的最值，一元二次不等式解的情况和判别式△的关系即可求出p：a≤1，q：a＜﹣1，或a＞3，而根据“p或q”为真，“p且q”为假知道p真q假，或p假q真两种情况，所以求出每种情况的a的取值范围并求并集即可．解答：解：由命题p知，x2在上的最小值为1，∴p：a≤1；由命题q知，不等式x2+（a﹣1）x+1＜0有解，∴△=（a﹣1）2﹣4＞0；∴a＞3或a＜﹣1；即q：a＞3，或a＜﹣1；∴若“p或q”为真，“p且q”为假，则p，q一真一假；∴；∴﹣1≤a≤1，或a＞3；∴实数a的取值范围为∪（3，+∞）．点评：考查二次函数在闭区间上的最值，一元二次不等式解的情况和判别式△的关系，以及p或q，p且q的真假和p，q真假的关系．18．已知函数f（x）=x3+（1﹣a） x2﹣a（a+2）x+b（a，b∈R）．（Ⅰ）若函数f（x）的图象过原点，且在原点处的切线斜率是﹣3，求a，b的值；（Ⅱ）若函数f（x）在区间（﹣1，1）上不单调，求a的取值范围．考点：利用导数研究函数的单调性；导数的几何意义．专题：导数的综合应用．分析：（Ⅰ）先求导数：f′（x）=3x2+2（1﹣a）x﹣a（a+2），再利用导数求出在x=0处的导函数值，再结合导数的几何意义即可求出切线的斜率．列出关于a，b等式解之，从而问题解决．（Ⅱ）根据题中条件：“函数f（x）在区间（﹣1，1）不单调，”等价于“导函数f′（x）在（﹣1，1）既能取到大于0的实数，又能取到小于0的实数”，由于导函数是一个二次函数，有两个根，故问题可以转化为到少有一根在区间（﹣1，1）内，先求两根，再由以上关系得到参数的不等式，解出两个不等式的解集，求其并集即可；解答：解析：（Ⅰ）由题意得f′（x）=3x2+2（1﹣a）x﹣a（a+2）又，解得b=0，a=﹣3或a=1（Ⅱ）函数f（x）在区间（﹣1，1）不单调，等价于导函数f′（x），在（﹣1，1有实数根但无重根．∵f′（x）=3x2+2（1﹣a）x﹣a（a+2）=（x﹣a），令f′（x）=0得两根分别为x=a与x=若a=即a=﹣时，此时导数恒大于等于0，不符合题意，当两者不相等时即a≠﹣时有a∈（﹣1，1）或者∈（﹣1，1）解得a∈（﹣5，1）且a≠﹣综上得参数a的取值范围是（﹣5，﹣）∪（﹣，1）点评：本小题主要考查函数单调性的应用、函数奇偶性的应用、不等式的解法等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．19．已知函数，g（x）=sinx•cosx．（Ⅰ）求函数y=f（x）图象的对称轴方程；（Ⅱ）求函数h（x）=f（x）+g（x）的值域．考点：二倍角的余弦；函数y=Asin（ωx+φ）的图象变换．专题：三角函数的求值．分析：（Ⅰ）f（x）利用二倍角的余弦函数公式化简，根据余弦函数的性质即可确定出函数y=f（x）图象的对称轴方程；（Ⅱ）将f（x）与g（x）代入h（x）中，整理后利用两角和与差的正弦函数公式化为一个角的正弦函数，根据正弦函数的值域即可确定出h（x）的值域．解答：解：（Ⅰ）由题知f（x）=﹣1=cos（2x+）﹣，∴y=f（x）的对称轴方程为2x+=kπ（k∈Z），即x=kπ﹣（k∈Z）；（Ⅱ）由题知h（x）=f（x）+g（x）=cos（2x+）﹣+sin2x=﹣=（cos2x+sin2x）﹣=sin（2x+）﹣，∵﹣1≤sin（2x+）≤1，即﹣1≤sin（2x+）﹣≤0，∴h（x）的值域为．点评：此题考查了二倍角的余弦函数公式，正弦函数的值域，以及余弦函数的对称性，熟练掌握公式是解本题的关键．20．已知函数f（x）=（1）求f（x）的定义域和值域；（2）若曲线f（x）在点P（x0，f（x0））（﹣＜x0＜）处的切线平行直线y=x，求在点P处的切线方程．考点：利用导数研究曲线上某点切线方程；利用导数研究函数的单调性．专题：综合题；导数的综合应用．分析：（1）化简函数，再求f（x）的定义域和值域；（2）求导数，确定切点的坐标，即可求在点P处的切线方程．解答：解：（1）=，∴f（x）的值域为．…（6分）（2）由题意得∴又∵，∴，∴切点为，切线方程为：和．…（12分）点评：本题考查三角函数的化简，考查导数知识的运用，考查学生分析解决问题的能力，属于中档题．21．已知函数f（x）=2sin（ωx+φ）（0＜φ＜π，ω＞0）为偶函数，且函数y=f（x）图象的两相邻对称轴间的距离为π．（1）求函数y=f（x）的解析式；（2）已知△ABC中角 A、B、C所对的边分别是a、b、c，且f（A+）=，c=2a，求sinC 的值．考点：三角函数中的恒等变换应用；函数y=Asin（ωx+φ）的图象变换．专题：三角函数的图像与性质．分析：（1）先根据函数对称轴之间的距离，即可得到函数的周期，利用函数的周期性和奇偶性即可求出求函数y=f（x）的解析式；（2）根据函数的解析式，利用三角函数边角关系即可得到结论．解答：解：（1）∵函数y=f（x）图象的两相邻对称轴间的距离为π，∴函数f（x）周期为2π．∴ω=1．∵f（x）=2sin（ωx+φ）（0＜φ＜π，ω＞0）为偶函数，∴当x=0时f（0）=2sinϕ=2，∴．即．（2），∴，又由于，∴，∴，∴．点评：本题主要考查三角函数的图象和性质，根据函数的对称性和奇偶性求出函数的解析式是解决本题的关键．。

2014-2015学年安徽省铜陵五中高三（上）10月月考数学试卷（文科）一、选择题（每小题5分，共50分）1．已知集合A={x|x2﹣x≤0}，函数f（x）=2﹣x（x∈A）的值域为B，则（∁R A）∩B为（） A．（1，2] B． C． D．（1，+∞）2．已知函数f（x）是R上的单调增函数且为奇函数，则f（1）的值（） A．恒为正数 B．恒为负数 C．恒为0 D．可正可负3．已知函数，则函数f的定义域是（）A． {x|x≠﹣1} B． {x|x≠﹣2} C． {x|x≠﹣1且x≠﹣2} D． {x|x≠﹣1或x≠﹣2}4．下列命题中，说法错误的是（）A．“若p，则q”的否命题是：“若￢p，则￢q”B．“∀x＞2，x2﹣2x＞0”的否定是：“∃x≤2，x2﹣2x≤0”C．“p∧q是真命题”是“p∨q是真命题”的充分不必要条件D．“若b=0，则函数f（x）=ax2+bx+c是偶函数”的逆命题是真命题5．设f（x）在x0可导，则等于（） A． 2f'（x0） B． f'（x0） C． 3f'（x0） D． 4f'（x0）6．函数y=f（x）的图象如图所示，则y=f′（x）的图象可能是（）A． B． C． D．7．为得到函数的图象，只需将函数y=sinx的图象（） A．向左平移个长度单位 B．向右平移个长度单位C．向左平移个长度单位 D．向右平移个长度单位8．函数y=sin（2x+）图象的对称轴方程可能是（）A． x=﹣ B． x=﹣ C． x= D． x=9．数y=Asin（ωx+φ）+B（A＞0，φ＞0，|φ|＜，x∈R）的部分图象如图所示，则函数的表达式为（）A． B．C． D．10．若△ABC的内角A，B，C满足6sinA=4sinB=3sinC，则cosB=（）A． B． C． D．二、填空题（每小题5分，共25分）11．曲线y=xe x+2x+1在点（0，1）处的切线方程为．12．命题：∃x∈R，x2﹣x+1=0的否定是．13．函数的最大值是．14．△ABC中，角A，B，C所对的边分别为a，b，c，若acosA=bsinB，则sinAcosA+cos2B= ．15．对于下列命题：①在△ABC中，若sin2A=sin2B，则△ABC为等腰三角形；②在△ABC中，角A，B，C的对边分别为a，b，c，若a=4，b=10，A=，则△ABC有两组解；③设a=sin，b=cos，c=tan，则a＜b＜c；④将函数y=sin（3x+）的图象向左平移个单位，得到函数y=cos（3x+）的图象．其中正确命题的编号是．（写出所有正确结论的编号）三、解答题16．定义在R上的奇函数f（x）满足f（x）=f（x+4），且x∈（0，2]时，f（x）=．（1）求f（x）在上的解析式；（2）判断f（x）在上的单调性，并给予证明；（3）当λ为何值时，关于方程f（x）=λ在上有实数解？17．已知命题P：“对任意x∈，x2﹣a≥0”，命题q：“存在x∈R，x2+（a﹣1）x+1＜0”若“p 或q”为真，“p且q”为假命题，求实数a的取值范围．18．已知函数f（x）=x3+（1﹣a） x2﹣a（a+2）x+b（a，b∈R）．（Ⅰ）若函数f（x）的图象过原点，且在原点处的切线斜率是﹣3，求a，b的值；（Ⅱ）若函数f（x）在区间（﹣1，1）上不单调，求a的取值范围．19．已知函数，g（x）=sinx•cosx．（Ⅰ）求函数y=f（x）图象的对称轴方程；（Ⅱ）求函数h（x）=f（x）+g（x）的值域．20．已知函数f（x）=（1）求f（x）的定义域和值域；（2）若曲线f（x）在点P（x0，f（x0））（﹣＜x0＜）处的切线平行直线y=x，求在点P处的切线方程．21．已知函数f（x）=2sin（ωx+φ）（0＜φ＜π，ω＞0）为偶函数，且函数y=f（x）图象的两相邻对称轴间的距离为π．（1）求函数y=f（x）的解析式；（2）已知△ABC中角 A、B、C所对的边分别是a、b、c，且f（A+）=，c=2a，求sinC的值．2014-2015学年安徽省铜陵五中高三（上）10月月考数学试卷（文科）参考答案与试题解析一、选择题（每小题5分，共50分）1．已知集合A={x|x2﹣x≤0}，函数f（x）=2﹣x（x∈A）的值域为B，则（∁R A）∩B为（） A．（1，2] B． C． D．（1，+∞）考点：交、并、补集的混合运算．专题：函数的性质及应用．分析：利用集合的交、并、补集的混合运算法则直接求解．解答：解：∵集合A={x|x2﹣x≤0}，函数f（x）=2﹣x（x∈A）的值域为B，∴A={x|0≤x≤1}，B={x|1≤x≤2}，∴（∁R A）∩B={x|x＜0或x＞1}∩{x|1≤x≤2}={x|1＜x≤2}=（1，2]．故选：A．点评：本题考查集合的交、并、补集的混合运算，是基础题，解题时要认真审题，注意不等式的合理运用．2．已知函数f（x）是R上的单调增函数且为奇函数，则f（1）的值（） A．恒为正数 B．恒为负数 C．恒为0 D．可正可负考点：奇偶性与单调性的综合．专题：计算题．分析：根据奇函数的定义，我们易求了f（0）的值，然后根据函数f（x）是R上的单调增函数，我们即可判断出f（1）的值的符号．解答：解：∵函数f（x）是R上的奇函数∴f（0）=0，又∵f（x）在R上递增，∴f（1）＞f（0）=0，故选A．点评：本题考查的知识点是函数奇偶性与单调性的综合应用，其中根据奇函数的定义，判断出f（0）=0，是解答本题的关键．3．已知函数，则函数f的定义域是（）A． {x|x≠﹣1} B． {x|x≠﹣2} C． {x|x≠﹣1且x≠﹣2} D． {x|x≠﹣1或x≠﹣2}考点：函数的定义域及其求法．专题：计算题．分析：定义域是自变量x的取值范围所组成的集合，所以，我们要求出 f中x的取值范围．通过求出f的表达式来解决问题．解答：解：由函数，得f=，∴综合得x≠﹣1且x≠﹣2故选C．点评：复合函数的定义域是经常被考查的，所以要理解其解题时要注意的问题：综合考虑各个式子有意义．4．下列命题中，说法错误的是（）A．“若p，则q”的否命题是：“若￢p，则￢q”B．“∀x＞2，x2﹣2x＞0”的否定是：“∃x≤2，x2﹣2x≤0”C．“p∧q是真命题”是“p∨q是真命题”的充分不必要条件D．“若b=0，则函数f（x）=ax2+bx+c是偶函数”的逆命题是真命题考点：命题的真假判断与应用．专题：简易逻辑．分析：根据四种命题，全称命题的否定，充要条件的定义，偶函数的定义，逐一判断四个结论的正误，可得答案．解答：解：“若p，则q”的否命题是：“若￢p，则￢q”，故A正确；“∀x＞2，x2﹣2x＞0”的否定是：“∃x＞2，x2﹣2x≤0”，故B错误；“p∧q是真命题”⇔“p，q均为真命题”，“p∨q是真命题”⇔“p，q中存在真命题”，故“p∧q是真命题”是“p∨q是真命题”的充分不必要条件，即C正确；“若b=0，则函数f（x）=ax2+bx+c是偶函数”的逆命题为“若f（x）=ax2+bx+c是偶函数，则b=0”为真命题，故D正确．故选：B点评：本题以命题的真假判断为载体考查了四种命题，全称命题的否定，充要条件的定义，偶函数的定义等知识点，难度不大，属于基础题．5．设f（x）在x0可导，则等于（） A． 2f'（x0） B． f'（x0） C． 3f'（x0） D． 4f'（x0）考点：极限及其运算．专题：计算题．分析：由函数在某点的导数的定义可得 f′（x0）=，而要求的式子可化为+3，由此得出结论．解答：解：∵f（x）在x0可导，∴f′（x0）=．∴==+=f′（x0）+3=f′（x0）+3f′（x0）=4f′（x0），故选D．点评：本题考查极限及其运算，求解的关键有二，一是熟练掌握导数的定义，二是导数极限定义式的格式记忆准确，如此才能想到改变分子上两个函数式的顺序得出正确答案．此也是本题的一个易错点，极易出错，解决的办法就是对定义掌握准确，属于基础题．6．函数y=f（x）的图象如图所示，则y=f′（x）的图象可能是（）A． B． C． D．考点：函数的图象；导数的运算．专题：导数的概念及应用．分析：先看定义域，然后先依据原函数的单调性，判断导函数的符号，还无法辨别的再根据原函数增减的快慢判断导函数的绝对值的大小．解答：解：依据原函数图象可看出①当x＜0时，函数y=f（x）递增，所以此时f′（x）＞0，y=f′（x）的图象在x轴上方；②当x＞0时，函数y=f（x）递减，所以f′（x）＜0，y=f′（x）的图象在x轴下方．故选D点评：判断原函数与导函数图象之间的关系，主要是依据三点：在定义域内的某区间上①原函数递增，则导函数为正，图象在x轴上方；原函数递减，则导函数为负，图象在x轴下方；②极值点处的导数为零；③原函数增或减得越快（慢），则导函数的绝对值越大（小）．7．为得到函数的图象，只需将函数y=sinx的图象（） A．向左平移个长度单位 B．向右平移个长度单位C．向左平移个长度单位 D．向右平移个长度单位考点：函数y=Asin（ωx+φ）的图象变换．专题：计算题．分析：利用诱导公式将y=cos（x+）转化为y=sin（x+），利用平移知识解决即可．解答：解：∵y=cos（x+）=cos（﹣x﹣）=sin=sin（x+），∴要得到y=sin（x+）的图象，只需将函数y=sinx的图象向左平移个长度单位，故选C．点评：本题考查函数y=Asin（ωx+φ）的图象变换，将y=cos（x+）转化为y=sin（x+）是关键，考查理解与转化的能力，属于中档题．8．函数y=sin（2x+）图象的对称轴方程可能是（）A． x=﹣ B． x=﹣ C． x= D． x=考点：函数y=Asin（ωx+φ）的图象变换．分析：令2x+=求出x的值，然后根据k的不同取值对选项进行验证即可．解答：解：令2x+=，∴x=（k∈Z）当k=0时为D选项，故选D．点评：本题主要考查正弦函数对称轴的求法．属基础题．9．数y=Asin（ωx+φ）+B（A＞0，φ＞0，|φ|＜，x∈R）的部分图象如图所示，则函数的表达式为（）A． B．C． D．考点：由y=Asin（ωx+φ）的部分图象确定其解析式．专题：计算题．分析：通过函数的表达式的形式结合图象，求出B，A，求出函数的周期，得到ω，函数经过（2，3）以及φ的范围求出φ的值，得到选项．解答：解：由题意可知A=2，B=1，T==6，ω==，因为函数经过（2，3）所以3=2sin（×2+φ）+1，|φ|＜，φ=﹣，所以函数的表达式为；故选A．点评：本题考查三角函数的解析式的求法，函数图象的应用，注意周期的求法以及φ的求法是本题的关键，考查计算能力．10．若△ABC的内角A，B，C满足6sinA=4sinB=3sinC，则cosB=（）A． B． C． D．考点：三角函数的恒等变换及化简求值．专题：三角函数的图像与性质．分析：由题意利用正弦定理，推出a，b，c的关系，然后利用余弦定理求出cosB的值．解答：解：△ABC的内角A，B，C满足6sinA=4sinB=3sinC，所以6a=4b=3c，不妨令a=2，b=3，c=4，所以由余弦定理：b2=a2+c2﹣2accosB，所以cosB=，故选D．点评：本题是基础题，考查正弦定理，余弦定理的应用，考查计算能力，常考题型．二、填空题（每小题5分，共25分）11．曲线y=xe x+2x+1在点（0，1）处的切线方程为y=3x+1 ．考点：导数的几何意义．专题：计算题．分析：根据导数的几何意义求出函数y在x=0处的导数，从而求出切线的斜率，再用点斜式写出切线方程，化成斜截式即可；解答：解：y′=e x+x•e x+2，y′|x=0=3，∴切线方程为y﹣1=3（x﹣0），∴y=3x+1．故答案为：y=3x+1点评：本题考查了导数的几何意义，同时考查了导数的运算法则，本题属于基础题．12．命题：∃x∈R，x2﹣x+1=0的否定是∀x∈R，x2﹣x+1≠0 ．考点：特称命题；命题的否定．专题：计算题．分析：利用特称命题的否定是全称命题，写出结果即可．解答：解：因为特称命题的否定是全称命题，所以∃x∈R，x2﹣x+1=0的否定是：∀x∈R，x2﹣x+1≠0．故答案为：∀x∈R，x2﹣x+1≠0．点评：本题考查特称命题与全称命题的否定关系，考查基本知识的应用．13．函数的最大值是2 ．考点：三角函数的最值；运用诱导公式化简求值．专题：计算题．分析：先根据两角和与差的正弦公式进行化简，再由正弦函数的性质即可得到其最大值．解答：解：由．故答案为：2点评：本题主要考查两角和与差的正弦公式和正弦函数的性质﹣﹣最值．考查考生对正弦函数的性质的掌握和应用．三角函数式高考的一个必考点，重点在对于基础知识的考查．14．△ABC中，角A，B，C所对的边分别为a，b，c，若acosA=bsinB，则sinAcosA+cos2B= 1 ．考点：正弦定理；三角函数的化简求值．专题：计算题．分析：利用正弦定理化简已知的等式，得到sinAcosA=sin2B，代入所求的式子中，利用同角三角函数间的基本关系化简，即可求出所求式子的值．解答：解：∵acosA=bsinB，由正弦定理得：sinAcosA=sinBsinB=sin2B，则sinAcosA+cos2B=sin2B+cos2B=1．故答案为：1点评：此题考查了正弦定理，以及同角三角函数间的基本关系，熟练掌握正弦定理是解本题的关键．15．对于下列命题：①在△ABC中，若sin2A=sin2B，则△ABC为等腰三角形；②在△ABC中，角A，B，C的对边分别为a，b，c，若a=4，b=10，A=，则△ABC有两组解；③设a=sin，b=cos，c=tan，则a＜b＜c；④将函数y=sin（3x+）的图象向左平移个单位，得到函数y=cos（3x+）的图象．其中正确命题的编号是③，④．（写出所有正确结论的编号）考点：命题的真假判断与应用．分析：①运用三角函数的等价转换，②运用三角形正余弦定理，③考察的是三角函数的周期，④是函数图象的平移，向左平移n个单位，则自变量要加上n，向右平移n个单位，则变成自变量减去n解答：解：①：由题意可知，A=B满足条件，但是我们有sin（π﹣2A）=sin2A，∴存在π﹣2A=2B，∴2A+2B=π时，即A+B=90°时，也满足条件，∴故①错．②：知道两边和一个相对应的夹角，可以运用正弦定理，得：，∴sinB=＞1，∴此时△ABC无解，即画不出这样的图形．故②错；③：∵sinx、cosx是周期函数，且周期为2π，tanx也为周期函数，周期为π，∴sin=sin=﹣，cos=cos=﹣，tan=tan=∴a＜b＜c，故③正确；④：由函数图象左移个单位可知，函数变为 y=sin=sin=cos（3x+）∴故④正确．故答案为：③④．点评：三角函数等价转换，对称性，周期性，单调性，以及函数的平移和正余弦定理是常考点三、解答题16．定义在R上的奇函数f（x）满足f（x）=f（x+4），且x∈（0，2]时，f（x）=．（1）求f（x）在上的解析式；（2）判断f（x）在上的单调性，并给予证明；（3）当λ为何值时，关于方程f（x）=λ在上有实数解？考点：奇偶性与单调性的综合．专题：函数的性质及应用．分析：（1）由条件可得函数的周期为4，设x∈，根据f（﹣x）===﹣f（x），求得f（x）=．再根据奇函数的定义可得f（0）=0，从而求得可得，f（x）在上的解析式．（2）根据f（0）=0，当x∈（0，2]时，由于f（x）=1﹣＞0，且f（x）随着x的增大而增大，可得f（x）在上是增函数．再利用函数的单调性的定义进行证明．（3）由题意可得，本题即求函数λ=f（x）在上的值域，再利用函数的单调性求得函数f（x）在上的值域．解答：解：（1）∵奇函数f（x）满足f（x）=f（x+4），故函数的周期为4．由于x∈（0，2]时，f（x）=，设x∈，故 f（﹣x）===﹣f（x），∴f（x）=．再根据奇函数的定义可得f（0）=0，可得，f（x）在上的解析式为f（x）=．（2）在上，f（0）=0，当x∈（0，2]时，由于f（x）==1﹣＞0，且f（x）随着x的增大而增大，故f（x）在上是增函数．证明：设0≤x1＜x2≤2，则由f（x1）﹣f（x2）=﹣=＜0，可得f（x1）＜f（x2），故f（x）在上是增函数．（3）由题意可得，本题即求函数λ=f（x）在上的值域．利用函数的单调性求得函数f（x）在上的值域为 {λ|y=0，或＜λ≤，或﹣≤λ＜﹣}，故λ的范围为：{λ|y=0，或＜λ≤，或﹣≤λ＜﹣}．点评：本题主要考查函数的周期性、单调性和奇偶性的应用，求函数的解析式和函数的值域，体现了转化的数学思想，属于基础题．17．已知命题P：“对任意x∈，x2﹣a≥0”，命题q：“存在x∈R，x2+（a﹣1）x+1＜0”若“p 或q”为真，“p且q”为假命题，求实数a的取值范围．考点：复合命题的真假．专题：简易逻辑．分析：根据二次函数的最值，一元二次不等式解的情况和判别式△的关系即可求出p：a≤1，q：a＜﹣1，或a＞3，而根据“p或q”为真，“p且q”为假知道p真q假，或p假q真两种情况，所以求出每种情况的a的取值范围并求并集即可．解答：解：由命题p知，x2在上的最小值为1，∴p：a≤1；由命题q知，不等式x2+（a﹣1）x+1＜0有解，∴△=（a﹣1）2﹣4＞0；∴a＞3或a＜﹣1；即q：a＞3，或a＜﹣1；∴若“p或q”为真，“p且q”为假，则p，q一真一假；∴；∴﹣1≤a≤1，或a＞3；∴实数a的取值范围为∪（3，+∞）．点评：考查二次函数在闭区间上的最值，一元二次不等式解的情况和判别式△的关系，以及p或q，p且q的真假和p，q真假的关系．18．已知函数f（x）=x3+（1﹣a） x2﹣a（a+2）x+b（a，b∈R）．（Ⅰ）若函数f（x）的图象过原点，且在原点处的切线斜率是﹣3，求a，b的值；（Ⅱ）若函数f（x）在区间（﹣1，1）上不单调，求a的取值范围．考点：利用导数研究函数的单调性；导数的几何意义．专题：导数的综合应用．分析：（Ⅰ）先求导数：f′（x）=3x2+2（1﹣a）x﹣a（a+2），再利用导数求出在x=0处的导函数值，再结合导数的几何意义即可求出切线的斜率．列出关于a，b等式解之，从而问题解决．（Ⅱ）根据题中条件：“函数f（x）在区间（﹣1，1）不单调，”等价于“导函数f′（x）在（﹣1，1）既能取到大于0的实数，又能取到小于0的实数”，由于导函数是一个二次函数，有两个根，故问题可以转化为到少有一根在区间（﹣1，1）内，先求两根，再由以上关系得到参数的不等式，解出两个不等式的解集，求其并集即可；解答：解析：（Ⅰ）由题意得f′（x）=3x2+2（1﹣a）x﹣a（a+2）又，解得b=0，a=﹣3或a=1（Ⅱ）函数f（x）在区间（﹣1，1）不单调，等价于导函数f′（x），在（﹣1，1有实数根但无重根．∵f′（x）=3x2+2（1﹣a）x﹣a（a+2）=（x﹣a），令f′（x）=0得两根分别为x=a与x=若a=即a=﹣时，此时导数恒大于等于0，不符合题意，当两者不相等时即a≠﹣时有a∈（﹣1，1）或者∈（﹣1，1）解得a∈（﹣5，1）且a≠﹣综上得参数a的取值范围是（﹣5，﹣）∪（﹣，1）点评：本小题主要考查函数单调性的应用、函数奇偶性的应用、不等式的解法等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．19．已知函数，g（x）=sinx•cosx．（Ⅰ）求函数y=f（x）图象的对称轴方程；（Ⅱ）求函数h（x）=f（x）+g（x）的值域．考点：二倍角的余弦；函数y=Asin（ωx+φ）的图象变换．专题：三角函数的求值．分析：（Ⅰ）f（x）利用二倍角的余弦函数公式化简，根据余弦函数的性质即可确定出函数y=f（x）图象的对称轴方程；（Ⅱ）将f（x）与g（x）代入h（x）中，整理后利用两角和与差的正弦函数公式化为一个角的正弦函数，根据正弦函数的值域即可确定出h（x）的值域．解答：解：（Ⅰ）由题知f（x）=﹣1=cos（2x+）﹣，∴y=f（x）的对称轴方程为2x+=kπ（k∈Z），即x=kπ﹣（k∈Z）；（Ⅱ）由题知h（x）=f（x）+g（x）=cos（2x+）﹣+sin2x=﹣=（cos2x+sin2x）﹣=sin（2x+）﹣，∵﹣1≤sin（2x+）≤1，即﹣1≤sin（2x+）﹣≤0，∴h（x）的值域为．点评：此题考查了二倍角的余弦函数公式，正弦函数的值域，以及余弦函数的对称性，熟练掌握公式是解本题的关键．20．已知函数f（x）=（1）求f（x）的定义域和值域；（2）若曲线f（x）在点P（x0，f（x0））（﹣＜x0＜）处的切线平行直线y=x，求在点P处的切线方程．考点：利用导数研究曲线上某点切线方程；利用导数研究函数的单调性．专题：综合题；导数的综合应用．分析：（1）化简函数，再求f（x）的定义域和值域；（2）求导数，确定切点的坐标，即可求在点P处的切线方程．解答：解：（1）=，∴f（x）的值域为．…（6分）（2）由题意得∴又∵，∴，∴切点为，切线方程为：和．…（12分）点评：本题考查三角函数的化简，考查导数知识的运用，考查学生分析解决问题的能力，属于中档题．21．已知函数f（x）=2sin（ωx+φ）（0＜φ＜π，ω＞0）为偶函数，且函数y=f（x）图象的两相邻对称轴间的距离为π．（1）求函数y=f（x）的解析式；（2）已知△ABC中角 A、B、C所对的边分别是a、b、c，且f（A+）=，c=2a，求sinC 的值．考点：三角函数中的恒等变换应用；函数y=Asin（ωx+φ）的图象变换．专题：三角函数的图像与性质．分析：（1）先根据函数对称轴之间的距离，即可得到函数的周期，利用函数的周期性和奇偶性即可求出求函数y=f（x）的解析式；（2）根据函数的解析式，利用三角函数边角关系即可得到结论．解答：解：（1）∵函数y=f（x）图象的两相邻对称轴间的距离为π，∴函数f（x）周期为2π．∴ω=1．∵f（x）=2sin（ωx+φ）（0＜φ＜π，ω＞0）为偶函数，∴当x=0时f（0）=2sinϕ=2，∴．即．（2），∴，又由于，∴，∴，∴．点评：本题主要考查三角函数的图象和性质，根据函数的对称性和奇偶性求出函数的解析式是解决本题的关键．。

铜陵市第五中学2015届高三第三次月考化学试题时间：90分钟满分：100分一选择题（每题只有一个正确选项，每题3分共48分）1.对下列定量实验中的基本操作和仪器的描述正确的是( )A.用托盘天平称取 NaOH固体20.0 gB.将用水润湿的pH试纸，浸入稀盐酸溶液，测定溶液的pHC.滴定管的0刻度线在上部，而量筒的0刻度线在下部D.在配制一定物质的量浓度的溶液时，定容后，经摇匀后发现液面低于刻度线，此时再加入蒸馏水使其液面与刻度持平2.下列除去杂质的方法中，正确的是（）A、除去铜粉中混有的铁：加足量稀硝酸，过滤B、除去N2中少量的CO：通过足量灼热的CuO粉末C、除去KCl溶液中的少量CaCl2：加适量Na2CO3溶液，过滤D、除去CO2中的少量的HCl：通过足量的饱和碳酸氢钠溶液3. 用下列实验装置完成对应的实验(部分仪器已省略)，能达到实验目的的是（）4.设N A为阿伏加德罗常数。

下列叙述中正确的是( )A．常温常压下，3.4g NH中含N—H键数目为0.6N A3中充分燃烧，转移的电子数为0.3N A B．0.1 mol铁在0.1 mol Cl2）所含的电子数为9N AC．15g甲基（—14CH3）中所含氯原子数为0.3N AD．标准状况下，2.24L氯仿（CHCl35．下列各组离子在碱性条件下能大量共存，而在强酸性条件下能发生氧化还原反应的是( )A.Mg2+、Na+、SO42-、Cl—B.K+、CO32-、Cl—、NO3—C.Na+、K+、NO3—、SO32—D.NH4+、Na+、SO42-、NO3—6.在下列氧化还原反应中，水作为氧化剂的是（）A．C+ H2O CO+ H2 B.3NO2+H2O＝2HNO3+NOC．2Na2O2+2H2O＝4NaOH+O2↑D．2F2+2H2O＝4HF+O27．从海水中提取溴，主要反应为：2Br—+Cl2=2Cl—+Br2，下列说法正确的是A．溴离子具有氧化性 B. 氯气是还原剂C．该反应属于复分解反应 D. 氯气的氧化性比溴单质强8.下列叙述正确的是( )A．发生化学反应时失去电子越多的金属原子，还原能力越强B．金属阳离子被还原后，一定得到该元素的单质C．核外电子数相同的原子，一定是同种元素的原子D．能与酸反应的氧化物，一定是碱性氧化物9．下列实验设计及其对应离子方程式均正确的是()A．Na2O2与H2O反应制备O2：Na2O2＋H2O===2Na＋＋2OH－＋O2↑B．用FeCl3溶液腐蚀铜线路板：Cu＋2Fe3＋===Cu2＋＋2Fe2＋C．将氯气溶于水制备次氯酸：Cl2＋H2O===2H＋＋Cl－＋ClO－D．用浓盐酸酸化的KMnO4与H2O2反应，证明H2O2具有还原性：2MnO－4＋6H＋＋5H2O2===2Mn2＋＋5O2↑＋8H2O10.在一定条件下，RO3n－和氟气可发生如下反应：RO3n－＋F2＋2OH－＝RO4－＋2F－＋H2O从而可知在RO3n－中，元素R的化合价是( )A．＋4 B．＋5 C．＋6 D．＋711.根据反应式：(1)2Fe3＋+2I－=2Fe2＋+I2，(2)Br2+2Fe2＋=2Br－+2Fe3＋，可判断离子的还原性从强到弱的顺序是( )A．Br－、Fe2＋、I－B．I－、Fe2＋、Br－C．Br－、I－、Fe2＋D．Fe2＋、I－、Br－12.下列现象或应用中，不能．．用胶体知识解释的是( )A．在饱和FeCl3溶液中逐滴加入NaOH溶液，产生红褐色沉淀B．用微波手术刀进行外科手术，可使开刀处的血液迅速凝固而减少失血C．清晨，在茂密的树林，常常可以看到从枝叶间透过的一道道光柱D．肾功能衰竭等疾病引起的血液中毒，可利用血液透析进行治疗13．对于以下反应：①KHCO3溶液与石灰水反应②Na2SO3溶液与稀盐酸反应③Si与烧碱溶液反应④Fe与稀硝酸反应改变反应物用量时，不．能用同一个离子方程式表示的是( )A．①②③ B．①②④ C．①③④ D．②③④14．锌与很稀的硝酸反应生成硝酸锌、硝酸铵和水。