
4.1 一个四元对称信源?
?????=??????4/14/1324/14/110)(X P X ,接收符号Y = {0, 1, 2, 3},其失真矩阵为?????
???????0111
101111011110,求D max 和D min 及信源的R(D)函数,并画出其曲线(取4至5个点)。解: 0041041041041),(min )(43041141141141),()(min min min max =?+?+?+?===?+?+?+?===∑∑i
j i j i i j i i j j y x d x p D y x d x p D D 因为n 元等概信源率失真函数:
??
? ??-??? ??-+-+=a D a D n a D
a D n D R 1ln 11ln ln )( 其中a = 1, n = 4, 所以率失真函数为:
()()D D D D D R --++=1ln 13
ln
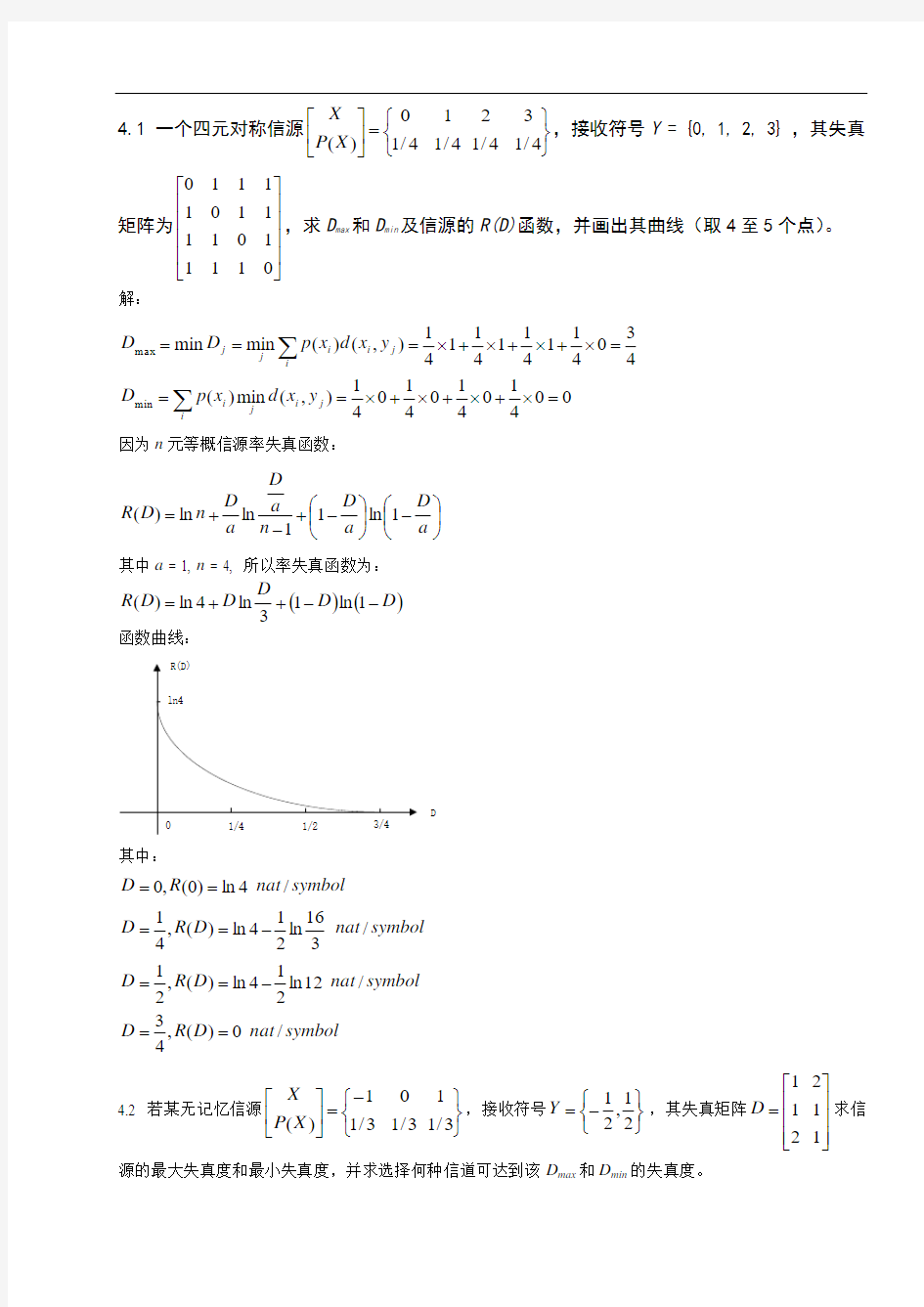
4ln )( 函数曲线:
D 其中:
symbol nat D R D symbol nat D R D symbol nat D R D symbol
nat R D /0)(,4
3/12ln 2
14ln )(,21/3
16ln 214ln )(,41/4ln )0(,0==-==-==== 4.2 若某无记忆信源??????-=??????3/113/13/101)(X P X ,接收符号??????-=21,21Y ,其失真矩阵????
??????=112211D 求信源的最大失真度和最小失真度,并求选择何种信道可达到该D max 和D min 的失真度。
4.3 某二元信源??????=??????2/12/110)(X P X 其失真矩阵为??
????=a a D 00求这信源的D max 和D min 和R(D)函数。
解:
0021021),(min )(202121),()(min min min max =?+?===?+?===∑∑i
j i j i i j i i j j y x d x p D a a y x d x p D D 因为二元等概信源率失真函数:
??
? ??-=a D H n D R ln )( 其中n = 2, 所以率失真函数为:
??
??????? ??-??? ??-+-=a D a D a D a D D R 1ln 1ln 2ln )( 4.4 已知信源X = {0, 1},信宿Y = {0, 1, 2}。设信源输入符号为等概率分布,而且失真函数??????∞∞=1100D ,求信源的率失真函数R(D)。
4.5 设信源X = {0, 1, 2, 3},信宿Y = {0, 1, 2, 3, 4, 5, 6}。且信源为无记忆、等概率分布。失真函数定义为
???????∞======其他
且且53,21
41,010),(j i j i j i y x d j i 证明率失真函数R(D)如图所示。
log2
2log2
D
4.6 设信源X = {0, 1, 2},相应的概率分布p (0) = p (1) = 0.4,p (2) = 0.2。且失真函数为 )2,1,0,(10),(=???≠==j i j i j i y x d j i
(1) 求此信源的R(D);
(2) 若此信源用容量为C 的信道传递,请画出信道容量C 和其最小误码率P k 之间的曲线关系。
4.7 设0 < α, β < 1, α + β = 1。试证明:αR(D ’) +βR(D ”) ≥ R(αD ’ +βD ”)
4.8 试证明对于离散无记忆N 次扩展信源,有R N (D) = NR(D)。其中N 为任意正整数,D ≥ D min 。
4.9 设某地区的“晴天”概率p (晴) = 5/6,“雨天”概率p (雨) = 1/6,把“晴天”预报为“雨天”,把“雨天”
预报为“晴天”造成的损失为a 元。又设该地区的天气预报系统把“晴天”预报为“晴天”,“雨天”预报为“雨天”的概率均为0.9;把把“晴天”预报为“雨天”,把“雨天”预报为“晴天”的概率均为0.1。试计算这种预报系统的信息价值率v (元/比特)。
4.10 设离散无记忆信源?
?????=??????3/13/13/1)(321x x x X P X 其失真度为汉明失真度。 (1) 求D min 和R(D min ),并写出相应试验信道的信道矩阵;
(2) 求D max 和R(D max ),并写出相应试验信道的信道矩阵;
(3) 若允许平均失真度D = 1/3,试问信源的每一个信源符号平均最少有几个二进制符号表示?
解:
???????≠-+=-+==?+?+?==∑j i e n e j i e n x y p y x d x p D sa sa sa i j i
j i j i ,)1(1,)1(11)/(0031031031),(min )(min
4.11 设信源?
?????-=??????p p x x X P X 1)(21(p < 0.5),其失真度为汉明失真度,试问当允许平均失真度D = 0.5p 时,每一信源符号平均最少需要几个二进制符号表示?
解:
因为二元信源率失真函数:
??
? ??-=a D H p H D R )()( 其中a = 1(汉明失真), 所以二元信源率失真函数为:
)()()(D H p H D R -= 当2
p D =时 []symbol nat p p p p p p p p p H p H p R /21ln 212ln 2)1ln()1(ln 2)(2??
??????? ??-??? ??-++--+-=??? ??-=??? ??
反比例函数知识点及典型例题 反比例函数这一章是初中数学的一个重点,也是初中数学的一个核心知识点。由反比例函数的图像和性质衍生出了好多数学问题,这对“数形结合”思想还有点欠缺的中学生来说无疑是一个难点。 一、反比例函数知识要点点拨 1、反比例函数的图象和性质: 反比例函数 (0)k y k x = ≠ k 的符号 0k > 0k < 图象 性质 ①x 的取值范围是0x ≠, y 的取值范围是0y ≠. ②当0k >时,函数图象的两个分支分别在第一、第三象限.在每 个象限内,y 随x 的增大而减小. ①x 的取值范围是0x ≠, y 的取值范围是0y ≠. ②当0k <时,函数图象的两个分支分别在第二、第四象 限.在每个象限内,y 随x 的增大而增大. 反比例函数的图象既是轴对称图形,又是中心对称图形,它有两条对称轴,对称中心是坐标原点. 2、反比例函数与正比例函数(0)y kx k =≠的异同点: 函数 正比例函数 反比例函数 x y O x y O
解析式 (0)y kx k =≠ (0)k y k x = ≠ 图象 直线,经过原点 双曲线,与坐标轴没有交点 自变量取值范围 全体实数 0x ≠的一切实数 图象的位置 当0k >时,在一、三象限; 当0k <时,在二、四象限. 当0k >时,在一、三象限; 当0k <时,在二、四象限. 性质 当0k >时,y 随x 的增大而增大; 当0k <时,y 随x 的增大而减小. 当0k >时,y 随x 的增大而 减小; 当0k <时,y 随x 的增大而增大. 二,、典型例题 例 1 下面函数中,哪些是反比例函数? (1)3 x y -=;(2)x y 8-=;(3)54-=x y ;(4)15-=x y ;(5).8 1=xy 解:其中反比例函数有(2),(4),(5). 说明:判断函数是反比例函数,依据反比例函数定义,x k y =)0(≠k , 它也可变形为1-=kx y 及k xy =的形式,(4),(5)就是这两种形式. 例 2在以下各小题后面的括号里填写正确的记号.若这个小题成正比例关系,填 (正);若成反比例关系,填(反);若既不成正比例关系又不成反比例关系,填(非). (1)周长为定值的长方形的长与宽的关系 ( ); (2)面积为定值时长方形的长与宽的关系 ( ); (3)圆面积与半径的关系 ( ); (4)圆面积与半径平方的关系 ( ); (5)三角形底边一定时,面积与高的关系 ( ); (6)三角形面积一定时,底边与高的关系 ( );
第二章 随机变量及其分布 1、解: 设公司赔付金额为X ,则X 的可能值为; 投保一年内因意外死亡:20万,概率为0.0002 投保一年内因其他原因死亡:5万,概率为0.0010 投保一年内没有死亡:0,概率为1-0.0002-0.0010=0.9988 所以X 2、一袋中有5X 表示取出的三只球中的最大号码,写出随机变量X 的分布律 解:X 可以取值3,4,5,分布律为 10 61)4,3,2,1,5()5(1031)3,2,1,4()4(10 11)2,1,3()3(35 2 435 2 335 2 2=?= === ?==== ?= ==C C P X P C C P X P C C P X P 中任取两球再在号一球为中任取两球再在号一球为号两球为号一球为 也可列为下表 X : 3, 4,5 P :10 6, 103,101 3、设在15只同类型零件中有2只是次品,在其中取三次,每次任取一只,作不放回抽样,以X 表示取出次品的只数,(1)求X 的分布律,(2)画出分布律的图形。 解:任取三只,其中新含次品个数X 可能为0,1,2个。 35 22 )0(315313= ==C C X P 3512)1(3 15213 12=?==C C C X P 35 1)2(3 15 113 22= ?= =C C C X P 再列为下表 X : 0, 1, 2 P : 35 1, 3512,3522 4、进行重复独立实验,设每次成功的概率为p ,失败的概率为q =1-p (0
反比例函数知识点归纳和典型例题 知识点归纳 (一)反比例函数的概念 1.()可以写成()的形式,注意自变量x的指数为,在解决有关自变量指数问题时应特别注意系数这一限制条件; 2.()也可以写成xy=k的形式,用它可以迅速地求出反比例函数解析式中的k,从而得到反比例函数的解析式; 3.反比例函数的自变量,故函数图象与x轴、y轴无交点. (二)反比例函数的图象 在用描点法画反比例函数的图象时,应注意自变量x的取值不能为0,且x应对称取点(关于原点对称). (三)反比例函数及其图象的性质 1.函数解析式:() 2.自变量的取值范围: 3.图象: (1)图象的形状:双曲线. 越大,图象的弯曲度越小,曲线越平直. 越小,图象的弯曲度越大. (2)图象的位置和性质: 与坐标轴没有交点,称两条坐标轴是双曲线的渐近线. 当时,图象的两支分别位于一、三象限; 在每个象限内,y随x的增大而减小; 当时,图象的两支分别位于二、四象限; 在每个象限内,y随x的增大而增大. (3)对称性:图象关于原点对称,即若(a,b)在双曲线的一支上, 则(,)在双曲线的另一支上.
图象关于直线对称,即若(a,b)在双曲线的一支上, 则(,)和(,)在双曲线的另一支上.4.k的几何意义 如图1,设点P(a,b)是双曲线上任意一点,作PA⊥x轴于A点,PB⊥y轴于B点,则矩形PBOA的面积是(三角形PAO和三角形PBO的面积都是). 如图2,由双曲线的对称性可知,P关于原点的对称 点Q也在双曲线上,作QC⊥PA的延长线于C,则有三 角形PQC的面积为. 图1 图2 5.说明: (1)双曲线的两个分支是断开的,研究反比例函数的增减性时,要将两个分支分别讨论,不能一概而论. (2)直线 与双曲线的关系: 当 时,两图象没有交点; 当 时,两图象必有两个交点,且这两个交点关于原点成中心对称.
第1章 习 题 一、习题1.1 解:(1)利用题目中的数据,通过SAS 系统proc univariate 过程计算得到: 139.0=x 7.06387S = 49.898312=S 0.142众数= 51.0g 1-= 08192.5=CV 126129.0g 2-=由得到的数据特征可知道,偏度为负,所以呈做偏态, 峰度为负,所以均值两侧的极端值较少。 (2) 139.0=M 31.0=R 0.135Q 1= 5.144Q 3= 5.9R 131=-=Q Q 375.1394 1 2141M 31=++= ∧ Q M Q (3) 通过SAS 系统proc capability 得到直方图,并拟合正态分布曲线:
(4) 通过SAS 系统proc univariate 可以画出茎叶图,从茎叶图可以看出数据大致呈对称分布,由于所给数据都是整数,所以叶所代表的小位数都是0。 (5) 通过SAS 系统proc univariate 过程计算得到: 0.971571W 0= 00()H p P W W =≤= 0.1741 取0.05=α,因α>=0.1742p ,故不能拒绝0H ,认为样本来自正态总体分布。 通过画QQ图和经验分布曲线和理论分布函数曲线,从图中可以看出QQ图近似的在一条直线上,经验分布曲线的拟合程度也相当好,所以可以进一步说明此样本来自正态总体分布。
二、习题1.2 7.8574027=x 1.62568785 S = 2.642860982=S 0.13721437g 1= 20.6898884=CV -1.4238025g 2= 由得到的数据特征可知道,偏度为正,所以呈右偏态,峰度为负,所以均值两侧的极端值较少。 (2)
4.1 一个四元对称信源? ?????=??????4/14/1324/14/110)(X P X ,接收符号Y = {0, 1, 2, 3},其失真矩阵为????? ???????0111 101111011110,求D max 和D min 及信源的R(D)函数,并画出其曲线(取4至5个点)。 解: 0041041041041),(min )(43041141141141),()(min min min max =?+?+?+?===?+?+?+?===∑∑i j i j i i j i i j j y x d x p D y x d x p D D 因为n 元等概信源率失真函数: ?? ? ??-??? ??-+-+=a D a D n a D a D n D R 1ln 11ln ln )( 其中a = 1, n = 4, 所以率失真函数为: ()()D D D D D R --++=1ln 13 ln 4ln )( 函数曲线: D 其中: symbol nat D R D symbol nat D R D symbol nat D R D symbol nat R D /0)(,4 3/12ln 2 14ln )(,21/3 16ln 214ln )(,41/4ln )0(,0==-==-==== 4.2 若某无记忆信源??????-=??????3/113/13/101)(X P X ,接收符号??????-=21,21Y ,其失真矩阵???? ??????=112211D 求信源的最大失真度和最小失真度,并求选择何种信道可达到该D max 和D min 的失真度。
反比例函数 知识点及考点: (一)反比例函数的概念: 知识要点: 1、一般地,形如 y = x k ( k 是常数, k = 0 ) 的函数叫做反比例函数。 注意:(1)常数 k 称为比例系数,k 是非零常数; (2)解析式有三种常见的表达形式: (A )y = x k (k ≠ 0) , (B )xy = k (k ≠ 0) (C )y=kx -1 (k ≠0) 例题讲解:有关反比例函数的解析式 (1)下列函数,① 1)2(=+y x ②. 11 += x y ③21x y = ④.x y 21-=⑤2x y =-⑥13y x = ;其中是y 关于 x 的反比例函数的有:_________________。 (2)函数2 2 )2(--=a x a y 是反比例函数,则a 的值是( ) A .-1 B .-2 C .2 D .2或-2 (3)若函数1 1-= m x y (m 是常数)是反比例函数,则m =________,解析式为________. (4)如果y 是m 的反比例函数,m 是x 的反比例函数,那么y 是x 的( ) A .反比例函数 B .正比例函数 C .一次函数 D .反比例或正比例函数 练习:(1)如果y 是m 的正比例函数,m 是x 的反比例函数,那么y 是x 的( ) (2)如果y 是m 的正比例函数,m 是x 的正比例函数,那么y 是x 的( ) (5)反比例函数(0k y k x = ≠) 的图象经过(—2,5, n ), 求1)n 的值; 2)判断点B (24,)是否在这个函数图象上,并说明理由 (6)已知y 与2x -3成反比例,且4 1 =x 时,y =-2,求y 与x 的函数关系式.
4.1 一个四元对称信源? ?????=??????4/14/1324/14/110)(X P X ,接收符号Y = {0, 1, 2, 3},其失真矩阵为????? ???????0111 101111011110,求D max 和D min 及信源的R(D)函数,并画出其曲线(取4至5个点)。 解: 0041041041041),(min )(43041141141141),()(min min min max =?+?+?+?===?+?+?+?===∑∑i j i j i i j i i j j y x d x p D y x d x p D D 因为n 元等概信源率失真函数: ?? ? ??-??? ??-+-+=a D a D n a D a D n D R 1ln 11ln ln )( 其中a = 1, n = 4, 所以率失真函数为: ()()D D D D D R --++=1ln 13 ln 4ln )( 函数曲线: D 其中: sym bol nat D R D sym bol nat D R D sym bol nat D R D sym bol nat R D /0)(,4 3/12ln 2 14ln )(,21/3 16ln 214ln )(,41/4ln )0(,0==-==-==== 4.2 若某无记忆信源??????-=??????3/113/13/101)(X P X ,接收符号??????-=21,21Y ,其失真矩阵???? ??????=112211D 求信源的最大失真度和最小失真度,并求选择何种信道可达到该D max 和D min 的失真度。 4.3 某二元信源??????=??????2/12/110)(X P X 其失真矩阵为?? ????=a a D 00求这信源的D max 和D min 和R(D)
X Y -9 -8-7-6-5-4-3-2-1 1110987654321 -8-7-6-5-4-3-2-1 9 876543210X Y -9 -8-7-6-5-4-3-2-1 11109876543 21 -8-7-6-5-4-3-2-19 8 7 6 5 4 3 2 1 0反比例函数 一、经典内容解析 1.反比例函数的概念 (1) (k ≠0)可以写成(k ≠0)的形式,注意自变量x 的指数为-1,在解决有关 自变量指数问题时应特别注意系数k ≠0这一限制条件; (2) (k ≠0)也可以写成xy=k 的形式,用它可以迅速地求出反比例函数解析式中的 k ,从而得到反比例函数的解析式; (3) 反比例函数 的自变量x ≠0,故函数图象与x 轴、y 轴无交点. 解析式 x k y = (k 为常数,且0k ≠) 自变量取值范围 0≠x 的实数 图 象 图象的性质 双曲线 0k > 0k < 示意图 位置 两个分支分别位于 一、三象限 两个分支分别位于 二、四象限 变化趋势 在每个象限内,y 随x 的增大而减小 在每个象限内,y 随x 的增大而增大 对称性 是轴对称图形,直线x y ±=是它的两条对称轴 是中心对称图形,对称中心为坐标原点 3.反比例函数的性质(与正比例函数对比) 函数解析式 正比例函数 y=kx (k ≠0) 反比例函数 (k ≠0) 自变量的 取值范围 全体实数 x ≠0 图 象 直线,经过原点 双曲线,与坐标轴没有交点
图象位置 (性质) 当k>0时,图象经过一、三象限;当 k<0时,图象经过二、四象限. 当k>0时,图象的两支分别位于一、三 象限;当k<0时,图象的两支分别位 于二、四象限. 性质 (1) 当k>0时,y随x的增大而增大; 当k<0时,y随x的增大而减小. (2) 越大,图象越靠近y轴. (1) 当k>0时,在每个象限内y随x的 增大而减小;当k<0时,在每个象限 内y随x的增大而增大. (2) 越大,图 象的弯曲度越小,曲线越平直. 注: (1) 双曲线的两个分支是断开的,研究反比例函数的增减性时,要将两个分支分别讨论, 不能一概而论. (2) 正比例函数与反比例函数, 当时,两图象没有交点; 当时,两图象必有两个交点, 且这两个交点关于原点成中心对称. (3) 反比例函数与一次函数的联系. 4.反比例函数中比例系数k的几何意义 (1)过双曲线(k≠0) 上任意一点作x轴、y轴的垂线,所得矩形的面积为. (2)过双曲线(k≠0) 上任意一点作一坐标轴的垂线,连接该点和原点,所得三角形
第四章信息率失真函数(第九讲) (2课时) 主要内容:(1)平均失真和信息率失真函数(2)离散信源和连续信源的R(D)计算重点:失真函数、平均失真、信息率失真函数R(D)、信息率失真函数的计算。 难点:信息率失真函数R(D)、信息率失真函数的计算。 作业:4、lo 说明:本堂课推导内容较多,枯燥平淡,不易激发学生兴趣,要注意多讨论用途。另外,注意,解题方法。多加一些内容丰富知识和理解。 §4-1引言 (一)引入限失真的必要性: 失真在传输中是不可避免的; 接收者(信宿)无论是人还是机器设备,都有一定的分辨能力与灵敏度,超过分辨能力与灵敏度的信息传送过程是毫无意义的; 即使信宿能分辨、能判别,但对通信质量的影响不大,也可以称它为允许范围内的失真; 我们的目的就是研究不同的类型的客观信源与信宿,在给定的Qos要求下的最大允许(容忍)失真D,及其相应的信源最小信息率R(D). 对限失真信源,应该传送的最小信息率是R(D),而不是无失真情况下的信源爛H(U). 显然H(U)2R(D). 当且仅当D=0时,等号成立; 为了定量度量D,必须建立信源的客观失真度量,并与D建立定量关系; R(D)函数是限失真信源信息处理的理论基础; (二)R(D)函数的定义 信源与信宿联合空间上失真测度的定义:d (见叩:t/xV^/r[0,oo) 其屮:u*U(单消息信源空I'可) v y eV (单消息信宿空间) 则有 万=Y工〃(吧 称7为统计平均失真,它在信号空I'可屮可以看作一类“距离”,它有性质 1〉= 0,当比=Vj 2〉min 〃(吧)=°
3〉05〃(比/匕)<00 对离散信源:i=j=l,2............. n , d(upj) = djj, 则有: d 」0,当;可(无失真) 厂]〉0,当iHj (有失真) 若取冷为汉明距离,则有: Jo,当i = j (无失真) 厂[1,当iHj (有失真) 对连续信源,失真可用二元函数d(u,v)表示。 推而广之,d(u,v)可表示任何用V 表达U 时所引进的失真,误差,损失,风险,甚至是 主观感觉 上的差异等等。 进一步定义允许失真D 为平均失真的上界: D>d =工=工工〃£皿???对离散 ? ? ? ? 在讨论信息率失真函数时,考虑到信源与信宿之I'可有一个无失真信道,称它为试验信 道,对离散信源可记为p 〃,对限失真信源这一试验信道集合可定义为: P D =\P ji -D>d = YLP :P J^ 根据前面在互信息中已讨论过的性质: 1(U\ I,p ;j\ 且互信息是门的上凸函数,其极限值存在且为信道容量:C = max/(卫: p< ? 这里,我们给出其对偶定义: R(D)= mi 1Y U # ) m"pQp2,_ D P j f P D 陆 j i P D 即互信息是◎的下凸函数。其极限值存在且为信息率失真函数。 它还存在下列等效定义: D(R) = minD>d =工工门叽 < P 泸 P R i J P R = {? : /(t/;V) < R (给定速率)} 称D(R)为失真信息率函数,是R(D)的逆函数,它是求在允许最大速率情况下的最大 失真Do 至此,我们已给定R(D)函数一个初步描述。 则有: d(u. v)= (w-仍 H = \u-v
第十七章 反比例函数 一、基础知识 1. 定义:一般地,形如x k y =(k 为常数,o k ≠)的函数称为反比例函数。x k y = 还可以写成kx y =1- 2. 反比例函数解析式的特征: ⑴等号左边是函数y ,等号右边是一个分式。分子是不为零的常数k (也叫做比例系数k ),分母中含有自变量x ,且指数为1. ⑵比例系数0≠k ⑶自变量x 的取值为一切非零实数。 ⑷函数y 的取值是一切非零实数。 3. 反比例函数的图像 ⑴图像的画法:描点法 ① 列表(应以O 为中心,沿O 的两边分别取三对或以上互为相反的数) ② 描点(有小到大的顺序) 连线(从左到右光滑的曲线) ⑵反比例函数的图像是双曲线,x k y =(k 为常数,0≠k )中自变量0≠x ,函 数值0≠y ,所以双曲线是不经过原点,断开的两个分支,延伸部分逐渐靠近坐标轴,但是永远不与坐标轴相交。 ⑶反比例函数的图像是是轴对称图形(对称轴是x y =或x y -=)。 ⑷反比例函数x k y = (0≠k )中比例系数k 的几何意义是:过双曲线x k y = (0≠k )上任意引x 轴y 轴的垂线,所得矩形面积为k 。 4 5. 点的坐标即可求出k ) 6.“反比例关系”与“反比例函数”:成反比例的关系式不一定是反比例函数, 但是反比例函数x k y =中的两个变量必成反比例关系。 7. 反比例函数的应用二、例题 【例1】如果函数2 22 -+=k k kx y 的图像是双曲线,且在第二,四象限内,那么的值 是多少?【解析】有函数图像为双曲线则此函数为反比例函数x k y = ,(0≠k )
即kx y =1-(0≠k )又在第二,四象限内,则0
第三-四章 概率与离散变量的概率分布练习题 一、填空 1.用古典法计算概率.在应用上有两个缺点:①它只适用于有限样本点的情况;②它假设( )。 2.分布函数)(x F 和)(x P 或?)(x 的关系,就像向上累计频数和频率的关系一样。所不同的是,)(x F 累计的是( )。 3.如果A 和B ( ),总有P(A/B)=P 〔B/A 〕=0。 4.若事件A 和事件B 不能同时发生,则称A 和B 是( )事件。 4.在一副扑克牌中单独抽取一次,抽到一张红桃或爱司的概率是(1/4 );在一副扑克牌中单独抽取一次,抽到一张红桃且爱司的概率是( 1/52 )。 二、单项选择 1.随机试验所有可能出现的结果,称为( D )。A 基本事件; B 样本;C 全部事件;D 样本空间。 2.在次数分布中,频率是指( ) A.各组的频率相互之比 B.各组的分布次数相互之比 C.各组分布次数与频率之比 D.各组分布次数与总次数之比 3.以等可能性为基础的概率是(A )。A 古典概率;B 经验概率;C 试验概率;D 主观概率。 4.古典概率的特点应为( A )。 A 基本事件是有限个,并且是等可能的; B 基本事件是无限个,并且是等可能的; C 基本事件是有限个,但可以是具有不同的可能性; D 基本事件是无限的,但可以是具有不同的可能性。 5.任一随机事件出现的概率为( D )。A 在–1与1之间;B 小于0;C 不小于1;D 在0与1之间。 6.若P (A )=0.2,P(B )=0.6,P (A/B )=0.4,则)(B A P =( D )。A 0.8 B 0.08 C 0.12 D 0.24。 7.若A 与B 是任意的两个事件,且P (AB )=P (A )·P (B ),则可称事件A 与B (C )。 A 等价 B 互不相容 C 相互独立 D 相互对立。 8.若相互独立的随机变量X 和Y 的标准差分别为6与8,则(X +Y )的标准差为(B )。A 7 B 10 C 14 D 无法计算。 9.如果在事件A 和B 存在包含关系A ?B 的同时,又存在两事件的反向包含关系A ?B ,则称事件A 与事件B (A )A 相等 B 互斥 C 对立 D 互相独立 10.二项分布的数学期望为(C )。A n(1-n)p B np(1- p) C np D n(1- p)。 11.关于二项分布,下面不正确的描述是(A )。 A 它为连续型随机变量的分布; B 二项分布的数学期望)(X E =μ=np ,变异数)(X D =2 σ=npq ; C 它的图形当p =0.5时是对称的,当p ≠ 0.5时是非对称的,而当n 愈大时非对称性愈不明显; D 二项分布只受成功事件概率p 和试验次数n 两个参数变化的影响。 12.事件A 在一次试验中发生的概率为 4 1 ,则在3次独立重复试验中,事件A 恰好发生2次的概率为(C )。 A 21 B 161 C 64 3 D 649 13.设随机变量ξ~B ????6,12,则P (ξ=3)的值为( A ) A.516 B.316 C.58 D.716 14.设随机变量ξ ~ B (2,p ),随机变量η ~ B (3,p ),若P (ξ ≥1) =59,则P (η≥1) =( )A.13 B.59 C.827 D.19 27 解析:∵P (ξ≥1) =2p (1-p )+p 2=59, ∴p =13 ,∴P (η≥1) =C 13????13????232+C 23????132????23+C 33????133=1927,故选D. 15.在4次独立重复试验中,随机事件A 恰好发生1次的概率不大于其恰好发生2次的概率,则事件A 在一次试验中发生的概率p 的取值范围是( A ) A .[0.4,1) B .(0,0.6] C .(0,0.4] D .[0.6,1)
习题一 1 设总体X 的样本容量5=n ,写出在下列4种情况下样本的联合概率分布. 1)),1(~p B X ; 2))(~λP X ; 3)],[~b a U X ; 4))1,(~μN X . 解 设总体的样本为12345,,,,X X X X X , 1)对总体~(1,)X B p , 11223344555 11 1 55(1) (,,,,)()(1)(1)i i n x x i i i i x x P X x X x X x X x X x P X x p p p p -==-========-=-∏∏ 其中:5 1 15i i x x ==∑ 2)对总体~()X P λ 11223344555 1 1 555 1 (,,,,)()! ! i x n i i i i i x i i P X x X x X x X x X x P X x e x e x λ λ λλ-==-========== ∏∏ ∏ 其中:5 1 15i i x x ==∑ 3)对总体~(,)X U a b 5 511511,,1,...,5 (,,)()0i i i i a x b i f x x f x b a ==?≤≤=?==-??? ∏∏ ,其他 4)对总体~(,1) X N μ ()() ()2 55 55/2 22 1511 1 1 (,,)()=2exp 2i x i i i i i f x x f x x μπμ-- -===??==-- ??? ∑∏
2 为了研究玻璃产品在集装箱托运过程中的损坏情况,现随机抽取20个集装箱检查其产品损坏的件数,记录结果为:1,1,1,1,2,0,0,1,3,1,0,0,2,4,0,3,1,4,0,2,写出样本频率分布、经验分布函数并画出图形. 解 设(=0,1,2,3,4)i i 代表各箱检查中抽到的产品损坏件数,由题意可统计出如下的样本频率分布表1.1: 经验分布函数的定义式为: ()()() (1)10,(),,=1,2,,1,1,n k k k x x k F x x x x k n n x x +
反比例函数知识点归纳总结与典型例题 (一)反比例函数的概念: 知识要点: 1、一般地,形如 y = x k ( k 是常数, k = 0 ) 的函数叫做反比例函数。 注意:(1)常数 k 称为比例系数,k 是非零常数; (2)解析式有三种常见的表达形式: (A )y = x k (k ≠ 0) , (B )xy = k (k ≠ 0) (C )y=kx -1 (k ≠0) 例题讲解:有关反比例函数的解析式 (1)下列函数,① 1)2(=+y x ②. 11+= x y ③21x y = ④.x y 21 -=⑤2 x y =-⑥13y x = ;其中是y 关 于x 的反比例函数的有:_________________。 (2)函数2 2 )2(--=a x a y 是反比例函数,则a 的值是( ) A .-1 B .-2 C .2 D .2或-2 (3)若函数1 1-= m x y (m 是常数)是反比例函数,则m =________,解析式为________. (4)反比例函数(0k y k x = ≠) 的图象经过(—2,5, n ), 求1)n 的值; 2)判断点B (24, (二)反比例函数的图象和性质: 知识要点: 1、形状:图象是双曲线。 2、位置:(1)当k>0时,双曲线分别位于第________象限内;(2)当k<0时, 双曲线分别位于第________象限内。 3、增减性:(1)当k>0时,_________________,y 随x 的增大而________; (2)当k<0时,_________________,y 随x 的增大而______。 4、变化趋势:双曲线无限接近于x 、y 轴,但永远不会与坐标轴相交 5、对称性:(1)对于双曲线本身来说,它的两个分支关于直角坐标系原点____________;(2)对于k 取互为相反数的两个反比例函数(如:y = x 6 和y = x 6 -)来说,它们是关于x 轴,y 轴___________。 例题讲解: 反比例函数的图象和性质: (1)写出一个反比例函数,使它的图象经过第二、四象限 . (2)若反比例函数 2 2 )12(--=m x m y 的图象在第二、四象限,则m 的值是( ) A 、 -1或1; B 、小于 1 2 的任意实数; C 、-1; D、不能确定 (3)下列函数中,当0x <时,y 随x 的增大而增大的是( ) A .34y x =-+ B .123y x =-- C .4 y x =- D .12y x =. (4)已知反比例函数2 y x -= 的图象上有两点A (1x ,1y ),B (2x ,2y ),且12x x <,
习题与解答5.2 1. 以下是某工厂通过抽样调查得到的10名工人一周内生产的产品数 149 156 160 138 149 153 153 169 156 156 试由这批数据构造经验分布函数并作图. 解 此样本容量为10,经排序可得有序样本: (1)(2)(3)(4)(5)(6)(7)(8)(9)(10)138,149,153,156,160,169 x x x x x x x x x x ========== 其经验分布函数及其图形分别如下 ()01380.11490.31530.51560.81600.91691n x F
()037.50.1547.50.3557.50.7567.50.977.51n x x F
反比例函数练习题 一、精心选一选!(30分) 1.下列 函数中,图象经过点(11)-,的反比例函数解析式是( ) A .1 y x = B .1y x -= C .2y x = D .2y x -= 2. 反 比例函数2 k y x =-(k 为常数,0k ≠)的图象位于( ) A.第一、二象限 B.第一、三象限 C.第二、四角限 D.第三、四象限 3.已知 反比例函数y = x 2 k -的图象位于第一、第三象限,则k 的取值范围是( ). (A )k >2 (B ) k ≥2 (C )k ≤2 (D ) k <2 4.反 比例函数x k y = 的图象如图所示,点M 是该函数图象上一点,MN 垂直于x 轴,垂足是点N ,如果S △MON =2,则k 的值为( ) (A)2 (B)-2 (C)4 (D)-4 5.对于反比 例函数2 y x = ,下列说法不正确...的是( ) A .点(21)--,在它的图象上 B .它的图象在第一、三象限 C .当0x >时,y 随x 的增大而增大 D .当0x <时,y 随x 的增大而减小 6.反比 例函数 2 2)12(--=m x m y ,当x >0时,y 随x 的增大而增大,则m 的值时( ) A 、±1 B 、小于 2 1 的实数 C 、-1 D 、1 7.如 图,P 1、P 2、P 3是双曲线上的三点,过这三点分别作y 轴的垂线,得到三个三角形P 1A 1O 、P 2A 2O 、P 3A 3O ,设它们的面积分别是S 1、S 2、S 3,则( )。 A 、S 1<S 2<S 3 B 、S 2<S 1<S 3 C 、S 3<S 1<S 2 D 、S 1=S 2=S 3 8.在同 一直角坐标系中,函数x y 2 - =与x y 2=图象的交点个数为( ) A .3 B .2 C .1 D .0 9.已知 甲、乙两地相距s (km ),汽车从甲地匀速行驶到乙地,则汽车行驶的时间t (h )与行驶速度v (km/h )的函数关系图象大致是( ) 10.如图,直线y=mx 与双曲线y=x k 交于A 、B 两点,过点A 作AM ⊥x 轴,垂足为M ,连结BM,若ABM S ?=2,则k 的值是( ) A .2 B 、m-2 C 、m D 、 4
4.1 一个四元对称信源,接收符号Y = {0, 1, 2, 3},其失??????=??????4/14/1324/14/110)(X P X 真矩阵为,求D max 和D min 及信源的R(D)函数,并画出其曲线(取4至5个点)。????????????0111101111011110解: 0041041041041),(min )(43041141141141),()(min min min max =?+?+?+?===?+?+?+?===∑∑i j i j i i j i i j j y x d x p D y x d x p D D 因为n 元等概信源率失真函数:??? ??-??? ??-+-+=a D a D n a D a D n D R 1ln 11ln ln )(其中a = 1, n = 4, 所以率失真函数为: ()()D D D D D R --++=1ln 13ln 4ln )(函数曲线: D 其中:symbol nat D R D symbol nat D R D symbol nat D R D symbol nat R D /0)(,43/12ln 214ln )(,21/316ln 214ln )(,41/4ln )0(,0==-==-====4.2 若某无记忆信源,接收符号,其失真矩阵求信??????-=??????3/113/13/101)(X P X ??????-=21,21Y ??????????=112211D 源的最大失真度和最小失真度,并求选择何种信道可达到该D max 和D min 的失真度。
4.3 某二元信源其失真矩阵为求这信源的D max 和D min 和R(D)??????=??????2/12/110)(X P X ?? ????=a a D 00函数。解:0021021),(min )(202121),()(min min min max =?+?===?+?===∑∑i j i j i i j i i j j y x d x p D a a y x d x p D D 因为二元等概信源率失真函数:??? ??-=a D H n D R ln )(其中n = 2, 所以率失真函数为: ????????? ??-??? ??-+-=a D a D a D a D D R 1ln 1ln 2ln )(4.4 已知信源X = {0, 1},信宿Y = {0, 1, 2}。设信源输入符号为等概率分布,而且失真函数,求信源的率失真函数R(D)。??????∞∞=1100D 4.5 设信源X = {0, 1, 2, 3},信宿Y = {0, 1, 2, 3, 4, 5, 6}。且信源为无记忆、等概率分布。失真函数定义为 证明率失真函数R(D)如图所示。???????∞ ======且且且且53,21 41,010),(j i j i j i y x d j i log22log2D 4.6 设信源X = {0, 1, 2},相应的概率分布p (0) = p (1) = 0.4,p (2) = 0.2。且失真函数为)2,1,0,(10),(=???≠==j i j i j i y x d j i (1) 求此信源的R(D); (2) 若此信源用容量为C 的信道传递,请画出信道容量C 和其最小误码率P k 之间的曲线关系。 4.7 设0 < α, β < 1, α + β = 1。试证明:αR(D’) +βR(D”) ≥ R(αD’ +βD”) 4.8 试证明对于离散无记忆N 次扩展信源,有R N (D) = NR(D)。其中N 为任意正整数,D ≥ D min 。 4.9 设某地区的“晴天”概率p (晴) = 5/6,“雨天”概率p (雨) = 1/6,把“晴天”预报为“雨天”,把“雨天”预报为“晴天”造成的损失为a 元。又设该地区的天气预报系统把“晴天”预报为“晴天”,“雨天”预报为“雨天”的概率均为0.9;把把“晴天”预报为“雨天”,把“雨天”预报为“晴天”的概率均为
反比例函数典型例题
————————————————————————————————作者:————————————————————————————————日期: ?
反比例函数的典型例题一 例 下面函数中,哪些是反比例函数? (1)3x y - =;(2)x y 8-=;(3)54-=x y ;(4)15-=x y ;(5).8 1=xy 解:其中反比例函数有(2),(4),(5). 说明:判断函数是反比例函数,依据反比例函数定义,x k y =)0(≠k ,它也可变形为1-=kx y 及k xy =的形式, (4),(5)就是这两种形式. 反比例函数的典型例题二 例 在以下各小题后面的括号里填写正确的记号.若这个小题成正比例关系,填(正);若成反比例关系,填(反);若既不成正比例关系又不成反比例关系,填(非). (1)周长为定值的长方形的长与宽的关系 ( ); (2)面积为定值时长方形的长与宽的关系 ( ); (3)圆面积与半径的关系 ( ); (4)圆面积与半径平方的关系 ( ); (5)三角形底边一定时,面积与高的关系 ( ); (6)三角形面积一定时,底边与高的关系 ( ); (7)三角形面积一定且一条边长一定,另两边的关系 ( ); (8)在圆中弦长与弦心距的关系 ( ); (9)x 越来越大时,y 越来越小,y与x的关系 ( ); (10)在圆中弧长与此弧所对的圆心角的关系 ( ). 答: 说明:本题考查了正比例函数和反比例函数的定义,关键是一定要弄清出二者的定义. 反比例函数的典型例题三 例 已知反比例函数6 2 )2(--=a x a y ,y 随x 增大而减小,求a 的值及解析式. 分析 根据反比例函数的定义及性质来解此题. 解 因为6 2 )2(--=a x a y 是反比例函数,且y 随x的增大而减小, 所以???>--=-.02, 162a a 解得???>±=. 2,5a a 所以5=a ,解析式为x y 2 5-= . 反比例函数的典型例题四
第三 - 四章 概率与离散变量的概率分布练习题 一、填空 1.用古典法计算概率.在应用上有两个缺点:①它只适用于有限样本点的情况;②它假设( )。 2.分布函数 F ( x) 和 P( x) 或 ( x) 的关系,就像向上累计频数和频率的关系一样。所不同的是, F ( x) 累计的是( )。 3.如果 A 和 B ( ),总有 P(A/B) = P 〔 B/A 〕= 0。 4.若事件 A 和事件 B 不能同时发生,则称 A 和 B 是( )事件。 4.在一副扑克牌中单独抽取一次,抽到一张红桃或爱司的概率是( 1/4 );在一副扑克牌中单独抽取一次,抽到一张红 桃且爱司的概率是( 1/52 )。 二、单项选择 1.随机试验所有可能出现的结果,称为( D )。 A 基本事件; B 样本; C 全部事件; D 样本空间。 2.在次数分布中,频率是指( ) A. 各组的频率相互之比 B. 各组的分布次数相互之比 C.各组分布次数与频率之比 D.各组分布次数与总次数之比 3.以等可能性为基础的概率是( A )。 A 古典概率; B 经验概率; C 试验概率; D 主观概率。 4.古典概率的特点应为( A )。 A 基本事件是有限个,并且是等可能的; B 基本事件是无限个,并且是等可能的; C 基本事件是有限个,但可以是具有不同的可能性; D 基本事件是无限的,但可以是具有不同的可能性。 5.任一随机事件出现的概率为( D )。A 在–1 与 1之间; B 小于 0;C 不小于 1;D 在 0与1之间。 6.若 P ( A )= 0.2,P( B )= 0.6,P ( A/B )= 0.4,则 P( A B) =( D )。 A 0.8 B 0.08 C 0.12 D 0.24 。 7.若 A 与 B 是任意的两个事件,且 P ( AB )= P ( A )· P (B ),则可称事件 A 与B (C )。 A 等价 B 互不相容 C 相互独立 D 相互对立。 8.若相互独立的随机变量 X 和 Y 的标准差分别为 6 与 8,则( X +Y )的标准差为( B )。A 7 B 10 C 14 D 无法计算。 9.如果在事件 A 和 B 存在包含关系 A B 的同时,又存在两事件的反向包含关系 A B A 与事件 B ) ,则称事件 (A A 相等 B 互斥 C 对立 D 互相独立 10.二项分布的数学期望为( C )。A n(1-n)p B np(1- p) C np D n(1- p) 。 11.关于二项分布,下面不正确的描述是( A )。 A 它为连续型随机变量的分布; B 二项分布的数学期望 E(X)= = np ,变异数 D ( X ) = 2 = npq ; C 它的图形当 p = 0.5 时是对称的,当 p ≠ 0.5 时是非对称的,而当 n 愈大时非对称性愈不明显; D 二项分布只受成功事件概率 p 和试验次数 n 两个参数变化的影响。 12.事件 A 在一次试验中发生的概率为 1 , 则在 3 次独立重复试验中,事件 A 恰好发生 2 次的概率为 ( C ) 。 4 A 1 B 1 C 3 D 9 2 16 64 64 13.设随机变量 ξ~ B 6, 1 ,则 P(ξ= 3)的值为 ( A ) A. 5 B. 3 C. 5 D. 7 2 16 16 8 16 5 ,则 P( η≥1) = ( )A. 1 5 8 19 14.设随机变量 ξ~ B(2, p),随机变量 η ~ B(3, p),若 P(ξ≥ 1) =9 3 B.9 C. 27 D. 27 2 5 1 1 1 2 2 2 1 2 2 3 1 3 19 解析: ∵ P(ξ≥ 1) = 2p(1-p)+ p = 9, ∴p = 3 , ∴P(η≥ 1) = C 3 3 3 +C 3 3 3 + C 3 3 = 27,故选 D. 15.在 4 次独立重复试验中,随机事件 A 恰好发生 1 次的概率不大于其恰好发生 2 次的概率,则事件 A 在一次试验中 发生的概率 p 的取值范围是 ( A ) A .[0.4,1) B . (0,0.6] C . (0,0.4] D . [0.6,1)