
阿波罗尼斯圆及其应用 数学理论 1.“阿波罗尼斯圆”:在平面上给定两点B A ,,设P 点在同一平面上且满足,λ=PB PA 当0>λ且1≠λ时,P 点的轨迹是个圆,称之为阿波罗尼斯圆。 (1=λ时P 点的轨迹是线段AB 的中垂线) 2.阿波罗尼斯圆的证明及相关性质 定理:B A ,为两已知点,Q P ,分别为线段AB 的定比为)1(≠λλ的内外分点,则以PQ 为直径的圆O 上任意点到B A ,两点的距离之比为.λ 证 (以1>λ为例) 设λ===QB AQ PB AP a AB ,,则 1 ,1,1,1-=-=+=+=λλλλλλa BQ a AQ a PB a AP . 由相交弦定理及勾股定理知 ,1,1222222222 -=+=-=?=λλλa BC AB AC a BQ PB BC 于是,1,122-=-=λλλa AC a BC .λ=BC AC 而C Q P ,,同时在到B A ,两点距离之比等于λ的曲线(圆)上,不共线的三点所确定的圆是唯一的,因此,圆O 上任意一点到B A ,两点的距离之比恒为.λ 性质1.当1>λ时,点B 在圆O 内,点A 在圆O 外; 当10<<λ时,点A 在圆O 内,点B 在圆O 外。 性质2.因AQ AP AC ?=2 ,过AC 是圆O 的一条切线。 若已知圆O 及圆O 外一点A ,可以作出与之对应的点,B 反之亦然。 性质3.所作出的阿波罗尼斯圆的直径为122-=λλa PQ ,面积为.12 2?? ? ??-λλπa 性质4.过点A 作圆O 的切线C AC (为切点),则CQ CP ,分别为ACB ∠的内、外角平分线。 性质5.过点B 作圆O 不与CD 重合的弦,EF 则AB 平分.EAF ∠
――――――阿波罗尼斯问题详细解答
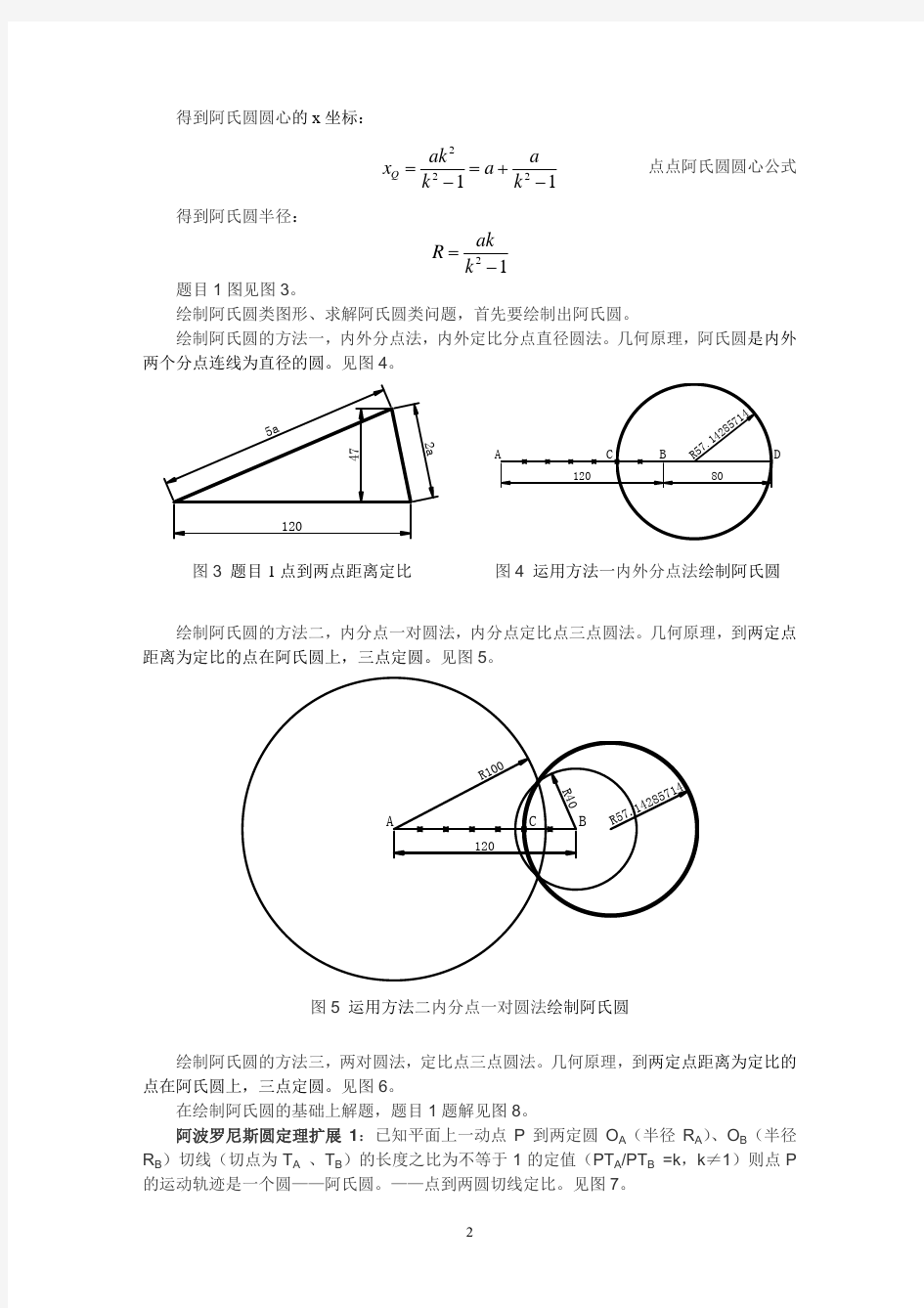
1
序号 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 附录
目
录
内
容
阿波罗尼斯是一个什么样的人?
什么是阿波罗尼斯问题?
阿波罗尼斯问题有多少个子问题?
怎样作一条线段的垂直平分线?
怎样过线段上一点作该线段的垂线?
怎样过圆上一点作该圆的切线?
怎样作两个圆的公切线?
什么叫反演变换?
怎样作反演圆内一点的反演点?
怎样作反演圆外一点的反演点?
怎样作一条直线的反演图形?
怎样作一个圆的反演图形?
怎样才能让一条直线经过反演变换后保持不变?
怎样才能让一个圆经过反演变换后保持不变?
怎样作线段 a、b 的比例中项 c?
什么叫圆的幂?怎样作出圆的幂?
什么是圆的根轴(或等幂轴)?怎样作出圆的根轴?
什么是圆的根心?怎样作出圆的根心?
什么叫相(位)似中心?怎样作出相(位)似中心?
什么叫相(位)似点?什么叫正相(位)似点?什么叫逆相似点?
什么叫两圆周的共同幂?
什么叫相似轴?怎样作出相似轴?
阿波罗尼斯问题之一:点点点
阿波罗尼斯问题之二:线线线
阿波罗尼斯问题之三:点线线
阿波罗尼斯问题之四:点点线
阿波罗尼斯问题之五:点点圆
阿波罗尼斯问题之六:点圆圆
阿波罗尼斯问题之七:点线圆
阿波罗尼斯问题之八:线圆圆
阿波罗尼斯问题之九:线线圆
阿波罗尼斯问题之十:圆圆圆
米勒问题和米勒定理
页码 03 03 03 03 04 04 05 06 06 06 07 08 10 10 10 11 11 13 13 14 16 17 17 18 19 22 26 31 35 41 47 55 69
2
阿波罗尼斯圆性质及其应用 背景展示 阿波罗尼斯是古希腊著名数学家,与欧几里得、阿基米德被称为亚历山大时期数学三巨匠,他对圆锥曲线有深刻而系统的研究,主要研究成果集中在他的代表作《圆锥曲线》一书,阿波罗尼斯圆是他的研究成果之一 (人教A 版124页B 组第3题)已知点M 与两个定点O(0,0),A(3,0)点距离的比为,求点M 的轨迹方程。 (人教A 版144页B 组第2题)已知点M 与两个定点 距离的比是一个正数m,求点M 的轨迹方程,并说明轨迹是什么图形(考虑m=1和m )。 公元前3世纪,古希腊数学家阿波罗尼斯(Apollonius)在《平面轨迹》一书中,曾研究了众多的平面轨迹问题,其中有如下著名结果:到平面上两定点距离比等于定值的动点轨迹为直线或圆.(定值为1时是直线,定值不是1时为圆) 定义:一般的平面内到两顶点A ,B 距离之比为常数( )的点的轨迹为圆,此圆称为阿波罗尼斯圆 类型一:求轨迹方程 1.已知点M 与两个定点()0,0O ,()0,3A 的距离的比为21,求点M 的轨迹方程 2.已知()02>=a a AB ,()0≥=λλMB MA ,试分析M 点的轨迹 3.(2006年高考四川卷第6题)已知两定点A (-2,0),B (1,0),如果动点P 满足条件 ,则点P 的轨迹所包围的图形面积等于( ) A . B. C. D.9 类型二:求三角形面积的最值 4.(2008江苏卷)满足条件AB = 2,AC = BC 的?ABC 的面积的最大值是 5.(2011浙江温州高三模拟)在等腰 ABC 中,AB=AC ,D 为AC 的中点,BD=3,则 ABC 面积的最大值为 6.在ABC 中,AC=2,AB=mBC(m>1),恰好当B=时 ABC 面积的最大,m=
1、欧拉(Euler)线: 同一三角形的垂心、重心、外心三点共线,这条直线称为三角形的欧拉线;且外心与重心的距离等于垂心与重心距离的一半 证明:利用向量,简单明了 设H,G,O,分别为△ABC的垂心、重心、外心.,D为BC边上的中点。 ∵向量OH=向量OA+向量AH =向量OA+2向量OD (1) =向量OA+向量OB+向量BD+向量OC+向量CD =向量OA+向量OB+向量OC; 而向量OG=向量OA+向量AG =向量OA+1/3(向量AB+向量AC) (2) =1/3[向量OA+(向量OA+向量AB)+(向量OA+向量AC)] =1/3(向量OA+向量OB+向量OC). ∴向量OG=1/3向量OH, ∴O、G、H三点共线且OG=1/3OH。 2、九点圆: 任意三角形三边的中点,三高的垂足及三顶点与垂心间线段的中点,共九个点共圆,这个圆称为三角形的九点圆;其圆心为三角形外心与垂心所连线段的中点,其半径等于三角形外接圆半径的一半。
证明:如右图所示,△ABC的BC边垂足为D,BC边中点为L。证法为以垂心H为位似中心,1/2为位似比作位似变换。 连结HL并延长至L',使LL'=HL;做H关于BC的对称点D'。 显然,∠BHC=∠FHE=180°-∠A,所以∠BD'C=∠BHC=180°-∠A,从而A,B,D',C四点共圆。 又因为BC和HL'互相平分于L,所以四边形BL'CH为平行四边形。故∠BL'C=∠BHC=180°-∠A,从而A,B,L',C四点共圆。 综上,A,B,C,D',L'五点共圆。显然,对于另外两边AB,AC边上的F,N,E,M也有同样的结论成立,故A,B,C,D',L',F',N',E',M'九点共圆。此圆即△ABC的外接圆⊙O。 接下来做位似变换,做法是所有的点(⊙O上的九个点和点O本身)都以H为位似中心进行位似比为1/2的位似变换。那么,L'变到了L(因为HL'=2HL),D'变到了D(因为D'是H关于BC的对称点),B变到了Q,C变到了R(即垂心与顶点连线的中点)。其它各点也类似变换。O点变成了OH中点V。 位似变换将圆仍映射为圆(容易用向量证明),因此原来在⊙O上的九个点变成了在⊙V上的九个点,且⊙V 的半径是⊙O的一半。 这就证明了三角形三边的中点,三高的垂足和三个欧拉点都在一个圆上。 3、费尔马点: 已知P为锐角△ABC内一点,当∠APB=∠BPC=∠CPA=120°时,PA+PB+PC的值最小,这个点P称为△ABC的费尔马点。 证明:如图,以△ABC三边为边向外作等边△ABD、△BCE、△ACF, 连接CD、BF、AE交于点O,试证:O是费马点。 证明:在△ACD、△ABF中, AD=AB,∠DAC=∠BAF,AC=AF ∴△ACD≌△ABF(SAS)
阿波罗尼斯圆性质及其应用探究 背景展示 阿波罗尼斯是古希腊著名数学家,与欧几里得、阿基米德被称为亚历山大时期数学三巨匠,他对圆锥曲线有深刻而系统的研究,主要研究成果集中在他的代表作《圆锥曲线论》一书,阿波罗尼斯圆是他的研究成果之一。 1.“阿波罗尼斯圆”:在平面上给定两点B A ,,设P 点在同一平面上且满足 ,λ=PB PA 当0>λ且1≠λ时,P 点的轨迹是个圆,称之为阿波罗尼斯圆。 (1=λ时P 点的轨迹是线段AB 的中垂线) 2.阿波罗尼斯圆的证明. . 角坐标系中点为原点建立平面直轴,所在的直线为证明:以AB x AB ()()(), 不妨设y x P a B a A ,,0,,0,-()()22 222222,,,,PA PA PB PA PB x a y x a y PB λλλ??=∴==∴++=-+??Q ()( )()() 0112112222222=-++--+-∴a ax y x λλλλ ( ) () 2 22 2 222222 221211,01112??? ??-=+??? ? ??-+-∴=-+-+-+∴λλλλλλλa y a x a ax y x λλλλλ=??? ??-=+???? ? ?-+-∴PB PA a y a x 的解都满足又以上过程均可逆,2 22 2 221211 .120,11222为半径的圆上运动为圆心,以在以综上,动点-=???? ??-+λλλλa r a C P 3.阿波罗尼斯圆的性质. 性质1 点A 、点B 在圆心C 的同侧; 当1>λ时,点B 在圆C 内,点A 在圆C 外; 当10<<λ时,点A 在圆C 内,点B 在圆C 外。 (). ,1 1 ,012111122222的右侧当然也在点的右侧, 在点点所示,时,如图证明:当A B C a a a a a ∴>-+∴>-=--+>λλλλλλ
1、几何中的著名定理1、勾股定理(毕达哥拉斯定理) 2、射影定理(欧几里得定理) 3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分 4、四边形两边中心的连线的两条对角线中心的连线交于一点 5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。 6、三角形各边的垂直一平分线交于一点。 7、从三角形的各顶点向其对边所作的三条垂线交于一点 8、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足不L,则AH=2OL 9、三角形的外心,垂心,重心在同一条直线上。 10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上, 11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上 12、库立奇*大上定理:(圆内接四边形的九点圆) 圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。 13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式: r=(s-a)(s-b)(s-c)ss为三角形周长的一半 14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点 15、中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有
AB2+AC2=2(AP2+BP2) 16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有 n×AB2+m×AC2=(m+n)AP2+mnm+nBC2 17、波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB 中点M和对角线交点E的直线垂直于CD 18、阿波罗尼斯定理:到两定点A、B的距离之比为定比m:n(值不为1)的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上 19、托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD×BC=AC 20、以任意三角形ABC的边BC、CA、AB为底边,分别向外作底角都是30度的等腰△BDC、△CEA、△AFB,则△DEF是正三角形, 21、爱尔可斯定理1:若△ABC和三角形△都是正三角形,则由线段AD、BE、CF的重心构成的三角形也是正三角形。 22、爱尔可斯定理2:若△ABC、△DEF、△GHI都是正三角形,则由三角形△ADG、△BEH、△CFI的重心构成的三角形是正三角形。 23、梅涅劳斯定理:设△ABC的三边BC、CA、AB或其延长线和一条不经过它们任一顶点的直线的交点分别为P、Q、R则有 BPPC×CQQA×ARRB=1 24、梅涅劳斯定理的逆定理:(略) 25、梅涅劳斯定理的应用定理1:设△ABC的∠A的外角平分线交边CA于Q、∠C的平分线交边AB于R,、∠B的平分线交边CA于Q,则P、Q、R三点共线。 26、梅涅劳斯定理的应用定理2:过任意△ABC的三个顶点A、B、C作它的外接圆的切线,分别和BC、CA、AB的延长线交于点P、Q、R,则P、Q、R 三点共线 27、塞瓦定理:设△ABC的三个顶点A、B、C的不在三角形的边或它们的延长线上的一点S连接面成的三条直线,分别与边BC、CA、AB或它们的延长
“阿波罗尼斯圆”的应用举例 【例】 阿波罗尼斯是古希腊著名数学家,与欧几里得、阿基米德被称为亚历山大时期数学三巨匠,他对圆锥曲线有深刻而系统的研究,主要研究成果击中在他的代表作《圆锥曲线》一书,阿波罗尼斯圆是他的研究成果之一,指的是:已知动点M 与两定点A 、B 的距离之比为 λ(0λ>, 1λ≠) ,那么点M 的轨迹就是阿波罗尼斯圆.下面,我们来研究与此相关的一个问题.已知圆: 221x y +=和点1,02A ??- ??? ,点()1,1B , M 为圆O 上动点,则2MA MB +的最小值为( ) A. 6 B. 7 C. 10 D. 11答案 C 解析 令2=MA MC ,则12 MA MC =. 由题意可得圆221x y +=是关于点A,C 的阿波罗尼斯圆,且1=2 λ。 设点C 坐标为(),C m n , 则()()2 2221212 x y MA MC x m y n ??++ ???==-+-。 整理得2222 2421333m n m n x y x y ++-+++=。
由题意得该圆的方程为221x y +=, ∴2224020113m n m n +==+-????? =???? ,解得2{ 0m n =-=。 ∴点C 的坐标为(-2,0)。 ∴2MA MB MC MB +=+, 因此当点M 位于图中的12,M M 的位置时, 2MA MB MC MB +=+的值最小,且为10,故选C. 【练习】 1.设椭圆与双曲线有共同的焦点F 1(-1,0),F 2(1,0),且椭圆长轴是双曲线实轴的2倍,则椭圆与双曲线的交点轨迹是( ) A .双曲线 B .一个圆
阿波罗尼斯圆 一、适用题型 1、已知两个线段长度之比为定值; 2、过某动点向两定圆作切线,若切线张角相等; 3、向量的定比分点公式结合角平分线; 4、线段的倍数转化; 二、基本理论 (一)阿波罗尼斯定理(又称中线长公式) 设三角形的三边长分别为c b a ,,,中线长分别为c b a m m m ,,,则: 2 2222 222222222 1221221c b a m c b a m b c a m a c b +=++=++= + (二)阿波罗尼斯圆 一般地,平面内到两个定点距离之比为常数(1)λλ≠的点的轨迹是圆,此圆被叫做“阿波罗尼斯圆” ()()()()则,若设不妨设,,1,0,0,0,,0,y x P a BP AP a B a A ≠>>=-λλλ ()()2222y a x y a x +-=++λ 化简得:2 22 2 221211??? ??-=+???? ? ?-+-a y a x λλλλ 轨迹为圆心a a 12011222-??? ? ??-+λλλλ,半径为,的圆
(三)阿波罗尼斯圆的性质 1、满足上面条件的阿波罗尼斯圆的直径的两端是按照定比λ内分AB 和外分AB 所得的两个分点; 2、直线CM 平分ACB ∠,直线CN 平分ACB ∠的外角; 3、 BN AN BM AM = 4、CN CM ⊥ 5、内在圆点内; 在圆时,点O A O B ,101<<>λλ; 6、若AD AC ,是切线,则CD 与AO 的交点即为B ; 7、若点B 做圆O 的不与CD 重合的弦EF ,则AB 平分EAF ∠; 三、补充说明 1、关于性质1的证明 定理:B A ,为两已知点,Q P ,分别为线段AB 的定比为()1≠λλ的内、外分点,则以PQ 为直径的圆O 上任意点到B A ,两点的距离之比等于常数λ。 证明:不妨设1>λ 1 ,1,1,1,-= -=+=+==λλλλλλa BQ a AQ a BP a AP CD PQ O B a AB ,则 垂直的弦的与直径作圆过点设 由相交弦定理及勾股定理得:
阿波罗尼斯(Apollonius)圆
法二: 设平面上有不同的两点A,B ,那么该平面上使得 k PB PA = 为定值k (1≠k )的P 的轨迹是一个圆。
这个定理的证明方法很多。下面是笔者的分析与证明,希望读者喜欢。 如图,P是平面上一动点,A、B是两定点,PA:PB= m:n ,M是AB的内分点(M在线段AB上),N是AB的外分点(N在AB的延长线上)且AM:MB=AN:NB=m:n,则P点的轨迹是以MN为直径的圆。 下面先证明两个定理: 一、如图一,已知M是BC上一点,且AB:AC=BM:MC, 求证:AM平分∠BAC(三角形内角平分线定理的逆定理) 证明:过C点作CD∥AM交BA的延长线于D,则AB:AD=BM:MC ∵AB:AC=BM:MC, ∴AB:AD =AB:AC, ∴AC=AD,∴∠D=∠3, ∵CD∥AM,∴∠1=∠D,∠2=∠3,∴∠1=∠2,∴AM平分∠BAC。 二、如图二,N是BC延长线上一点,BN:CN=AB:AC,求证:AN平分∠BAC的邻补角∠EAC. 证明:∵CD∥AN交AB于D,则BN:CN=AB:AD. ∵BN:CN=AB:AC ∴AB:AD=AB:AC,AD=AC,∴∠3=∠4. ∵DC∥AN,∴∠1=∠3,∠2=∠4 ∴∠1=∠2 ∴AN平分∠BAC的邻补角∠EAC
有了上面的证明,阿波罗尼斯圆定理的证明就不难了,证明如下: 连结PM、PN,∵M为AB的内分点 PA:PB=AM:MB =m:n,∴PM平分∠APB ∵N为AB的外分点,AN:BN=PA:PB =m:n ∴PN平分∠BPE ∵∠APB+∠BPE=180o,又∠2=∠APB/2,∠3=∠BPE/2 ∴∠2+∠3=(∠APB+∠BPE)/2即∠MPN=90o ∴动点P到MN的中点O的距离等于MN(定值)的一半(直角三角形斜边上的中线等于斜边的一半),点P的轨迹,是以定比m:n内分和外分定线段AB的两个分点的连线为直径的圆
高考数学文化内容预测三:阿波罗尼斯圆问题 一、高考考试大纲数学大纲分析及意义: 普通高考考试大纲数学修订,加强了对数学文化的考查。针对这一修订提出以下建议: 建议教师对数学文化这一概念认真学习,结合教材内容学习,特别是教材中渗透数学文化的内容要充分重视,重点研究;结合近年新课标试题中出现的与数学文化有关的试题进行学习,重点关注题源、考法命题形式。 其主要意义为: (1)增加中华优秀传统文化的考核内容,积极培育和践行社会主义核心价值观,充分发挥高考命题的育人功能和积极导向作用. (2)能力要求:经命题专家精细加工,再渗透现代数学思想和方法;在内涵方面,增加了基础性、综合性、应用性、创新性的要求. 二、往年新课标高考实例解析及2017年高考数学文化试题预测: 往年新课标高考实例分析: 分析一:古代数学书籍《九章算术》、《数书九章》等为背景 近年来在全国高考数学试题中,从《九章算术》中选取与当今高中数学教学相映的题材背景. (1)2015年高考全国卷Ⅰ,此题源于《九章算术》卷第五《商功》之[二五],将古代文化“依垣”和现代教育元素“圆锥”结合. (2)2015年高考全国卷Ⅱ,此题源于《九章算术》卷第一《方田》之[六]:“又有九十一分之四十九.问约之得几何?”“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也.以等数约之”,后人称之为“更相减损术”. (3)2015年高考湖北卷,此题背景源于《九章算术》卷第五《商功》之[一五].今有阳马,广五尺,袤七尺,高八尺.问积几何;之[一六]今有鳖臑,下广五尺,无袤;上袤四尺,无广,高七尺.问积几何.考题将“阳马”,“鳖臑”相结合,以《选修2-1》P109例4为源进行有机整合.巧妙嫁接,精典设问,和谐优美的考题呼之即出. 分析二:课后阅读或课后习题如阿波罗尼圆为背景 从2005-2013年多次涉及考题,全国卷2011年16题以此为命题背景的其他省市:江苏:2008年13题、2013年17题.2009-2013年湖北高考连续出现等等. 数学文化题型背景预测: 预测1:古代数学书籍《九章算术》、《数书九章》等数为背景的数学文化类题目. 预测2:高等数学衔接知识类题目.如微积分、初等数学和高等数学的桥梁,由高中向大学的知识过渡衔接. 预测3:课本阅读和课后习题的数学文化类题目.如必修3中,辗转相除法、更相减损术、秦九韶算法、二进制、割圆术等。 预测4:中外一些经典的数学问题类题目.如:回文数、匹克定理、角谷猜想、哥尼斯堡七桥问题、四色猜想等经典数学小问题值得注意。
从课本中的阿波罗尼斯圆问题 探讨数学文化在教学中的渗透 靖江市第一高级中学 数学组 印栋 E-mail: yde2003@https://www.doczj.com/doc/6a10407431.html, 邮编:214500 克莱因在其名著《西方文化中的数学》中指出:数学是一种精神,一种理性的精神.正是这种精神,激发、促进、鼓舞并驱使人类的思维得以运用到最完善的程度,亦正是这种精神,试图决定性地影响人类的物质、道德和社会生活;试图回答有关人类自身存在提出的问题;努力去理解和控制自然;尽力去探求和确立已经获得知识的最深刻的和最完美的内涵.因此,美国数学学会主席魏尔德说:“数学是一种会不断进化的文化”.正是数学与文化以及数学文化的不断交融及相互促进,才使数学在人类文明的发展中起到了举足轻重的作用并获得了如此多的赞誉.在新课程改革中,数学文化不再是被孤立的装饰品,而是渗透在相关模块和专题中. 新课标《苏教版·必修2》在第2章平面解析几何初步第2.2节圆与方程介绍了圆的标准方程和一般方程后编排了这样一道习题: 习题2.2(1)10.已知点)(y x M ,与两个定点)03()00(,,, A O 的距离之比为2/1,那么点M 的坐标应满足什么关系?画出满足条件的点M 所形成的曲线. 分析:由于有了课上推导圆标准方程的过程可作为参照,大部分学生不需费太多的气力就可以解出上述的问题,解法如下. 解析:由题知2/1/=MA MO ,将距离公式代入可得 12 =, 化简整理即得到该曲线的方程为: 4)1(22=++y x . 因此,所求点M 所形成的曲线是以(-1,0)为圆心,2为半径的圆(图略). 这道题实际上源自约公元前262~前190的古希腊人阿波罗尼斯(Apollonius of Perga ,也有文献上将其名字翻译为“阿波罗尼奥斯”)在其巨著《圆锥曲线论》给出的一个著名的几何问题:“在平面上给定两点A 、B ,设P 点在同一平面上且满足λ=PB PA /,当λ大于0且λ≠1时,P 点的轨迹是个圆”,这个圆我们称之为“阿波罗尼斯圆”,这个结论称作“阿波罗尼斯轨迹”. 同上题一样,我们用解析法完全可以证明:与A 、B 距离之比等于λ的动点轨迹为圆.但如果每题都先用解析法求出圆的方程,再根据圆心及半径作出圆,显然很费事,特别是对一些选择题或填空题如此解法实在小题大做,能 否找出阿 波罗尼斯圆的简捷作法?下述定理可给出明 确答案. 定理:A 、B 为两已知点,P 、Q 分别为 线段A B 的定比为λ(λ≠1)的内、外分点,则以P 、Q 为直径的
阿波罗尼斯圆性质及其应用 背景展示 阿波罗尼斯是古希腊著名数学家,与欧几里得、阿基米德被称为亚历山大时期数学三巨匠,他对圆锥曲线有深刻而系统的研究,主要研究成果集中在他的代表作《圆锥曲线》一书,阿波罗尼斯圆是他的研究成果之一 (人教A版124页B组第3题)已知点M与两个定点O(0,0),A(3,0)点距离的比为,求点M的轨迹方程。 (人教A版144页B组第2题)已知点M与两个定点距离的比是一个正数m,求点M的轨迹方程,并说明轨迹是什么图形(考虑m=1和m)。 公元前3世纪,古希腊数学家阿波罗尼斯(Apollonius)在《平面轨迹》一书中,曾研究了众多的平面轨迹问题,其中有如下著名结果:到平面上两定点距离比等于定值的动点轨迹为直线或圆.(定值为1时是直线,定值不是1时为圆) 定义:一般的平面内到两顶点A,B距离之比为常数()的点的轨迹为圆,此圆称为阿波罗尼斯圆
类型一:求轨迹方程 1.已知点M 与两个定点()0,0O ,()0,3A 的距离的比为2 1 ,求点M 的轨迹方程 2.已知()02>=a a AB ,()0≥=λλMB MA ,试分析M 点的轨迹 3.(2006年高考四川卷第6题)已知两定点A (-2,0),B (1,0),如果动点P 满足条件,则点P 的轨迹所包围的图形面积等于( ) A . B. C. D.9 类型二:求三角形面积的最值 4.(2008江苏卷)满足条件AB = 2,AC = BC 的?ABC 的面积的最大值是 5.(2011浙江温州高三模拟)在等腰ABC 中,AB=AC ,D 为AC 的中点,BD= 3,则ABC 面积的最大值为 6.在ABC 中,AC=2,AB=mBC(m>1),恰好当B=时 ABC 面积的最大,m= 类型三:定点定值问题
2020中考数学线段最值问题之阿波罗尼斯圆(阿氏圆) 【知识背景】 阿波罗尼斯与阿基米德、欧几里德齐名,被称为亚历山大时期数学三巨匠。阿波罗尼斯对圆锥曲线有深刻而系统的研究,其主要研究成果集中在他的代表作《圆锥曲线》一书,阿波罗尼斯圆是其研究成果之一,本文主要讲述阿波罗尼斯圆在线段最值中的应用,下文中阿波罗尼斯圆简称为“阿氏圆”。 【定 义】 阿氏圆是指:平面上的一个动点P 到两个定点A ,B 的距离的比值等于k ,且k≠1的点P 的轨迹称之为阿氏圆。即: )1(≠=k k PB PA ,如下图所示: 上图为用几何画板画出的动点P 的轨迹,分别是由图中红色和蓝色两部分组成的的圆,由于是静态文档的形式,无法展示动图,有兴趣的可以用几何画板试一试。 【几何证明】 证明方法一:初中纯几何知识证明:阿氏圆在高中数学阶段可以建立直角坐标系,用解析几何的方式来确定其方程。但在初中阶段,限于知识的局限性,我们可以采用纯几何的证明方式,在证明前需要先明白角平分线定理及其逆定理,请看下文: 知识点1:内角平分线定理及逆定理
若AD 是∠BAC 的角平分线,则有: CD BD AC AB = 。即“两腰之比”等于“两底边之比”。 其逆定理也成立:即CD BD AC AB = ,则有:AD 是∠BAC 的角平分线。 知识点2:外角平分线定理及其逆定理 若AD 是△ABC 外角∠EAC 的角平分线,则有 CD BD AC AB = 。即“两腰之比”等于“两底边之比”。 其逆定理也成立:即CD BD AC AB = ,则有:AD 是外角∠EAC 的角平分线。 【阿氏圆的证明】 有了上述两个知识储备后,我们开始着手证明阿氏圆。
超级名圆——阿波罗尼斯圆 一、问题背景 1.(苏教版选修2-1,P63例2)求平面内到两个定点A,B 的距离之比等于2的动点M 的轨迹. 【解】以B A ,所在的直线为x 轴,线段AB 的垂直平分线为y 轴,建立平面直角坐标系xOy , 令a AB 2=,则B A ,两点的坐标分别为()()0,,0,a a -. 设M 点坐标为()y x ,,依题意,点M 满足 2=MB MA , 由2 2 22)(,)(y a x MB y a x MA +-=++=得2)()(2 2 22=+-++y a x y a x , 化简整理,得0310332 2 2 =+-+a ax y x , 所以动点M 的轨迹方程为0310332 22=+-+a ax y x . 2.(苏教版必修2,P112第12题)已知点M(x,y)与两个定点O(0,0),A(3,0)的距离之比为1:2, 那么点M 的坐标应满足什么关系?画出满足条件的点M 所构成的曲线. 【解】由两点间距离公式得22y x MO += ,22)3(y x MA +-=, 则2:1)3(:2 222=+-+y x y x ,化简得4)1(2 2 =++y x , 即点M 是以(-1,0)为圆心,2=r 的圆.(图略) 二、阿波罗尼斯圆 阿波罗尼斯(Apollonius of Perga Back ),古希腊人(262BC~190BC ),与阿基米德、欧几里德一起被誉为古希腊三大数学家,他写了八册《圆锥曲线论》(Conics ),其中有七册流传下来,书中详细讨论了圆锥曲线的各种性质,如切线、共轭直径、极与极轴、点到锥线的最短与最长距离等,圆锥曲线的性质几乎囊括殆尽,阿波罗尼斯曾研究了众多的平面轨迹问题,阿氏圆是他的论著中的一个著名问题: 已知平面上两定点A 、B ,则所有满足 ()1≠=λλPB PA 的点P 的轨迹是一个以定比n m :内分和外分定线段AB 的两个分点的连线为直径的圆. 这是著名的阿波罗尼斯轨迹定理,以内外分点为直径的圆被后人称为阿波罗尼斯圆,简称阿氏圆.
到两点点的距离之和为定值(大于两定点距离)的点的轨迹是椭圆. 到两点点的距离之差为定值(小于两定点距离)的点的轨迹是双曲线 那么到两定点的距离之比为定值的点的轨迹是什么呢? 没错就是阿氏圆. 阿氏圆定理(全称:阿波罗尼斯圆定理),具体的描述: 一动点P到两定点A、B的距离之比等于定比m:n,则P点的轨迹,是以定比m:n内分和外分定线段AB的两个分点的连线为直径的圆.这个轨迹最先由古希腊数学家阿波罗尼斯发现,该圆称为阿波罗尼斯圆,简称阿氏圆. 【分析】 令B为坐标原点,A的坐标为(a,0).则动点P(x,y).满足PA/PB=k(为实数,且不为±1) 得(k2-1)(x2+y2)+2ax-a2=0, 当k不为±1时,它的图形是圆. 当k为±1时,轨迹是两点连线的中垂线. 【典型例题】 问题提出:如图1,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP、BP,求AP+1/2BP的最小值. (1)尝试解决:为了解决这个问题,下面给出一种解题思路: 如图2,连接CP,在CB上取点D,使CD=1, 则有CD/CP=CP/CB=1/2, 又∵∠PCD=∠BCP,∴△PCD∽△BCP. ∴PD/BP=1/2,∴PD=1/2BP, ∴AP+1/2BP=AP+PD.
请你完成余下的思考,并直接写出答案:AP +1/2BP 的最小值为. (2)自主探索:在“问题提出”的条件不变的情况下, 1/3AP +BP 的最小值为. (3)拓展延伸:已知扇形COD 中,∠COD =90°,OC =6,OA =3,OB =5,点P 是弧CD 上一点,求2PA +PB 的最小值. 10.(3分)(2015?贵港)如图,已知P 是⊙O 外一点,Q 是⊙O 上的动点,线段PQ 的中点为M ,连接OP ,OM .若⊙O 的半径为2,OP=4,则线段OM 的最小值是( ) A . 0 B . 1 C . 2 D . 3 18.如图,在ABC ?中, 90,8,6ACB BC AC ∠=?==,以点C 为圆心,4为半径的圆上有一个动点D .连接AD 、BD 、CD ,则 12BD AD +的最小值是 .
A P B 阿波罗尼斯圆问题 一【问题背景】 苏教版《数学必修2》第12题: 已知点(,)M x y 与两个定点(0,0),(3,0)O A 的距离之比为1 2 ,那么点M 的坐标应满足什么关系画出满足条件的点M 所构成的曲线. 二、【阿波罗尼斯圆】 公元前3世纪,古希腊数学家阿波罗尼斯(Apollonius )在《平面轨迹》一书中,曾研究了众多的平面轨迹问题,其中有如下结果: 到两定点距离之比等于已知数的动点轨迹为直线或圆. 如图,点B A ,为两定点,动点P 满足PB PA λ=, 则1=λ时,动点P 的轨迹为直线;当1≠λ时,动点P 的轨迹为圆, 后世称之为阿波罗尼斯圆. 证:设PB PA m m AB λ=>=,02)(.以AB 中点为原点,直线AB 为x 轴建立平面直角坐标系,则),,(0m A -) ,(0m B . 又设),(y x C ,则由PB PA λ=得2 2 2 2 )()(y m x y m x +-=++λ, 两边平方并化简整理得)()()()(2 22222211121λλλλ-=-++--m y x m x , 当1=λ时,0=x ,轨迹为线段AB 的垂直平分线; 当1>λ时,2 2 2 22222)1(4)11(-=-+-λλλλm y m x ,轨迹为以点)0,11(22m -+λλ为圆心,122-λλm 长为半径的圆. 上述课本习题的一般化情形就是阿波罗尼斯定理. 三、【范例】 例1 满足条件BC AC AB 2,2= =的三角形ABC 的面积的最大值是 . 解:以AB 中点为原点,直线AB 为x 轴建立平面直角坐标系,则), ,(01-A ) ,(01B ,设),(y x C ,由BC AC 2=得22 22121y x y x +-?=++)()(,
阿波罗尼斯圆的应用 【例1】(2008·江苏13)满足条件2AB =,2AC BC =的三角形ABC 的面积的最大值为_________. 【解析】法一:设△ABC 中角A ,B ,C 所对的边分别为a ,b ,c . 由题知,2c =,2b a =. 由余弦定理可知,2222242cos 322cos c a b ab C a a C ==+?=?,解得22cos 22C a = ?, ∴2222242132sin 1cos 1822C C a a a ??=?=??=?+? ? ??? . 设△ABC 的面积为S ,则有2 222242111sin sin sin 242S ab C a b C a C ??=== ??? 42221311(12)816216a a a =?+?=??+,当23a =,26b =时,有max 22S =. 法二:以线段AB 的中点O 为原点,AB 所在直线为x 轴建立平面直角坐标 系. 可记(10)A ?, ,(10)B ,. 设()(0)C x y y ≠,,由2AC BC =可知2222(1)2(1)x y x y ++=??+,化简可得22(3)8(0)x y y ?+=≠,可 知点C 的轨迹是以点P (3,0)为圆心,22为半径的圆(去掉左、右顶点). 当点C 为该圆的上、下顶点时,不妨假设(322)C ,,△ABC 的面积S 最 大,此时max 112222222 S AB PC ==??=. 【总结】本题法一运用解三角形的知识,以边长a 为参数,建立△ABC 的面积S 关于a 的函数讨论S 的最大值,虽说思路明确但是计算量相对较为庞大;法二灵活运用2AC BC =的关系,通过解析几何的手法探讨出点C 的运动轨迹是一个圆,通过数形结合的思想求出S 的最大值,使得计算相对简单. 本题法二中的圆我们可以称之为阿波罗尼斯圆,其机理是到两定点距离比值为定值(不为1)的点的轨迹为圆. 运用这种思路,我们也可以解决类似的题型例2. 【例2】在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若6a b +=,4c =,求△ABC 面积S 的最大值. 【解析】法一:由题知22236a b ab ++=,222cos 16a b ab C +?=,联立两式,可解得 10cos 1C ab =?,∴2 22221010020sin 1cos 11C C ab a b ab ??=?=??=?+ ??? . 于是有22222211sin sin 525525592520242a b S ab C a b C ab +????===?≤?=??= ? ????? ,当且仅当3a b ==时,取“=”;即max 25S =. 法二:由题知6CB CA +=,4AB =,以线段AB 的中点O 为原点,AB 所在直线为x 轴建立平面直 角坐标系. 可记(20)A ?,,(20)B ,. 由椭圆的定义知,点C 的轨迹是以A ,B 为焦点,6为长轴长的椭圆(去掉长轴端点),其方程为22 1(0)95 x y y +=≠. 当点C 为该椭圆的短轴端点时,不妨假设(05)C ,,△ABC 的面积S 最大,此 时max 11452522 S AB OC ==??=. 【总结】类似地,我们可以灵活运用6CB CA +=的关系,推知点C 的轨迹是一个椭圆,从而可以运用类似阿波罗尼斯圆的方法讨论△ABC 的面积S 的最大值.
阿氏圆几何画板作法及应用 我们知道,到两定点 F 1、F 2 的距离之和为定值(大于 F 1F 2)的点 M 的轨迹为椭圆,而距离之差为定值 (小于 F 1F 2)的点 M 的轨迹为双曲线,那么圆是否有相类似的结论呢?答案是肯定的,事实上满足到两定 点 F 1、F 2 的距离之比为定值 t(t>0 且 t ≠ 1) 点 M 的轨迹为圆, 这个结论是阿波罗尼 (Apollonius ,约前 260~ 前 190) 发现的,所以往往称为阿波罗尼圆。但圆的这一性质比较“隐晦” ,为帮助学生直观理解需要我们 创设“所见即所得”的教学情境,本文以几何画板 5.0 为例谈谈在画板环境中阿波罗尼圆的构造方式,并 与读者分享画板中自定义工具功能的实现与应用。 一、阿波罗尼圆的画板实现 1. 几何构造法实现阿波罗尼圆 步骤 1、构造一直线上两点 F 、 F ,新建参数 t ,其初值赋为 2; 1 2 步骤 2、度量计算 t 并标记为比 值,双击 t 1 点 F 标记为中心, 选中 F 按标记比值缩放 得 到 点 1 2 P ; 步骤 3、度量计算 t 并标记为比 值,双击 t 1 点 F 标记为中心, 选中 F 按标记比值缩放 得到点得 1 2 到点 Q ; 图 1 步骤 4、构造线段 PQ 并构造线段 PQ 的 中 点 C ,以 C 为圆心以 P 为圆上一点构造圆 C 。 试试效果如何?取圆 C 上任意一点 M 构造线段 MF 1、MF 2,并先后选中两线段度量比值,拖动点 M 会 发 现比值不变并且与参数 t 值恒相等(如图 1 所示)。 2. 解析构造法实现阿波罗尼圆 步骤 1、在 x 轴上任取两点 F 1、 F 2, 度量其横 坐标将标签分别设为 x 1、 x 2,新建参数 t 初值赋为 3; 步骤 2、计算 x 1 tx 2 ,选中后点击 〖绘图〗 1 t 菜单中的〖在轴上绘制点〗命令,在弹出 窗口中选 择“绘制”按纽得到点 P ; 图 2 步骤 3、计算 x 1 tx 2 ,重复步骤 2 可得到点 Q ; 1 t 步骤 4、同方法一,以 PQ 为直径构造圆 C 。 我们也可仿照方法一验证效果(如图 2 所示)。 3. 实现方法构造详解及比较 从以上构造过程我们可以发现,确实阿波罗尼圆关键在于找到 圆与直线 F F 的交点 P 、Q (因为圆 C 以 PQ 为直径)。事实上, P 、 Q 两点一个在 线段 FF 内 1 2 1 2 一个在线段 F 1F 2 外,于是这两个点便称为圆的内分点、外分点;更进 一步地,如 果参数 t>1 ,则 Q 点在 F 1F 2 的延长线上,此时圆 C 偏向 F 2 一侧;如果 0 《阿波罗尼斯圆及其简单应用》教学设计 一.教学目标 根据课程标准与教学内容并结合学生实际,确定本节课的教学目标为: 1.知识与技能 了解阿波罗尼斯圆及其文化背景,掌握阿波罗尼斯圆的简单性质并能应用性质解决问题。 2.过程与方法 通过具体例子引导学生自主合作、探究、抽象概括,对阿波罗尼斯圆由感性认识上升到理性认识的过程,体会从特殊到一般的数学研究方法,渗透数形结合的思想. 3.情感、态度与价值观 通过学生对问题的自主探究,培养学生的独立思考能力和抓主要矛盾解决问题的能力.在问题逐步深入的研究中唤起学生追求真理,乐于创新的情感需求,引发学生渴求知识的强烈愿望,树立科学的人生观、价值观. 二.重难点分析 重点:阿波罗尼斯圆及其性质的理解和应用. 难点:阿波罗尼斯圆性质的推导及其应用. 三.教学过程 (一)引入:由椭圆、双曲线定义提出问题:到两定点距离之比为定值的点的轨迹是什么? 引例点M到椭圆 22 22 1 1312 x y +=的左焦点和右焦点的距离的比为2:3. 求点M满足的 方程,并画出草图. 设计意图:先提出问题,激发学生进一步探究的欲望.再以课本练习题引入,说明问题源于课本,但又高于课本,提醒学生重视课本,用好课本,发掘课本的潜在价值。 (二)抽象概括: 阿波罗尼斯 (Apollonius of Perga,也有文献上将其名字翻译为“阿波罗尼奥斯”)约公元前262~前190,古希腊人.阿波罗尼斯与欧几里得、阿基米德合称为亚历山大时期的“数学三杰”.在其巨著《圆锥曲线论》给出了一个著名的几何问题: “在平面上给定相异两点A、B,设点P在同一平面内且满足,P点的 轨迹是个圆”,这个圆我们称之为“阿波罗尼斯圆”,又称阿氏圆.这个结论称作“阿波罗尼斯轨迹定理”. 以阿波罗尼斯圆为背景的考题在历年高考中频频出现,备受青睐。《普通高中数学课程标准(实验)》在不同部分对数学文化的内涵和价值做了阐述,首次明确提出数学课程要“体现数学的文化价值”。 设计意图:抽象概括,形成概念,渗透数学文化,体现课程标准. (三)阿波罗尼斯圆再探究 1.设定点(,0),(,0)(0)A c B c c ->,点P 在同一平面上且满足(0,1)PA PB λλλ=>≠P 点的 轨迹是以__________为圆心,半径为_________的圆. 2.在平面上给定相异两点A 、B ,点P 在同一平面上且满足 (0,1)PA PB λλλ=>≠ ,则P 点的轨迹是圆.若此圆与直线AB 交于,M N 两点,则 ____,____.MA NA MB NB == 由此你能得到什么结论?(提示:以引例为研究对象,再抽象概括) 设计意图:分解难点,提炼重点,从两个不同角度给出阿波罗尼斯圆的快速作 图法,为后面的应用做好铺垫.培养学生合作交流的能力和抽象概括能力. (四)阿波罗尼斯圆的应用 巩固练习1.(06四川)已知两定点).0,1(),0,2(B A -如果动点P 满足PB PA 2=,则点P 的轨迹所围成的平面图形的面积是________________. 解析:此题若用常规思路先求点P 的轨迹方程,再求半径和面积自然可以求解.但对于填空题大可不必“小题大做”,若应用性质2可以很快确定点P 的轨教学设计《阿波罗尼斯圆及其简单应用》