
72
x = B(0,4)
A(6,0)
E
F
x
y
O
二次函数与四边形综合专题
一.二次函数与四边形的形状
例1. 如图,抛物线223y x x =--与x 轴交A 、B 两点(A 点在B 点左侧),直线l 与抛物线交于A 、C 两点,其中C 点的横坐标为2.
(1)求A 、B 两点的坐标及直线AC 的函数表达式;
(2)P 是线段AC 上的一个动点,过P 点作y 轴的平行线交抛物线于E 点,求线段PE 长度的最大值; (3)点G 是抛物线上的动点,在x 轴上是否存在点F ,使A 、C 、F 、G 这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F 点坐标;如果不存在,请说明理由.
解:(1)令y=0,解得11x =-或23x =∴A (-1,0)B (3,0);将C 点的横坐标x=2代入223y x x =-- 得y=-3,∴C (2,-3)∴直线AC 的函数解析式是y=-x-1 (2)设P 点的横坐标为x (-1≤x ≤2)则P 、E 的坐标分别为:
P (x ,-x-1),E (2(,23)x x x --
∵P 点在E 点的上方,PE=22(1)(23)2x x x x x -----=-++
∴当12x =时,PE 的最大值=9
4
(3)存在4个这样的点F ,分别是1234(1,0),(3,0),(470),(47,0)F F F F -+-,
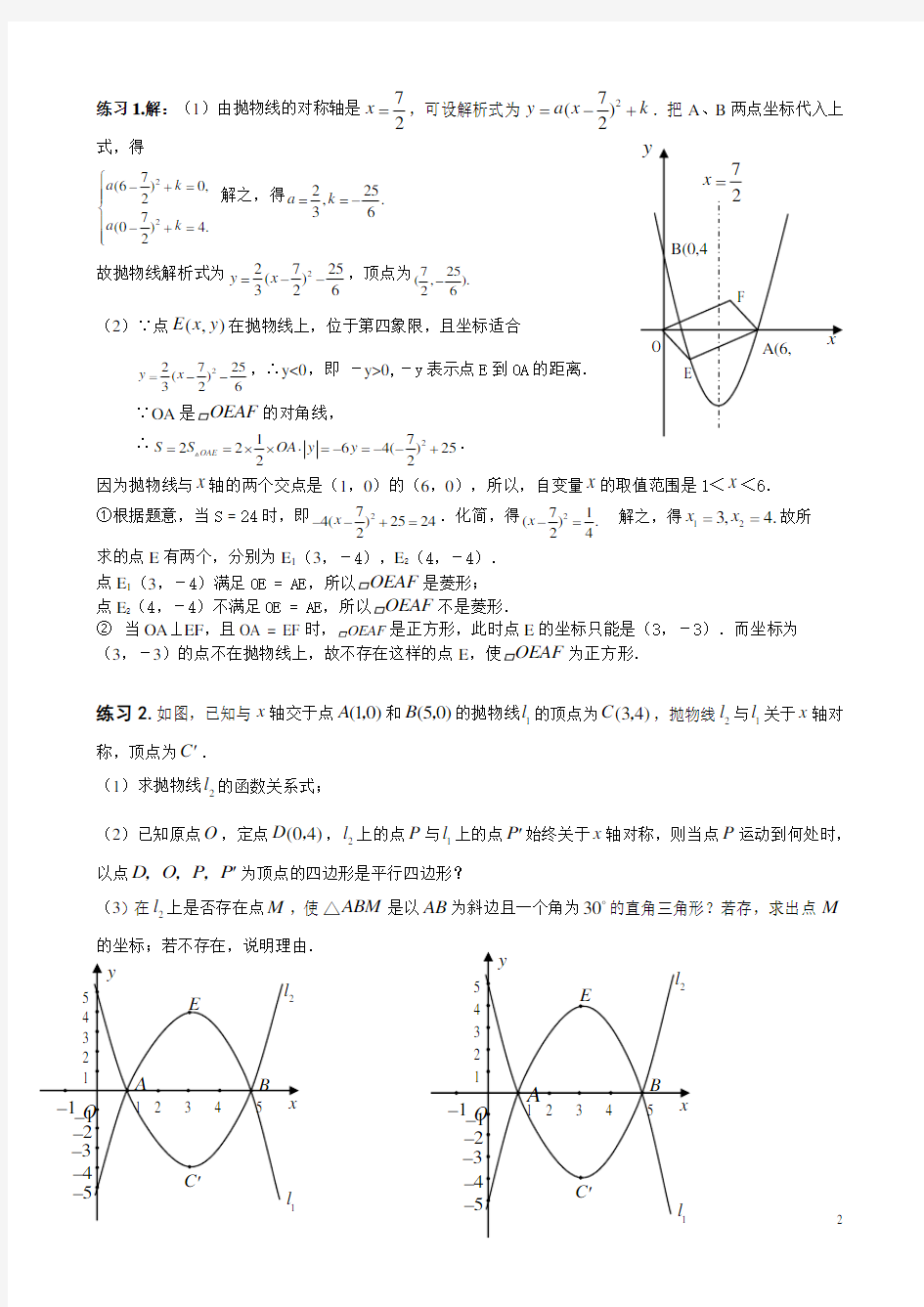
练习1.如图,对称轴为直线7
2
x =
的抛物线经过点A (6,0)和B (0,4). (1)求抛物线解析式及顶点坐标;
(2)设点E (x ,y )是抛物线上一动点,且位于第四象限,四边形OEAF 是以OA 为对角线的平行四边形.求平行四边形OEAF 的面积S 与x 之间的函数关系式,并写出自变量x 的取值范围; ①当平行四边形OEAF 的面积为24时,请判断平行四边形OEAF 是否为菱形?
②是否存在点E ,使平行四边形OEAF 为正方形?若存在,求出点E 的坐标;若不存在,请说明理由.
A
7
2
x =
B(0,4
A(6,
E
F
x
y
O
练习1.解:(1)由抛物线的对称轴是72x =,可设解析式为2
7()2
y a x k =-+.把A 、B 两点坐标代入上式,得
227(6)0,27(0) 4.2
a k a k ?-+=????-+=?? 解之,得225,.36a k ==- 故抛物线解析式为22725()3
2
6
y x =--,顶点为725(,).2
6
-
(2)∵点(,)E x y 在抛物线上,位于第四象限,且坐标适合
22725()326
y x =
--,∴y<0,即 -y>0,-y 表示点E 到OA 的距离. ∵OA 是OEAF 的对角线,
∴2172264()252
2
OAE S S OA y y ==???=-=--+ .
因为抛物线与x 轴的两个交点是(1,0)的(6,0),所以,自变量x 的取值范围是1<x <6. ①根据题意,当S = 24时,即274()25242
x --+=.化简,得271().2
4
x -= 解之,得123, 4.x x ==故所
求的点E 有两个,分别为E 1(3,-4),E 2(4,-4).
点E 1(3,-4)满足OE = AE ,所以OEAF 是菱形;
点E 2(4,-4)不满足OE = AE ,所以OEAF 不是菱形.
② 当OA ⊥EF ,且OA = EF 时,OEAF 是正方形,此时点E 的坐标只能是(3,-3).而坐标为 (3,-3)的点不在抛物线上,故不存在这样的点E ,使OEAF 为正方形.
练习2.如图,已知与x 轴交于点(10)A ,
和(50)B ,的抛物线1l 的顶点为(34)C ,,抛物线2l 与1l 关于x 轴对称,顶点为C '.
(1)求抛物线2l 的函数关系式;
(2)已知原点O ,定点(04)D ,
,2l 上的点P 与1l 上的点P '始终关于x 轴对称,则当点P 运动到何处时,以点D O P P ',,,为顶点的四边形是平行四边形?
(3)在2l 上是否存在点M ,使ABM △是以AB 为斜边且一个角为30
的直角三角形?若存,求出点M 的坐标;若不存在,说明理由.
5-
4- 3- 2- 1- 1
2 3
4 5 5
4
3
2 1 A E
B
C '
1- O 2l
l
x
y
4-
3-
2-
1- 1 2 3 4 5 5
4
3
2
1 A
E
B
C '
1- O 2l
x
y
练习3. 如图,已知抛物线1C 与坐标轴的交点依次是(40)A -,,(20)B -,,(08)E ,
. (1)求抛物线1C 关于原点对称的抛物线2C 的解析式;
(2)设抛物线1C 的顶点为M ,抛物线2C 与x 轴分别交于C D ,两点(点C 在点D 的左侧),顶点为N ,四边形MDNA 的面积为S .若点A ,点D 同时以每秒1个单位的速度沿水平方向分别向右、向左运动;
与此同时,点M ,点N 同时以每秒2个单位的速度沿坚直方向分别向下、向上运动,直到点A 与点D 重合为止.求出四边形MDNA 的面积S 与运动时间t 之间的关系式,并写出自变量t 的取值范围; (3)当t 为何值时,四边形MDNA 的面积S 有最大值,并求出此最大值;
(4)在运动过程中,四边形MDNA 能否形成矩形?若能,求出此时t 的值;若不能,请说明理由.
二.二次函数与四边形的面积
例1.如图10,已知抛物线P :y=ax 2
+bx+c(a ≠0) 与x 轴交于A 、B 两点(点A 在x 轴的正半轴上),与y 轴交于点C ,矩形DEFG 的一条边DE 在线段AB 上,顶点F 、G 分别在线段BC 、AC 上,抛物线P 上部分点的横坐标对应的纵坐标如下:
x … -3 -2 1 2 … y
…
-52
-4
-52
…
(1) 求A 、B 、C 三点的坐标;
(2) 若点D 的坐标为(m ,0),矩形DEFG 的面积为S ,求S 与m 的函数关系,并指出m 的取值范围;
(3) 当矩形DEFG 的面积S 取最大值时,连接DF 并延长至点M ,使FM=k ·DF ,若点M 不在抛物线P 上,求k 的取值范围.
图10
练习1.如图,平面直角坐标系中有一直角梯形OMNH ,点H 的坐标为(-8,0),点N 的坐标为(-6,-4). (1)画出直角梯形OMNH 绕点O 旋转180°的图形OABC ,并写出顶点A ,B ,C 的坐标(点M 的对应点为A , 点N 的对应点为B , 点H 的对应点为C ); (2)求出过A ,B ,C 三点的抛物线的表达式;
(3)截取CE =OF =AG =m ,且E ,F ,G 分别在线段CO ,OA ,AB 上,求四边形BEFG 的面积S 与m 之间的函数关系式,并写出自变量m 的取值范围;面积S 是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由;
(4)在(3)的情况下,四边形BEFG 是否存在邻边相等的情况,若存在,请直接写出此时m 的值,并指出相等的邻边;若不存在,说明理由.
练习2.如图,正方形ABCD 的边长为2cm ,在对称中心O 处有一钉子.动点P ,Q 同时从点A 出发,点P 沿A B C →→方向以每秒2cm 的速度运动,
到点C 停止,点Q 沿A D →方向以每秒1cm 的速度运动,到点D 停止.P ,Q 两点用一条可伸缩的细橡皮筋联结,设x 秒后橡皮筋扫过的面积为2
cm y .
(1)当01x ≤≤时,求y 与x 之间的函数关系式; (2)当橡皮筋刚好触及钉子时,求x 值;
(3)当12x ≤≤时,求y 与x 之间的函数关系式,并写出橡皮筋从触及钉子到运动停止时POQ ∠的变化范围;
(4)当02x ≤≤时,请在给出的直角坐标系中画出y 与x 之间的函数图象.
B C P
O D Q
A B
P
C
O
D
Q A
y
3
2
1
O
1
2 x
练习3. 如图,已知抛物线l 1:y =x 2-4的图象与x 轴相交于A 、C 两点,B 是抛物线l 1上的动点(B 不与A 、C 重合),抛物线l 2与l 1关于x 轴对称,以AC 为对角线的平行四边形ABCD 的第四个顶点为D . (1) 求l 2的解析式;
(2) 求证:点D 一定在l 2上;
(3) □ABCD 能否为矩形?如果能为矩形,求这些矩形公共部分的面积(若只有一个矩形符合条件,则求此矩形的面积);如果不能为矩形,请说明理由. 注:计算结果不取近似值 .
三.二次函数与四边形的动态探究
例1.如图1,在平面直角坐标系中,有一张矩形纸片OABC ,已知O (0,0),A (4,0),C (0,3),点P 是OA 边上的动点(与点O 、A 不重合).现将△PAB 沿PB 翻折,得到△PDB ;再在OC 边上选取适当的点E ,将△POE 沿PE 翻折,得到△PFE ,并使直线PD 、PF 重合.
(1)设P (x ,0),E (0,y ),求y 关于x 的函数关系式,并求y 的最大值;
(2)如图2,若翻折后点D 落在BC 边上,求过点P 、B 、E 的抛物线的函数关系式;
(3)在(2)的情况下,在该抛物线上是否存在点Q ,使△PEQ 是以PE 为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q 的坐标.
例2. 已知抛物线y =ax2+bx +c 与x 轴交于A 、B 两点,与y 轴交于点C ,其中点B 在x 轴的正半轴上,
图2
O
C
A B
x
y D
P
E F 图
1
F
E P
D y x
B
A C O
点C 在y 轴的正半轴上,线段OB 、OC 的长(OB (1)求A 、B 、C 三点的坐标; (2)求此抛物线的表达式; (3)连接AC 、BC ,若点E 是线段AB 上的一个动点(与点A 、点B 不重合),过点E 作EF ∥AC 交BC 于点F ,连接CE ,设AE 的长为m ,△CEF 的面积为S ,求S 与m 之间的函数关系式,并写出自变量m 的取值范围; (4)在(3)的基础上试说明S 是否存在最大值,若存在,请求出S 的最大值,并求出此时点E 的坐标,判断此时△BCE 的形状;若不存在,请说明理由. 例3. 如图,矩形ABCD 中,AB =3,BC =4,将矩形ABCD 沿对角线A 平移,平移后的矩形为EFGH (A 、E 、C 、G 始终在同一条直线上),当点E 与C 重时停止移动.平移中EF 与BC 交于点N ,GH 与BC 的延长线交于点M ,EH 与DC 交于点P ,FG 与DC 的延长线交于点Q .设S 表示矩形PCMH 的面积,S '表示矩形NFQC 的面积. (1) S 与S '相等吗?请说明理由. (2)设AE =x ,写出S 和x 之间的函数关系式,并求出x 取何值时S 有最大值,最大值是多少? (3)如图11,连结BE ,当AE 为何值时,ABE ?是等腰三角形. 练习1.如图12, 四边形OABC 为直角梯形,A (4,0),B (3,4),C (0,4). 点M 从O 出发以每 x N M Q P H G F E D C B A 图11 Q P N M H G F E D C B A 图10 秒2个单位长度的速度向A 运动;点N 从B 同时出发,以每秒1个单位长度的速度向C 运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N 作NP 垂直x 轴于点P ,连结AC 交NP 于Q ,连结MQ . (1)点 (填M 或N )能到达终点; (2)求△AQM 的面积S 与运动时间t 的函数关系式,并写出自变量t 的取值范围,当t 为何值时,S 的值最大; (3)是否存在点M ,使得△AQM 为直角三角形?若存在,求出点M 的坐标,若不存在,说明理由. 练习2. 实验与探究 (1)在图1,2,3中,给出平行四边形ABCD 的顶点A B D ,,的坐标(如图所示),写出图1,2,3 中的顶点C 的坐标,它们分别是(52), , , ; (2)在图4中,给出平行四边形ABCD 的顶点A B D ,,的坐标(如图所示),求出顶点C 的坐标(C 点坐标用含a b c d e f ,,,,,的代数式表示); 归纳与发现 (3)通过对图1,2,3,4的观察和顶点C 的坐标的探究,你会发现:无论平行四边形ABCD 处于直角坐标系中哪个位置,当其顶点坐标为()()()()A a b B c d C m n D e f ,,,,,,,(如图4)时,则四个顶 点的横坐标a c m e ,,,之间的等量关系为 ;纵坐标b d n f ,,,之间的等量关系为 y C ()A (40)D , (12)B , O x 图1 y C ()A (0)D e , ()B c d , O x 图2 y C ()A a b , ()D e b , ()B c d , O x 图3 y C ()A a b , ()D e f , ()B c d , O x 图4 图12 y x P Q B C N M O A 7 2 x = B(0,4 A(6, E F x y O (不必证明); 运用与推广 (4)在同一直角坐标系中有抛物线2(53)y x c x c =---和三个点15192222G c c S c c ????- ? ????? ,,,,(20)H c ,(其中0c >).问当c 为何值时,该抛物线上存在点P ,使得以G S H P ,,,为顶点的四边形是平行四边形?并求出所有符合条件的P 点坐标. 参考答案: 一.二次函数与四边形的形状 例1.解:(1)令y=0,解得11x =-或23x =∴A (-1,0)B (3,0); 将C 点的横坐标x=2代入223y x x =--得y=-3,∴C (2,-3)∴直线AC 的函数解析式是y=-x-1 (2)设P 点的横坐标为x (-1≤x ≤2)则P 、E 的坐标分别为:P (x ,-x-1), E (2(,23)x x x --∵P 点在E 点的上方,PE=22(1)(23)2x x x x x -----=-++ ∴当12x = 时,PE 的最大值=94 (3)存在4个这样的点F ,分别是1234(1,0),(3,0),(470),(47,0)F F F F -+-, 练习1.解:(1)由抛物线的对称轴是72x =,可设解析式为2 7()2 y a x k =-+.把A 、B 两点坐标代入上式,得 227(6)0,27(0) 4.2 a k a k ? -+=????-+=?? 解之,得225,.36a k ==- 故抛物线解析式为22725 ()326y x = --,顶点为725(,).26 - (2)∵点(,)E x y 在抛物线上,位于第四象限,且坐标适合 22725 ()326 y x = --, ∴y<0,即 -y>0,-y 表示点E 到OA 的距离.∵OA 是OEAF 的对角线, ∴217 2264()2522 OAE S S OA y y ==? ??=-=--+ . 因为抛物线与x 轴的两个交点是(1,0)的(6,0),所以,自变量x 的取值范围是1<x <6. 5 -4 -3 -2 -1-1 2 3 D 5 5 4 3 2 1 A C E M B C ' 1-O 2 l 1 l x y ① 根据题意,当S = 24时,即274()25242 x --+=.化简,得271 ().24x -= 解之,得123, 4.x x == 故所求的点E 有两个,分别为E 1(3,-4),E 2(4,-4). 点E 1(3,-4)满足OE = AE ,所以OEAF 是菱形; 点E 2(4,-4)不满足OE = AE ,所以OEAF 不是菱形. ② 当OA ⊥EF ,且OA = EF 时,OEAF 是正方形,此时点E 的 ③ 坐标只能是(3,-3). 而坐标为(3,-3)的点不在抛物线上,故不存在这样的点E , 使OEAF 为正方形. 练习2.解:(1)由题意知点C '的坐标为(34)-, .设2l 的函数关系式为2(3)4y a x =--. 又 点(1 0)A ,在抛物线2(3)4y a x =--上,2(13)40a ∴--=,解得1a =. ∴抛物线2l 的函数关系式为2(3)4y x =--(或265y x x =-+). (2)P 与P '始终关于x 轴对称, PP '∴与y 轴平行. 设点P 的横坐标为m ,则其纵坐标为265m m -+,4OD = ,22654m m ∴-+=, 即2652m m -+=±.当2652m m -+=时,解得36m =±.当2652m m -+=-时,解得32m =±.∴当点P 运动到(362)-,或(362)+,或(322)--,或(322)+-,时, P P OD ' ∥,以点D O P P ',,,为顶点的四边形是平行四边形. (3)满足条件的点M 不存在.理由如下:若存在满足条件的点M 在2l 上,则 90AMB ∠= ,30BAM ∠= (或30ABM ∠= ), 11 4222 BM AB ∴==?=. 过点M 作ME AB ⊥于点E ,可得30BME BAM ∠=∠= . 11 2122 EB BM ∴==?=,3EM =,4OE =. ∴点M 的坐标为(43)-,. 但是,当4x =时,2 46451624533y =-?+=-+=-≠-. ∴不存在这样的点M 构成满足条件的直角三角形. 练习 3. 解(1)点(40)A -, ,点(20)B -,,点(08)E ,关于原点的对称点5- 4- 3- 2- 1- 1 2 3 4 5 5 4 3 2 1 A E B C ' 1- O 2l 1l x y 分别为(40)D ,,(20)C ,,(08)F -,. 设抛物线2C 的解析式是 2 (0)y ax bx c a =++≠,则16404208a b c a b c c ++=??++=??=-?,,.解得1 68a b c =-??=??=-? ,, . 所以所求抛物线的解析式是268y x x =-+-. (2)由(1)可计算得点(31)(31)M N --,,,. 过点N 作NH AD ⊥,垂足为H . 当运动到时刻t 时,282AD OD t ==-,12NH t =+. 根据中心对称的性质OA OD OM ON ==,,所以四边形MDNA 是平行四边形.所以2ADN S S =△.所以,四边形MDNA 的面积2(82)(12)4148S t t t t =-+=-++. 因为运动至点A 与点D 重合为止,据题 意可知04t <≤.所以,所求关系式是2 4148S t t =-++,t 的取值范围是04t <≤. (3)781 444 S t ??=-- + ?? ?,(04t <≤).所以74t =时,S 有最大值814. 提示:也可用顶点坐标公式来求. (4)在运动过程中四边形MDNA 能形成矩形. 由(2)知四边形MDNA 是平行四边形,对角线是AD MN ,,所以当AD MN =时四边形MDNA 是矩形.所以OD ON =.所以 2222OD ON OH NH ==+. 所以22420t t +-=.解之得126262t t =-=--,(舍). 所以在运动过程中四边形MDNA 可以形成矩形,此时62t =-. [点评]本题以二次函数为背景,结合动态问题、存在性问题、最值问题,是一道较传统的压轴题,能力要求较 高。 二.二次函数与四边形的面积 例1. 解:(1)解法一:设)0(2 ≠++=a c bx ax y ,任取x,y 的三组值代入,求出解析式2 142 y x x = +-, 令y=0,求出124,2x x =-=;令x=0,得y=-4,∴ A 、B 、C 三点的坐标分别是A(2,0),B(-4,0),C(0,-4) ··································· 解法二:由抛物线P 过点(1,-52),(-3,5 2 -)可知, 抛物线P 的对称轴方程为x=-1, 又∵ 抛物线P 过(2,0)、(-2,-4),则由抛物线的对称性可知, 点A 、B 、C 的坐标分别为 A(2,0),B(-4,0),C(0,-4) . (2)由题意,AD DG AO OC = ,而AO=2,OC=4,AD=2-m ,故DG=4-2m , ······ 又 BE EF BO OC = ,EF=DG ,得BE=4-2m ,∴ DE=3m , ∴DEFG s =DG·DE=(4-2m) 3m=12m-6m 2 (0<m <2) . 注:也可通过解Rt△BOC 及Rt △AOC ,或依据△BOC 是等腰直角三角形建立关系求解. (3)∵SDEFG=12m-6m 2 (0<m <2),∴m=1时,矩形的面积最大,且最大面积是6 . 当矩形面积最大时,其顶点为D(1,0),G(1,-2),F(-2,-2),E(-2,0), 设直线DF 的解析式为y=kx+b ,易知,k=23,b=-23,∴22 33y x =-, 又可求得抛物线P 的解析式为:21 42 y x x =+-, 令2233x -=21 42x x +-,可求出3 611--=x . 设射线DF 与抛物线P 相交于点N , 则N 的横坐标为161 3 --,过N 作x 轴的垂线交x 轴于H ,有 FN HE DF DE = =161 233---- =5619-+, 点M 不在抛物线P 上,即点M 不与N 重合时,此时k 的取值范围是 k≠5619 -+且k >0. 说明:若以上两条件错漏一个,本步不得分. 若选择另一问题: (2)∵AD DG AO OC =,而AD=1,AO=2,OC=4,则DG=2,又∵FG CP AB OC = , 而AB=6,CP=2,OC=4,则FG=3, ∴DEFG s =DG·FG=6. 练习1.解:利用中心对称性质,画出梯形OABC . ················· 1分 ∵A ,B ,C 三点与M ,N ,H 分别关于点O 中心对称, ∴A (0,4),B (6,4),C (8,0) ··················· 3分 (写错一个点的坐标扣1分) (2)设过A ,B ,C 三点的抛物线关系式为 ,∵抛物线过点A (0,4), ∴.则抛物线关系式为. ·············· 4分 将B (6,4), C (8,0)两点坐标代入关系式,得 ··············· 5AB ,垂足为G ,则sin ∠FEG =sin ∠CAB = 分 解得····················· 6分 所求抛物线关系式为:.········ 7分 (3)∵OA=4,OC=8,∴AF=4-m ,OE=8-m . ·········· 8分 ∴ OA (AB+OC ) AF ·AG OE ·OF CE ·OA ( 0< <4) ········ 10分 ∵. ∴当时,S 的取最小值. 又∵0<m <4,∴不存在m 值,使S 的取得最小值. ······· 12分 (4)当时,GB=GF ,当 时,BE=BG . 14分 练习2.[解] (1)当01x ≤≤时,2AP x =,AQ x =,21 2 y AQ AP x == ,即2y x =. (2)当1 2 A B C D ABPQ S S = 正方形四边形时,橡皮筋刚好触及钉子,22BP x =-,AQ x =,()21122222 2 x x -+?=?, 4 3 x ∴= . (3)当413x ≤≤时,2AB =,22PB x =-,AQ x =,2223222 AQ BP x x y AB x ++-∴==?=- , 即32y x =-. 作OE AB ⊥,E 为垂足. 当 4 23 x ≤≤时,22BP x =-,AQ x =,1OE =, BEOP OEAQ y S S =+梯形梯形12211122 x x +-+=?+?3 2x =, 即3 2 y x =.90180POQ ≤∠≤或180270POQ ≤∠≤ (4)如图所示: 练习3. 解](1) 设l 2的解析式为y =ax 2+bx +c (a ≠0), ∵l 1与x 轴的交点为A (-2,0),C (2,0),顶点坐标是(0,- 4),l 2与l 1关于x 轴对称, ∴l 2过A (-2,0),C (2,0),顶点坐标是(0,4), ∴420,420,4. a b c a b c c -+=??++=?=?? ∴ a =-1,b =0,c =4,即l 2的解析式为y = -x 2+4 . (还可利用顶点式、对称性关系等方法解答) 3 2 1 O 1 2 x y 4 3 (2) 设点B (m ,n )为l 1:y =x 2-4上任意一点,则n = m 2-4 (*). ∵ 四边形ABCD 是平行四边形,点A 、C 关于原点O 对称,∴ B 、D 关于原点O 对称, ∴ 点D 的坐标为D (-m ,-n ) . 由(*)式可知, -n =-(m 2-4)= -(-m )2+4,即点D 的坐标满足y = -x 2+4,∴ 点D 在l 2上. (3) □ABCD 能为矩形. 过点B 作BH ⊥x 轴于H ,由点B 在l 1:y =x 2-4上,可设点B 的坐标为 (x 0,x 02-4),则OH =| x 0|,BH =| x 02-4| . 易知,当且仅当BO = AO =2时,□ABCD 为矩形. 在Rt △OBH 中,由勾股定理得,| x 0|2+| x 02-4|2=22,(x 02-4)( x 02-3)=0,∴x 0=±2(舍去)、x 0=±3 . 所以,当点B 坐标为B ( 3 ,-1)或B ′(- 3 ,-1)时,□ABCD 为矩形, 此时,点D 的坐标分别是D (- 3 ,1)、D ′( 3 ,1). 因此,符合条件的矩形有且只有2个,即矩形ABCD 和矩形AB ′CD ′ . 设直线AB 与y 轴交于E ,显然,△AOE ∽△AHB , ∴ EO AO = BH AH ,∴1 223EO =+. ∴ EO =4-23 . 由该图形的对称性知矩形ABCD 与矩形AB ′CD ′重合部分是菱形, 其面积为S =2S ΔACE =2×12 × AC ×EO =2×1 2 ×4×(4-2 3 )=16 - 8 3 . 三.二次函数与四边形的动态探究 例1.解: (1) 由已知PB 平分∠APD ,PE 平分∠OPF ,且PD 、PF 重合,则∠BPE =90°.∴∠OPE +∠APB =90°. 又∠APB +∠ABP =90°,∴∠OPE =∠PBA . ∴Rt △POE ∽Rt △BPA .∴ PO BA OE AP = .即34x y x =-.∴y =2114 (4)333 x x x x -=-+(0<x <4). 且当x =2时,y 有最大值13 . (2)由已知,△PAB 、△POE 均为等腰三角形,可得P (1,0),E (0,1),B (4,3). 设过此三点的抛物线为y =ax 2+bx +c ,则1,0,164 3.c a b c a b c =??++=??++=? ∴1,23, 21.a b c ? =???=-??=??? y = 213 122 x x -+. (3)由(2)知∠EPB =90°,即点Q 与点B 重合时满足条件.直线PB 为y =x -1,与y 轴交于点(0,-1). 将PB 向上平移2个单位则过点E (0,1), ∴该直线为y =x +1. 由21, 1 31,22y x y x x =+???=-+?? 得5,6.x y =?? =?∴Q(5,6). 故该抛物线上存在两点Q (4,3)、(5,6)满足条件. 例2.解: (1)解方程x 2-10x +16=0得x 1=2,x 2=8 ……………………1分 ∵点B 在x 轴的正半轴上,点C 在y 轴的正半轴上,且OB <OC ∴点B 的坐标为(2,0),点C 的坐标为(0,8) 又∵抛物线y =ax 2+bx +c 的对称轴是直线x =-2 ∴由抛物线的对称性可得点A 的坐标为(-6,0) …………………4分 (2)∵点C (0,8)在抛物线y =ax 2+bx +c 的图象上,∴c =8,将A (-6,0)、B (2,0)代入表达 式,得 解得 ∴所求抛物线的表达式为y =x 2 x +8 ………………………7分 (3)依题意,AE =m ,则BE =8-m ,∵OA =6,OC =8,∴AC =10 ∵EF ∥AC ∴△BEF ∽△BAC ∴ 即 ,∴EF = ∴= ∴FG =·=8-m ∴S =S △BCE -S △BFE =(8-m )×8-(8-m )(8-m ) =(8-m )(8-8+m )=(8-m )m =-m 2+4m …………10分 自变量m 的取值范围是0<m <8 …………………………11分 (4)存在.理由:∵S =-m 2+4m =-(m -4)2+8 且-<0, ∴当m =4时,S 有最大值,S 最大值=8 ………………………12分 ∵m =4,∴点E 的坐标为(-2,0) ∴△BCE 为等腰三角形. …………………………14分 (以上答案仅供参考,如有其它做法,可参照给分) 例3解: (1)相等。理由是:因为四边形ABCD 、EFGH 是矩形, 所以,,EGH EGF ECN ECP CGQ CGM S S S S S S ??????=== 所以,EGH ECP CGM EGF ECN CGQ S S S S S S ??????--=-- 即:S S '= (2)AB =3,BC =4,AC =5,设AE =x ,则EC =5-x ,34(5),,5 5 PC x MC x =-= 所以12(5)25 S PC MC x x ==- ,即21212(05)25 5 S x x x =-+≤≤ 配方得:2125()3252S x =- -+,所以当5 2 x =时,S 有最大值3 (3)当AE =AB =3或AE =BE =5 2或AE =3.6时,ABE ?是等腰三角形 练习1. 解: (1)点 M 1分 (2)经过t 秒时,NB t =,2OM t = 则3CN t =-,42AM t =-∵BCA ∠=MAQ ∠=45 ∴ 3QN CN t ==- ∴ 1 PQ t =+ ∴11(42)(1) 22AMQ S AM PQ t t ==-+ △22t t =-++ ∴2219224 S t t t ??=-++=--+ ??? ∵02t ≤≤∴当1 2 t = 时,S 的值最大. (3)存在.设经过t 秒时,NB =t ,OM=2t 则3CN t =-,42AM t =-∴BCA ∠=MAQ ∠=45 ①若90AQM ∠= ,则PQ 是等腰Rt △MQA 底边MA 上的高∴PQ 是底边MA 的中线 ∴ 12PQ AP MA == ∴11(42)2t t +=- ∴12t = ∴点M 的坐标为(1,0) ②若90QMA ∠= ,此时QM 与QP 重合∴QM QP MA ==∴142t t +=-∴1t = ∴点M 的坐标为(2,0) 练习2.解: (1)()e c d +,,()c e a d +-,. (2)分别过点A B C D ,,,作x 轴的垂线,垂足分别为1 111A B C D ,,,,分别过A D ,作1AE BB ⊥于E ,1DF CC ⊥于点F . 在平行四边形ABCD 中,CD BA =,又11BB CC ∥, 180EBA ABC BCF ABC BCF FCD ∴∠+∠+∠=∠+∠+∠= . EBA FCD ∴∠=∠. 又90BEA CFD ∠=∠= , BEA CFD ∴△≌△. AF DF a c ∴==-,BE CF d b ==-. 设()C x y ,.由e x a c -=-,得x e c a =+-. 由y f d b -=-,得y f d b =+-.()C e c a f d b ∴+-+-,. y C ()A a b , ()D e f , ()B c d , E F 1B 1A 1C 1D O x (3)m c e a =+-,n d f b =+-.或m a c e +=+,n b d f +=+. (4)若GS 为平行四边形的对角线,由(3)可得1(27)P c c -,.要使1P 在抛物线上, 则有274(53)(2)c c c c c =--?--,即2 0c c -=. 10c ∴=(舍去),21c =.此时1(27)P -, . 若SH 为平行四边形的对角线,由(3)可得2(32)P c c ,,同理可得1c =,此时2(32)P ,. 若GH 为平行四边形的对角线,由(3)可得(2)c c -,,同理可得1c =,此时3(12)P -,. 综上所述,当1c =时,抛物线上存在点P ,使得以G S H P ,,,为顶点的四边形是平行四边形. 符合条件的点有1(27)P -, ,2(32)P ,,3(12)P -,. 练习3.解:⑴由Rt △AOB ≌Rt △CDA 得OD=2+1=3,CD=1 ∴C 点坐标为(-3,1), ∵抛物线经过点C, ∴1= (-3)2 a +(-3)a-2,∴2 1 = a 。 ∴抛物线的解析式为22 1 212-+= x x y . ⑵在抛物线(对称轴的右侧)上存在点P 、Q ,使四边形ABPQ 是正方形。 以AB 边在AB 右侧作正方形ABPQ 。过P 作PE ⊥OB 于E ,QG ⊥x 轴于G ,可证△PBE ≌△AQG ≌△BAO , ∴PE =AG =BO =2,BE =QG =AO =1,∴P 点坐标为(2,1),Q 点坐标为(1,-1)。 由(1)抛物线22 1 212-+= x x y 。当x =2时,y =1,当x =,1时,y =-1。∴P 、Q 在抛物线上。 故在抛物线(对称轴的右侧)上存在点P (2,1)、Q (1,-1),使四边形ABPQ 是正方形。 ⑵另解:在抛物线(对称轴的右侧)上存在点P 、Q ,使四边形ABPQ 是正方形。 延长CA 交抛物线于Q ,过B 作BP ∥CA 交抛物线于P ,连PQ ,设直线CA 、BP 的解析式分别为y=k 1x+b 1, y=k 2x+b 2, ∵A (-1,0),C (-3,1),∴CA 的解析式2121-- =x y ,同理BP 的解析式为2 1 21+-=x y , 解方程组??? ??? ? -+=--=2212121212x x y x y 得Q 点坐标为(1,-1),同理得P 点坐标为(2,1)。 由勾股定理得AQ =BP =AB =5,而∠BAQ =90°, ∴四边形ABPQ 是正方形。故在抛物线(对称轴的右侧)上存在点P (2,1)、Q (1,-1),使四边形ABPQ 是正方形。 ⑵另解:在抛物线(对称轴的右侧)上存在点P 、Q ,使四边形ABPQ 是正方形。如图,将线段CA 沿CA 方向平移至AQ , ∵C (-3,1)的对应点是A (-1,0),∴A (-1,0)的对应点是Q (1,-1),再将线段AQ 沿AB 方向平移至BP ,同理可得P (2,1) ∵∠BAC =90°,AB =AC ∴四边形ABPQ 是正方形。经验证P (2,1)、Q (1,-1)两点均在抛物线221212-+=x x y 上。 ⑶结论②AG BG AF BF =成立, 证明如下:连EF ,过F 作FM ∥BG 交AB 的延长线于M ,则△AMF ∽△ABG , ∴AG BG AF MF =。由⑴知△ABC 是等腰直角三角形, ∴∠1=∠2=45°。∵AF =AE ,∴∠AEF =∠1=45°。∴∠EAF =90°,EF 是⊙O ′的直径。 ∴∠EBF =90°。∵FM ∥BG ,∴∠MFB =∠EBF =90°,∠M =∠2=45°,∴BF =MF ,∴AG BG AF BF = 二次函数中动点与特殊四边形综合问题解析与训练 一、知识准备: 抛物线与直线形的结合表形式之一是,以抛物线为载体,探讨是否存在一些点,使其能构成某些特殊四边形,有以下常风的基本形式 (1)抛物线上的点能否构成平行四边形 (2)抛物线上的点能否构成矩形,菱形,正方形 特殊四边形的性质与是解决这类问题的基础,而待定系数法,数形结合,分类讨论是解决这类问题的关键。 二、例题精析 ㈠【抛物线上的点能否构成平行四边形】 例一、(2013河南)如图,抛物线2 y x bx c =-++与直线 1 2 2 y x =+交于,C D两点,其 中点C在y轴上,点D的坐标为 7 (3,) 2 。点P是y轴右侧的抛物线上一动点,过点P作 PE x ⊥轴于点E,交CD于点F. (1)求抛物线的解析式; (2)若点P的横坐标为m,当m为何值时,以,,, O C P F为顶点的四边形是平行四边形?请说明理由。 【解答】(1)∵直线 1 2 2 y x =+经过点C,∴(0,2) C ∵抛物线2 y x bx c =-++经过点(0,2) C,D 7 (3,) 2 ∴22727 332 2c b b c c =?? =? ?∴??=-++??=?? ∴抛物线的解析式为2 7 22 y x x =-++ (2)∵点P 的横坐标为m 且在抛物线上 ∴2 71 (,2),(,2)22 P m m m F m m -+ ++ ∵PF ∥CO ,∴当PF CO =时,以,,,O C P F 为顶点的四边形是平行四边形 ① 当03m <<时,2 271 2(2)322 PF m m m m m =-+ +-+=-+ ∴2 32m m -+=,解得:121,2m m == 即当1m =或2时,四边形OCPF 是平行四边形 ② 当3m ≥时,2 217 (2)(2)32 2 PF m m m m m =+--+ +=- 232m m -= ,解得:123322 m m += =(舍去) 即当132 m += 时,四边形OCFP 是平行四边形 练习1:(2013?盘锦)如图,抛物线y=ax 2+bx+3与x 轴相交于点A (﹣1,0)、B (3,0), 与y 轴相交于点C ,点P 为线段OB 上的动点(不与O 、B 重合),过点P 垂直于x 轴的直线与抛物线及线段BC 分别交于点E 、F ,点D 在y 轴正半轴上,OD=2,连接DE 、OF . (1)求抛物线的解析式; (2)当四边形ODEF 是平行四边形时,求点P 的坐标; 二次函数(平行四边形) 1.如图,在平面直角坐标系xOy中,抛物线y=(x﹣m)2﹣m2+m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.(1)当m=2时,求点B的坐标; (2)求DE的长? (3)①设点D的坐标为(x,y),求y关于x的函数关系式?②过点D作AB的平行线,与第(3)①题确定的函数图象的另一个交点为P,当m为何值时,以,A,B,D,P为顶点的四边形是平行四边形? 解答:解:(1)当m=2时,y=(x﹣2)2+1, 把x=0代入y=(x﹣2)2+1,得:y=2, ∴点B的坐标为(0,2). (2)延长EA,交y轴于点F, ∵AD=AC,∠AFC=∠AED=90°,∠CAF=∠DAE, ∴△AFC≌△AED, ∴AF=AE, ∵点A(m,﹣m2+m),点B(0,m), ∴AF=AE=|m|,BF=m﹣(﹣m2+m)=m2, ∵∠ABF=90°﹣∠BAF=∠DAE,∠AFB=∠DEA=90°, ∴△ABF∽△DAE, ∴=,即:=, ∴DE=4. (3)①∵点A的坐标为(m,﹣m2+m), ∴点D的坐标为(2m,﹣m2+m+4), ∴x=2m,y=﹣m2+m+4, ∴y=﹣?++4, ∴所求函数的解析式为:y=﹣x2+x+4, ②作PQ⊥DE于点Q,则△DPQ≌△BAF, (Ⅰ)当四边形ABDP为平行四边形时(如图1), 点P的横坐标为3m, 点P的纵坐标为:(﹣m2+m+4)﹣(m2)=﹣m2+m+4, 把P(3m,﹣m2+m+4)的坐标代入y=﹣x2+x+4得: ﹣m2+m+4=﹣×(3m)2+×(3m)+4, 解得:m=0(此时A,B,D,P在同一直线上,舍去)或m=8.(Ⅱ)当四边形ABDP为平行四边形时(如图2), 点P的横坐标为m, 点P的纵坐标为:(﹣m2+m+4)+(m2)=m+4, 把P(m,m+4)的坐标代入y=﹣x2+x+4得: m+4=﹣m2+m+4, 解得:m=0(此时A,B,D,P在同一直线上,舍去)或m=﹣8,综上所述:m的值为8或﹣8. 中考:四边形精华试题附参考答案 一、选择题 1.(深圳市龙城中学下学期质量检测数学试题)下列命题,真命题是 ( ) A. 两条直线被第三条直线所截,同位角相等 B. 两组对角分别相等的四边形是平行四边形 C. 在同一个圆中,相等的弦所对的弧相等 D. 对角线相等的四边形是矩形 答案:B 2.(深圳市龙城中学下学期质量检测数学试题)如图2,M 是ABCD 的AB 边中点,CM 交BD 于点E , 则图中阴影部分的 面积ABCD 的面积的比是 ( ) A. 1:3 B.1:4 C. 1:6 D.5:12 答案:A 3.(嘉兴市秀洲区模拟)把矩形ABCD 沿EF 对折后使两部分叠合,如图所示.若115AEF ∠=?, 则∠1= ( ) A.50° B.55° C.60° D.65° 答案 A 4.(2010学年度武汉市九年级复习备考数学测试试卷16)如图, 直角梯形ABCD 中,AB ⊥CD ,AE ∥CD 交BC 于E ,O 是AC 的中点,3=AB ,2=AD ,3=BC ,下列结论:①∠CAE=30°;②四边形ADCE 是菱形;③ABE ADC S S ??=2;④OB ⊥CD.其中正确的结论是( ) A .①②④ B. ②③④ C .①③④ D .①②③④ 答:D 5.(2010年武汉市中考模拟数学试题(26))已知如图,在ABCD 中,E 、F 分别为边AB 、CD 的中点BD 是对角线,AG ∥DB ,交CB 的延长线于G ,连接GF ,若AD ⊥BD.下列结论:①DE ∥BF ;②四边形BEDF 是菱形;③FG ⊥AB ;④S △BFG= 其中正确的是( ) A. ①②③④ B. ①② C. ①③ D. ①②④ G F E D C B A 答:D 6.(2010年武汉市中考模拟数学试题(27))如图,ABCD 、CEFG 是正方形,E 在CD 上,直 A B E O D C 第4题图 (第3题图) 1 A B D C E F 14 ABCD S 备战2020年中考数学压轴题之二次函数 专题06 二次函数背景下的特殊四边形存在性判定 【方法综述】 知识准备:特殊四边形包括平行四边形、菱形、矩形和正方形。它们的判定方法如下:平行四边形的判定方法: 两组对边分别平行的四边形是平行四边形;两组对角分别相等的四边形是平行四边形 两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形 两条对角线互相平分的四边形是平行四边形; 矩形判的定方法 有一个角是直角的平行四边形是矩形;对角线相等的平行四边形是矩形 有三个角是直角的四边形是矩形 菱形判定方法 有一组邻边相等的平行四边形是菱形;对角线互相垂直的平行四边形是菱形 四条边相等的四边形是矩形 正方形的判定方法 平行四边形+矩形的特性;平行四边形+菱形的特性 解答时常用的技巧: (1).根据平行四边形的对角线互相平分这条性质,应用中点坐标公式,可以采用如下方法: 已知点A、B、C三点坐标已知,点P在某函数图像上,是否存在以点A、B、C、P为顶点的四边形为平行四边形,求点P的坐标。 如,当AP、BC为平行四边形对角线时,由中点坐标公式,可得 a+m=c+e,n+b=d+f 则m= c+e-a;n= d+f-b,点P坐标可知,将其带入到函数关系式进行验证,如果满足函数关系式,即为所求P点,同理,根据分类讨论可以得到其它情况的解答方法。 (2).菱形在折叠的情况下,可以看成是等腰三角形以底边所在直线折叠所得,因此,菱形的存在性讨论,亦可以看做等腰三角形的存在性讨论。 (3).矩形中的直角证明出来常规直角的探究外,还有主要是否由隐形圆的直径所对圆周角得到。 【典例示范】 类型一平行四边形的存在性探究 例1:如图,在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点. (1)求抛物线的解析式; (2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S,求S关于m的函数关系式,并求出S的最大值; (3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能使以点P,Q,B,O为顶点的四边形为平行四边形(要求PQ∥OB),直接写出相应的点Q的坐标. 【答案】(1)y=1 2 x2+x-4;(2)当m=-2时,S有最大值,S最大=4;(3)满足题意的Q点的坐标有三 个,分别是(-2+2-,(-2-2+,(-4,4). 【思路引导】 (1)已知抛物线与x轴的两个交点的横坐标,一般选用两点式,利用待定系数法求解即可; 72 x = B(0,4) A(6,0) E F x y O 二次函数与四边形综合压轴题专题汇编 一.二次函数与四边形的形状 例1.(浙江义乌市) 如图,抛物线223y x x =--与x 轴交A 、B 两点(A 点在B 点左侧),直线l 与抛物线交于A 、C 两点,其中C 点的横坐标为2. (1)求A 、B 两点的坐标及直线AC 的函数表达式; (2)P 是线段AC 上的一个动点,过P 点作y 轴的平 行线交抛物线于E 点,求线段PE 长度的最大值; (3)点G 是抛物线上的动点,在x 轴上是否存在点F ,使A 、C 、F 、G 这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F 点坐标;如果不存在,请说明理由. 练习1.(河南省实验区) 23.如图,对称轴为直线7 2 x = 的抛物线经过点 A (6,0)和 B (0,4). (1)求抛物线解析式及顶点坐标; (2)设点E (x ,y )是抛物线上一动点,且位于第四象限,四边形OEAF 是以OA 为对角线的平行四边形.求平行四边形OEAF 的面积S 与x 之间的函数关系式,并写出自变量x 的取值范围; ①当平行四边形OEAF 的面积为24时,请判断平行四边形OEAF 是否为菱形? ②是否存在点E ,使平行四边形OEAF 为正方形?若存在,求出点E 的坐标;若不存在,请说明理由. A 练习 2.(四川省德阳市)25.如图,已知与x 轴交于点(10)A ,和(50)B ,的抛物线1l 的顶点为 (34)C ,,抛物线2l 与1l 关于x 轴对称,顶点为C '. (1)求抛物线2l 的函数关系式; (2)已知原点O ,定点(04)D ,,2l 上的点P 与1l 上的点P '始终关于x 轴对称,则当点P 运动到何处时,以点D O P P ',,,为顶点的四边形是平行四边形? (3)在2l 上是否存在点M ,使ABM △是以AB 为斜边且一个角为30 的直角三角形?若存, 求出点M 的坐标;若不存在,说明理由. 练习3.(山西卷)如图,已知抛物线1C 与坐标轴的交点依次是(40)A -, ,(20)B -,,(08)E ,. (1)求抛物线1 C 关于原点对称的抛物线2C 的解析式; (2)设抛物线1C 的顶点为M ,抛物线2C 与x 轴分别交于 C D ,两点(点C 在点D 的左侧),顶点为N ,四边形MDNA 的 面积为S .若点A ,点D 同时以每秒1个单位的速度沿水平方向分别向右、向左运动;与此同时,点M ,点N 同时以每秒2个单位的速度沿坚直方向分别向下、向上运动,直到点A 与点D 重合为止.求出四边形MDNA 的面积S 与运动时间t 之间的关系式,并写 出自变量t 的取值范围; (3)当t 为何值时,四边形MDNA 的面积S 有最大值,并求出此最大值; (4)在运动过程中,四边形MDNA 能否形成矩形?若能,求出此时t 的值;若不能,请说明理由. 5- 4- 3- 2- 1- 1 2 3 4 5 5 4 3 2 1 A E B C ' 1- O 2l 1l x y 一、平行四边形真题与模拟题分类汇编(难题易错题) 1.如图,在正方形ABCD中,E是边BC上的一动点(不与点B、C重合),连接DE、点C 关于直线DE的对称点为C′,连接AC′并延长交直线DE于点P,F是AC′的中点,连接DF.(1)求∠FDP的度数; (2)连接BP,请用等式表示AP、BP、DP三条线段之间的数量关系,并证明; (3)连接AC,若正方形的边长为2,请直接写出△ACC′的面积最大值. 【答案】(1)45°;(2)BP+DP2AP,证明详见解析;(32﹣1. 【解析】 【分析】 (1)证明∠CDE=∠C'DE和∠ADF=∠C'DF,可得∠FDP'=1 2 ∠ADC=45°; (2)作辅助线,构建全等三角形,证明△BAP≌△DAP'(SAS),得BP=DP',从而得△PAP'是等腰直角三角形,可得结论; (3)先作高线C'G,确定△ACC′的面积中底边AC为定值2,根据高的大小确定面积的大小,当C'在BD上时,C'G最大,其△ACC′的面积最大,并求此时的面积. 【详解】 (1)由对称得:CD=C'D,∠CDE=∠C'DE, 在正方形ABCD中,AD=CD,∠ADC=90°, ∴AD=C'D, ∵F是AC'的中点, ∴DF⊥AC',∠ADF=∠C'DF, ∴∠FDP=∠FDC'+∠EDC'=1 2 ∠ADC=45°; (2)结论:BP+DP2AP, 理由是:如图,作AP'⊥AP交PD的延长线于P', ∴∠PAP'=90°, 在正方形ABCD中,DA=BA,∠BAD=90°,∴∠DAP'=∠BAP, 由(1)可知:∠FDP=45° ∵∠DFP=90° ∴∠APD=45°, ∴∠P'=45°, ∴AP=AP', 在△BAP和△DAP'中, ∵ BA DA BAP DAP AP AP ' = ? ? ∠=∠ ? =' ? ? , ∴△BAP≌△DAP'(SAS),∴BP=DP', ∴DP+BP=PP'=2AP; (3)如图,过C'作C'G⊥AC于G,则S△AC'C=1 2 AC?C'G, Rt△ABC中,AB=BC2, ∴AC22 (2)(2)2 +=,即AC为定值, 当C'G最大值,△AC'C的面积最大, 连接BD,交AC于O,当C'在BD上时,C'G最大,此时G与O重合, 【例1】 已知:如图,在平面直角坐标系xOy 中,直线3 64 y x =-+与x 轴、y 轴的交点分 别为A B 、, 将OBA ∠对折,使点O 的对应点H 落在直线AB 上,折痕交x 轴于点.C (1)直接写出点C 的坐标,并求过A B C 、、三点的抛物线的解析式; (2)若抛物线的顶点为D ,在直线BC 上是否存在点P ,使得四边形ODAP 为平行四边形?若存在,求出点P 的坐标;若不存在,说明理由; (3)设抛物线的对称轴与直线BC 的交点为T Q , 为线段BT 上一点,直接写出QA QO -的取值范围. 【例2】 如图,点O 是坐标原点,点(0)A n ,是x 轴上一动点(0)n <.以AO 为一边作矩形AOBC ,点C 在第二象限,且2OB OA =.矩形AOBC 绕点A 逆时针旋转90?得矩形AGDE .过点A 的直线y kx m =+(0)k ≠交y 轴于点F ,FB FA =.抛物线2y ax bx c =++过点E 、F 、G 且和直线AF 交于点H ,过点H 作HM x ⊥轴,垂足为点M . ⑴ 求k 的值; ⑵ 点A 位置改变时,AMH ?的面积和矩形AOBC 的面积的比值是否改变?说明你的理由. 【例3】 如图1,Rt ABC ?中,90A ∠=?,3 tan 4 B = ,点P 在线段AB 上运动,点Q 、R 分别在线段BC 、AC 上,且使得四边形APQR 是矩形.设AP 的长为x ,矩形APQR 的面积为y ,已知y 是x 的函数,其图 象是过点()1236,的抛物线的一部分(如图2所示). (1)求AB 的长; (2)当AP 为何值时,矩形APQR 的面积最大,并求出最大值. R Q B C A 二次函数与平行四边形综合 二次函数平行四边形存在性问题例题 一.解答题(共9小题) 1.如图,抛物线经过A(﹣1,0),B(5,0),C(0,)三点. (1)求抛物线的解析式; (2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标; (3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由. 2.如图,在平面直角坐标系中,直线y=﹣3x﹣3与x轴交于点A,与y轴交于点C.抛物线y=x2+bx+c经过A,C两点,且与x轴交于另一点B(点B在点A右侧). (1)求抛物线的解析式及点B坐标; (2)若点M是线段BC上一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值; (3)试探究当ME取最大值时,在x轴下方抛物线上是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由. 3.已知:如图,在平面直角坐标系xOy中,直线与x轴、y轴的交点 分别为A、B两点,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x 轴于点C. (1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式; (2)若(1)中抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP 为平行四边形?若存在,求出点P的坐标;若不存在,说明理由; (3)若把(1)中的抛物线向左平移3.5个单位,则图象与x轴交于F、N(点F 在点N的左侧)两点,交y轴于E点,则在此抛物线的对称轴上是否存在一点Q,使点Q到E、N两点的距离之差最大?若存在,请求出点Q的坐标;若不存在,请说明理由. 4.已知:如图,在平面直角坐标系xOy中,直线与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C. (1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式; (2)若抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四边形?若存在,求出点P的坐标;若不存在,说明理由; (3)设抛物线的对称轴与直线BC的交点为T,Q为线段BT上一点,直接写出|QA ﹣QO|的取值范围. 5.如图,Rt△OAB如图所示放置在平面直角坐标系中,直角边OA与x轴重合, 第一讲:矩形、菱形训练学习(1)—2014年中考数学四边形专题 一、矩形的学习 例题1(2013浙江省绍兴,15,5分)如图,在矩形ABCD中,点E,F分别在BC,CD上,将△ABE沿AE 折叠,使点B落在AC上的点B`处,又将△CEF沿EF折叠, 使点C落在直线EB`与AD的交点C`处.则BC∶AB的值为. 例题2.(2013安徽,14,5分)如图,P是矩形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论: ①S1+S2=S3+S4②S2+S4= S1+ S3 ③若S3=2 S1,则S4=2 S2④若S1= S2,则P点在矩形的对角线上 其中正确的结论的序号是_________________(把所有正确结论的序号都填在横线上). 相应练习一 1.(2013年吉林省,第22题、7分.)如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC. (1)求证:△ADC △ECD; (2)若BD=CD,求证四边形ADCE是矩形. 2.(2013贵州六盘水,22,12分)如图11,已知E 是ABCD 中BC 边的中点,连接AE 并延长AE 交DC 的延长线于点F . (1)求证:△ABE ≌△FCE . (2)连接AC 、BF ,若∠AEC =2∠ABC ,求证:四边形ABFC 为矩形. 3.(2013湖南湘潭,19,6分)如图,矩形ABCD 是供一辆机动车停放的车位示意图,已知m BC 2=, m CD 4.5=,?=∠30DCF ,请你计算车位所占的宽度EF 约为多少米? 二、菱 形 的 学 习 例题3(2013深圳市 20 ,8分)如图7,将矩形ABCD 沿直线EF 折叠,使点C 与点A 重合,折痕交AD 于点E ,交BC 于点F ,连接AF 、CE , (1)求证:四边形AFCE 为菱形; (2)设,,,AE a ED b DC c ===请写出一个a 、b 、c 三者之间的数量关系式 'A 二次函数与特殊四边形判定 ★1.在平面直角坐标系xOy 中,抛物线W 的表达式为y =14x 2-x , D 是抛物线W 的顶点. (1)将抛物线W 向右平移4个单位,再向下平移32个单位,得到抛物线 W ′,求抛物线W ′的表达式及其顶点F 的坐标; (2)若点M 是x 轴上的一点,点N 是抛物线W ′上的一点,则是否存在这样的点M 和点N ,使得以D 、F 、M 、N 为顶点的四边形是平行四边形?若存在,求出点M 的坐标;若不存在,请说明理由. ★2.已知二次函数y=ax2+bx+c(a≠0)的图象过点A(-1,0)、B(0,1),且与x轴有唯一交点. (1)求二次函数y=ax2+bx+c(a≠0)的表达式; (2)若将(1)中的抛物线沿y轴向下平移m个单位后与x轴的两个交点分别为C、D(点C在点D的左边),当∠CBD=90°时,求m的值; (3)在(2)中平移后的抛物线上是否存在一点E,使以C、D、B、E为顶点的四边形是矩形?若存在,请求出点E的坐标;若不存在,请说明理由. ★3.已知抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,顶点M关于x轴的对称点是M′. (1)求抛物线的表达式; (2)若直线AM′与此抛物线的另一个交点为C,求△CAB的面积; (3)是否存在抛物线y=ax2+bx+c(a≠0)的图象过点在过A(-1,0),B(3,0)两点,其顶点P关于x轴的对称点为Q,使得四边形APBQ 为正方形?若存在,求出此抛物线的表达式;若不存在,请说明理由. ★4.如图,在平面直角坐标系中,已知△ABE的边AB在x轴上,A(-1,0),OB=4OA,OE=2,抛物线C经过△ABE的三个顶点. (1)求抛物线C的表达式; (2)将抛物线C向下平移m个单位得到抛物线C′,使抛物线C′与直线BE有且只有一个公共点M,试求点M的坐标及m的值; (3)若点P是抛物线C′上一点,Q是y轴上一点,是否存在这样的点P,使得以点A、P、Q、M为顶点的四边形为平行四边形,若存在,请求出点P的坐标;若不存在,请说明理由. 第4题图 中考数学四边形选择题 (08黑龙江哈尔滨)10.如图,将边长为8cm 的正方形纸片ABCD 折叠,使点D 落在BC 边中 点E 处,点A 落在点F 处,折痕为MN ,则线段CN 的长是( A ). (A )3cm (B )4cm (C )5cm (D )6cm (08辽宁沈阳)8.如图所示,正方形ABCD 中,点E 是CD 边上一点,连接AE , 交对角线BD 于点F ,连接CF ,则图中全等三角形共有( C ) A .1对 B .2对 C .3对 D .4对 (08辽宁十二市)5.下列命题中正确的是( A ) A .两条对角线互相平分的四边形是平行四边形 B .两条对角线相等的四边形是矩形 C .两条对角线互相垂直的四边形是菱形 D .两条对角线互相垂直且平分的四边形是正方形 (08山东滨州)10、如图,在矩形ABCD 中,动点P 从点B 出发,沿BC 、CD 、DA 运动至点A 停止,设点P 运动的路程为x ,△ABP 的面积为y ,如果y 关于x 的函数图象如图2所 示,则△ABC 的面积是( A ) 9 4x y O P D A 、10 B 、16 C 、18 D 、20 (08山东济宁)4.若梯形的面积为2 8cm ,高为2cm ,则此梯形的中位线长是( B ) A .2cm B .4cm C .6cm D .8cm (08山东聊城)9.把一张正方形纸片按如图所示的方法对折两次后剪去两个角,那么打开以后的形状是( C ) A .六边形 B .八边形 C .十二边形 D .十六边形 A D C E F B 第8题图 第9题图 (08山东临沂)11.如图,菱形ABCD 中,∠B =60°,AB =2,E 、F 分别是BC 、CD 的中点,连接AE 、EF 、AF ,则△AEF 的周长为( B ) A . 32 B . 33 C . 34 D . 3 (08山东泰安)4.如图,下列条件之一能使 ABCD 是菱形的为( A ) ①AC BD ⊥ ②90BAD ∠= ③AB BC = ④AC BD = A .①③ B .②③ C .③④ D .①②③ (08山东威海)10.将矩形纸片ABCD 按如图所示的方式折叠,得到菱形AECF .若AB =3,则BC 的长为 D A .1 B .2 C .2 D .3 (08山东潍坊)3.如图,梯形ABCD 中,AD BC ∥,AD AB =,BC BD =,100A =∠,则C =∠( ) A .80 B .70 C .75 D .60 (08山东潍坊)11.在平行四边形ABCD 中,点1A ,2A ,3A ,4A 和1C ,2C ,3C ,4C 分别是AB 和CD 的五等分点,点1B ,2B 和1D ,2D 分别是BC 和DA 的三等分点,已知四边形4242A B C D 的面积为1,则平行四边形ABCD 的面积为( ) A .2 B .3 5 C . 53 D .15 (08年江苏常州)顺次连接菱形各边中点所得的四边形一定是( B ) A.等腰梯形 B.正方形 C.平行四边形 D.矩形 (08年江苏连云港)7.已知AC 为矩形ABCD 的对角线,则图中1∠与2∠一定不相等的是( D ) A . B . C . D . (08年江苏南京)6.如图,将一张等腰梯形纸片沿中位线剪开,拼成一个新的图形, 这个新的图形可以是下列图形中的( B ) A .三角形 B .平行四边形 C .矩形 D .正方形 A B C D (第4题) A E A B D A B 1 2 3 4 B A C 1 2 B A D C B A C 1 2 D 1 2 B A D C (第6题) 《二次函数专题提优》:特殊四边形存在性问题 (一)、平行四边形存在性原理: 1、实验与探究: (1)、在图1,2,3中,给出平行四边形ABCD的顶点A B D ,,的坐标(如图所示),写出图1,2,3中的顶点C的坐标,它们分别是(52) , ,,; ( 2)、在图4 中,给出平行四边形ABCD 的顶点A B D ,,的坐标(如图所示),求出顶点C的坐标(C点坐标用含 a b c d e f ,,,,,的代数式表示); 归纳与发现: (3)、通过对图1,2,3,4的观察和顶点C的坐标的探究,你会发现:无论平行四边形ABCD处于直角坐标系中哪个位置,当其顶点坐标为 ()()()() A a b B c d C m n D e f ,,,,,,,(如图4)时,则四个顶点的横坐标a c m e ,,,之间的等量关系为;纵坐标b d n f ,,,之间的等量关系为(不必证明); 运用与推广: (4)、在同一直角坐标系中有抛物线 2(53) y x c x c =---和三个点 1519 2222 G c c S c c ???? - ? ? ???? ,,, , (20) H c,(其 中0 c>).问当c为何值时,该抛物线上存在点P,使得以G S H P ,,,为顶点的四边形是平行四边形? 并求出所有符合条件的P点坐标. 图1图2图3 图4 (二)、平行四边形的存在性问题: 2、在平面直角坐标系xOy 中,已知抛物线 c bx ax y + + =2的对称轴是x=1,并且经过(?2,?5)和(5,?12)两点。 (1)、求此抛物线的解析式; (2)、设此抛物线与x轴交于A. B 两点(点A 在点B的左侧),与y轴交于C 点,D是线段BC上一点(不与点B. C 重合),若以B. O、D为顶点的三角形与△BAC相似,求点D的坐标; (3)、点P在y轴上,点M在此抛物线上,若要使以点P、M、A. B为顶点的四边形是平行四边形, 请你直接写出点M的坐标 3、如图,抛物线y=ax2+bx+c交x轴于点A(-3,0),点B(1,0),交y轴于点E(0,-3),点C是点A关于点B 的对称点,点F是线段BC的中点,直线l过点F且与y轴平行,直线y=-x+m过点C,交y轴于点D. (1)、求抛物线的函数表达式; (2)、点K为线段AB上一动点,过点K作x轴的垂线与直线CD交于点H,与抛物线交于点G,求线段HG长度的最大值; (3)、在直线l上取点M,在抛物线上取点N,使以点A,C,M,N为顶点的四边形是平行四边形,求点N的坐标. A x B C D H E F G K O x y l A B C D H E F G K O y l 备用图 图① ●探究 (1)在图1中,已知线段AB,CD,其中点分别为E,F。 ①若A(-1,0),B(3,0),则E点坐标为__________; ②若C(-2,2),D(-2,-1),则F点坐标为__________; (2)在图2中,已知线段AB的端点坐标为A(a,b),B(c,d),求出图中AB中点D的坐标(用含a,b,c,d的代数式表示),并给出求解过程; ●归纳 无论线段AB处于直角坐标系中的哪个位置, 当其端点坐标为A(a,b),B(c,d),AB中点为D(x,y)时,x=_________,y=___________;(不必证明) ●运用 在图2中,一次函数y=x-2与反比例函数的图象交点为A,B。 ①求出交点A,B的坐标; ②若以A,O,B,P为顶点的四边形是平行四边形,请利用上面的结论求出顶点P的坐标。 图 2 图 3 图1 以二次函数为载体的平行四边形存在性问题是近年来中考的热点,其图形复杂,知识覆盖面广,综合性较强,对学生分析问题和解决问题的能力要求高.对这类题,常规解法是先画出平行四边形,再依据“平行四边形的一组对边平行且相等”或“平行四边形的对角线互相平分”来解决.由于先要画出草图,若考虑不周,很容易漏解.为此,笔者另辟蹊径,借助探究平行四边形顶点坐标公式来解决这一类题. 1 两个结论,解题的切入点 数学课标,现行初中数学教材中没有线段的中点坐标公式,也没有平行四边形的顶点坐标公式,我们可帮助学生来探究,这可作为解题的切入点。 1.1 线段中点坐标公式 平面直角坐标系中,点A 坐标为(x 1,y 1),点B 坐标为(x 2,y 2),则线段AB 的中点坐标为(221x x +,2 21y y +). 证明 : 如图1,设AB 中点P 的坐标为(x P ,y P ).由x P -x 1=x 2-x P ,得x P = 2 21x x +,同理y P =221y y +,所以线段AB 的中点坐标为(221x x +,221y y +). 1.2 平行四边形顶点坐标公式 □ABCD 的顶点坐标分别为A (x A ,y A )、B (x B ,y B )、C (x C ,y C )、D (x D ,y D ),则:x A +x C =x B +x D ;y A +y C =y B +y D . 证明: 如图2,连接AC 、BD ,相交于点E . ∵点E 为AC 的中点, ∴E 点坐标为(2C A x x +,2 C A y y +). 又∵点E 为B D 的中点, ∴ E 点坐标为( 2D B x x +,2D B y y +). ∴x A +x C =x B +x D ;y A +y C =y B +y D . 即平行四边形对角线两端点的横坐标、纵坐标之和分别相等. 2 一个基本事实,解题的预备知识 如图3,已知不在同一直线上的三点A 、B 、C ,在平面内另找一个点D ,使以A 、B 、C 、D 为顶点的四边形是平行四边形.答案有三种:以AB 为对角线的□ACBD 1,以AC 为对角线的□ABCD 2,以BC 为对角线的□ABD 3C . 2021模拟年中考数学复习专题练:《四边形综合》 1.如图①所示,已知正方形ABCD和正方形AEFG,连接DG,BE. (1)发现:当正方形AEFG绕点A旋转,如图②所示. ①线段DG与BE之间的数量关系是; ②直线DG与直线BE之间的位置关系是; (2)探究:如图③所示,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE时,上述结论是否成立,并说明理由. (3)应用:在(2)的情况下,连接BG、DE,若AE=1,AB=2,求BG2+DE2的值(直接写出结果). 2.如图1,在正方形ABCD中,点E是CD上一点(不与C,D两点重合),连接BE,过点C作CH⊥BE于点F,交对角线BD于点G,交AD边于点H,连接GE, (1)求证:△DHC≌△CEB; (2)如图2,若点E是CD的中点,当BE=8时,求线段GH 的长; (3)设正方形ABCD的面积为S1,四边形DEGH的面积为S2,当的值为时,的值为. 3.在平面直角坐标系中,四边形AOBC是矩形,点O(0,0),点A(6,0),点B(0,8).以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,点O,B,C的对应点分别为D,E,F,记旋转角为α(0°<α<90°). (I)如图①,当α=30°时,求点D的坐标; (Ⅱ)如图②,当点E落在AC的延长线上时,求点D的坐标;(Ⅲ)当点D落在线段OC上时,求点E的坐标(直接写出结果即可). 4.如图,BD是平行四边形ABCD的对角线,DE⊥AB于点E,过点E的直线交BC于点G,且BG=CG. (1)求证:GD=EG. (2)若BD⊥EG垂足为O,BO=2,DO=4,画出图形并求出四边形ABCD的面积. (3)在(2)的条件下,以O为旋转中心顺时针旋转△GDO,得到△G′D'O,点G′落在BC上时,请直接写出G′E的长. 5.(1)【探索发现】 如图1,在正方形ABCD中,点M,N分别是边BC,CD上的点,∠MAN=45°,若将△DAN绕点A顺时针旋转90°到△BAG位置,可得△MAN≌△MAG,若△MCN的周长为8,则正方形ABCD的边长为. 第十八讲二次函数与平行四边形综合 一、教学内容 1.二次函数的表示 , 二次函数图像与性质; 2.平行四边形的性质和判定; 3.函数图像与平行四边形的综合应用,典型应用、图像题; 二、例题细看 【例 1】已知:如图,在平面直角坐标系 将OBA 对折,使点O的对应点xOy 中,直线 y 3 与 x 轴、y轴的交点分别为 A、B , x 6 4 H 落在直线 AB 上,折痕交x 轴于点C. ( 1)直接写出点 C 的坐标,并求过A、B、C 三点的抛物线的解析式; ( 2)若抛物线的顶点为 D ,在直线BC上是否存在点P ,使得四边形ODAP 为平行四边形?若存在,求出点P 的坐标;若不存在,说明理由; ( 3)设抛物线的对称轴与直线BC的交点为 T ,Q 为线段BT上一点,直接写出 QA QO 的取值范围 . 【考点分析】二次函数综合题 y B H 1 O1 C A x D T 【PEC分析】( 1)点 A 的坐标是纵坐标为 0,得横坐标为 8,所以点 A 的坐标为( 8, 0); 点B 的坐标是横坐标为 0,解得纵坐标为 6,所以点 B 的坐标为( 0, 6); 由题意得: BC是∠ ABO的角平分线,所以OC=CH, BH=OB=6 ∵AB=10,∴ AH=4,设 OC=x,则 AC=8-x 由勾股定理得: x=3 ∴点 C 的坐标为( 3, 0)将此三点代入二次函数一般式,列的方程组即可求得; ( 3)如图,由对称性可知QO=QH,|QA-QO|=|QA-QH| .当点 Q与点 B 重合时, Q、 H、 A 三点共线,|QA-QO|取得最大值4(即为 AH的长);设线段OA的垂直平分线与直线 BC的交点为 K,当点 Q与点 K 重合时, |QA-QO|取得最小值 0. 【跟踪练习】例 1.(浙江义乌市 ) 如图,抛物线y x22x 3与x轴交A、B两点(A点在B点左侧),直线 l 与抛物线交于A、C两点,其中C点的横坐标为2. ( 1)求 A 、 B 两点的坐标及直线AC 的函数表达式; ( 2)P 是线段 AC 上的一个动点,过 P 点作 y 轴的平行线交抛物线于 E 点,求线段 PE 长度的最大值; ( 3)点 G 是抛物线上的动点,在x 轴上是否存在点F,使 A 、C、 F、 G 这样的四个点为顶点的四边 形是平行四边形?如果存在,求出所有满足条件的 F 点坐标;如果不存在,请说明理由. A 【例 2】如图,点O是坐标原点,点A(n ,0) 是 x 轴上一动点(n 0) .以 AO 为一边作矩形AOBC ,点C在第二象限,且OB 2OA .矩形AOBC 绕点 A 逆时针旋转90 得矩形AGDE .过点 A 的直线 y kx m ( k 0) 交y轴于点F,FB FA .抛物线y ax 2bx c 过点E、F、G且和直线AF 交于点 H ,过点 H 作 HM x 轴,垂足为点M . ⑴求 k 的值; ⑵点 A 位置改变时,AMH 的面积和矩形AOBC的面积的比值是否改变?说明你的理由. y C B D G M F E A O x H 【 PEC分析】( 1 )由题意知O B=2OA=2n,在直角三角形AEO 中, OF=OB-BF=-2n-AF,因此可用勾股定理求出AF 的表达式,也就求出了FB 的长,由于 F 的坐标为( 0 , m )据此可求出m , n 的关系式,可用 n 替换掉一次函数中m 的值,然后将 A 点的坐标代入即可求出k 的值. ( 2 )思路同( 1)一样,先用n 表示出 E、 F、 G 的坐标,然后代入抛物线的解析式中,得出 a ,b , c 与n 的函数关系式,然后用n 表示出二次函数的解析式,进而可用n 表示出 H 点的坐标,然后求出△AMH 72 x = B(0,4) A(6,0) E F x y O 二次函数与四边形综合专题 一.二次函数与四边形的形状 例1. 如图,抛物线2 23y x x =--与x 轴交A 、B 两点(A 点在B 点左侧),直线l 与抛物线交于A 、C 两点,其中C 点的横坐标为2. (1)求A 、B 两点的坐标及直线AC 的函数表达式; (2)P 是线段AC 上的一个动点,过P 点作y 轴的平行线交抛物线于E 点,求线段PE 长度的最大值; (3)点G 是抛物线上的动点,在x 轴上是否存在点F ,使A 、C 、F 、G 这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F 点坐标;如果不存在,请说明理由. 解:(1)令y=0,解得11x =-或23x =∴A (-1,0)B (3,0);将C 点的横坐标x=2代入2 23y x x =-- 得y=-3,∴C (2,-3)∴直线AC 的函数解析式是y=-x-1 (2)设P 点的横坐标为x (-1≤x ≤2)则P 、E 的坐标分别为: P (x ,-x-1),E (2(,23)x x x -- ∵P 点在E 点的上方,PE=22(1)(23)2x x x x x -----=-++ ∴当12x =时,PE 的最大值=9 4 (3)存在4个这样的点F ,分别是1234(1,0),(3,0),(470),(47,0)F F F F -+-, 练习1.如图,对称轴为直线7 2 x = 的抛物线经过点A (6,0)和B (0,4). (1)求抛物线解析式及顶点坐标; (2)设点E (x ,y )是抛物线上一动点,且位于第四象限,四边形OEAF 是以OA 为对角线的平行四边形.求平行四边形OEAF 的面积S 与x 之间的函数关系式,并写出自变量x 的取值范围; ①当平行四边形OEAF 的面积为24时,请判断平行四边形OEAF 是否为菱形? ②是否存在点E ,使平行四边形OEAF 为正方形?若存在,求出点E 的坐标;若不存在,请说明理由. A 2020年中考数学试题分类 四边形 一、选择题 10.(2020广州)如图5,矩形ABCD 的对角线AC ,BD 交于点O ,6AB =,8BC =,过点O 作OE ⊥AC ,交AD 于点E ,过点E 作EF ⊥BD ,垂足为F ,则OE EF +的值为( * ). (A ) 485 (B )325 (C )24 5 (D ) 12 5 【答案】C 8.(2020陕西)如图,在?ABCD 中,AB =5,BC =8.E 是边BC 的中点,F 是?ABCD 内一点,且∠BFC =90°.连接AF 并延长,交CD 于点G .若EF ∥AB ,则DG 的长为( ) A . B . C .3 D .2 【解答】解:∵E 是边BC 的中点,且∠BFC =90°, ∴Rt △BCF 中,EF =BC =4, ∵EF ∥AB ,AB ∥CG ,E 是边BC 的中点, ∴F 是AG 的中点, ∴EF 是梯形ABCG 的中位线, ∴CG =2EF ﹣AB =3, 又∵CD =AB =5, ∴DG =5﹣3=2, 故选:D . 图5 O F E D C B A 5.(2020乐山)如图,在菱形ABCD 中,4AB =,120BAD ∠=?,O 是对角线BD 的中点,过点O 作OE CD ⊥ 于点E ,连结OA .则四边形AOED 的周长为( ) A. 9+ B. 9+ C. 7+ D. 8 【答案】B 【详解】∵四边形ABCD 是菱形,O 是对角线BD 的中点, ∵AO∵BD , AD=AB=4,AB∵DC ∵∵BAD=120o, ∵∵ABD=∵ADB=∵CDB=30o, ∵OE∵DC , ∵在RtΔAOD 中,AD=4 , AO=1 2 AD =2 ,= 在RtΔDEO 中,OE= 1 2 OD =,3=, ∵四边形AOED 的周长为 故选:B. 7.(2020贵阳)菱形的两条对角线长分别是6和8,则此菱形的周长是( ) A. 5 B. 20 C. 24 D. 32 【答案】B 【详解】解:如图所示,根据题意得AO =1842 ?=,BO =1 632?=, ∵四边形ABCD 是菱形, ∵AB =BC =CD =DA ,AC∵BD , ∵∵AOB 是直角三角形, ∵AB 5=, ∵此菱形的周长为:5×4=20. 故选:B .二次函数与特殊四边形综合问题专题训练(有答案)
二次函数中考平行四边形含答案
中考数学练习题:四边形专题
二次函数背景下的特殊四边形存在性判定(解析版)
二次函数与四边形综合压轴题专题汇编(含答案)
人教中考数学综合题专题复习【平行四边形】专题解析含详细答案
二次函数与平行四边形综合.
二次函数平行四边形存在性问题例题
2014年中考数学四边形专题复习:四边形的证明与计算 (2)
二次函数与四边形判定
全国中考数学四边形选择题(含答案)
《二次函数专题提优》 :特殊四边形存在性问题
(完整版)二次函数中平行四边形通用解决方法
2021年中考数学复习专题练:《四边形综合 》(含答案)
二次函数与平行四边形综合
中考数学二次函数与四边形综合专题汇总-共17页
2020年中考数学试题分类专题之 四边形