求三角形内一点到三个顶点距离之和的最小值求三角形内一点到三个顶点最短值

求三角形内一点到三个顶点距离之和的最小值求三角形内一点到三个顶点距离之和的最小值1、已知三角形ABC中，AC=3，BC=4，AB=5，P是三角形ABC内一点，求PA+PB+PC的最小值.解：由题意三角形ABC为直角三角形，以直角顶点C为原点，CB为x轴，CA为y轴建立坐标系（如图）则C（0，0）A（0，3）B（4，0）以B为旋转中心，将△BPC绕点B逆时钟旋转60°至△BP'C'，连接PP'、CC'、AC'则△BPP'，△BCC'均为等边三角形所以PB=PP'，PC=P'C'所以PA+PB+PC=AP+PP'+P'C'≥AC'而C'（2，-2√3）所以AC'=√[（0-2）²+（3+2√3）²]=√（25+12√3）.即PA+PB+PC的最小值等于AC'的长√（25+12√3）.2、已知三角形ABC中，AB=10，AC=17，BC=21，P 是三角形ABC内一点，求PA+PB+PC的最小值.解：过A作AD⊥BC于D，设BC=x，则CD=21-x由勾股定理得AD²=10²-x²=17²-(21-x）²，解得x=6，AD=8，DC=15以D为坐标原点，BC为x轴，DA为y轴建立坐标系（如图）则A（0，8）B（-6，0）C（15，0）以C为旋转中心，将△CPB绕点C逆时钟旋转60°至△CP'B'，连接PP'、BB'、AB'则△CPP'，△CBB'均为等边三角形所以PC=PP'，PB=P'B'所以PA+PB+PC=AP+PP'+P'B'≥AB'而B'（9/2，-21√3/2）所以AB'=√[（0-9/2）²+（8+21√3/2）²]=√（415+168√3）.即PA+PB+PC的最小值等于AB'的长√（415+168√3）.【补充说明】（1）如图，以△ABC的三边为边，分别向外作等边三角形BCD、ACE、ABF，连接AD、BE、CF，则（1）AD、BE、CF交于一点P，且∠APB=∠APC=∠BPC=120°，（2）P到A、B、C三顶点距离的和最小，且PA+PB+PC=AD=BE=CF。

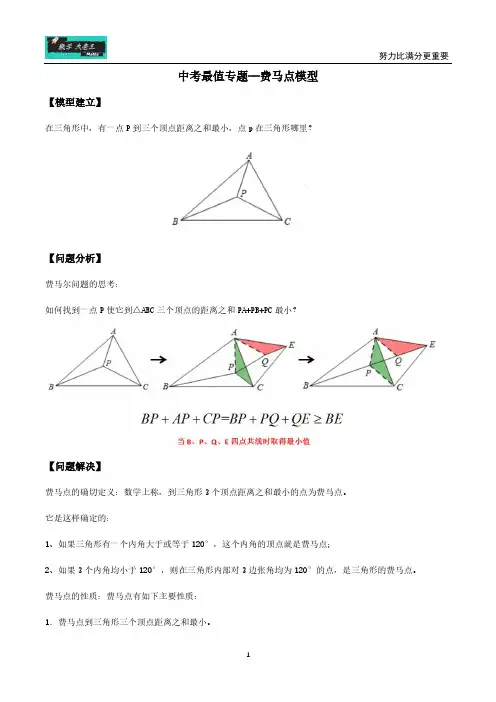
中考最值专题--费马点模型【模型建立】在三角形中，有一点P到三个顶点距离之和最小，点p在三角形哪里？【问题分析】费马尔问题的思考：如何找到一点P使它到△ABC三个顶点的距离之和PA+PB+PC最小？【问题解决】费马点的确切定义：数学上称，到三角形3个顶点距离之和最小的点为费马点。

它是这样确定的：1、如果三角形有一个内角大于或等于120°，这个内角的顶点就是费马点；2、如果3个内角均小于120°，则在三角形内部对3边张角均为120°的点，是三角形的费马点。

费马点的性质：费马点有如下主要性质：1．费马点到三角形三个顶点距离之和最小。

2．费马点连接三顶点所成的三夹角皆为120°。

【模型总结】费马点最小值快速求解：费尔马问题告诉我们，存在这么一个点到三个定点的距离的和最小，解决问题的方法是运用旋转变换. 秘诀：以△ABC任意一边为边向外作等边三角形，这条边所对两顶点的距离即为最小值。

费马点最值模型典例讲解例1. 如图，矩形ABCD是一个长为1000米，宽为600米的货场，A、D是入口，现拟在货场内建一个收费站P，在铁路线BC段上建一个发货站台H，设铺设公路AP、DP以及PH之长度和为l，求l的最小值．变式练习>>>1．如图，某货运场为一个矩形场地ABCD，其中AB＝500米，AD＝800米，顶点A，D为两个出口，现在想在货运广场内建一个货物堆放平台P，在BC边上（含B，C两点）开一个货物入口M，并修建三条专用车道PA，PD，PM．若修建每米专用车道的费用为10000元，当M，P建在何处时，修建专用车道的费用最少？最少费用为多少？（结果保留整数）【注】本题旋转△AEB、△BEC也都可以，但都必须绕着定点旋转！变式练习>>>2．若P为锐角△ABC的费马点，且∠ABC=60°，PA=3，PC=4, 求PB的值.例题3. 已知：△ABC是锐角三角形，G是三角形内一点。

三角形任意一点到三个顶点的距离在平面几何学中，三角形是一个非常重要的概念。

我们知道，三角形由三条边和三个顶点组成。

本文将探讨三角形中的一个问题，即任意一点到三个顶点的距离。

首先，我们来介绍一下三角形的基本概念。

三角形是由三条边连接而成的图形，在三角形中，每个顶点都与其他两个顶点通过一条边相连接。

三角形的三个顶点可以用大写字母A、B、C表示，相应的边则用小写字母a、b、c表示。

在三角形中，任意一点都可以与三个顶点构成三条线段，我们将分别计算这三条线段的长度，并称之为该点到三个顶点的距离。

以三角形ABC为例，我们假设任意一点为P，其到顶点A的距离为d1，到顶点B的距离为d2，到顶点C的距离为d3。

我们的目标是求出这三个距离的值。

为了计算这些距离，我们可以利用平面几何的相关知识。

根据勾股定理，我们知道，在直角三角形中，两条直角边的平方和等于斜边的平方。

因此，我们可以利用勾股定理来计算线段的长度。

以距离d1为例，我们可以将线段AP与线段AC看作直角三角形的两条直角边，线段AC为斜边。

根据勾股定理，可以得到以下等式：d1^2=AP^2+AC^2同理，我们可以得到以下等式：d2^2=BP^2+BC^2d3^2=CP^2+CA^2通过求解这三个等式，我们就可以得到d1、d2和d3的值。

在实际应用中，可以利用坐标几何的方法来计算这些距离。

首先，我们可以将三角形ABC的三个顶点坐标表示为A(x1,y1)、B(x2, y2)和C(x3,y3)。

假设任意一点P的坐标为P(x,y)。

根据坐标几何的知识，我们知道两点之间的距离可以使用勾股定理来计算。

因此，我们可以得到以下等式：d1=√[(x-x1)^2+(y-y1)^2]d2=√[(x-x2)^2+(y-y2)^2]d3=√[(x-x3)^2+(y-y3)^2]通过计算上述等式，我们就可以得到任意一点到三个顶点的距离。

在实际应用中，计算这些距离可以帮助我们解决一些几何问题。

三⾓形内有没有⼀个点到三边距离之和最⼩不论是不是内⼼, ⼀个点到三边的距离都是垂线段的长度, 相互之间不能直接⽐较.正确的结论是这样的:①若三⾓形不等腰,则平⾯上到三边距离和最⼩的点是最⼤内⾓的顶点.②若三⾓形等腰, ⽽底边⼤于腰,则到三边距离和最⼩的点是顶⾓的顶点.③若三⾓形等腰, ⽽底边⼩于腰,则底边上(内部和端点)任意⼀点到三边距离和相等, 并为平⾯上点到三边距离和的最⼩值.④若三⾓形等边,则三⾓形内任意⼀点到三边距离和相等, 并为平⾯上点到三边距离和的最⼩值.证明不难, 关键是如下特殊情况.借⽤下⾯的图, P是△AMN的⼀边MN所在直线上任意⼀点.PE, PF分别为到另两边的垂线段. 设AM ≥ AN, NK MJ分别是AM, AN边上的⾼.则有如下结论:1) MJ ≥ NK.2) 当P不在线段MN上, 有PE+PF > NK.3) 若AM = AN, 且P在线段MN上, 有PE+PF = NK.4) 若AM > AN, P在线段MN上且不与N重合, 则PE+PF > NK.证明:1) ∵AN·MJ/2 = S△AMN = AM·NK/2, ∴AN·MJ = AM·NK.⼜∵AM ≥ AN, ∴MJ ≥ NK.2) 若P在M左侧, 则PE+PF ≥ PE > MJ ≥ NK. 若P在N的右侧, 则PE+PF ≥ PF > NK. 因此PE+PF > NK对直线MN上不在线段MN 上的P点均成⽴.3) ∵S△AMP = AM·PF/2, S△ANP = AN·PE/2,∴S△AMN = S△AMP+S△AMP = (AM·PF+AN·PE)/2.⼜∵S△AMN = AM·NK/2, ∴AM·NK = AM·PF+AN·PE (*).∵AM = AN, ∴NK = PF+PE.4) 接上⾯(*)式.∵AM > AN, PE > 0,∴AM·NK = AM·PF+AN·PE < AM·PF+AM·PE = AM·(PE+PF),∴NK < PE+PF.向左转|向右转回到⼀般情况.如图, 设P是△ABC所在平⾯上任意⼀点, PD, PE, PF分别为其到三边的垂线段.过P作BC的平⾏线, 交AB, AC于M, N.不妨设AB ≥ AC, 则有AM ≥ AN. 设NK, NL为N到AB, BC的垂线段.∵MN // BC, ∴PD = NL.⽽上⾯的特殊情况已证PE+PF ≥ NK, ∴PD+PE+PF ≥ NL+NK.即P到三边距离和不⼩于N到三边距离和.这样就完成了第⼀步放缩, 将平⾯上的点变到⼀条边所在的直线上.再对N使⽤上⾯的特殊情况(N在直线AC上运动),可知AB ≥ BC时, N到三边的距离和不⼩于C到三边的距离和 (由AB ≥ AC, 此时AB为最⼤边). ⽽BC ≥ AB, N到三边的距离和不⼩于A到三边的距离和, (由AB ≥ AC, 此时BC为最⼤边).总结起来, N到三边的距离和不⼩于最⼤内⾓的顶点到三边的距离和.这样就完成了第⼆步放缩, 将直线上的点变到⼀点.因此平⾯上到△ABC三边距离和的最⼩值⼀定在其最⼤内⾓的顶点取得.⽽当△ABC有两边或三边相等, 上述放缩过程中的部分"≥"能成⽴等号.此时可能有更多的点取得最⼩值.具体来说, 当三⾓形等腰, 且底边⼩于腰, 最⼤内⾓是底⾓.底边上的点到三边(另两边)的距离和为定值, 即都等于最⼩值.但对底边之外的点, 第⼀步放缩的不等号是严格的, 因此不能取得最⼩值.当三⾓形等边, 两步放缩都能取得等号(对三⾓形内的点).因此最⼩值在三⾓形内的任意点处取得(其实也可以直接⽤△APB, △BPC, △CPA的⾯积证明).⾄此结论证毕.如果⾮要说内⼼到三边距离的极值性质, 那就是"到三边距离的最⼤值最⼩".这个其实很显然, ⽽且意义不⼤, 所以就不写了.。

求三角形内一点到三个顶点距离之和的最小值1、已知三角形ABC中，AC=3，BC=4，AB=5，P是三角形ABC内一点，求PA+PB+PC的最小值.解：由题意三角形ABC为直角三角形，以直角顶点C为原点，CB为x轴，CA为y轴建立坐标系（如图）则C（0，0）A（0，3）B（4，0）以B为旋转中心，将△BPC绕点B逆时钟旋转60°至△BP'C'，连接PP'、CC'、AC'则△BPP'，△BCC'均为等边三角形所以PB=PP'，PC=P'C'所以PA+PB+PC=AP+PP'+P'C'≥AC'而C'（2，-2√3）所以AC'=√[（0-2）²+（3+2√3）²]=√（25+12√3）. 即PA+PB+PC的最小值等于AC'的长√（25+12√3）.2、已知三角形ABC中，AB=10，AC=17，BC=21，P 是三角形ABC内一点，求PA+PB+PC的最小值.解：过A作AD⊥BC于D，设BC=x，则CD=21-x由勾股定理得AD²=10²-x²=17²-(21-x）²，解得x=6，AD=8，DC=15以D为坐标原点，BC为x轴，DA为y轴建立坐标系（如图）则A（0，8）B（-6，0）C（15，0）以C为旋转中心，将△CPB绕点C逆时钟旋转60°至△CP'B'，连接PP'、BB'、AB'则△CPP'，△CBB'均为等边三角形所以PC=PP'，PB=P'B'所以PA+PB+PC=AP+PP'+P'B'≥AB'而B'（9/2，-21√3/2）所以AB'=√[（0-9/2）²+（8+21√3/2）²]=√（415+168√3）.即PA+PB+PC的最小值等于AB'的长√（415+168√3）. 【补充说明】（1）如图，以△ABC的三边为边，分别向外作等边三角形BCD、ACE、ABF，连接AD、BE、CF，则（1）AD、BE、CF交于一点P，且∠APB=∠APC=∠BPC=120°，（2）P到A、B、C三顶点距离的和最小，且PA+PB+PC=AD=BE=CF。

一点到三角形三个顶点距离之和最小值在平面几何中，三角形是最基本的几何形状之一，它由三条线段组成，这三条线段称为边。

而三角形的三个顶点即为连接这三条边的点。

现在的问题是，给定一个点P和一个三角形ABC，如何确定点P到三角形ABC三个顶点的距离之和最小值呢？我们可以通过画图来观察一下这个问题的特点。

假设点P在三角形ABC的内部，我们可以发现，点P到三个顶点的距离之和是一个固定值，即三角形的周长。

但是，如果点P不在三角形ABC的内部，而是在三角形的外部，情况就变得复杂一些。

我们可以假设点P在三角形ABC的外部，且点P到三个顶点的距离之和最小。

那么，我们可以发现，点P到三个顶点的连线会与三角形的三条边相交。

以点P到边AB上的交点为例，我们可以发现，如果我们将点P沿着边AB的方向移动一点点，点P到三个顶点的距离之和会变小。

同理，点P到边AC和边BC上的交点也具有相同的性质。

这样一来，我们可以得出一个结论：点P到三角形ABC三个顶点的距离之和最小，当且仅当点P到三角形ABC的三条边上的交点重合。

这个交点有一个特殊的名字，叫做三角形ABC的费马点。

费马点是指在平面上给定一个点P，使得点P到三角形ABC三个顶点的距离之和最小。

费马点的特点是，它到三个顶点的连线夹角相等，即∠APB = ∠BPC = ∠CPA。

现在，我们来考虑一下如何求解费马点。

我们可以通过以下步骤来实现：1. 首先，我们需要计算出三角形ABC的三条边的长度，假设分别为a、b、c。

2. 然后，我们可以根据三角形的边长和角度关系，利用三角函数来求解费马点的坐标。

3. 假设费马点的坐标为(x, y)，我们可以得到以下方程组：(x - xA)^2 + (y - yA)^2 = a^2(x - xB)^2 + (y - yB)^2 = b^2(x - xC)^2 + (y - yC)^2 = c^2其中，(xA, yA)、(xB, yB)、(xC, yC)分别为三角形ABC的三个顶点的坐标。

三角形中点到三个顶点的距离正方形、长方形以及正多边形，都是能轻易被我们认识的形状，其中，三角形则也是三种形状中最常见的形状之一。

三角形是一种基本的平面图形，由三条相联的线段组成，其特征可以完全用三个点表示。

在三角形中，由三个点（称为顶点）构成三个边，其中，每一条边都是从一个顶点到另一个顶点形成的，三条边相互连接后，构成三角形。

其中，三条边是三角形的三条边，而三个顶点则是三角形的三个顶点。

我们可以将三条边连接起来，从而完成三角形的构成，也可以记录三条边的长度，也可以知道三个顶点的位置。

本文的主题是三角形中点到三个顶点的距离，那么，首先要明确的是，三角形中每一个顶点到另外两个顶点的距离都是相同的，也就是说，三角形的三条边的长度都是相等的。

假设三角形的三个顶点分别为A、B、C，那么，A点到B点的距离等于B点到C点的距离，也等于C点到A点的距离，等于三条边的长度。

那么，三角形的面积可以根据以上计算公式来确定，即：面积 =（1/2）×三条边的长度×角度内切边线的长度由于三条边的长度都是相等的，因此，三角形的面积可以用以下计算公式来确定：面积 =（1/2）×三条边的长度的平方另外，经过一定的几何推导，得出了如下的计算公式：点到三个顶点距离之和=三条边长度之和=2×三角形面积÷角度内切边线的长度可以看出，点到三个顶点距离之和与三角形的面积有一定的联系，因此，可以根据三角形的三条边的长度，来确定点到三个顶点的距离之和。

除此之外，如果我们知道了点到三个顶点的距离之和，也可以通过以上公式来求出三角形的面积。

再比如，若想求出三角形的面积，可以先求出内切边线的长度，再用以下公式：面积 =（1/2）×三条边的长度×角度内切边线的长度根据以上知识，我们就可以计算出三角形中点到三个顶点的距离之和以及面积，从而了解三角形的基本知识。

总之，三角形是一种常见的平面图形，它由三条相联的线段组成，其特征可以完全用三个点表示，而每一条边都是从一个顶点到另一个顶点形成的，三条边相互连接后，构成三角形。

费马点问题1．费马点在三角形内部，到三角形三个顶点的距离之和最小的点叫做费马点．2．基本模型如图，在锐角△ABC 内有一点O ，分别连接OA 、OB 、OC ，求证：当∠AOB ＝∠AOC ＝∠BOC ＝120°时，OA ＋OB ＋OC 最小．证明：将△APC 绕点C 旋转60°至△A ′P ′C ，则△PP ′C 是等边三角形，∴OA ＋OB ＋OC ＝BP ＋PP ′＋P ′A ≥BA ′，此时∠BPC ＝180°－∠CPP ′＝120°，∠A ′P ′C ＝180°－∠CP ′P ＝120°，∴∠APC ＝∠A ′P ′C ＝120°，∴∠AOB ＝∠AOC ＝∠BOC ＝120°．3．基本结论（1）对于一个各角都不超过120°的三角形，费马点是对各边的张角都是120°的点．（2）对于有一个角超过120°的三角形，费马点就是这个内角的顶点．（不作研究）4．基本题型（1）两点之间线段最短（2）垂线段最短（3）加权问题加权费马点，旋转加缩放，系数先化一，必为勾股数．A BCPABP PCP′P′A′APBC类型1：经典费马点问题：两点之间线段最短【例题1】如图，△ABC 中，∠ACB ＝90°，∠ABC ＝60°，BC＝P 是△ABC 内一动点，将△ACP 绕点A 逆时针旋转60°得到△ADE ，连接PE 、BD ，则PA ＋PB ＋PC 的最小值为___________．【例题2】如图，等边△ABC 中，AB ＝2，若点P 是△ABC 内部一个动点，则PA ＋PB ＋PC 的最小值为__________．【例题3】如图，Rt △ABC 中，∠ABC ＝90°，AB ＝2，BC ＝P 是△ABC 内一个动点，则P A ＋PB ＋PC 的最小值为__________．【例题4】如图，正方形ABCD 内一动点E ，到顶点A 、B 、C 的距离之和AE ＋BE ＋CE____________．PEDCBA ABCPABCPE DCBA【例题5】如图，△ABC 中，AB ＝5，BC ＝3，∠ABC ＝60°，若点P 是△ABC 内一个动点，则P A ＋PB ＋PC 的最小值为__________．【例题6】如图，在△ABC 中，AB ＝AC ＝4，∠CAB ＝30°，AD ⊥BC ，垂足为D ，P 为线段AD 上的一动点，连接PB 、PC ，则P A ＋2PB 的最小值为_____________．【例题7】如图，在△MNG 中，MN ＝6，∠M ＝75°，MG ＝4O 为△MNG 内一点，则点O 到△MNG 三个顶点的距离之和的最小值为____________．【例题8】如图，锐角三角形ABC 中，∠ACB ＝60°，AB ＝7，BC ＝5，AC ＝8，D 为△ABC 内一点，BD ＝1，△ABC 内有动点P ，则P A ＋PC ＋PD 的最小值为_________．PCAGNABCD P类型2：动态费马点问题：垂线段最短【例题9】如图，已知矩形ABCD，AB＝4，BC＝6，点M为矩形内一点，点E为BC边上任意一点，则MA＋MD＋ME的最小值为___________．【例题10】如图，四个村庄坐落在矩形ABCD的四个顶点上，AB＝10公里，BC＝15公里，现在要设立两个车站E、F，则EA＋EB＋EF＋FC＋FD的最小值为__________公里．类型3：加权费马点——缩放法，旋转系数大的线段【例题11】如图，在△ABC中，AB＝4，BC＝6，∠ABC＝30°，P是△ABC内一动点，则P APB＋PC的最小值为___________．【例题12】如图，在△ABC中，AB＝AC＝4，∠BAC＝90°，点P为△ABC内一点，则12P A＋PBPC的最小值为___________．AB CDEMAB CDEFPC BAAB CP【例题13】如图，点P是边长为2的等边△ABC内一点，则P A＋PB＋12PC的最小值为_________．AB CP费马点问题1．费马点在三角形内部，到三角形三个顶点的距离之和最小的点叫做费马点．2．基本模型如图，在锐角△ABC 内有一点O ，分别连接OA 、OB 、OC ，求证：当∠AOB ＝∠AOC ＝∠BOC ＝120°时，OA ＋OB ＋OC 最小．证明：将△APC 绕点C 旋转60°至△A ′P ′C ，则△PP ′C 是等边三角形，∴OA ＋OB ＋OC ＝BP ＋PP ′＋P ′A ≥BA ′，此时∠BPC ＝180°－∠CPP ′＝120°，∠A ′P ′C ＝180°－∠CP ′P ＝120°，∴∠APC ＝∠A ′P ′C ＝120°，∴∠AOB ＝∠AOC ＝∠BOC ＝120°．3．基本结论（1）对于一个各角都不超过120°的三角形，费马点是对各边的张角都是120°的点．（2）对于有一个角超过120°的三角形，费马点就是这个内角的顶点．（不作研究）4．基本题型（1）两点之间线段最短（2）垂线段最短（3）加权问题加权费马点，旋转加缩放，系数先化一，必为勾股数．A BCPABP PCP′P′A′APBC类型1：经典费马点问题：两点之间线段最短【例题1】如图，△ABC中，∠ACB＝90°，∠ABC＝60°，BC＝P是△ABC内一动点，将△ACP绕点A逆时针旋转60°得到△ADE，连接PE、BD，则PA＋PB＋PC的最小值为___________．【答案】7．【例题2】如图，等边△ABC中，AB＝2，若点P是△ABC内部一个动点，则PA＋PB＋PC的最小值为__________．【答案】（提示：将△ABP绕点A顺时针旋转60°得到△AB′P′）【例题3】如图，Rt△ABC中，∠ABC＝90°，AB＝2，BC＝P是△ABC内一个动点，则P A＋PB＋PC的最小值为__________．【答案】（提示：将△ABP绕点A顺时针旋转60°得到△AB′P′）【例题4】如图，正方形ABCD内一动点E，到顶点A、B、C的距离之和AE＋BE＋CE____________．【答案】2．（提示：将△ABE绕点A顺时针旋转60°得到△AB′E′，∠B′BP＝90°－60°＝30°，设B′P＝x，则PB＝，B′B＝BC＝2x，在Rt△B′PC中，x2＋(＋2x)2＝)2，解得x＝1，∴BC＝PEDCBAABCP P′A′MPCBAAB CPP′B′NMPCBAEDCBAABCDEPB′E′2）【例题5】如图，△ABC 中，AB ＝5，BC ＝3，∠ABC ＝60°，若点P 是△ABC 内一个动点，则P A ＋PB ＋PC 的最小值为__________．【答案】7．（提示：将△ABP 绕点A 顺时针旋转60°得到△AB ′P ′）【例题6】如图，在△ABC 中，AB ＝AC ＝4，∠CAB ＝30°，AD ⊥BC ，垂足为D ，P 为线段AD 上的一动点，连接PB 、PC ，则P A ＋2PB 的最小值为_____________．【答案】．（提示：费马点）【例题7】如图，在△MNG 中，MN ＝6，∠M ＝75°，MG ＝4O 为△MNG 内一点，则点O 到△MNG 三个顶点的距离之和的最小值为____________．【答案】（提示：将△MOG 绕点M 顺时针旋转60°得到△MO ′G ′）【例题8】如图，锐角三角形ABC 中，∠ACB ＝60°，AB ＝7，BC ＝5，AC ＝8，D 为△ABC 内一点，BD ＝1，△ABC 内有动点P ，则P A ＋PC ＋PD 的最小值为_________．PCB AABCPP′B′EF P′B′PD CBAGNG′O′HNMOGABCD PC′P′PFE D CBA【答案】1．（提示：将△APC绕点A逆时针旋转60°得到△AP′C′）类型2：动态费马点问题：垂线段最短【例题9】如图，已知矩形ABCD，AB＝4，BC＝6，点M为矩形内一点，点E为BC边上任意一点，则MA＋MD＋ME的最小值为___________．【答案】4＋（提示：将△AMD绕点D顺时针旋转60°得到△A′M′D）【例题10】如图，四个村庄坐落在矩形ABCD的四个顶点上，AB＝10公里，BC＝15公里，现在要设立两个车站E、F，则EA＋EB＋EF＋FC＋FD的最小值为__________公里．【答案】15＋（提示：将△AMD绕点D顺时针旋转60°得到△A′M′D）类型3：加权费马点——缩放法，旋转系数大的线段【例题11】如图，在△ABC中，AB＝4，BC＝6，∠ABC＝30°，P是△ABC内一动点，则P APB＋PC的最小值为___________．【答案】（提示：将△ABP绕点B逆时针旋转90°得到△A′BP′）AB CDEMAB CDEFE′B′C′F′NMFEDCBAPCBA ABCEPP′A′【例题12】如图，在△ABC 中，AB ＝AC ＝4，∠BAC ＝90°，点P 为△ABC 内一点，则12P A ＋PBPC 的最小值为___________．【答案】．（提示：方法1，将△APC 缩小到原来的12，并绕点C 顺时针旋转90°得到△AP ′C ′；方法2，原式＝12(P A ＋2PBPC )，将△APC 扩大到原来的2倍，并绕点C 顺时针旋转90°得到△A ′P ′C ）【例题13】如图，点P 是边长为2的等边△ABC内一点，则P A ＋PB ＋12PC 的最小值为___________．【答案】（提示：方法1，将△APC 缩小到原来的12，并绕点A 逆时针旋转60°得到△AP ′C ′；方法2，将△APC缩小到原来的，并绕点C 逆时针旋转30°得到△A ′P ′C ；方法3，原式＝12(A ＋2PB＋PC )，将△APC扩大到原来的C 顺时针旋转90°得到△A ′P ′C ）A BCPP′A′PEC B AABCPABCE PC′P′ABCPA′P′。

线段最值系列—费马点模型学号：姓名：【问题背景】“费马点”是指位于三角形内且到三角形三个顶点距离之和最短的点.若给定一个三角形△ABC的话，从这个三角形的费马点P到三角形的三个顶点A、B、C的距离之和比从其它点算起的都要小.这个特殊点对于每个给定的三角形都只有一个.若三角形有一内角大于等于120°，则此钝角的顶点就是距离和最小的点.【构图模型】问题：如图1，如何找点P使它到△ABC三个顶点的距离之和PA+PB+PC最小？图文解析：如图1，把△APC绕C点顺时针旋转60°得到△A′P′C，连接PP′．则△CPP′为等边三角形，CP= PP′，P A =P′A′，∴P A+PB+PC= P′A′+ PB+ PP′≥B C′．∵点A′可看成是线段CA绕C点顺时针旋转60°而得的定点，BA′为定长，∴当B、P、P′、A′ 四点在同一直线上时，P A+PB+PC最小．最小值为BA.′【如图1和图2，利用旋转、等边等条件转化相等线段.】∴∠APC=∠A′ P′C=180°-∠CP′P=180°-60°=120°，∠BPC=180°-∠P′PC=180°-60°=120°，∠APC=360°-∠BPC-∠APC=360°-120°-120°=120°.因此，当△ABC的每一个内角都小于120°时，所求的点P对三角形每边的张角都是120°；当有一内角大于或等于120°时，所求的P点就是钝角的顶点．费马点问题告诉我们，存在这么一个点到三个定点的距离的和最小，解决问题的方法是运用旋转变换．【构图总结】利用旋转、等边等条件转化相等线段，将三条线段转化成首尾相连的三条线段，利用两点之间线段最短进而解决该问题.【典型例题】例1（2019⋅武汉）如图，在△MNG中，MN=6，∠M=75°，MG=42，点O是△MNG内一点，则点O到△MNG三个顶点的距离和的最小值是______．例2如图，已知矩形ABCD，AB=4，BC=6，点M为矩形内一点，点E为BC边上任意一点，则MA+MD+ME的最小值为______．ON G图2AB CDME图1图2例1图例2图例3 如图1，已知一次函数y =x +3的图象与x 轴、y 轴分别交于A 、B 两点，抛物线c bx x y ++-=2过A 、B 两点，且与x 轴交于另一点C ． （1）求b 、c 的值；*（2）点D 为AC 的中点，点E 在线段BD 上，且BE =2ED ，连接CE 并延长交抛物线于点M ，求点M 的坐标；（3）将直线AB 绕点A 按逆时针方向旋转15°后交y 轴于点G ，连接CG ，如图2，P 为△ACG 内一点，连接P A 、PC 、PG ，分别以AP 、AG 为边，在他们的左侧作等边△APR ，等边△AGQ ，连接QR ，求P A +PC +PG 的最小值．例4 如图，在平面直角坐标系中，点A 的坐标为（－1,0），点B 的坐标为（4，0），经过点A 点B 抛物线y =x ²+bx +c 与y 轴交于点C . （1）求抛物线的关系式.*（2）△ABC 的外接圆与y 轴交于点D ，在抛物线上是否存在点M 使S △MBC =S △DBC ，若存在，请求出点M 的坐标.（3）点P 是直线y = -x 上一个动点，连接PB ，PC ，当PB +PC +PO 最小时，求点P 的坐标及其最小值.图1 图2备用图线段最值系列—费马点模型课堂检测学号： 姓名：1.如图，四个村庄坐落在矩形ABCD 的四个顶点上，AB ＝10公里，BC ＝15公里，现在要设立两个车站E ，F ，则EA +EB +EF +FC +FD 的最小值为 公里．2.小颖在学习“两点之间线段最短”查阅资料时发现：ABC ∆内总存在一点P 与三个顶点的连线的夹角相等，此时该点到三个顶点的距离之和最小． 【特例】如图1，点P 为等边ABC ∆的中心，将ACP ∆绕点A 逆时针旋转60︒得到ADE ∆，从而有DE PC =，连接PD 得到PD PA =，同时12060180APB APD ∠+∠=︒+︒=︒，180ADP ADE ∠+∠=︒，即B 、P 、D 、E 四点共线，故：PA PB PC PD PB DE BE ++=++=．在ABC ∆中，另取一点P '，易知点P '与三个顶点连线的夹角不相等，可证明B 、P '、D '、E 四点不共线，所以P A P B P C PA PB PC '+'+'>++，即点P 到三个顶点距离之和最小．【探究】（1）如图2，P 为ABC ∆内一点，120APB BPC ∠=∠=︒，证明PA PB PC ++的值最小； 【拓展】（2）如图3，ABC ∆中，6AC =，8BC =，30ACB ∠=︒，且点P 为ABC ∆内一点，求点P 到三个顶点的距离之和的最小值．。

三角形内一点到各顶点距离最短的证明(费马问题)在三角形ABC内找一点P，使其到三个顶点的距离和是最小。

（P称为费马点）这是费马给伽利略的学生和助手托里析利（E. TOrricelli 1608～1647）考虑的一个几何难题。

托里析里在对物体运动，流体力学及大气压力有研究，他发明水银柱气压计，由此证明大气是有压力。

他对费马的这个问题给出了几何解决方法，先来介绍五十多年前一位英国人霍夫曼（J.E. Hofmann）以及匈牙利数学家笛波·伽累依（Tibor Gallai）先后想出同样的一个解决方法。

霍夫曼及伽累依是怎样考虑费马的问题呢？先假设△ABC没有一个角大于120°。

在△ABC内任取一点P，如图，向外作一正△PBP' 与C隔于BP，作正△ABC′与C隔于AB，容易看出，∠1=∠2，A'B=AB，P'B=PB，则△APB≌△A'BP'，进而PA=P'A'。

即PA+PB+PC=P'A'+P'P+PC。

A'和C是定点，若要使距离和最小，则需要P'P在A'C上。

此时，∠3=180-60=120，则∠4=∠3=120。

同理可证其余各角都是120。

这就导出一则画法：向△ABC外作正△ABA'，作其外接圆交A'C 于P，P就是费马点。

又或者向△ABC外任作两正△,把它的顶点连接相对的三角形顶点,产生的2条连线交点为费马点.以下是托里析利的方法：以AB，AC为边向外作两个正三角形其外接圆交于A和P。

过A的PA的垂线、过B的PB的垂线、过C的PC 的垂线交成△XYZ，如图。

按作图方法知道∠APB=120，但∠PBX=∠PAX=90，于是∠X=60，同理∠Y=∠Z=60，则△XYZ是等边三角形。

假定有一个不与P重合的点P'，过P'向这个等边三角形引垂线P'A'、P'B'、P'C'，注意到直角三角形斜边大于直角边，又考虑一下维维亚尼定理(正三角内的点到三边距离之和为定值)，于是P'A +P'B +P'C现在再考虑在△ABC中有一个内角(比如说A)≥120°时，极值点P在哪里．(这时，三角形内没有费马点)如图4－37所示，设P为△ABC内任一点，将△APC 绕A点旋转，使C转到BA延长线上的C′点，P转到P′．这时的旋转角度为18O°-A≤60°，所以PP′≤AP．于是PA+PB+PC≥BP+PP′+P′C≥BC′=AB+AC．上式等号当且仅当P点与A点重合时成立．这就是说，当A≥120°时，极值点P是顶点A．综上可知，当△ABC的每一内角均小于120°时，使PA+PB+PC最小的极值点是三角形的费马点；当有一个内角≥120°时，极值点是最大角的顶点．在物理有一个这样的“最小势能原理”（也称为狄利克雷原理Principle of Dirichlet ）：“一个物体或系统当处于平衡位置时，它的势能是最小。

第8讲费马点最值模型(解析版)中考数学几何模型8：费马点最值模型XXX问题思考：如何找一点P使它到△ABC三个顶点的距离之和PA+PB+PC最小？解法：费马点的定义是指到三角形三个顶点距离之和最小的点。

费马点有如下主要性质：到三角形三个顶点距离之和最小，连接三顶点所成的三夹角皆为120°。

费马点最小值快速求解方法是运用旋转变换，以△XXX任意一边为边向外作等边三角形，这条边所对两顶点的距离即为最小值。

典题探究：已知：△ABC是锐角三角形，G是三角形内一点。

∠AGC=∠AGB=∠BGC=120°.求证：GA+GB+GC的值最小.证明：将△BGC逆时针旋转60°，连GP,DB.则△CGB≌△CPD；∴∠CPD=∠CGB=120°,CG=CP,GB=PD。

BC=DC,∠GCB=∠PCD.∵∠GCP=60°,∴∠BCD=60°,∴△GCP 和△BCD都是等边三角形。

∵∠AGC=120°,∠CGP=60°.∴A、G、P三点一线。

∵∠CPD=120°,∠CPG=60°.∴G、P、D三点一线。

∴AG、GP、PD三条线段同在一条直线上。

∵GA+GC+GB=GA+GP+PD=AD.∴G点是等腰三角形内到三个顶点的距离之和最小的那一点。

变式练：如图，P是边长为1的等边△ABC内的任意一点，求t=PA+PB+PC的取值范围。

解法：将△BPC绕点B顺时针旋转60°得到△BP'C'，易知△BPP'为等边三角形。

从而PA+PB+PC=PA+PP'+P'C'≥AC'（两点之间线段最短），从而t≥3.过P作BC的平行线分别交AB、AC于点M、N，易知MN=AN=AM。

因为在△BMP和△PNC中，PB∠ANM=∠AMN，所以XXX<AM。

PB+PC≥MN，从而t=PA+PB+PC≥AM+MN=3.所以t的取值范围为[3,∞)。

D
A
A
E
B
C
B
C
D
A
D
E
P
B
C
B
A E
P C
F
在图三的模型里有结论：（1）∠BPD=60°；（2）连接 AP，AP 平分∠DPE． 有这两个结论便足以说明∠PAB=∠BPC=∠CPA=120°． 但是在这里有个小小的要求，细心的同学会发现，这个图成立的一个必要条件是 ∠BAC<120°，若 BAC 120 ,这个图就不是这个图了，会长成这个样子：
如图，以 MG 为边作等边△MGH，连接 NH，则 NH 的值即为所求的点 O 到△MNG 三个顶
点的距离和的最小值．（此处不再证明）
M
H
N
G
过点 H 作 HQ⊥NM 交 NM 延长线于 Q 点，
根据∠NMG=75°，∠GMH=60°，可得∠HMQ=45°，
∴△MHQ 是等腰直角三角形，
∴MQ=HQ=4，
最小值．至于点 P 的位置？这不重要！
D A
B
C
如何求 BD？考虑到△ABC 和△ACD 都是特殊的三角形，过点 D 作 DH⊥BA 交 BA 的延长线于 H 点，根据勾股定理， BD2 = BH 2 + DH 2 即可得出结果．
H
D A
B
C
【练习】如图，已知矩形 ABCD，AB=4，BC=6，点 M 为矩形内一点，点 E 为 BC 边上任意 一点，则 MA+MD+ME 的最小值为______．
∴NH= NQ2 + HQ2 = 100 +16 = 2 29 ．
Q 4 M
4 H
6
N
G
【练习】如图，在△ABC 中，∠ACB=90°，AB=AC=1，P 是△ABC 内一点，求 PA+PB+PC 的最小值．

三角形内一点到各顶点距离最短的证明(费马问题)在三角形ABC内找一点P，使其到三个顶点的距离和是最小。

（P称为费马点）这是费马给伽利略的学生和助手托里析利（E. TOrricelli 1608～1647）考虑的一个几何难题。

托里析里在对物体运动，流体力学及大气压力有研究，他发明水银柱气压计，由此证明大气是有压力。

他对费马的这个问题给出了几何解决方法，先来介绍五十多年前一位英国人霍夫曼（J.E. Hofmann）以及匈牙利数学家笛波·伽累依（Tibor Gallai）先后想出同样的一个解决方法。

霍夫曼及伽累依是怎样考虑费马的问题呢？先假设△ABC没有一个角大于120°。

在△ABC内任取一点P，如图，向外作一正△PBP' 与C隔于BP，作正△ABC′与C隔于AB，容易看出，∠1=∠2，A'B=AB，P'B=PB，则△APB≌△A'BP'，进而PA=P'A'。

即PA+PB+PC=P'A'+P'P+PC。

A'和C是定点，若要使距离和最小，则需要P'P在A'C上。

此时，∠3=180-60=120，则∠4=∠3=120。

同理可证其余各角都是120。

这就导出一则画法：向△ABC外作正△ABA'，作其外接圆交A'C 于P，P就是费马点。

又或者向△ABC外任作两正△,把它的顶点连接相对的三角形顶点,产生的2条连线交点为费马点.以下是托里析利的方法：以AB，AC为边向外作两个正三角形其外接圆交于A和P。

过A的PA的垂线、过B的PB的垂线、过C的PC 的垂线交成△XYZ，如图。

按作图方法知道∠APB=120，但∠PBX=∠PAX=90，于是∠X=60，同理∠Y=∠Z=60，则△XYZ是等边三角形。

假定有一个不与P重合的点P'，过P'向这个等边三角形引垂线P'A'、P'B'、P'C'，注意到直角三角形斜边大于直角边，又考虑一下维维亚尼定理(正三角内的点到三边距离之和为定值)，于是P'A +P'B +P'C现在再考虑在△ABC中有一个内角(比如说A)≥120°时，极值点P在哪里．(这时，三角形内没有费马点)如图4－37所示，设P为△ABC内任一点，将△APC 绕A点旋转，使C转到BA延长线上的C′点，P转到P′．这时的旋转角度为18O°-A≤60°，所以PP′≤AP．于是PA+PB+PC≥BP+PP′+P′C≥BC′=AB+AC．上式等号当且仅当P点与A点重合时成立．这就是说，当A≥120°时，极值点P是顶点A．综上可知，当△ABC的每一内角均小于120°时，使PA+PB+PC最小的极值点是三角形的费马点；当有一个内角≥120°时，极值点是最大角的顶点．在物理有一个这样的“最小势能原理”（也称为狄利克雷原理Principle of Dirichlet ）：“一个物体或系统当处于平衡位置时，它的势能是最小。

初中数学最值问题专题4 费马点中三线段模型与最值问题【专题说明】费马点”是指位于三角形内且到三角形三个顶点距高之和最短的点。

主要分为两种情况：（1）当三角形三个内角都小于120°的三角形，通常将某三角形绕点旋转60度，从而将“不等三爪图”中三条线段转化在同一条直线上，利用两点之间线段最短解决问题。

（2）当三角形有一个内角大于120°时，费马点就是此内角的顶点.费马点问题解题的核心技巧：旋转60° 构造等边三角形将“不等三爪图”中三条线段转化至同一直线上利用两点之间线段最短求解问题【模型展示】问题：在△ABC内找一点P，使得P A+PB+PC最小．APB C【分析】在之前的最值问题中，我们解决的依据有：两点之间线段最短、点到直线的连线中垂线段最短、作对称化折线段为直线段、确定动点轨迹求最值等．（1）如图，分别以△ABC中的AB、AC为边，作等边△ABD、等边△ACE．（2）连接CD、BE，即有一组手拉手全等：△ADC≌△ABE．（3）记CD、BE交点为P，点P即为费马点．（到这一步其实就可以了）（4）以BC为边作等边△BCF，连接AF，必过点P，有∠P AB=∠BPC=∠CP A=120°．在图三的模型里有结论：（1）∠BPD=60°；（2）连接AP，AP平分∠DPE．有这两个结论便足以说明∠P AB=∠BPC=∠CP A=120°．原来在“手拉手全等”就已经见过了呀，只是相逢何必曾相识！【例题】1、如图，四边形ABCD 是菱形，AB =4，且∠ABC =∠ABE =60°，G 为对角线BD （不含B 点）上任意一点，将∠ABG 绕点B 逆时针旋转60°得到∠EBF ，当AG +BG +CG 取最小值时EF 的长（ ）A ．B ．C ．D ．2、如图，将ABC ∆绕点A 逆时针旋转60°得到ADE ∆，DE 与BC 交于点P ，可推出结论：PA PC PE +=问题解决：如图，在MNG ∆中，6MN =，75M ∠=︒，MG =O 是MNG ∆内一点，则点O 到MNG ∆三个顶点的距离和的最小值是___________3、如图，四边形ABCD是菱形，A B=6，且∠ABC=60° ，M是菱形内任一点，连接AM，BM，CM，则AM+BM+CM的最小值为________．4、如图，∠ABC中，∠BAC＝30°且AB＝AC，P是底边上的高AH上一点．若AP+BP+CP的最小值为，则BC＝_____．5、如图，四边形ABCD 是正方形，∠ABE 是等边三角形，M 为对角线BD （不含B 点）上任意一点，将BM 绕点B 逆时针旋转60°得到BN ，连接EN 、AM 、CM .∠ 求证：∠AMB ∠∠ENB ；∠ ∠当M 点在何处时，AM ＋CM 的值最小；∠当M 点在何处时，AM ＋BM ＋CM 的值最小，并说明理由； ∠ 当AM ＋BM ＋CM 的最小值为13 时，求正方形的边长.EA DB CNMF EA DB CNM6、在正方形ABCD中，点E为对角线AC（不含点A）上任意一点，AB=（1）如图1，将∠ADE绕点D逆时针旋转90°得到∠DCF，连接EF；∠把图形补充完整（无需写画法）；∠求2EF的取值范围；(2)如图2，求BE+AE+DE的最小值．专题4 费马点中三线段模型与最值问题答案【专题说明】费马点”是指位于三角形内且到三角形三个顶点距高之和最短的点。

三角形内一点到三个顶点距离之和三角形是几何中最常见的图形，它有三个边和三个顶点组成。

在几何中，三角形内一点到三个顶点的距离之和是一个有趣的概念，它涉及到三角形的关系性和距离的概念。

在本文中，我们将探讨三角形内一点到三个顶点距离之和的概念，以及它的计算方法。

首先，让我们来看一个关于三角形内一点到三个顶点距离之和的定义：三角形内一点到三个顶点距离之和，即指三角形内一点到三个顶点的距离之和，等于三角形的周长。

也就是说，三角形内一点到三个顶点的距离之和等于三角形的周长。

其次，让我们来看一个关于三角形内一点到三个顶点距离之和的计算方法：首先，设三角形的三个顶点分别为A、B、C，其中P为三角形内的一点，令AP、PB、CQ分别为P 到A、B、C的距离。

那么，三角形内一点P到三个顶点A、B、C的距离之和可以用下面的公式来表示：AP + PB + CQ = AB + BC + CA，其中AB、BC、CA分别为三角形的三个边的边长。

三角形内一点到三个顶点距离之和的概念与三角形的关系性和距离有关联。

由于三角形内一点P到三个顶点A、B、C的距离之和等于三角形的周长，因此可以推出，对于任意一个三角形，它的周长总是等于三角形内一点P到三个顶点A、B、C的距离之和。

此外，三角形内一点到三个顶点距离之和的概念也可以用来计算三角形的面积。

由于三角形的周长等于三角形内一点P到三个顶点A、B、C的距离之和，而三角形的面积又与周长和三角形内角的大小有关，因此可以通过计算三角形内一点P到三个顶点A、B、C的距离之和，来计算三角形的面积。

以上就是关于三角形内一点到三个顶点距离之和的概念及其计算方法的介绍。

三角形内一点到三个顶点距离之和的概念与三角形的关系性和距离有关联，可以用来计算三角形的周长和面积。

本文只是对三角形内一点到三个顶点距离之和的概念及其计算方法的简单介绍，其他更深入的内容，比如三角形内一点到三个顶点距离之和的具体应用，还需要进一步深入研究。

求三角形内一点到三个顶点距离之和的最小值1、已知三角形ABC中，AC=3 , BC=4 , AB=5 , P是三角形ABC内一点，求PA+PB+PC 的最小值.AC∖∖ ∖ √∖∖ fVc解：由题意三角形ABC为直角三角形，以直角顶点C为原点，CB为X轴，CA为y轴建立坐标系（如图）则C（0，0）A（0，3）B（4，0）以B为旋转中心，将△ BPC绕点B逆时钟旋转60°至厶BP'C',连接PP'、CC'、AC'则厶BPP'，△ BCC'均为等边三角形所以PB=PP' ，PC=P'C'所以PA+PB+PC=AP+PP'+P'≥AC'而C'（2，-2√3）所以AC'=√[ （0-2）2+ （3+2√3 ）2]= √（25+12√3 ）即PA+PB+PC 的最小值等于AC'的长√ （25+12√3）.2、已知三角形ABC 中，AB=10 , AC=17 , BC=21 , P是三角形ABC内一点，求PA+PB+PC 的最小值.解：过A作AD丄BC于D ,设BC=X ,贝U CD=21-x由勾股定理得AD2=102-x2=172-(21-x ) 2 ,解得x=6 , AD=8 , DC=15以D为坐标原点，BC为X轴，DA为y轴建立坐标系(如图) 则A (0 , 8) B (-6 , 0) C (15 , 0 )以C为旋转中心，将△ CPB绕点C逆时钟旋转60°至厶CP'B',连接PP'、BB'、AB'则厶CPP' , △ CBB'均为等边三角形所以PC=PP' , PB=P'B'所以PA+PB+PC=AP+PP'+P'≥AB'而B' (9/2 , -21√3/2 )所以AB'=√[ (0-9/2 ) 2+ (8+21√3/2 ) 2]= √(415+168√3).即PA+PB+PC 的最小值等于AB'的长√( 415+168√3 ).【补充说明】(1 )如图，以△ ABC的三边为边，分别向外作等边三角形BCD、ACE、ABF，连接AD、BE、CF，贝U(1 ) AD、BE、CF 交于一点P,且∠ APB= ∠ APC= ∠BPC=120 , (2 ) P到A、B、C三顶点距离的和最小，且证明：∙∙∙AF=AB , ∠ FAC= ∠ BAE , AC=AE •••△AFC S ABE∙∙∙ CF=BE同理可证厶BCF S BDA , CF=AD∙∙∙ AD=BE=CF.•••△ AFC s ABE∙∙∙∠ AFC= ∠ ABE∙∙∙∠BPF= ∠ BAF=60 , ∠ BPC=120同理可证∠ APB= ∠ APC=120∙∙∙∠ APB= ∠ APC= ∠ BPC=120至于P到三顶点距离之和为何最小上面两题已明。