matlab计量经济学 相关分析
- 格式:doc
- 大小:172.50 KB
- 文档页数:15
伍德⾥奇---计量经济学第2章部分计算机习题详解(MATLAB)班级:⾦融学×××班姓名:××学号:×××××××C2.1 401K.RAW prate=β0+β1mrate解:(ⅰ)求出计划的样本中平均参与率和平均匹配率.所以,平均参与率为87.36,平均匹配率为0.73.(ⅱ)报告结果以及样本容量和R2.β1=mrate i?mrate(prate i?prate)ni=1mrate i?mrate2ni=1=cov(x,y)var(x)β0=prate?β1mrate=A?β1B R2=SSESST所以β1= 5.8611;所以β0= 83.07.= 0.0747, n=1534.且R2=SSESST(ⅲ)解释⽅程中的截距和mrate的系数.⽅程中的截距β0意味着,当mrate= 0时,预测的参与率是83.07%。
⽽系数mrate意味着员⼯每投⼊⼀美元,prate的预期变化为5.86个百分点。
(ⅳ)当mrate=3.5时,求出prate的预测值。
只是⼀个合理的预测吗?解释这⾥出现的情况.由(ⅱ)可得prate=83.07+5.86mrate,所以当mrate=3.5时,prate= 83.07 + 5.86 * 3.5 = 103.58,即prate的预测值是103.85.这不是⼀个合理的预测,因为最多只可能有100%的参与率,不可能超过100% 。
(ⅴ)prate的变异中,有多少是由mrate解释的?这是⼀个⾜够⼤的量吗?在prate的变异中,有7.47% 是由mrate解释的,这不是⼀个⾜够⼤的量,意味着还有许多其他因素影响计划的参与率。
C2.2 CEOSAL2.RAW lo g salary=β0+β1ceoten+u解:(ⅰ)求出样本中的平均年薪和平均任期.所以,平均年薪为865.86,平均任期为7.95.(ⅱ)有多少位CEO尚处于担任CEO的第⼀年(即ceoten=0)?最长的CEO任期是多少?所以,有5位CEO尚处于担任CEO的第⼀年;所以,最长的CEO任期是37年。
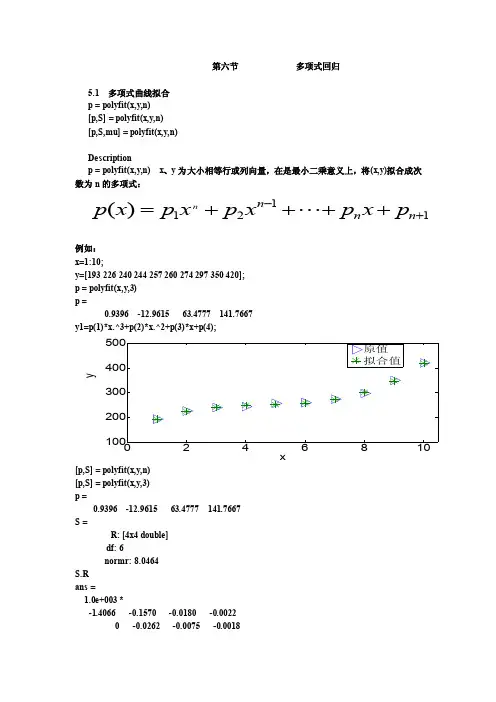
第六节 多项式回归5.1 多项式曲线拟合 p = polyfit(x,y,n) [p,S] = polyfit(x,y,n) [p,S,mu] = polyfit(x,y,n)Descriptionp = polyfit(x,y,n) x 、y 为大小相等行或列向量,在是最小二乘意义上,将(x,y)拟合成次数为n 的多项式:1121)(+-++++=n n n p x p x p x p x p n例如: x=1:10;y=[193 226 240 244 257 260 274 297 350 420]; p = polyfit(x,y,3) p =0.9396 -12.9615 63.4777 141.7667y1=p(1)*x.^3+p(2)*x.^2+p(3)*x+p(4);xy[p,S] = polyfit(x,y,n) [p,S] = polyfit(x,y,3) p =0.9396 -12.9615 63.4777 141.7667 S =R: [4x4 double] df: 6normr: 8.0464 S.R ans =1.0e+003 *-1.4066 -0.1570 -0.0180 -0.0022 0 -0.0262 -0.0075 -0.00180 0 -0.0019 -0.00140 0 0 0.0005normr是残差的模,即:norm(y-y1)ans =8.0464[p,S,MU] = polyfit(x,y,n)[p,S,MU] = polyfit(x,y,3)p =26.0768 23.2986 18.6757 255.1312S =R: [4x4 double]df: 6normr: 8.0464MU =5.50003.0277MU是x均值和x的标准差即std(x)S.Rans =5.1959 0.0000 2.7682 0.00000 -3.7926 -0.0000 -2.37310 0 1.1562 0.00000 0 0 -2.0901P它等于:[p,S] = polyfit((x-mean(x))./std(x),y,3)p =26.0768 23.2986 18.6757 255.1312S =R: [4x4 double]df: 6normr: 8.0464>> S.Rans =5.1959 0.0000 2.7682 0.00000 -3.7926 -0.0000 -2.37310 0 1.1562 0.00000 0 0 -2.09015.2 多项式估计y= polyval(p,x)[y,DELT A] = polyval(p,x,S)y= polyval(p,x) 返回给定系数p和变量x值的多项式的预测y = P(1)*x^N + P(2)*x^(N-1) + ... + P(N)*x + P(N+1)x=1:10;y= polyval([3 2],x)y =5 8 11 14 17 20 23 26 29 32[3 2]有两个数,因此为一次多项式,即y=3x+2如:x=1:10;y=[193 226 240 244 257 260 274 297 350 420];p=polyfit(x,3)y1= polyval(p,x)norm(y-y1)ans =8.0464如果是矩阵,则polyval(p,x)为对应x的每一个预测值。

计量经济学常见问题汇总转载请联系计量经济学相关问题1计量经济学是分析啥的?包含些什么内容?计量经济学的主要⽤途或⽬的主要有两个⽅⾯:1、理论检验。
2、预测应⽤。
研究对象:计量经济学的两⼤研究对象:横截⾯数据(Cross-sectional Data)和时间序列数据(Time-series Data)。
前者旨在归纳不同经济⾏为者是否具有相似的⾏为关联性,以模型参数估计结果显现相关性;后者重点在分析同⼀经济⾏为者不同时间的资料,以展现研究对象的动态⾏为。
新兴计量经济学研究开始切⼊同时具有横截⾯及时间序列的资料,换⾔之,每个横截⾯都同时具有时间序列的观测值,这种资料称为追踪资料 (Panel data,或称⾯板资料分析)。
追踪资料研究多个不同经济体动态⾏为之差异,可以获得较单纯横截⾯或时间序列分析更丰富的实证结论。
涉及到的相关学科:计量经济学是结合经济理论与数理统计,并以实际经济数据作定量分析的⼀门学科。
计量经济学以古典回归分析⽅法为出发点。
依据数据形态分为:横截⾯数据回归分析、时间序列分析、⾯板数据分析等。
依据模型假设的强弱分为:参量计量经济学、⾮参量计量经济学、半参量计量经济学等。
常运⽤的软件:EViews、Gretl、MATLAB 、Stata、R、SAS、SPSS等……2什么叫做伪回归若是所建⽴的回归模型在经济意义上没有因果关系,那么这个就是伪回归,例如路边⼩树年增长率和国民经济年增长率之间存在很⼤的相关系数,但是建⽴的模型却是伪回归。
如果你直接⽤数据回归,那肯定存在正相关,⽽其实这个是没有意义的回归。
3在什么情况下,应将变量取对数再进⾏回归?为避免伪回归,消除异⽅差,在不改变时间序列的性质及相关性的前提下,为获得平稳数据,通常会对时间序列取⾃然对数。
对数据进⾏平稳性检验是研究中不可或缺的步骤,因为时间序列分析法只适⽤于平稳的数据。
那么什么情况下会对数据取对数呢?第⼀,关于对数的问题,若是⾃⼰选取的变量数据,⾥⾯有部分⼩于0,或者负数,需要重新考量下,看是否数据或者其他问题,此时肯定是没法取对数;第⼆,针对CD 等⽣产函数等类型的数据分析,由于建模需要,⼀般需要取对数,此类情况⼀般会在柯布道格拉斯函数基础上,引⼊新的变量,包括但不局限于资本和劳动等变量;第三,平时在⼀些数据处理中,经常会把原始数据取对数后进⼀步处理。

matlab 自相关法Matlab自相关法是一种常用的信号处理方法,在信号处理、统计分析等领域具有广泛的应用。
本文将介绍Matlab自相关法的基本原理、算法实现及其在实际应用中的应用案例。
一、Matlab自相关法的基本原理自相关法是一种基于信号的统计分析方法,用于研究信号的相关性和周期性。
在Matlab中,自相关函数可以通过调用相关函数实现。
自相关函数定义如下:Rxx(tau) = E(x(t)x(t+tau))其中,x(t)为原始信号,tau为时间延迟。
二、Matlab自相关法的算法实现1. 读取信号数据需要将待分析的信号数据读入到Matlab中,可以通过load函数或者importdata函数实现。
2. 计算自相关函数利用Matlab的相关函数,可以方便地计算自相关函数。
具体的调用方法为:Rxx = xcorr(x)其中,x为原始信号数据。
3. 绘制自相关函数图像通过调用plot函数,可以将自相关函数的结果以图像的形式展示出来。
可以设置横轴为时间延迟tau,纵轴为自相关函数的值Rxx。
三、Matlab自相关法的应用案例1. 信号分析自相关法可以用于信号的分析,比如检测信号中的周期性成分。
通过计算自相关函数,可以得到信号的周期性特征。
2. 语音识别在语音识别领域,自相关法被广泛应用。
利用自相关函数可以提取语音信号中的共振峰信息,从而实现语音识别。
3. 图像处理在图像处理中,自相关法可以用于图像的模板匹配。
通过计算图像的自相关函数,可以实现图像的特征匹配和目标检测。
四、总结本文介绍了Matlab自相关法的基本原理、算法实现及其在实际应用中的应用案例。
通过使用Matlab自相关函数,可以方便地进行信号分析、语音识别和图像处理等任务。
希望本文对读者理解和应用Matlab自相关法有所帮助。

MATLAB是一款功能强大的数学软件,广泛应用于科学计算、工程仿真、数据分析等领域。
自相关和偏相关是在时间序列分析中常用的统计方法,用于研究数据点之间的相关性和相关程度。
下面将分别对MATLAB中的自相关和偏相关进行详细介绍。
一、自相关1. 自相关的概念自相关是一种用于衡量时间序列数据中各个数据点之间相关性的统计方法。
在MATLAB中,自相关函数可以通过调用`autocorr`来实现。
自相关函数的输出结果为数据序列在不同滞后期下的相关系数,从而可以分析出数据在不同时间点上的相关程度。
2. 自相关的计算方法在MATLAB中,通过调用`autocorr`函数可以很方便地计算出时间序列数据的自相关系数。
该函数的语法格式为:```[r,lags] = autocorr(data,maxLag)```其中,`data`为输入的时间序列数据,`maxLag`为最大滞后期。
函数会返回计算得出的自相关系数数组`r`以及对应的滞后期数组`lags`。
3. 自相关的应用自相关函数可以用于分析时间序列数据中的周期性和趋势性,帮助我们了解数据点之间的相关关系。
通过自相关函数的计算和分析,我们可以找出数据序列中的周期模式,预测未来的趋势变化,以及识别数据中的潜在规律。
二、偏相关1. 偏相关的概念偏相关是用来衡量时间序列数据中两个数据点之间相关性的统计指标,消除了滞后效应对相关性的影响。
在MATLAB中,可以使用`parcorr`函数来计算偏相关系数。
偏相关系数可以帮助我们更准确地分析数据点之间的相关关系,找到数据中的特征和规律。
2. 偏相关的计算方法在MATLAB中,通过调用`parcorr`函数可以计算出时间序列数据的偏相关系数。
函数的语法格式为:```[acf,lag] = parcorr(data,maxLag)其中,`data`为输入的时间序列数据,`maxLag`为最大滞后期。
函数会返回计算得出的偏相关系数数组`acf`以及对应的滞后期数组`lag`。

利用MATLAB进行统计分析使用 MATLAB 进行统计分析引言统计分析是一种常用的数据分析方法,可以帮助我们理解数据背后的趋势和规律。
MATLAB 提供了一套强大的统计工具箱,可以帮助用户进行数据的统计计算、可视化和建模分析。
本文将介绍如何利用 MATLAB 进行统计分析,并以实例展示其应用。
一、数据导入和预处理在开始统计分析之前,首先需要导入数据并进行预处理。
MATLAB 提供了多种导入数据的方式,可以根据实际情况选择合适的方法。
例如,可以使用`readtable` 函数导入Excel 表格数据,或使用`csvread` 函数导入CSV 格式的数据。
导入数据后,我们需要对数据进行预处理,以确保数据的质量和准确性。
预处理包括数据清洗、缺失值处理、异常值处理等步骤。
MATLAB 提供了丰富的函数和工具,可以帮助用户进行数据预处理。
例如,可以使用 `fillmissing` 函数填充缺失值,使用 `isoutlier` 函数识别并处理异常值。
二、描述统计分析描述统计分析是对数据的基本特征进行概括和总结的方法,可以帮助我们了解数据的分布、中心趋势和变异程度。
MATLAB 提供了多种描述统计分析的函数,可以方便地计算数据的均值、标准差、方差、分位数等指标。
例如,可以使用 `mean` 函数计算数据的均值,使用 `std` 函数计算数据的标准差,使用 `median` 函数计算数据的中位数。
此外,MATLAB 还提供了 `histogram`函数和 `boxplot` 函数,可以绘制数据的直方图和箱线图,从而更直观地展现数据的分布特征。
三、假设检验假设检验是统计分析中常用的推断方法,用于检验关于总体参数的假设。
MATLAB 提供了多种假设检验的函数,可以帮助用户进行单样本检验、双样本检验、方差分析等分析。
例如,可以使用 `ttest` 函数进行单样本 t 检验,用于检验一个总体均值是否等于某个给定值。
可以使用 `anova1` 函数进行单因素方差分析,用于比较不同组之间的均值差异是否显著。

计量经济学简单线性回归OLS的Matlab程序wxh10002011-09-21先写OLS.m的M文件,用来代替regress函数;(目前对regress函数不太了解,这里特别感谢潘晓炜同学的提醒)-----------------------------------------------------------------------------------↓function [beta_0 beta_1]=OLS(y,x)%Ordinary Linear Regression%其中x,y为样本构成的向量;%回归方程为Simple regression: y=beta_0+x*beta_1+u;%y_mean=mean(y);%x_mean=mean(x);%beta_1=((x-x_mean)*(y-y_mean)')/((x-x_mean)*(x-x_mean)');%beta_0=y_mean-beta_1*x_mean;%其中u为服从N(0,sigma^2)随机变量;y_mean=mean(y);x_mean=mean(x);beta_1=((x-x_mean)*(y-y_mean)')/((x-x_mean)*(x-x_mean)');beta_0=y_mean-beta_1*x_mean;-----------------------------------------------------------------------------------↑然后写OLS_test.m的M文件,用来进行模拟;-----------------------------------------------------------------------------------↓function [b_0 b_1]=OLS_test(beta_0,beta_1,n,a,b,sigma)%已知beta_0,beta_1,由OLS回归得b_0,b_1.两者进行比较得到估计效果;%y=beta_0+beta_1*x+u来得到;%x为随机向量,u为服从N(0,sigma^2)随机变量;%n为模拟数据量,比如1,10,100,1000等;%x=a+b*rand(1,n);%产生(a,a+b)区间上的随机向量;%mu= ;sigma= ;%随机矩阵服从均值为mu,方差为sigma的正态分布%M= ;N= %M,N为产生[M,N]的随机矩阵%x=mu+sqrt(sigma)*randn(M,N);%x为新生成的矩阵[M,N],服从均值为mu,方差为sigma的正态分布;x=a+b*rand(1,n);%产生(a,a+b)区间上的随机向量;%随机矩阵服从均值为0,方差为sigma的正态分布u=sqrt(sigma)*randn(1,n);y=beta_0+beta_1*x+u;%用OLS函数进行回归即可:[beta_0 beta_1]=OLS(y,x);[b_0 b_1]=OLS(y,x);sprintf('已知参数\n\tbeta_0=%0.5g\n\tbeta_1=%0.5g\n模拟后,OLS估计值为\n\tbeta_0=%0.5g\n\tbeta_1=%0.5g',beta_0,beta_1,b_0,b_1) -----------------------------------------------------------------------------------↑运行结果如下:-----------------------------------------------------------------------------------↓>> [b_0 b_1]=OLS_test(20,0.7,2,1,99,1)ans =已知参数beta_0=20beta_1=0.7模拟后,OLS估计值为beta_0=19.394beta_1=0.72626>> [b_0 b_1]=OLS_test(20,0.7,100,1,99,1)ans =已知参数beta_0=20beta_1=0.7模拟后,OLS估计值为beta_0=19.894beta_1=0.70479>> [b_0 b_1]=OLS_test(20,0.7,10000,1,99,1)ans =已知参数beta_0=20beta_1=0.7模拟后,OLS估计值为beta_0=19.988beta_1=0.70018。

常用统计分析软件常用的统计分析软件有很多,下面我将介绍一些常见的统计分析软件及其特点。
1. SPSS(Statistical Package for the Social Sciences):是一款统计分析软件,具有强大的数据处理、数据分析和报告生成功能。
它可进行描述性统计、假设检验、方差分析、回归分析、聚类分析、因子分析等常用统计分析。
2. SAS(Statistical Analysis System):是一种完整的统计分析解决方案,包含数据管理、数据分析、统计建模和数据可视化等功能。
它适用于大规模数据的处理和分析,具有高效、稳定和灵活的特点。
3.R:是一种免费的开源统计分析软件,拥有丰富的统计分析函数和高级绘图功能。
R语言具有强大的数据处理能力和灵活的编程特点,适用于各种统计分析及数据可视化的需求。
4. Python:是一种通用的编程语言,也可以进行统计分析。
配合一些科学计算库(如NumPy、SciPy、Pandas等),Python可以进行各种统计分析任务,包括数据处理、数据分析、机器学习等。
5. Excel:是一种常用的电子表格软件,也可以进行一些简单的统计分析。
Excel提供了一些常用的统计函数和图表功能,对于小规模数据的分析和可视化比较便捷。
6.MATLAB:是一种功能强大的数学计算软件,也可以用于统计分析。
MATLAB提供了丰富的数学和统计函数,可以进行各种统计分析任务,包括回归分析、方差分析、时间序列分析等。
7. Stata:是一种统计分析软件,广泛应用于社会科学研究。
Stata 具有易用的用户界面和灵活的命令语言,提供了丰富的统计分析函数和专门的模块,满足各种统计分析需求。
8. Minitab:是一种易学易用的统计分析软件,广泛应用于工业和质量管理等领域。
Minitab提供了丰富的统计分析和质量管理工具,方便用户进行数据处理和分析,能够生成报告和图表。
9. Gretl:是一种专门用于计量经济学研究的统计分析软件。

8.9.因为n-1=14,所以样本容量为n=15。
b .RSS=TSS-ESS=66042-65965=77。
c .ESS 的自由度为2,因为它是一个三变量模型。
RSS 的自由度为12,因为15-3=12。
d .9988.02==TSS ESS R ,9986.01)1(122=--⋅--=-k n n R R 。
e .采用联合假设,即两个变量的系数联合或同时为零。
这个假设表明两个解释变量联合对应变量Y 无影响。
f .不能,因为它们是联合对Y 的影响,而不是各自的。
8.11a .所有解释变量都与应变量Y 正相关。
在其他条件保持不变的情况下,空调的BTU 比率每增加一个百分点,空调价格平均上升0.023元。
同样地,在其他条件不变时,能量效率每增加一个百分点,空调价格平均上升19.729元。
类似地,在其他条件不变时,设定数每增加一点,空调价格平均上升7.653元。
当1X =2X =3X =0时,空调价格平均为-68.236元。
b .因为84.02=R ,所以我们可以说84%被样本回归直线解释,拟合度相当高,回归结果有经济意义。
而且它说明了解释量对空调价格的影响。
c . 下面我们进行检验联合假设:0:20=βH vs 0:21>βH)15(753.16.4005.0023.0)(095.0222t Se t =>==-=∧∧ββ 所以我们拒绝零假设,也就是说空调的BTU 比率对价格有正向影响。
d .)15,3(F 3.287425.2641984.011484.0110.9522=>=---=---=k n R k R F 能够拒绝零假设:三个解释量在很大程度上没能解释空调价格的变动。
8.12a . 边际消费倾向是每额外增加1美元个人可支配收入所增加的消费支出,所以边际消费倾向就是2X 的系数,即MPC=0.93。

Matlab中的自相关与互相关分析方法介绍引言:自相关与互相关是信号处理领域中常用的分析方法。
在Matlab中,我们可以利用相关函数进行这些分析。
本文将介绍自相关与互相关的概念,以及在Matlab 中如何利用相关函数进行分析。
一、自相关分析自相关是一种用于分析信号的统计方法,它可以衡量信号在不同时间点间的相关性。
在Matlab中,我们可以使用xcorr函数进行自相关分析。
该函数的基本语法为:[R, lags] = xcorr(x)其中,x是输入信号,R是自相关结果,lags是延迟时间。
自相关分析结果的解释可以通过图形来进行。
可以使用stem函数绘制自相关信号的图像。
例如,下面的代码将绘制自相关结果的图像:stem(lags, R)title('自相关结果')xlabel('延迟时间')ylabel('相关系数')通过图像可以直观地观察到信号在不同时间点间的相关性。
自相关结果的峰值表示信号具有一定的周期性,在延迟时间上可以找到对应的周期。
二、互相关分析互相关用于分析两个信号之间的相关性。
在Matlab中,我们可以使用xcorr函数进行互相关分析。
该函数的基本语法为:[R, lags] = xcorr(x, y)其中,x和y是输入信号,R是互相关结果,lags是延迟时间。
互相关分析的结果也可以通过图形来进行解释。
可以同时绘制两个信号和它们的互相关结果。
例如,下面的代码将绘制两个信号和它们的互相关结果的图像:subplot(2, 1, 1)plot(x)title('信号x')xlabel('时间')ylabel('幅值')subplot(2, 1, 2)plot(y)title('信号y')xlabel('时间')ylabel('幅值')figure()stem(lags, R)title('互相关结果')xlabel('延迟时间')ylabel('相关系数')通过图像可以观察到两个信号之间的相关性。

matlab基础及在经济学与管理科学中的应用MATLAB是一种强大的数值计算和科学编程软件,广泛应用于经济学和管理科学领域。
它提供了许多功能和工具,可以帮助经济学家和管理科学家分析数据、建立模型、进行预测和优化问题等。
在经济学中,MATLAB可以用于经济模型的建立和求解。
经济学家可以使用MATLAB来构建供求模型、动态优化模型、一般均衡模型等,并通过数值方法求解这些模型。
此外,MATLAB还可以用于经济统计分析、计量经济学模型估计、博弈论分析等。
在管理科学中,MATLAB可以用于优化问题的求解。
管理科学家常常需要在资源有限的情况下做出最佳决策,例如生产调度、库存管理、运输路线规划等。
MATLAB提供了各种优化算法和工具,可以帮助管理科学家解决这些问题。
此外,MATLAB还具有数据可视化和绘图功能,可以帮助经济学家和管理科学家将数据以图表的形式展示出来,更好地理解和传达研究结果。
总之,MATLAB在经济学和管理科学中的应用非常广泛,它提供了丰富的数值计算和科学编程功能,可以帮助研究者进行数据分析、模型建立和优化问题求解等工作。
如何使用MATLAB进行数据分析一、引言MATLAB是一种强大的数据分析工具,广泛应用于各个领域。
在本文中,我们将介绍如何使用MATLAB进行数据分析。
我们将从数据预处理开始,包括数据清洗和数据变换;接着讨论数据可视化的方法,如绘制折线图、柱状图和散点图;最后,我们将探讨一些常用的数据分析技术,如回归分析和聚类分析。
二、数据预处理数据预处理是数据分析的重要一步。
首先,我们需要进行数据清洗,即处理数据中的缺失值、异常值和重复值。
MATLAB提供了许多函数来处理这些问题,如isnan()函数判断缺失值,isoutlier()函数判断异常值,unique()函数去除重复值。
此外,我们还可以对数据进行变换,以便更好地进行分析。
常用的数据变换方法包括对数转换、标准化和归一化等。
在MATLAB中,log()函数用于进行对数转换,zscore()函数可进行标准化,而minmax()函数则可实现归一化。
三、数据可视化数据可视化是数据分析中必不可少的一环。
通过可视化,我们可以更直观地理解数据的分布和关系。
在MATLAB中,我们可以使用plot()函数绘制折线图,bar()函数绘制柱状图,scatter()函数绘制散点图。
此外,MATLAB还提供了许多其他的绘图函数,如histogram()函数绘制直方图、pie()函数绘制饼图等,可以根据需要选择合适的函数进行数据可视化。
四、数据分析技术除了数据预处理和数据可视化,MATLAB还提供了丰富的数据分析技术。
其中,回归分析是用于分析两个或多个变量之间关系的方法。
MATLAB提供了regress()函数来进行回归分析,可以计算出拟合直线或曲线的系数和误差。
另外,聚类分析是将相似的对象组合在一起的方法。
MATLAB 中的kmeans()函数可以根据数据的特征将其分为多个簇。
除了回归分析和聚类分析,MATLAB还支持其他各种统计分析方法,如方差分析、主成分分析等。
根据具体需求,选择合适的方法进行数据分析。
Matlab中的参数估计方法介绍1. 引言参数估计是统计学中的一个重要概念,它涉及到对总体参数进行估计的方法和技巧。
在Matlab中,有多种参数估计的方法可以使用,可以根据具体问题和数据的分布特点选择合适的方法进行估计。
本文将介绍几种常见的参数估计方法,并通过代码示例展示其在Matlab中的应用。
2. 极大似然估计(Maximum Likelihood Estimation,MLE)极大似然估计是一种常用的参数估计方法,其核心思想是寻找最有可能产生观测数据的参数值。
在Matlab中,通过`mle`函数可以方便地进行极大似然估计。
以正态分布为例,假设观测数据服从正态分布,我们希望估计其均值和标准差。
首先,我们需要定义正态分布的似然函数,然后利用`mle`函数进行参数估计。
```matlabdata = normrnd(0, 1, [100, 1]); % 生成100个服从标准正态分布的观测数据mu0 = 0; % 均值的初始值sigma0 = 1; % 标准差的初始值paramEstimates = mle(data, 'distribution', 'normal', 'start', [mu0, sigma0]);```3. 最小二乘估计(Least Squares Estimation,LSE)最小二乘估计是一种通过最小化观测值与估计值之间的残差平方和来估计参数的方法。
在Matlab中,可以使用`lsqcurvefit`函数进行最小二乘估计。
以非线性回归为例,假设观测数据符合一个非线性模型,我们希望通过最小二乘估计来估计模型中的参数。
首先,我们需要定义模型函数和初始参数值,然后利用`lsqcurvefit`函数进行参数估计。
```matlabx = linspace(0, 10, 100)';y = 2 * exp(-0.5 * x) + 0.05 * randn(size(x)); % 生成符合非线性模型的观测数据model = @(theta, x) theta(1) * exp(-theta(2) * x); % 定义非线性模型函数theta0 = [1, 1]; % 参数的初始值thetaEstimates = lsqcurvefit(model, theta0, x, y);```4. 贝叶斯估计(Bayesian Estimation)贝叶斯估计是一种基于贝叶斯理论的参数估计方法,它使用观测数据和先验信息来计算参数的后验概率分布。
MATLAB中基于GARCH模型对股票指数的拟合与预测——以恒生指数为例周丹文(南京审计大学, 江苏 南京 211815)[摘 要]从股票指数的基础时间序列出发,分析了时间序列的性质以及股票指数的特性。
并以此为基础,运用经济统计与计量经济学,选取恒生指数2009年10月至2019年10月十年间日收盘价进行分析,同时利用MATLAB的金融工具分析箱,建立GARCH模型,对恒生指数的日收益率进行建模与预测。
结果表明,GARCH模型能够较好地拟合样本数据的对数收益率;在短期内,模型同样拥有较好的预测效果。
[关键词]股票指数;时间序列分析;GARCH;MATLAB[中图分类号] F830.59 [文献标识码] A [文章编号] 2095-3283(2020)04-0077-04 Fitting and Prediction of Stock Index Based on GARCH Model in MATLAB— Take the Hang Seng Index as An ExampleZhou Danwen(Nanjing Audit University ,Nanjing Jiangsu 211815)Abstract: Based on the basic time series of stock index, this paper analyzes the properties of time series and stock index. On this basis, with the knowledge of economic statistics and econometrics, the daily closing price of Hang Seng Index from October 2009 to October 2019 is selected to analysis. GARCH models are established by using the Financial Toolbox of MATLAB to model and predict the daily yield of Hang Seng Index. The results show that GARCH model can fit the logarithmic rate of return of sample data well, and in the short term, the model also has a good prediction effect.Key Words: Stock Index; Time Series Analysis; GARCH; MATLAB一、研究背景(一)股票指数股票指数是用来度量股票行情的一种指标, 反映了股票市场总体价格水平及其变动趋势,一般由证券交易所或其他金融服务机构编制,用以为股民提供一个衡量股市价值变化的参考依据。
MATLAB中的多变量数据分析方法探究导言多变量数据分析是一种通过研究多个相关变量之间的关系来揭示数据内在规律的方法。
在科学研究和实践应用中,我们经常需要分析多个变量之间的相互作用,以便进行预测、优化方案或者发现变量之间的相关机制。
MATLAB作为一种强大的数学计算工具,提供了丰富的多变量数据分析方法来应对各种问题。
一、主成分分析主成分分析(Principal Component Analysis, PCA)是一种常用的无监督学习方法,用于将高维数据降维到低维空间。
其目标是通过找到数据中最大方差的方向,实现数据的降维,同时保留尽可能多的信息。
PCA可以帮助我们获得数据集的主要结构和特征,用于可视化、分类和聚类等任务。
在MATLAB中,我们可以使用pca函数进行主成分分析。
该函数根据输入的数据矩阵,计算出数据的主成分,并返回主成分的系数矩阵、方差贡献率以及属性载荷矩阵等信息。
通过分析主成分的方差贡献率,我们可以选择适合的维度来表示原始数据。
二、因子分析因子分析(Factor Analysis)是一种统计方法,用于分析多个变量之间的相关性和结构。
其基本思想是将多个观测变量解释为共同驱动的一组潜在因子,从而实现数据的降维和模型简化。
在MATLAB中,我们可以使用factoran函数进行因子分析。
该函数通过最大似然估计方法,估计因子的系数矩阵和测量误差,从而得到潜在因子和观测变量之间的关系。
通过分析因子的载荷矩阵,我们可以了解变量之间的共同因素以及它们与潜在因子之间的关系。
三、聚类分析聚类分析(Cluster Analysis)是一种将样本集合划分为相似子集的无监督学习方法。
它通过计算样本之间的相似度来度量样本的距离,并将相似的样本聚集在一起。
聚类分析可以帮助我们发现数据中的群组结构和相似模式。
在MATLAB中,我们可以使用kmeans函数进行聚类分析。
该函数通过迭代计算样本与聚类中心之间的距离,将样本分配到不同的簇中。
第一节相关分析1.1协方差命令:C = cov(X)当X为行或列向量时,它等于var(X) 样本标准差。
X=1:15;cov(X)ans =20>> var(X)ans =20当X为矩阵时,此时X的每行为一次观察值,每列为一个变量。
cov(X)为协方差矩阵,它是对称矩阵。
例:x=rand(100,3);c=cov(x)c=0.089672 -0.012641 -0.0055434-0.012641 0.07928 0.012326-0.0055434 0.012326 0.082203c的对角线为:diag(c)ans =0.08970.07930.0822它等于:var(x)ans =0.0897 0.0793 0.0822sqrt(diag(cov(x)))ans =0.29950.28160.2867它等于:std(x)ans =0.2995 0.2816 0.2867命令:c = cov(x,y)其中x和y是等长度的列向量(不是行向量),它等于cov([x y])或cov([x,y])例:x=[1;4;9];y=[5;8;6];>> c=cov(x,y)c =16.3333 1.16671.16672.3333>> cov([x,y])ans =16.3333 1.16671.16672.3333COV(X)、 COV(X,0)[两者相等] 或COV(X,Y)、COV(X,Y,0) [两者相等],它们都是除以n-1,而COV(X,1) or COV(X,Y,1)是除以nx=[1;4;9];y=[5;8;6]; >> cov(x,y,1) ans =10.8889 0.7778 0.7778 1.5556它的对角线与var([x y],1) 相等 ans =10.8889 1.5556 协差阵的代数计算: [n,p] = size(X);X = X - ones(n,1) * mean(X);Y = X'*X/(n-1); Y 为X 的协差阵1.2 相关系数(一)命令:r=corrcoef(x)x 为矩阵,此时x 的每行为一次观察值,每列为一个变量。
r 为相关系数矩阵。
它称为Pearson 相关系数例:x=rand(18,3);r=corrcoef(x) r =1.0000 0.1509 -0.2008 0.1509 1.0000 0.1142 -0.2008 0.1142 1.0000 r 为对称矩阵,主对角阵为1 命令:r=corrcoef(x,y)其中x 和y 是等长度的列向量(不是行向量),它等于cov([x y])或cov([x,y]),或x 和y 是等长度的行向量,r=corrcoef(x,y)它则等于r=corrcoef(x ’,y ’), r=corrcoef([x ’,y ’])例:x=[1;4;9];y=[5;8;6]; corrcoef(x,y) ans =1.0000 0.1890 0.1890 1.0000 corrcoef([x,y]) ans =1.0000 0.1890 0.1890 1.0000 C = COV(X)R ij =C(i,j)/SQRT(C(i,i)*C(j,j))如:X=[1 2 7 4 ;5 12 7 8;9 17 11 17];()()()()y y x x y y x x 22∑∑∑-⋅---=rcov(X) ans =16.0000 30.0000 8.0000 26.0000 30.0000 58.3333 13.3333 46.6667 8.0000 13.3333 5.3333 14.6667 26.0000 46.6667 14.6667 44.3333 corrcoef(X) ans =1.0000 0.9820 0.8660 0.9762 0.9820 1.0000 0.7559 0.9177 0.8660 0.7559 1.0000 0.9538 0.9762 0.9177 0.9538 1.0000 则有:30/sqrt(16*58.3333) ans =0.9820命令:[r,p]=corrcoef[….]它还将返回p 值,原假设是变量之间不相关。
例:x = [430 335 520 490 470 210 195 270 400 480]; y=[30 21 35 42 37 20 8 17 35 25]; [r,p]=corrcoef(x,y) r =1.0000 0.8594 0.8594 1.0000 p =1.0000 0.0014 0.0014 1.0000P 矩阵主对角矩阵全为1,当总体变量X 和Y 都服从正态分布,并且总体相关系数等于0时,有:)2(~122---=n t rn r tP 矩阵的计算,即上例中0.0014的算法。
4.75408594.012108594.01222=--⨯=--=rn r t (1-tcdf(4.7540,8))*2 得:0.0014在显著性水平0.05下,0.0014小于0.05,拒绝两总体不相关的原假设,即销售量与气温相关。
命令:[r,p,rlo,rup]=corrcoef(….)rlo 与rup 是与r 矩阵大小相同的矩阵,rlo 为相关系数r 的下限,rup 为相关系数r的上限。
在缺失情况下,置信度为95%。
例:x = [430 335 520 490 470 210 195 270 400 480]; y=[30 21 35 42 37 20 8 17 35 25]; [r,p,rlo,rup]=corrcoef(x,y) r =1.0000 0.8594 0.8594 1.0000 p =1.0000 0.0014 0.0014 1.0000 rlo =1.0000 0.5006 0.5006 1.0000 rup =1.0000 0.9662 0.9662 1.0000因此销售量与气温相关系数95%的置信区间为 [0.5006,0.9662]如果要求99%的销售量与气温相关系数的置信区间: [r,p,rlo,rup]=corrcoef(x,y,'alpha',0.01) 注意不是:[r,p,rlo,rup]=corrcoef(x,y,0.01) r =1.0000 0.8594 0.8594 1.0000 p =1.0000 0.0014 0.0014 1.0000 rlo =1.0000 0.3071 0.3071 1.0000 rup =1.0000 0.9786 0.9786 1.0000得销售量与气温相关系数99%的置信区间为[0.3071,0.9786]比95%的置信区间[0.5006,0.9662]更宽。
rlo和rup具体怎么算出来的还没弄明白。
帮助文件是这样说的:The confidence bounds are based on an asymptotic normal distribution of 0.5*log((1+R)/(1-R)), with an approximate variance equal to 1/(n-3).命令:[...]=corrcoef(...,'param1',val1,'param2',val2,...)例:[...]=corrcoef(...,'alpha',0.01) 是求在置信度为99%,求r置信区间。
[...]=corrcoef(...,'rows', 'all') 只计算两个变量(两列)所有观察值(所有行)都存在的两个变量。
缺失情况下,就是用这种方法计算。
例:x =[ 3 9 2 345 NaN6 66NaN 4 9 78 7 33 99 14 11 22][r,p,rlo,rup]=corrcoef(x,'rows', 'all')r =NaN NaN NaN NaNNaN NaN NaN NaNNaN NaN 1.0000 -0.5296NaN NaN -0.5296 1.0000p =NaN NaN NaN NaNNaN NaN NaN NaNNaN NaN 1.0000 0.3587NaN NaN 0.3587 1.0000rlo =NaN NaN NaN NaNNaN NaN NaN NaNNaN NaN 1.0000 -0.9623NaN NaN -0.9623 1.0000rup =NaN NaN NaN NaNNaN NaN NaN NaNNaN NaN 1.0000 0.6619NaN NaN 0.6619 1.0000说明:NaN表示不存在数据,在x中,只有第四列和每五列每行的数据都存在,[r,p,rlo,rup]=corrcoef(x,'rows', 'all')只计算第三列和第四列的相关系数及相应的区间。
即:[r,p,rlo,rup]=corrcoef(x(:,3), x(:,4))r =1.0000 -0.5296-0.5296 1.0000p =1.0000 0.35870.3587 1.0000rlo =1.0000 -0.9623-0.9623 1.0000rup =1.0000 0.66190.6619 1.0000命令:[r,p,rlo,rup]=corrcoef(x,'rows', 'complete')如果某行含有N aN,则去掉所有含NaN的行,再计算相关系数和区间。
例:x =[ 3 9 2 345 NaN6 66NaN 4 9 78 7 33 99 14 11 22][r,p,rlo,rup]=corrcoef(x,'rows', 'complete')r =1.0000 0.3883 0.6080 -0.76300.3883 1.0000 -0.4956 0.29950.6080 -0.4956 1.0000 -0.9771-0.7630 0.2995 -0.9771 1.0000p =1.0000 0.7462 0.5840 0.44750.7462 1.0000 0.6699 0.80640.5840 0.6699 1.0000 0.13650.4475 0.8064 0.1365 1.0000rlo =1 NaN NaN NaNNaN 1 NaN NaNNaN NaN 1 NaNNaN NaN NaN 1rup =1 NaN NaN NaNNaN 1 NaN NaNNaN NaN 1 NaNNaN NaN NaN 1[r,p,rlo,rup]=corrcoef(x,'rows', 'complete')与去掉二、三行所得矩阵再求corrcoef相同。