连续传递函数离散化的方法与原理
- 格式:doc
- 大小:3.31 MB
- 文档页数:46


连续传递函数离散化的方法与原理连续传递函数离散化是将连续时间域中的传递函数转换为离散时间域中的传递函数的过程。
在控制系统设计中,离散化是非常重要的一步,因为大多数数字控制器本质上只能处理离散的输入和输出信号。
离散化方法的选择对系统的稳定性、性能和可实现性都有很大的影响。
离散化方法分为两大类:时域方法和频域方法。
时域方法根据传递函数的时间响应,或者根据传递函数的微分方程进行转换。
频域方法通过拉普拉斯变换和z变换之间的等价关系进行转换。
时域离散化方法:1. 脉冲响应不变法(Impulse Invariance Method):这是最常用的离散化方法之一、它通过将连续时间系统的脉冲响应对应到离散时间系统的单位冲激响应上来实现离散化。
该方法的原理是保持连续系统和离散系统的单位冲激响应相同,从而尽可能保持系统的动态特性。
2. 零阶保持法(Zero Order Hold Method):这个方法假设连续时间系统在每个采样周期内是恒定的,即将采样周期内的连续时间系统输出等效为一个恒定值。
这个方法的原理是根据离散系统的输出间隔和连续时间系统的采样间隔,使用插值方法得到离散系统的输出值。
3. 一阶保持法(First Order Hold Method):这个方法在零阶保持法的基础上改进,考虑了连续时间系统在每个采样周期内的变化趋势。
它假设连续时间系统在每个采样周期内是线性变化的。
通过插值方法得到离散系统的输出值。
4. 向后微分法(Backward Difference Method):这个方法根据连续时间系统微分方程中的向后差分近似来实现离散化。
它假设离散时间系统输出的变化率等于连续时间系统输出的变化率。
频域离散化方法:1. 频率响应匹配法(Frequency Response Matching Method):这个方法将连续时间系统和离散时间系统的频率响应函数进行匹配,使它们在一定频率范围内的增益和相位相近。
通过频率响应函数的等价性,可以使用拉普拉斯变换和z变换之间的关系得到离散时间系统的传递函数。
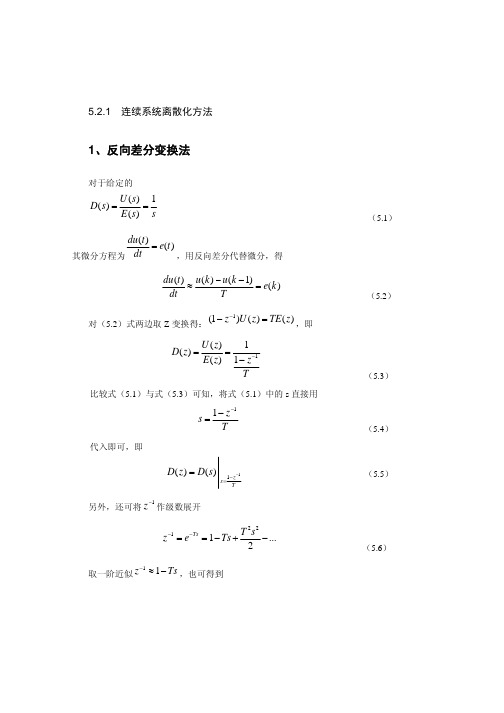

连续函数离散化-以SOGI为例0. 引⾔0.1 本⽂内容基于SOGI函数,将s域传递函数转换为离散的z域函数,并以m语⾔形式进⾏实现,在simulink中封装为m-function并进⾏验证0.2 学到什么离散化⽅法函数程序实现⽅法1. SOGI简介以TI官⽅⽂档中单相锁相环中SOGI应⽤为例框图如下所⽰正弦信号经过SOGI可得到同相信号及正交信号2. 传递函数同相传递函数H d(s)=v′v(s)=kωn ss2+kωn s+ω2n正交信号传递函数为H q(s)=qv′v(s)=kω2ns2+kωn s+ω2n3. 离散化采⽤双线性变换将s域函数离散⾄Z域3.1 ⼿动离散双线性变换公式为s=2T sz−1 z+1将式3代⼊式1得到H d(z)=kωn2T sz−1z+1(2T sz−1z+1)2+kωn(2T sz−1z+1)+ω2n这⾥使⽤以下两个替换x=2kωn T sy=(ωn T s)2得到H d (z )=x x +y +4+−x x +y +4z −21−2(4−y )x +y +4z −1−x −y −4x +y +4z −2=b 0+b 2z −21−a 1z −1−a 2z −2同理得到正交函数的离散形式H q (z )=k ⋅y x +y +4+2k ⋅y x +y +4z −1+k ⋅y x +y +4z −21−2(4−y )z −1−x −y −4z −2=qb 0+qb 1z −1+qb 2z −21−a 1z −a 2z 3.2 基于MATLAB 的离散⽅法看完上⾯的离散过程,很明显,太⿇烦,有没有简单点的⽅法呢?哎,还真有,MATLAB 只需要⼀条命令就能搞定MATLAB 中c2d 命令可通过多种离散⽅法将连续函数离散化,这⾥为保持⼀致,同样以双线性变换(tustin )为例进⾏介绍(了解更多c2d 命令,请点击)具体⽤法如下sysd = c2d(sys,Ts,'method')其中,sys 与sysd 分别为离散前后函数,Ts 为采样周期,method 为离散化⽅式,这⾥就是tustin直接给出离散过程的MATLAB 代码%%定义s 为传递函数s = tf('s');%%定义各参数k = 0.5;Wn = 100*pi; %%50HzTs = 1e-4; %%10kHz%%写出传递函数Hd_s = k*Wn*s/(s^2+k*Wn*s+Wn^2);Hq_s = k*Wn^2/(s^2+k*Wn*s+Wn^2);Hd_z = c2d(Hd_s,Ts,'tustin')Hq_z = c2d(Hq_s,Ts,'tustin')运⾏结果为Hd_z =0.007791 z^2 - 0.007791-----------------------z^2 - 1.983 z + 0.9844Sample time: 0.0001 secondsDiscrete-time transfer function.Hq_z =0.0001224 z^2 + 0.0002448 z + 0.0001224---------------------------------------z^2 - 1.983 z + 0.9844Sample time: 0.0001 secondsDiscrete-time transfer function.3.3 对⽐()()()()()()()()()上⾯已经给出了采⽤MATLAB进⾏离散的结果,采⽤同样的参数,这⾥基于式5-8,给出传统计算⽅式的结果Parameter value Parameter valueb00.0078qb00.00012238b10qb10.00024476b2-0.0078qb20.00012238a1 1.9834a2-0.9844可能会看到,这⾥系数正负号与MATLAB计算出结果有所不同,这⾥实际结果没错哈,认为错了的⾃⼰好好检查!4.SOGI的程序实现既然已经得到离散的SOGI函数,如何将其写成程序呢,这⾥以MATLAB语⾔为例,C语⾔同理4.1 离散序列的获得根据式7和8,我们知道U o(z) i(z)=b0+b2z−21−a1z−1−a2z−2U qo(z)i==qb0+qb1z−1+qb2z−2 1−a1z−1−a2z−2容易写成序列⽅程U o(k)−a1U o(k−1)−a2U o(k−2)=b0U i(k)+b2U i(k−2)U qo(k)−a1U qo(k−1)−a2U qo(k−2)=qb0U i(k)+qb1U i(k−1)+qb2U i(k−2)4.2 封装⼀个m-function根据上⾯的式⼦我们很容易可以写出相应的程序,但为了在simulink中验证程序的正确性,我们在这⾥把SOGI封装为⼀个m-function块以便使⽤不了解Matlab的function块功能的⾃⾏百度很容易知道,对于⼀个完整的SOGI函数,有⼀个输⼊端,两个输出端。

传递函数离散化公式函数离散化是指将连续函数转化为离散函数,即在一定的区间内将连续函数的取值按照一定的间隔进行采样。
离散化公式的设计需要考虑到采样间隔的选择、采样点的选取以及近似误差的控制等因素。
下面介绍两种常见的离散化公式:等间隔离散化和最小二乘离散化。
1.等间隔离散化:等间隔离散化是指将函数的定义域等距地划分成若干个小区间,并在每个区间内选择一个采样点。
等间隔离散化的离散化公式如下:x_i=a+i*h,i=0,1,2,...,N其中,x_i是第i个采样点的坐标,a是定义域的起始点,h是采样的间隔,N是离散化的个数。
2.最小二乘离散化:最小二乘离散化是一种基于最小二乘法的离散化方法,它通过最小化离散函数与原始连续函数之间的均方误差来选择合适的采样点。
最小二乘离散化的离散化公式如下:E=Σ[f(x)-f_i(x_i)]^2其中,E是误差,f(x)是原始连续函数,f_i(x_i)是离散函数,x_i 是采样点的坐标。
在最小二乘离散化中,我们需要根据给定的误差函数f(x)来选择合适的离散函数f_i(x_i)。
具体的选择方式包括:2.1多项式插值:多项式插值是一种常用的最小二乘离散化方法,它通过在每个小区间内使用一个多项式来逼近原始函数。
插值公式如下:f_i(x)=a_0+a_1*(x-x_i)+a_2*(x-x_i)^2+...+a_n*(x-x_i)^n其中,a_0,a_1,...,a_n是待定系数,n是多项式的次数。
2.2样条插值:样条插值是一种更加平滑的最小二乘离散化方法,它通过在每个小区间内使用多个低次多项式来逼近原始函数。
样条插值公式如下:f_i(x)=a_0+a_1*(x-x_i)+a_2*(x-x_i)^2+...+a_n*(x-x_i)^n,x∈[x_i,x_{i+1}]其中,a_0,a_1,...,a_n是待定系数,n是每个小区间内多项式的次数。
需要注意的是,离散化公式的选择应根据具体情况进行判断。

传递函数离散化是指将连续的传递函数模型离散化为离散的点,以便进行数值计算。
传递函数是一种常用的电路建模方法,它可以用来描述电路的频率响应特性。
传递函数离散化的基本思想是,通过对传递函数进行采样,将连续的传递函数转换为离散的点。
这样就可以使用计算机来进行数值计算了。
传递函数离散化的方法有很多种,例如:
•均匀采样法:在频率范围内均匀地采样传递函数,得到若干个离散点。
•重心采样法:在频率范围内的重心处采样传递函数,得到若干个离散点。
•自适应采样法:根据传递函数的形态自动调整采样点的分布,使得采样点能够更准确地反映传递函数的形态。
传递函数离散化是一种常用的数值计算方法,它可以用于对电路的频率响应特性进行建模和分析。
Tustin方法(也称为Bilinear变换或双线性变换)是一种用于将连续时间系统(模拟系统)离散化为离散时间系统的方法之一。
它是一种广泛使用的数值方法,尤其适用于将连续时间系统转换为数字控制系统。
Tustin方法的离散化步骤如下:1. 连续时间系统:首先,考虑一个具有传递函数H(s)的连续时间系统,其中s是复变量。
传递函数通常具有以下形式:H(s)=N(s) D(s)其中,N(s)和D(s)是多项式,表示系统的分子和分母。
2. 替换s:使用Tustin方法,我们将s替换为离散时间z上的特定映射。
Tustin方法使用双线性变换:s=2Tz−1 z+1其中,T是采样时间。
3. 替换H(s):将s替换为上述表达式,得到离散时间系统的传递函数:H(z)=N(2Tz−1z+1) D(2Tz−1z+1)4. 优化H(z):通常,为了方便分析和实现,可以对H(z)进行代数化简,例如通过因式分解或部分分数展开。
5. 数字实现:将H(z)转换为数字控制系统的形式,例如差分方程或脉冲响应。
示例:假设有一个连续时间系统的传递函数为:H(s)=s+1s2+3s+2采样时间T为 0.1 秒,应用Tustin方法:s=2Tz−1 z+1将其代入传递函数,进行代数化简,最终得到离散时间系统的传递函数。
这就是Tustin方法的基本过程。
它是一种将连续时间系统转换为离散时间系统的常用方法,具有一定的数值稳定性和频率响应特性。
在数字控制系统设计中,经常使用这样的方法来进行系统离散化。
传递函数离散化为差分方程
传递函数是控制系统中非常重要的概念,它是用于描述输入和输
出之间关系的数学表达式。
但是,在处理实际的控制系统问题时,常
常需要将传递函数离散化为差分方程,以便在数字计算机上进行处理。
下面,我们将分步骤阐述如何将传递函数离散化为差分方程。
第一步:将传递函数转化为拉氏变换
在进行离散化之前,需要将传递函数转化为拉氏变换。
拉氏变换是用
于将时域信号转化为复频域信号的数学工具。
将传递函数转化为拉氏
变换的过程,可以使用MATLAB等数学软件进行实现。
第二步:将拉氏变换转化为Z变换
将传递函数转化为拉氏变换后,需要将其进一步转化为Z变换。
Z变换是一种用于将离散时间信号转化为复频域信号的数学工具,在数字控
制系统中得到广泛应用。
第三步:将Z变换离散化为差分方程
将Z变换离散化为差分方程是离散化传递函数的最后一步。
差分方程
是描述离散时间系统的数学表达式,可以用于数值计算和仿真。
总结:传递函数通过拉氏变换和Z变换的转化,最终可以离散化
为差分方程,这使得设计师能够更好地理解和处理数字控制系统的问题。
离散化传递函数的过程非常重要,它是数字控制系统工程中的基
本步骤。
希望读者能够通过本篇文章,更好地理解如何将传递函数离
散化为差分方程。
连续函数离散化 Prepared on 22 November 2020连续函数离散化替换法传递函数是控制系统应用最广泛的模型描述形式,连续系统为S域的传递函数G(S),离散系统为Z域的脉冲传递函数G(Z)。
替换法的基本思想:对给定的连续系统模型G(S),设法找到S域到Z域的某种映射关系,将S域的变量映射到Z平面上,由此得到与连续系统G(S)相对应的离散系统的脉冲传递函数G(Z)。
然后,再由G(Z)通过Z反变换得到系统的时域离散模型——差分方程,从而快速求解。
根据Z变换理论,S域到Z域的最基本的映射关系是:Ts e Z =或Z Ts ln 1= 其中T是采样周期若直接将这个映射关系代入G(S)得到G(Z)将会很复杂,不便于计算,实际应用中是利用Z变换理论的基本映射关系进行简化处理,得到近似的离散模型。
简单替换法由幂级数展开式: +++++=!!212n x x x e nx取近似式:Ts e Z Ts +≈=1或:TZ s 1-= 用此式代入G(S)就得到G(Z),这就是简单替换法,又称Euler 法。
例:二阶连续系统s s s U s Y s G 50400)()()(2+==,001.0=T 解:简单替换法TZ s 1-=代入G(s) 001.0=T 代入双线性替换法 取近似式:2121Ts Tse Z Ts -+==或)1()1(2+-=Z T Z s 用此式代入G(S)就得到G(Z),这就是双线性替换法,又称Tustin 变换。
相当于数值积分法中的梯形法,有较好的性能。
例:二阶连续系统ss s U s Y s G 50400)()()(2+==,001.0=T 用双线性替换法建立差分方程。
解:双线性替换:)1()1(2+-=z T z s 代入G(s) 001.0=T 代入域离散相似法离散相似法将连续系统模型处理成与之等效的离散模型的一种方法。
设计一个离散系统模型,使其中的信息流与给定的连续系统中的信息流相似。
目录第一章模拟化设计基础 1 第一节步骤 1 第二节在MATLAB中离散化 3 第三节延时e-Ts环节的处理 5 第四节控制函数分类 6 第二章离散化算法10 摘要10 比较11 第一节冲击响应不变法(imp,无保持器直接z变换法) 11 第二节阶跃响应不变法(zoh,零阶保持器z变换法) 11 第三节斜坡响应不变法(foh,一阶保持器z变换法) 11 第四节后向差分近似法12 第五节前向差分近似法14 第六节双线性近似法(tustin) 15 第七节预畸双线性法(prevarp) 17 第八节零极点匹配法(matched) 18 第三章时域化算法19 第一节直接算法1—双中间变量向后递推19 第二节直接算法2—双中间变量向前递推20 第三节直接算法3—单中间变量向后递推21 第四节直接算法4—单中间变量向前递推(简约快速算法) 21 第五节串联算法22 第六节并联算法23 第四章数字PID控制算法24 第一节微分方程和差分方程25 第二节不完全微分25 第三节参数选择26 第四节c51框架27 第五章保持器33 第一节零阶保持器33 第二节一阶保持器30 附录两种一阶离散化方法的结果的比较31第一章 模拟化设计基础数字控制系统的设计有两条道路,一是模拟化设计,一是直接数字设计。
如果已经有成熟的模拟控制器,可以节省很多时间和部分试验费用,只要将模拟控制器离散化即可投入应用。
如果模拟控制器还不存在,可以利用已有的模拟系统的设计经验,先设计出模拟控制器,再进行离散化。
将模拟控制器离散化,如果用手工进行,计算量比较大。
借助数学软件MATLAB 控制工具箱,可以轻松地完成所需要的全部计算步骤。
如果需要的话,还可以使用MATLAB 的SIMULINK 工具箱,进行模拟仿真。
第一节 步骤步骤1 模拟控制器的处理在数字控制系统中,总是有传输特性为零阶保持器的数模转换器(DAC ),因此,如果模拟控制器尚未设计,则应以下图的方式设计模拟控制器,即在对象前面加上一个零阶保持器,形成一个新对象Ts 1e G s s ()--,然后针对这个新对象求模拟控制器D(s)。
事实上,模拟控制器一般是已经设计好的,无法或不方便更改了,离散化后的系统只好作为近似设计了。
然而,按照上述思路,可否将已有的控制器除以一个零阶保持器再离散化呢?还没有这方面的实际经验。
D(s)xue-模拟控制器1-e -TssG(s)对象以下假设选定的G(s),D(s)如下图,而且不对G(s)作添加保持器的预处理。
xue-D(s)=8s+2s+15.G(s)=20s(s+2)步骤2 离散化模拟控制器离散化模拟控制器之前,先要确定离散化算法和采样时间。
离散化算法有好几种,第二章中有详细的论述,现假定采用双线性变换法。
确定采样时间,需要考虑被控对象的特性,计算机的性能,以及干扰信号的影响等,初步可按采样时间T<0.1Tp ,Tp 为被控对象时间常数,或T=(0.125~0.25)τ,为被控对象的纯滞后,初步确定后再综合平衡其它因素,当然这需要一定的经验,现在假定取0.05秒。
假设模拟控制器为s 2D s 8s 15+=⋅+(),在MATLAB 中,用c2d 函数进行离散化,过程为:转换结果为:xue-D(z)=6.1091(z-0.9048)z-0.4545D(s)=8s+2s+15.G(s)=20s(s+2)步骤3 检验数字控制器的性能数字控制器的性能项目比较多,我们仅以直流增益,频率特性,零极点分布说明。
直流增益 dcgain(dz)返回直流增益1.0667ds=zpk(-2,-15,8) %建立模拟控制器的s 传递函数dz=c2d(ds,0.05,'tustin') %将模拟控制器按tustin 方法转换为z 传递函数的数字控制频率特性 bode(ds,'r',dz,'g') 伯德图,见下页左图 零极点分布 pzmap(dz) 零极点分布图,见下页右图步骤4 离散化控制对象为了进行模拟仿真,需要对控制对象进行离散化,由于步骤1所说的原因,应把被控对象视为零阶保持器与原对象的串连,即应对Ts1e G s s ()--进行离散化,这时可在c2d 函数中使用零阶保持器(zoh)方法,如果认为不需要添加零阶保持器,即直接对G(s)离散化,则应在c2d 函数中使用冲击响应不变法(imp )。
借用零阶保持器(zoh)方法,将对象20G s s s 2()()=+带一阶保持器离散化的过程如下:转换结果为:D(z)xue -D(z)=6.1091(z-0.9048)z-0.4545G1(z)=Z(1-e-TssG(s))G1(z)=0.024187(z-0.9672)(z-1)(z-0.9048)步骤5 模拟仿真求离散系统的闭环传递函数和连续系统的闭环传递函数。
离散系统的闭环传递函数为:CZ D z G 1z TR 1D z G 1z ()()()()=+连续系统的闭环传递函数为:CS D s G s TR 1D s G s =+()()()()用MATLAB 算TR CZ 与TR CS :结果为: C Z 2 0.14776(z-0.9048)(z-0.9048)(z-1)(z-0.4545)(z+0.9672)T R (z-0.4545)(z-0.9047)(z-0.9048)(z-1)(z -1.307z+0.5975)=trcz=dz*g1z/(1+dz*g1z) trcs=ds*gs/(1+ds*gs)...... %模拟控制器D(s)转换为D(z)的过程见前 gs=zpk([ ],[0,-2],20) %建立对象的s 传递函数g1z=c2d(gs,0.05,'zoh') %借用c2d 函数进行带零阶保持器的对象的离散化2CS 22160s(s +2)(s +15)TR s(s +15)(s +2)(s +15s +160)=用MATLAB 函数STEP 画阶跃响应图形:响应图形为:步骤6 求数字控制器的时域表达式 上面已经求出, 连续传递函数s 2D s 8s 15+=+⋅()的tustin 离散式为11U z 61091z 09048 6.1091-5.527z D z E z z 0454*******z ---===--().(.)()()..,或 11U z 61091E z 5527E z z 04545U z z ().().().()--=-+。
对上式取z 反变换,得时域表达式u k 61091e k 5527e k 104545u k 1=--+-().().().(),根据此式就可以写出计算u k ()的程序代码来了。
除上述步骤之外,在编写程序代码时,还需要考虑几个问题: ① ADC 位数ADC 位数是一个硬件问题,在系统设计时,就应该结合控制算法,仔细分析ADC 位数对控制精度的影响。
② 数据类型在控制算法中有3种数据类型可以采用:无符号整数,定点数,浮点数。
我们知道,无符号整数运算既是最简单和速度最快的运算,又是定点数运算和浮点数运算的基础。
在数据动态范围比较小的情况下,应尽可能用无符号整数运算代替定点数运算和浮点数运算。
浮点数运算是一整套运算,包括加,减,乘,除,对阶,规格化,溢出处理等一系列子程序,使用浮点数的程序,将占用比较多的代码空间和比较长的运行时间。
不论使用汇编语言还是c 语言,对于是否使用浮点数运算,都应进行比较仔细的酌斟。
③ 数值计算误差数值计算引入的误差有3个方面,一是定点数字长不够或者浮点数有效数字过少,一是两个相近的数相减,一是加减乘除次数过多。
在程序设计中,应优化算法以避免计算误差的引入。
hold on %图形保持step(trcs,'r',2) %画连续系统的阶跃响应图,红色,终止时间为2秒 step(trcz,'b',2) %画离散系统的阶跃响应图,兰色,终止时间为2秒第二节 在MATLAB 中离散化1. 建立s 降幂传递函数 ① 建立多项式型s 降幂传递函数 方法1. sys = tf(num,den) 方法2. s = tf('s'),再令sys = f(s) 例: 已知03215s 3G 025s 125s s...+=++,用tf 函数建立多项式型s 降幂传递函数,0G tf 153********([.],[..])=,若G 0以零极点形式给出,即已知0305s 1G s s 1025s 1(.)()(.)+=++,仍可用tf 函数建立多项式型s 降幂传递函数,但需用多项式乘法函数conv 配合,G0=tf(conv([3],[0.5 1]),conv(conv([1 0],[1 1]),[0.25 1])) ② 建立零极点型s 传递函数 方法1. sys = zpk(z,p,k)方法2. s = zpk('s'),再令sys = f(s)。
2. 传递函数的转换① 将任意形式的s 传递函数转换为s 降幂传递函数 sys = tf(sys) ② 将任意形式的s 传递函数转换为s 零极点传递函数 sys = zpk(sys)3. 建立z 传递函数① 将连续传递函数转换为离散传递函数 sysd = c2d(sysc,t,method) ② 建立多项式形式的z 传递函数 方法1. sys = tf(num,den,∆t) 方法2. z = tf('z',∆t),再令sys = f(z) ③ 建立零极点z 传递函数 方法1. sys = zpk(z,p,k,∆t)方法2. z = zpk('z',∆t),再令sys = f(z) 4. 建立z -1格式的传递函数直接根据分子和分母建立z -1格式的传递函数sys_z = filt(num,den,∆t)当已有多项式形式的z 降幂传递函数时,按以下步骤:① 取z 降幂传递函数a 的分子多项式系数 [num,den] = tfdata(sys_s,'v') ② 建立z -1格式的传递函数sys_z = filt(num,den,∆t)5. 将多项式形式的高阶z -1降幂传递函数转换为并联传递函数,按以下步骤: ① “手工”将z -1降幂传递函数a 改写成多项式形式的z 降幂传递函数b 。
② 取z 降幂传递函数b 的分子多项式系数num 和分母多项式系数den 。
③ 利用residue 函数取z 降幂传递函数b 的分项分式,[an ad ak]=residue(num,den)。
分项结果可能出现共轭复数,在这种情况下应将含有共轭复数的分式合并成二次有理质分式。