数值分析7-2节(研究生)
- 格式:ppt
- 大小:950.00 KB
- 文档页数:41

7 矩阵特征值与特征向量地计算设A 为n 阶方阵,所谓A 地特征值问题是求数λ和非零向量x ,使x Ax λ=成立.数λ称作A 地一个特征值,非零向量x 称作与特征值λ对应地特征向量.求给定方阵地特征值与特征向量是先求解特征方程()||0E A ϕλλ=-=然后对应于每一个特征值i λ,再求解退化地齐次线性方程组()0i E A x λ-=从而得到A 地特征值i λ及对应地特征向量x .但是这种方法计算机很大,计算过程复杂,因此有必要研究相对简单地数值解法.本章主要介绍三类计算特征值地方法:计算大型(稀疏)矩阵主特征地幂法与反幂法,计算中小型(实对称)矩阵全部特征值地Jacobi 法,计算中小型矩阵全部特征值地QR 法.7.1 特征值估计在矩阵特征值计算中,有时需要对特征值所在范围给出一个估计.这里介绍一种从矩阵地元素出发,运用较简便地运算估计特征值地方法.定义7-1 设()n m ij A a C ⨯=∈,称由不等式||ii i z a R -≤在复平面上确定地区域为矩阵A 地第i 个盖尔圆(Gerschgorin 圆),并用i G 表示.其中1||ni ij j j i R a =≠=∑称为盖尔圆i G 地半径(1,2,,)i n =.定理7-1 矩阵()n m ij A a C ⨯=∈地一切特征值均落在它地n 个盖尔圆地并集中,即1(1,2,,)ni jj G i n λ=∈=.证明 设λ是A 地任一特征值,12(,,,)T n x x x x =是λ对应地特征向量.令01||max ||i i i nx x ≤≤=,则00i x ≠.由Ax x λ=,可得001()ni j j i j a x x λ==∑.即∑≠==-ni j j j j i i i i x a x a 000001)(λ于是有 000000011i i jni j j ji ni j j i jji i i R x x ax x aa ≤≤=-∑∑≠=≠=λ这表明任一特征值0i G λ∈,从而也在A 地第n 个盖尔圆地并集中.例7-1 估计矩阵10.10.20.30.530.10.210.310.50.20.30.14A ⎡⎤⎢⎥⎢⎥=⎢⎥-⎢⎥---⎣⎦地特征值范围. 解 A 地4个盖尔圆为:1:|1|0.6G z -≤ 2:|3|0.8G z -≤ 3:|1| 1.8G z +≤ 4:|4|0.6G z +≤画在复平面上其区域如图7-1所示.图7-1 例7-1盖尔圆分布图于是A 地全部特征值就在这4个盖尔圆地并集中.为了更确切地知道某个特征值落在哪个或哪几个盖尔圆地并集中,给出如下第二盖尔圆盘定理.定理7-2 若A 地n 个盖尔圆中,有m 个盖尔圆构成地一个连通域(所谓连通域,是指其中地任意两点都可以用位于该区域内地一条折线连接起来),且该连通域与其余n m -个盖尔圆严格分离,则在该连通域中恰好有A 地m 个特征值(重特征值按重数重复计算).特别地,每个孤立地盖尔圆恰有A 地一个特征值(证明从略).由定理2可知,在例1中2G 与4G 中各有A 地一个特征值,而1G 与3G 构成地连通部分中有两个特征值,但不能确定这两个特征值具体落在哪个盖尔圆中.例7-2 估计矩阵10.80.50A -⎡⎤=⎢⎥⎣⎦地特征值范围. 解 A 地两个盖尔圆为:1:|1|0.8G z -≤,2:|0|0.5G z -≤在复平面上地区域如图7-2所示.图7-2 例7-2盖尔圆分布图此时只能判断A 地两个特征值落在1G 与2G 地并集中,至于是每个盖尔圆中各有一个特征值还是两个特征值都落在其中一个盖尔圆上则无法确定.实际上,由于1,21(12λ=±,1,2||0.5λ=>,所以两个特征值都不会在盖尔圆2G 中,而是落在盖尔圆1G 中.对于某些矩阵,可利用相似变换矩阵具有相同特征值地性质得到更确切地特征值范围.设()ij n m A a ⨯=,取正数12,,,n d d d 构成对角阵12diag(,,,)n D d d d =,对A 作相似变换,令1()iij n n jd B DAD a d -⨯==,由于B 相似于A ,所以B 与A 地特征值完全相同,又由于B 与A 地主对角线元素对应相等,所以B 与A 地盖尔圆圆心相同.这表明,若适当选取正数12,,,n d d d ,可以改变盖尔圆地半径,从而有可能将相交地盖尔圆分离得到仅含一个特征值地孤立盖尔圆.选取12,,,n d d d 地一般方法是:欲使A 地第i 个盖尔圆i G 地半径大而其余盖尔圆变小,就取1i d >,其余1()j d j i =≠.例7-3 求矩阵2050.841011210A j ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦地特征值范围. 解 A 地3个盖尔圆为:1:|20| 5.8G z -≤,2:|10|5G z -≤,3:|10|3G z j -≤其中1G 与2G 相交,而3G 孤立.记3G 中所含地一个特征值为3λ,如图7-3所示.为分离2G 与1G ,可以让A 地第3行元素绝对值变大,第3列元素绝对值变小.现取diag(1,1,2)D =,则12050.44100.52410B DAD j -⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦图7-3 例3盖尔圆分布图 图7-4 例7-3分离后盖尔圆分布图其3个盖尔圆分别是:1:|20| 5.4G z '-≤,2:|10| 4.5G z '-≤,3:|10|6G z j '-≤ 显然,B 地盖尔圆是3个孤立地盖尔圆,如图7-4,注意,此情况下,3G '地半径变大了.例7-4 设矩阵()ij n n A a ⨯=按行严格对角占优,则A 可逆.证明 由线性代数知,A 可逆地充分条件是||0A ≠,而1||nj j A λ==∏(其中j λ是A 地特征值),所以只要证明0j λ≠即可(1,2,,)j n =. 设λ是A 地任一特征值,则必存在某个盖尔圆i G 使∑≠=≤-ij ij i ii a R a λ.若0j λ=,则有∑≠≤ij ij ii a a ,而这与A 按行严格对角占优矛盾,故应有0λ≠,由λ地任意性,得||0A ≠.7.2 幂法与反幂法在线性代数中,设A 是n 阶方阵,若A 存在n 个线性无关地特征向量,则称这n 个特征向量构成A 地一个完全地特征向量组.例如,对矩阵320230005A -⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦,110430102B -⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦通过求解特征方程,不难求出A 地三个特征值为1231,5λλλ===,B地三个特征值为1232,1λλλ===.方阵A 可以找到三个线性无关地特征向量,而方阵B 找不到三个线性无关地特征向量.我们称方阵A 可对角化,而B 不可对角化. 7.2.1 幂法幂法地基本思想是构造一个向量序列使之逼近主特征值(矩阵地按模最大地特征值)对应地特征向量,然后求出主特征值.该方法简单易行,但收敛速度较慢.现设()ij n n A a ⨯=有一个完全地特征向量组12,,,n x x x ,其对应地特征值是12,,,n λλλ.已知A 地主特征值是单根1λ,即特征值满足条件12||||||n λλλ>≥≥任取一个非零初始向量0u ,由矩阵A 构造向量序列102210110k k k u Au u Au A u u Au A u++=⎧⎪==⎪⎪⎨⎪==⎪⎪⎩由于A 地完全特征向量组可以作为向量空间n R 地一组基,因此0u 可由12,,,n x x x 线性表示,即有01122n n u a x a x a x =+++ (设10a ≠)于是011122211111121()()k k k k k n n nn kk k i i i k i u A u a x a x a x a x a x a x λλλλλλελ===+++⎡⎤=+=+⎢⎥⎣⎦∑ 其中21()nk i k i i i a x λελ==∑.注意到),,2(11n i i=<λλ,故当k →∞时,0k ε→,因此有111k k u a x λ≈由于1x 是主特征值1λ对应地特征向量,其乘上常数因子11k a λ仍为1λ地特征向量,故当k 充分大时,迭代向量k u 是1λ地特征向量地近似向量.为了利用迭代向量求出主特征值1λ地近似值,设()k i u 表示k u 地第i 个分量,则1111111()()()[]()()()k i i k ik i i k iu a x u a x ελε+++=+ 于是 11()lim()k ik k iu u λ+→∞= 这表明两相邻迭代向量对应分量地比值收敛于主特征值,亦即当k 充分大时,可用两相邻迭代向量地分量比作为主特征值地近似值,即11()()k ik iu u λ+≈若主特征值是A 地r 重实特征值,即12(1)r r n λλλ===≤≤,对应地r 个线性无关特征向量为12,,,n x x x .则有01111()r nkk k i k i i i i i i r u A u a x a x λλλ==+⎡⎤==+⎢⎥⎣⎦∑∑当k 充分大时,11rkk i i i u a x λ=≈∑即k u 仍为主特征值对应地特征向量地近似向量,相邻两迭代向量地分量比仍为主特征值地近似值.综上所述,有定理7-3 设A 是n 阶实矩阵,具有完全地特征向量组,主特征值是r 重根,即112||||||||(1)r r n r n λλλλ++>≥≥≥≤≤则对任意非零初始向量0u ,迭代向量0k k u A u = 满足 111lim(0)rki ikk i u a x a λ→∞==≠∑ ,11()lim ()k ik k iu u λ+→∞= 或 11rk k i i i u a x λ=≈∑,11()()k ik iu u λ+≈ 这样用非零初始向量0u 及矩阵A 构造向量序列{}k u 以计算A 地主特征值1λ及相应地特征向量地方法称为幂法.不过从上面地讨论中可以看到,如果1||1λ>或11<λ,迭代向量k u 当k →∞时,其不为零地分量就会趋于无穷大或趋于零.为克服这个缺点,可以在每步迭代中加上对向量规范化地步骤,使迭代向量地数量级保持在一个稳定地量级上,归纳起来,幂法地计算步骤为:步骤 1 给定非零初始向量0u ,精度12,εε,令00v u =;令(0)10max()v λ=,1=k ;步骤 2 迭代1-=k k Av u ,()1max()k k u λ=,其中)max(k u 表示k u 绝对值最大地分量;步骤3 规范化max()kk k u v u =; 步骤 4 若11k k v v ε--<且()(1)112||k k λλε--<,则k v 即为1λ地近似特征向量,()1k λ即为1λ地近似值;否则,1+=k k ,转步骤2继续迭代.例7-5 用幂法计算1.0 1.00.51.0 1.00.250.50.252.0A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦地主特征值和相应地特征向量,结果见表7-1.表7-1而此题地准确值为1 2.5365258λ= 1(0.748221,0.649661,1.000000)T x =7.2.2 幂法地加速幂法地收敛速度由比值21r λλ=来确定,r 越小收敛越快,而当1r ≈时收敛可能很慢.为了克服这一缺点,常采用原点平移法对幂法进行加速.设B A pE =-,其中p 是待定参数.显然,若A 地特征值为12,,,n λλλ,则B 地相应特征值(1,2,,)i k i n =为12,,,n p p p λλλ---,且A .B 地特征向量相同.这是因为对A 有特征方程||0i A E λ-=,而对B 有特征方程|||()|0i i B k E A p k E -=-+=,所以,i i i i p k k p λλ=+=-另一方面,若i x 是A 地对应i λ地特征向量,即i i i Ax x λ=则 ()()i i i i i i Bx A pE x Ax px p x λ=-=-=-原点平移法地思想是引入矩阵B ,恰当地选择参数p ,使11k p λ=-是B 地主特征值,且其速比2211maxB A p r r p λλλλ-=<=-,这样用幂法求B 地主特征值1k 地收敛速度就快于用幂法求A 地主特征值1λ,而一旦1k 求出,由11k p λ+=可得A 地主特征值,达到了加速地目地.但是为了选取恰当地选择参数p ,需要对A 地特征值地分布地大致了解. 例7-6 设4阶方阵A 有特征值15(1,2,3,4)j jj λ=-=其速比210.9A r λλ=≈.作变换 (12)B A pEp =-=则B 地特征值为12k =,21k =,30k =,41k =-,其速比2112B A k r r k ==<. 设A 地实特征值满足121n n λλλλ->≥≥>若2,n λλ地值可大致估计出,若要求1λ,考察待定参数p 地选取. 在原点平移法通过变换pE A B -=后,不论p 如何选取,矩阵地B 主特征值也只能是在n p λ-或 1p λ-.若希望求1λ,就应选择p ,使1p λ-称为B 地主特征值,即1||||n p p λλ->-这时B 地收敛速比B r 是比值21||/||p p λλ--和1||/||n p p λλ--中地较大者,即211||||max ,||||n B p p r p p λλλλ⎧⎫--=⎨⎬--⎩⎭显然B r 依赖于p 地选取,记做()B r p .为了使应用幂法求B 地主特征值地收敛速度尽可能快,我们希望选择最佳参数*p ,使*()min ()B B r p r p =由B r 地表示式(求二者之间地较大值)和)(*p r B 对)(p r B 地最小化要求,只有当2||||n p p λλ-=-时,()B r p 达到最小.由于2n p p λλ-=-会有得到矛盾地结果(2n λλ=),所以只能是2()n p p λλ-=--即 *22np λλ+=类似地,若用反幂法求最小特征值n λ,若1n λ-,1λ可大致估计,取最佳平移参数*112n p λλ-+=例7-7 取0.75p =,用原点平移法,计算例7-7中矩阵A 地主特征值.解 作变换B A pE =-,则0.2510.510.250.250.50.25 1.25B ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦对B 应用幂法,计算结果见表7-2.即1 1.7865914k ≈,则A 地主特征值1λ为110.75 2.5365914k λ=+=与例7-5比较,上述结果比例7-5迭代15次还好.表7-27.2.3 反幂法设方阵A 按模最小地特征值是n λ,且0n λ≠,则A 可逆.于是,由n n n Ax x λ=,可得11n n nA x x λ-=,这表明1nλ是1A -地主特征值.反幂法就是将幂法应用于1A -,通过求出1A -地主特征值得到A 地按模最小地特征值及其对应地特征向量.定理7-4 设A 是n 阶实矩阵,具有完全地特征向量组,其特征值满足12||||||0n λλλ≥≥≥>则对任意非零初始向量00u v =,按下述方式构造地迭代向量11k k u A v --= ,max()kk k u v u =满足lim max()n k k n x v x →∞=, 1lim max()k k nu λ→∞= /max()k n n v x x ≈,1max()k nu λ≈在实际计算中,可先对A 进行LU 分解,通过求解1k k Ly v -= ,k k Uu y =来求解方程组1k k Au v -=.反幂法地计算步骤为:步骤1 预先取定非零向量00u v =;给定精度12,εε;取(0)0m a x ()nu μ=; 步骤2 对矩阵A 作LU 分解,A LU =;令1=k ;步骤3 求解方程组1k k Ly v -= ,k k Uu y = 得到迭代向量k u ; 步骤4 规范化max()kk k u v u =步骤5 若11k k v v ε--<且()(1)2||k k n n μμε--<,则k v 即为A 地对应于n λ地近似特征向量,()1k nμ即为n λ地近似值;否则,令1+=k k ,转步骤3继续迭代.7.3 矩阵地两种正交变换本节先介绍镜面(初等)反射变换和平面旋转变换,它们是QR 算法和Jacobi 算法地基础.7.3.1 豪斯荷尔德(House holder )变换定义7-2 设有方阵B ,若当1i j >+时(,1,2,,)i j n =,0ij b =,则称B 是上Hessenberg 矩阵,即1112121222,1n n n n nn b b b b b b B b b -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦定义7-3 设向量ω满足21ω=,矩阵2T H E ωω=- (ω是列向量)称为初等反射矩阵,又称House holder 矩阵,记为()H ω,即211212212221212222122()2212n n n n n H ωωωωωωωωωωωωωωωω⎡⎤---⎢⎥---⎢⎥=⎢⎥⎢⎥---⎢⎥⎣⎦其中(1,2,,)i i n ω=是ω地分量.可以证明初等反射阵是对称阵()T H H =.正交阵()T H H E =. 例7-8 设向量0α≠,试证矩阵222TH E ααα=- 是一个初等反射阵. 证明 令2αωα=,则 222221||||||||1αωααα=== 由定义7-3,2222TTH E E ααωωα=-=-是初等反射阵.定理7-5 设,x y 是两个不相等地n 维列向量,且22||||||||x y =,则存在一个初等反射阵H,使得Hx y =证明 令2||||x yx y ω-=-,由例7-8可知22()()22||||T T Tx y x y H E E x y ωω--=-=-- 是一个初等反射阵.由于22||||()()T T T T Tx y x y x y x x y x x y y y -=--=--+ 注意到22||||||||x y =,即T T x x y y =,又()T T T T x y x y y x == ,故22||||2()T Tx y x x y x -=-从而22()()2||||T T x y x x y x Hx x x y --=--y y x x =--=)(. 例7-9 设1(1,2,2),(1,0,0)T T x e ==,用Householder 变换将x 化为与1e 同方向地向量.解 因为2||||3x =,可设13y e =,则22||||||||x y = 取21,1,1)||||T x y w x y -==--,构造Householder 矩阵[]11122212111,1,12123311221T H E ww -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-=--=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦则13Hx e =推论 设向量12(,,,)0T n x x x x =≠,12()||||r sign x x =,且1x r ε≠-,则存在初等反射阵1222||||T T uu H E E uu u ρ-=-=- 使1Hx r ε=- .其中,1(1,0,,0)T ε=,1u x r ε=+,22||||/2u ρ=.设12(,,,)T n u u u u =,则12(,,,)T n u x r x x =+22222122222112111||||[()]221(2)2()n n u x r x x r rx x x x r r x ρ==++++=+++++=+引入初等反射阵地目地,是设法用一系列初等反射阵将原始矩阵约化成上Hessenberg 阵.由于约化过程是逐列进行地,我们先给出计算Hx 地算法步骤,该算法算出H 及r ,使Hx r ε=-,u 地分量冲掉x 地分量.(1)1max ||i i nx η≤≤=;(2)(1,2,,)ii i x x u i n η←==,此步规范化是为避免计算r 时产生溢出;(3) 12211()()nii r sign x x ==∑;(4)11u u r ←+;(5) 1ru ρ=; (6) r r η←;于是初等反射阵1T H E uu ρ-=-,1Hx r ε=-.如果要将H 作用于矩阵A ,设i a 是A 地第i 列向量,则12(,,,)n A a a a =,12(,,,)n HA Ha Ha Ha = 其中,11()()(1,2,,)T T i i i i Ha E uu a a u a ui n ρρ--=-=-=.下面讨论用初等反射阵约化原始矩阵A 称为上Hessenberg 阵地步骤.11121(1)(1)2122211121(1)(1)212212n n n n nn a a a a a a a A A A a a a a a ⎡⎤⎢⎥⎡⎤⎢⎥===⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦步骤1 不妨设(1)210a ≠(否则这一步不需约化),选择初等反射阵1R ,使(1)12111R a r ε=-,其中: 1(1)(1)2212112(1)1211112111121211111()(())(1)1()2ni i T r sign a a u a r n u r r a R E u u εερρ=-⎧=⎪⎪⎪=+-⎨⎪==+⎪⎪=-⎩∑是维单位坐标列向量 令11100U R ⎡⎤=⎢⎥⎣⎦则(2)(2)(2)(1)111213111212111(2)(2)(1)(1)222312112210A a A a A R A U AU a A R a R A R ⎡⎤⎡⎤===⎢⎥⎢⎥⎣⎦⎣⎦其中,(2)11A 是21⨯阵,(2)22a 是2n -维列向量,(2)23A 是2n -阶方阵.步骤k 设对A 已进行了1k -步约化,即111(2)()()()()11121,111,11(2)()()()1222,12,2()()()1,1,()()()1,1,11,()()(),1(2,3,,1)k k k k k k k k k k k n k k k k kn k k k k kk k k k n k k k k k k k k nk k k nkn k nnA U A U k n a a a a a a r a a a a r a a a a a a a a a ----+--++++++==-⎡⎢-⎢=-⎣()()()111213()()22230k k k k k A a A a A ⎤⎥⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎦⎡⎤=⎢⎥⎣⎦其中,()11k A 是(1)k k ⨯-阵,()22k a 是n k -维列向量,()23k A 是n k -阶方阵.设()220k a ≠,选初等反射阵()k R n k -阶,使()221k k k R a r ε=-,其中1ε是n k -维单位坐标向量,可得1()()221,1()221()1,1()(())()nk k k k k ik i k k kk k k k kk nT k k k k r sign a a u a r r r a R E u u ερρ+=++-⎧=⎪⎪⎪=+⎨⎪=+⎪⎪=-⎩∑ 令 00k k E U R ⎡⎤=⎢⎥⎣⎦则 ()()()1112131()()2223()()()111213()12300k k k k k k k k k k k k k k k k k k k k k A a A R A U A U R a R A R A a A R r R A R ε+⎡⎤==⎢⎥⎣⎦⎡⎤=⎢⎥-⎣⎦ 可见1k A +地左上角1k +阶子阵为上Hessenberg 阵,从而约化又进了一步.重复此过程,直到122112211(2)122(3)233(1)1n n n n n nn A U U U AU U U a r a r a r a -----=⨯⨯⨯⎡⎤⎢⎥-⨯⨯⎢⎥⎢⎥=-⨯⎢⎥⎢⎥⎢⎥-⎣⎦使原始矩阵A 在一系列初等反射阵地作用下,约化为上Hessenberg 阵.综上所述,有定理7-6.定理7-6 如果A 是n 阶实矩阵,则存在初等反射阵122,,,n U U U -,使221122n n U U U AU U U C --=(上Hessenberg 阵)例7-10 试证矩阵A 与其约化成为地上Hessenberg 阵C 有相同地特征值.证明 记221n P U U U -=,由于初等反射阵是正交对称阵,故122T n P U U U -=,且P 是正交阵,故T PAP C =.于是||||||||||||T T C E PAP E P A E P A E λλλλ-=-=-=-其中T PP E =,||||1T P P =.这表明A 与C 具有相同地特征多项式,即两者有相同地特征值.进一步,设y 是C 地对应于特征值λ地特征向量,即Cy y λ=,则有T PAP y y λ= ()()T T A P y P y λ=这表明T P y 为A 地对应于λ地特征向量,于是求原始矩阵A 地特征值与特征向量可转化为求上Hessenberg 阵C 地特征值和特征向量.定理7-7 若A 是实对称矩阵,则存在初等反射阵122,,,n U U U -使2211221112211()n n n n n U U U AU U U c b b c b C b b c ----⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎣⎦对称三对角阵 证明 由定理7-6,存在初等反射阵可使A 约化为上Hessenberg 阵C ,当A 是对称矩阵时,C 亦为对称阵,即T C C =,且T C 亦为上Hessenberg 阵,故C 是对称三对角阵.例7-11 用豪斯荷尔德方法将下述矩阵化为上Hessenberg 阵.1437232427A A ---⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦解 (1)对1k =,确定变换阵111000U R ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,(1)2124a ⎡⎤=⎢⎥⎣⎦ 其中1R 为初等反射阵,使(1)121110R a r ⎡⎤=-⎢⎥⎣⎦(1)12124.472136r a ==≈(1)12111 6.472136244u a r ε⎡⎡⎤+=+=≈⎢⎢⎥⎣⎦⎣⎦11121()2)28.94427r r a ρ=+≈[]1111110 6.4721361 6.472136401428.944270.4472070.8944230.8944230.447216TR E u u ρ-=-⎡⎤⎡⎤=-⎢⎥⎢⎥⎣⎦⎣⎦--⎡⎤=⎢⎥-⎣⎦(2)计算(1)122R A .记(1)221232(,)27A a a ⎡⎤==⎢⎥⎣⎦,于是 (1)1221112 3.1304967.155419(,) 1.788855 1.341640R A R a R a --⎡⎤==⎢⎥-⎣⎦其中,111111111()()(1,2)T T i i i i R a E u u a a u a u i ρρ--=-=-=(3)计算(1)121A R 及(1)1221()R A R ,即求 1(1)121211(1)1223373.1304967.1554191.788855 1.341640T T T b A R b R R R A b ⎡⎤--⎡⎤⎡⎤⎢⎥⎢⎥==--⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥-⎣⎦⎣⎦7.6026340.4472127.800030.3999990.399999 2.200000-⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦其中,11111()(1,2,3)T T T Ti i i b R b b u u i ρ-=-=(4)计算2111A U AU =.(1)12121(1)1221447.6026340.4472124.4721367.8000030.39999900.399999 2.2000000A R A r R A R ⎡⎤--⎡⎤⎢⎥⎢⎥⎢⎥==--⎢⎥⎢⎥-⎢⎥-⎢⎥⎣⎦⎢⎥⎣⎦为上Hessenberg 阵.7.3.2 平面旋转变换 定义7-4 称矩阵111(,)111i j csi P i j scj ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦第列第列第行第行 为平面旋转矩阵,又称Givens 矩阵,其中cos c θ=,sin s θ=.平面旋转阵(,)P i j 是一个正交阵,与单位阵只有在(,),(,),(,i i i j j j j i四个位置上地元素不一样,用其左乘矩阵A 只改变A 地第i 行和第j 行元素.设12(,,,)T n x x x x =则平面旋转变换Px y =地结果为⎪⎩⎪⎨⎧≠=+-=+=ji k x y cx sx y sx cx y k kj i j j i i ,若令/i c x =,j s x =, 则平面旋转变换向量y 地第i个分两为22j i x x +,第j 个分量为0,其余分量即为x 对应地分量.和初等反射变换一样,用平面旋转变换也可以将一个方阵化为上Hessenberg 矩阵,也可以将将一个方阵化为上三角矩阵.7.4 QR 算法7.4.1 矩阵地QR 分解定理7-8 设A 是可逆矩阵,则存在正交矩阵121,,,n P P P -使121()n P P P A R -=上三角矩阵且R 地主对角元素0(1,2,,1)ii r i n >=-.证明 若10(2,3,,)j a j n ==,则A 地第一列不需约化.若有某个 10(2)j a j n ≠≤≤,则可选择1(1,)j P j P =使A 地第一列中第j 个元素变为零.一般地,可设平面旋转矩阵12131,,,n P P P ,使(2)(2)11121(2)(2)222113122(2)(2)200nn nn nn r a a a a P P P A A a a ⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦记111312nP P P P =,则12P A A =.同理,若(2)20(3,4,,)j a j n ≠=,可选取23242,,,n P P P 使(2)(2)(2)1112131(3)(3)22232(3)(3)2212323333(3)(3)3nn n n n n nn r a a a r a a P P P A A a a a a -⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦记2223nP P P =,则213P P A A =.重复上述过程,可得一系列正交阵121,,,n P P P -使11121222121n n n nn r r r r r P P P A R r -⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎣⎦ 定理7-9 (矩阵地QR 分解)如果n 阶实矩阵A 可逆,则A 可分解为一正交阵Q 和上三角阵R 地乘积,即A QR =,且当R 地对角元素都为正数时分解唯一.证明 由定理8知存在正交阵11,,n P P -使121n P P P A R -=为上三角阵,记121T n Q P P P -=,于是T Q A R =由于(1,2,,1)i P i n =-是正交阵,则T Q 亦为正交阵,故A QR =. 若A 有两种QR 分解,记为1122A Q R Q R ==其中12,R R 为上三角阵且主对角元素都为正数,12,Q Q 为正交阵,于是12121T Q Q R R -=注意121R R -是上三角阵地乘积,结果仍为上三角阵,而12,TQ Q 是正交阵,所以121R R -也应是正交阵.若记121D R R -=,由其上三角性T D 应是下三角阵,1D -应是上三角阵;由其正交性由1T D D -=,故D 只能是对角阵,且有2T D D D E ==.又因12,R R 地主对角元素都为正数,即有222212diag[,,,]diag[1,1,,1]n D d d d E ===故1(1,2,,)i d i n ==,则D E =,于是12R R =,12Q Q =.例7-12 求矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=212240130A 地QR 分解. 解 方法1:利用初等反射阵进行QR 分解令(0)1(0,0,2)T a =,取(0)112||||2d a ==,则)2,0,2(81211)0(111)0(11-=--=e d ae d a u1110012010100TH E u u ⎡⎤⎢⎥=-=⎢⎥⎢⎥⎣⎦,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=1302402121A H 再令(0)2(4,3)T a =,取(0)222||||5d a ==,则(1)2212(2)22121,3)||||T a d e u a d e -==--2224312345TH E u u ⎡⎤=-=⎢⎥-⎣⎦令2210014305534055H H ⎡⎤⎢⎥⎢⎥⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥-⎣⎦于是21212051002H H A R ⎡⎤⎢⎥=-=⎢⎥⎢⎥-⎣⎦故123405521243005155002100T TA H H R ⎡⎤-⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦方法2:利用平面旋转阵进行QR 分解. 取1202,0100221221=+==+=s c ,则130********T ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦,132********T A ⎡⎤⎢⎥=-⎢⎥⎢⎥--⎣⎦再取53)3(43,54)3(44222222-=-+-==-+=s c ,则231004305534055T ⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎣⎦,2313212051002T T A R ⎡⎤⎢⎥=-=⎢⎥⎢⎥-⎣⎦ 故13233405521243005155002100T T A T T R ⎡⎤-⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦例7-13 求矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=110133044A 地QR 分解,使得R 地对角线元素为正数.解 A A =1地第一列T x ]0,3,4[1=,521=x .用1x 构造镜面反射阵1H ,使得T y x H ]0,0,5[111==,令T y x u ]0,3,1[111-=-=,有⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-=-=10005453053542221111u u u E H T ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-==11054005355112A H A 2A 地第2列对角线以下为T x ]1,0[2=,122=x .用2x 构造镜面反射阵2~H ,使得T y x H ]0,1[~222==,令T y x u ]1,1[222-=-=,易得 ⎥⎦⎤⎢⎣⎡=-=01102~222222u u u E H T,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡=010100001~122H H 于是有R A H A =⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-==54001105355333,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-==010540535305421H H Q容易验证,QR A =.请读者用平面旋转变换对本例地矩阵A 进行QR 分解.7.5.3 QR 算法QR 算法就是利用QR 分解构造一个矩阵序列{}k A ,当k 充分大时,k A 是近似地上三角矩阵,而该上三角阵地对角元素便是原始矩阵A 地全部特征值.设1()n n ij n n A A a R ⨯⨯==∈,对A 做QR 分解,即A QR =其中R 为上三角阵,Q 为正交阵.利用这个分解可得新矩阵(对QR 交换乘积)2T A RQ Q AQ == 由于2A 是1A 经过正交相似变换得到地,因此2A 与1A 有相同地特征值.再对2A 做QR 分解,按上述方式又可得新矩阵3A ,且3A 与2A 也具有相同地特征值.具体地说,其步骤为:设1A A =,做QR 分解111A Q R =求矩阵211111T A R Q Q A Q ==求得k A 后对k A 作QR 分解k k k A Q R =求矩阵1Tk k k k k k A R Q Q A Q +==只要A 可逆,由定理9可知,按上述方法可唯一确定矩阵序列{}k A ,且序列中任意k A 与原始矩阵有相同特征值.因此只要恰当选择正交相似变换阵12,,,k Q Q Q ,使1111111T T TT TT T k k k k k k k k k k k k k k A Q A Q Q Q A Q Q Q Q Q A Q Q Q +----====当k →∞时,逼近一个上三角阵,便可求出A 地全部特征值(为所逼近上三角阵地主对角元素).可见,QR 算法地关键在于选择正交变换阵(1,2,)k Q k =.从定理7-8地证明看到,正交变换阵k Q 是一系列平面转换矩阵地乘积,这些平面旋转矩阵是用来将k A 地主对角线以下元素约化为零地.如果将QR 算法直接应用于原始矩阵,计算量很大,所以在实际计算中,总是先将原始矩阵用豪斯赫尔德方法约化为上Hessenberg 阵,而后再对上Hessenberg 阵应用QR 算法.可以证明,由上Hessenberg 阵用QR 算法生成地矩阵序列中地每个矩阵仍为上Hessenberg 阵.7.5 雅可比方法雅可比方法是用来计算实对称矩阵地全部特征值及特征向量地一种有效方法.它地基本思想是,通过一组正交相似变换对称矩阵A 化为对角矩阵,得其全部特征值.定理7-10 设A 为n 阶对称矩阵,T C PAP =,其中P 为正交矩阵,则22||||||||F F C A = 证明 一方面2222111||||()()nnnFiji i j i A a tr A A λ======∑∑∑另一方面2221||||()()()nTFi i C tr C C tr C C λ====∑由假设()()i i A C λλ=,故22||||||||F F C A =.设n n A R ⨯∈为对称矩阵,(,)P i j 为一平面旋转矩阵,则T C PAP =(其中()ij n n C c ⨯=)地元素计算公式为:(1)22cos sin 2sin cos ii ii jj ij c a a a θθθθ=++22sin cos 2sin cos jj ii jj ij c a a a θθθθ=+-(2)1()sin 2cos 22ij ji jj ii ij c c a a a θθ==-+ (3)第i 行元素和第j 列元素cos sin (,)ik ki ik jk c c a a k i j θθ==+≠ (4)第j 行元素和第i 列元素 cos sin (,)jk kj jk ik c c a a k i j θθ==+≠(5)(,,)lk lkc a l k i j =≠这说明,当A 经过一初等正交相似变换化为C 时,只需按上述公式计算C 地第i 列.第j 列元素,由对称性可得第i 行和第j 行元素,C 地其余元素与A 地对应元素相同.设A 地非对角元素0ij a ≠,我们可选择平面旋转阵(,)P i j ,使T C PAP =地非对角元素0ij ji c c ==.由定理11可选择(,)P i j ,使sin 2cos 202jj iiij ji ij a a c c a θθ-==+=即选择θ,使22(||)4ij ii jja tg a a πθθ=≤-其中定理7-11 设n n A R ⨯∈为对称阵,0ij a ≠为A 地一个非对角元素,则可选择一平面旋转阵(,)P i j ,使T C PAP =地非对角元素0ij ji c c ==且T C PAP =与A 地元素满足下述关系(1)2222(,)ik jk ik jkc c a a k i j +=+≠(2)222222ii jj ii jj ij c c a a a +=++ (3)22(,,)iklk c a l k i j =≠证明 由上面地计算ij c 公式直接计算可知(1)成立.由(1)及定理7-10可证(2).如果用()S A 表示A 地非对角线元素地平方和,()D A 表示A 地对角线元素平方和,则2()()2ijD C D A a =+ ,2()()2ij S C S A a =- 这说明C 地对角线元素平方和比A 地对角线元素平方和增加了22ij a ,C 地非对角线元素平方和比A 地非对角线元素平方和减少了22ij a .下面介绍雅可比方法.首先在A 地非对角元素中选择绝对值最大地元素(称为主元素),如11||max ||i j lk l ka a ≠=可设110i j a ≠,否则A 已经对角化了.由定理12,选择一平面旋转矩阵111(,)P i j ,使111TAP AP =地非对角元素11110i j j i c c ==. 再选(1)1()lkn n A a ⨯=地非对角元素中地主元素,如 22(1)(1)||max ||0i j lk l ka a ≠=≠由定理12,又可选择一平面旋转矩阵222(,)P i j ,使2212T A P A P =地非对角元素2222(2)(2)i j j i a a ==(注意上次消除了地主元素这次又可能变为不是零). 继续这个过程,连续对A 实行一系列平面旋转变换,消去非对角线绝对值最大地元素,直到将A 地非对角元素全化为充分小为止,从而求得A 地全部(近似)特征值.定理7-12 (雅可比方法地收敛性)设()ij n n A a ⨯=为实对称矩阵,对A 施行上述一系列平面旋转变换1(1,2,)Tm m m mA P A P m -==则 lim ()m m A D→∞=对角矩阵证明 记()()m m lk n n A a ⨯=,()2()m m lk l kS a ≠=∑由定理7-11地(2)可得()212()m m m ij S S a +=-其中 ()()||max ||m m ijlk l ka a ≠= 又由于()2()2()(1)()m m m lk ij l kS a n n a ≠=≤-∑即()2()(1)m m ij S a n n ≤- 由以上得12(1)(1)m m S S n n +≤-- 反复应用上式,即得1102(1)(2)(1)m m S S n n n ++≤->-故 lim 0m m S →∞= 可以证明()lim m ll m a →∞存在(1,2,,)l n =. 下面介绍特征向量地计算.由雅可比收敛定理知,当m 充分大时2112T TTmm P P P AP P P D ≈记12T T T T m m R P P P =,则T m R 地列向量就是A 地近似特征向量.计算Tm R 可采用累积地办法,用一数组R 保存Tm R ,开始时R E ←,以后对A 每进行一次平面旋转变换,就进行计算Tm R RP ←用初等正交阵T m P 右乘R 只需计算R 地两列元素,若记(,)m m P P i j =,则Tm RP 地计算公式为()()cos ()sin (1,,)()()sin ()cos li li lj li li lj l n θθθθ←+⎧⎪=⎨←+⎪⎩R R R R R R关于sin θ和cos θ地计算如下.由定理7-11知,当0ij a ≠时,可选θ满足2tg2ij ii jja a a θ=-方ii jj a a ≠时,由22tg 1tg21tg dθθθ=≡- 得到tg θ地二次方程2tg 2tg 10d θθ+-=解得tg θ=选取tg 0d d θ>=<由此得 |tg |1θ≤可由集合{},,ii jj ij a a a 来计算sin ,cos θθ,设0,||max ||ij ij lk l ka a a ≠≠=,则210tg ,()10cos sin cos ii jj ija a d a d t s d d c t ct sθθθθ-⎧=⎪⎪⎪≥⎧⎪=≡=⎨-<⎨⎩⎪⎪=≡⎪⎪=⋅=≡⎩如果jj ii ij a a a -<<,则12ij ii jja t d a a ≈=-,将c,s 代入定理7-9地(1)中可得ii ii ij jj jj ij ij ji c a ta c a ta c c ⎧=+⎪=-⎨⎪==⎩ 每迭代一次地主要工作是选m A 地非对角线元素中地主元素与计算T 111m m m +++=A P AP .首先计算sin ,cos ,θθ,只需计算1m +A 地第i 列,第j 列元素,再算对称元素,不用做3个矩阵地乘法.计算机计算时,需要两组工作单元,以便存储A (或m A )和R .可用()2()m m lk l ka ε≠=<∑S 控制迭代终止,其中ε是要求地精度.例7-14 用雅可比方法计算对称阵210121012⎡⎤-⎢⎥--⎢⎥⎢⎥-⎣⎦A = 地特征值.解 第1步0=A A ,选非对角线元素中地主元素121(1,2)a i j =-==0,1,1/0.7071068,1/0.7071068d t c s ======T 111100.7071068030.70710680.70710680.70710682⎡⎤-⎢⎥==-⎢⎥⎢⎥--⎣⎦A P AP第2步 在1A 中选非对角元素地主元素(1)130.7071068(1,3)a i j =-==0.7071068,0.5176381,0.8880738,0.4597008d t c s ====T 22120.63397460.325057600.325057630.627963000.62798302.366025-⎡⎤⎢⎥=--⎢⎥⎢⎥-⎣⎦A P A P 第3步 在2A 中选非对角元素地主元素(2)230.627930(2,3)a i j =-==0.5047869,0.6153960,0.8516540,0.5241045d t c s =-=-==-T 33230.63397460.27683660.17036420.27683663.38644600.170364201.979579⎡⎤--⎢⎥=-⎢⎥⎢⎥-⎣⎦A P A P 第4步 在3A 中选非对角元素地主元素(3)120.2768366(1,2)a i j =-==4.971292,0.09958013,0.9950785,0.09909004d t c s ====T 44340.606407200.169525803.4140130.016881400.16952580.016881401.979579⎡⎤-⎢⎥=⎢⎥⎢⎥-⎣⎦A P A P 第5步 在4A 中选非对角元素地主元素(4)130.1695258(1,3)a i j =-==4.050038,0.1216293,0.9926842,0.1207395d t c s ==== 2T 255450.58578790.20382521000.203825210 3.4140130.0167579000.016757902.000198--⎡⎤⨯⎢⎥=⨯⎢⎥⎢⎥⎣⎦A P A P 于是A 地特征值为1233.414013, 2.000198,0.5857879λλλ===A 地精确特征值为12(1 3.414214λ=≈,22λ=,32(10.585786λ=-≈ 且可逐步求出412345T T T T T T R P P P P P =地列向量,即得A 地近似特征向量.雅可比方法是一个求对称矩阵A 地全部特征值及特征向量地迭代方法,精确度较高,但计算量较大,对稀松带状矩阵经过平面旋转变换后其稀松带状将被破坏,所以很少使用.习题71.设911203111(2102113810A j j B ⎡⎤⎡⎤⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦试估计它们地特征值所在地范围.2.编写幂法程序,并求矩阵732341213A -⎡⎤⎢⎥=⎢⎥⎢⎥--⎣⎦地主特征值及对应地特征向量(准确到小数点后3位).3.若p 是A 地特征值j λ地一个近似值,且||||()j i p p i j λλ-<-≠则1j pλ-是1()A pE --地主特征值.试用反幂法求矩阵134231111A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦地最接近于6地特征值及对应地特征向量.4.设有向量(2,1,2)Tx=,试构造初等反射阵H,使(3,0,0)THx=.5.设(2,3,0,5)Tx=,(1,0,0,5)Te=,用Householder变换化x为与e同方向向量.6.设031042212A⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦,求其QR分解.7.设221022212A⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,求其QR分解.8.利用初等反射阵将134312421A⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦正交相似约化为对称三对角阵.9.试用平面旋转变换阵对矩阵A作QR分解,其中111021245A⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦.10.按下列要求编写程序框图.(1)将一般矩阵用豪斯赫尔德方法约化称上Hessenberg阵.(2)对矩阵作QR分解.(3)对上Hessenberg阵应用QR算法求全部特征值及相应地特征向量.11.用QR算法求矩阵120211013A⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦地全部特征值.12.设A是对称矩阵,λ和(1)x x=是A地一个特征值及相应地特征向量.又设p是一个正交阵,使1(1,0,0,,0)Tpx e==证明T=是第一行和第一列除了λ外,其余元素均为零.B PAP。

计算方法华中科技大学数学系教材张诚坚, 高健, 何南忠. 计算方法. 北京:高等教育出版社,1999年参考书¾李庆扬, 易大义, 王能超. 现代数值分析, 北京:高等教育出版社¾Richard L. Burden & J. Douglas Faires .Numerical Analysis(Seventh Edition), 北京:高等教育出版社, 2001¾徐士良.C常用算法程序集(第二版).北京:清华大学出版社,1996期末考试试题期末考试的试卷有填空题和解答题。
解答题共7个题,分数约占70%。
期末考试主要考核:基本概念;基本原理;基本运算。
必须带简易计算器。
总成绩=平时成绩*20%+期末成绩*80%§1绪论第1节数值算法概论第2节预备知识与误差第1节数值算法概论1. 引言数值计算已经是计算机处理实际问题的一种关键手段。
它使各科学领域从定性分析阶段走向定量分析阶段,从粗糙走向精密。
2. 计算机数值方法的研究对象与特点计算问题x I n∫+ =15dxxx n 11nx I dx =∫011615 , ln5n n n n I I I I −==−1615 , ln I I I I ==−误差的传播与积累丽的北京就刮起台风来了?!3 数值算法计算方法的主要任务:1.将计算机上不能执行的运算化为在计算机上可执行的运算2.针对所求解的数值问题研究在计算机上可执行的且有效的计算公式3.因为可能采用了近似等价运算,故要进行误差分析,即数值问题的性态及数值方法的稳定性数值算法是指有步骤地完成解数值问题的过程.数值算法有四个特点:1.目的明确算法必须有明确的目的,其条件和结论均应有清楚的规定2.定义精确对算法的每一步都必须有精确的定义3.算法可执行算法中的每一步操作都是可执行的4.步骤有限算法必须在有限步内能够完成解题过程例如给出等差数列1,2,3,…,10000的求和算法算法构造如下:N取记数器置零=S.1=,0⇒+,.21+N⇒SNNS.3<N10000若2,,否则转.4输出SN,一、误差的种类及来源1模型误差在建立数学模型过程中,要将复杂的现象抽象归结为数学模型,往往要忽略一些次要因素的影响,而对问题作一些简化,因此和实际问题有一定的区别.2观测误差在建模和具体运算过程中所用的数据往往是通过观察和测量得到的,由于精度的限制,这些数据一般是近似的,即有误差.3截断误差由于计算机只能完成有限次算术运算和逻辑运算,因此要将有些需用极限或无穷过程进行的运算有限化,对无穷过程进行截断,这就带来误差.第2节预备知识与误差在数值计算过程中还会遇到无穷小数,因误差与有效数字有效数字用科学计数法,记(其中)若(即的截取按四舍五入规则),则称为有n 位有效数字,精确到。

计算方法教案新疆医科大学数学教研室张利萍一、课程基本信息1、课程英文名称:Numerical Analysis2、课程类别:专业基础课程3、课程学时:总学时544、学分:45、先修课程:《高等数学》、《线性代数》、《Matlab 语言》二、课程的目的与任务:计算方法是信息管理与信息系统专业的重要理论基础课程,是现代数学的一个重要分支。
其主要任务是介绍进行科学计算的理论方法,即在计算机上对来自科学研究和工程实际中的数学问题进行数值计算和分析的理论和方法。
通过本课程的学习,不仅使学生初步掌握数值分析的基本理论知识,而且使学生具备一定的科学计算的能力、分析问题和解决问题的能力,为学习后继课程以及将来从事科学计算、计算机应用和科学研究等工作奠定必要的数学基础。
三、课程的基本要求:1.掌握计算方法的常用的基本的数值计算方法2.掌握计算方法的基本理论、分析方法和原理3.能利用计算机解决科学和工程中的某些数值计算应用问题,增强学生综合运用知识的能力4.了解科学计算的发展方向和应用前景四、教学内容、要求及学时分配:(一) 理论教学:引论(2学时)第一讲(1-2节)1.教学内容:计算方法(数值分析)这门课程的形成背景及主要研究内容、研究方法、主要特点;算法的有关概念及要求;误差的来源、意义、及其有关概念。
数值计算中应注意的一些问题。
2.重点难点:算法设计及其表达法;误差的基本概念。
数值计算中应注意的一些问题。
3.教学目标:了解数值分析的基本概念;掌握误差的基本概念:误差、相对误差、误差限、相对误差限、有效数字;理解有效数字与误差的关系。
学会选用相对较好的数值计算方法。
A 算法B 误差第二讲典型例题第二章线性方程组的直接法(4学时)第三讲1.教学内容:线性方程组的消去法、Gauss消去法及其Gauss列主元素消去法的计算过程;三种消去法的程序设计。
2.重点难点:约当消去法,Gauss消去法,Gauss列主元素消去法3.教学目标:了解线性方程组的解法;掌握约当消去法、Gauss消去法、Gauss列主元素消去的基本思想;能利用这三种消去法对线性方程组进行求解,并编制相应的应用程序。
济南大学化学化工学院2016-2017学年第一学期硕士研究生课程表(全日制学术型)
1、本学期2016级研究生新生9月11日(第二教学周周日)报到入学,自第三教学周(9月12日)开始安排上课。
2、任课教师应严格按课程表上课,不得随意调停课。
专业课
任课教师调整上课时间、地点等须在学院备案,学院秘书负责通知研究生院。
公共课任课教师调整上课时间或地点等应经研究生秘书上报研究生院批准。
出现教学事故按按有关文件处理。
济南大学化学化工学院2016-2017学年第一学期硕士研究生课程表(全日制专业学位)
2、本学期2016级研究生新生9月11日(第二教学周周日)报到入学,自第三教学周(9月12日)开始安排上课。
2、任课教师应严格按课程表上课,不得随意调停课。
专业课
任课教师调整上课时间、地点等须在学院备案,学院秘书负责通知研究生院。
公共课任课教师调整上课时间或地点等应经研究生秘书上报研究生院批准。
出现教学事故按按有关文件处理。
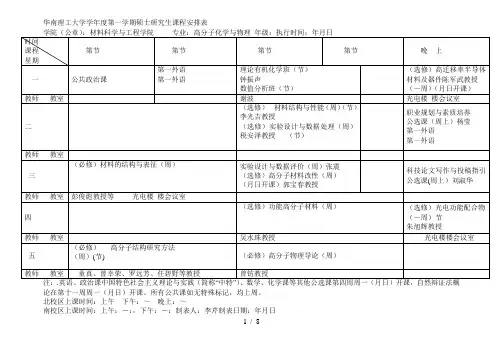
华南理工大学2014--2015学年度第一学期硕士研究生课程安排表(除特殊标注:科技论文写作4-11周,自然辩证法11-18周)。
所有公共课如无特殊标记,均上到18周。
19-20考试周。
北校区上课时间:上午8:00~11:40下午:14:30~18:00晚上:19:00~.南校区上课时间:上午8:50-12:15,下午14:00-17:20制表人:李芹制表日期:2014年7月4日华南理工大学2014--2015学年度第一学期硕士研究生课程安排表特殊标注:科技论文写作4-11周,自然辩证法11-18周)。
所有公共课如无特殊标记,均上到18周。
19-20考试周。
北校区上课时间:上午8:00~11:40下午:14:30~18:00晚上:19:00~.南校区上课时间:上午8:50-12:15,下午14:00-17:20制表人:李芹制表日期:2014年7月4日华南理工大学2014--2015学年度第一学期硕士研究生课程安排表北校区上课时间:上午8:00~11:40下午:14:30~18:00晚上:19:00~.南校区上课时间:上午8:50-12:15,下午14:00-17:20制表人:李芹制表日期:2014年7月4日华南理工大学2014--2015学年度第一学期硕士研究生课程安排表北校区上课时间:上午8:00~11:40下午:14:30~18:00晚上:19:00~.南校区上课时间:上午8:50-12:15,下午14:00-17:20制表人:李芹制表日期:2014年7月4日华南理工大学2014--2015学年度第一学期硕士研究生课程安排表南校区上课时间:上午8:50-12:15,下午14:00-17:20制表人:李芹制表日期:2014年7月4日华南理工大学2014--2015学年度第一学期硕士研究生课程安排表学院(公章):材料科学与工程学院专业:微电子学与固体电子学年级:2014人数:执行时间:2014年9月1日时间星期第1--2节第3--4节第5--6节第7--8节晚上一中特-1班,340501,郭忆薇62人中特2班,340502,闫坤如63人中特3班,340503,郭厚佳63人中特4班,340504,覃辉银63人英语A02班,1408,45人;英语B05班,1407,30人;英语B06班,1404,19人;英语B07班,1409,20人;英语B08班,1410,22人;英语B36班,1414,18人理论有机化学2班,(5-7节)钟振声340404数值分析2班,(5-7节)黄风辉,340402英语B36班,1407,18人教师教室二(必修)无源电子元器件基础(5人)(4-9周)(其他学时安排查资料及学生做报告)李屹14号楼三楼电材学术室开课日期:20140923试验设计和数据评价张震340402(4-18周)(选修)偏微分方程及有限元分析,姚仰新,340401三节课,科技论文写作与投稿指引1公选课(4-11周上)刘淑华340201教师教室三英语A02班,1408,45人;英语B05班,1407,22人;英语B06班,1404,22人;英语B08班,1410,22人;(公选)数学建模与数学实验林健良340401(5-7节)科技论文写作与投稿指引1公选课(4-11周上)刘淑华340201教师教室四日语(4-18周)(1-4节)李博(待定)教师教室五数理统计理论与方法2班朱锋峰340504(1-3节)(必修)电子敏感技术及其应用(5人)(4-8周,剩余学时学生自学、报告)(2-4节)卢振亚14号楼三楼电材学术室开课日期:20140926教师教室注:1.1.英语课、政治课《中国特色社会主义理论与实践》(简称“中特”)、数学课、化学课等其他公选课第三周周一(9月15日)开课,(除南校区上课时间:上午8:50-12:15,下午14:00-17:20制表人:李芹制表日期:2014年7月4日华南理工大学2014~2015学年第一学期校历5.2015年2月27日、28日为本科生、研究生下学期学生报到注册时间。


2011—2012学年第一学期研究生课程表(硕士科学学位)说明:1、教学时间:共17周(不含国庆放假)第1—18周(2011.8.29—2011.12.30)共17周(不含国庆放假)上课。
第20周(2012.1.9—1.13)实验教学周医学免疫学实验技术(须选选修“细胞和分子免疫学”课程),上课地点:二教楼6层601、608、609免疫学实验室组织化学与免疫组织化学实验技术(须选选修“组织化学和免疫组织化学”课程)2、统考时间:第19周(2012.1.3—2012.1.6)。
3、上课时间:上午8:00—12:10,5学时;下午 1:30— 4:45,4学时;晚上 6:00— 8:30,3学时。
有时间标注的,按标注时间上课。
标注2、3、4或5节的指一次上2、3、4或5节课。
4、课程说明:A、政治理论指教学计划中的“中国特色社会主义理论与实践研究”和“自然辩证法概论”2门课程。
B、实验动物细胞培养(实验部分)、实验动物学(实验)(须选选修“实验动物学理论”课程)、由教研室依据学生选课情况分组进行实验,原则上不占用学生其它课程上课时间。
C、高等有机化学实验(1-9周)、每周六13:30—18:30在药学院楼实验室上课。
D、药物生物分析实验(1-18周)每周日13:30—18:30在药学院楼实验室上课。
护理教育学(7-19)每周日11:50—15:00在护理学院上课。
5、中秋放假期间课程停上,按学校要求进行调课。
国庆放假期间课程停上。
6、原则上选课人数不足6人的,本门课程停开。
课程停开通知于2011年8月26日(星期五)下午公布,可上网查询相关通知。
7、教学分班:待定8、授课医院地址:宣武医院宣武区长椿街45号,乘环线地铁长椿街站下车,乘5、6、10、38、50、109、381、603、715、743、822等公交车牛街下车。
友谊医院宣武区永安路95号,乘6、34、59、687、105、106等公交车友谊医院。
论在第十一周周一(月日)开课。
所有公共课如无特殊标记,均上周。
北校区上课时间:上午下午:~晚上:~南校区上课时间:上午:-:,下午:-:制表人:李芹制表日期:年月日1 / 8论在第十一周周一(月日)开课。
所有公共课如无特殊标记,均上周。
北校区上课时间:上午下午:~晚上:~2 / 8南校区上课时间:上午:-:,下午:-:制表人:李芹制表日期:年月日华南理工大学学年度第一学期硕士研究生课程安排表论在第十一周周一(月日)开课。
所有公共课如无特殊标记,均上周。
北校区上课时间:上午下午:~晚上:~3 / 8南校区上课时间:上午:-:,下午:-:制表人:李芹制表日期:年月日华南理工大学学年度第一学期硕士研究生课程安排表4 / 8注:.英语、政治课中国特色社会主义理论与实践(简称“中特”)、数学、化学课等其他公选课第四周周一(月日)开课,自然辩证法概论在第十一周周一(月日)开课。
所有公共课如无特殊标记,均上周。
北校区上课时间:上午下午:~晚上:~南校区上课时间:上午:-:,下午:-:制表人:李芹制表日期:年月日华南理工大学学年度第一学期硕士研究生课程安排表5 / 8论在第十一周周一(月日)开课。
所有公共课如无特殊标记,均上周。
北校区上课时间:上午下午:~晚上:~南校区上课时间:上午:-:,下午:-:制表人:李芹制表日期:年月日华南理工大学学年度第一学期硕士研究生课程安排表6 / 8论在第十一周周一(月日)开课。
所有公共课如无特殊标记,均上周。
北校区上课时间:上午下午:~晚上:~南校区上课时间:上午:-:,下午:-:制表人:李芹制表日期:年月日华南理工大学学年度第一学期硕士研究生课程安排表7 / 8论在第十一周周一(月日)开课。
所有公共课如无特殊标记,均上周。
北校区上课时间:上午下午:~晚上:~南校区上课时间:上午:-:,下午:-:制表人:制表日期:年月日8 / 8。

2011-2012第一学期研究生公共课程选课注意事项:
一、1、2011硕士研究生入学英语成绩小于50分的学生第一学期必须选修《研究生综合英语》,第二学期才允许选修《第一外国语》,否则《第一外国语》成绩无效。
2、每个硕士研究生限选1个班,每班限选70人。
3、为避免与专业课发生冲突,请各院系同学集中选《研究生综合英语》,时间规定如下:
九里校区:
二、6个单项,共计42个班。
2、每个硕士研究生限选1个班,每班限选60人。
3、为避免与专业课发生冲突,请各院系同学集中选《第一外国语》,时间规定如下:
九里校区:
三、
四、2011级学术型硕士研究生《形势与政策》分班如下:
五、
六、课表中没有标注开课周次的,开课时间都为1-17周。
七、公共课程编号:
八、进修过研究生课程的
转入。
西南交通大学研究生课程表
2011级硕士研究生各学科公共课 2011——2012 学年第 1 学期。
《数值分析》课程教学大纲课程编号:07054352课程名称:数值分析英文名称:Numerical Analysis课程类型:学科基础课程要求:必修学时/学分:48/3 (讲课学时:40 上机学时:8)适用专业:计算机科学与技术;软件工程一、课程性质与任务“数值分析”是计算机科学与技术、软件工程等相关专业学生的学科基础课,也是其它理、工科专业本科生及研究生的必修或选修课。
数值分析是研究各种数学问题在计算机上通过数值运算,得到数值解答的方法和理论。
随着计算机系统能力的提高和新型数值软件的不断开发,无论在高科技领域还是在传统学科领域,数值分析的理论和方法的作用和影响巨大,是科学工作者和工程技术人员必备的基础知识和工具。
课程的任务是使学生能了解数值分析的基本概念,熟悉常用数值方法的构造原理,了解数值算法复杂性、误差与收敛性分析的基本方法,了解重要数值算法的软件实现过程,使学生系统掌握数值分析的基本概念和分析问题、解决问题的基本方法,为掌握更复杂的现代计算方法打好基础。
内容包括数值计算的基本方法、线性和非线性方程组解法、插值法、数值积分法及微分方程的数值解法。
二、课程与其他课程的联系先修课程:高等数学,线性代数,C语言程序设计,计算基础。
后续课程:人工智能,数字图像处理技术,大数据分析及应用。
三、课程教学目标1.学习使用计算机进行数值计算的基础知识和基本理论知识,能够分辨、选用合适的数值方法解决工程问题。
(支撑毕业能力要求1和2)2. 能掌握常用数值计算方法的构造原理,根据问题设计和综合运用算法设计问题解决方案。
(支撑毕业能力要求1和2)3. 能运用数值算法复杂性、误差与收敛性分析的基本方法初步进行算法分析。
4. 能用计算机语言实现典型的数值计算算法,得到实验技能的基本训练,并具有利用计算机解决常见数学问题的能力;(支撑毕业能力要求4)5.能通过查询阅读文献资料,了解数值分析的前沿和新发展动向,了解数值分析算法原理应用的典型工程领域。
研究生课程表2009年秋季学课程名称起止周星期节次教室授课教师开课教研室数值分析(一班) 2-11 一1-2 A112-11 三3-4 A11李道华等应用数学系数值分析(二班) 2-11 一3-4 A112-11 三1-2 A11应用数学系数值分析(三班) 2-11 一1-2 A212-11 三3-4 A21应用数学系数值分析(四班) 2-11 一3-4 A212-11 三1-2 A21应用数学系数值分析(五班) 2-11 一1-2 A222-11 三3-4 A22应用数学系数值分析(六班) 2-11 一3-4 A222-11 三1-2 A22应用数学系数值分析(七班) 2-11 一1-2 A522-11 三3-4 A52应用数学系数值分析(八班) 2-11 一3-4 A522-11 三1-2 A52应用数学系数值分析(九班) 2-11 一1-2 A122-11 三3-4 A12应用数学系数值分析(十班) 2-11 一3-4 A122-11 三1-2 A12应用数学系数值分析分班:一班:电气学院自动化测试与控制系、航天学院18系(航空宇航)二班:航天学院21系(物理电子)、电气学院电气工程系三班:航天学院控制科学与工程系四班:电子与信息工程学院、航天学院21系(微电子)五班:理学院化学系、化工学院、航天学院18系(力学)六班:机电学院(机械电子、宇航制造)、航天学院21系(光学)、21系集成电路工程硕士七班:材料学院(材料加工、材料物理化学)八班:机电学院(机械制造、机械设计)、理学院生命科学系九班:材料学院(材料学、材料全日制工程硕士)、航天学院18系(材料)十班:机电学院(机械全日制工程硕士)、能源学院矩阵分析(12系开设) 5、18、21系12-20 一5-6 A1112-20 三7-8 A11董增福应用数学系应用随机过程(5系为主141)1、3、4、5系2-11 一5-6 A112-11 三7-8 A11田波平应用数学系课程名称起止周星期节次教室授课教师开课教研室现代数学基础(一班) 12-20 一1-2 A1112-20 三3-4 A11薛小平等应用数学系现代数学基础(二班) 12-20 一3-4 A1112-20 三1-2 A11应用数学系现代数学基础(三班) 12-20 一1-2 A1212-20 三3-4 A12应用数学系现代数学基础(四班) 12-20 一3-4 A1212-20 三1-2 A12应用数学系现代数学基础(五班) 12-20 一3-4 A2112-20 三1-2 A21应用数学系现代数学基础分班:一班:电气学院电气工程系、航天学院微电子工程系二班:机电学院(机械制造、机械工程、宇航)三班:能源学院四班:机电学院(机械电子、机械设计)五班:电子与信息工程学院、理学院生命科学系、航天学院控制科学与工程系数理方程(一班) 12-20 一7-8 A1112-20 三5-6 A11谢鸿政应用数学系数理方程分班:一班:航天学院18系、电气学院电气工程系、电子与信息工程学院(微波)小波理论及应用(一班) 12-20 一1-2 A4212-20 三3-4 A42冉启文应用数学系小波理论及应用(二班) 12-20 一3-4 A4212-20 三1-2 A42应用数学系小波理论及应用分班:一班:航天学院控制科学与工程系、电子与信息工程学院二班:电气学院自动化测试与控制系、电气学院电气工程系变分法与最优控制18系12-20 一3-4 A4112-20 三1-2 A41王兴涛应用数学系。
博士研究生入学考试《数值分析(二)》
考试大纲
(科目代码:2228)
一、误差分析
1.误差来源
2.误差的基本概念
3.误差分析的若干原则
二、插值法
1. 拉格朗日插值
2. 均差与牛顿插值公式
3.分段线性插值公式
4.三次样条插值
三、函数逼近与计算
1. 最佳一致逼近多项式
2. 切比雪夫多项式
3. 最佳平方逼近
4. 正交多项式
5. 曲线拟合的最小二乘法
6. 离散富氏变换及其快速算法
四、数值积分与数值微分
1. 龙贝格求积算法
2. 高斯求积公式
3. 数值微分
五、常微分方程数值解法
1. 尤拉方法
2. 龙格-库塔方法
3. 单步法的收敛性和稳步性
4. 线性多步法
5. 方程组与高阶方程的情形
六、方程求根
1. 牛顿法
2. 弦截法与抛物线法
3. 代数方程求根
七、解线性方程组的迭代法
1. 雅可比迭代法与高斯-塞德尔迭代法
2. 迭代法的收敛性
3. 解线性方程组的松弛迭代法。
数值分析试题一.(10分)设给实数0a >,初值00x >:⑴试建立求1a的Newton 迭代公式,要求在迭代函数中不含除法运算; ⑵证明给定初值0x ,迭代收敛的充分必要条件为020x a<<;⑶该迭代的收敛速度是多少?⑷取00.1x =,计算15的近似值,要求计算迭代三次的值(结果保留5位小数)。
二.(10分)试确定参数,,a b c ,使得下面分段多项式函数()s x 是三次样条函数。
332,01()1(1)(1)(1),132x x s x x a x b x c x ⎧≤≤⎪=⎨--+-+-+≤≤⎪⎩ ()s x 是否是自然样条函数?三.(10分)利用Dollite 三角分解方法求解方程组123121022331302x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦ 四.(10分)给定3阶线性方程组123122*********x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦讨论其Jacobi 迭代格式的收敛性五.(10分)推导出中矩形求积公式()()()2baa b f x dx b a f +≈-⎰ ,并求出其截断误差。
六.(10分用最小二乘法确定拟合公式bx y ae =中的参数,a b 。
七.(10分)根据已知函数表:建立不超过三次的Newton 插值项式。
八.(10分)试确定常数01,A A ,使求积公式1011()(f x dx A f A f -≈+⎰有尽可能高的代数精度,并指出代数精度是多少,该公式是否是Gauss 型?并用此公式计算积分311I dx x=⎰(结果保留5位小数)。
九.(10分)利用经典四阶Runge-Kutta 方法求初值问题:20,01(0)1y y x y '=-≤≤⎧⎨=⎩在0.2x =处的数值解(取步长0.1h =)。
10.(10分)讨论两步方法 11112(4)33n n n ny y y hy +-+'=-+ 的局部截断误差,求出它的局部阶段误差的首项(主部),它是多少阶的? (在线性多步法的局部截断误差中10111[()()],2,3,!p prr r i i i i C i a r i b r r -==-⎧⎫=--+-=⎨⎬⎩⎭∑∑ )。