偶数阶幻方
- 格式:pdf
- 大小:841.10 KB
- 文档页数:6

填幻方技巧什么是幻方?幻方是一种数学谜题,它由一个n×n 的方阵组成,其中填充了从1到 n^2 的整数,使得每一行、每一列以及对角线上的数字之和都相等。
幻方有着悠久的历史,可以追溯到几百年前。
幻方的分类根据幻方的特性和规则,我们可以将其分为以下几类:奇阶幻方奇阶幻方是指边长为奇数的幻方。
例如3阶、5阶、7阶等。
奇阶幻方最早出现在中国古代文献中,并且在各种文化中得到广泛应用。
偶阶幻方偶阶幻方是指边长为偶数的幻方。
例如4阶、6阶、8阶等。
偶阶幻方相对于奇阶幻方来说更加复杂,因为它们需要遵循特定的构造规则。
多重幻方多重幻方是指在同一个正方形中同时存在多个不同边长的完美平衡填充数字的方式。
这种类型的幻方通常具有更高级别的难度和挑战性。
填幻方的技巧下面将介绍一些填写幻方的技巧,帮助你更好地解决幻方谜题:1. 奇阶幻方的填写技巧对于奇阶幻方,最简单的方法是使用“Siamese method”(中文名:暹罗法)来填写。
这种方法可以确保你能够快速而准确地填写奇阶幻方。
暹罗法的基本步骤如下: - 将数字1放在第一行中间的位置。
- 从数字2开始,按照以下规则进行填写: - 如果当前位置的右上角为空,则将数字放在右上角。
- 如果当前位置超出第一行,则将数字放在下一列的最后一个位置。
- 如果当前位置超出最后一列,则将数字放在第一列的相同行。
- 如果当前位置已经被占用,则将数字放在当前位置下面一行。
2. 偶阶幻方的填写技巧对于偶阶幻方,填写起来相对更加困难。
有许多不同的方法和算法可以用来构造偶阶幻方,其中著名且常用的方法是“LUX method”(中文名:LUX法)。
LUX法的基本步骤如下: - 将数字1放在第一行中间的位置。
- 从数字2开始,按照以下规则进行填写: - 如果当前位置的右上角为空,则将数字放在右上角。
- 如果当前位置超出第一行,则将数字放在下一列的最后一个位置。
- 如果当前位置超出最后一列,则将数字放在第一列的相同行。

幻方知识点总结一、幻方的定义。
幻方是一种将数字安排在正方形格子中,使每行、每列和对角线上的数字之和都相等的数学结构。
例如,一个简单的三阶幻方(3×3的方格):begin{array}{ccc}hline8 1 6 hline3 5 7 hline4 9 2 hlineend{array}这里每行、每列和两条对角线上的数字之和都是15。
二、幻方的阶数。
1. 阶数的概念。
- 幻方的阶数是指幻方的行数(或列数),用n表示。
常见的有三阶幻方(n = 3)、四阶幻方(n=4)等。
2. 不同阶数幻方的特点。
- 三阶幻方。
- 是最基本、最常见的幻方。
它的数字组合相对固定,中心数字具有特殊性质。
在三阶幻方中,中心数字是这9个数字的平均数。
例如在上面的三阶幻方中,数字是1 - 9,它们的平均数是5,正好是中心数字。
- 四阶幻方。
- 构造相对复杂一些。
四阶幻方的幻和(每行、每列、对角线数字之和)计算为:(1 + 2+3+·s+16)÷4=(16×(16 + 1)÷2)÷4= 34。
三、幻方的构造方法。
1. 奇数阶幻方(以三阶幻方为例)——罗伯法。
- 把1(或最小的数)放在第一行正中。
- 按以下规律排列剩下的数:- 每一个数放在前一个数的右上一格。
- 如果这个数所要放的格已经超出了最顶行,那么就把它放在底行,仍然要放在右一列。
- 如果这个数所要放的格已经超出了最右列,那么就把它放在最左列,仍然要放在上一行。
- 如果这个数所要放的格已经填好了其他的数,或者同时超出了顶行和右列,那么就把这个数放在前一个数的下一行同一列的格内。
2. 偶数阶幻方(以四阶幻方为例)——对称交换法。
- 先将1 - 16按顺序填入4×4的方格中。
- 然后将对角线上的数字(从左上角到右下角和从右上角到左下角)进行对称交换。
例如,交换1和16,4和13,6和11,7和10,就可以得到一个四阶幻方。
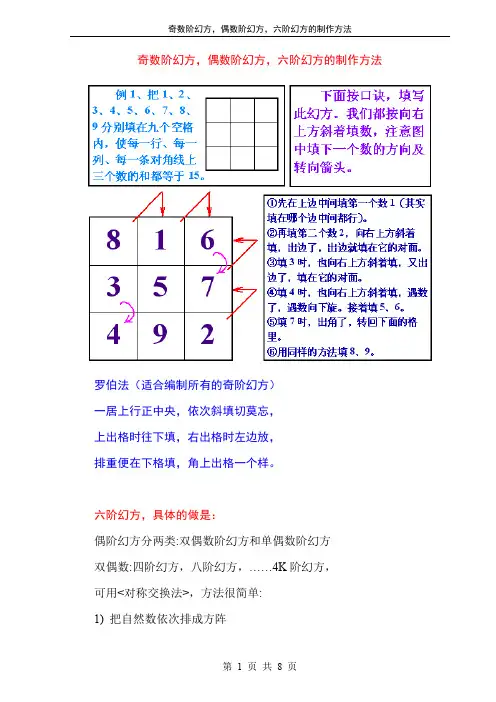
奇数阶幻方,偶数阶幻方,六阶幻方的制作方法罗伯法(适合编制所有的奇阶幻方)一居上行正中央,依次斜填切莫忘,上出格时往下填,右出格时左边放,排重便在下格填,角上出格一个样。
六阶幻方,具体的做是:偶阶幻方分两类:双偶数阶幻方和单偶数阶幻方双偶数:四阶幻方,八阶幻方,……4K阶幻方,可用<对称交换法>,方法很简单:1) 把自然数依次排成方阵2) 把幻方划成4×4的小区,每个小区划对角线3) 把这些对角线所划到的数,保持不动4) 把没划到的数,按幻方的中心,以中心对称的方式,进行对调幻方完成!单偶数:六阶幻方,十阶幻方,……4K+2阶幻方方法是很繁的,有一种称<同心方阵法>:1) 把幻方分成两个区:一是边框一圈;二是里面一个双偶数方阵,2) 把(3+8K)到(16K2 +8K+2)按双偶数幻方方法填入双偶数方阵3) 把余下的数,在边上试填,调整到符合为止六阶幻方(4×1+2,k=1)就是把11~26填入中间4×4方格中传说在很久很久以前,黄河里跃起一匹龙马,马背上驮着一幅图;洛水里也浮出一只神龟,龟背上也驮着一幅图。
这两幅图上都用圆点来表示一组数字,马背上的那幅称为“河图”,龟背上的那幅称为“洛书”。
(参见图1)再后来,经过人们研究,发现图中右边的那幅“洛书”,其实是一幅纵横图,即用1到9这9个数字组成一幅数字图,使它横的每行相加、竖的每列相加以及对角线相加,其和都等于15(参见图2)。
我们知道,纵横图就是今天所说的“幻方”,一般地,是指把从1到十的自然数排成纵横各有m 个数,并且使同行、同列及同一对角线上的n个数的和都相等的一种方阵,其中涉及的是组合数学的问题。
而前面所说的“洛书”,就是我国最早的一个三阶幻方。
图1 河图洛书图2 纵横图长期以来,纵横图一直被看作是一种数字游戏。
一直到南宋时期的数学家杨辉,才真正把它作为一个数学问题而加以深入的研究。

偶数阶幻方的解法
偶数阶幻方是指由奇数个数字构成的正方形矩阵,其中每行、每列和对角线上的数字之和都相等。
下面是一种经典的解法:
1. 填充数字:将1填充到幻方的左上角的第一行中间位置,然后顺序填充2、3、4等数字到右上角、右下角和左下角的位置,直到填满所有的空格。
填充的顺序是从上到下、从右到左。
2. 调整数字:将填充的数字中最大的数字和最小的数字交换,然后将次大的数字和次小的数字交换,以此类推。
这一步的目的是保证幻方的对角线上的数字之和仍然相等。
3. 调整行:从第二行开始,将前一行的最后一个数字放到当前行的第一个位置,然后将剩下的数字依次右移一位。
这一步的目的是保证幻方的每行的数字之和相等。
4. 调整列:从第二列开始,将前一列的最后一个数字放到当前列的第一个位置,然后将剩下的数字依次下移一位。
这一步的目的是保证幻方的每列的数字之和相等。
5. 完成:重复步骤3和步骤4,直到幻方的每行和每列的数字
之和都相等。
最后得到的矩阵就是一个解法。
需要注意的是,对于偶数阶幻方,不同的填充和调整顺序可能会得到不同的解法。
上述的步骤只是其中一种可能的解法。

偶数阶幻方二阶幻方不存在。
如果存在着二阶幻方,那么这个幻方的幻和为123452+++=。
这表明这个幻方的四个角上的四个数1,2,3,4,只能是1,4和2,3分别占据两组对角线,但是在这种情况下行、列的和只能是3,7或4,6,而不能是5。
所以偶数阶幻方如果存在,只能是四阶以上。
四阶幻方四阶幻方的幻和为121516344++++= 。
我们试着排一个四阶幻方。
首先将1,2,,15,16 这16个数按自然顺序写入44⨯方阵中,通过简单计算不难发现,两条对角线上的四个数之和都是34,而各行各列上的四个数之和都不是34。
我们来调整,因为两条对角线上的四个数之和都是34,所以我们在调整的时候应当使对角线上的数不离开对角线。
第一行12343424+++-=-, 第四行131415163424+++-=,如果将1,16对调,将4,13对调,这样不仅第一行与第四行的四个数之和都是34,第一列和第四列的四个数之和也都是34,同样将6,11对调,将7,10对调,就调整好了第二、三行(列)。
对于四阶幻方,我们称和为17的两数为互补两数。
因此,我们可以总结四阶幻方的排法:首先将1,2,,15,16 这16个数按自然顺序写入44⨯方阵中,然后把对角线上的数都换成它的补数,即得。
六阶幻方六阶幻方的幻和为图 1123456789101112131415161235361116++++= ,要排出一个六阶幻方,我们能借用四阶幻方的经验吗?如果我们将1,2,,35,36 像图2一样,排成一个66⨯方阵,虽然也有两条对角线上六个数的和为111,但是我们立即发现,无论怎么调整,也得不出六阶幻方。
所以要排出六阶幻方,我们必须另想办法。
观察图2,我们看到一个66⨯方阵可以划分为四个33⨯方阵,如果我们把1,2,,35,36 平均分为四段,每一段排成一个三阶幻方,将这四个三阶幻方拼成一个66⨯方阵,情形将如何呢?第一段,1,2,3,,8,9 用杨辉的方法(以下我们都用杨辉方法),排成幻方A :()492357 816A 幻和为15A H =;第二段,10,11,,17,18 ,排成幻方B :()131811121416 171015B 幻和为42B H =;第三段,19,20,,26,27 ,排成幻方C :()222720212325 261924C 幻和为69C H =;第四段,28,29,,35,36 ,排成幻方D :()313629303234 352830D 幻和为96D H =。

幻方常规解法汇总按目前填写幻方的方法,是把幻方分成了三类,即奇数阶幻方、双偶阶幻方、单偶阶幻方。
下面按这三类幻方,列出最常用解法(考试用,不求强大,只求有效!)。
奇数阶幻方(罗伯法)奇数阶幻方最经典的填法是罗伯法。
填写的方法是:把1(或最小的数)放在第一行正中;按以下规律排列剩下的(n×n -1)个数:1、每一个数放在前一个数的右上一格;2、如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列;3、如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行;4、如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在前一个数的下一行同一列的格内;5、如果这个数所要放的格已经有数填入,那么就把它放在前一个数的下一行同一列的格内。
例,用该填法获得的5阶幻方:17 24 1 8 1523 5 7 14 164 6 13 20 2210 12 19 21 311 18 25 2 9双偶数阶幻方(对称交换法)所谓双偶阶幻方就是当n可以被4整除时的偶阶幻方,即4K阶幻方。
在说解法之前我们先说明一个“互补数”定义:就是在n阶幻方中,如果两个数的和等于幻方中最大的数与1的和(即n×n+1),我们称它们为一对互补数。
如在三阶幻方中,每一对和为10的数,是一对互补数;在四阶幻方中,每一对和为17的数,是一对互补数。
双偶数阶幻方的对称交换解法:先看看4阶幻方的填法:将数字从左到右、从上到下按顺序填写:1 2 3 45 6789 1011121314 15 16内外四个角对角上互补的数相易,(方阵分为两个正方形,外大内小,然后把大正方形的四个对角上的数字对换,小正方形四个对角上的数字对换)即(1,16)(4,13)互换(6,11)(7,10)互换即可。
16 2 3 135 11 10 89 7 6 124 14 15 1对于n=4k阶幻方,我们先把数字按顺序填写。

巧填幻方一、什么叫幻方?(通俗点说)把一些有规律的数填在纵横格数都相等的正方形图内,使每一行、每一列和每一条对角线上各个数之和都相等。
这样的方阵图叫做幻方。
幻方又分为奇数阶幻方和偶数阶幻方。
奇数阶幻方是指横行、竖列都是单数(即3、5、7、9……)的方阵图。
偶数阶幻方是指横行、竖列都是双数(即4、6、8、10……)的方阵图。
二、奇数阶幻方在第一行居中的方格内放1,依次向右上方填入2、3、4…,如果右上方已有数字,则向下移一格继续填写。
(1) 将1放在第一行中间一列;(2) 从2开始直到n×n止各数依次按下列规则存放:按 45°方向向右上方行走,每一个数存放的行比前一个数的行数减1,列数加1(3) 如果行列范围超出矩阵范围,则回绕。
例如1在第1行,则2应放在最下一行,列数同样加1;(4) 如果按上面规则确定的位置上已有数,或上一个数是第1行第n列时,则把下一个数放在上一个数的下面。
例:3阶幻方例:5阶幻方三、偶阶幻方1、双偶阶幻方:四阶幻方,八阶幻方,....,4m阶幻方,采用对称元素交换法。
将幻方等分成m×m个4阶幻方,将各4阶幻方中对角线上的方格内数字与n阶(n=4×m)幻方内以中心点为对称点的对角数字进行交换。
首先把数1到n×n按从上至下,从左到右顺序填入矩阵,然后将方阵的所有4×4子方阵中的两对角线上位置的数关于方阵中心作对称交换,即a(i,j)与a(n-1-i,n-1-j)交换,所有其它位置上的数不变。
(或者将对角线不变,其它位置对称交换也可)1) 把自然数依次排成方阵2) 把幻方划成4*4的小区,每个小区划对角线,3) 把这些对角线所划到的数,保持不动,4) 把没划到的数,按幻方的中心,以中心对称的方式,进行对调。
例:4阶幻方第一步,先把1放在4阶幻方4个角的任意一个角格,按同一个方向按顺序依次填写其余数。
如下所示:第二步,进行对称交换(有两种对称交换的方法)。

一、幻方按照阶数可分成了三类,即奇数阶幻方、双偶阶幻方、单偶阶幻方。
二、奇数阶幻方(劳伯法)奇数阶幻方最经典的填法是罗伯法。
填写的方法是:把1(或最小的数)放在第一行正中;按以下规律排列剩下的(n×n-1)个数:(1)每一个数放在前一个数的右上一格;(2)如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列;(3)如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行;(4)如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在底行且最左列;(5)如果这个数所要放的格已经有数填入,那么就把它放在前一个数的下一行同一列的格内。
例,用该填法获得的5阶幻方:三、单偶数阶幻方(斯特拉兹法)所谓单偶阶幻方就是当n不可以被4整除时的偶阶幻方,即4K+2阶幻方。
如(n=6,10,14……)的幻方。
单偶数阶幻方最经典的填法是斯特拉兹法。
填写的方法是:以10阶幻方为例。
这时,k=2。
(1)把魔方阵分为A,B,C,D四个象限,这样每一个象限肯定是奇数阶。
用罗伯法,依次在A象限,D象限,B象限,C象限按奇数阶幻方的填法填数。
(2)在A象限的中间行、中间格开始,按自左向右的方向,标出k格。
A象限的其它行则标出最左边的k格。
将这些格,和C象限相对位置上的数互换位置。
(3)在B象限所有行的中间格,自右向左,标出k-1格。
(注:6阶幻方由于k-1=0,所以不用再作B、D象限的数据交换),将这些格,和D象限相对位置上的数互换位置。
四、源代码如下,已加详细注释#include<stdio.h>#include<stdlib.h>int array[15][15];intinit(int degree) //初始化{inti;int j;for(i=0; i<=degree+1; i++)for(j=0; j<=degree+1; j++)array[i][j] = 0;return 0;}inttest_print(int x, int y, int w, int h) //测试用的,输出以(x,y)为原点,宽为w,高为h,这个区域的数值{inti;int j;for(i=y; i<=y+h-1; i++){for(j=x; j<=x+w-1; j++){printf("%2d ",array[i][j]);}printf("\n");}return 0;}intlao_bo_er(int degree, int x, int y, intnum) //劳伯法{inti;int j;int k;i = y;j = degree/2 + x;for(k=num; k<=num+degree*degree-1; k++){array[i][j] = k;if((k-num+1)%degree == 0){ //如果这个数所要放的格已经有数填入i = (i-y+1)%degree+y;}else{ //每一个数放在前一个数的右上一格i = (i-y-1+degree)%degree+y;j = (j-x+1)%degree+x;}}return 0;}intseq_range(int degree) //把数字按顺序填{inti;int j;intnum;num = 1;for(i=1; i<=degree; i++){for(j=1; j<=degree; j++){array[i][j] = num++;}}return 0;}intsi_te_la_zi(int degree, int x, int y, intnum) //斯特拉兹法{intdeg;int k;int temp;inti;int j;deg = degree/2;lao_bo_er(deg, x, y, num); //用罗伯法,依次在A象限,D象限,B象限,C象限按奇数阶幻方的填法填数lao_bo_er(deg, x+deg, y, num+2*deg*deg);lao_bo_er(deg, x, y+deg, num+3*deg*deg);lao_bo_er(deg, x+deg, y+deg, num+deg*deg);k = (degree-2)/4;for(i=1; i<=deg; i++){ //A象限和C象限对换数据for(j=1; j<=k; j++){temp = array[i][j];array[i][j] = array[i+deg][j];array[i+deg][j]=temp;}for(j=deg+deg/2+1; j>=deg+deg/2-k+3; j--){temp = array[i][j];array[i][j] = array[i+deg][j];array[i+deg][j]=temp;}}for(i=j=1; j<=deg/2+k; j++){ //B象限和D象限对换数据temp = array[i+deg/2][j];array[i+deg/2][j] = array[i+deg+deg/2][j];array[i+deg+deg/2][j]=temp;}return 0;}inthai_er_fa(int degree) //海尔法{inti;int j;int complement;intdeg;seq_range(degree);complement = degree*degree+1;deg = degree/4;for(i=0; i<deg; i++){for(j=0; j<deg; j++){ //对角线上的数字换成和它互补的数array[i*4+1][j*4+1] = complement -array[i*4+1][j*4+1];array[i*4+1][j*4+4] = complement -array[i*4+1][j*4+4];array[i*4+4][j*4+1] = complement -array[i*4+4][j*4+1];array[i*4+4][j*4+4] = complement -array[i*4+4][j*4+4];array[i*4+2][j*4+2] = complement -array[i*4+2][j*4+2];array[i*4+2][j*4+3] = complement -array[i*4+2][j*4+3];array[i*4+3][j*4+2] = complement -array[i*4+3][j*4+2];array[i*4+3][j*4+3] = complement -array[i*4+3][j*4+3];}}return 0;}int main(){int degree;printf("please input the degree\n");scanf("%d",°ree);init(degree);if(degree%2 == 1){ //奇数阶幻方lao_bo_er(degree,1,1,1);test_print(1,1,degree,degree);}else if(degree%4 == 2){ //双偶阶幻方si_te_la_zi(degree, 1, 1, 1);test_print(1,1,degree,degree);}else{ //单偶阶幻方hai_er_fa(degree);test_print(1,1,degree,degree);}return 0;}。

幻方的构造所谓幻方(magic square),也叫纵横图,就是在n×n的方阵中,放入从1开始的n2个自然数;在一定的布局下,其各行、各列和两条对角线上的数字之和正好都相等。
这个和数就叫“幻方常数”或“幻和”。
对于任意n阶的幻方来说,其幻方常数S和方阵阶数n的关系是:1n(n2+1)S=2例如3阶的幻方常数是15,4阶的幻方常数是34,5阶的幻方常数是65……那么,如何构造幻方呢?下面我们分几种情况分别进行说明:一、奇数阶幻方奇数阶幻方,也就是幻方阶数为奇数的幻方,如:3阶、5阶、7阶……幻方,那么如何构造这样的幻方呢?对所有奇数阶幻方的构造,我们都可以采取“连续摆数法”,其法则如下:把“1”放在中间一列最上边的方格中,从它开始,按对角线方向(比如说按从左下到右上的方向)顺次把由小到大的各数放入各方格中,如果碰到顶,则折向底,如果到达右侧,则转向左侧,如果进行中轮到的方格中已有数或到达右上角,则退至前一格的下方。
按照这一法则构成5阶幻方的示例如下图:按上述法则构成11阶幻方如下图:二、4阶幻方构造4阶幻方我们可以采取“对角线法”,即首先按从上到下、从右向左(也可按从左到右、从上到下)的次序把1—16填入4阶方阵中,然后将两条主对角线上元素按中心轴对称原则互相交换就行,也就是1和16互换、6和11互换、4和13互换、7和10互换,见下图:三、6阶幻方构造6阶幻方,我们可以采用“斯特雷奇法”,即首先将6阶幻方分成ABCD四个3阶幻方,然后按ABCD的顺序将每个3阶幻方用“连续摆数法”填上,3阶方阵A填数字1—9,B填10—18,C填19—27,D填28—36,如下图:然后将A中的8、5和4分别和D中的35、32和31交换,形成6阶幻方,如下图:四、双偶数阶幻方双偶数阶幻方,即n=2·2m形式的幻方,我们可以采取“对称法”(symmetrical method)。
即将双偶数阶幻方分成上、下、左、右4个小方阵,首先在左上角方阵中布点:每行每列任取一半方格打上“○”号;然后向其余3个方阵映象,使每个小方阵中各有一半方格被“○”所占据。

没法,组合数学还考幻方构造。
这东西不看解法真不会写,虽然没见有啥用,但还是记录下,免得日后再找。
按目前填写幻方的方法,是把幻方分成了三类,即奇数阶幻方、双偶阶幻方、单偶阶幻方。
下面按这三类幻方,列出最常用解法(考试用,不求强大,只求有效!)。
奇数阶幻方(罗伯法)奇数阶幻方最经典的填法是罗伯法。
填写的方法是:把1(或最小的数)放在第一行正中;按以下规律排列剩下的(n×n-1)个数:1、每一个数放在前一个数的右上一格;2、如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列;3、如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行;4、如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在前一个数的下一行同一列的格内;5、如果这个数所要放的格已经有数填入,那么就把它放在前一个数的下一行同一列的格内。
例,用该填法获得的5阶幻方:17241815235714164613202210121921311182529双偶数阶幻方(对称交换法)所谓双偶阶幻方就是当n可以被4整除时的偶阶幻方,即4K阶幻方。
在说解法之前我们先说明一个“互补数”定义:就是在 n 阶幻方中,如果两个数的和等于幻方中最大的数与 1 的和(即n×n+1),我们称它们为一对互补数。
如在三阶幻方中,每一对和为 10 的数,是一对互补数;在四阶幻方中,每一对和为 17 的数,是一对互补数。
双偶数阶幻方的对称交换解法:先看看4阶幻方的填法:将数字从左到右、从上到下按顺序填写:12345678910111213141516内外四个角对角上互补的数相易,(方阵分为两个正方形,外大内小,然后把大正方形的四个对角上的数字对换,小正方形四个对角上的数字对换)即(1,16)(4,13)互换(6,11)(7,10)互换即可。
16231351110897612414151对于n=4k阶幻方,我们先把数字按顺序填写。

没法,组合数学还考幻方构造。
这东西不看解法真不会写,虽然没见有啥用,但还是记录下,免得日后再找。
按目前填写幻方的方法,是把幻方分成了三类,即奇数阶幻方、双偶阶幻方、单偶阶幻方。
下面按这三类幻方,列出最常用解法(考试用,不求强大,只求有效!)。
奇数阶幻方(罗伯法)奇数阶幻方最经典的填法是罗伯法。
填写的方法是:把1(或最小的数)放在第一行正中;按以下规律排列剩下的(n×n-1)个数:1、每一个数放在前一个数的右上一格;2、如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列;3、如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行;4、如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在前一个数的下一行同一列的格内;5、如果这个数所要放的格已经有数填入,那么就把它放在前一个数的下一行同一列的格内。
例,用该填法获得的5阶幻方:双偶数阶幻方(对称交换法)所谓双偶阶幻方就是当n可以被4整除时的偶阶幻方,即4K阶幻方。
在说解法之前我们先说明一个“互补数”定义:就是在 n 阶幻方中,如果两个数的和等于幻方中最大的数与 1 的和(即n×n+1),我们称它们为一对互补数。
如在三阶幻方中,每一对和为 10 的数,是一对互补数;在四阶幻方中,每一对和为 17 的数,是一对互补数。
双偶数阶幻方的对称交换解法:先看看4阶幻方的填法:将数字从左到右、从上到下按顺序填写:的四个对角上的数字对换,小正方形四个对角上的数字对换)即(1,16)(4,13)互换(6,11)(7,10)互换即可。
对于n=4k阶幻方,我们先把数字按顺序填写。
写好后,按4×4把它划分成k×k 个方阵。
因为n是4的倍数,一定能用4×4的小方阵分割。
然后把每个小方阵的对角线,象制作4阶幻方的方法一样,对角线上的数字换成互补的数字,就构成幻方。
以8阶幻方为例:(1) 先把数字按顺序填。
幻方解法
幻方,就是对于一个n×n的方阵,将1—n²这n²个数填入其中,使每行每列以及对角线上的数字之和都相等的方阵。
幻方分为奇数阶幻方(n=2k+1)、单偶数幻方
(n=4k+2)、双偶数幻方(n=4k)三种,每种幻方解法不同,但都有其固定的解。
下面我来具体介绍下幻方的解法:
1.奇数阶幻方
①将1填入第一行中间位置
②向右上方向依次填入
③如果上方出格了,则将其填入最后一行与其同列的位置
④如果右方出格了,则将其填入第一列与其同行的位置
⑤如果右上都出格,则将其填入第一列最后一格
⑥如果将要填入的方格已有数字,则填入上一个数字的下方
这里已三阶幻方为例:
2.双偶数阶幻方(n=4k):
①先将1,2,3……n²依次填入方阵中
②拟出方阵对角线
③对角线上数字不动,将其余所有数字移至与其中心对称的位置
这里以四阶幻方为例
↓
↓ 3.单偶数阶幻方(n=4k+2):
①先将1,2,3……n平方依次填入方阵中
②拟出对角线,将对角线上所有数字移至与其中心对称的位置。
③从方阵左半部分的每一列数字中抽出一对上下对称的数字互换位置(每一列抽出一对)
④从方阵上半部分的每一行数字中抽出一对左对称的数字互换位置(每一行抽出一对)
注:已经移动过或换过位置的数字不能再移动或换位
这里以六阶幻方为例:
↓
↓②↓
↓
↓③↓
↓
↓④↓。
Advances in Applied Mathematics 应用数学进展, 2023, 12(4), 2043-2048 Published Online April 2023 in Hans. https:///journal/aam https:///10.12677/aam.2023.124208双偶数阶幻方构造规律的矩阵化朱雅妮*,刘兴祥#延安大学数学与计算机科学学院,陕西 延安收稿日期:2023年3月26日;录用日期:2023年4月21日;发布日期:2023年4月29日摘要以和幻方的定义及性质为基础,利用矩阵化解决双偶数阶(4n 阶)幻方,通过分块矩阵的运算,给出双偶数阶幻方构造的通法。
关键词和幻方,双偶数阶幻方,分块矩阵Matrix of Construction Law of Magic Squares of Double Even OrderYani Zhu *, Xingxiang Liu #College of Mathematics and Computer Science, Yan’an University, Yan’an ShaanxiReceived: Mar. 26th , 2023; accepted: Apr. 21st , 2023; published: Apr. 29th, 2023AbstractBased on the definition and properties of sum magic squares, the paper solves the magic squares of double even order (4n order) by matrix, and gives the general method of constructing magic squares of double even order by the operation of block matrix.KeywordsSum Magic Square, Magic Square of Double Even Order, Block Matrix*第一作者。
偶数阶幻方二阶幻方不存在。
如果存在着二阶幻方,那么这个幻方的幻和为123452+++=。
这表明这个幻方的四个角上的四个数1,2,3,4,只能是1,4和2,3分别占据两组对角线,但是在这种情况下行、列的和只能是3,7或4,6,而不能是5。
所以偶数阶幻方如果存在,只能是四阶以上。
四阶幻方四阶幻方的幻和为121516344++++= 。
我们试着排一个四阶幻方。
首先将1,2,,15,16 这16个数按自然顺序写入44⨯方阵中,通过简单计算不难发现,两条对角线上的四个数之和都是34,而各行各列上的四个数之和都不是34。
我们来调整,因为两条对角线上的四个数之和都是34,所以我们在调整的时候应当使对角线上的数不离开对角线。
第一行12343424+++-=-, 第四行131415163424+++-=,如果将1,16对调,将4,13对调,这样不仅第一行与第四行的四个数之和都是34,第一列和第四列的四个数之和也都是34,同样将6,11对调,将7,10对调,就调整好了第二、三行(列)。
对于四阶幻方,我们称和为17的两数为互补两数。
因此,我们可以总结四阶幻方的排法:首先将1,2,,15,16 这16个数按自然顺序写入44⨯方阵中,然后把对角线上的数都换成它的补数,即得。
六阶幻方六阶幻方的幻和为图 1123456789101112131415161235361116++++= ,要排出一个六阶幻方,我们能借用四阶幻方的经验吗?如果我们将1,2,,35,36 像图2一样,排成一个66⨯方阵,虽然也有两条对角线上六个数的和为111,但是我们立即发现,无论怎么调整,也得不出六阶幻方。
所以要排出六阶幻方,我们必须另想办法。
观察图2,我们看到一个66⨯方阵可以划分为四个33⨯方阵,如果我们把1,2,,35,36 平均分为四段,每一段排成一个三阶幻方,将这四个三阶幻方拼成一个66⨯方阵,情形将如何呢?第一段,1,2,3,,8,9 用杨辉的方法(以下我们都用杨辉方法),排成幻方A :()492357 816A 幻和为15A H =;第二段,10,11,,17,18 ,排成幻方B :()131811121416 171015B 幻和为42B H =;第三段,19,20,,26,27 ,排成幻方C :()222720212325 261924C 幻和为69C H =;第四段,28,29,,35,36 ,排成幻方D :()313629303234 352830D 幻和为96D H =。
偶数阶幻方的一种制作方法-双偶阶、单偶阶幻方
1. 双偶阶幻方(对称交换法)
n为偶数,且能被4整除(n=4,8,12,16,20……) (n=4k,k=1,2,3,4,5……)
先说明一个定义。
互补:如果两个数字的和,等于幻方最大数和最小数的和,即 n×n+1,称为互补。
先看看4阶幻方的填法:将数字从左到右、从上到下按顺序填写:
这个方阵的对角线,已经用颜色标出。
将对角线上的数字,换成与它互补(同色)的数字。
这里,n×n+1 = 4×4+1 = 17;把1换成17-1 = 16;把6换成17-6 = 11;把11换成17-11 = 6……换完后就是一个四阶幻方。
对于n=4k阶幻方,我们先把数字按顺序填写。
写好后,按4×4把它划分成k×k个方阵。
因为n是4的倍数,一定能用4×4的小方阵分割。
然后把每个小方阵的对角线,象制作4阶幻方的方法一样,对角线上的数字换成互补的数字,就构成幻方。
2. 单偶阶幻方(斯特雷奇Ralph Strachey法)
n为偶数,且不能被4整除(n=6,10,14,18,22……) (n=4k+2,k=1,2,3,4,5……)
这是三种里面最复杂的幻方。
以n=10为例,10=4×2+2,这时k=2
(1)把方阵分为A,B,C,D四个象限,这样每一个象限肯定是奇数阶。
用楼梯法,依次在A象限,D象限,B象限,C象限按奇数阶幻方的填法填数。
(2)在A象限的中间行、中间格开始,按自左向右的方向,标出k 格。
A象限的其它行则标出最左边的k格。
将这些格,和C象限相对位置上的数,互换位置。
(3)在B象限任一行的中间格,自右向左,标出k-1列。
(注:6阶幻方由于k-1=0,所以不用再作B、D象限的数据交换),将B象限标出的这
些数,和D象限相对位置上的数进行交换,就形成幻方。
下面是6阶幻方的填法:6=4×1+2,这时k=1
看起来很麻烦,其实掌握了方法就很简单了。