
第2章逻辑代数及其化简
2-1 分别将十进制数29.625,127.175和378.425转换成二进制数。
解答:
(29.625)10=(1,1101.101)2
(127.175)10=(111,1111.0010,1100,…)2
(378.425)10=(1,0111,1010.0110,1100,…)2
2-2 分别将二进制数101101.11010111和101011.101101转换成十进制数。
解答:
(101101.11010111)2=(45.83984375)10
(101011.101101)2=(43.703125)10
2-3 分别将二进制数100110.100111和101011101.1100111转换成十六进制数。解答:
(100110.100111)2=(0010,0110.1001,1100)2=(26.9C)16
(101011101.1100111)2=(1,0101,1101.1100,1110)2=(15D.CE)16
2-4 分别将十六进制数3AD.6EBH和6C2B.4A7H转换成二进制数。
解答:
(3AD.6EB)16=(11,1010,1101.0110,1110,1011)2
(6C2B.4A7)16=(110,1100,0010,1011.0100,1010,0111)2
2-5 试用真值表法证明下列逻辑等式:
++=+
(1) AB A C BC AB C
++=++
(2) AB AB BC AB AB AC
++=++
(3) AB BC C A AB BC CA
+++=+
(4) AB AB BC AC A BC
+++=+
(5) AB BC CD D A ABCD ABCD
++=+
(6) AB AB ABC A B
证明:
++=+
(1) AB A C BC AB C
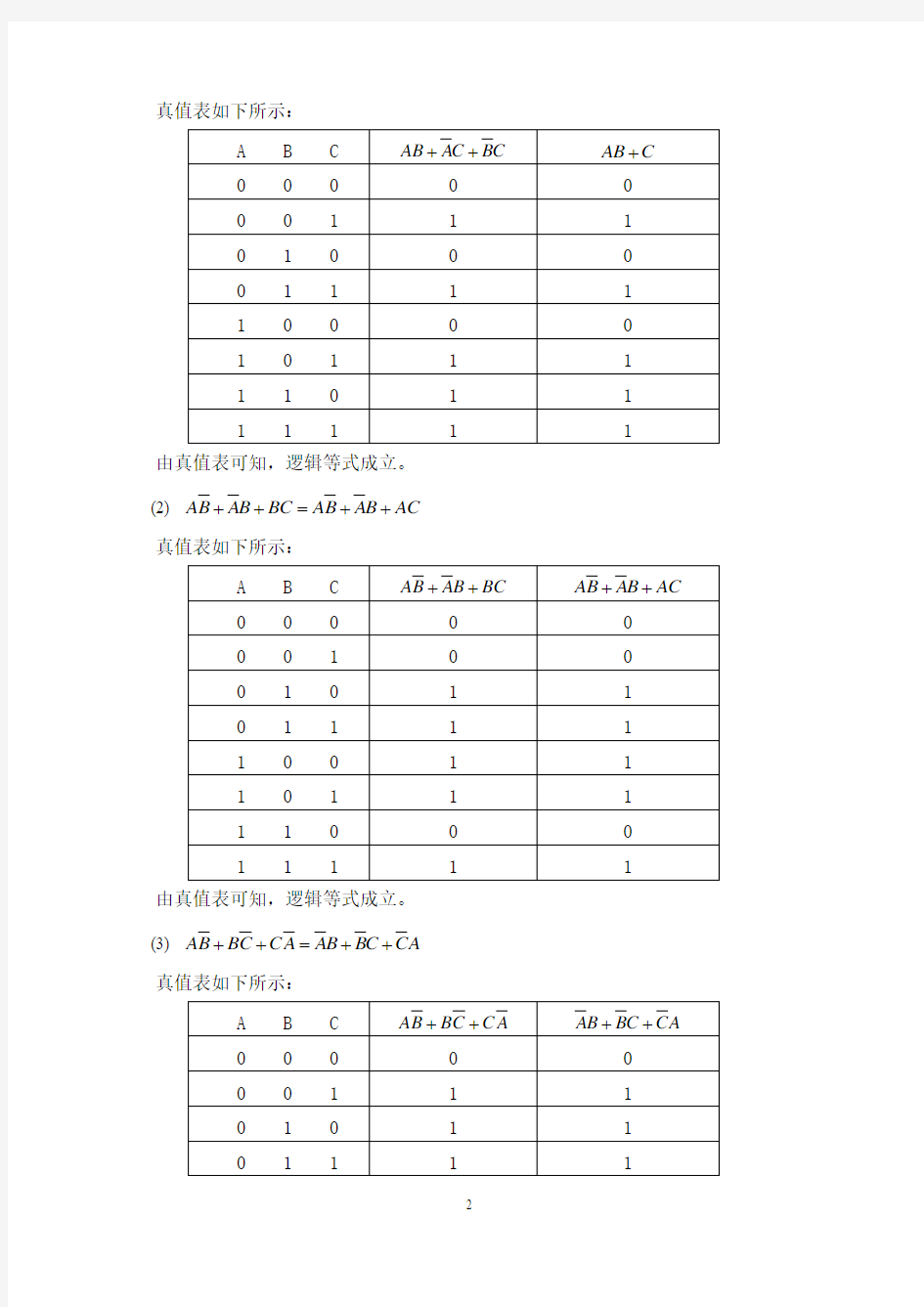
真值表如下所示:
由真值表可知,逻辑等式成立。
++=++ (2) AB AB BC AB AB AC 真值表如下所示:
由真值表可知,逻辑等式成立。
++=++ (3) AB BC C A AB BC CA 真值表如下所示:
由真值表可知,逻辑等式成立。
+++=+
(4) AB AB BC AC A BC
真值表如下所示:
由真值表可知,逻辑等式成立。
+++=+
(5) AB BC CD D A ABCD ABCD 真值表如下所示:
由真值表可知,逻辑等式成立。 (6) AB AB ABC A B ++=+ 真值表如下所示:
由真值表可知,逻辑等式成立。
2-6 求下列各逻辑函数F 的反函数F 和对偶式F ¢: (1) 1F A ABC A C =++
(2) 2()()()F A B A AB C A B C AB ABC =++++++ (3) 3F A B CD ADB =+++ (4) 4F AB BD C AB B D =+++++
(5) ()()5F AB AB BC BC =++ (6) 6F CD CD A C DB =+++ 解答:
(1) 1F A ABC A C =++
1()()F A A B C A C =+++ 1'()()F A A B C A C =+++
(2) 2()()()F A B A AB C A B C AB ABC =++++++
2()()()F AB AA B C A BC A B A B C =+++++++ 2'()()()F AB AA B C A BC A B A B C =+++++++ (3) 3F A B CD ADB =+++
3F ABC DA D B =+++
3'F ABC DA D B =+++
(4) 4F AB BD C AB B D =+++++
4()()()F A B B D C A B BD =+++ 4'()()()F A B B D C A B BD =+++ (5) ()()5F AB AB BC BC =++
5()()()()F A B A B B C B C =+++++ 5'()()()()F A B A B B C B C =+++++
(6) 6F CD CD A C DB =+++
6()()()()F C D C D A C D B =++++ 6'()()()()F C D C D A C D B =++++
2-7 某逻辑电路有A 、B 、C 共3个输入端,一个输出端F ,当输入信号中有奇数个1时,输出F 为1,否则输出为0,试列出此逻辑函数的真值表,写出其逻辑函数表达式,并画出逻辑电路图。 解答:
由题意可列出真值表如下:
由真值表可以得到函数表达式为:F ABC ABC ABC ABC =+++
逻辑电路如图T2-7所示:
A B C A B C A B C A B C
F
图T2-7
2-8 设计一个3人表决电路,要求:当输入A 、B 、C 中有半数以上人同意时,决议才能通过,但A 有否决权,如A 不同意,即使B 、C 都同意,决议也不能通过。 解答:
定义变量A 、B 、C ,1代表同意,0代表不同意;F 为结果,1代表通过,0代表不能通过。 由题意可列出真值表如下:
由真值表可以得到函数表达式为F ABC ABC ABC =++,化简可以得到F AC AB =+。
2-9 试用代数公式法证明题2-5中的各等式。
(1)AB A C BC AB C ++=+
证明:
()AB AC BC AB A B C
AB ABC AB C
++=++=+=+
(2)AB AB BC AB AB AC ++=++
证明:
()AB AB BC AB BC AB
AB BC AC AB AB AB AC
++=++=+++=++ (3)AB BC C A AB BC CA ++=++
证明:
()()()
()()()AB BC C A AB BC BC C A AB C A AB BC C A CA AB BC
AB CA BC AB BC C A CA BC AB AB BC CA
++=+++++=+++++=++++++++=++
(4)AB AB BC AC A BC +++=+
证明:
(1)AB AB BC AC A BC AC
A C BC A BC
+++=++=++=+
(5)AB BC CD D A ABCD ABCD +++=+ 证明:
()()()()
()()AB BC CD DA A B B C C D D A AB A C BC CD CA DA ABCD ABCD
+++=++++=++++=+ (6)AB AB ABC A B ++=+
证明:
()()AB AB ABC AB A B ABC
A ABC A
B B A B
++=+++=+++=+ 2-10 证明下列异或运算公式: (1) 0A A ?
(2) 1A A ?
(3) 0A A ?
(4) 1A A
?
(5) AB AB A ?
(6) A B A B ??
解答:
(1)0A A ⊕= 证明:
000A A AA AA ⊕=+=+=
(2)1A A ⊕= 证明:
11101011A A A A A ⊕=+=+=+=
(3)0A A ⊕= 证明:
00010A A A A A A ⊕=+=+=
(4)1A A ⊕=
证明:
1A A AA AA AA AA A A ⊕=+=+=+=
(5)AB AB A ⊕=
证明:
()()AB AB AB AB AB AB AB A B A B AB AB AB A ⊕=+=+++=+=
(6)A B A B ⊕=⊕
证明:
()()A B AB AB AB AB AB AB ABAB
A B A B AB AB A B
⊕=+=+=+==++=+=⊕
2-11 用公式法化简下列逻辑函数为最简与或式: (1) 1()F AB AB AB AB CD =+++ (2) 2F ABC AC ABC AC =+++ (3) 3()()F AB AB A B AB =++ (4) 4()()F A AB A BC C =+++ (5) 5()F AB A CD B C D =+++
(6) 6()()()F A B A AB C A B C AB ABC =++++++ 解答:
(1) 1()F AB AB AB AB CD =+++ 化简:
1()()
()()F AB AB AB AB CD A AB AB CD A B AB CD AB AB CD AB
=+++=++=++=+=
(2) 2F ABC AC ABC AC =+++ 化简:
2()()()()F ABC AC ABC AC A BC C ABC AC A B C ABC AC ABC ABC AC
A BC AC A BC AC ABC A
B
C AC ABC AB AC AC ABC AB A ABC A
A BC
=+++=+++=+++=++=⊕+=+=+++=+++=++=+=+
(3) 3()()F AB AB A B AB =++ 化简: 3()()()000F AB AB A B AB AB AB AB ABAB ABAB =++=+=+=+=
(4) 4()()F A AB A BC C =+++ 化简: 4()()()()()0F A AB A BC C A B A B C A B ABC =+++=+++=+=
(5) 5()F AB A CD B C D =+++ 化简:
5()()()()()()()()
()()()()
F AB ACD B C D A B A C D B C D AA AC AD AB BC BD B C D AC AB BC AD BD B C D AC AB AD BD B C D AC AB AD B C D ABC AC ACD AB ABC ABD ABD ACD AD AC AB AD
=+++=+++++=+++++++=++++++=+++++=++++=++++++++=++
(6) 6()()()F A B A AB C A B C AB ABC =++++++ 化简:
6()()()()F A B A AB C A B C AB ABC A AB C A BC AB ABC AC A BC AB ABC A BC AB A B BC A B C
=++++++=+++++=++++=++=++=++
2-12 用卡诺图化简下列逻辑函数为最简与或式: (1) 1(3,5,6,7)F m =?
(2) 2(4,5,6,7,8,9,10,11,12,13)F m =? (3) 3(2,3,6,7,10,11,12,15)F m =? (4) 4(1,3,4,5,8,9,13,15)F m =
?
(5) 5(1,3,4,6,7,9,11,12,14,15)F m =? (6) 6(0,2,4,7,8,9,12,13,14,15)F m =?
解答:
(1) 13,5,6,7F m
=
∑() 卡诺图:
由卡诺图可知:13,5,6,7F m
AC AB BC ==++∑()
(2) 24,5,6,7,8,9,10,11,12,13F m
=
∑() 卡诺图:
由卡诺图可知:2F AB AC ++
(3) 32,3,6,7,10,11,12,15F m
=
∑() 卡诺图:
由卡诺图可知:
32,3,6,7,10,11,12,15
F m ABCD A C BC CD
==+++
∑()
(4)
4134,5,8,9,13,15
F m
=∑(,,)卡诺图:
由卡诺图可知:
4134,5,8,9,13,15
F m ABD ABC ABD ABC
==+++
∑(,,)
(5)
5134,6,7,9,11,12,1415
F m
=∑(,,,)卡诺图:
由卡诺图可知:
5134,6,7,9,11,12,1415
F m BD BD CD
==++
∑(,,,)
(6)
6024,7,8,9,12,13,14,15
F m
=∑(,,)卡诺图:
10
由卡诺图可知:
6024,7,8,9,12,13,14,15F m AB AC CD ABC BCD ==++++∑(,,) 2-13 对具有无关项0AB AC +=的下列逻辑函数进行化简: (1) 1F AC AB =+ (2) 2F A C AB =+
(3) 3F ABC ABD ABD ABCD =+++ (4) 4F BCD ABCD ABC ABD =+++ (5)5F ACD ABCD ABD ABCD =+++ (6) 6F BCD ABCD ABCD =++
解答:
(1) 1F AC AB =+
1F AC AB AC AB AB AC AC B AC =+=+++=++
(2) 2F A C AB =+
解:
2F A C AB A C AB AB AC B C =+=+++=+
(3) 3F ABC ABD ABD ABCD =+++
3F ABC ABD ABD ABCD AB AC ABC AB ABCD AB AC ABC B ABCD AC AC B ACD AC B C ACD B C AD
=+++++=++++=+++=+++=++=++
(4) 4F BCD ABCD ABC ABD =+++
4F BCD ABCD ABC ABD
BCD ABCD ABC ABD AB AC
BCD ACD ABC ABD AB AC ABCD ACBD ABC AB AC AB CD AC BD ABC CD BD ABC
=+++=+++++=+++++=++++=++++=++
(5) 5F ACD ABCD ABD ABCD =+++
5F ACD ABCD ABD ABCD
ACD ABCD ABD ABCD AB AC ACD ABD ABD ABCD AB AC
ACD AD ABCD AB AC AD ABCD AB AC AD BCD AB AC AD BCD
=+++=+++++=+++++=++++=+++=+++=+
(6) 6F BCD ABCD ABCD =++
6F BCD ABCD ABCD
BCD ABCD ABCD AB AC BCD AB BCD AC ABD BCD AB AD BCD AC BCD BCD AD
=++=++++=++++=++++=++
2-14 化简下列具有无关项?的逻辑函数: (1) 1(0,1,3,5,8)(10,11,12,13,14,15)F m =+
?邋
(2) 2(0,1,2,3,4,7,8,9)(10,11,12,13,14,15)F m =+?邋 (3) 3(2,3,4,7,12,13,14)(5,6,8,9,10,11)F m =+?邋 (4) 4(0,2,7,8,13,15)(1,5,6,9,10,11,12)F m =+?邋 (5) 5(0,4,6,8,13)(1,2,3,9,10,11)F m =+?邋 (6) 6(0,2,6,8,10,14)(5,7,13,15)F m =+
?邋
解答:
(1)1(0,1,3,5,8)(10,11,12,13,14,15)F m φ=
+∑∑
卡诺图如图所示:
由卡诺图可知:1F ABD BCD BCD =++
(2)2(0,1,2,3,4,7,8,9)(10,11,12,13,14,15)F m φ=
+∑∑
卡诺图如图所示:
由卡诺图可知:2F B CD CD =++
(3)3(2,3,4,7,12,13,14)(5,6,8,9,10,11)F m φ=
+∑∑
卡诺图如图所示:
由卡诺图可知:3F AC A C BD =++
(4)4(0,2,7,8,13,15)(1,5,6,9,10,11,12)F m φ=
+∑∑
卡诺图如图所示:
由卡诺图可知:4F BD BD =+
(5)5(0,4,6,8,13)(1,2,3,9,10,11)F m φ=
+∑∑
卡诺图如图所示:
由卡诺图可知:5F B AD ACD =++
(6)6(0,2,6,8,10,14)(5,7,13,15)F m φ=
+∑∑
卡诺图如图所示:
由卡诺图可知:6F BD CD =+
2-15 用Multism2001将下列逻辑函数式化简为与或形式。
(1)Y(A ,B ,C ,D ,E)='''''''
'''())ABCD E A B D E AC DE AC
BE C D ++++
(2)Y(A ,B ,C ,D ,E)=∑m(0,4,11,15,16,19,20,23,27,31)
(3)Y(A ,B ,C ,D ,E)=∑m(1,3,5,8,9,12,13,18,19,22,23,24,25,28,29)
(4)Y(A ,B ,C ,D ,E ,F)=∑m(0,4,8,11,12,15,16,17,20,21,27,31,32,36,59,63)
(5)Y(A ,B ,C ,D ,E ,F)= ∑m(3,7,9,11,13,15,16,19,27,29,36,41,43,45,47,48)
(6)Y(A ,B ,C ,D ,E ,F)= ∑m(0,4,9,11,15,25,27,31,32,41,45,53,59,63) +∑Φ(13,29,36,43,47,57,61) 解答:
(1)
(,,,,)'''''''('')'F A B C D E ABCD E A B D E AC DE A C BE C D =++++
在Logic Convert 底部的逻辑表达式框内输入函数表达式,先得到对应真值表,再对真值表进行
化简,可以得到最简与或形式:
(,,,,)''''''''''F A B C D E A B D E A B C A CE AC DE BCD E =++++
即(,,,,)F A B C D E ABDE ABC ACE ACDE BCDE =++++ (2)
(,,,,)(0,4,11,15,16,19,20,23,27,31)F A B C D E m =∑
在Logic Convert 对应真值表中的最小项设置为1,对真值表进行简化,可以得到最简与或形式:
(,,,,)'''F A B C D E B D E ADE BDE =++
即:(,,,,)F A B C D E BDE ADE BDE =++
(3)
(,,,,)(1,3,5,8,9,12,13,18,19,22,23,24,25,28,29)F A B C D E m =∑
在Logic Convert 对应真值表中的最小项设置为1,对真值表进行简化,可以得到最简与或形式:
(,,,,)'''''''F A B C D E A B C E A D E AB D BD =+++
即(,,,,)F A B C D E ABCE ADE ABD BD =+++ (4)
(,,,,)(0,4,8,11,12,15,16,17,20,21,27,31,32,36,59,63)F A B C D E m =∑
在Logic Convert 对应真值表中的最小项设置为1,对真值表进行简化,可以得到最简与或形式:
(,,,,)''''''''''''F A B C D E A B E F A BC E A CEF B C E F BCEF =++++
即(,,,,)F A B C D E ABEF ABCE ACEF BCEF BCEF =++++
(5)
(,,,,)(3,7,9,11,13,15,16,19,27,29,36,41,43,45,47,48)F A B C D E m =∑
在Logic Convert 对应真值表中的最小项设置为1,对真值表进行简化,可以得到最简与或形式:
(,,,,)'''''''''''''''
F A B C D E A B EF A D EF A CDE F AB C DE F B CF BC D E F =+++++
即:(,,,,)''F A B C D E A B EF ADEF ACDEF ABCDEF BCF BCDEF =+++++
(6)
(,,,,)(0,4,9,11,15,25,27,31,32,41,45,53,59,63)
(13,29,36,43,47,57,61)
F A B C D E m φ=+∑∑
在Logic Convert 对应真值表中的最小项设置为1,将无关项设置为×对真值表进行简化,可以得到最简与或形式: (,,,,)'''''F A B C D E B C E F ABDE F CF =++
即:(,,,,)F A B C D E BCEF ABDEF CF =++
第8章 §8.5 逻辑代数公式化简习题2 1 第8章 §8.5 逻辑代数公式化简习题2 (一)考核内容 1、第8章掌握逻辑运算和逻辑门;掌握复合逻辑运算和复合逻辑门;掌握逻辑函数的表示方法;掌握逻辑代数的基本定理和常用公式;掌握逻辑函数的化简方法。 8.6 逻辑函数的化简 8.6. 1 化简的意义 1、所谓化简就是使逻辑函数中所包含的乘积项最少,而且每个乘积项所包含的变量因子最少,从而得到逻辑函数的最简与–或逻辑表达式。 逻辑函数化简通常有以下两种方法: (1)公式化简法 又称代数法,利用逻辑代数公式进行化简。它可以化简任意逻辑函数,但取决于经验、技巧、洞察力和对公式的熟练程度。 (2)卡诺图法 又称图解法。卡诺图化简比较直观、方便,但对于5变量以上的逻辑函数就失去直观性。 2、逻辑函数的最简形式 同一逻辑关系的逻辑函数不是唯一的,它可以有几种不同表达式,异或、与或、与或非—非、与非—与非、或与非、与或非、或非—或非。 一个逻辑函数的表达式可以有与或表达式、或与表达式、与非-与非表达式、或非-或非表达式、与或非表达式5种表示形式。 (1)与或表达式:AC B A Y += (2)或与表达式:Y ))((C A B A ++= (3)与非-与非表达式:Y AC B A ?= (4)或非-或非表达式:Y C A B A +++= (5)与或非表达式:Y C A B A += 3、公式化简法 (1)、并项法:利用公式A B A AB =+,把两个乘积项合并起来,消去一个变量。 例题1: B B A A B =+= (2)、吸收法:利用公式 A A B A =+,吸收掉多余的乘积项。 例题2:E B D A AB Y ++= B A E B D A B A +=+++= (3)、消去法:利用公式B A B A A +=+,消去乘积项中多余的因子。 例题3:AC AB Y += C B A A C B A ++=++= (4)、配项消项法:利用公式C A AB BC C A AB +=++,在函数与或表达式中加上多余的项— —冗余项,以消去更多的乘积项,从而获得最简与或式。 例题4: B A C AB ABC Y ++=
逻辑代数化简练习 一、选择题 1. 以下表达式中符合逻辑运算法则的是 。 A.C ·C =C 2 B.1+1=10 C.0<1 D.A +1=1 2. 逻辑变量的取值1和0可以表示: 。 A.开关的闭合、断开 B.电位的高、低 C.真与假 D.电流的有、无 3. 当逻辑函数有n 个变量时,共有 个变量取值组合? A. n B. 2n C. n 2 D. 2n 4. 逻辑函数的表示方法中具有唯一性的是 。 A .真值表 B.表达式 C.逻辑图 D.卡诺图 5.F=A B +BD+CDE+A D= 。 A.D B A + B.D B A )(+ C.))((D B D A ++ D.))((D B D A ++ 6.逻辑函数F=)(B A A ⊕⊕ = 。 A.B B.A C.B A ⊕ D. B A ⊕ 7.求一个逻辑函数F 的对偶式,可将F 中的 。 A .“·”换成“+”,“+”换成“·” B.原变量换成反变量,反变量换成原变量 C.变量不变 D.常数中“0”换成“1”,“1”换成“0” E.常数不变 8.A+BC= 。 A .A + B B.A + C C.(A +B )(A +C ) D.B +C 9.在何种输入情况下,“与非”运算的结果是逻辑0。 A .全部输入是0 B.任一输入是0 C.仅一输入是0 D.全部输入是1 10.在何种输入情况下,“或非”运算的结果是逻辑0。 A .全部输入是0 B.全部输入是1 C.任一输入为0,其他输入为1 D.任一输入为1 二、判断题(正确打√,错误的打×) 1. 逻辑变量的取值,1比0大。( )。 2. 异或函数与同或函数在逻辑上互为反函数。( )。 3.若两个函数具有相同的真值表,则两个逻辑函数必然相等。( )。 4.因为逻辑表达式A+B+AB=A+B 成立,所以AB=0成立。( ) 5.若两个函数具有不同的真值表,则两个逻辑函数必然不相等。( ) 6.若两个函数具有不同的逻辑函数式,则两个逻辑函数必然不相等。( ) 7.逻辑函数两次求反则还原,逻辑函数的对偶式再作对偶变换也还原为它本身。( )
《抽象代数基础》习 题 答 解 于延栋编 盐城师范学院数学科学学院二零零九年五月
第一章 群 论 §1 代数运算 1.设},,,{c b a e A =,A 上的乘法”“?的乘法表如下: 证明: ”“?适合结合律. 证明 设z y x ,,为A 中任意三个元素.为了证明”“?适合结合律,只需证明 )()(z y x z y x ??=??. 下面分两种情形来阐明上式成立. I.z y x ,,中至少有一个等于e . 当e x =时,)()(z y x z y z y x ??=?=??; 当e y =时,)()(z y x z x z y x ??=?=??; 当e z =时,)()(z y x y x z y x ??=?=??. II .z y x ,,都不等于e . (I)z y x ==.这时,)()(z y x e x x z z e z y x ??=?===?=??. (II)z y x ,,两两不等.这时,)()(z y x x x e z z z y x ??=?==?=??. (III)z y x ,,中有且仅有两个相等. 当y x =时,x 和z 是},,{c b a 中的两个不同元素,令u 表示},,{c b a 中其余的那个元素.于是,z z e z y x =?=??)(,z u x z y x =?=??)(,从而,)()(z y x z y x ??=??.同理可知,当z y =或x z =时,都有)()(z y x z y x ??=??. 2.设”“?是集合A 上一个适合结合律的代数运算.对于A 中元素,归纳定义∏=n i i a 1为: 111a a i i =∏=,111 1+=+=????? ??=∏∏r r i i r i i a a a . 证明: ∏∏∏+==+==???? ??????? ??m n k k m j j n n i i a a a 1 11.
习题7.7 3.指出下列方程所表示的曲线. (1)???==++;3, 25222x z y x (2)???==++;1,3694222y z y x (3)???-==+-;3, 254222x z y x (4)???==+-+.4,08422y x z y 【解】 (1)表示平面3=x 上的圆周曲线1622=+z y ; (2)表示平面1=y 上的椭圆19 32322 2=+z x ; (3)表示平面3-=x 上的双曲线14 162 2=-y z ; (4)表示平面4=y 上的抛物线642-=x z . 4.求() () ?????=++=++Γ2, 21, :2 22 2 222Rz z y x R z y x 在三个坐标面上的投影曲线. 【解】 (一)(1)、(2)联立消去z 得 2224 3R y x = + 所以,Γ在xoy 面上的投影曲线为 ?????==+.0, 4 322 2z R y x (二)(1)、(2)联立消去y 得 R z 2 1 = 所以,Γ在zox 面上的投影曲线为 .23.0,21R x y R z ≤ ?? ? ??==
(三)(1)、(2)联立消去x 得 R z 21 = 所以,Γ在yoz 面上的投影曲线为 .23.0, 21R y x R z ≤ ????? == 6.求由球面224y x z --= ①和锥面() 223y x z += ②所围成的立体在xoy 面上的投影区域. 【解】联立①、②消去z 得 122=+y x 故Γ在xoy 面上的投影曲线为 ? ??==+.0, 122z y x 所以,球面和锥面所围成的立体在xoy 面上的投影区域为(){}1|,22≤+=y x y x D . 习题7.8 2.设空间曲线C 的向量函数为(){} t t t t t r 62,34,122--+=,R t ∈.求曲线C 在与 20=t 相应的点处的单位切向量. 【解】因(){}64,4,2-=t t t r ,故C 相应20=t 的点处的切向量为 (){}2,4,42='r . C 相应20=t 的点处的单位切向量为 (){}.31,32,322,4,4612? ?????±=± =' 3.求曲线32,,:t z t y t x ===Γ在点)1,1,1(0M 处的切线方程和法平面方程. 【解】0M 对应参数1=t .Γ在0M 点处的切线方向为
高等数学第六版上册课后习题答案及解析 第一章 习题1-1 1. 设A =(-∞, -5)?(5, +∞), B =[-10, 3), 写出A ?B , A ?B , A \B 及A \(A \B )的表达式. 解 A ?B =(-∞, 3)?(5, +∞), A ? B =[-10, -5), A \ B =(-∞, -10)?(5, +∞), A \(A \B )=[-10, -5). 2. 设A 、B 是任意两个集合, 证明对偶律: (A ?B )C =A C ?B C . 证明 因为 x ∈(A ?B )C ?x ?A ?B ? x ?A 或x ?B ? x ∈A C 或x ∈B C ? x ∈A C ?B C , 所以 (A ?B )C =A C ?B C . 3. 设映射f : X →Y , A ?X , B ?X . 证明 (1)f (A ?B )=f (A )?f (B ); (2)f (A ?B )?f (A )?f (B ). 证明 因为 y ∈f (A ?B )??x ∈A ?B , 使f (x )=y ?(因为x ∈A 或x ∈B ) y ∈f (A )或y ∈f (B ) ? y ∈f (A )?f (B ), 所以 f (A ?B )=f (A )?f (B ). (2)因为 y ∈f (A ?B )??x ∈A ?B , 使f (x )=y ?(因为x ∈A 且x ∈B ) y ∈f (A )且y ∈f (B )? y ∈ f (A )?f (B ), 所以 f (A ?B )?f (A )?f (B ). 4. 设映射f : X →Y , 若存在一个映射g : Y →X , 使X I f g =ο, Y I g f =ο, 其中I X 、 I Y 分别是X 、Y 上的恒等映射, 即对于每一个x ∈X , 有I X x =x ; 对于每一个y ∈Y , 有I Y y =y . 证明: f 是双射, 且g 是f 的逆映射: g =f -1. 证明 因为对于任意的y ∈Y , 有x =g (y )∈X , 且f (x )=f [g (y )]=I y y =y , 即Y 中
第2章逻辑代数及其化简 2-1 分别将十进制数,和转换成二进制数。 解答: 10=(1,2 …)2 10=(111,,1100, ,1100,…)2 10=(1,0111, 2-2 分别将二进制数101101.和转换成十进制数。 解答: (101101.)2=(45.)10 2=10 2-3 分别将二进制数和转换成十六进制数。 解答: =(26.9C)16 2=(0010,,1100)2 =16 2=(1,0101,,1110)2 2-4 分别将十六进制数和6C2B.4A7H转换成二进制数。解答:
16=(11,1010,,1110,1011)2 (6C2B.4A7)16=(110,1100,0010,,1010,0111)2 2-5 试用真值表法证明下列逻辑等式: (1) AB A C BC AB C (2) AB AB BC AB AB AC (3) AB BC C A AB BC CA (4) AB AB BC AC A BC (5) AB BC CD D A ABCD ABCD (6) AB AB ABC A B 证明: (1) AB A C BC AB C ++=+ 真值表如下所示:
由真值表可知,逻辑等式成立。 (2) AB AB BC AB AB AC ++=++ 真值表如下所示:
由真值表可知,逻辑等式成立。 (3) AB BC C A AB BC CA ++=++ 真值表如下所示:
由真值表可知,逻辑等式成立。 (4) AB AB BC AC A BC +++=+ 真值表如下所示:
由真值表可知,逻辑等式成立。(5) AB BC CD D A ABCD ABCD +++=+ 真值表如下所示:
高等数学课后习题及解答 1. 设u=a-b+2c,v=-a+3b-c.试用a,b,c 表示2u-3v. 解2u-3v=2(a-b+2c)-3(-a+3b-c) =5a-11b+7c. 2. 如果平面上一个四边形的对角线互相平分,试用向量证明它是平 行四边形. 证如图8-1 ,设四边形ABCD中AC 与BD 交于M ,已知AM = MC ,DM 故 MB . AB AM MB MC DM DC . 即AB // DC 且|AB |=| DC | ,因此四边形ABCD是平行四边形. 3. 把△ABC的BC边五等分,设分点依次为D1,D2,D3,D4,再把各 分点与点 A 连接.试以AB=c, BC=a 表向量 证如图8-2 ,根据题意知 1 D 1 A, 1 D 2 A, D 3 A, D A. 4 1 D3 D4 BD1 1 a, 5 a, D1D2 a, 5 5 1 D 2 D 3 a, 5 故D1 A=- (AB BD1)=- a- c 5
D 2 A =- ( AB D A =- ( AB BD 2 BD )=- )=- 2 a- c 5 3 a- c 3 =- ( AB 3 BD 4 )=- 5 4a- c. 5 4. 已知两点 M 1(0,1,2)和 M 2(1,-1,0) .试用坐标表示式表示 向量 M 1M 2 及-2 M 1M 2 . 解 M 1M 2 =(1-0, -1-1, 0-2)=( 1, -2, -2) . -2 M 1M 2 =-2( 1,-2,-2) =(-2, 4,4). 5. 求平行于向量 a =(6, 7, -6)的单位向量 . a 解 向量 a 的单位向量 为 ,故平行向量 a 的单位向量为 a a 1 = ( 6,7, -6)= 6 , 7 , 6 , a 11 11 11 11 其 中 a 6 2 72 ( 6)2 11. 6. 在空间直角坐标系中,指出下列各点在哪个卦限? A (1,-2,3), B ( 2, 3,-4), C (2,-3,-4), D (-2, -3, 1). 解 A 点在第四卦限, B 点在第五卦限, C 点在第八卦限, D 点在第三卦限 . 7. 在坐标面上和在坐标轴上的点的坐标各有什么特征?指出下列各点的位置: A ( 3, 4, 0), B ( 0, 4,3), C ( 3,0,0), D ( 0, D A 4
《电子线路》教学导学案 课题名称:逻辑代数的基本定律及应用实施课时2课时教学目标 (知识与技能,过程与方法,情感、态度与价 值观)1.熟悉逻辑代数的基本定律2.会运用这些定律解题 教学重点逻辑代数的基本定律应用 教学难点逻辑代数的基本定律的应用 教学资源无 教学实施过程: 教学内容: 复习: 1.默写各种门电路的符号,函数表达式 2.默写各门电路逻辑功能 B、引入 逻辑代数的作用:把一个逻辑电路的简化问题变成相应的逻辑函数式的化简,为设计和认识逻辑电路带来方便。 C、新授 一、逻辑代数基本定律 1.交换律: A+B = B+A A·B = B·A 2.结合律: A +(B+C)=(A+B)+ C A ·(B+C)=(A·B)·C 3.分配律: A + B·C=(A+B)·(A+C) A ·(B+C)=A·B+A·C 4.互补律: 1 = +A A 教师活动: 要求每位学生拿出空白 纸 教师提问 简单讲述引入 教师讲解有哪些基本定 律,告诉学生该如何记 忆,可以让学士快速记 忆5分钟后在试着默写 学生活动: 回答教师提问 注意听讲 尝试记忆 尝试默写
0=?A A 5.反演律(摩根定律) ???? ?+=??=+B A B A B A B A 练习:用列真值表的方法验证摩根定律 6.逻辑函数式在等号两边的各项不可任意消去。 “=”表明逻辑功能是相同的,不是数值相等。 例: ①A +=A +C 则=C 因为当=1,可能B≠C ②=AC ,则B = C 因为A =时有可能B C 二、逻辑函数式的化简 1.并项法: 1=+A A 例:B B A AB =+ () B A C C B A C B A C B A =+=+ 2.吸收法: A +AB = A 3.消去法:B A B A A +=+ 例:() B A C AB C B C A AB ++=++C AB AB ?+== A B + C 4.配项法:() B B A A += 例1:() BC A A C A AB BC C A AB +++=++ C A BC A ABC AB +++= C A AB += 例2:求证:B A AB B A B A +=+ 证:()() B A B A B A B A ++=? B A AB += 要求学生分两大组用真值表的方法验证摩根定律 讲解化简过程中注意事项 讲解例题,各种方法的使用 可以让学生先试着化简 在仔细讲解 运用真值表的方法验证摩根定律完成任务一 注意听讲 完成对应练习完成任务二 边仔细听讲,边仔细思考试着化简
第一章 第二章 第一章 1. 如果在群G 中任意元素,a b 都满足222()ab a b =, 则G 是交换群. 证明: 对任意,a b G ∈有abab aabb =. 由消去律有ab ba =. □ 2. 如果在群G 中任意元素a 都满足2a e =,则G 是交换群. 证明: 对任意,a b G ∈有222()ab e a b ==. 由上题即得. □ 3. 设G 是一个非空有限集合, 它上面的一个乘法满足: (1) ()()a bc ab c =, 任意,,a b c G ∈. (2) 若ab ac =则b c =. (3) 若ac bc =则a b =. 求证: G 关于这个乘法是一个群. 证明: 任取a G ∈, 考虑2{,,,}a a G ??. 由于||G <∞必然存在最 小的i +∈ 使得i a a =. 如果对任意a G ∈, 上述i 都是1, 即, 对任意x G ∈都有2x x =, 我们断言G 只有一个元, 从而是幺群. 事实上, 对任意,a b G ∈, 此时有: ()()()ab ab a ba b ab ==, 由消去律, 2bab b b ==; 2ab b b ==, 再由消去律, 得到a b =, 从而证明了此时G 只有一个元, 从而是幺群. 所以我们设G 中至少有一个元素a 满足: 对于满足 i a a =的最小正整数i 有1i >. 定义e G ∈为1i e a -=, 往证e
为一个单位元. 事实上, 对任意b G ∈, 由||G <∞, 存在 最小的k +∈ 使得k ba ba =. 由消去律和i 的定义知k i =: i ba ba =, 即be b =. 最后, 对任意x G ∈, 前面已经证明了有最小的正整数k 使得k x x =. 如果1k =, 则2x x xe ==, 由消去律有x e = 从而22x e e ==, 此时x 有逆, 即它自身. 如果1k >, 则11k k k x x xe xx x x --====, 此时x 也有逆: 1k x -. □ 注: 也可以用下面的第4题来证明. 4. 设G 是一个非空集合, G 上有满足结合律的乘法. 如果该乘法 还满足: 对任意,a b G ∈, 方程ax b =和ya b =在G 上有解, 证明: G 关于该乘法是一个群. 证明: 取定a G ∈. 记ax a =的在G 中的一个解为e . 往证e 是G 的单位元. 对任意b G ∈, 取ya b =的一个解c G ∈: ca b =. 于是: ()()be ca e c ae ca b ====. 得证. 对任意g G ∈, 由gx e =即得g 的逆. □ 5. 找两个元素3,x y S ∈使得222()xy x y =/. 解: 取(12)x =, (13)y =. □ 6. 对于整数2n >, 作出一个阶为2n 的非交换群. 解: 二面体群n D . □ 7. 设G 是一个群. 如果,a b G ∈满足1r a ba b -=, 其中r 是正整数, 证 明: i i i r a ba b -=, i 是非负整数.
逻辑代数化简试
————————————————————————————————作者:————————————————————————————————日期:
逻辑代数化简练习 一、选择题 1. 以下表达式中符合逻辑运算法则的是 。 A.C ·C =C 2 B.1+1=10 C.0<1 D.A +1=1 2. 逻辑变量的取值1和0可以表示: 。 A.开关的闭合、断开 B.电位的高、低 C.真与假 D.电流的有、无 3. 当逻辑函数有n 个变量时,共有 个变量取值组合? A. n B. 2n C. n 2 D. 2n 4. 逻辑函数的表示方法中具有唯一性的是 。 A .真值表 B.表达式 C.逻辑图 D.卡诺图 5.F=A B +BD+CDE+A D= 。 A.D B A + B.D B A )(+ C.))((D B D A ++ D.))((D B D A ++ 6.逻辑函数F=)(B A A ⊕⊕ = 。 A.B B.A C.B A ⊕ D. B A ⊕ 7.求一个逻辑函数F 的对偶式,可将F 中的 。 A .“·”换成“+”,“+”换成“·” B.原变量换成反变量,反变量换成原变量 C.变量不变 D.常数中“0”换成“1”,“1”换成“0” E.常数不变 8.A+BC= 。 A .A + B B.A + C C.(A +B )(A +C ) D.B +C 9.在何种输入情况下,“与非”运算的结果是逻辑0。 A .全部输入是0 B.任一输入是0 C.仅一输入是0 D.全部输入是1 10.在何种输入情况下,“或非”运算的结果是逻辑0。 A .全部输入是0 B.全部输入是1 C.任一输入为0,其他输入为1 D.任一输入为1 二、判断题(正确打√,错误的打×) 1. 逻辑变量的取值,1比0大。( )。 2. 异或函数与同或函数在逻辑上互为反函数。( )。 3.若两个函数具有相同的真值表,则两个逻辑函数必然相等。( )。 4.因为逻辑表达式A+B+AB=A+B 成立,所以AB=0成立。( ) 5.若两个函数具有不同的真值表,则两个逻辑函数必然不相等。( ) 6.若两个函数具有不同的逻辑函数式,则两个逻辑函数必然不相等。( ) 7.逻辑函数两次求反则还原,逻辑函数的对偶式再作对偶变换也还原为它本身。( )
近世代数习题解答 第三章环与域 1加群、环的定义 1. 证明,本节内所给的加群的一个子集作成一个子群的条件是充分而且必要的. 证 (ⅰ)若S 是一个子群 则S b a S b a ∈+?∈, '0是S 的零元,即a a =+'0 对G 的零元,000' =∴=+a a 即.00S a a s ∈-=-∴∈ (ⅱ)若S b a S b a ∈+?∈, S a S a ∈-?∈ 今证S 是子群 由S S b a S b a ,,∈+?∈对加法是闭的,适合结合律, 由S a S a ∈-?∈,而且得S a a ∈=-0 再证另一个充要条件: 若S 是子群,S b a S b a S b a ∈-?∈-?∈,, 反之S a a S a a S a ∈-=-?∈=-?∈00 故S b a b a S b a ∈+=--?∈)(, 2. },,,0{c b a R =,加法和乘法由以下两个表给定: + 0 a b c ? 0 a b c 0 0 a b c 0 0 0 0 0 a a 0 c b a 0 0 0 0 b b c 0 a b 0 a b c c c b a 0 c 0 a b c 证明,R 作成一个环 证R 对加法和乘法的闭的. 对加法来说,由.9.2习题6,R 和阶是4的非循环群同构,且为交换群. 乘法适合结合律Z xy yz x )()(= 事实上. 当0=x 或a x =,)(A 的两端显然均为0. 当b x =或x=c,)(A 的两端显然均为yz .
这已讨论了所有的可能性,故乘法适合结合律. 两个分配律都成立xz xy z y x +=+)( zx yx x z y +=+)( 事实上,第一个分配律的成立和适合律的讨论完全一样, 只看0=x 或a x =以及b x =或c x =就可以了. 至于第二个分配律的成立的验证,由于加法适合交换律,故可看 0=y 或a y =(可省略a z z ==,0的情形)的情形,此时两端均为zx 剩下的情形就只有 0,0)(=+=+=+x x bx bx x b b 0,0)(=+=+=+x x cx cx x c c 0,0)(=+=+==+x x cx bx ax x c b ∴R 作成一个环. 2交换律、单位元、零因子、整环 1. 证明二项式定理 n n n n n b b a a b a +++=+- 11)()( 在交换环中成立. 证用数学归纳法证明. 当1=n 时,显然成立. 假定k n =时是成立的: k i i k k i k k k k b b a b a a b a +++++=+-- )()()(11 看1+=k n 的情形)()(b a b a k ++ ))()()((11b a b b a b a a k i i k k i k k k ++++++=-- 1111111)]()[()()(++--+++++++++=+k i i k k i k i k k k k b b a b a a b a 1111 11)()(+-+++++++++=k i i k k i k k k b b a b a a (因为)()()(11 k r k r k r -++=) 即二项式定理在交换环中成立. 2. 假定一个环R 对于加法来说作成一个循环群,证明R 是交换环. 证设a 是生成元 则R 的元可以写成 na (n 整数) 2)]([)]([))((nma aa m n ma a n ma na === 2))((mna na ma =
近世代数课后习题参考答案 第四章 整环里的因子分解 1 素元、唯一分解 1. 证明:0不是任何元的真因子。 证 当0≠a 时 若b a 0=则0=a 故矛盾 当0=a 时,有00ε= (ε 是单位) 就是说0是它自己的相伴元 2. 我们看以下的整环I ,I 刚好包含所有可以写成 m m n (2 是任意整数,0≥n 的整数) 形式的有理数,I 的哪些个元是单位,哪些个元是素元? 证 1)I 的单位 总可以把m 表为 p p m k (2=是0或奇数,k 非负整数)我们说 1±=p 时,即k m 2±=是单位,反之亦然 2)I 的素元 依然是k p p m k ,(2=的限制同上) 我们要求 ⅰ)0≠p ⅱ)1±≠p ⅲ)p k 2只有平凡因子 满足ⅰ)—— ⅲ)的p 是奇素数 故p m k 2=而p 是奇素数是n m 2 是素元,反之亦然, 3.I 是刚好包含所有复数b a bi a ,(+整数)的整环,证明5不是I 的素元,5有没有唯一分解? 证 (1)I 的元ε是单位,当而且只当12 =ε 时, 事实上,若bi a +=ε是单位 则11-=εε 2 ' 2 2 1ε ε = 即2 '2 1εε=
但2 22 b a +=ε 是一正整数,同样2 ' ε也是正整数, 因此,只有12 =ε 反之,若12 2 2 =+=b a ε ,则0,1=±=b a 或1,0±==b a 这些显然均是单位 此外,再没有一对整数b a ,满足122=+b a ,所以I 的单位只有i ±±,1。 (2)适合条件52 =α 的I 的元α一定是素元。 事实上,若52 =α 则0≠α 又由α)1(也不是单位 若2 2 2 5,λβ α βλα=== 则12=β或52=β ββ?=12是单位λαβλ?=?-1 2 是α的相伴元 λλ β ?=?=152 2 是单位βαλβ?=?-1 是α的相伴元 不管哪种情形,α只有平凡因子,因而α是素元。 (3)I 的元5不是素元。 若βα=5则2 2 25λβ= 这样,2 β只可能是25,5,1 当52=β由)1(β是单位 当152 2 =?=λ β 由)1(λ是单位 此即λβ,中有一是5的相伴元 现在看52 =β 的情形 5,2 2 2 =+=+=b a bi a β β可能的情形是 ???==21b a ??=-=21b a ???-==21b a ???-=-=21 b a ???==12b a ? ??-==12b a ???=-=12b a ???-=-=12 b a 显然)2)(2(5i i -+= 由(2)知52 =β 的β是素元,故知5是素元之积 (4)5的单一分解 )21)(21(5i i -+=)21)(1)(21)(1(i i --+-= )21)()(21)(()21)()(21)((i i i i i i i i --+=-+-= i ±±,1均为单位 2 唯一分解环 1.证明本节的推论 证 本节的推论是; 一个唯一分解环I 的 n 个元n a a a ,,21 在I 里一定有最大公因子 ,
逻辑代数的化简算法 观察函数 1.该函数有四个逻辑变量,可表示成 Y=f(A、B、C、D) 2.该函数有三个乘积项:第一项有四个因子——四个变量在乘积项中都出现了。第二项有三个因子——缺少变量B(或)。第三项缺少变量C、D(或、)。 3.第一个乘积项是A、B、C、D的一个最小项,其余二项均不是A、B、C、D的最小项。 最小项:n个逻辑变量A1、A2、…… An组成的逻辑系统中含n个因子的乘积项——每个变量(或)在乘积项中只出现一次,称这样的乘积项为最小项。 两个逻辑变量A、B有22=4个最小项,分别是:、、、。 三个逻辑变量A、B、C有23=8个最小项,分别是:、、、、、 、、。 四个逻辑变量A、B、C、D有24=16个最小项。 练习:写出A、B、C、D的十六个最小项。 最小项的性质: (1)对变量的任意一组取值,只有一个最小项为1,其余最小项全为0。二变量A、B的最小项为:、、、。对A、B的任意一组取值: A=0 B=0 =1 其余三项全为0,即===0 A=0 B=1 = 1 其余三项全为0
A=1 B=0 = 1 其余三项全为0 A=1 B=1 = 1 其余三项全为0 (2)全体最小项之和为1。(读者自己证明) (3)任意两个最小项的乘积为0。 最小项的编号: 三变量A、B、C的八组取值000、001、……111能分别使八个最小项的值为1,又与十进制数0,1……7的二进制数表示相同。用0~7编号八个最小项,记为:m0、m1、m2、m3、m4、 m5、m6、m7,则m7=m111=,……m4=m100=,m0=m000=。 练习:读者试写出四变量A、B、C、D的十六个最小项m0、m1 (15) 逻辑函数的最小项之和形式 任何逻辑函数都可化为最小项之和的标准形式 例:将下列函数化为最小项之和的形式 反函数的最小项之和表示 例:求二变量A,B的逻辑函数的反函数。 解一:
逻辑代数化简练习 一、选择题 1、 以下表达式中符合逻辑运算法则的就是 。 A 、C ·C =C 2 B 、1+1=10 C 、0<1 D 、A +1=1 2、 逻辑变量的取值1与0可以表示: 。 A 、开关的闭合、断开 B 、电位的高、低 C 、真与假 D 、电流的有、无 3、 当逻辑函数有n 个变量时,共有 个变量取值组合? A 、 n B 、 2n C 、 n 2 D 、 2n 4、 逻辑函数的表示方法中具有唯一性的就是 。 A 、真值表 B 、表达式 C 、逻辑图 D 、卡诺图 5、F=A B +BD+CDE+A D= 。 A 、D B A + B 、D B A )(+ C 、))(( D B D A ++ D 、))((D B D A ++ 6、逻辑函数F=)(B A A ⊕⊕ = 。 A 、 B B 、A C 、B A ⊕ D 、 B A ⊕ 7.求一个逻辑函数F 的对偶式,可将F 中的 。 A 、“·”换成“+”,“+”换成“·” B 、原变量换成反变量,反变量换成原变量 C 、变量不变 D 、常数中“0”换成“1”,“1”换成“0” E 、常数不变 8.A+BC= 。 A 、A + B B 、A + C C 、(A +B )(A +C ) D 、B +C 9.在何种输入情况下,“与非”运算的结果就是逻辑0。 A.全部输入就是0 B 、任一输入就是0 C 、仅一输入就是0 D 、全部输入就是1 10.在何种输入情况下,“或非”运算的结果就是逻辑0。 A.全部输入就是0 B 、全部输入就是1 C 、任一输入为0,其她输入为1 D 、任一输入为1 二、判断题(正确打√,错误的打×) 1. 逻辑变量的取值,1比0大。( )。 2. 异或函数与同或函数在逻辑上互为反函数。( )。 3.若两个函数具有相同的真值表,则两个逻辑函数必然相等。( )。 4.因为逻辑表达式A+B+AB=A+B 成立,所以AB=0成立。( ) 5.若两个函数具有不同的真值表,则两个逻辑函数必然不相等。( ) 6.若两个函数具有不同的逻辑函数式,则两个逻辑函数必然不相等。( ) 7.逻辑函数两次求反则还原,逻辑函数的对偶式再作对偶变换也还原为它本身。( ) 8.逻辑函数Y=A B +A B+B C+B C 已就是最简与或表达式。( ) 9.因为逻辑表达式A B +A B +AB=A+B+AB 成立,所以A B +A B= A+B 成立。( )
大学数学A (1)课后复习题 第一章 一、选择题 1.下列各组函数中相等的是. …….. ……..…………………………………………………………………………………….( ) A .2 ln )(,ln 2)(x x g x x f == B .0 )(,1)(x x g x f == C .1)(,11)(2-=-?+= x x g x x x f D .2)(|,|)(x x g x x f == 2.下列函数中为奇函数的是. ……. …….. …………………………………………………………………………………….( ). A .)1ln()(2++=x x x f B .| |)(x e x f = C .x x f cos )(= D .1 sin )1()(2--= x x x x f 3.极限??? ? ?+++∞→22221lim n n n n n 的值为………………………………………………………………………..…….( ) A .0 B .1 C .2 1 D .∞ 4.极限x x x x sin lim +∞→的值为.. …….. ……..……………………………………………………………………………...…….( ) A .0 B .1 C .2 D .∞ 5.当0→x 时,下列各项中与 2 3 x 为等价无穷小的是…………………………………………………….( ) A .)1(3-x e x B .x cos 1- C .x x sin tan - D .)1ln(x + 6.设12)(-=x x f ,则当0→x 时,有…………………………………………………………………………..…….( ). A .)(x f 与x 是等价无穷小 B .)(x f 与x 同阶但非等价无穷小 C .)(x f 是比x 高阶的无穷小 D .)(x f 是比x 低阶的无穷小 7.函数)(x f 在点x 0可导是)(x f 在点x 0连续的____________条件. ………...………………....…..( ) A .充分不必要 B .必要不充分 C .充要 D .既不充分也不必要 8.设函数?? ? ??<≤--<≤≤≤-=01,110, 21,2)(2x x x x x x x f ,则下述结论正确的是……………………………………….( )
第 2 章 逻辑代数和逻辑函数化简 基本概念:逻辑代数是有美国数学家 George Boole 在十九世纪提出 , 因此也称 布尔代数 , 是分析和设计数字逻辑电路的数学工具。 也叫开关代数, 是研究只用 0 和 1 构成的数字系统的数学。 基本逻辑运算和复合逻辑运算 基本逻辑运算:“与”、“或”、“非”。 复合逻辑运算:“与非”、“或非”、“与或非”、“异 或”、“同或”等。 A B 基本逻辑运算 ~ 220V F 1. “与”运算①逻辑含义:当决定事件成立的所有条件全部具 备时,事件才会发生。 ②运算电路:开关 A 、B 都闭合,灯 F 才亮。 ③表示逻辑功能的方法: 真值表 A B F 灯 F 的状态代表 开关 A 、B 的状态代 0 0 表输入: 0 1 0 输出: 1 0 0 “ 0”表示亮; “0”表示断开; 1 1 1 表达式: F A B = ? 逻辑符号: A & FA FA F B B B 国家标准 以前的符号 欧美符号 功能说明: 有 0 出 0,全 1 出 1。 在大规模集成电路可编程逻辑器件中的表示符号: A B A B A B & F F F
通过“ ?”接入到此线上的输入信号都是该与门的一个输入端。推广:当有 n 个变量时: F=A 1A 2 A 3 ? ? ? A n “与”运算的几个等式: 0?0=0,0?1=0, 1?1=1 A?0=0(0-1 律), A?1=A (自等律),A?A=A (同一律), A?A?A=A (同一律)。 2. “或”运算①逻辑含义:在决定事件成立的所有条件中,只 要具备一个,事件就会发生。 A ②运算电路: 开关 A 、B 只要闭合一个,灯 F 就亮。 B ~220V F ③表示逻辑功能的方法: 逻辑功能: 有 1 出 1,全 0 出 0。 真值表:(略) 表达式: F=A+B 逻辑符号: A ≥ 1 F A FA F B + B B 国家标准 以前的符号 欧美符号 推广:当有 n 个变量时: F=A 1+A 2+ A 3+? ? ? +A n “或”运算的几个等式: 0+0=0,0+1=1, 1+1=1 A+0=A (自等律) A+1=1( 0-1 律),A+A=A (同一律)。 上次课小结:与、或的功能、表达式等,几个等式。 3.“非”运算 ①逻辑含义:当决定事件的条件具备时, 事件不 发生;当条件不具备时,事件反而发生了。 R ②运算电路:开关 A 闭合,灯 F 不亮。 ~ 220V A F ③表示逻辑功能的方法: 逻辑功能: 入 0 出 1,入 1 出 0。 真值表:(略) 表达式: F= A
2019年广西满分作文:毕业前的最后一堂课时光飞逝,白马过隙。2019高考如约而至,距离我的那年高考也已有二十岁的年份。烈日的阳光,斑驳的光影,仿佛又把我拉进了在宽窄巷子的学堂里最后冲刺的时光。 高中即将毕业,意味着每个人将为人生方向的开启选好时光的阀门,单纯的学历生涯即将告一段落。课堂上朗朗整齐的晨读和起立,行礼的流程将渐行远去。它是青春懵懂的里程,也是最为单纯的诗书礼仪,课桌黑板走廊都将记录这里每个人在经历人生的最后一课,无论是同学还是老师。 记得1999年炙热的炎夏,当年的二十八中还隐藏在老成都皇城宽窄巷子里面,距离高考还有一周,同学们已经不再像之前那样紧张忙碌的复习节奏,三三两两,甚至结伴到学校周围看看能不能捡到老皇城留下的一砖半瓦,为自己这里的高中学涯留点念想。 还记得是用过学校食堂的午餐,在最后一节考前动员课上完以后,大家就会各自回到家中,为最后到来的大考最最后的准备。课堂的气氛很是轻松,甚至我和我的同桌还在讨论中午学校食堂红椒肉丝的白糖是否搁多了,随着班主任走进教室,踏上讲台,一如既往地喊道:上课!接着就是值日生的“起立敬礼老师好”的三重奏,最后一节课的师生礼仪完毕后,班主任转身在黑板上用粉笔撰写了四个大字“勇往直前”,语重心长的寄语和感慨在此不表,大家彼此默契的拿出早已准备好的记事本开始彼此留言签名,数言珍语,寥寥几笔都赫然纸上。 人生最后一堂课,没有习题的讲解和紧张备考的威严氛围。三年同窗,彼此单纯的朝夕相处和课桌校园间的点滴生活早已让这个班级凝成了一片经脉。“聚是一团火,散是满天星,不求桃李满天下,只愿每人福满多。”班主任最后这句话至今印刻脑海。二十载已过,当时班主任的心境早已能够理解,也希望每年高考时,同学志愿看天下!
《近世代数》作业 一.概念解释 1.代数运算 2.群的第一定义 3.域的定义 4.满射 5.群的第二定义 6.理想 7.单射 8.置换 9.除环 10.一一映射 11.群的指数 12.环的单位元 二.判断题 1.Φ是集合n A A A ??? 21列集合D 的映射,则),2,1(n i A i =不能相同。 2.在环R 到环R 的同态满射下,则R 的一个子环S 的象S 不一定是R 的一个子环。 3.设N 为正整数集,并定义ab b a b a ++= ),(N b a ∈,那么N 对所给运算 能作成一个群。 4.假如一个集合A 的代数运算 适合交换率,那么在n a a a a 321里)(A a i ∈,元的次序可以交换。 5.在环R 到R 的同态满射下,R 得一个理想N 的逆象N 一定是R 的理想。 6.环R 的非空子集S 作成子环的充要条件是: 1)若,,S b a ∈则S b a ∈-; 2),,S b a ∈,则S ab ∈。 7.若Φ是A 与A 间的一一映射,则1-Φ是A 与A 间的一一映射。 8.若ε是整环I 的一个元,且ε有逆元,则称ε是整环I 的一个单位。 9.设σ与τ分别为集合A 到B 和B 到C 的映射,如果σ,τ都是单射,则τσ是A 到C 的映射。 10.若对于代数运算 ,,A 与A 同态,那么若A 的代数运算 适合结合律,则A 的代数运算也适合结合律。 11.整环中一个不等于零的元a ,有真因子的冲要条件是bc a =。 12.设F 是任意一个域,*F 是F 的全体非零元素作成的裙,那么* F 的任何有限子群 G 必为循环群。 13. 集合A 的一个分类决定A 的一个等价关系。 ( ) 14. 设1H ,2H 均为群G 的子群,则21H H ?也为G 的子群。 ( ) 15. 群G 的不变子群N 的不变子群M 未必是G 的不变子群。 ( ) 三.证明题 1. 设G 是整数环Z 上行列式等于1或-1的全体n 阶方阵作成集合,证明:对于方阵的普通乘法G 作成一个 群。 2.设G=(a )是循环群,证明:当∞=a 时,G=(a )与整数加群同构。