
轴对称最值问题(线段和最小或差最大)(北师
版)
一、单选题(共8道,每道12分)
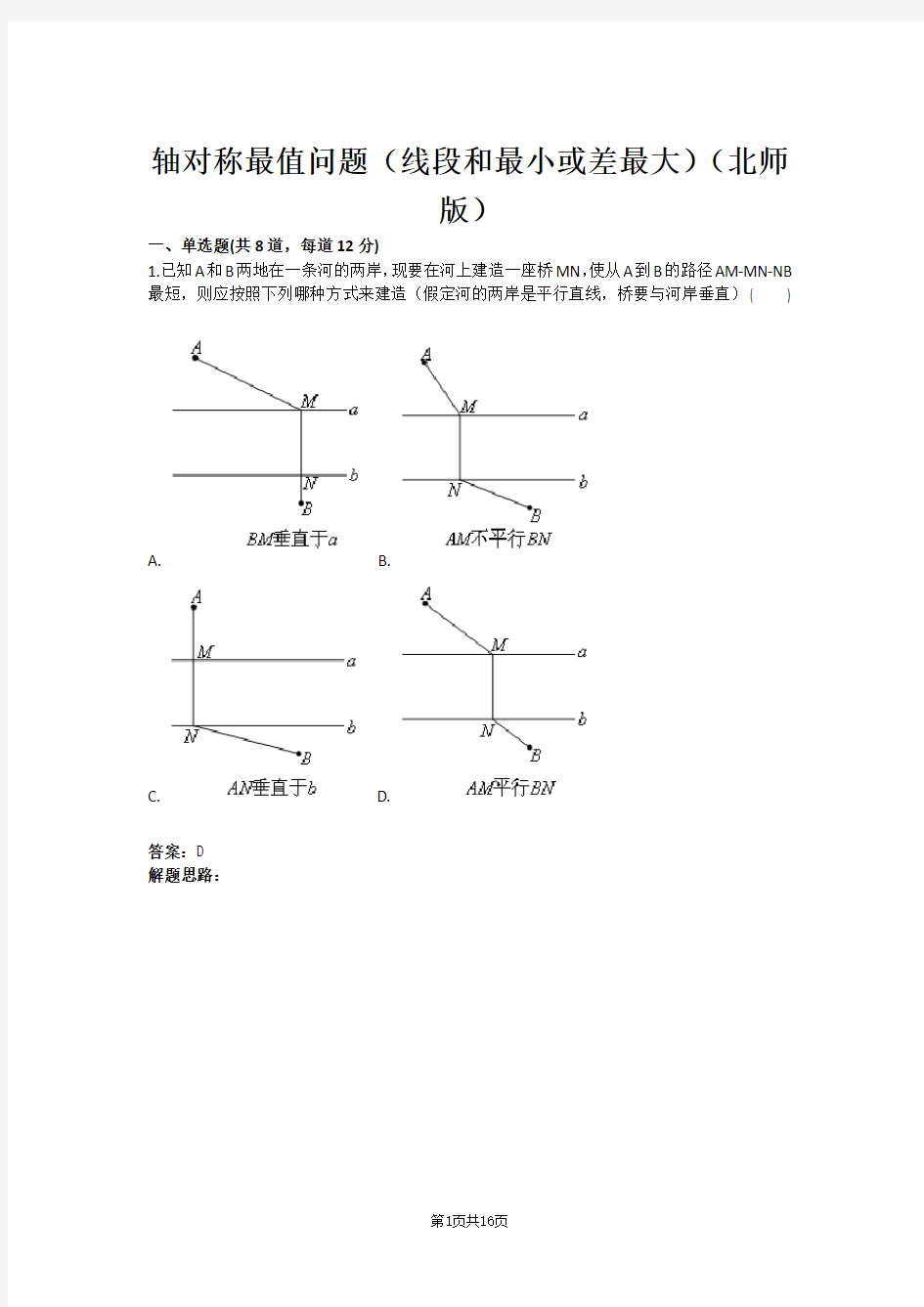
1.已知A和B两地在一条河的两岸,现要在河上建造一座桥MN,使从A到B的路径AM-MN-NB 最短,则应按照下列哪种方式来建造(假定河的两岸是平行直线,桥要与河岸垂直)( )
A. B.
C. D.
答案:D
解题思路:
试题难度:三颗星知识点:轴对称最值问题
2.如图,已知A(1,3),B(5,1),长度为2的线段PQ在x轴上平行移动,当AP+PQ+QB 的值最小时,点P的坐标为( )
A. B.
C.(1,0)
D.(5,0)
答案:B
解题思路:
试题难度:三颗星知识点:轴对称最值问题
3.在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A,B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.若E,F为边OA上的两个动点,且EF=2,则当四边形CDEF的周长最小时,点F的坐标为( )
A. B.
C.(2,0)
D.(3,0)
答案:B
解题思路:
试题难度:三颗星知识点:轴对称最值问题
4.如图,当四边形PABN的周长最小时,a的值为( )
A. B.1 C.2 D.
答案:A
解题思路:
试题难度:三颗星知识点:轴对称最值问题
5.如图,两点A,B在直线MN的同侧,A到MN的距离AC=8,B到MN的距离BD=6,CD=4,P在直线MN上运动,则的最大值为( )
A. B.
C. D.
答案:C
解题思路:
试题难度:三颗星知识点:轴对称最值问题
6.如图,已知两点A,B在直线的异侧,A到直线的距离AC=6,B到直线的距离BD=2,CD=3,点P在直线上运动,则的最大值为( )
A. B.3 C.1 D.5
答案:D
解题思路:
试题难度:三颗星知识点:轴对称最值问题
7.如图,已知两点A,B在直线的异侧,A到直线的距离AC=5,B到直线的距离BD=2,DC=4,点P在直线上运动,则的最大值为( )
A.1
B.5
C.3
D.2
答案:B
解题思路:
试题难度:三颗星知识点:轴对称最值问题
8.如图,在平面直角坐标系中,已知A(0,1),B(3,-4),在x轴上有一点P,当的值最大时,点P的坐标是( )
A. B.(-1,0)C.(0,0) D.(3,0)
答案:B
解题思路:
试题难度:三颗星知识点:轴对称最值问题
学生做题后建议通过以下问题总结反思
问题1:解决几何最值问题的理论依据有哪些?
问题2:解决几何最值问题的主要方法是______,通过变化过程中_____________的分析,利用_______________________等手段把所求量进行转化,构造出符合几何最值问题理论依据的___________进而解决问题.
问题3:如图,已知A(1,3),B(5,1),长度为2的线段PQ在x轴上平行移动,AP+PQ+QB 的值最小时,P点的坐标为( )
A.B.C.(1,0)D.(5,0)
本题的特征是什么?目标是什么?如何操作?
问题4:如图,两点A,B在直线MN的同侧,A到MN的距离AC=8,B到MN的距离BD=6,CD=4,P在直线MN上运动,则的最大值为( )
A.B.C.D.
本题的特征是什么?目标是什么?如何操作?
问题5:轴对称最值问题—线段和最小和线段差最大问题中,他们的理论依据分别是什么?问题6:轴对称最值问题—线段和最小和线段差最大问题中,操作时有什么不同?
5W2H分析法--案例分析 企业管理 2008-08-25 14:50 阅读936 评论8 字号:大中小 “5W”是五个英文字母的词头,即“WHAT、WHO、WHEN、WHERE、WHY”,翻译成汉语就是“何事、何人、何时、何地,何因”,这原本是新闻写作的五大要素,外资企业现在也将此要求用于企业管理,并在“5 W”的基础上再加上了“2H”,“2H”也是两个英文单词的词头,即“HOW DO、HOW MUCH”,翻译成汉语是 “怎样做、需要花费多少钱”。 “5W2H”还是所有外资企业的管理者在提交报告时不可缺少的内容,如果一份报告中没有这些内容,或者这些内容交代得不清楚,那么绝对不会是一份质量高的工作报告。 5W2H分析法又叫七何分析法,5W2H法是第二世界大战中美国陆军兵器修理部首创。简单、方便,易于理解、使用,富有启发意义,广泛用于企业管理和技术活动,对于决策和执行性的活动措施也非常有帮助, 也有助于弥补考虑问题的疏漏。 (1)WHY——为什么为什么要这么做理由何在原因是什么 (2)WHAT——是什么目的是什么做什么工作 (3)WHERE——何处在哪里做从哪里入手 (4)WHEN——何时什么时间完成什么时机最适宜 · (5)WHO——谁由谁来承担谁来完成谁负责 (6)HOW——怎么做如何提高效率如何实施方法怎样(7)HOW MUCH——多少做到什么程度数量 如何质量水平如何费用产出如何 发明者用五个以w开头的英语单词和两个以H开头的英语单词进行设问,发现解决问题的线索,寻找发明思路,进行设计构思,从而搞出新的发明项目,这就叫做5W2H法。 提出疑问于发现问题和解决问题是极其重要的。创造力高的人,都具有善于提问题的能力,众所周知,提出一个好的问题,就意味着问题解决了一半。提问题的技巧高,可以发挥人的想象力。相反,有些问题提出来,反而挫伤我们的想象力。发明者在设计新产品时,常常提出:为什么(Why);做什么(What);何人做(Who);何时(When);何地(Where);如何(How);多少(How much)。这就构成了5W2 H法的总框架。如果提问题中常有“假如……”、“如果……”、“是否……”这样的虚构,就是一种设问,设问需要 更高的想象力。 在发明设计中,对问题不敏感,看不出毛病是与平时不善于提问有密切关系的。对一个问题追根刨底,有可能发现新的知识和新的疑问。所以从根本上说,学会发明首先要学会提问,善于提问。阻碍提问的因素,一是怕提问多,被别人看成什么也不懂的傻瓜,二是随着年龄和知识的增长,提问欲望渐渐淡薄。如果提问得不到答复和鼓励,反而遭人讥讽,结果在人的潜意识中就形成了这种看法:好提问、好挑毛病的人是扰乱别人的讨厌鬼,最好紧闭嘴唇,不看、不闻、不问,但是这恰恰阻碍了人的创造性的发挥。
初中几何中线段和(差)的最值问题 一、两条线段和的最小值。 基本图形解析: 一)、已知两个定点: 1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧: (2)点A 、B 在直线同侧: A 、A ’ 是关于直线m 的对称点。 2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。 (1)两个点都在直线外侧: (2)一个点在内侧,一个点在外侧: (3)两个点都在内侧: (4)、台球两次碰壁模型 变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、 E 点,使得围成的四边形ADEB 周长最短. 变式二:已知点A 位于直线m,n 的内侧 , 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短. 二)、一个动点,一个定点: (一)动点在直线上运动: 点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧: 2、两点在直线同侧: (二)动点在圆上运动 点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧: 2、点与圆在直线同侧: 三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。( 原理用平移知识解) (1)点A 、B 在直线m 两侧: 过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左 平移PQ 长,即为P 点,此时P 、Q 即为所求的点。 (2)点A 、B 在直线 m 同侧: m m A m A B m n n n m n n n m m n m n m n m m m m m
线段差的最大值与线段和的最小值问题 有关线段差的最大值与线段和的最小值问题的主要应用原理是:1、两点这间线段最短。2、三角形的任意两边之和大于第三边(找和的最小值)。3、三角形的任意两边之差小于第三边(找差的最大值)。 作图找点的关键:充分利用轴对称,找出对称点,然后,使三点在一条直线上。即利用线段的垂直平分线定理可以把两条线段、三条线段、四条线段搬在同一条直线上。证明此类问题,可任意另找一点,利用以上原理来证明。 一两条线段差的最大值: (1)两点同侧:如图,点P在直线L上运动,画出一点P,使︱PA-PB︱取最大值。 作法:连结AB并延长AB交直线L于点P。点P即为所求。︱PA-PB︱=AB 证明:在直线L上任意取一点P。,连结PA、PB,︱PA-PB︱<AB p' (2两点异侧:如图,如图,点P在直线L上运动,画出一点P,使︱PA-PB︱取最大值。作法:1、作B关于直线L的对称点B。 B 2、连结AB并延长AB交直线L于点P。点P即为所求。︱PA-PB︱=AB 证明:在直线L上任意取一点P。,连结PA、PB、PB。︱PA-PB︱=︱PA-PB︱<AB
(三角形任意两边之差小于第三边) 二、两条线段和的最小值问题: (1))两点同侧:如图,点P在直线L上运动,画出一点P使PA+PB取最小值。 (三角形的任意两边之和大于第三边(找和的最小值),PA+PB=AB (2)两点异侧:如图,点P在直线L上运动,画出一点P使PA+PB取最小值。 (两点之间线段最短) 三、中考考点: 08年林金钟老师的最后一题:如图,在矩形ABCO中,B(3,2),E(3,1),F(1,2)在X轴与Y轴上是否分别存在点M、N,使得四边形EFNM的周长最小?若存在,请求出周长的最小值,若不存在,请说明理由。 提示:EF长不变。即求FN+NM+MF的最小值。利用E关于X轴的对称点E,F的对称点F,把这三条线段搬到同一条直线上。
线段、角的轴对称性 [趣题导学] 如图1.4-1,初二(1)班与初二(2)班这两个班的学生分别在M、N两处参加劳动,现要在道路AB、AC的交叉区域内设一个茶水供应点P,使P到两条道路的距离相等,且使PM=PN,你能找出符合条件的点P,并简要说明理由吗? 图1.4-1 图1.4-2 解答:P点如图1.4-2所示,作∠BAC的角平分线AD,作线段MN的垂直平分线EF,AD 与EF交于点P,因为AD平分∠BAC,所以点P到两条道路AB、AC的距离相等,又因为点P在线段MN的中垂线上,所以PM=PN。 [双基锤炼] 一、选择题 1、下列图形中,不是轴对称图形的是() A. 两条相交直线 B. 线段 C.有公共端点的两条相等线段 D.有公共端点的两条不相等线段 2、到三角形的三个顶点距离相等的点是() A.三条角平分线的交点 B.三条中线的交点 C.三条高的交点 D.三条边的垂直平分线的交点 3、有下列图形:(1)两个点;(2)一条线段;(3)一个角;(4)一个长方形;(5)两条相交直线;(6)两条平行线。其中轴对称图形共有() A、3个 B、4个 C、5个 D、6个 4、已知:在△ABC中,AD为∠BAC的角平分线上,DE⊥AB,F为AC上一点,且∠DFA=1000,则() A.DE>DF B.DE 专题一.线段和(差)的最值问题 【知识依据】 1.线段公理——两点之间,线段最短; 2.对称的性质——①关于一条直线对称的两个图形全等;②对称轴是两个对称图形对应点连线的垂直平分线; 3.三角形两边之和大于第三边; 4.三角形两边之差小于第三边; 5、垂直线段最短。 一、已知两个定点: 1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧: (2)点A 、B 在直线同侧: A 、A ’ 是关于直线m 的对称点。 2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。 (1)两个点都在直线外侧: P m A B m A B m A B P m A B A' n m A B Q P n m A B P'Q' (2)一个点在内侧,一个点在外侧: (3)两个点都在内侧: (4)、台球两次碰壁模型 变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短. 变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短. n m A B Q P n m A B B'Q P n m A B B'A' n m A B m n A B E D m n A B A'B'm n A P Q m n A A' 二、一个动点,一个定点: (一)动点在直线上运动: 点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧: 2、两点在直线同侧: (二)动点在圆上运动:点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧: 2、点与圆在直线同侧: m n A P m n A B m n A P m n A A'B m O A P'P m O B A B' m O A P m O A B A' 线段和(差)的最值问题 此类问题特点:1.两个定点,一个定点;2. 线段和最小值,线段差最大值 一、线段和最小值问题 若在一条直线m上,求一点P,使PA+PB最小; (1)两侧/异侧型:定点A、 B在直线m(动点P所在直线)两侧:直接连接A、B两点交直线m于一点P,该点P即为所求点。(PA+PB=AB) (2)同侧型:定点A、B在动点P所在直线m同侧:(方法:一找二作三连): 一找:找定点A、B,动点P及动点所在的直线m;二作:任选一个定点做对称;三连:连接对称点与另一个定点,其连线交动点所在直线于一点P,该点P即为所求。(PA+PB=PA’+PB=A’B) m A B P m A B 二、线段差最大值问题 若在一条直线m上,求一点P,使得最大 (1)同侧型:定点A、B在直线m(动点P所在直线)两侧:直接连接A、B两点交直线m于一点P,该点P即为所求点。() (2)两侧/异侧型:定点A、B在直线m(动点P所在直线)两侧:任选一个定点做对称;三连:连接对称点与另一个定点,其连线交动点所在直线m于一点P,该点P即为所求点。() 线段和最小值练习题 1.如图1,在锐角三角形ABC中,AB=,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值为. 2. 如图2所示,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点.若AE=2,EM+CM的最小值为. 3.如图3,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=4,AB=5,BC=6,点P是AB上一个动点,当PC+PD的和最小时,PB的长为__________. 图1 图2 图3 图4 4. 如图4,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为. 5. 如图5,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为________cm. 6.已知正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.则PB +PE的最小值是 7. 如图6,已知正方形ABCD的边长为8,点M在DC上,且DM=2,N是AC上的一个动点,则DN+MN的最小值为. 8.如图7,在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ 周长的最小值为cm.(结果不取近似值) 图5 图6 图7 9. 如图8,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则PA+PC的最小值是. 2.4线段、角的轴对称性(4) 教学目标 1.能利用所学知识提出问题并能解决实际问题; 2.能利用角平分线性质定理和逆定理证明相关结论,做到每一步有根有据;3.经历探索角的轴对称应用的过程,在解决问题的过程中培养思考的严谨性和表达的条理性. 教学重点综合运用角平分线的性质定理和逆定理解决问题. 教学难点学会证明点在角平分线上. 教学过程 开场白 同学们,上节课我们知道了“角平分线上的点到角两边距离相等”,而且“角的内部到角两边距离相等的点在角的平分线上”.这两个定理能用来解决什么问题呢? 例2 已知:△ABC的两内角∠ABC、∠ACB的角平分线相交于点P.求证:点P在∠A的角平分线上. 分析:要证明点P在∠A的角平分线上,根据角的内部到角两边距离相等的点在角平分线上,只要点P到∠A两边的距离相等,所以过点P做两边的垂线段PD、PE,证出PD=PE,而要证PD=PE,因为点P是∠ABC、∠ACB的角平分线的交点,根据角平分线的性质,点P到∠ABC、∠ACB两边的距离都相等,所以只要做出BC边上的垂线段PF,就可得PD=PF,PE=PF,从而PD=PE,所以得证. 通过解决上述问题,你发现三角形的三个内角的角平分线有什么位置关系? 例3 已知:如图2-28,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足为E、F.求证:AD垂直平分EF. 分析:要证AD垂直平分EF, 只要证:,. 已知∠BAD=∠CAD,DE⊥AB,DF⊥AC, 只要证, 只要证. …… 指导学生完成练习. 解完题后,说说你的发现,提出你的问题. 练习:课本P56练习. 学生发现:三角形两外角的角平分线与第三个角的角平分线所在的直线相交于一点;可能提出“三角形三个外角的角平分线所在直线是否相交于一点的问题”. 布置作业 课本P58-59习题2.4,分析第9、10、11题的思路,任选2题写出过程. For personal use only in study and research; not for commercial use 线段差的最大值与线段和的最小值问题 有关线段差的最大值与线段和的最小值问题的主要应用原理是:1、两点这间线段最短。2、三角形的任意两边之和大于第三边(找和的最小值)。3、三角形的任意两边之差小于第三边(找差的最大值)。 作图找点的关键:充分利用轴对称,找出对称点,然后,使三点在一条直线上。即利用线段的垂直平分线定理可以把两条线段、三条线段、四条线段搬在同一条直线上。证明此类问题,可任意另找一点,利用以上原理来证明。 一两条线段差的最大值: (1)两点同侧:如图,点P在直线L上运动,画出一点P,使︱PA-PB︱取最大值。作法:连结AB并延长AB交直线L于点P。点P即为所求。︱PA-PB︱=AB 证明:在直线L上任意取一点P。,连结PA、PB,︱PA-PB︱<AB (2两点异侧:如图,如图,点P在直线L上运动,画出一点P,使︱PA-PB︱取最大值。作法:1、作B关于直线L的对称点B。 B 2、连结AB并延长AB交直线L于点P。点P即为所求。︱PA-PB︱=AB 证明:在直线L上任意取一点P。,连结PA、PB、PB。︱PA-PB︱=︱PA-PB︱<AB (三角形任意两边之差小于第三边) 二、两条线段和的最小值问题: (1))两点同侧:如图,点P在直线L上运动,画出一点P使P A+PB取最小值。 (三角形的任意两边之和大于第三边(找和的最小值),P A+PB=AB (2)两点异侧:如图,点P在直线L上运动,画出一点P使P A+PB取最小值。 (两点之间线段最短) 三、中考考点: 08年林金钟老师的最后一题:如图,在矩形ABCO中,B(3,2),E(3,1),F(1,2)在X轴与Y轴上是否分别存在点M、N,使得四边形EFNM的周长最小?若存在,请求出周长的最小值,若不存在,请说明理由。 提示:EF长不变。即求F N+NM+MF的最小值。利用E关于X轴的对称点E,F的对称点F,把这三条线段搬到同一条直线上。 线段、角的轴对称性 [知识要点] 1.线段的垂直平分线 性质定理:线段的垂直平分线上的点到线段两端的距离相等。 判定定理:到线段两端的距离相等的点在这条线段的垂直平分线上。 2.角平分线 性质定理:角平分线上任意一点到角的两边的距离相等。 判定定理:到角的两边距离相等的点在这个角的平分线上。 3.尺规作图 作线段的垂直平分线和角的平分线 [点睛例题] 例1.如图,C是∠AOB内一点,C1、C2分别是点C关于OA、OB的对称点,若C1、C2的连线交OA于D,交OB于E,C1C2=4.5cm,则△CDE的周长为() A.4.5cmB.6.5cmC.5.5cmD.无法求 例2.如图,在△ABC中,点O是∠ABC的平分线与线段BC的垂直平分线的交点,则下列结论不一定成立的是() A.OB=OCB.OD=OFC.OA=OB=OCD.BD=DC 例3.如图,A、B、C是新建的三个居民小区,我们已经在到三个小区距离相等的地方修建了一所学校,现规划修建居民小区D,其要求是: (1)到学校的距离与其它小区到学校的距离一样; (2)控制人口密度,有利于生态环境建设,试确定居民小区D的位置. [点睛习题] 1、如图,等腰△ABC的周长为21,底边BC = 5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为() A.13 B.14C.15D.16 2、已知,如图,△ABC中,∠ABC与∠ACB的平分线交于点P, 那么点P是否在∠BAC的平分线上?为什么? 3、下列说法:(1)若直线PE是线段AB的中垂线,则EA=EB,PA=PB;(2)若EA=EB,PA=PB,则直线PE垂直平分线段AB;(3)若PA=PB,则点P必是线段AB的中垂线上的点;(4)若AE=BE,则经过点E的直线垂直平分线AB,其中正确的个数为() A.1个B.2个C.3个D.4个 4、已知,如图,△ABC的两个外角的平分线交于点P,那么点P是否在∠BAC的平分线上?为什么? 5.如图,△ABC中,DE垂直平分AC交AB于E,∠A=30°,∠ACB=80°,则∠BCE=____°。 6.小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片(如图①);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图②)。小明认为△AEF是等腰三角形,你同意吗?请说明理由。 (2)实践与运用 将矩形纸片ABCD沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图③);再沿过点E的直线折叠,使点D落在BE上的点D′处,折痕为EG(如图④);再展平纸片(如图⑤)。求图⑤中∠α的大小。 第二章 2.4 线段、角的轴对称性 一.选择题(共10小题) 1.(2016?湖州)如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是() A.8 B.6 C.4 D.2 2.(2016?淮安)如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧, 分别交AC,AB于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是() A.15 B.30 C.45 D.60 3.(2016?德州)如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大 于AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD 的度数为() A.65° B.60° C.55° D.45° 4.如图,已知点P是∠AOB角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,DM=4cm,如果点C是OB上一个动点,则PC的最小值为() A.2 B.2C.4 D.4 5.如图,在已知的△ABC中,按以下步骤作图: ①分别以B,C为圆心,以大于BC的长为半径作弧,两弧相交于两点M,N; ②作直线MN交AB于点D,连接CD. 若CD=AC,∠A=50°,则∠ACB的度数为() A.90° B.95° C.100°D.105° 6.如图,锐角三角形ABC中,直线l为BC的垂直平分线,射线m平分∠ABC,l与m相交于P点.若∠A=60°,∠ACP=24°,则∠ABP等于() A.24° B.30° C.32° D.42° 7.如图,△ABC中,AB边的垂直平分线交AB于点E,交BC于点D,已知AC=5cm,△ADC 的周长为17cm,则BC的长为() A.7cm B.10cm C.12cm D.22cm 8.三角形ABC的三条内角平分线为AE、BF、CG,下面的说法中正确的个数有() ①△ABC的内角平分线上的点到三边距离相等 ②三角形的三条内角平分线交于一点 ③三角形的内角平分线位于三角形的内部 ④三角形的任一内角平分线将三角形分成面积相等的两部分. A.1个B.2个C.3个D.4个 9.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为() A.11 B.5.5 C.7 D.3.5 10.如图所示,点P为△ABC三边垂直平分线的交点,PA=6,则点P到点C的距离为PC满足() A.PC<6 B.PC=6 C.PC>6 D.以上都不对 二.填空题(共6小题) 11. (2016?西宁)如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PC=4,则PD=______. 12.(2016?遵义)如图,在△ABC中,AB=BC,∠ABC=110°,AB的垂直平分线DE交AC于点D,连接BD,则∠ABD=_____ _度. 线段、角的轴对称性 例1.如图,在△ABC 中,∠C=90°,AB 的垂直平分线DE 交AC 于D ,垂足为E ,若∠A=30°,CD=3. (1)求∠BDC 的度数. (2)求AC 的长度. 举一反三:如图,△ABC 中,AB 、AC 的垂直平分线分别交BC 于D 、E ,垂足分别是M 、N . (1)若△ADE 的周长是10,求BC 的长; (2)若∠BAC=100゜,求∠DAE 的度数. 例2.如图,已知∠AOB 及点C 、D ,求作一点P ,使PC=PD ,并且使点P 到OA 、OB 的距离相等。 例3.如图,AD 平分∠BAC ,EF 垂直平分AD 交BC 的延长线于F ,连接AF .求证:∠B=∠CAF · C B O A · D 举一反三:已知△ABC 中,AD 是∠BAC 的平分线,AD 的垂直平分线交BC 的延长线于F . 求证:∠BAF=∠ACF . 【课堂巩固】 1.在△ABC 中,AB=BC ,BD 平分∠ABC ,下列说法不正确的是( ) A 、BD 平分AC B 、AD ⊥BD C 、AD 垂直平分BC , D 、BD 垂直平分AC 2.如图,在△ABC 中,∠C = 90°,AD 平分∠BAC ,且CD = 5,则点D 到AB 的距离为 . 3.如图:在△ABC 中,∠C=90° AD 是∠BAC 的平分线,DE ⊥AB 于E ,F 在AC 上,BD=DF ; 说明:(1)CF=EB . (2)AB=AF+2EB . 4.如图,DE ⊥AB 于E ,DF ⊥AC 于F ,若BD=CD 、BE=CF . (1)求证:AD 平分∠BAC ; (2)直接写出AB+AC 与AE 之间的等量关系 C B A D 5W2H分析方法 前言 在企业管理或者生活中我面临: 对问题不敏感,视问题为常态或者看不出毛病,这往往与平时不善于提问有密切关系的。如果我们对一个问题追根刨底,有可能发现新的知识和新的疑问。 所以:从根本上说,学会发明或设计首先要学会提问,善于提问。 现在阻碍提问的因素: 一是怕提问多,被别人看成什么也不懂的傻瓜: 二是随着年龄和知识的增长,提问欲望渐渐淡薄。 如果提问得不到答复和鼓励,反而遭人讥讽,结果在潜意识中就形成了这种看法:好提问、好挑毛病的人是扰乱别人的讨厌鬼,最好紧闭嘴唇,不看、不闻、不问,但是这恰恰阻碍了人的创造性的发挥。 5w2H的定义 5w2H分析法又叫七何分析法,5w2H法是第二世界大战中美国陆军 兵器修理部首创。 5w2H分析法简单、方便,易于理解、使用,富有启发意义,广泛用于企业管理和技术活动,对于决策和执行性的活动措施也非常有帮助,也有助于弥补考虑问题的疏漏。 如图:发明者用五个以W开头的英语单词和两个以H开头的英语单 词进行设问。发现解决问题的线索,寻找出创新和发明新项目的思路,更进一步进行设计构思,从而搞出新的发明项目,这就叫做5w2H法 5W分别是: 1) Why:为什么?为什么要这么做?理由何在?原因是什么? 2) What:是什么?目的是什么?做什么工作? 3) Where:何处?在哪里做?从哪里入手? 4) When:何时?什么时间完成?什么时机最适宜? 5) Who:谁?由谁来承担?谁来完成?谁负责? 2H分别是: 1) How:怎么做?如何提高效率?如何实施?方法怎样? 2) How much:多少?做到什么程度?数量如何?质 量水平如何?费用产出如何? 线段和差最值的存在性问题解题策略 专题攻略 两条动线段的和的最小值问题,常见的是典型的“牛喝水”问题,关键是指出一条对称轴“河流”(如图1). 三条动线段的和的最小值问题,常见的是典型的“台球两次碰壁”或“光的两次反射”问题,关键是指出两条对称轴“反射镜面”(如图2). 两条线段差的最大值问题,一般根据三角形的两边之差小于第三边,当三点共线时,两条线段差的最大值就是第三边的长.如图3,PA 与PB 的差的最大值就是AB ,此时点P 在AB 的延长线上,即P ′. 解决线段和差的最值问题,有时候求函数的最值更方便,本讲不涉及函数最值问题. 图1 图2 图3 例题解析 例? 如图1-1,抛物线y =x 2 -2x -3与x 轴交于A 、B 两点,与y 轴交于点C ,点P 是抛物线对称轴上的一个动点,如果△PAC 的周长最小,求点P 的坐标. 图1-1 【解析】如图1-2,把抛物线的对称轴当作河流,点A 与点B 对称,连结BC ,那么在△PBC 中,PB +PC 总是大于BC 的.如图1-3,当点P 落在BC 上时,PB +PC 最小,因此PA +PC 最小,△PAC 的周长也最小. 由y =x 2 -2x -3,可知OB =OC =3,OD =1.所以DB =DP =2,因此P (1,-2). 图1-2 图1-3 例?如图,抛物线21442 y x x =-+与y 轴交于点A ,B 是OA 的中点.一个动点G 从点B 出发,先经过x 轴上的点M ,再经过抛物线对称轴上的点N ,然后返回到点A .如果动点G 走过的路程最短,请找出点M 、N 的位置,并求最短路程. 几何中线段和,差最值问题 一、解决几何最值问题的通常思路 两点之间线段最短; 直线外一点与直线上所有点的连线段中,垂线段最短; 三角形两边之和大于第三边或三角形两边之差小于第三边(重合时取到最值) 是解决几何最值问题的理论依据,根据不同特征转化是解决最值问题的关键.通过转化减少变量,向三个定理靠拢进而解决问题;直接调用基本模型也是解决几何最值问题的高效手段. 一般处理方法: 常用定理: 两点之间,线段最短(已知两个定点时) 垂线段最短(已知一个定点、一条定直线时) 三角形三边关系(已知两边长固定或其和、差固定时) 二、典型题型 1.如图:点P 是∠AOB 内一定点,点M 、N 分别在边OA 、OB 上运动,若∠AOB =45°,OP =32,则△PMN 的周长的最小值为 6 . 2.如图,当四边形P ABN 的周长最小时,a = 4 7 . 线段和(周长)最小 转化 构造三角形 两点之间,线段最短 垂线段最短 P A +PB 最小, 需转化, 使点在线异侧 |P A -PB |最大, 需转化,使点在线同侧 线段差最大 线段最大(小)值 三角形三边关系定理 三点共线时取得最值 平移 对称 旋转 使点在线异侧 (如下图) 使点在线同侧 (如下图) 使目标线段与定长线段构成三角形 平移 对称 旋转 l B'A B P l B'B A P 3.如图,A、B两点在直线的两侧,点A到直线的距离AM=4,点B到直线的距离BN=1,且MN=4,P为直线上的动点,|P A﹣PB|的最大值为5. D P B′ N B M A 4.动手操作:在矩形纸片ABCD中,AB=3,AD=5.如图所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点A′在BC边上可移动的最大距离为 2 . 5.如图,直角梯形纸片ABCD,AD⊥AB,AB=8,AD=CD=4,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.当P落在直角梯形ABCD 内部时,PD的最小值等于8- 5 4. 6.如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为1 2 . 教案1.4线段、角的轴对称性(2) 【学习目标】: 1、让学生经历角的折叠过程探索角的对称性,并发现角平分线的性质和判定点在一个角的平分线上的方法; 2、使学生会运用角平分线的性质定理解决生活中的相关问题; 3、培养学生实践探索的科学习惯; 4、在“操作—探究—归纳—说理”的过程中学会有条理地思考和表达,提高演绎推理能力. 【重点难点】:角平分线的性质和判定 【预习指导】: 1、在一张薄纸上任意画一个角(∠AOB ),折纸,使两边OA、OB重合,你发现折痕与∠ AOB有什么关系? 结论: 2、在∠AOB的内部任意取折痕上的一点P,分别画点P到OA和OB的垂线段PC和PD,再 沿原折痕重新折叠,由此你能发现角平分线上的点有什么性质? 结论: 几何符号:∵ ∴ 3、反之,如果一个角内一点具备到这个角两边的距离相等,那么这个点的位置有何特征?结论: 几何符号:∵ ∴ 【典题选讲】: 例1、任意画∠O,在∠O的两边上分别截取OA、OB,使OA=OB,过点A画OA的垂线,过点B画OB的垂线,设两条垂线相交于点P,点O在∠APB的平分线上吗?为什么? P B A 例2、已知:如图,在ΔABC中.O是∠B、∠C外角的平分线的交点,那么点O在∠A的平分线上吗?为什么? F 【学习体会】: 【课堂练习】: 1、 画一画:已知∠AOB 和C 、D 两点,请在图中标出一点E ,使得点E 到OA 、OB 的距离相等,而且E 点到C 、D 的距离也相等. 2、 已知:在ΔABC 中,D 是BC 上一点,DF ⊥AB 于E,DE ⊥AC 于F,且DE=DF. 线段AD 与EF 有何关系?并说明理由. 3、 已知:在∠ABC 中,D 是∠ABC 平分线上一点,E 、F 分别在AB 、AC 上,且DE=DF. 试判断∠BED 与∠BFD 的关系,并说明理由. ( 编写者:李晓红) O B A C D · · A C 线段、角的轴对称性—知识讲解 责编:陆海霞 【学习目标】 1.理解线段的垂直平分线的概念,掌握线段的垂直平分线的性质及判定,会画已知线段的垂直平分线,能运用线段的垂直平分线的性质解决简单的数学问题及实际问题. 2. 理解角平分线的画法,掌握角平分线的性质,理解三角形的三条角平分线的性质,熟练运用角的平分线 的性质解决问题. (2)用符号语言表示角的内部到角两边距离相等的点在角的平分线上 若PE⊥AD于点E, 角平分线的画法 角平分线的尺规作图 【典型例题】 类型一、线段的轴对称性 1、如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为() A.13 B.15 C.17 D.19 【变式】(2015?黄岛区校级模拟)某旅游景区内有一块三角形绿地ABC,如图所示,现要在道路AB的边缘上建一个休息点M,使它到A,C两个点的距离相等.在图中确定休息点M的位置. 2、如图所示,如果将军从马棚M出发,先赶到河OA上的某一位置P,再马上赶到河OB上的某一位置Q, 然后立即返回校场N.请为将军重新设计一条路线(即选择点P和Q),使得总路程MP+PQ+QN最短. 【变式】如图所示,将军希望从马棚M出发,先赶到河OA上的某一位置P,再马上赶到河OB上的某一位置Q.请为将军设计一条路线(即选择点P和Q),使得总路程MP+PQ最短. 类型二、角的轴对称性 3、如图, △ABC中, ∠C = 90 , AC = BC, AD平分∠CAB, 交BC于D, DE⊥AB于E, 且AB=6cm, 则△DEB的周长为( ) A. 4cm B. 6cm C.10cm D. 以上都不对 求线段和(差)的最值问题 【知识依据】:1.线段公理——两点之间,线段最短;2.对称的性质——①关于一条直线对称的两个图形全等;②对称轴是两个对称图形对应点连线的垂直平分线;3.三角形两边之和大于第三边;4.三角形两边之差小于第三边。5、垂直线段最短 一、已知两个定点: 1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧: (2)点A 、B 在直线同侧: A 、A ’ 是关于直线m 的对称点。 2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。 (1)两个点都在直线外侧: m m A B m A B m n m n (2)一个点在内侧,一个点在外侧: (3)两个点都在内侧: (4)、台球两次碰壁模型 变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短. 变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短. n m A n n n m 二、一个动点,一个定点: (一)动点在直线上运动: 点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧: 2、两点在直线同侧: (二)动点在圆上运动 点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧: 2、点与圆在直线同侧: m n m n m n m m m m m 中考二轮复习之线段和(差)的最值问题 一、两条线段和的最小值。 填空题: 1.如图,正方形的边长为2,E为的中点,P是上一动点.则的最小值是. 2.如图,⊙O的半径为2,点A、B、C在⊙O上,⊥,∠60°,P是上一动点,则的最小值是. 3.如图,在锐角△中,=42,∠=45°,∠的平分线交于点D,M、N分别是和上的动点,则的最小值是. 4.如图,在四边形中,∠=90°,∥,=4,=5,=6,点P是上一个动点,当+的和最小时,的长为. 5.已知A(-2,3),B(3,1),P点在x轴上,若+长度最小,则最小值为.若—长度最大,则最大值为. 6.如图,是半径为1的⊙O的直径,点A在⊙O 第1题第2题第3题第4题 上,∠=30°,B为弧的中点,P是直径上一动点,则+的最小值为. 7、如图,菱形中,2,∠120°,点P,Q,K分别为线段,,上的任意一点,则的最小值为 8、如图,正方形的边长是2,∠的平分线交于点E,若点P、Q 分别是和上的动点,则的最小值为. 综合题: 1.如图,∠45°,P是∠内一点,10,Q、R分别是、上的动点,求△周长的最小值. 2.如图,已知平面直角坐标系,A,B两点的 坐标分别为A(2,-3),B(4,-1) 设M,N分别为x轴和y轴上的动点,请问: 是否存在这样的点M(m,0),N(0,n),使四 边形的周长最短?若存在,请求出m=,n=(不必写解答过程);若不存在,请说明理由. 中考赏析: 1.著名的恩施大峡谷(A)和世界级自然保护区星斗山(B)位于笔直的沪渝高速公路X同侧,50、B到直线X的距离分别为10和40,要在沪渝高速公路旁修建一服务区P,向A、B两景区运送游客.小民设计了两种方案,图(1)是方案一的示意图(与直线X垂直,垂足为P),P到A、B的距离之和S1=+,图(2)是方案二的示意图(点A关于直线X的对称点是A',连接'交直线X于点P),P到A、B的距离之和S2=+. (1)求S1、S2,并比较它们的大小; (2)请你说明S2=+的值为最小; (3)拟建的恩施到张家界高速公路Y与沪渝高速公路垂直,建立如图(3)所示的直角坐标系,B到直线Y的距离为30,请你在X旁和Y旁各修建一服务区P、Q,使P、A、B、Q组成的四边形的周长最小.并求出这个最小值. 初中几何中线段和(差)的最值问题 一、两条线段和的最小值。 基本图形解析: 一)、已知两个定点: 1、在一条直线m 上,求一点P,使P A+PB 最小; (1)点A 、B 在直线m 两侧: (2)点A 、B 在直线同侧: 2、在直线m 、n 上分别找两点P、Q,使PA+P Q+QB 最小。 (1)两个点都在直线外侧: (2)一个点在内侧,一个点在外侧: (3)两个点都在内侧: m m B m A B m n m n n m n n n m (4)、台球两次碰壁模型 变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短. 变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA +PQ+Q A周长最短. 二)、一个动点,一个定点: (一)动点在直线上运动: 点B在直线n上运动,在直线m 上找一点P,使PA +PB 最小(在图中画出点P和点B ) 1、两点在直线两侧: 2、两点在直线同侧: (二)动点在圆上运动 点B 在⊙O 上运动,在直线m 上找一点P,使PA+P B最小(在图中画出点P 和点B ) 1、点与圆在直线两侧: m n m n m n m m 2、点与圆在直线同侧: 三)、已知A 、B 是两个定点,P 、Q 是直线m上的两个动点,P 在Q 的左侧,且PQ间长度恒定,在直线m上要求P 、Q 两点,使得PA+P Q+QB 的值最小。(原理用平移知识解) (1)点A 、B 在直线m两侧: 作法:过A 点作AC ∥m,且AC长等于PQ长,连接BC ,交直线m 于Q,Q 向左平移PQ 长,即为P点,此时P 、Q 即为所求的点。 (2)点A 、B 在直线m同侧: 基础题 1.如图1,∠AO B=45°,P 是∠AO B内一点,PO =10,Q、R 分别是OA 、OB 上的动点,求△PQR 周长的最小值为 . 2、如图2,在锐角三角形ABC 中,AB=4 ,∠BAC=45°,∠B AC的平分线交B C于点D, M,N分别是AD 和AB上的动点,则BM+MN的最小值为 . m O A P m O A B m A B E Q P m A B Q m A Q m A C Q P 二次函数中线段和、差最值问题 姓名: 1、如图,已知抛物线y=ax2+bx+3与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).(1)求抛物线的解析式;(2)在(1)中抛物线的对称轴上是否存在点D,使△BCD的周长最小?若存在,求出点D的坐标,若不存在,请说明理由;并求出周长的最小值;(3)若点E是(1)中抛物线上的一个动点,且位于直线AC的下方,试求△ACE的最大面积及E点的坐标. 2、如图,△ABC的三个顶点坐标分别为A(-2,0)、B(6,0)、C(0,3 2 -),抛物线y=ax2+bx+c (a≠0)经过A、B、C三点。(1)求直线AC的解析式;(2)求抛物线的解析式;(3)若抛物线的顶点为D,在直线AC上是否存一点P,使得△BDP的周长最小,若存在,求出P点的坐标;若不存在,请说明理由。 3、如图,已知直线 1 1 2 y x =+与y轴交于点A,与x轴交于点D,抛物线2 1 2 y x bx c =++与直 线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0)。⑴求该抛物线的解析式; ⑵动点P在x轴上移动,当△PAE是直角三角形时,求点P的坐标P。⑶在抛物线的对称轴上找一点M,使|| AM MC -的值最大,求出点M的坐标。 4、如图8,对称轴为直线x =2的抛物线经过点A (-1,0),C (0,5)两点,与x 轴另一交点为B ,已知M (0,1),E (a ,0),F (a +1,0),点P 是第一象限内的抛物线上的动点.(1)求此抛物线的解析式.(2)当a =1时,求四边形MEFP 面积的最大值,并求此时点P 的坐标.(3)若△PCM 是以点P 为顶点的等腰三角形,求a 为何值时,四边形PMEF 周长最小?请说明理由. 图8 O A E F B M C P x y 备用图 A O M C E F x B y P线段和差最值问题
线段和差最值问题-经典模型(新)
2.4线段、角的轴对称性(4)
线段差的最大值与线段和的最小值问题
八年级数学——线段和角的轴对称性
线段角的轴对称性单元练习
线段、角的轴对称性专题练习
5W2H分析方法
中考数学压轴题解题策略:线段和差最值的存在性问题
经典几何中线段和差最值(含答案)
线段角的轴对称性教案
线段、角的轴对称性
中考数学之_线段和(差)的最值问题
中考复习线段和差的最大值与最小值拔高
初中几何中线段和与差最值问题
二次函数中线段和差最值问题