
初中几何中线段和(差)的最值问题
一、两条线段和的最小值。 基本图形解析: 一)、已知两个定点:
1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:
(2)点A 、B 在直线同侧:
A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。 (1)两个点都在直线外侧:
(2)一个点在内侧,一个点在外侧:
(3)两个点都在内侧:
m
m
B m
A B
m
n m
n
n m
n
n
n
m
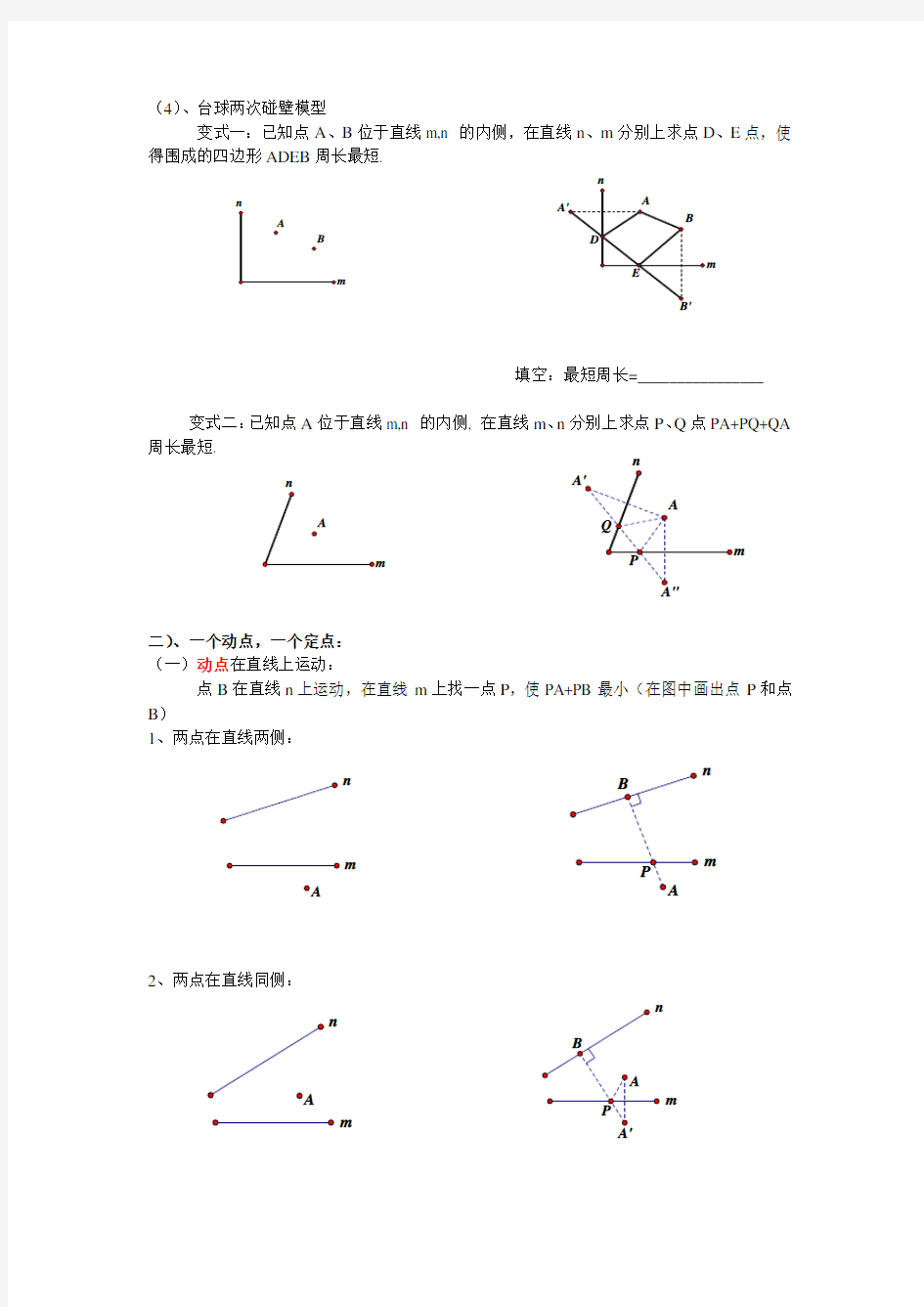
(4)、台球两次碰壁模型
变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.
填空:最短周长=________________
变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.
二)、一个动点,一个定点: (一)动点在直线上运动:
点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B )
1、两点在直线两侧:
2、两点在直线同侧:
m
n
m n
m n
m
(二)动点在圆上运动
点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧:
2、点与圆在直线同侧:
三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。(原理用平移知识解) (1)点A 、B 在直线m 两侧:
过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。 (2)点A 、B 在直线m 同侧:
m
m
m
m
Q
练习题 1.如图,∠AOB =45°,P 是∠AOB 内一点,PO =10,Q 、R 分别是OA 、OB 上的动点,求△PQR 周长的最小值为 .
2、 如图1,在锐角三角形ABC 中,AB=4
,∠BAC=45°,∠BAC 的平分线交BC 于点D ,
M,N 分别是AD 和AB 上的动点,则BM+MN 的最小值为 .
3、如图,在锐角三角形ABC 中 ,
AB=BAC=45,BAC 的平分线交BC 于D ,M 、N 分别是AD 和AB 上的动点,则BM+MN 的最小值是多少?
4、如图4所示,等边△ABC 的边长为6,AD 是BC 边上的中线,M 是AD 上的动点,E 是AC 边上一点.若AE=2,EM+CM 的最小值为 .
5、如图3,在直角梯形ABCD 中,∠ABC =90°,AD ∥BC ,AD =4,AB =5,BC =6,点P 是AB 上一个动点,当PC +PD 的和最小时,PB 的长为__________.
6、 如图4,等腰梯形ABCD 中,AB=AD=CD=1,∠ABC=60°,P 是上底,下底中点EF 直线上的一点,则PA+PB 的最小值为 .
Q
7、如图5菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为.
8、如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是
9、如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为________cm.
10、如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为
11、如图,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.则PB+PE的最小值是
12、如图6所示,已知正方形ABCD的边长为8,点M在DC上,且DM=2,N是AC上的一个动点,则DN+MN的最小值为.
13、如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为.
14、如图7,在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为 cm.(结果不取近似值).
15、如图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则P A+PC的最小值是.
16、如图8,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为( )
(A)2 (B) (C)1 (D)2
解答题
1、如图9,正比例函数y=x的图象与反比例函数y=(k≠0)在第一象限的图象交于A
点,过A点作x轴的垂线,垂足为M,已知三角形OAM的面积为1.
(1)求反比例函数的解析式;
(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.
2、如图,一元二次方程x2+2x-3=0的二根x1,x2(x1<x2)是抛物线y=ax2+bx+c 与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).
(1)求此二次函数的解析式;
(2)设此抛物线的顶点为P,对称轴与AC相交于点Q,求点P和点Q的坐标;(3)在x轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标.
3、如图10,在平面直角坐标系中,点A的坐标为(1,),△AOB的面积是.
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的解析式;
(3)在(2)中抛物线的对称轴上是否存在点C,使△AOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;
4.如图,抛物线y =35x 2-18
5x +3和y 轴的交点为A ,M 为OA 的中点,若有一动点P ,自
M 点处出发,沿直线运动到x 轴上的某点(设为点E ),再沿直线运动到该抛物线对称轴上
的某点(设为点F ),最后又沿直线运动到点A ,求使点P 运动的总路程最短的点E ,点F 的坐标,并求出这个最短路程的长.
5.如图,已知在平面直角坐标系xOy 中,直角梯形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =AB =2,OC =3,过点B 作BD ⊥BC ,交OA 于点D .将∠DBC 绕点B 按顺时针方向旋转,角的两边分别交y 轴的正半轴、x 轴的正半轴于点E 和F . (1)求经过A 、B 、C 三点的抛物线的解析式;
(2)当BE 经过(1)中抛物线的顶点时,求CF 的长; (3)在抛物线的对称轴上取两点P 、Q (点Q 在点P 的上方),且PQ =1,要使四边形BCPQ 的周长最小,求出P 、Q 两点的坐标.
6.如图,已知平面直角坐标系,A,B两点的坐标分别为A(2,-3),B(4,-1)若C(a,0),D(a+3,0)是x轴上的两个动点,则当a为何值时,四边形ABDC的周长最短.
7、如图11,在平面直角坐标系中,矩形的顶点O在坐标原点,顶点A、B分别在x
轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.
(1)若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标;
(2)若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标.
二、求两线段差的最大值问题 (运用三角形两边之差小于第三边) 基本图形解析:
1、在一条直线m 上,求一点P ,使PA 与PB 的差最大; (1)点A 、B 在直线m 同侧:
解析:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P ’A —P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。 (2)点A 、B 在直线m 异侧:
解析:过B 作关于直线m 的对称点B ’,连接AB ’交点直线m 于P,此时PB=PB ’,PA-PB 最大值为AB ’ 练习题
1. 如图,抛物线y =-14x 2
-x +2的顶点为A ,与y 轴交于点B .
(1)求点A 、点B 的坐标;
(2)若点P 是x 轴上任意一点,求证:P A -PB ≤AB ; (3)当P A -PB 最大时,求点P 的坐标.
B
m
m
2. 如图,已知直线y =2
1
x +1与y 轴交于点A ,与x 轴交于点D , 抛物线y =
2
1x 2
+bx +c 与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为(1,0).
(1)求该抛物线的解析式;
(3)在抛物线的对称轴上找一点M ,使|AM -MC |的值最大,求出点M 的坐标.
3、在直角坐标系中,点A 、B 的坐标分别为(-4,-1)和(-2,-5);点P 是y 轴上的一个动点,⑴点P 在何处时,PA +PB 的和为最小?并求最小值。⑵点P 在何处时,∣PA —PB ∣最大?并求最大值。
4. 如图,直线y =-3x +2与x 轴交于点C ,与y 轴交于点B ,点A 为y 轴正半轴上的一点,⊙A 经过点B 和点O ,直线BC 交⊙A 于点D . (1)求点D 的坐标;
(2)过O ,C ,
D 三点作抛物线,在抛物线的对称轴上是否存在一点P ,使线段PO 与PD 之差的值最大?若存在,请求出这个最大值和点P 的坐标.若不存在,请说明理由.
5、抛物线的解析式为2
23y x x =-++,交x 轴与A 与B,交y 轴于C , ⑴在其对称轴上是否存在一点P ,使⊿APC 周长最小,若存在,求其坐标。 ⑵在其对称轴上是否存在一点Q ,使∣QB —QC ∣的值最大,若存在求其坐标。
6、已知:如图,把矩形OCBA放置于直角坐标系中,OC=3,BC=2,取AB的中点M,连接MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.
(1)试直接写出点D的坐标;
(2)已知点B与点D在经过原点的抛物线上,点P在第一象限内的该抛物线上移动,过点P作PQ⊥x轴于点Q,连接OP.
①若以O、P、Q为顶点的三角形与△DAO相似,试求出点P的坐标;
②试问在抛物线的对称轴上是否存在一点T,使得|TO-TB|的值最大?
7、如图,已知抛物线C1的解析式为y=-x2+2x+8,图象与y轴交于D点,并且顶点A在双曲线上.
(1)求过顶点A的双曲线解析式;
(2)若开口向上的抛物线C2与C1的形状、大小完全相同,并且C2的顶点P始终在C1上,证明:抛物线C2一定经过A点;
(3)设(2)中的抛物线C2的对称轴PF与x轴交于F点,且与双曲线交于E点,当D、O、E、F四点组成的四边形的面积为16.5时,先求出P点坐标,并在直线y=x上求一点M,使|MD-MP|的值最大.
8、如图,已知抛物线经过A(3,0),B(0,4),
(1).求此抛物线解析式
(2)若抛物线与x轴的另一交点为C,求点C关于直线AB的对称点C’的坐标
(3)若点D是第二象限内点,以D为圆心的圆分别与x轴、y轴、直线AB相切于点E、F、H,问在抛物线的对称轴上是否存在一点一点P,使得|PH-P A|的值最大?若存在,求出该最大值;若不存在,请说明理由。
D C
B A A B C
D A B
C D
三、其它非基本图形类线段和差最值问题
1、求线段的最大值与最小值需要将该条线段转化到一个三角形中,在该三角形中,其他两边是已知的,则所求线段的最大值为其他两线段之和,最小值为其他两线段之差。
2、在转化较难进行时需要借助于三角形的中位线及直角三角形斜边上的中线。
3、线段之和的问题往往是将各条线段串联起来,再连接首尾端点,根据两点之间线段最短以及点到线的距离垂线段最短的基本依据解决。
1、如图,在△ABC 中,∠C =90°,AC =4,BC =2,点A 、C 分别在x 轴、y 轴上,当点A
在x 轴上运动时,点C 随之在y 轴上运动,在运动过程中,点B 到原点的最大距离是( ) A . 222 B .52 C 。 62 D . 6
2、已知:在△ABC 中,BC=a ,AC=b ,以AB 为边作等边三角形ABD. 探究下列问题:
(1)如图1,当点D 与点C 位于直线AB 的两侧时,a=b=3,且∠ACB=60°,则CD= ;
(2)如图2,当点D 与点C 位于直线AB 的同侧时,a=b=6,且∠ACB=90°,则CD= ;
(3)如图3,当∠ACB 变化,且点D 与点C 位于直线AB 的两侧时,求 CD 的最大值及相应的∠ACB 的度数.
图1 图2 图3
3、在Rt △ABC 中,∠ACB =90°,tan ∠BAC =
1
2
. 点D 在边AC 上(不与A ,C 重合),连结BD ,F 为BD 中点. (1)若过点D 作DE ⊥AB 于E ,连结CF 、EF 、CE ,如图1. 设CF kEF ,则k = ; (2)若将图1中的△ADE 绕点A 旋转,使得D 、E 、B 三点共线,点F 仍为BD 中点,如图2所示.求证:BE -DE =2CF ;
(3)若BC =6,点D 在边AC 的三等分点处,将线段AD 绕点A 旋转,点F 始终为BD
中点,求线段CF 长度的最大值.
B C
A D
E F
B D
E A F
C
B
A
C
1
图2
图备图
4、如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、C M.⑴ 求证:△AMB≌△ENB;
⑵ ①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,并说明理由;
3 时,求正方形的边长.
⑶ 当AM+BM+CM的最小值为1
B C
5、如图,二次函数y=-x2+bx+c与x轴交于点B和点A(-1,0),与y轴交于点C,与一次函数y=x+a交于点A和点D.
(1)求出a、b、c的值;
(2)若直线AD上方的抛物线存在点E,可使得△EAD面积最大,求点E的坐标;
(3)点F为线段AD上的一个动点,点F到(2)中的点E的距离与到y轴的距离之和记为d,求d的最小值及此时点F的坐标.
专题四线段和的最小值问题 纵观贵阳5年中考,2014年和年两年连续考查了利用对称求线段和最小值的几何问题.设置在第24题、25题,以解答题的形式出现,分值为12分,难度较大. 预计2017贵阳中考还会设计利用图形变换考查此类问题的几何综合题,复习时要加大训练力度. ,中考重难点突破) 线段的最小值 【经典导例】 【例】(六盘水中考)(1)观察发现 如图①,若点A,B在直线m同侧,在直线m上找一点P,使AP+BP的值最小,做法如下:作点B关于直线m的对称点B′,连接AB′,与直线m的交点就是所求作的点P,线段AB′的长度即为AP+BP的最小值.
如图②,在等边三角形ABC 中,AB =2,点E 是AB 的中点,AD 是高,在AD 上找一点P ,使BP +PE 的值最小,做法如下: 作点B 关于AD 的对称点,恰好与点C 重合,连接CE 交AD 于一点,则这点就是所求作的点P ,故BP +PE 的最小值为________. (2)实践运用 如图③,已知⊙O 的直径CD 为2,︵AC 的度数为60°,点B 是︵AC 的中点,在直径CD 上作出点P ,使BP +AP 的值最小,则BP +AP 的最小值为________. (3)拓展延伸 如图④,点P 是四边形ABCD 内一点,分别在边AB ,BC 上作出点M ,点N ,使PM +PN 的值最小,保留作图痕迹,不写作法. 【解析】(1)利用作法得到CE 的长为BP +PE 的最小值;由AB =2,点E 是AB 的中点,根据等边三角形的 性质得到CE ⊥AB ,∠BCE =21 ∠BCA =30°,BE =1,再根据含30°的直角三角形三边的关系得到CE 的长度.C E 的长为BP +PE 的最小值.∵在等边三角形ABC 中,AB =2,点E 是AB 的中点,∴CE ⊥AB ,∠BCE =21 ∠BCA =30°,BE =1,∴CE =BE =.故答案为;(2)过B 点作弦BE ⊥CD ,连接AE 交CD 于P 点,连接OB ,O E ,OA ,PB ,根据垂径定得到CD 平分BE ,即点E 与点B 关于CD 对称,则AE 的长就是BP +AP 的最小值.
初中几何中线段和(差)的最值问题 一、两条线段和的最小值。 基本图形解析:( 对称轴为:动点所在的直线上) 一)、已知两个定点: 1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧: (2)点A 、B 在直线同侧: A 、A ’ 是关于直线m 的对称点。 2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。 m m A B m B m A B m
(1)两个点都在直线外侧: (2)一个点在内侧,一个点在外侧: (3)两个点都在内侧: n m n n m n n n m
(4)、台球两次碰壁模型 变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、 m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短. 填空:最短周长=________________ 变式二:已知点A 位于直线m,n 的内侧, 在直线m 、 n 分别上求点P 、Q 点PA+PQ+QA 周长最短.
二)、一个动点,一个定点: (一)动点在直线上运动: 点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧: 2、两点在直线同侧: m n m n m n m
(二)动点在圆上运动 点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧: 2、点与圆在直线同侧: 三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度 m m m m
初中数学《最值问题》典型例题 一、解决几何最值问题的通常思路 两点之间线段最短; 直线外一点与直线上所有点的连线段中,垂线段最短; 三角形两边之和大于第三边或三角形两边之差小于第三边(重合时取到最值) 是解决几何最值问题的理论依据,根据不同特征转化是解决最值问题的关键.通过转化减少变量,向三个定理靠拢进而解决问题;直接调用基本模型也是解决几何最值问题的高效手段. 轴 对 称 最 值 图形 l P B A N M l B A A P B l 原理两点之间线段最短两点之间线段最短三角形三边关系 特征 A,B为定点,l为定直 线,P为直线l上的一 个动点,求AP+BP的 最小值 A,B为定点,l为定直线, MN为直线l上的一条动线 段,求AM+BN的最小值 A,B为定点,l为定直线, P为直线l上的一个动 点,求|AP-BP|的最大值转化 作其中一个定点关于定 直线l的对称点 先平移AM或BN使M,N 重合,然后作其中一个定 点关于定直线l的对称点 作其中一个定点关于定 直线l的对称点 折 叠 最 值 图形 B' N M C A B 原理两点之间线段最短 特征 在△ABC中,M,N两点分别是边AB,BC上的动点,将△BMN沿MN翻折, B点的对应点为B',连接AB',求AB'的最小值. 转化转化成求AB'+B'N+NC的最小值 1.如图:点P是∠AOB内一定点,点M、N分别在边OA、OB上运动,若∠AOB=45°,OP=32,则△PMN 的周长的最小值为. 【分析】作P关于OA,OB的对称点C,D.连接OC,OD.则当M,N是CD与OA,OB的交点时,△PMN 的周长最短,最短的值是CD的长.根据对称的性质可以证得:△COD是等腰直角三角形,据此即可求解.【解答】解:作P关于OA,OB的对称点C,D.连接OC,OD.则当M,N是CD与OA,OB的交点时,△PMN的周长最短,最短的值是CD的长. ∵PC关于OA对称, ∴∠COP=2∠AOP,OC=OP 同理,∠DOP=2∠BOP,OP=OD ∴∠COD=∠COP+∠DOP=2(∠AOP+∠BOP)=2∠AOB=90°,OC=OD.
例说求函数的最大值和最小值的方法 例1.设x 是正实数,求函数x x x y 32+ +=的最小值。 解:先估计y 的下界。 55)1(3)1(5)21(3)12(222≥+- +-=+-+ ++-=x x x x x x x y 又当x =1时,y =5,所以y 的最小值为5。 说明 本题是利用“配方法”先求出y 的下界,然后再“举例”说明这个下界是可以限到的。“举例”是必不可少的,否则就不一定对了。例如,本题我们也可以这样估计: 77)1(3)1(7)21(3)12(222-≥-+ +-=-++ ++-=x x x x x x x y 但y 是取不到-7的。即-7不能作为y 的最小值。 例2. 求函数1 223222++--=x x x x y 的最大值和最小值。 解 去分母、整理得:(2y -1)x 2+2(y +1)x +(y +3)=0. 当2 1≠y 时,这是一个关于x 的二次方程,因为x 、y 均为实数,所以 ?=[2(y +1)]2-4(2y -1)(y +3)≥0, y 2+3y --4≤0, 所以 -4≤y ≤1 又当3 1-=x 时,y =-4;x =-2时,y =1.所以y min =-4,y max =1.
说明 本题求是最值的方法叫做判别式法。 例3.求函数152++-=x x y ,x ∈[0,1]的最大值 解:设]2,1[1∈=+t t x ,则x =t 2-1 y = -2(t 2-1)+5t = -2t 2+5t +1 原函数当t =169,45=x 即时取最大值8 33 例4求函数22 3,5212≤≤+--=x x x x y 的最小值和最大值 解:令x -1=t ( 121≤≤t ) 则t t t t y 4142+=+= y min =5 1,172max =y 例5.已知实数x ,y 满足1≤x 2+y 2≤4,求f (x )=x 2+xy +y 2的最小值和最大值 解:∵)(2 122y x xy +≤ ∴6)(23 ),(2222≤+≤++=y x xy y x y x f 又当2==y x 时f (x ,y )=6,故f (x ,y )max =6 又因为)(2122y x xy +- ≥
几何中线段和,差最值问题 一、解决几何最值问题的通常思路 两点之间线段最短; 直线外一点与直线上所有点的连线段中,垂线段最短; 三角形两边之和大于第三边或三角形两边之差小于第三边(重合时取到最值) 是解决几何最值问题的理论依据,根据不同特征转化是解决最值问题的关键.通过转化减少变量,向三个定理靠拢进而解决问题;直接调用基本模型也是解决几何最值问题的高效手段.
一般处理方法: 常用定理: 两点之间,线段最短(已知两个定点时) 垂线段最短(已知一个定点、一条定直线时) 三角形三边关系(已知两边长固定或其和、差固定时) 二、典型题型 1.如图:点P 是∠AOB 内一定点,点M 、N 分别在边OA 、OB 上运动,若∠AOB =45°,OP =△PMN 的周长的最小值为 6 . 2.如图,当四边形P ABN 的周长最小时,a = 4 7 . P A +P B 最小, 需转化, 使点在线异侧 B l
3.如图,A、B两点在直线的两侧,点A到直线的距离AM=4,点B到直线的距离BN=1,且MN=4,P为直线上的动点,|P A﹣PB|的最大值为5. 4.动手操作:在矩形纸片ABCD中,AB=3,AD=5.如图所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点 P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点A′在BC 边 上可移动的最大距离为 2 . 5.如图,直角梯形纸片ABCD,AD⊥AB,AB=8,AD=CD=4,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.当P落在直角梯形ABCD内部时,PD 6.如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B 在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O
函数的最大值和最小值教案 1.本节教材的地位与作用本节主要研究闭区间上的连续函数最大值和最小值的求法和实际应用,分两课时,这里是第一课时,它是在学生已经会求某些函数的最值,并且已 经掌握了性质:“如果f(x)是闭区间[a,b]上的连续函数,那么 f(x)在闭区间[a,b]上有最大值和最小值” ,以及会求可导函数的极值之后进行学习的,学好这一节,学生将会求更多的函数的 最值,运用本节知识可以解决科技、经济、社会中的一些如何使成本最低、产量最高、效益最大等实际问题.这节课集中体现了数形结合、理论联系实际等重要的数学思想方法,学好本节,对于进一步完善学生的知识结构,培养学生用数学的意识都具有极为重要的意义. 2.教学重点会求闭区间上连续开区间上可导的函数的最值. 3.教学难点高三年级学生虽然已经具有一定的知识基础,但由于对求函数极值还不熟练,特别是对优 化解题过程依据的理解会有较大的困难,所以这节课的难点是理解确定函数最值的方法. 4.教学关键本节课突破难点的关键是:理解方程f′(x)=0的解,包含有指定区间内全部可能的极值点. 【教学目标】根据本节教材在高中数学知识体系中的地位和作用,结合学生已有的认知水平,制定本节如下的 教学目标: 1.知识和技能目标 (1)理解函数的最值与极 值的区别和联系. (2)进一步明确闭区间[a,b]上的连续函数
f(x),在[a,b]上必有最大、最小值. (3)掌握用导数法求上述 函数的最大值与最小值的方法和步骤. 2.过程和方法目标(1)了解开区间内的连续函数或闭区间上的不连续函数不一定有 最大、最小值. (2)理解闭区间上的连续函数最值存在的可能 位置:极值点处或区间端点处. (3)会求闭区间上连续,开区 间内可导的函数的最大、最小值. 3.情感和价值目标 (1) 认识事物之间的的区别和联系. (2)培养学生观察事物的能力,能够自己发现问题,分析问题并最终解决问题. (3)提高 学生的数学能力,培养学生的创新精神、实践能力和理性精神. 【教法选择】根据皮亚杰的建构主义认识论,知识是个体在 与环境相互作用的过程中逐渐建构的结果,而认识则是起源于主 客体之间的相互作用. 本节课在帮助学生回顾肯定了闭区间 上的连续函数一定存在最大值和最小值之后,引导学生通过观察 闭区间内的连续函数的几个图象,自己归纳、总结出函数最大值、最小值存在的可能位置,进而探索出函数最大值、最小值求解的 方法与步骤,并优化解题过程,让学生主动地获得知识,老师只是 进行适当的引导,而不进行全部的灌输.为突出重点,突破难点, 这节课主要选择以合作探究式教学法组织教学. 【学法指导】对于求函数的最值,高三学生已经具备了良好的知识基础,剩下 的问题就是有没有一种更一般的方法,能运用于更多更复杂函数 的求最值问题?教学设计中注意激发起学生强烈的求知欲望,使 得他们能积极主动地观察、分析、归纳,以形成认识,参与到课堂
D C B A A B C D A B C D 几何中线段的最值问题 一、 一条线段的最值问题一 (1)借助旋转求最值 2013通州一模 24.已知:2AD =,4BD =,以AB 为一边作等边三角形ABC .使C 、D 两点落在直线AB 的两侧. (1)如图,当∠ADB=60°时,求AB 及CD 的长; (2)当∠ADB 变化,且其它条件不变时,求CD 的 最大值,及相应∠ADB 的大小. 2011丰台一模 25.已知:在△ABC 中,BC=a ,AC=b ,以AB 为边作等边三角形ABD. 探究下列问题: (1)如图1,当点D 与点C 位于直线AB 的两侧时,a=b=3,且∠ACB=60°,则CD= ; (2)如图2,当点D 与点C 位于直线AB 的同侧时,a=b=6,且∠ACB=90°,则CD= ; (3)如图3,当∠ACB 变化,且点D 与点C 位于直线AB 的两侧时,求 CD 的最大值及相应的∠ACB 的度数. A D B C
图1 图2 图3 (2)借助直角三角形性质求最值 (1)勾股定理 (2)直角三角形斜边中线等于斜边一半 (3)直角三角形斜边的两条重要的线段,一是斜边上的高,另一个是斜边上的中线,直角三角形斜边上的高是直角顶点到斜边上所有点之中距离最短的,其长度可以用两直角边乘积除 以斜边求得. 【例1】如图,在ΔABC中,∠C=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C 随之在y轴上运动,在运动过程中,点B到原点的最大距离是 【例2】如图,△ABC 是边长为定值m的正三角形,C点与原点重合,点B在第一象限点,点A 在x轴上。 ②求出AC边上的高线BD的长度; ③当点C在y轴的正半轴滑动时,试求出点O到CA距离的最大值; ④已知点P是△ABC内切圆的圆心,请求出OP的最大值。
For personal use only in study and research; not for commercial use 线段差的最大值与线段和的最小值问题 有关线段差的最大值与线段和的最小值问题的主要应用原理是:1、两点这间线段最短。2、三角形的任意两边之和大于第三边(找和的最小值)。3、三角形的任意两边之差小于第三边(找差的最大值)。 作图找点的关键:充分利用轴对称,找出对称点,然后,使三点在一条直线上。即利用线段的垂直平分线定理可以把两条线段、三条线段、四条线段搬在同一条直线上。证明此类问题,可任意另找一点,利用以上原理来证明。 一两条线段差的最大值: (1)两点同侧:如图,点P在直线L上运动,画出一点P,使︱PA-PB︱取最大值。作法:连结AB并延长AB交直线L于点P。点P即为所求。︱PA-PB︱=AB 证明:在直线L上任意取一点P。,连结PA、PB,︱PA-PB︱<AB (2两点异侧:如图,如图,点P在直线L上运动,画出一点P,使︱PA-PB︱取最大值。作法:1、作B关于直线L的对称点B。 B
2、连结AB并延长AB交直线L于点P。点P即为所求。︱PA-PB︱=AB 证明:在直线L上任意取一点P。,连结PA、PB、PB。︱PA-PB︱=︱PA-PB︱<AB (三角形任意两边之差小于第三边) 二、两条线段和的最小值问题: (1))两点同侧:如图,点P在直线L上运动,画出一点P使P A+PB取最小值。 (三角形的任意两边之和大于第三边(找和的最小值),P A+PB=AB (2)两点异侧:如图,点P在直线L上运动,画出一点P使P A+PB取最小值。 (两点之间线段最短) 三、中考考点: 08年林金钟老师的最后一题:如图,在矩形ABCO中,B(3,2),E(3,1),F(1,2)在X轴与Y轴上是否分别存在点M、N,使得四边形EFNM的周长最小?若存在,请求出周长的最小值,若不存在,请说明理由。 提示:EF长不变。即求F N+NM+MF的最小值。利用E关于X轴的对称点E,F的对称点F,把这三条线段搬到同一条直线上。
专题10 几何最值问题【十二个基本问题】
1.如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为() A.61cm B.11cm C.13cm D.17cm 第1题第2题第3题第4题 ' 2.已知圆锥的底面半径为r=20cm,高h=20 15cm,现在有一只蚂蚁从底边上一点A出发.在侧面上爬行一周又回到A点,蚂蚁爬行的最短距离为________. 3.如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC 于F,则EF的最小值为() A.2 B.C.D. 4.如图,在矩形ABCD中,AB=10,BC=5.若点M、N分别是线段AC,AB上的两个动点,则BM+MN的最小值为() A.10 B.8 C.5 3 D.6 5.如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C处. (1)请你画出蚂蚁能够最快到达目的地的可能路径; (2)当AB=4,BC=4,CC=5时,求蚂蚁爬过的最短路径的长. (3)在(2)的条件下,求点B到最短路径的距离. · 6.如图,已知P为∠AOB内任意一点,且∠AOB=30°,点P、P分别在OA、OB上,求作点P、P,使△PPP的周长最小,连接OP,若OP=10cm,求△PPP的周长.
7.如图,E ,F 是正方形ABCD 的边AD 上两个动点,满足AE =DF .连接CF 交BD 于点G ,连接BE 交AG 于点H .若正方形的边长为2,则线段DH 长度的最小值是________. ? 第7题 第8题 第9题 8.如图,在等腰Rt △ABC 中,∠BAC =90°,AB =AC ,BC =4 2,点D 是AC 边上一动点,连接BD ,以AD 为直径的圆交BD 于点E ,则线段CE 长度的最小值为 . 9.如图,⊙O 的半径为1,弦AB =1,点P 为优弧(⌒)AB 上一动点,AC ⊥AP 交直线PB 于点C ,则△ABC 的最大面积是( ) A .12 B .22 C .32 D .34 10.如图,已知抛物线y =-x +bx +c 与一直线相交于A (-1,0),C (2,3)两点,与y 轴交于 点N .其顶点为D . (1)抛物线及直线AC 的函数关系式; (2)设点M (3,m ),求使MN +MD 的值最小时m 的值; (3)若抛物线的对称轴与直线AC 相交于点B ,E 为直线AC 上的任意一点,过点E 作EF ∥BD 交抛物线于点F ,以B ,D ,E ,F 为顶点的四边形能否为平行四边形若能,求点E 的坐标;若不能,请说明理由; (4)若P 是抛物线上位于直线AC 上方的一个动点,求△APC 的面积的最大值. ~
导数在函数求最大值和最小值中的应用 例1.求函数f (x )=5x + . 解析:由3040x x +??-? ≥≥得f (x )的定义域为-3≤x ≤4,原问题转化为求f (x )在区间[-3, 4]上的最值问题。 ∵ y ’=f ’(x ) =5 在[-3,4]上f ’(x )>0恒成立, ∴ f (x )在[-3,4]上单调递增. ∴ 当x =-3时y min =-15-7, 当x =4时y max =20+27, ∴ 函数的值域为[-15-7,20+27]. 例2.设32f (a ),f (-1)
线段最值问题 1、“对称+点点最值”如图,在正方形ABCD中,AB=8,AC与BD交于点O,N是OC的中点,点M在BC边上,且BM=6,P为对角线BD上一点,则PM+PN的最小值为 2、“对称+点点最值”如图,在矩形ABCD中,AB=6,AD=8,E、 F、 G、H分别在矩形ABCD 的边AD、AB、BC、CD上。若AF=2,DH=5,E、G分别为AD、BC上的动点, 求四边形EFGH周长的最小值 3、“双对称 +点点最值”如图,在边长为6的菱形 ABCD中, AC是其对角线,∠B=60°,点P在 CD上,CP=2,点M在AD上,点N在AC上,则△PMN周长的最小值为 4、“双对称+点点最值”如图,∠AOB=30°,点P为∠AOB内一点,且OP=10,点M,N分别为OA,OB上的动点求△PMN周长的最小值 5、“平移+点点最值”如图,菱形ABCD的边长为3,∠BAD=60°,点E、F是对角线AC上的两点,且EF=1,点E在点F的左侧,求DE+BF的最小值。
6、“平移+对称+点点最值”(1)如图,菱形ABCD 的边长为3,∠BAD=60°,点E 、F 是对角线AC 上的两点,且EF=1,点E 在点F 的左侧,求DE+DF 的最小值。 (2)如图,矩形ABCD 中,AD =2,AB =4,AC 为对角线,E 、F 分别为边AB 、CD 上的动点,且EF ⊥AC 于点M ,连接AF 、CE ,求AF +CE 的最小值. (3)如图,sinC=3/5,长度为2的线段ED 在射线CF 上滑动,点B 在射线CA 上,BC=5,则△BDE 的周长的最小值为_____. (4)如图,在平面直角坐标系中,矩形ABCD 的顶点B 在原点,点A 、C 在坐标轴上,点D 的坐标为(6,4),E 为CD 的中点,点P 、Q 为BC 边上两个动点,且PQ =2,要使四边形APQE 的周长最小,则点P 的坐示应为______________. 7、“三对称+点点最值”如图,矩形ABCD 的边AB=3,BC=4,点E 为CD 边上一点,且CE=1,点F 、G 、H 分别是AD 、AB 、BC 边上的动点,则四边形EFGH 周长的最小值是多少? A B C D E F M x
二次函数的最大值和最小值问题
————————————————————————————————作者: ————————————————————————————————日期:
二次函数的最大值和最小值问题 高一数学组主讲人---------蒋建平 本节课的教学目标: 重点:掌握闭区间上的二次函数的最值问题 难点:理解并会处理含参数的二次函数的最值问题 核心: 区间与对称轴的相对位置 思想: 数形结合、分类讨论 一、复习引入 1、二次函数相关的知识点回顾。 (1)二次函数的顶点式: (2)二次函数的对称轴: (3)二次函数的顶点坐标: 2、函数的最大值和最小值的概念 设函数)(x f 在0x 处的函数值是)(0x f ,如果不等式)()(0x f x f ≥对于定义域内任意x 都成立,那么)(0x f 叫做函数)(x f y =的最小值。记作)(0min x f y = 如果不等式)()(0x f x f ≤对于定义域内任意x 都成立,那么)(0x f 叫做函数)(x f y =的最小值。记作)(0max x f y = 二、新课讲解:二次函数最大值最小值问题探究 类型一:无限制条件的最大值与最小值问题 例1、(1)求二次函数322 ++-=x x y 的最大值 . (2)求二次函数x x y 422-=的最小值 . 本题小结:求无条件限制时二次函数最值的步骤 1、配方,求二次函数的顶点坐标。 2、根据二次函数的开口方向确定是函数的最大值还是最小值。 3、求出最值。
类型二:轴定区间定的最大值与最小值问题 例2、(1)求函数])1,3[(,232-∈-+=x x x y 的最大值 ,最小值 . (2)求函数])3,1[(232∈-+=x x x y 的最大值 ,最小值 . (3)求函数])2,5[(232 --∈-+=x x x y 的最大值 与最小值 . 本题小结:求轴定区间定时二次函数最值的步骤 1、配方,求二次函数的顶点坐标或求对称轴,画简图。 2、判断顶点的横坐标(对称轴)是否在闭区间内。 3、计算闭区间端点的值,并比较大小。 类型三:轴动区间定的最大值与最小值问题 例3、求函数)(32R a ax x y ∈++=在]1,1[-上的最大值。
中考数学压轴题解题策略(8) 线段和差最值的存在性问题解题策略 《挑战压轴题·中考数学》的作者上海马学斌 专题攻略 两条动线段的和的最小值问题,常见的是典型的“牛喝水”问题,关键是指出一条对称轴“河流”(如图1). 三条动线段的和的最小值问题,常见的是典型的“台球两次碰壁”或“光的两次反射”问题,关键是指出两条对称轴“反射镜面”(如图2). 两条线段差的最大值问题,一般根据三角形的两边之差小于第三边,当三点共线时,两条线段差的最大值就是第三边的长.如图3,P A与PB的差的最大值就是AB,此时点P在AB的延长线上,即P′. 解决线段和差的最值问题,有时候求函数的最值更方便,本讲不涉及函数最值问题. 图1 图2 图3 例题解析 例?如图1-1,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C,点P 是抛物线对称轴上的一个动点,如果△P AC的周长最小,求点P的坐标. 图1-1 【解析】如图1-2,把抛物线的对称轴当作河流,点A与点B对称,连结BC,那么在△PBC中,PB+PC总是大于BC的.如图1-3,当点P落在BC上时,PB+PC最小,因此P A+PC最小,△P AC的周长也最小. 由y=x2-2x-3,可知OB=OC=3,OD=1.所以DB=DP=2,因此P(1,-2). 图1-2 图1-3
例?如图,抛物线21442 y x x =-+与y 轴交于点A ,B 是OA 的中点.一个动点G 从点B 出发,先经过x 轴上的点M ,再经过抛物线对称轴上的点N ,然后返回到点A .如果动点G 走过的路程最短,请找出点M 、N 的位置,并求最短路程. 图2-1 【解析】如图2-2,按照“台球两次碰壁”的模型,作点A 关于抛物线的对称轴对称的点A ′,作点B 关于x 轴对称的点B ′,连结A ′B ′与x 轴交于点M ,与抛物线的对称轴交于点N . 在Rt △AA ′B ′中,AA ′=8,AB ′=6,所以A ′B ′=10,即点G 走过的最短路程为10.根据 相似比可以计算得到OM =83,MH =43,NH =1.所以M (83 , 0),N (4, 1). 图2-2 例? 如图3-1,抛物线248293 y x x =-++与y 轴交于点A ,顶点为B .点P 是x 轴上的一个动点,求线段P A 与PB 中较长的线段减去较短的线段的差的最小值与最大值,并求出相应的点P 的坐标. 图3-1 【解析】题目读起来像绕口令,其实就是求|P A -PB |的最小值与最大值. 由抛物线的解析式可以得到A (0, 2),B (3, 6).设P (x , 0). 绝对值|P A -PB |的最小值当然是0了,此时P A =PB ,点P 在AB 的垂直平分线上(如图3-2).解方程x 2+22=(x -3)2+62,得416x =.此时P 41(,0)6 . 在△P AB 中,根据两边之差小于第三边,那么|P A -PB |总是小于AB 了.如图3-3,当点
§ 4函数的最大值最小值问题 最值与极值的重要区别: 极值是一点X 。局部的形态; 最值是某区间整体的形态。 先讨论必要 性: X 。是f (x)在(a b 内的最大(小)值, =X 。必是f (x)在(a,b)的极大(小)值点, =X 。是f (x)的稳定点或不可导点. 稳定点 f(x)在[a,b ]的可能的最值点:S 不可导点 ,区间端点 F 面就两种常见的情形给出判别法,以最大值为例说明. 1 ?闭区间情形 设f (x)在a,b 1连续,这时f (x)在l.a, b 1必有最大值. 则将所有稳定点、不可导点和区间端点的函数值进行比较 (如果可能的 话),最大者即是最大值. 2.开区间情形 设f(x)在(a,b)可导,且在(a,b)有最大值.若在(a,b)内有唯一的 稳定点X 。,则X 。是最大值点. 注意强调最值的存在性 例1 一块边长为a 的正方形,在四个角上截去同样大小的正方形, 做成无盖的盒,问截去多大的小方块能使盒的容积最大?
图5-13 解设x为截去的小方块的边长,则盒的容积为 V(x)二x(a 2,) ,x 100,) 显然,V(x)在(0,a)可导,且 2 ' 2 V (x) =(a _2x) _4x(a _2x) =(a_2x)(a _6x) 令V (x) = 0得x =—或x =—。因此在(0,—)中有唯一一的稳定点—o 2 6 2 6 由实际问题本身知V(x)在(0,-)中必有最大值,故知最大值为 2 V(—) -a3。即截去的小的方块边长为-时,盒的容积最大。 6 2 7 6 例2求函数f (x) = 2x3 -9x2 +12x在1-1,3】的最大值和最小值 解2x3-9x212x =x 2(x-9)2 15, IL 4 8 因此f(x) =(2x3-9x2 12x)sgnx,x 〔-1,3 1, f (x) =(6x2-18x 12)sgn x = 6(x-1)(x -2)sgn x, x (T,0) _? (0,3) 故f (x)的稳定 点为x=1,x=2,不可导为x=0。 比较所有可能的最值点的函数值: f(-1)= 2 3f, (0) f 0, =(1f) 5〒(f2) =4, 即得最大值为f(-1) = 23,最小值为f(0)=0。 例3 在正午时,甲船恰在乙船正南82处,以速度V1=20km h向正东开出;乙船也正以速度v =16km h向正南开去(图5—15).已知两船航向不变,试证:下午二时,两船相距最近.
中考数学最值问题总结 考查知识点:1、“两点之间线段最短”,“垂线段最短”,“点关于线对称”,“线段的平移”。 (2、代数计算最值问题 3、二次函数中最值问题) 问题原型:饮马问题 造桥选址问题 (完全平方公式 配方求多项式取值 二次函数顶点) 出题背景变式:角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等。 解题总思路:找点关于线的对称点实现“折”转“直” 几何基本模型: 条件:如下左图,A 、B 是直线l 同旁的两个定点. 问题:在直线l 上确定一点P ,使PA PB +的值最小. 方法:作点A 关于直线l 的对称点A ',连结A B '交l 于 点P ,则PA PB A B '+=的值最小 例1、如图,四边形ABCD 是正方形,△ABE 是等边三 角形,M 为对角线BD (不含B 点)上任意一点,将BM 绕点B 逆时针旋转60°得到BN ,连接EN 、AM 、CM . (1)求证:△AMB ≌△ENB ; (2)①当M 点在何处时,AM+CM 的值最小; ②当M 点在何处时,AM+BM+CM 的值最小,并说明理由; (3)当AM+BM+CM 的最小值为 时,求正方形的边长。 例2、如图13,抛物线y=ax 2+bx +c(a≠0)的顶点为(1,4),交x 轴于A 、B ,交y 轴于D ,其中B 点的坐标为(3,0) (1)求抛物线的解析式 (2)如图14,过点A 的直线与抛物线交于点E ,交y 轴于点F ,其中E 点的横坐标为2,若直线PQ 为抛物线的对称轴,点G 为PQ 上一动点,则x 轴上是否存在一点H ,使D 、G 、F 、H 四点围成的四边形周长最小.若存在,求出这个最小值及G 、H 的坐标;若不存在,请说明理由. (3)如图15,抛物线上是否存在一点T ,过点T 作x 的垂线,垂足为M ,过点M 作直线M N ∥BD ,交线段AD 于点N ,连接MD ,使△DNM ∽△BMD ,若存在,求出点T 的坐标;若不存在,说明理由. A B A ' ′ P l
初中几何中线段和(差)的最值问题 一、两条线段和的最小值。 基本图形解析: 一)、已知两个定点: 1、在一条直线m 上,求一点P,使P A+PB 最小; (1)点A 、B 在直线m 两侧: (2)点A 、B 在直线同侧: 2、在直线m 、n 上分别找两点P、Q,使PA+P Q+QB 最小。 (1)两个点都在直线外侧: (2)一个点在内侧,一个点在外侧: (3)两个点都在内侧: m m B m A B m n m n n m n n n m
(4)、台球两次碰壁模型 变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短. 变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA +PQ+Q A周长最短. 二)、一个动点,一个定点: (一)动点在直线上运动: 点B在直线n上运动,在直线m 上找一点P,使PA +PB 最小(在图中画出点P和点B ) 1、两点在直线两侧: 2、两点在直线同侧: (二)动点在圆上运动 点B 在⊙O 上运动,在直线m 上找一点P,使PA+P B最小(在图中画出点P 和点B ) 1、点与圆在直线两侧: m n m n m n m m
2、点与圆在直线同侧: 三)、已知A 、B 是两个定点,P 、Q 是直线m上的两个动点,P 在Q 的左侧,且PQ间长度恒定,在直线m上要求P 、Q 两点,使得PA+P Q+QB 的值最小。(原理用平移知识解) (1)点A 、B 在直线m两侧: 作法:过A 点作AC ∥m,且AC长等于PQ长,连接BC ,交直线m 于Q,Q 向左平移PQ 长,即为P点,此时P 、Q 即为所求的点。 (2)点A 、B 在直线m同侧: 基础题 1.如图1,∠AO B=45°,P 是∠AO B内一点,PO =10,Q、R 分别是OA 、OB 上的动点,求△PQR 周长的最小值为 . 2、如图2,在锐角三角形ABC 中,AB=4 ,∠BAC=45°,∠B AC的平分线交B C于点D, M,N分别是AD 和AB上的动点,则BM+MN的最小值为 . m O A P m O A B m A B E Q P m A B Q m A Q m A C Q P
几何中线段的最值问题 Document number:PBGCG-0857-BTDO-0089-PTT1998
D C B A A B C D A B C D 几何中线段的最值问题 一、 一条线段的最值问题一 (1)借助旋转求最值 2013通州一模 24.已知:2AD =,4BD =,以AB 为一边作等边三角形ABC .使C 、D 两点落在直线AB 的两侧. (1)如图,当∠ADB=60°时,求AB 及CD 的长; (2)当∠ADB 变化,且其它条件不变时,求CD 的 最大值,及相应∠ADB 的大小. 2011丰台一模 25.已知:在△ABC 中,BC=a ,AC=b ,以AB 为边作等边三角形ABD. 探究下列问题: (1)如图1,当点D 与点C 位于直线AB 的两侧时,a=b=3,且∠ACB=60°,则CD= ; (2)如图2,当点D 与点C 位于直线AB 的同侧时,a=b=6,且∠ACB=90°,则CD= ; (3)如图3,当∠ACB 变化,且点D 与点C 位于直线AB 的两侧时,求 CD 的最大值及相应的∠ACB 的度数. A D B C
图1 图2 图3 (2)借助直角三角形性质求最值 (1)勾股定理 (2)直角三角形斜边中线等于斜边一半 (3)直角三角形斜边的两条重要的线段,一是斜边上的高,另一个是斜边上的中线,直角三角形斜边上的高是直角顶点到斜边上所有点之中距离最短的,其长 度可以用两直角边乘积除以斜边求得. 【例1】如图,在ΔABC中,∠C=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点的最大距离是 【例2】如图,△ABC 是边长为定值m的正三角形,C点与原点重合,点B在第一象限点,点A 在x轴上。 ②求出AC边上的高线BD的长度; ③当点C在y轴的正半轴滑动时,试求出点O到CA距离的最大值; ④已知点P是△ABC内切圆的圆心,请求出OP的最大值。 2011海淀一模
求线段和(差)的最值问题 【知识依据】:1.线段公理——两点之间,线段最短;2.对称的性质——①关于一条直线对称的两个图形全等;②对称轴是两个对称图形对应点连线的垂直平分线;3.三角形两边之和大于第三边;4.三角形两边之差小于第三边。5、垂直线段最短 一、已知两个定点: 1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧: (2)点A 、B 在直线同侧: A 、A ’ 是关于直线m 的对称点。 2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。 (1)两个点都在直线外侧: m m A B m A B m n m n
(2)一个点在内侧,一个点在外侧: (3)两个点都在内侧: (4)、台球两次碰壁模型 变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短. 变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短. n m A n n n m
二、一个动点,一个定点: (一)动点在直线上运动: 点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧: 2、两点在直线同侧: (二)动点在圆上运动 点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧: 2、点与圆在直线同侧: m n m n m n m m m m m
初中几何中线段和(差)的最值练习题 1、如图,在锐角三角形ABC中,AB=42,∠BAC=45°,∠BAC的平分线交BC于点D,M、N 分别是AD和AB上的动点,则BM+MN的最小值为 _______________ 1题2题3题 2、如图所示,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点.若AE=2,EM+CM的最小值为______________. . 3、如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=4,AB=5,BC=6,点P是AB 上一个动点,当PC+PD的和最小时,PB的长为__________. 4、已知:等腰梯形ABCD中,AB=AD=CD=1,∠ABC=60°,P是上底,下底中点EF直线上的一点,则PA+PB的最小值为_______________ . 图6 图7 图9 图8 6、如图6菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为_____________
. 7、如图7,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是 --------------- 8、如图8,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为 ________cm 9、如图9,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为_____________. 10、如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.则PB+PE的最小值是 _________. 11.如图2,∠AOB=45°,P是∠AOB内一定点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值.(要求画出示意图,写出解题过程 10题11题12题13题 12、如图所示,已知正方形ABCD的边长为8,点M在DC上,且DM=2,N是AC上的一个动点,则DN+MN的最小值为_____________. 13、如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE 上的动点,则DQ+PQ的最小值为_____________. 14、如图,在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为_____ cm.(结果不取近似值). 14题 15、已知:⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则PA+PC的最小值是 ______________. 16、如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,P