密码学中的可证明安全性 杨波
- 格式:pdf
- 大小:1.57 MB
- 文档页数:118

cca安全证明方法CCA安全证明方法随着互联网的发展,网络安全问题越来越受到人们的关注。
在这个信息化时代,保护个人隐私和企业机密已经成为了一项重要的任务。
而在网络安全领域,CCA安全证明方法是一种非常有效的保护手段。
一、什么是CCA安全证明方法CCA安全证明方法是一种密码学中的概念,全称为“Chosen Ciphertext Attack Security”。
它是一种用于衡量加密算法安全性的标准,也是一种用于评估加密算法强度的方法。
简单来说,CCA安全证明方法是指在攻击者可以选择密文的情况下,加密算法仍然能够保证安全。
二、CCA安全证明方法的分类根据加密算法的不同,CCA安全证明方法可以分为对称加密算法和非对称加密算法两种。
1. 对称加密算法对称加密算法是指加密和解密使用同一个密钥的加密算法。
在对称加密算法中,CCA安全证明方法主要有两种:IND-CCA1和IND-CCA2。
IND-CCA1是指在攻击者可以选择密文的情况下,加密算法仍然能够保证安全,但是攻击者不能够获得解密后的明文。
IND-CCA2是指在攻击者可以选择密文的情况下,加密算法仍然能够保证安全,并且攻击者可以获得解密后的明文。
2. 非对称加密算法非对称加密算法是指加密和解密使用不同密钥的加密算法。
在非对称加密算法中,CCA安全证明方法主要有两种:CCA1和CCA2。
CCA1是指在攻击者可以选择密文的情况下,加密算法仍然能够保证安全,但是攻击者不能够获得解密后的明文。
CCA2是指在攻击者可以选择密文的情况下,加密算法仍然能够保证安全,并且攻击者可以获得解密后的明文。
三、CCA安全证明方法的应用CCA安全证明方法在实际应用中非常广泛。
在电子商务、在线支付、电子邮件等领域,都需要使用加密算法来保护数据的安全性。
而CCA 安全证明方法可以帮助我们评估加密算法的安全性,从而选择更加安全的加密算法来保护数据。
此外,CCA安全证明方法还可以用于评估数字签名算法的安全性。





密码学笔记(5)——Rabin密码体制和语义安全性⼀、Rabin密码体制 Rabin密码体制是RSA密码体制的⼀种,假定模数n=pq不能被分解,该类体制对于选择明⽂攻击是计算安全的。
因此,Rabin密码体制提供了⼀个可证明安全的密码体制的例⼦:假定分解整数问题是整数上不可⾏的,那么Rabin密码体制是安全的。
Thm1 (Rabin密码体制)设n=pq,其中p和q是素数,且p,q \equiv 3 (mod \, 4),设P=C=Z^{\star}_{n},且定义\kappa =\{(n,p,q)\}对K=(n,p,q),定义e_{K}(x)=x^{2} (mod \, n)和d_{K}=\sqrt{y} (mod \, n)n为公钥,p和q为私钥。
注:条件p,q \equiv 3 (mod \, 4)可以省去,条件P=C=Z^n_{\star}也可以弱化为P=C=Z^n,只是在使⽤更多的限制性描述的时候,简化了许多⽅⾯的计算和密码体制分析。
注意看到这个函数y=x^{2}对于加密来说不是⼀个单射,所以解密不能以⼀种明显的⽅式完成,特别的,对于y \equiv x^{2} (mod \, n),对于某⼀个x \in Z^{\star}_{n},存在y模n的是个解,除⾮有其他的冗余信息,否则⽆法确认是那⼀个值。
从Bob的观点来看解密问题,它有⼀个密⽂y,要想得到x使得x^2 \equiv y(mod \, n)这是⼀个关于Z_{n}中未知元x的⼆次⽅程,解密需要求出模n的平⽅根,等价于求解以下两个同余⽅程。
z^{2} \equiv y (mod \, p)z^{2} \equiv y (mod \, q)虽然我们可以利⽤Euler准则来判断y是否为⼀个模p或模q的⼆次剩余。
事实上,如果加密正确的执⾏,y是⼀个模p和模q的⼆次剩余,遗憾的是它并不能帮助我们找到y。
当p \equiv 3(mod \, 4)时,有⼀个简单公式来计算模p的⼆次剩余的平⽅根,假定y是⼀个模p的⼆次剩余,且y \equiv 3 (mod \, 4)那么有\begin{align} (\pm y^{\frac {p+1}{4}})^{2} \equiv & y^{\frac{p+1}{2}} (mod \, p) \\ \equiv & y^{\frac{p-1}{2}}y (mod \, p) \\ \equiv & y(mod \, p) \\ \end{align}这⾥⼜⼀次使⽤了Euler准则,即当y是⼀个模p的⼆次剩余时,有y^{\frac{p-1}{2}} \equiv 1 (mod \, p),因此,y模p的两个平⽅根为\pm y^{\frac{p+1}{4}} (mod \, p),同样的讨论可以知道,y模q的两个平⽅根为\pm y^{\frac{p+1}{4}} (mod \, q),再利⽤中国剩余定理可以得到y模n的四个平⽅根。

混合离散对数及安全认证摘要:近二十年来,电子认证成为一个重要的研究领域。
其第一个应用就是对数字文档进行数字签名,其后Chaum希望利用银行认证和用户的匿名性这一性质产生电子货币,于是他提出盲签名的概念。
对于所有的这些问题以及其他的在线认证,零知识证明理论成为一个非常强有力的工具。
虽然其具有很高的安全性,却导致高负荷运算。
最近发现信息不可分辨性是一个可以兼顾安全和效率的性质。
本文研究混合系数的离散对数问题,也即信息不可识别性。
我们提供一种新的认证,这种认证比因式分解有更好的安全性,而且从证明者角度看来有更高的效率。
我们也降低了对Schnorr方案变形的实际安全参数的Girault的证明的花销。
最后,基于信息不可识别性,我们得到一个安全性与因式分解相同的盲签名。
1.概述在密码学中,可证明为安全的方案是一直以来都在追求的一个重要目标。
然而,效率一直就是一个难以实现的属性。
即使在现在对于认证已经进行了广泛的研究,还是很少有方案能兼顾效率和安全性。
其原因就是零知识协议的广泛应用。
身份识别:关于识别方案的第一篇理论性的论文就是关于零知识的,零知识理论使得不用泄漏关于消息的任何信息,就可以证明自己知道这个消息。
然而这样一种能够抵抗主动攻击的属性,通常需要许多次迭代来得到较高的安全性,从而使得协议或者在计算方面,或者在通信量方面或者在两个方面效率都十分低下。
最近,poupard和stern提出了一个比较高效的方案,其安全性等价于离散对数问题。
然而,其约减的代价太高,使得其不适用于现实中的问题。
几年以前,fiege和shamir就定义了比零知识更弱的属性,即“信息隐藏”和“信息不可分辨”属性,它们对于安全的识别协议来说已经够用了。
说它们比零知识更弱是指它们可能会泄漏秘密消息的某些信息,但是还不足以找到消息。
具体一点来说,对于“信息隐藏”属性,如果一个攻击者能够通过一个一次主动攻击发现秘密消息,她不是通过与证明者的交互来发现它的。
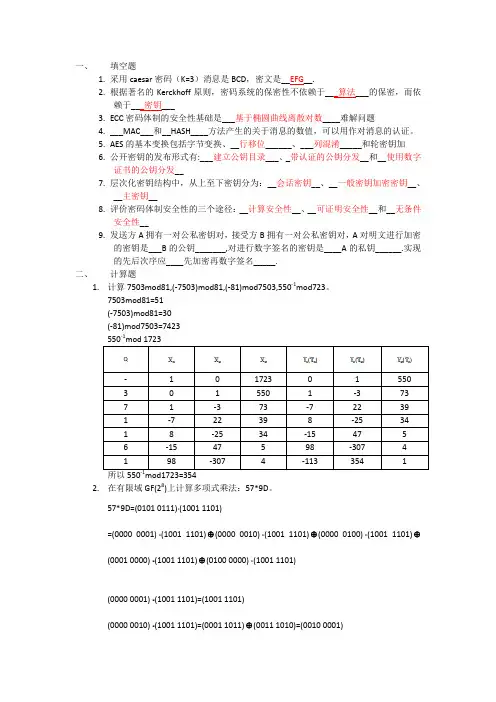
一、填空题1.采用caesar密码(K=3)消息是BCD,密文是__EFG__.2.根据著名的Kerckhoff原则,密码系统的保密性不依赖于___算法___的保密,而依赖于___密钥___3.ECC密码体制的安全性基础是___基于椭圆曲线离散对数____难解问题4.___MAC___和__HASH____方法产生的关于消息的数值,可以用作对消息的认证。
5.AES的基本变换包括字节变换、__行移位______、___列混淆_____和轮密钥加6.公开密钥的发布形式有:___建立公钥目录___、_带认证的公钥分发__和__使用数字证书的公钥分发__7.层次化密钥结构中,从上至下密钥分为:__会话密钥__、__一般密钥加密密钥__、__主密钥__8.评价密码体制安全性的三个途径:__计算安全性__、__可证明安全性__和__无条件安全性__9.发送方A拥有一对公私密钥对,接受方B拥有一对公私密钥对,A对明文进行加密的密钥是___B的公钥_______,对进行数字签名的密钥是____A的私钥______.实现的先后次序应____先加密再数字签名_____.二、计算题1.计算7503mod81,(-7503)mod81,(-81)mod7503,550-1mod723。
7503mod81=51(-7503)mod81=30(-81)mod7503=7423-1() ()()所以550mod1723=3542.在有限域GF(28)上计算多项式乘法:57*9D。
57*9D=(0101 0111)(1001 1101)=(0000 0001)(1001 1101)⊕(0000 0010)(1001 1101)⊕(0000 0100)(1001 1101)⊕(0001 0000)(1001 1101)⊕(0100 0000)(1001 1101)(0000 0001)(1001 1101)=(1001 1101)(0000 0010)(1001 1101)=(0001 1011)⊕(0011 1010)=(0010 0001)(0000 0100)(1001 1101)=(0000 0010)(0010 0001)=(0100 0010)(0001 0000)(1001 1101)=(0000 1000)[(0000 0010)(1001 1101)]=(0000 1000)(0010 0001)=(0000 0100)(0100 0010)=(0000 0010)(1000 0100)=(0001 1011)⊕(0000 1000)=(0001 0011)(0100 0000)(1001 1101)=(0010 0000)[(0000 0010)(1001 1101)]=(0010 0000)(0010 0001)=(0001 0000)(0100 0010)=(0000 1000)(1000 0100)=(0000 0100)[(0001 1011)(0000 1000)]=(0000 0100)(0001 0011)=(0000 0010)(0010 0110)=(0100 1100)所以:(0101 0111)(1001 1101)= (1001 1101)⊕(0010 0001)⊕(0100 0010)⊕(0001 0011)⊕(0100 1100)=(1010 0001)=A1三、简答题1.简述密码算法中对称、非对称算法各自的优缺点,及分析如何将两者进行结合应用。

第四节Shannon理论简介密码体制安全性标准计算安全性(computational security) 可证明安全性(provable security)无条件安全性(unconditional security)计算安全性这种度量涉及到攻击密码体制所作的计算上的努力。
如果使用最好的算法攻破一个密码体制需要至少N次操作,这里的N是一个特定的非常大的数字,我们可以定义这个密码体制是计算安全的。
可证明安全性另外一种途径是将密码体制的安全性归结为某个经过深入研究的数学难题。
例如,可以证明这样一类命题:如果给定的整数是不可分解的,那么给定的密码体制是不可破解的。
我们称这种类型的密码体制是可证明安全的。
注: 这种途径只是说明了安全性和另一个问题是相关的,并没有完全证明是安全的。
无条件安全性这种度量考虑的是对攻击者的计算量没有限制的时候的安全性。
即使提供了无穷的计算资源,也是无法被攻破的,我们定义这种密码体制是无条件安全的。
问题:计算安全性、可证明安全性、无条件安全性中哪种安全标准更实用?在上面三种安全标准的判定中,只有无条件安全性和信息论有关,即通过信息论来证明传递过程中无信息泄露。
下面来建立密码学中的信息论模型。
密码学中的信息论模型密码系统的保密性能及破译一个密码系统都和信息论密切相关。
我们知道,信息的传输是由通信系统完成的,而信息的保密则是由密码系统来完成。
在通信过程中发送方发出的信息在信道中进行传输时往往受到各种干扰,使m出错而变成m′,一般m′≠m。
合法接收者要从m′恢复m,必须识别m′中哪些信息是出错的。
为此他要求发送方对m进行适当编码,即按一定的规则增加部分码字,使合法接收者通过译码器把m′中的错误纠正过来。
对消息m进行加密的作用类似于对m进行干扰,密文c相当于被干扰的信息m′,破译者相当于在有干扰的信道下的接收者, 他要设法去掉这种“干扰”恢复原明文。
密码系统图示信源M加密器解密器信宿M信道m c c m密钥k破译者c这样便出现了如下问题: 密码设计者在设计密码体制时, 要尽可能地使破译者从密文c中少获得原明文信息, 而破译者则要从密文c中尽可能多地获得原明文信息。

可证明安全k—out—of—n不经意传输方案的安全分析与改进作者:李璐瑶戴明青龙来源:《计算机应用》2014年第05期摘要:不经意传输是密码学研究的一个重要内容。
对一种可证明安全的k-out-of-n不经意传输方案安全性进行了分析。
该方案的构造方法很新颖,具有很高的计算效率和传输效率。
但是分析发现其存在一个明显漏洞,可以使得接收者能够获得发送者发送的全部信息,从而违背了不经意传输的安全性要求。
详细分析后,通过引入一个随机数对该方案进行了改进,改进后的方案消除了原方案存在的漏洞,并且传输开销和计算开销与原方案相同,方案安全性同样是建立在判断性DiffieHellman (DDH)问题为困难问题的假设之上。
关键词:不经意传输;可证明安全;密码分析;判断性DiffieHellman假设;安全计算中图分类号:TP319文献标志码:A0引言不经意传输(Oblivious Transfer, OT)是密码学研究的一个重要领域,是其他很多密码协议设计的基础。
不经意传输在实践中具有广泛应用,包括网上商品交易、合同签名、隐私信息恢复、不经意多项式估值、隐私保留的审计等[1-4]。
不经意传输这一术语首次由Rabin提出[5]。
文献[5]提出的OT协议是一种双方参与协议,协议实现的是发送者发送一个bit消息给接收者,接收者接收该消息的概率为1/2。
协议要求发送者不能获得接收者是否成功接收到该消息的任何信息。
其后研究人员在文献[1]的基础上提出了很多不同类型的OT协议,包括:1)1outof2 OT (OT12)协议[6]。
该协议实现的是发送者同时发送两个消息给接收者,接收者可以随意选择得到其中一个消息,协议要求接收者不能获得另一个消息的任何信息,同时发送者不能获得接收者选择的任何信息。
2)1outofn OT (OT1n)协议[7-8]。
该协议是OT12的简单推广,实现的是发送者同时发送n个消息给接收者,接收者随意选择得到其中一个消息,协议要求接收者不能获得其余消息的任何信息,同时发送者不能获得接收者选择的任何信息。

安全多方计算技术在密码学中的应用密码学作为一门研究信息安全的学科,一直以来都备受关注。
随着信息技术的不断发展,传统的密码学方法逐渐暴露出一些安全性的问题。
为了应对这些挑战,安全多方计算技术进入了密码学领域,并取得了显著的成果。
本文将从安全多方计算技术的基本原理、密码学中的应用以及未来的发展趋势等方面进行探讨。
一、安全多方计算技术的基本原理安全多方计算技术是指在多方参与计算的情况下,确保计算结果的安全性和隐私性的一种方法。
它能够在不暴露各方私密输入的情况下,实现计算结果的正确性。
其基本原理包括安全协议、秘密共享以及零知识证明等。
首先,安全协议是实现安全多方计算的基础。
各方在进行计算前,通过建立安全协议来确定计算过程和涉及到的操作。
这些安全协议可以确保计算过程的正确性和隐私性。
其次,秘密共享是安全多方计算的关键技术之一。
通过将参与计算的私密输入进行分割和分发给各方,可以确保参与方之间的私密输入不被泄露。
各方只有在进行计算时才能恢复出完整的输入信息,并参与到计算中。
最后,零知识证明可以在安全多方计算过程中证明某个事实的真实性,而无需泄露与之相关的任何私密输入。
这样可以保证计算过程的安全性和隐私性,同时提供不可抵赖性的证明。
二、安全多方计算在密码学中的应用1. 秘密共享在数字签名算法中,秘密共享技术可以用于生成签名密钥,保护私钥的安全性。
多方共享私钥后,只有在所有参与方齐心协力的情况下,才能恢复出完整的私钥,并进行签名操作。
这样一来,即便有一方的私钥被泄露,也无法独自进行签名,提高了签名算法的安全性。
2. 安全多方计算在密码协议中的应用安全多方计算技术可以用于密码协议中的安全关键操作,例如密钥交换、访问控制等。
通过多方共同参与计算,在不泄露私密输入的情况下,生成协议中所需的临时密钥或验证信息。
3. 安全多方计算在云安全中的应用云计算作为一种高效的数据存储和计算方式,对数据的安全性提出了更高的要求。
将安全多方计算技术应用于云安全中,可以实现在云环境中进行隐私保护、数据共享等操作,保障用户数据的安全。
密码主要功能:1.机密性:指保证信息不泄露给非授权的用户或实体,确保存储的信息和传输的信息仅能被授权的各方得到,而非授权用户即使得到信息也无法知晓信息内容,不能使用。
2.完整性:是指信息未经授权不能进行改变的特征,维护信息的一致性,即信息在生成、传输、存储和使用过程中不应发生人为或非人为的非授权篡改(插入、替换、删除、重排序等),如果发生,能够及时发现。
3.认证性:是指确保一个信息的来源或源本身被正确地标识,同时确保该标识的真实性,分为实体认证和消息认证。
消息认证:向接收方保证消息确实来自于它所宣称的源;实体认证:参与信息处理的实体是可信的,即每个实体的确是它所宣称的那个实体,使得任何其它实体不能假冒这个实体。
4.不可否认性:是防止发送方或接收方抵赖所传输的信息,要求无论发送方还是接收方都不能抵赖所进行的行为。
因此,当发送一个信息时,接收方能证实该信息的确是由所宣称的发送方发来的;当接收方收到一个信息时,发送方能够证实该信息的确送到了指定的接收方。
信息安全:指信息网络的硬件、软件及其系统中的数据受到保护,不受偶然的或者恶意的原因而遭到破坏、更改、泄露、否认等,系统连续可靠正常地运行,信息服务不中断。
信息安全的理论基础是密码学,根本解决,密码学理论对称密码技术——分组密码和序列密码——机密性;消息认证码——完整性,认证性;数字签名技术——完整性,认证性,不可否认性;1949年Shannon发表题为《保密系统的通信理论》1976年后,美国数据加密标准(DES)的公布使密码学的研究公开,密码学得到了迅速发展。
1976年,Diffe和Hellman发表了《密码学的新方向》,提出了一种新的密码设计思想,从而开创了公钥密码学的新纪元。
置换密码置换密码的特点是保持明文的所有字符不变,只是利用置换打乱了明文字符的位置和次序。
列置换密码和周期置换密码使用密码设备必备四要素:安全、性能、成本、方便。
密码体制的基本要求:1.密码体制既易于实现又便于使用,主要是指加密函数和解密函数都可以高效地计算。