大地电磁测深法(MT)二维倾子正演研究
- 格式:pdf
- 大小:9.58 MB
- 文档页数:9


第34卷第2期2004年2月数学的实践与认识M A TH EM A T I CS I N PRA CT I CE AND TH EO R YV o l 134 N o 12 Feb .,2004 电法勘探中的数学模型胡建德(中央民族大学信息与计算科学系,北京 100081)摘要: 文章介绍了地球物理勘探中大地电磁法(M T )在二维构造上的数学模型和正反演方法,也给出了可控源音频大地电磁测深(CSAM T )的二维正演数学模型.关键词: 大地电磁;CSAM T ;Backus 2Gilbert 线性反演收稿日期:2003204228电法勘探是综合地球物理勘探方法中的基本方法之一[1].电磁测深方法是用变频进行测深的一个电法勘探分支.利用天然电磁场(由太阳辐射的变异、大气圈下层电荷的移动、雷雨放电等产生)做场源的称为大地电磁(测深)法(M T )[1,2],使用人工电磁场做场源的称为可控源频率测深法.电磁场以电磁波的形式向地下传播时,不同的频率对应着不同的电磁波长和穿透深度,场强随深度的增加而衰减.电磁测深方法观测不同频率的电磁波在地表的响应,即电磁场的水平分量,来推导或反演地球内部的岩石电性结构,以适应矿产普查或构造研究的需要.本文给出了二维构造条件下M T 响应的数学模型和正反演方法和以线电流源为激发源时二维构造上电磁响应(CSAM T )的数学模型及正演算法.1 二维构造条件下的M T 数学模型取如图1所示的二维构造区域,设二维构造走向为X 轴向,则电阻率Θ分布只沿Y 和Z 两个方向上变化.在每一种岩层内部,电阻率是各向同性的.如果以e -i Ξt 表示电磁场随时间变化的关系,并考虑到大地电磁场主要是由电磁感应引起的,用实用单位制,则麦克斯韦图1 二维构造示意图方程可表达为×E =i ΞΛH(1.1) ×H =ΡE(1.2) H =0(1.3) E =0(1.4)式中E ,H 分别表示电磁场强度,Ρ电导率,Ξ圆频率,Λ磁导率.由于电阻率沿走向X 是稳定的,对于垂直入射的平面电磁波,有5E 5x =5H5x=0(1.5)将(115)代入(111)(112)的展开式中,可得如下两组相互独立的偏振波5E z 5y-5E y5z=iΞΛH x, 5H x5z=ΡE y, 5H x5y=-ΡE z(1.6)5H z y-5H yz=ΡE x, 5E xz=iΞΛH y, 5E xy=-iΞΛH z(1.7)(116)和(117)式分别称为TM波和T E波方式,并可化为如下的霍姆赫兹方程: T E方式: 52E x y2+52E xz2=-iΞΛΡE x(1.8)TM方式:5 5y 1Ρ5H x5y+55z1Ρ5H x5z=-iΞΛH x(1.9)适当地选取边界条件,则(118)和(119)式可表达为如下形式的泛函极值问题,即求J(V)=∫∫8a5V5y2+a5V5z2+b V2d y d z+∫#(c V2-dV)d s(1.10)最小.式中V表示E x或H y,在8上合理地作网格剖分,用有限元法可求出节点上的V值,进而计算断面上的大地电磁响应[2—4].2 M T资料的二维反演计算方法为构造反演算法,引入如下响应函数:V=1E x5E x5z U=1ΡH x5H x5z(2.1) 则(1.8)和(1.9)分别变为5V5z+V2+1E x52E x5y2+iΞΛΡ=0(2.2)5U5z+ΡU2+1H x55y1Ρ5H x5y+iΞΛ=0(2.3)设当Ρ=Ρ0时,V0和E x,0满足方程(212),U0和H x,0满足方程(213).令Ρ=Ρ0+∆Ρ, V=V0+∆V, U=U0+∆U(2.4)由于趋肤效应,场的垂直梯度一般较水平梯度大很多,因而将(212)(213)中{ }项用Ρ0对应的1E x,052E x,05y2和1H x,055y1Ρ05H x,05y近似代替,则两方程变为只对z微分的黎卡提方程:5V5z+V2+iΞΛΡ+1E x,052E x,05y2=0(2.5) 5U5z+ΡU2+iΞΛ+1H x,055y1Ρ05H x,05y=0(2.6)将(214)式代入上式并忽略∆V,∆U的二次项,则有55z∆V+2V0∆V+iΞΛ∆Ρ=0(2.7)55z∆U+2U0Ρ∆U+U20∆Ρ=0(2.8)其解为:82数 学 的 实 践 与 认 识34卷∆V (z )=1E 2x ,0(z )∫∞i ΞΛE 2x ,0(l )∆Ρ(l )d l(2.9)∆U (z )=1H2x ,0(z )∫∞1Ρ0(l )5H x ,0(l )5l2∆Ρ(l )d l (2.10)上式的积分限实际上是从地表z =0到某一深度即8的下边界Z m ax ,在此深度电磁场已近似衰减为0.令z =0则∆V (0)=1E 2x ,0(0)∫Z m ax0i ΞΛE 2x ,0(z )∆Ρ(z )d z (2.11)∆U (0)=1H2x ,0(0)∫Z m ax1Ρ0(z )5H x ,0(z )5z2∆Ρ(z )d z (2.12)地球的导电性可以有105到106级次的变化,令m (z )=-ln Ρ(z ),则∆m (z )=-∆Ρ(z ) Ρ0(z ).令G (z )=-i ΞΛE x ,0(z )E x ,0(0)2Ρ0(z )(2.13)H (z )=-1Ρ0(z )Hx ,0(0)5Hx ,0(z )5z2Ρ0(z )(2.14)则(2111)(2112)对于每个测点y 不同的观测频率f i 有∆V i (y ,0)=∫Z m axG i(y ,z )∆m (y ,z )d z(2.15)∆U i(y ,0)=∫Z m axH i(y ,z )∆m (y ,z )d z(2.16)这里得到了形式上与一维连续介质情况下相同的∆V i 或∆U i 与函数∆m 之间的线性泛函关系[5].核函数G (y ,z )或H (y ,z )是F rechet 导数,∆V 、∆U 以及G 、H 都是复数.若将(2115)(2116)分别写为∆V 或∆U 的振幅方程和相位方程,并考虑到在任何测点y 上第i 个频率的观测误差∆V i 或∆U i 已近似为深度的函数,则这些方程都可归类为如下形式的F redho l m 方程:∆V i =∫Z m axG i(z )∆m (z )d z , i =1,2,…,n (2.17)利用B acku s 2Gilbert 反演法[5—7],可对(2117)求∆m (z )的L 2范数最小解.即求在满足(2117)的约束条件下使I n =∫Z m ax∆m 2(z )d z(2.18)最小.按第一D irich let 准则知:∆m (z )=g T (z )(GG T )-1∆V(2.19)式中G 由(2117)中的G i (z )确定,g 则由下式定义g (z )=(G 1(z ),G 2(z ),…,G n (z ))T(2.20)对于每个测点,根据∆m (y ,z )修改Ρ0(y ,z ),最后求得新的二维模型Ρ(y ,z ):Ρ(y ,z )=Ρ0(y ,z )(1-∆m (y ,z ))(2.21)并以新的Ρ(y ,z )为初始模型进行迭代,直至∆V i 的均方相对误差足够小为止.对理论数据和实测资料的反演计算显示了良好的效果[8,9].922期胡建德:电法勘探中的数学模型3 CSAM T二维正演数学模型在图1所示的二维构造中,若用长导线在X轴向作激励源,并设其具有频率为Ξ的谐变电流I x=I0e-iΞt(3.1)则由麦克斯韦方程组可以导出满足电场E x的微分方程及边界条件为52E x 5y2+52E x5z2+Κ2E x=-iΞΛI0∆(y-y0)∆(z-z0)(3.2)5E x5n A O E,=05E x5n+Α1E x A B,B C=05E x5n+Α2E x ED=0式中:Κ2=Ξ2ΛΕ+iΞΛΡ, Α1=Κ0k1(Κ0r)k0(Κ0r)co sΗ, Α2=∞I0是电流源的电流强度幅值,Ε是介电常数.k0(Κ0r)和k1(Κ0r)分别是零阶和一阶修正的贝赛尔函数,Η是从线源到计算点的径向矢量r和边界外法线n之间的夹角.Κ0是空气中的波数,Κ0=ΞΛ0Ε0.与上述边值问题等价的泛函极值问题是求J(E x)=-iΞΛI0E x(0,0)+∫∫85E x5y2+5E x5z2-Κ2E2x d y d z+∫A B,B CΑ1E2x d s+∫EDΑ2E2x d s(3.3)极小.使用有限元法,可求得线源二维问题的解[11,12].对不同模型的计算结果及分析,为资料解释提供了依据[10,13].大地电磁测深法具有不需供电设备,使用的频率范围大、勘探深度大、等值范围小等优点,多用于地壳结构和区域地质构造的研究,也用于油气、水资源及工程地质勘探等方面.可探源频率测深法具有分辨力较高、各向异性影响小、测量参数多便于综合分析、工效高等优点,已广泛应用于找水、找油和矿产地质勘探.在复杂构造条件下建立电磁方法的数学模型并作正反演研究有着重要的实际意义.参考文献:[1] 日丹诺夫M C著,潘玉玲,王守坦译1电法勘探[M].中国地质大学出版社,1990.178—185.[2] 陈乐寿,王光锷1大地电磁测深法[M].北京地质出版社,19901[3] W illiam L Rodi.A T echnique fo r i m p roving the accuracy of finite elem ent so luti ons fo r m agneto telluric data[J].Geophys,J R A str Soc,1976,44:483—505.[4] 胡建德,蔡纲1用三角形二次插值有限元法计算二维大地电磁测深曲线[J].石油地球物理勘探,1984,(4):358—367.[5] O ldenburg D W,王家映1在地球物理学中的线性反演理论[J].地球科学,1984,9(3):133—147.[6] Sm ith J T,Booker J R.M agneto telluric inversi on fo r m ini m um structure[J].Geophysics,1988,53:1565—03数 学 的 实 践 与 认 识34卷1576.[7] 傅淑芳,朱仁益1地球物理反演问题[M ].地质出版社,1998.119—147.[8] 吴广耀,胡建德1大地电磁资料的二维连续模型自动反演[J ].地球科学,1990,15(增刊):23—25.[9] 吴小平,吴广耀,胡建德1二维最平模型的大地电磁快速反演[J ].地球科学,1994,19(6):821—830.[10] 石昆法1可控源音频大地电磁法理论与应用[M ].科学出版社,19991[11] 陈明生,严又生1二维水平电偶极变频测深阻抗视电阻率的有限元正演计算[J ].地球物理学报,1987,30(2):201—208.[12] 胡建德,阎述,陈明生等1线电流源声频大地电磁测深的二维正演计算及响应特点[J ].现代地质,1997,11(2):203—209.[13] 胡建德,管建和,向礼明等1M T 二维正演的混合剖分算法及其在线源CSAM T 正演计算中的应用[J ].现代地质,1996,10(1):129—135.M athematical M odels i n Electromagnetic SurveyHU J ian 2de(D ep t of M athem atics ,Ch iina U n iversity fo r N ati onalities ,Beijing 100081,Ch ina )Abstract : A b rief in troducti on is given to the 22D M T fo rw ard and inverse calcu lati on and to a 22D CSAM T model.Keywords : M T ;CSAM T ;Backu s 2Gilbert linear inversi on132期胡建德:电法勘探中的数学模型。
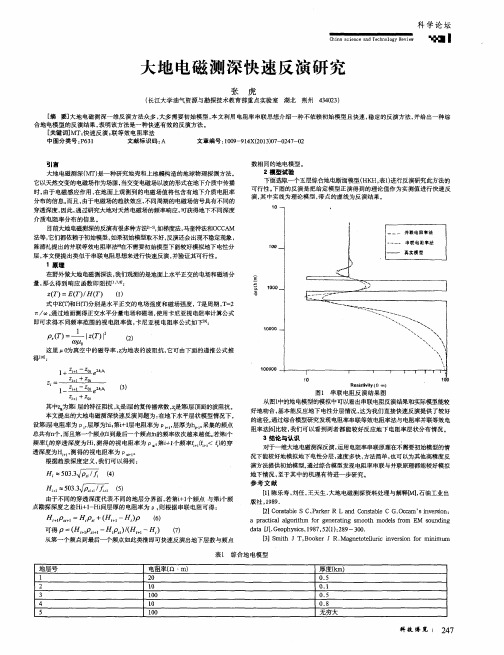



第39卷第2期注為科修Vol.39No.2 2021年4月JIANGXI SCIENCE Apr.2021 doi:10.13990/j.H e1001-3679.2021.02.022ZTEM三维正演响应特征分析王宇(东华理工大学,330013,南昌)摘要:天然源频率域航空电磁法(ZTEM)对于地下异常体的探测有着显著的优势,其正演响应特征的分析对提高勘探精度有着重要的意义。
简要地论述了ZTEM基本原理,基于交错网格有限差分法开展三维ZTEM正演模拟,首先正演模拟复杂模型的倾子响应,研究表明倾子数据对横向电性分界面反映准确;其次通过大量的模型试算,分析了影响ZTEM正演响应的主要因素。
结果显示,不同地电条件下的倾子响应幅值不同,进一步加深了对ZTEM三维正演响应特征的认识,对ZTEM的实际应用和异常解释提供了依据。
关键词:ZTEM;倾子;正演模拟;影响因素中图分类号:P631文献标识码:A文章编号:1001-3679(2021)02-318-05Anomaly Feature Analysis of3D Response ofAero-Electromagnetic Metiod of Nateral SourceWANG Y u(East China Institute of Technology,330013,Nanchang,PRC)Abstract:Z一Axis Tipper Electromaaneticc(ZTEM)has obvious advantaaet for the detection of underground abnormaO bodies,and play an importani role in improving the detection accuracy vic iis forward response analysis.The basic pOncipOe of ZTEM was baefly discussed and3D ZTEM foavard modeling was ccrWed out based on the staggered一gWd f n iie dpferencc method.Firstly,we calculai-ed the tipper wsponse of compix modei,wspectiveiy,whose resulis show thai tipper dati can accurate io the underawund hoWzontai electWcai interace;secondly,through calculate a iarae number of model,the main factors affecting the ZTEM forward response are analyzed.The results showed that the tipper response under dmerent geoelectric condition is dmerent,which further deepen the understanding of3D forward response of ZTEM,and a basis for the practicoi application and the intewwtation of anomalies of ZTEM.Key words:ZTEM;tipper;forvard modeling;influence factor0引言为了克服在复杂地形条件(尤其沙漠、沼泽等特殊地区)下音频大地电磁法难于施工的难题,b and Zang提出天然源频率域航空电磁法,称为Z轴倾子电磁法(ZTEM)⑴。
大地电磁(MT)法在深部矿产勘探中的分辨率探讨
夏时斌;闵刚;邱林;张中
【期刊名称】《工程地球物理学报》
【年(卷),期】2012(009)005
【摘要】面对固体矿资源的日益枯竭,开展第二深度(> 500m)找矿迫在眉睫,大地电磁(MT)法勘探深度大,受高阻屏蔽小,在深部找矿中具有重要的地位.本文以某矿区实际地电模型为例,利用成都理工大学开发的MTSoft2D软件对其进行正演模拟和occam反演计算,探讨大地电磁法对地电模型中异常体的分辨能力,为MT法在深部矿产勘探领域提供理论支持.
【总页数】6页(P531-536)
【作者】夏时斌;闵刚;邱林;张中
【作者单位】成都理工大学地球探测与信息技术教育部重点实验室,四川成都610059;成都理工大学地球探测与信息技术教育部重点实验室,四川成都610059;成都理工大学地球探测与信息技术教育部重点实验室,四川成都610059;成都理工大学地球探测与信息技术教育部重点实验室,四川成都610059
【正文语种】中文
【中图分类】P631.3
【相关文献】
1.综合电法在矿产勘探中对深部找矿靶区定位的研究与应用 [J], 周伟;葛海涛
2.华北地台地热勘探中利用大地电磁测深法(MT)圈定热田范围和探讨地热形成机
制 [J], 战双庆;汪启年
3.音频大地电磁测深法在老挝万象盆地钾镁盐矿产勘探中的运用效果 [J], 朱自串; 周丹; 李德文; 余润龙
4.矿产勘探中综合电法对深部找矿靶区定位影响分析 [J], 石金国
5.大地电磁测深法(MT)在无为盆地周边勘探中的应用 [J], 周月;官大维
因版权原因,仅展示原文概要,查看原文内容请购买。
正演:已知地质模型,求出其测量数据。
反演:已知测量数据,反求出地质模型。
反演方法是建立在正演计算的基础上的。
切线法是利用异常曲线上一些特征点的切线的交点坐标间的关系求解反问题的一类方法。
该方法具有简单、快速和不受正常场选择的影响等优点。
反演解释中遇到的问题:1.叠加异常的相互影响 2.场源物性参数的不均匀性问题3.测量误差与数值计算的影响4.反演的多解性问题水平层对称四级装置电阻率测深曲线的定性解释主要是确定电阻率测深曲线的类型,确定电性层分层,并建立电性层与实际地层的对应关系。
定性解释应该结合已知的地质情况进行,尽量利用已有的钻孔柱状图、电测井资料等。
定量解释就是要根据电阻率测深曲线获得一组关于水平地层厚度和电阻率的参数。
因为使用水平地层模型,一般要求满足野外测量的地形平坦,地层产状也比较平缓的条件才能得到比较准确的定量解释结果。
一维电阻率的四种方法:特征点法、直接反演法、正演拟合法、自动反演法。
解析法又称为任意点法或特征点法。
解析法是由简单条件下的规则地质体异常公式出发,分析求解出异常任意点坐标、特征点坐标以及异常值与地质体的位置、几何参数以及物性参数之间的解析表达式,再在实际异常的剖面上取出任意点或特征点的坐标或异常值,然后将它们代入解出的解析式,经过简单计算求得实际异常的反演结果。
最优化选择法就是将实测异常曲线与理论异常曲线进行对比,使理论曲线拟合实测曲线的一种异常解释方法。
这种对比拟合常采用逐渐逼近的方式。
选择法解释异常的步骤可以归纳为:1.场源初始模型的给出;2.初始模型体理论异常的计算;3.将理论异常曲线和实测异常曲线对比,视二者拟合情况决定是否修改模型体;4.若拟合得不好,修改初始模型体,然后重复123步骤,知道拟合好为止。
上述步骤的实现,是在给出场源初始模型的情况下,通过一系列的数学计算最后给出计算结果,此种计算即称为最优化选择法。
根据速度模型,沿地震波的传播路径,研究传播时间和距离关系的方法称为射线追踪法。
二维反演与一维反演有着很多的不同之处,主要表现在:(1)要拟合的数据是一条剖面上几个测点处的视电阻率的曲线(2)首先要确定模型的类型 (3)正演是用数值方法做近似计算,所需时间较长,因而数据相对参数的偏导数要用近似的解析方法或其它快速方法来求取。
也就是说实现二维反演重点要确定初始模型和对偏导数的计算。
一.初始模型的确定初始模型方法的的确定一般可分为两大类:一类是定性的方法,一类是定性的方法 ,用以确定初始模型的形态类型。
另一类是定量的方法 ,用以确定初始模型的参数值。
任一初始模型的确定,都同时兼用这两类方法,以期获得最佳的初始模型 。
定性的方法主要是通过仔细分析剖面上的实测数据,绘制各种剖面或平面剖面图来研究 地下结构的电性变化与地电层的结构,为定量解释提供分析依据 。
而定量方法,到目前为止有两种。
一种是根据理论计算结果,用函数拟合的方法来确定初始模型与视电阻率曲线特征值之间的关系式,并由此式及实测数据求出初始模型的参数。
另一种确定初始参数的方法 , 是将实测曲线进行一维形式化解释。
由于前者对于某一特定的模型,每次能给出的参数的个数是有限的,我们使用一维维博斯蒂克反演和改进的广义逆反演方法。
通过试算证明这种方法优于前者,并能给出比较接近实际情况的初始模型。
博斯蒂克反演方法的原理主要是基于大地电磁测深曲线低频渐近线的性质,通过把是电阻率随周期变化的曲线变换成真电阻率随深度变化的曲线,,利用变换曲线的倒数的即致电位置可确定分界面的深度,该方法配具有公式简单繁衍速度快的优点外,还能比较直观的揭示地下电性结构,能够为进一步的精确反演提供初始模型参数。
(1) 博斯蒂克反演方法:从水平层状介质的理论计算公式出发,可推到出当下半空间介质电阻率为无穷大和零这两种极限情况时,曲线低频渐近线分别满足的方程式:21a wuS ρ=(1),2a w u D ρ=(2),S 为下半空间上面多层介质的总纵向电导;D 为下半空间上面多层介质的总厚度。