A＊进路搜索算法的研究与实现

11网络通信技术Network Communication Technology电子技术与软件工程Electronic Technology & Software EngineeringA*（A-Star ）算法是一种静态路网中求解最短路径的直接搜索方法，因其灵活简便和对完整性及最优性的保证得以在机器人低维路径规划领域中广泛应用。

但同时也存在以下缺陷：一是在大规模环境中应用时，节点网络非常庞大，算法运行时间长；二是扩展节点时占用内存开销较大；三是计算复杂度依赖环境网格分辨率大小。

针对这些缺陷，已有很多学者提出了改进。

本文首先介绍A*算法原理并进行影响因素分析，然后从启发函数、搜索策略、数据存储与查找等方面介绍A*算法的改进方法及研究现状，进而展望了算法未来发展和面临的挑战。

1 A*算法原理A*算法是一种有序搜索算法，相比于Dijkstra 算法，加入了启发函数，使其朝着目标点有方向性的扩展节点，因此算法效率有了较大的提升。

A*算法的特点是，对于遍历的每一个节点，都采用一个评价函数f(n)来计算其通过该节点的代价，在每一次搜索时总是选择当前位置周围通行代价f(n)最小的点来扩展，如此从起始节点不断搜索直到找到目标节点，生成一条通行代价最小的路径。

关于评价函数的计算方式如下式：f(n)=g(n)+h(n) （1）其中，h(n)代表从当前点到目标点的估计代价，同时也是启发函数，g(n)计算方式为从起点到节点n 的实际行走距离。

2 算法分析由原理分析可知，影响A*算法搜索效率的主要因素是：2.1 启发函数的设置一般来说，从当前节点到目标点的启发函数一般小于实际路径代价，这样才可能得到最优解，但同时会增加扩展的节点数，增大算法时间开销。

理想情况是启发函数h(n)恰好等于实际路径代价，这样扩展节点最少，且刚好能找到最优路径。

2.2 访问open表寻找f(n)最小值的时间开销大传统的open 表可能采用Array 、List 、Queue 等结构来存储节点信息，随着搜索深度越深，要查找的节点就越多，每次扩展节点时都需要对open 表排序，查找f 最小值的节点，这会耗费部分时间，所以优化open 表的排序和查找是一个关键的改进方向。

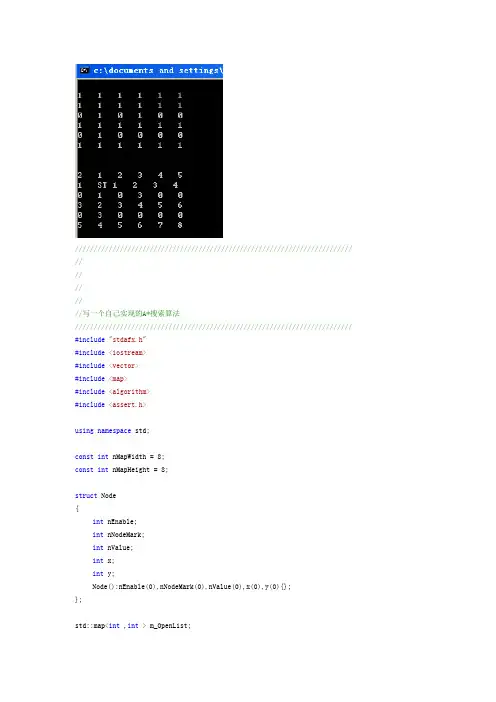
////////////////////////////////////////////////////////////////////////// //////////写一个自己实现的A*搜索算法////////////////////////////////////////////////////////////////////////// #include"stdafx.h"#include<iostream>#include<vector>#include<map>#include<algorithm>#include<assert.h>using namespace std;const int nMapWidth = 8;const int nMapHeight = 8;struct Node{int nEnable;int nNodeMark;int nValue;int x;int y;Node():nEnable(0),nNodeMark(0),nValue(0),x(0),y(0){};};std::map<int ,int > m_OpenList;std::map<int ,int > m_CloseList;std::vector<int> m_KeyList;Node m_MapNode[nMapWidth][nMapHeight];//计算openlist中靠前节点周围的节点void ComputerRound(int curx,int cury);//将一个新的节点加入到OPenList中void AddNodeToOpenList(Node* pNode,int nNum);//打印地图void Print(Node pNode[][nMapHeight]);void Print(Node pNode[][nMapHeight]){for (int n = 0; n < nMapWidth; ++n){for(int m = 0; m < nMapHeight; ++m){if (m == 0)cout<<endl;if (n == 0)cout<<pNode[n][m].nEnable/*<<"("<<" "<<pNode[n][m].nNodeMark<<")"*/<<" ";elsecout<<pNode[n][m].nEnable/*<<"("<<pNode[n][m].nNodeMark<<")"*/<<" ";}}}//将一个新的节点加入到OPenList中void AddNodeToOpenList(Node* pNode,int nNum){if(!pNode || !(pNode->nEnable))return;if (m_OpenList.empty()){m_OpenList[pNode->nNodeMark] = nNum;m_KeyList.push_back(pNode->nNodeMark);}else{std::map<int,int>::iterator itr = m_OpenList.find(pNode->nNodeMark);if (itr == m_OpenList.end()){std::map<int,int>::iterator itrQ = m_CloseList.find(pNode->nNodeMark);if (itrQ != m_CloseList.end()){if (nNum < (*itrQ).second){m_CloseList.erase(itrQ);}elsereturn;}else{m_OpenList[pNode->nNodeMark] =nNum;m_KeyList.push_back(pNode->nNodeMark);}}else{if ((*itr).second > nNum){m_OpenList[pNode->nNodeMark] =nNum;}}}}//将openlist中的一个靠前的节点展开到CloseList中void AddNodeToCloseList(Node* pNode,int nNum){if(!pNode)return;if (m_CloseList.empty()){m_CloseList[pNode->nNodeMark] = nNum;ComputerRound(pNode->x,pNode->y);}else{std::map<int,int>::iterator itrB = m_CloseList.find(pNode->nNodeMark);if(itrB == m_CloseList.end()){std::map<int,int>::iterator itrO = m_OpenList.find(pNode->nNodeMark);if (itrO != m_OpenList.end()){if ((*itrO).second < nNum){return;}else{std::vector<int>::iterator itrK =std::find(m_KeyList.begin(),m_KeyList.end(),(*itrO).first);if (itrK != m_KeyList.end())m_KeyList.erase(itrK);m_OpenList.erase(itrO);}}else{m_CloseList[pNode->nNodeMark] += nNum;ComputerRound(pNode->x,pNode->y);}}else{if (nNum < m_CloseList[pNode->nNodeMark])m_CloseList[pNode->nNodeMark] = nNum;}}}//探索是否该节点可行void TryNode(int nx,int ny,int curx, int cury){if (nx < 0 || ny < 0 || nx >= nMapWidth || ny >= nMapWidth)return;if (m_MapNode[nx][ny].nEnable == 0)return;int nNum = abs(nx - curx) + abs(ny - cury);std::map<int,int>::iterator itr = m_CloseList.find(m_MapNode[curx][cury].nNodeMark);if(itr != m_CloseList.end())nNum += (*itr).second;AddNodeToOpenList(&(m_MapNode[nx][ny]),nNum);}#define DesX 3#define DesY 4void ComputerRound(int curx,int cury){//对每一个当前节点执行以下操作TryNode(curx,cury+1,curx,cury);TryNode(curx+1,cury,curx,cury);TryNode(curx+1,cury+1,curx,cury);TryNode(curx-1,cury,curx,cury);TryNode(curx-1,cury-1,curx,cury);TryNode(curx-1,cury+1,curx,cury);TryNode(curx,cury-1,curx,cury);TryNode(curx+1,cury-1,curx,cury);}void main(){int nMark = 0;for (int n = 0; n < nMapWidth; ++n){for(int m = 0; m < nMapHeight; ++m){if (n != 2 || m == 3 || m == 1)m_MapNode[n][m].nEnable = 1;if (n == 4 && (m != 6))m_MapNode[n][m].nEnable = 0;m_MapNode[n][m].nNodeMark = ++nMark;m_MapNode[n][m].x = n;m_MapNode[n][m].y = m;}}Print(m_MapNode);AddNodeToCloseList(&(m_MapNode[1][1]),0);std::map<int,int>::iterator itr;while(!m_KeyList.empty()){itr = m_OpenList.find(*(m_KeyList.begin()));int nV = (*itr).first;int nNum =(*itr).second;std::vector<int>::iterator itrK =std::find(m_KeyList.begin(),m_KeyList.end(),(*itr).first);if (itrK != m_KeyList.end())m_KeyList.erase(itrK);itr = m_OpenList.erase(itr);AddNodeToCloseList(&(m_MapNode[(nV-1)/nMapWidth][(nV-1)%nMapWidth]),nNum);}cout<<endl;cout<<endl;std::map<int,int>::iterator itrC;for (int n = 0; n < nMapWidth; ++n){for(int m = 0; m < nMapHeight; ++m){if (m == 0)cout<<endl;if (m == 1 && n == 1){cout<<"ST"<<" ";continue;}itrC = m_CloseList.find(m_MapNode[n][m].nNodeMark);if (itrC != m_CloseList.end()){cout<<(*itrC).second<<" ";}elsecout<<"0"<<" ";}}getchar();}。

公共交通导航系统中的路径规划算法设计与实现随着城市人口的增长和交通拥堵问题的日益严重，公共交通导航系统已经成为现代城市交通管理的重要组成部分。

在实际应用中，旅客通常需要根据自己的起点和目的地，在公共交通网络中找到最优的路径，其中路径规划算法起到了至关重要的作用。

本文将介绍公共交通导航系统中的路径规划算法设计与实现，以便为旅客提供高效、准确的导航服务。

首先，路径规划算法的设计必须考虑到城市的交通网络特点和旅客的需求。

在公共交通导航系统中，交通网络一般可以表示为一个有向图，图中的每个节点表示一个交通站点，每条边表示两个站点之间的交通线路。

在路径规划过程中，算法需要综合考虑到行驶时间、车次间隔、换乘次数等因素，以及旅客的出行偏好（如少换乘、少步行等）。

因此，路径规划算法应具备高效性、准确性和可定制性。

其次，常用的路径规划算法包括Dijkstra算法、A*算法、最小换乘算法等。

Dijkstra算法是一种基于贪心策略的最短路径算法，可以用于计算公交车或地铁的最短路径。

该算法通过不断选择最短路径的节点来逐步扩展路径，直到到达目的地。

然而，Dijkstra算法的计算速度较慢，不适用于大规模的公交网络。

A*算法是一种启发式搜索算法，可以更加高效地搜索最优路径。

该算法利用启发函数来估计节点到目标节点的距离，从而在搜索过程中剪枝，减少搜索范围。

最小换乘算法是针对旅客在路径规划中通常希望尽量少换乘的需求而设计的。

该算法在搜索过程中，通过记录已经换乘的次数，以及一些换乘规则，来选择最少换乘的路径。

在路径规划算法的实现过程中，需要考虑到数据结构的选择和算法的优化。

首先，可以使用邻接表或邻接矩阵来表示公交网络的数据结构。

邻接表适用于稀疏图，能节省内存空间；邻接矩阵适用于稠密图，能提高查询效率。

其次，可以通过使用堆或优先队列等数据结构来优化最短路径算法的性能。

堆可以在O(logn)的时间内找到最小元素，适用于Dijkstra算法；优先队列可以根据节点的优先级进行排序，适用于A*算法。

无人驾驶车辆的路径规划算法研究与实现随着科技的不断发展，无人驾驶车辆正逐渐成为现实。

无人驾驶车辆的核心技术之一就是路径规划算法，它决定了车辆在复杂的路况中如何选择最佳路径，从而安全地到达目的地。

本文将对无人驾驶车辆的路径规划算法进行研究与实现。

一、无人驾驶车辆路径规划的重要性无人驾驶车辆处于复杂的交通环境中，能够精准地规划路径对确保车辆的安全和高效性至关重要。

路径规划算法需要综合考虑多种因素，如车辆当前位置、车速、交通流量、道路条件、行车规则等。

同时，路径规划算法还需要适应不同的路况，并能在实时性的要求下做出决策。

二、常见的路径规划算法1. A*算法A*算法是一种启发式搜索算法，通过计算起点到目标点的代价函数来搜索最优路径。

该算法考虑了启发式估计函数和已走过的实际代价，并通过不断更新优先级队列来找到最短路径。

A*算法在路径规划中被广泛使用，其算法简单且效果较好。

2. Dijkstra算法Dijkstra算法是一种无权图的最短路径算法，通过计算起点到当前节点的最短距离来更新其他节点的最短距离。

该算法可以应用于没有考虑交通流量和限制条件的简单路径规划问题。

3. RRT算法Rapidly-exploring Random Trees (RRT)算法是一种用于在高维空间中搜索快速路径的算法。

该算法以启发式的方式随机生成路线并逐渐扩展搜索空间，直到找到目标点为止。

RRT算法具有很高的搜索效率，适用于无人驾驶车辆的动态路径规划。

三、无人驾驶车辆路径规划算法的实现无人驾驶车辆的路径规划算法实现包括以下几个步骤：1. 车辆状态获取无人驾驶车辆需要实时获取车辆的状态信息，如当前位置、速度、方向等。

这些信息可以通过各类传感器获得。

获取到的状态信息将作为路径规划算法的输入。

2. 地图数据准备无人驾驶车辆需要准备基础地图数据，包括道路信息、交通标志、交通信号灯等。

地图数据可通过激光雷达、摄像头等传感器获取，并通过地图匹配算法进行处理和绘制。

智能导航系统中的路径规划算法与效率评估研究智能导航系统在现代交通生活中扮演着重要角色。

而路径规划算法作为智能导航系统的核心技术之一，主要负责寻找最优路径来引导用户到达目的地。

在这篇文章中，我们将探讨智能导航系统中的路径规划算法以及对其效率的评估研究。

一、路径规划算法概述路径规划算法是指在多个节点之间选择最佳路径的计算方法。

目前，常见的路径规划算法包括Dijkstra算法、A*算法、快速搜素算法等。

这些算法都是根据道路网络的拓扑结构以及节点间的距离、权值等因素进行路径选择。

1. Dijkstra算法Dijkstra算法是一种基于图的路径规划算法。

它通过在图中的节点之间进行迭代搜索，从起点开始，逐步扩展搜索范围，直到找到终点或搜索范围耗尽。

Dijkstra算法基于节点间的距离进行路径选择，通常适用于单源最短路径问题。

2. A*算法A*算法是一种启发式搜索算法，常用于路径规划问题。

它综合考虑了节点之间的距离以及估计到达目标节点的代价，通过启发函数对节点进行评估和排序。

A*算法具有较高的搜索效率和较好的路径质量。

3. 快速搜索算法快速搜索算法是一种基于经验法则的路径规划算法。

它采用启发式搜索策略，通过事先设置的启发式规则来指导路径选择。

快速搜索算法通常能够在较短的时间内找到满足搜索要求的路径。

二、路径规划算法的效率评估路径规划算法的效率评估是对算法性能的度量和比较。

其中，常见的效率评估指标包括算法执行时间、路径长度、搜索节点数等。

研究者通过实验和数据分析来评估不同算法在不同情况下的性能特点。

1. 算法执行时间算法执行时间是评估算法效率的一项重要指标。

通常，研究者会在相同的硬件环境下运行不同的路径规划算法，并统计其执行时间。

通过比较不同算法的执行时间，可以评估它们在搜索性能方面的差异。

2. 路径长度路径长度是指从起点到达目标节点所经过的节点数或距离。

通常，较短的路径长度代表更高的效率和更优的路径选择。

研究者可以通过实际案例，在相同起终点条件下，比较不同算法生成的路径长度，从而评估它们的效率。

计算机联锁软件设计及进路搜索算法的研究与应用徐鑫;陈光武【摘要】Based on the function which interlocking software needed to implement,this paper made module partition on interlocking program; adopted modularized design method to write interlocking software, engaged in analysing and comparing of different algorithm of route searching in route searching modules in particular, extracted a high efficiency searching algorithm, combined data structures of railway yard with algorithm, and applied this algorithm to design and development of interlocking softwar. In the end, this paper analysed security of interlocking software briefly.%本文根据联锁软件所要实现的功能,对联锁程序进行模块划分,采用模块化的设计方法编写联锁软件,并对进路搜索模块中不同算法进行分析比较,提炼出一种高效率的搜索算法,结合站场型数据结构将此算法应用到联锁软件的设计开发中.最后对联锁软件的安全性进行简要分析.【期刊名称】《铁路计算机应用》【年(卷),期】2011(020)001【总页数】4页(P49-52)【关键词】计算机联琐;模块化;进路搜索;数据结构【作者】徐鑫;陈光武【作者单位】兰州交通大学,光电技术与智能控制教育部重点实验室,兰州,730070;兰州交通大学,光电技术与智能控制教育部重点实验室,兰州,730070【正文语种】中文【中图分类】U284.3铁路车站联锁系统是铁路运输领域中的控制系统，以技术手段识别、减弱甚至消除车站内危及行车安全的不确定因素。

A算法在停车场寻车路径规划中的应用研究作者：吕博都美晔李璐君来源：《科学与信息化》2019年第11期摘要由于A*算法在进行启发式搜索时具有较高的算法效率，并且可以基于评估函数找到最优路径，本文针对在大型停车场中寻车困难的问题提出采用A*算法进行路线规划。

文章阐述了A*算法的原理及实现过程，并对停车场进行建模，通过仿真实验验证了算法应用于停车场寻车路径规划的可行性。

关键词 A*算法；路径规划；停车场引言随着经济的发展，中国汽车保有量及市场规模逐年增长。

为满足人们停车的需求，住宅区及大型商场的停车场面积增大、层数增加，提供大量车位的同时对用户寻车也造成了一定困难。

仅靠车位编号寻找车辆的方法效率较低，因此建立停车场寻车系统帮助用户寻找车辆位置，规划寻车路线十分重要。

最短路径算法是计算机科学、人工智能科学等研究的热点问题[1]。

两点间的所有路径中，一定有一条最佳的路径使时间和效率均为最优，这时就需要使用限制搜索区域内的最短路径算法[2]。

其中，A*算法由于其性能和准确性被广泛使用[3]。

1 A*算法原理与实现A*算法的原理是借助于开启列表（OpenList）和关闭列表（ClosedList）两个列表，通过估值函数来引导整个路径搜索的过程，快速寻找到一条最短的路径。

其中，开启列表和关闭列表是 A*算法在寻路搜索的过程中必须维护的两张表。

开启列表中存放着即将被访问但未被访问的节点，同时这些节点所对应着的估值值也被存放在该表中；而关闭列表中则存放着已经访问完成的节点。

估值函数用来引导寻路，其数学表达式为：F（n）=G（n） +H（n）（1）其中F（n）为估值函数；G（n）是已经计算出的从起始点到当前路点的实际路径长度；H（n）是估测从当前点到目标点路径长度的曼哈顿距离。

使用标准 A*算法进行寻找路径的流程见图1。

A*算法需要设置起始节点S和目标节点E，并建立两个空的List：OpenList 和ClosedList。

改进A^＊算法及其在GIS路径搜索中的应用
李志建;郑新奇;王淑晴;杨鑫
【期刊名称】《系统仿真学报》
【年(卷),期】2009()10
【摘要】路径选择在实际运用中主要追求的是最优而不是最短。

为此通常采用精
度换效率的策略。

这种策略虽然在一定程度上达到了路径搜索的任务要求,但如果
能在精度和效率之间综合取值的话,效果往往会更令人满意。

采用了一种改进的A*算法来实现这一目的。

主要是通过变权值的方式来控制算法的搜索精度和搜索效率。

实验证明,改进的A*算法可以实现最优路径的选择,且效率有很大的提高。

【总页数】4页(P3116-3119)
【作者】李志建;郑新奇;王淑晴;杨鑫
【作者单位】中国地质大学(北京)土地科学技术学院
【正文语种】中文
【中图分类】TP320.7
【相关文献】
1.改进Dijkstra算法在GIS导航应用中最短路径搜索研究
2.一种基于GIS最短路
径搜索的A*改进算法3.基于扩散方程的改进型路径搜索算法在机器人足球中的应
用4.一种新的最短路径搜索算法在GIS中的应用5.改进Dijkstra算法在停车场车
辆泊车路径搜索中的应用
因版权原因，仅展示原文概要，查看原文内容请购买。

A*寻路算法（For初学者）This article has been translated into Spanish and French. Other translations are welcome.While it is easy once you get the hang of it, the A* (pronounced A-star) algorithm can be complicated for beginners. There are plenty of articles on the web that explain A*, but most are written for people who understand the basics already. This one is for the true beginner.虽然掌握了A*（读作A-star）算法就认为它很容易，对于初学者来说，它却是复杂的。

网上有很多解释A*的文章，不过大多数是写给理解了基础知识的人。

本文是给初学者的。

This article does not try to be the definitive work on the subject. Instead it describes the fundamentals and prepares you to go out and read all of those other materials and understand what they are talking about. Links to some of the best are provided at the end of this article, under Further Reading.本文并不想成为关于这个主题的权威论文。

实际上它讨论了基础知识并为你做一些准备，以便进一步阅读其他资料和理解它们讨论的内容。

简述a算法的原理实现过程
A算法的原理实现过程如下：
1. 初始化：将起始节点的代价设置为0，将其他节点的代价设置为无穷大。

将起始节点标记为当前节点。

2. 计算启发函数值：对于当前节点，计算该节点到目标节点的预估代价，并将预估代价与起始节点到当前节点的实际代价相加，得到当前节点的总代价。

3. 扩展节点：对于当前节点，生成其相邻的未被访问的节点，并计算这些节点的总代价。

4. 选择下一个节点：从上一步生成的节点中，选择具有最小总代价的节点作为下一个要访问的节点。

5. 检查终止条件：如果下一个要访问的节点是目标节点，则算法结束。

6. 更新节点代价：将选定的下一个节点标记为当前节点，并更新其他节点的代价。

对于当前节点的相邻节点，如果从起始节点经过当前节点到达相邻节点的总代价比该节点的当前代价小，就更新相邻节点的代价为新的总代价，并将当前节点设置为相邻节点的父节点。

7. 重复步骤2到步骤6，直到找到目标节点或者无法再扩展新的节点。

8. 如果找到目标节点，则通过从目标节点追溯回起始节点的父节点，可以得到从起始节点到目标节点的最优路径。

如果无法找到目标节点，则算法失败。

总结起来，A算法的原理实现过程是通过不断地选择总代价最小的节点，然后扩展选定节点的相邻节点，更新节点的代价和父节点，直到找到目标节点或无法再扩展新的节点为止。

这种策略使得A算法在搜索过程中优先考虑实际代价较低且预估代价较低的路径，从而找到最优路径。

t(智乐圆入门1)A*(A星)算法(一)记得好象刚知道游戏开发这一行的时候老师就提到过A星算法,当时自己基础还不行,也就没有去看这方面的资料,前几天找了一些资料,研究了一天,觉的现在网上介绍A星算法的资料都讲的不够详细(因为我下的那个资料基本算是最详细的了- -但是都有一些很重要的部分没有说清楚....),所以我自己重新写一篇讲解A星算法的资料,还是借用其他资料的一些资源.不过转载太多了,只有谢谢原作者了:)我们将以下图作为地图来进行讲解,图中对每一个方格都进行了编号,其中绿色的方格代表起点,红色的方格代表终点,蓝色的方格代表障碍,我们将用A星算法来寻找一条从起点到终点最优路径,为了方便讲解,本地图规定只能走上下左右4个方向,当你理解了A星算法,8个方向也自然明白在地图中,每一个方格最基本也要具有两个属性值,一个是方格是通畅的还是障碍,另一个就是指向他父亲方格的指针(相当于双向链表结构中的父结点指针),我们假设方格值为0时为通畅,值为1时为障碍A星算法中,有2个相当重要的元素,第一个就是指向父亲结点的指针,第二个就是一个OPEN表,第三个就是CLOSE表,这两张表的具体作用我们在后面边用边介绍,第四个就是每个结点的F值(F值相当于图结构中的权值)而F = H + G;其中H值为从网格上当前方格移动到终点的预估移动耗费。

这经常被称为启发式的，可能会让你有点迷惑。

这样叫的原因是因为它只是个猜测。

我们没办法事先知道路径的长度，因为路上可能存在各种障碍(墙，水，等等)。

虽然本文只提供了一种计算H的方法，但是你可以在网上找到很多其他的方法,我们定义H 值为终点所在行减去当前格所在行的绝对值与终点所在列减去当前格所在列的绝对值之和,而G值为从当前格的父亲格移动到当前格的预估移动耗费,在这里我们设定一个基数10,每个H和G都要乘以10,这样方便观察好了,我们开始对地图进行搜索首先,我们将起点的父亲结点设置为NULL,然后将起点的G值设置为0,再装进open 表里面,然后将起点作为父亲结点的周围4个点20,28,30,38(因为我们地图只能走4个方向,如果是8方向,则要加个点进去)都加进open列表里面,并算去每个结点的H 值,然后再将起点从open列表删除,放进close表中,我们将放进close表的所有方格都用浅蓝色线条进行框边处理,所以这次搜索以后,图片变为如下格式,其中箭头代表的是其父结点其中每个格子的左下方为G值,右下方为H值,左上方为H值,我们拿28号格子为例来讲解一写F值的算法,首先因为终点33在4行7列,而28在4行2列,则行数相差为0,列数相差为5,总和为5,再乘以我们先前定的基数10,所以H值为50,又因为从28的父结点29移动到28,长度为1格,而29号为起点，G值为0,所以在父亲结点29的基础上移动到28所消耗的G值为(0 + 1) *10 = 10,0为父亲结点的G值,1为从29到28的消耗当前OPEN表中的值: 20,28,30,38 当前CLOSE表中的值: 29现在我们开始寻找OPEN列表中F值最低的,得出结点30的F值最低,且为40,然后将结点30从OPEN表中删除,然后再加入到CLOSE表中,然后在判断结点30周围4个结点,因为结点31为障碍,结点29存在于CLOSE表中,我们将不处理这两点,只将21和39号结点加入OPEN表中,添加完后地图变为下图样式当前OPEN表中的值: 20,28,38,21,39 当前CLOSE表中的值: 29,30接着我们重复上面的过程,寻找OPEN表中F值为低的值,我们发现OPEN表中所有结点的F值都为60,我们随即取一个结点,这里我们直接取最后添加进OPEN表中的结点,这样方便访问(因为存在这样的情况,所有从一个点到另外一个点的最短路径可能不只一条),我们取结点39,将他从OPEN表中删除,并添加进CLOSE表中,然后观察39号结点周围的4个结点,因为40号结点为障碍,所以我们不管它,而30号结点已经存在与OPEN表中了,所以我们要比较下假设39号结点为30号结点的父结点,30号结点的G值会不会更小,如果更小的话我们将30结点的父结点改为39号,这里我们以39号结点为父结点,得出30号结点的新G值为20,而30号结点原来的G值为10,并不比原来的小,所以我们不对30号进行任何操作,同样的对38号结点进行上述操作后我们也不对它进行任何操作,接着我们把48号结点添加进OPEN表中,添加完后地图变为下图样式当前OPEN表中的值: 20,28,38,21,48 当前CLOSE表中的值: 29,30,39以后的过程中我们都重复这样的过程,一直到遍历到了最后终点,通过遍历父结点编号,我们能够得出一条最短路径,具体完整的推导过程我就不写出来了,因为和刚才那几步是一样的，这里我再讲出一个特例,然后基本A星算法就没问题了上面的最后一推导中,我们在观察39号结点时,发现他周围已经有结点在OPEN表中了,我说"比较下假设39号结点为30号结点的父结点,30号结点的G值会不会更小,如果更小的话我们将30结点的父结点改为39号",但是刚才没有遇到G值更小的情况，所以这里我假设出一种G值更小的情况,然后让大家知道该怎么操作,假设以39号为父结点,我们得出的30号的新G值为5(只是假设),比30号的原G值10还要小,所以我们要修改路径,改变30号的箭头,本来他是指向29号结点的，我们现在让他指向39号结点,38号结点的操作也一样好了,A星算法的大体思路就是这样了，对于8方向的地图来说，唯一的改变就是G 值方面,在上下左右,我们的G值是加10,但是在斜方向我们要加14,其他的和上面讲的一样~~~:)PS: 今天下午去天门网络面试,我竟然连简历都没带- -空着个手带了个人就去了....都不晓得我当时杂想的...汗(智乐圆入门2)终于把A*寻路算法看懂了，虽然还有点小问题，但A*寻路算法我已经略知一二，帮助还不知道的朋友进入A*算法入门阶级，应该不成问题，下面就来看看A*算法的原理（以下讲解不带入任何程序语言，因此只要你看懂了下面所有的话，那么你可以随意用在任意程序语言中）在下也是初学，写这篇文章的目的只是让新手入门，因此高手看到这就飘过吧，当然愿意给予指点的高手请继续往下看前言：在文中可能会出现一些专业术语或者是我信口雌黄的话语，未免看官不明白，前面我先加以注解，具体意思可以从文中体会到方格：一个一个的小方块障碍物：挡着去路的东西目标方格：你想到达的方格操控方格：你控制的寻路对象标记：临时为某一个方格做的标记父标记：除了操控方格所创建的临时标记，每个标记都有个父标记，但父标记不是随便乱定的，请看下文开启标记列表：当该标记还未进行过遍历，会先加入到开启标记列表中关闭标记列表：当该标记已经进行过遍历，会加入到关闭标记列表中路径评分：通过某种算法，计算当前所遍历的标记离目标方格的路径耗费估值（后面会讲一种通用的耗费算法）首先描述一个环境，在一望无际的方格中，我身处某某方格，如今我想去某某方格，接下来我开始寻路！在脑海中，先创建开启标记列表、关闭标记列表，然后把我的初始位置设置为开始标记进行遍历，同时因为开始标记已经遍历过了，因此把开始标记加入到关闭列表。

科技信息2009年第21期SCIENCE&TECHNOLOGY INFORMATION0.引言移动机器人的路径规划是机器人学的一个重要研究领域，它是指在有障碍物的有限空间中，依据工作的实际需要，搜索出从起始点到目标点的一条较优，能避免障碍物的行走路径。

移动机器人的路径规划问题已经得到了广泛的研究，路径规划方法也是多种多样，不同的算法有七优劣。

A*算法是一种启发式搜索方法，通过估价函数在求解过程中的应用，克服了搜索过程形成的早熟现象。

该算法在每一步搜索过程中通过估价把当前的节点和以前的结点的估价值进行比较得到一个“最佳节点”，这样可以有效防止“最佳节点”的丢失。

通过仿真结果表明，采用本算法对机器人路径规划的的选择，在特点的环境下能够得到一条有效的路径规划方案。

1．机器人路径规划分析移动机器人在进行工作时，往往要求根据某一准则（如行走路线长度最短、能量消耗最小等），在工作空间中沿一条最优（或次优）的路径。

在对路径规划求解中分为离散空间和连续空间两种情况下的实现。

在离散空间下若栅格划分过粗，则规划精度较低；若栅格划分太细，则数据量又会太大。

本文主要介绍一种在连续空间下基于A*的移动机器人路径规划方法。

该方法在对规划空间利用连接图建模的基础上，通过A*得到较优的行走路径。

1.1规划空间的链接图建模进行机器人的路径规划时，首先必须对其自由空间进行描述，即进行规划空间建模。

链接图是自由空间建模中的一种比较好的方法，构造过程中作如下假设：1．1．1移动机器人在二维平面环境中移动，不考虑高度信息；1．1．2规划环境的边界及障碍物可用凸多边形描述；1．1．3通过对机器人大小等的考虑，可对规划环境边界适当地缩小，对障碍物的范围适当地扩大，机器人用点来表示，即“点机器人”。

连接图对自由空间进行建模的过程是：首先，用直线划分自由空间为凸多边形区域。

其次，设置各链接点的中间点为可能路径点。

再次，相互连接各凸多边形区域内的所有可能路径。