自振频率计算

结构自振周期计算公式结构自振是指结构体因受力作用，而发生固有频率的振动，是工程结构设计过程中的重要因素之一，其自振周期的计算也是工程分析与设计的重要参考。

一、结构自振周期计算的基本原理结构自振周期表示在定荷载作用下，结构体内存在的固有振动频率，而在房屋建筑等结构设计中，计算结构的自振周期可以给予工程师指导性的数据，从而判断结构的稳定性以及进行优化设计。

在分析自振周期时，振动方程为：$Mfrac{d^2u}{dt^2}+Ku=Fsin(wt)$其中：$M$为质量；$K$是刚度；$F$为外力；$w$为频率；$t$为时间。

由上述振动方程可推知，均布荷载情况下，自振周期可表示为： $T=2pisqrt{frac{M}{K}}$二、基于结构自振周期计算的工程实践1.建筑结构目前，建筑结构自振周期的计算方法多以勒温斯顿公式为指导，该公式如下：$T=2pisqrt{frac{mh}{3K}}$其中，$m$为梁或柱的质量，$h$为梁或柱的高度，而$K$为梁或柱的刚度。

由此可知，在建筑结构设计中，如果要实现某一特定的自振周期，就可以根据公式的参数来准确计算出梁或柱的质量和高度，进而实现设计要求。

2.机械结构在机械结构设计中，自振周期计算常用结构动力学公式：$T=2pisqrt{frac{J}{K}}$其中，$J$为动力学惯性矩，$K$为刚度。

由此可知，机械结构中要实现某一特定的自振周期，可以根据公式参数来计算动力学惯性矩和刚度，然后以计算结果为指导，从而实现设计要求。

三、结构自振周期计算的工程应用1.减小建筑物抗震性能近年来，随着自然灾害的增多，设计出具有良好抗震性能的建筑结构越来越受到重视，而结构自振周期的计算可以指导工程师控制结构的振动，从而减少结构层受到的震力，减少损坏层的概率，提高其受震抗力。

2.提高机械设备的耐久性耐久性是指机械设备承受外力时对结构持续不变的能力，而机械设备的自振周期可以提高设备的耐久性，使其可以承受外力的一定频率振动，从而提高设备的维护效率，延长其使用寿命。

线圈的自谐振频率线圈的自谐振频率是指线圈在没有外加电源的情况下，由于其自感和电容而产生的振荡频率。

线圈自谐振频率是一个重要的电磁学概念，对于电路设计和无线通信有着重要的意义。

线圈是由导线绕成的一个圆柱形或螺旋形的结构，它具有自感和电容的特性。

自感是指线圈中的电流在变化时会产生感应电动势，而电容则是指线圈的导线之间会存在电场。

当线圈的自感和电容达到平衡时，线圈会产生自谐振现象。

线圈的自谐振频率可以通过以下公式计算得到：自谐振频率= 1 / (2 * π * √(L * C))其中，L表示线圈的自感，C表示线圈的电容。

线圈的自谐振频率与线圈的自感和电容有关。

当线圈的自感或电容增大时，自谐振频率会下降；当线圈的自感或电容减小时，自谐振频率会上升。

这是因为线圈的自感和电容会影响线圈中电流的变化速度，从而影响自谐振频率。

线圈的自谐振频率在电路设计中有着重要的应用。

例如，在无线通信中，天线通常是由线圈组成的。

天线的自谐振频率决定了天线的工作频率范围。

如果天线的自谐振频率和通信频率相同，信号能够被有效地辐射出去；如果天线的自谐振频率和通信频率不匹配，信号的辐射效果会大大降低。

除了在通信领域，线圈的自谐振频率也在其他领域有着应用。

例如，在电子学中，自谐振频率可以用于设计振荡器和滤波器；在无线电领域，自谐振频率可以用于调谐电路和共振电路的设计。

为了提高线圈的自谐振频率，可以采取一些措施。

例如，可以增加线圈的绕组数目、增加线圈的导线长度或者增加线圈的电容。

这些措施都会增加线圈的自感和电容，从而提高自谐振频率。

线圈的自谐振频率是线圈在没有外加电源的情况下，由于其自感和电容而产生的振荡频率。

它是电路设计和无线通信中重要的概念，对于设计和优化电路具有重要意义。

通过合理调整线圈的自感和电容，可以实现所需的自谐振频率，从而提高电路的性能和效率。

速度计算
ap Fp

g
Fp p0e0.35 fn
按照理论计算或查表获得 根据规范取0.02～0.05
BL
取恒载和有效分布活荷载之和，楼层 有效分布活荷载：对办公建筑取 0.55kN/m2，对住宅可取0.3kN/m2
B CL
对边梁取1，对中= 0.001103 高 层 接近楼盖结构自振频率时人行走产生的作用力（kN） F p = 0.000656 建 筑 人们行走产生的作用力（kN），按表A.0.2采用 p0 = 0.3 混 楼盖结构竖向自振频率(Hz) fn = 17.5 凝 楼盖结构阻尼比，按表A.0.2采用 β = 0.02 土 ω 结 楼盖结构阻抗有效重量（kN) = 291.6 构 重力加速度 g = 9.8 技 术 楼盖单位面积有效重量(kN/m2) = 4.05 规 程 楼盖阻抗有效质量的分布宽度（m) B = 12 梁跨度（m) L = 6 垂直于梁跨度方向的楼盖受弯连续性影响系数 C = 2 蓝色框需输入，黄色框可选择，绿色框可查表获得。 楼盖振动峰值加速度(m/s2) ap

一、概述二阶系统是指具有两个自由度的动力系统，其特点包括自然振荡频率和阻尼比。

在工程学和科学领域中，对二阶系统的分析和控制具有重要意义。

本文将探讨二阶系统的自然振荡频率和阻尼比的相关公式，以便更好地理解和应用这些理论知识。

二、二阶系统的定义在探讨二阶系统的自然振荡频率和阻尼比之前，我们首先需要了解二阶系统的基本定义。

二阶系统是指具有两个因素或变量的动力系统，通常可以用微分方程或传递函数来描述其动态行为。

在工程学中，二阶系统的典型例子包括机械振动系统、电气电路系统等。

三、自然振荡频率的计算1. 自然振荡频率是指在没有外部干扰的情况下，系统的固有振荡频率。

对于二阶系统，其自然振荡频率可以通过以下公式进行计算：ω_n = √(k/m)其中，ω_n表示自然振荡频率，k表示系统的刚度，m表示系统的质量。

这个公式反映了系统的固有特性与其刚度和质量的关系，可以帮助工程师和科学家分析系统的振动行为。

四、阻尼比的计算2. 阻尼比是衡量系统阻尼效果的重要参数。

对于二阶系统，其阻尼比可以通过以下公式进行计算：ξ = c/(2*√(km))其中，ξ表示阻尼比，c表示系统的阻尼系数，k表示系统的刚度，m 表示系统的质量。

阻尼比反映了系统阻尼效果的强弱，对于振动系统的稳定性和响应特性具有重要影响。

五、实际应用以上介绍的自然振荡频率和阻尼比的公式，可以广泛应用于工程学和科学领域。

举例而言，在机械工程中，工程师可以利用这些公式来设计和优化振动系统，以确保系统的稳定性和性能。

在控制工程中，科学家可以利用这些公式来分析和改进控制系统的响应特性，以实现更好的控制效果。

六、结论通过上述分析，我们了解了二阶系统的自然振荡频率和阻尼比的相关公式，以及这些公式在实际应用中的重要性。

这些理论知识可以帮助工程师和科学家更好地理解和控制二阶系统的动态行为，为工程和科学领域的发展提供重要支持。

希望本文的内容能够对读者有所帮助，谢谢阅读！在工程学和科学领域中，二阶系统的自然振荡频率和阻尼比的计算与分析是非常重要的课题。

桥梁常用计算公式桥梁是道路、铁路、水路等交通工程中非常重要的基础设施。

在设计和施工过程中，需要进行一系列的计算来保证桥梁的稳定性和安全性。

下面是桥梁常用的计算公式和方法，供参考：1.静力平衡计算桥梁的静力平衡是保证桥梁结构稳定的基础。

在计算静力平衡时，常用的公式有：-受力平衡公式：对于简支梁，ΣFy=0，ΣMa=0；对于连续梁，ΣFy=0，ΣMa=0。

-桥墩反力计算公式：P=Q+(M/b)，其中P为桥墩反力，Q为桥面荷载，b为桥墩底宽度。

2.梁的弯矩计算桥梁在受到荷载作用时，会出现弯矩。

常用的梁的弯矩计算公式有：-点荷载的弯矩计算公式：M=Px；- 面荷载的弯矩计算公式：M=qx^2/2；-均布载荷的弯矩计算公式：M=qL^2/83.梁的挠度计算挠度是指梁在受荷载作用时的变形程度。

常用的梁的挠度计算公式有：-点荷载的挠度计算公式：δ=Px^2/(6EI)；- 面荷载的挠度计算公式：δ=qx^2(6L^2-4xL+x^2)/24EI；-均布载荷的挠度计算公式：δ=qL^4/(185EI)。

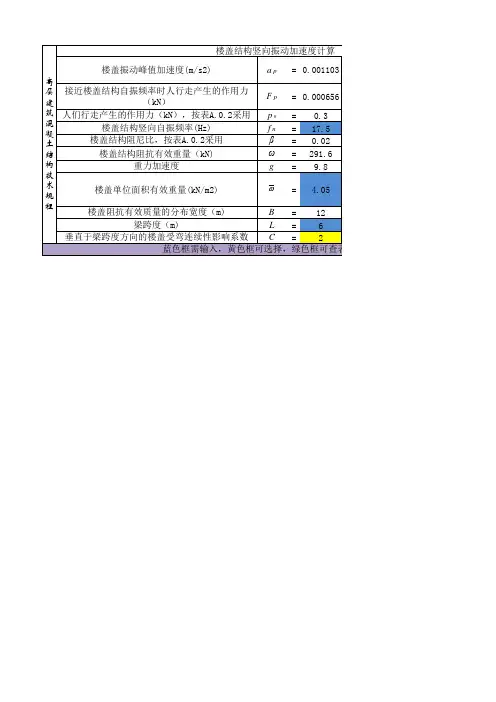
4.桥梁的自振频率计算自振频率是指桥梁结构固有的振动频率。

常用的自振频率计算公式有：-单跨梁自振频率计算公式：f=1/2π(1.875)^2(EI/ρA)^0.5/L^2；-多跨梁自振频率计算公式：f=1/2π(π^2(EI/ρA)^0.5/L^2+Σ(1.875)^2(EI/ρA)^0.5/L_i^2)。

5.破坏形态计算桥梁在受到荷载作用时可能发生不同的破坏形态，常用的破坏形态计算公式有：-弯曲破坏计算公式：M=P*L/4；-剪切破坏计算公式：V=P/2；-压弯破坏计算公式：M=P*L/2；-压剪破坏计算公式：V=P。

6.抗地震设计计算在地震区设计的桥梁需要进行抗地震设计，常用的抗地震设计计算公式有：-设计地震力计算公式：F=ΣW*As/g；-结构抗震强度计算公式：S=ηD*ηL*ηI*ηW*A。

其中，ΣW为结构作用力系数，As为地震地表加速度，g为重力加速度，ηD为调整系数，ηL为长度和工况调整系数，ηI为体型和影响系数，ηW为材料和连接性能系数，A为结构抗震强度。

固有频率自振频率自振圆频率固有频率、自振频率和自振圆频率，这三个概念在物理学和工程学中扮演着重要的角色。

它们涉及到振动系统的特性和行为，对于理解和设计振动系统具有重要意义。

本文将通过深度和广度的介绍，带你全面了解这三个概念的含义、联系和应用。

一、固有频率1.1 什么是固有频率固有频率是指振动系统在没有外力作用下的自然频率，也可以理解为系统固有的振动频率。

在物理学中，振动系统可以是机械系统、电子系统、光学系统等，它们都有各自的固有频率。

当振动系统受到外界扰动或激励时，如果激励频率接近系统的固有频率，将会发生共振现象，这对于一些特定的应用有着重要的意义。

1.2 固有频率的计算和影响因素振动系统的固有频率与系统的质量、刚度和阻尼等因素有关。

具体地，固有频率可以通过下式计算得出：\[f_0 = \frac{1}{2\pi}\sqrt{\frac{k}{m}}\]其中，\(f_0\)表示固有频率，\(k\)表示系统的刚度，\(m\)表示系统的质量。

从这个公式可以看出，固有频率与系统的质量和刚度成正比，与阻尼无关。

1.3 固有频率的应用固有频率在工程学中有着广泛的应用，比如在建筑结构设计中，为了避免共振现象的发生，需要对结构的固有频率进行分析和设计。

另外，在机械振动领域，对于机械系统的固有频率进行分析可以帮助预测系统的振动行为和稳定性。

二、自振频率2.1 什么是自振频率自振频率是指振动系统在受到外力激励时，系统本身的固有频率。

当激励频率接近系统的自振频率时，系统将呈现出共振现象，振幅会急剧增大。

自振频率是指在自由振动状态下，振动系统的固有频率。

2.2 如何计算自振频率自振频率可以通过系统的固有频率和阻尼比来计算。

在一般情况下，自振频率可以表示为：\[f_r = f_0\sqrt{1-\xi^2}\]其中，\(f_r\)表示自振频率，\(f_0\)表示固有频率，\(\xi\)表示阻尼比。

从这个公式可以看出，当阻尼比为0时，自振频率等于固有频率；当阻尼比接近于1时，自振频率将趋于0。

高层建筑结构的自振频率分析高层建筑结构是现代城市化进程中不可或缺的一部分，其结构的稳定性和安全性受到人们的广泛关注。

在设计和建造过程中，对于高层建筑的自振频率进行准确的分析和评估是非常重要的。

本文将对高层建筑结构的自振频率分析进行探讨。

一、引言高层建筑的自振频率是指在自由振动情况下，结构在一定的周期内完成一次完整的振动。

自振频率的分析可以帮助设计师确定结构的固有特性、响应特点以及对外界激励的敏感度。

二、自振频率的确定方法1. 简化模型法简化模型法是通过对高层建筑简化为某种能量稳定系统来进行自振频率的计算。

根据建筑高度、结构类型和材料参数等，可以将结构模型简化为梁、柱、墙等基本单元，并应用刚度矩阵法进行计算。

2. 有限元法有限元法是一种更为精确的计算自振频率的方法。

通过将结构划分为许多小单元，利用有限元法求解结构的模态方程，并求解出结构的固有频率与模态形态。

三、自振频率对结构的影响高层建筑的自振频率不仅仅是一个数值，它还反映了结构的稳定性和可行性。

较低的自振频率会导致建筑结构易受到外界激励的影响，引发共振现象，从而对结构的安全性产生威胁。

1. 天气影响根据结构自振频率的计算结果，可以预测高层建筑在不同天气条件下的响应情况。

较高的自振频率可以减小结构受风荷载等自然灾害的影响，提高结构的稳定性。

2. 人员舒适度高层建筑的自振频率还与人员的舒适度密切相关。

当结构振动频率与人的自然频率接近时，将引发人员在建筑内部产生不适感，影响日常工作和生活。

四、自振频率的优化措施为了提高高层建筑结构的稳定性和安全性，需要在设计过程中采取一些优化措施来控制自振频率。

1. 结构设计优化通过调整结构的刚度和质量分布来降低自振频率。

例如，在结构中加入钢筋混凝土剪力墙、叠层刚架等措施，可以有效提高结构的自振频率。

2. 阻尼措施在高层建筑中设置合适的阻尼器或阻尼装置，可以有效抑制结构的振动，降低结构的自振频率。

常见的阻尼措施包括液体阻尼器、摩擦阻尼器等。

通过算例表明,运用这些方法计算梁的自振频率和振动形式与 ansys 计算结果基本一致。 关键词：自振频率 复杂质量 振形 中图分类号：TU311.4
1．引言
在建筑工程、水利工程、煤炭、仪表装配等多层工业厂房中，在楼层上常常安装有压缩 机、离心机、通风机、破碎机、电动机、振动筛等旋转式(也有往复式的) 动力机器。由于 动力机器上楼，避免不了对楼层梁进行竖向振动分析。分析振动问题，首先要计算其自振特 性包括频率和振型。因为在实际工程中，楼层梁的布置首先要满足工艺设备布置的要求，因 此在一根梁上经常布置有数台设备(包括动力机器) 和支承着几根次梁,还支承着楼板传递的 荷载。总之，梁上作用的静和动荷载是比较复杂的。同时荷载的取值与实际的大小也不可能 完全相符,还有不确定性。另外梁的端部支承条件不完全是理论上的铰接或刚接，因此要精 确地计算其自振频率和振型是困难的，而在实际工程中进行复杂的分析一般必要性也不大。
换算系数 K j 时，首先确定连续梁第 2 ,3……n 振型集中质量作用处的值 y j ，然后按式(5) 计 算 K j [3]。
3．算例分析
计算下图等截面悬臂梁的自振频率和振形，截面尺寸为 500mm × 500mm。
图 1 悬臂梁示意图 Fig1 The sketch of cantilever
梁自由振动时的最大动能则为：
最大动能为：
∫ ∑ U max
=
1 2
ω
2
(
L 0
mu
y
2 (x
)
dx
+
n
m
j
y
2 j
)
j =1
由式(1) 得：
∫ Wmax
=
1 2
L EI ( d 2 y(x)

δ 11
δ 12
l3 4l 3 = , δ 22 = 3EI 3EI l3 = δ 21 = 2 EI
用 令
6 EI ml 3
乘上式， 乘上式，
m1 = 2m, m2 = m
(4 − λ )A1 + 3 A2 = 0 6 A1 + (8 − λ )A2 = 0
6 EI 1 ⋅ 2 = λ ，得 3 ml ω
2. 振型方程
) A1 + δ 12 m2 A2 = 0 ω2 1 δ 21m1 A1 + (δ 22 m2 − 2 ) A2 = 0 ω (δ 11m1 − 1
a 1 a 6 EI m − ω 2 A1 − 4 EI mA2 = 0 3 3 a a 1 − mA1 + m − 2 A2 = 0 EI 4 EI ω
y2 (t ) = − m1 &&1 (t )δ 21 − m2 &&2 (t )δ 22 y y
1 2 4 m − 2 A1 − mA2 = 0 EI ω 3EI 2 8 1 − mA1 + m − 2 A2 = 0 EI ω EI
y2 (t ) = − m1 &&1 (t )δ 21 − m2 &&2 (t )δ 22 y y
δ 11
a3 a3 = , δ 22 = 6 EI EI
用
12 EI ma 3
乘上式， 乘上式，
12 EI 1 ⋅ 2 = λ ，得 令 3 ma ω
δ 12 = δ 21
a3 =− 4 EI
(2 − λ )A1 − 3 A2 = 0 − 3 A1 + (12 − λ )A2 = 0

体系的最大位能：
1
多质点体系 Umax 2 F max
xn (t)
1 {X }T [K ]{X }
xi (t)
2
体系的最大动能：
多质点体系
Tmax
1 2
vmax
2
m
1 2{ X }T [M ]{ X }
2
体系按基本频率1作自由振动，相应的基本振型取一 种近似形式，即假设各质点的重力荷载Gi作为水平作用产 生的弹性变形曲线.
四、 结构自振周期和振型的计算
在进行结构的地震作用计算时，必须求出结 构的自振周期和振型，在进行最简单的计算（底 部剪力法）时，也要计算结构的基本周期。
结构自振周期的计算方法有： 1、理论与近似的计算 2、经验公式 3、试验方法等
(一)、理论与近似计算方法
1、近似方法1——能量法（Rayleigh法） 原理：能量守恒 一个无阻尼的弹性体系在自由振动中任何时
弯剪型
T1 1.7 T
顶点位移 单位为米,
可用于计算一般多高层框架结构的基本周期，顶点位移 的计算，按照框架在集中于楼盖的重力荷载作为水平作用产 以弯矩产生的变形为主，如剪力墙结构
剪切型变形：以剪力产生的变形为主，如框架结构
弯剪型变形：弯矩、剪力产生的变形都不能忽略，如
2、折算质量法
原理：在计算多质点体系的基本频率时， 用一个单质点体系代替原体系，使这个单质点 体系的自振周期与原体系的基本频率相等或接 近，这个单质点体系的质量就称为折算质量。 这个单质点体系的约束条件和刚度应与原体系 的完全相同。
折算质量应根据替代原体系的单质点体系振 动时的最大动能等于原体系的最大动能的条件 确定。
刻的总能量（位能与动能之和）不变。

电容自谐振频率是指电容在电路中产生的自然振荡频率，它是电容的固有属性。

在电路设计和分析中，对电容自谐振频率的了解是非常重要的。

本文将介绍电容自谐振频率的相关知识和应用。

一、电容自谐振频率的概念和计算电容自谐振频率是指电容在电路中自行振荡的频率，它与电容的电容值和电路中的电感值有关。

电容自谐振频率的计算公式为：f=1/2π√(LC)，其中f表示电容自谐振频率，L表示电路中的电感值，C表示电容的电容值。

根据公式可知，当电容 or 电感值增加时，电容自谐振频率会降低；反之，当电容 or 电感值减小时，电容自谐振频率会升高。

二、电容自谐振的效应在一些特定的电路中，电容自谐振频率可能会对电路产生一些独特的效应。

比如，在谐振电路中，电容自谐振频率可以实现对信号的筛选和增强，改善电路的稳定性；在滤波电路中，电容自谐振频率可以实现滤波作用，将噪声和干扰信号过滤掉；在振荡电路中，电容自谐振频率可以实现正弦波振荡，产生高精度的时钟信号和频率参考信号。

三、电容自谐振频率的应用电容自谐振频率有广泛应用。

比如，在音响领域，电容自谐振频率可应用于电子万能音响中的降噪电路和低音扩展电路等；在无线通信领域，电容自谐振频率可应用于天线匹配电路、振荡电路和滤波电路等；在电源设计领域，电容自谐振频率可应用于稳压电源中的滤波电路。

四、电容自谐振频率问题探讨在电容自谐振频率的实际应用中，有时会出现意料之外的问题。

比如，在一些特殊的电路中，电容自谐振频率可能会与其他频率重叠，导致电路的失真或不能正常工作。

这时需要通过调整电容或者调整其他元器件的参数，以避免频率冲突或碰撞。

同时，在电容的选型中，也需要考虑电容的质量、精度、稳定性等因素，以保证电容自谐振频率的正确性和稳定性。

五、本文总结本文介绍了电容自谐振频率的概念和计算公式，以及电容自谐振的效应和应用。

同时，本文也探讨了电容自谐振频率可能出现的问题和解决方法。

希望本文对读者了解电容自谐振频率有所帮助。

5pl4/ (384EI)。
因 ω=2πf ω(f ω 为第 1 自振频率), 则可得自
振频率以挠度表达的计算公式 :
fω
=
π 2
5g 384 Δst
按《规 范》 要求 , 令 fω ≥3Hz , 则可 得 Δst ≤ 0.035m 。 也就是说 , 不论桥的跨度有多大 , 其最大
挠度均不得超过 0.035m , 这对于跨度大的桥其要
对不同的桥型 、跨度和荷载大小来确定 。
— 53 —
SPST
特 种 结 构
2004 年第 1 期
二 、天桥的振动问题分析
天桥在人行荷载作用下的振动属于强迫振动
问题 。在这里将人行荷载模拟为如下简谐荷载 :
P(t)=F sinθt
(2)
式中 :F 为最大人行荷载 ;θ为荷载的圆频率 , θ=
2 πfθ;fθ为人行荷载的频率 , 取 2Hz 。
f
ω
≥
1 2π
4 π2f
2θ+n
q/
-
m
l
(12)
表 1 即为不同跨度梁板式主梁按式(12)计算
的需满足的最小自振频率(一般天桥的自重与活
荷载基本相当 , 因此本表计算时令 q ≈mg)。
表 1 主梁跨度与最小自振频率的关系
跨度 l(m)
最小自振频率 f ω(Hz)
20
25
30
35
40
3.38 3.16 2.99 2.87 2.78
y =C1sin ωt +C2cos ωt +m(ωF2-θ2)sinθt +ωg2 (6)
— 54 —
式(6)中的积分常数 C 1 和 C 2 由初始条件来

固有频率公式
固有频率公式是物理学中描述物体内部振动和波等动力现象的有效工具。

可以使用固有频率公式来计算物体在固定条件下（如无外力）的
内部振动情况。

本文将着重介绍固有频率公式的基础理论和计算方法：
1. 固有频率的基本概念
固有频率（也称自振频率）是一个物体在固定环境下起振动时达到的
最大振幅的振动频率。

可以通过控制环境条件改变来改变固有频率。

因此，固有频率是一个定量反映物体结构参数以及环境条件的技术指标。

2. 固有频率公式
固有频率公式是用于计算物体固有频率的核心公式，它由物理学家声
学研究室莱特尔及其同事们于1963年发表的声学理论中形成的。

该公
式可表示为：
f = 1/2π√(k/m)，
其中，f为固有频率，k为物体总质量的质量力学上的刚度系数，m为
物体总质量。

3. 应用
固有频率公式可用于计算建筑物、工业机械、家用电器等各种物体内部振动的情况，从而检测物体是否安全可靠、有效、可靠，以确保其服役期间能正常工作。

此外，固有频率公式还可用于调节物体的振动频率，使其达到最佳工作状态。

4. 研究发展
随着新型力学结构的发展，固有频率公式的研究也在不断发展。

最近几年，通过对建筑物安防、船舶设计、微动力系统设计等新型结构的研究，固有频率公式应用及精确性有了一定的提高，为把握物体的内部振动提供了新的可能性。

悬臂梁自振频率校验模型尺寸：横截面为1m×1m，高为10m。

材料参数：弹性模量2×1011Pa，泊松比0.167，密度2400Kg/m3。

边界条件：底端固定，法线为Y方向的两侧面设置链杆约束。

从表中可以看出，ADINA数值解中第1至3阶自振频率与精确解最为接近。

图1 悬臂梁第（1-5）阶振型图2 悬臂梁第（5-10）阶振型刚性坝面动水压力分布特性材料参数坝体：弹性模量2E20Pa ，泊松比0.167，密度2400Kg/m 3； 水体：体积模量2.56E9Pa ，密度1000Kg/m 3。

模型尺寸坝体：长10m ，宽1m ，高10m ；（ADINA-STRUCTURE 模块建模） 水体：长50m ，宽10m ，高10m 。

（ADINA-CFD 模块建模）单元类型坝体：3D-solid 水体：3D-fluid边界条件：水体两侧以及末端，底部全部设置Wall 边界，在近坝面设置流固耦合边界。

荷载条件：在坝体底部输入加速度时程a=sin2πt ，持续时间为5s 。

水体有限元模型 坝体模型模型示意图(单位:m )体积模量=1+20a E P μ 密度3=1000g/m K ρ加速度时程曲线动水压力沿高程分布图悬臂梁模态分析(1)干模态悬臂梁有限元模型单元类型：3d-Solid单元。

材料参数：弹性模量2×1010Pa，泊松比0.30，密度7800Kg/m3。

模型尺寸：长2.4m，高2.4m，宽0.5m。

计算方法：lanczos iteration，计算了10阶模态。

第一阶振型第二阶振型第三阶振型第四阶振型第五阶振型第六阶振型第七阶振型第八阶振型第九阶振型第十阶振型(2) 湿模态1）只考虑水体质量单元类型：3d-solid，3d-fluid（势流体单元）水体尺寸：长5m，宽2.4m，高2m。

水体材料参数：体积模量2.56e9Pa，密度1000Kg/m3。

第一阶振型第二阶振型第三阶振型第四阶振型第五阶振型第六阶振型第七阶振型第八阶振型第九阶振型第十阶振型2）在100m高水头作用下湿模态首先对100m水头作用下的悬臂梁进行了静力分析,而后在此基础上进行重启动分析,计算了10阶模态。

钢结构桥梁的自振频率分析钢结构桥梁是现代桥梁建设中常见的一种类型，它具有高强度、耐久性强、重量轻等优势。

然而，钢结构桥梁在使用过程中可能会受到外界环境和荷载的影响，进而产生自振现象。

自振频率是指桥梁结构在无外界干扰下的固有振动频率，对于钢结构桥梁的设计和安全评估具有重要意义。

本文将从理论分析与数值模拟两个方面进行钢结构桥梁的自振频率分析。

一、理论分析钢结构桥梁的自振频率可以通过结构的自由振动方程进行理论求解。

设桥梁结构振动形式为e^(jwt)，其中j为虚数单位，w为角频率。

将振动形式代入结构的自由振动方程，得到以下形式的特征方程：Mx''(t) + Cx'(t) + Kx(t) = 0其中，M为结构的质量矩阵，C为结构的阻尼矩阵，K为结构的刚度矩阵。

根据特征方程可求得桥梁结构的固有频率，即自振频率。

在实际应用中，钢结构桥梁的自振频率往往通过有限元方法进行计算。

有限元方法将桥梁结构离散为有限个节点，利用基于矩阵运算的数值计算方法求解结构的自由振动特征值。

通过有限元分析软件，我们可以得到钢结构桥梁在不同频率下的振型和自振频率。

二、数值模拟钢结构桥梁的自振频率分析也可以通过数值模拟方法进行求解。

数值模拟方法主要包括有限元方法、边界元方法、迭代法等。

其中，有限元方法是最常用、最有效的分析方法。

在数值模拟中，首先需要根据实际的桥梁几何形状和材料参数建立相应的数学模型。

然后，通过给定加载条件和边界条件，利用有限元软件对桥梁结构进行离散化处理，得到数值模型。

在数值模拟中，我们可以改变加载条件和边界条件，对桥梁进行动态响应分析，得到桥梁在不同频率下的振动响应。

通过寻找桥梁结构的最低自振频率，可以评估桥梁结构的振动特性，并为桥梁的设计和改进提供依据。

三、应用案例以下是一个实际的钢结构桥梁自振频率分析的案例。

某座长跨度的钢桁架桥的结构参数如下：跨度为40米，支座到桥面的高度为10米，主梁截面为I型钢，材料为Q345钢。