线性调频连续波时频分析中的余弦变换方法
- 格式:pdf
- 大小:268.30 KB
- 文档页数:4


傅里叶变换与余弦变换的关系
傅里叶变换和余弦变换是信号处理中常用的两种变换方法。
它们都是将信号从时域转换到频域的方法,但是它们的具体计算方法不同。
傅里叶变换将信号分解为一系列正弦波的加权和,可以精确地表示信号的频域特征。
而余弦变换将信号分解为一系列余弦函数的加权和,更适用于处理具有偶对称性的信号。
然而,傅里叶变换和余弦变换之间也存在一定的关系。
事实上,傅里叶变换可以看作是将信号分解为余弦函数和正弦函数的和,也就是说,傅里叶变换中的正弦函数实际上就是余弦变换中的偶函数,而余弦函数则对应着傅里叶变换中的偶函数。
因此,我们可以通过余弦变换来计算信号的傅里叶变换,也可以通过傅里叶变换来计算信号的余弦变换。
这种关系在实际信号处理中有着很重要的应用,比如在音频和图像处理中常常使用离散余弦变换(DCT)来压缩信号,而在通信系统中则广泛使用傅里叶变换来分析
和合成信号。
- 1 -。

线性调频连续波雷达的一种信号处理方法作者:雒海潮宋思盛来源:《现代电子技术》2010年第05期摘要:线性调频连续波(LFMCW)雷达具有距离和多普勒频率分辨率高,结构简单,体积小,重量轻和良好的低截获概率特性,得到了广泛的应用。
对线性调频连续波雷达的目标回波信号进行分析,使用差拍-频谱分析-MTD的方法进行仿真,从回波信号中提取目标的相位信息,从而获取目标的距离和速度信息,该方法可有效地抑制固定杂波,方便动目标检测。
关键词:LFMCW;差拍频率;FFT;MTD中图分类号:TN95文献标识码:A文章编号:1004-373X(2010)05-042-02Signal Processing Method for LFMCW RadarLUO Haichao,SONG Sisheng(Xi′an Electronic Engineering Research Institute,Xi′an,710100,China)Abstract:Characterized by high resolution for distance and doppler frequency,simple structure,small volume,low weight,and excellent Low Probability of Intercept(LPI),LFMCW radar has found wide applications.Target echo signal of LFMCW radar is fisrt analyzed with beat-spectrum analysis-MTD stimulation,then the phase information is obtained from target echo signal,hence the distance and speed of the target.The method can largely reduce fixed clutters,and it is very effective in moving target detection.Keywords:LFMCW;beat frequency;FFT;MTD线性调频连续波雷达(LFMCW)的距离速度模糊问题一直难以解决,文献[1]采用MTD频域配对方法,通过MTD简化差拍信号的频谱,并利用三角形线性调频连续波上、下扫频段多普勒频移的对称性,实现动目标的距离、速度去耦合,但其在多目标环境下难以准确配对。

delta离散余弦变换概述及解释说明1. 引言1.1 概述:本篇文章旨在介绍和解释delta离散余弦变换(Δ-DCT)的概念及其应用。
离散余弦变换(DCT)是一种常用的信号处理技术,广泛应用于图像、音频和视频等领域。
1.2 文章结构:本文分为五个主要部分进行讲述。
首先,在引言部分,我们将对文章进行概述,并介绍文章的整体结构。
然后,在第二部分中,我们将对delta离散余弦变换的定义与原理进行详细阐述。
接着,在第三部分中,我们将对delta离散余弦变换与传统离散余弦变换进行比较,并分析它们在不同方面的性能差异和优势。
在第四部分,我们将重点探讨delta离散余弦变换算法的实现方法,并提供一些实例进行分析。
最后,在总结与展望部分,我们将对研究工作进行总结并提出下一步的研究方向。
1.3 目的:本文旨在全面了解和解释delta离散余弦变换这一信号处理技术,并比较其与传统离散余弦变换之间的差异。
我们希望通过对算法的原理和实现方法进行详细介绍,为读者提供对该技术的深入理解。
同时,我们还将探讨delta离散余弦变换在不同领域中的应用,并分析其在性能方面的优势和局限性。
最后,我们将总结研究工作并展望未来的研究方向,以促进该领域的进一步发展。
2. Delta离散余弦变换的定义与原理:2.1 Delta离散余弦变换概述:Delta离散余弦变换(Δ-DCT)是一种改进的离散余弦变换(DCT)方法,它主要应用于图像和视频压缩、信号处理等领域。
与传统的DCT相比,Δ-DCT在保持了较好的性能的同时,还具有更低的计算复杂度。
2.2 离散余弦变换(DCT)的基本概念和原理:离散余弦变换是一种时频分析技术,它把一个时间序列或图像分解成一组互不重叠、按能量递减排列的正交基函数,得到对应的系数。
这些系数表示了输入信号或图像在不同频率上的能量分布情况。
DCT公式可以表示为:X(k) = Σx(n)*cos[π(k+0.5)n/N] , n=0,1,...,N-1, k=0,1,...,N-1其中,x(n)表示输入信号或图像中第n个采样点的值,X(k)表示第k个频率分量对应的系数。

1 Hilbert变换对于单频率信号有很高的时间分辨率和频率分辨率,但对于多频率成分信号它失去了物理意义,因而其瞬时属性就会没有任何意义,造成解释的困难。
1998年,Huang在NASA工作期间提出了一种新的信号处理方法,被称为Hilberto Huang变换(简称HHT变换),该方法包倉两个部分:经验模式分解(EmpiricalMode Decomposition.简称EMD)和希尔伯特(Hilbert)谱分析。
其中,EMD算法是HHT变换构成的核心。
采用EMD可将信号分解成拥有单分最特性的一组正交完备的,且呈现自适应特性的固有模态函数仃ntrinsic Mode Function,简称IMF),以此来刻画信号每个同部的振荡结构和频率分量,再借以希尔伯特变换(HilbertTransfonn简称HT)得到实信号的解析形式并获得具有明确物理意义的瞬时频率,进而得到信号的时间一频率一能最分布。
传统的HHT方法存在一定缺陷,针对HHT会产生虚假分最和模态混廉的问题,Peng等人提出了相应的改进算法,引入了小波包分解对信号进行预处理,使信号在进行EMD分解之前,通过小波包分解为一系列窄带信号:并利用归一化相关性甄别方法对EMD分解后得到IMF中的虚假分最进行相关性识别筛选,使得HHT的性能有了进一步提升。
Ki jewski. Correa将Morlet小波变换尺度•时间谱中的瞬时带宽信息剔除后,提取出小波脊并构成小波瞬时频率谱(WIFS) o而为了改善EMD分解中的模式混叠和端点飞异问题,01hede 和Walden基于离散小波包分解,提出了一种最大重叠离散小波包变换(maximal-ove dap discre te wavele t packet transform( MODWPT))的分解方法, 改进了传统离散小波变换对采样长度必须为2的指数幕的限制,并通过避免下采样,克服了离散小波尺度系数的不等变化循环变换问题。

正弦余弦函数的傅里叶变换正弦余弦函数的傅里叶变换是转化数学技术中一种有效的变化方式。
它可以使在实际应用中比较复杂的ipt文件表示的正弦余弦信号函数得到更加容易处理的两个量:频率和振幅。
具体来说,傅里叶变换可以把一个正弦余弦的波形作为函数的基础,对这个函数进行分析,然后把这个函数表示成一个抽象的振荡量,即频率和振幅,作为数学上的变换因子。
1、什么是正弦余弦函数的傅里叶变换正弦余弦函数的傅里叶变换是一种有效的变化方法,可以用来把实际应用中比较复杂的正弦余弦信号函数变换为两个更容易处理的量:频率和振幅。
傅里叶变换把一个正弦余弦函数作为输入,把它转化为频率和振幅组成的强度,这是一种有效和易于理解的变换方式。
2、正弦余弦函数的傅里叶变换的原理傅里叶变换的基本原理是,它把一个复杂的函数拆分成一系列的正弦余弦函数的线性组合,从而可以提取出一个函数的一系列特性。
这些特性包括这个函数在某个波长率上的振幅,以及这个振幅的叠加情况,从而表示出来的一个函数的形状,这就是正弦余弦函数的傅里叶变换。
3、正弦余弦函数傅里叶变换的应用正弦余弦函数的傅里叶变换最常用于信号处理和数据分析领域,它可以把一个复杂的信号函数变换为频率和强度来表达。
同时,傅里叶变换在电子工程中也被广泛应用,比如在机械设计中,用于压缩图像信息和处理3D图像数据,以及在声音信号处理中获得时域滤波器和相关参数。
4、正弦余弦函数傅里叶变换的好处正弦余弦函数的傅里叶变换具有几个显著的优势,其中最重要的是它实现了微分和积分之间的无缝转换,使得信号处理和数据分析计算更加准确和有效。
此外,由于傅里叶变换可以提取出一个正弦余弦函数的所有特性,因此可以更加客观地揭示出一个函数的特点,对正弦余弦函数的分析和识别更加准确、准确和有效。

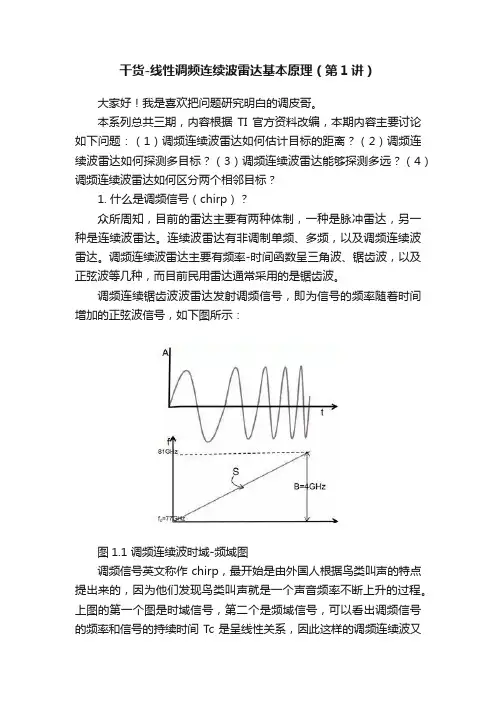
干货-线性调频连续波雷达基本原理(第1讲)大家好!我是喜欢把问题研究明白的调皮哥。
本系列总共三期,内容根据TI官方资料改编,本期内容主要讨论如下问题:(1)调频连续波雷达如何估计目标的距离?(2)调频连续波雷达如何探测多目标?(3)调频连续波雷达能够探测多远?(4)调频连续波雷达如何区分两个相邻目标?1. 什么是调频信号(chirp)?众所周知,目前的雷达主要有两种体制,一种是脉冲雷达,另一种是连续波雷达。
连续波雷达有非调制单频、多频,以及调频连续波雷达。
调频连续波雷达主要有频率-时间函数呈三角波、锯齿波,以及正弦波等几种,而目前民用雷达通常采用的是锯齿波。
调频连续锯齿波波雷达发射调频信号,即为信号的频率随着时间增加的正弦波信号,如下图所示:图1.1 调频连续波时域-频域图调频信号英文称作chirp,最开始是由外国人根据鸟类叫声的特点提出来的,因为他们发现鸟类叫声就是一个声音频率不断上升的过程。
上图的第一个图是时域信号,第二个是频域信号,可以看出调频信号的频率和信号的持续时间T c是呈线性关系,因此这样的调频连续波又称为线性调频连续波(LFMCW)。
LFMCW有几个主要的参数需要注意,分别是发射最大带宽B,调频斜率S,发射脉冲周期T c,发射信号起始频率fc。
这几个参数将在后面会有重要的作用,谨记。
上面的信号中斜率 :2. 单发单收线性调频连续波雷达顾名思义,单发单收雷达就是只有一个发射天线和一个接受天线,如下图所示。
图2.1 单发单收雷达如上图所示,频率综合器(Synth)生成调频信号,由发射天线(Tx ant)发射出去,电磁波打到物体上反射回来的信号叫做回波信号,回波信号被接收天线(Rx ant)接收,然后与发射信号进行混频(mixer),得到中频信号(IF signal)。
那么什么叫做混频呢?本科在高频电子线路中学习过,混频就是一个乘法器,将两个信号进行相乘,然后得到他们之间的信号频率差以及频率和。


fft分离正弦余弦Fast Fourier transform(FFT)分离正弦余弦是指使用FFT算法来将正弦波和余弦波进行分离的过程。
此分离可以帮助分析正弦余弦信号和应用自然处理信号中的调制版本。
FFT分离正弦余弦的基本原理是使用傅里叶变换来将一个复杂的信号分解成由许多小的正弦余弦成分构成的信号。
FFT的工作原理是将连续的时间域信号转换成频率域信号。
它使用一种叫做离散傅里叶变换(DFT)的算法。
DFT的工作原理是将一个连续的信号转换成一组可以构建的频率信号。
在FFT 分离正弦余弦之前,有必要了解傅里叶变换(FT)和离散傅里叶变换(DFT)。
傅里叶变换(FT)是一个把信号从时域或频域转换成另一个域的过程,它用一种叫做Fourier系数的技术来完成。
傅里叶变换(FT)能够将任何信号从时域转换到频域。
这是通过求解一个复杂的微分方程而实现的。
DFT则是一种可以将连续信号分解成一个定长的数值序列的技术。
DFT的基本原理是把一个复杂的信号分解成许多小的正弦余弦成分。
此类小的正弦余弦成分可以使用FFT分离出来。
使用FFT分离正弦余弦的做法是,先使用DFT变换时域信号,然后使用FFT变换频率域信号。
要执行DFT变换,首先需要定义一个定长时域信号,然后进行DFT变换。
接下来,依次应用FFT变换;从频率域求出每个正弦余弦成分的大小和相位;最后将正弦余弦成分排序,依次排列输出。
FFT分离正弦余弦是一个有用的信号处理技术,可以用于分析信号的频谱分布,检测和消除信号中的干扰,以及提取信号中的特征。
此外,它还可以用于对信号进行加密,从而增加系统的安全性。
第32卷第4期 2010年8月
探测与控制学报
Journal of Detection&Control Vo1.32 No.4
Aug.2010
线性调频连续波时频分析中的余弦变换方法 赵继广 ,宋一铄。,张智诠 (1.装甲兵工程学院控制工程系,北京100072;2.装备指挥技术学院,北京101416)
摘 要:LFM/CW测距系统中利用傅里叶变换进行时频分析从而得到差频信号的频率,针对其测距分辨力不 够高且运算量大、难于实现实时多距离分辨等问题,提出利用余弦变换进行时频分析的方法。利用余弦变换在 处理零初始相位单频信号时具有高频率分辨力这一优点,将其应用于处理LFM/CW体制测距系统的差频信 号从而提高测距分辨力。理论分析和仿真证实了在一定距离范围内,使用余弦变换处理差频信号可以得到近 似正确的频谱,相比使用傅里叶变换时其测距分辨力提高了一倍。 关键词:LFM/CW;初始相位;余弦变换;分辨力 . 中图分类号:TN911文献标志码:A 文章编号:1008—1194(2010)04—0065—04
Cosine Transform in Joint Time-frequency Analysis of LFM/CW Range Finder ZHAO Jiguang ”,SONG Yishuo ,ZHANG Zhiquan ((1.Dept of Control Engineering,Academy of Armored Force Engineering,Beijing 100072,China; 2.Academy of Equipment Command&Technology,Beijing 101416,China)
Abstract:Fourier transform was commonly used in LFM/CW range finder to analysis IF signals in frequency domain,and tO get the differential frequency signa1.Aiming at the problems of low distance resolution and the large calculation amount of Fourier transform,this paper presented a method with cosine transform tO do the joint time-frequency analysis for real time multi—distance recognition.The cosine tranforrn has the advantages of high frequency resolution when processing zero-initialization phase single frequency signal,and it was applied to the signal processing of the LFM/CW range finder tO promote the distance resolution.Theoretical analysis and simulations validated the fact that within certain distances,cosine transform gave the approximate correct spec— trum and featured a doubled distance resolution comparing tO that of Fourier transform. Key words:LFM/CW;initialization phase;cosine transform;resolution
0 引言 线性调频连续波(Linear Frequency Modula~ tion/Continuous Wave,LFM/cw)体制测距系统, 通过对回波信号与本振信号混频后得到的差频信号 频率的测量实现对目标距离的测量_1]。该测距系统 在一些距离范围内获得的差频信号的初始相位近似 为0,目前一般利用傅里叶变换进行时频分析_2]从 而得到差频信号的频率,但由于其测距分辨力不够 高且运算量大,因此难于实现实时多距离分辨。为 此,本文提出利用余弦变换进行时频分析的方法。 1傅里叶变换与余弦变换 傅里叶变换是进行频谱分析的重要方法,余弦 变换是傅里叶变换的一部分。傅里叶变换具有普适 性,对于一般信号都能给出正确的频谱。具体到一 些拥有特殊性质的信号,可以考虑利用其他时频分 析方法处理,从而突出某一方面的性能。例如对于 初始相位为0(或近似为O)的余弦信号,余弦变换不 *收稿日期:2010-03~21 修回日期:2010—06—17 基金项目:总装预研基金项目资助(9140A05070508BQ0103) 作者简介:赵继广(1967一),男,山东五莲人,博士,教授,研究方向:光电检测技术。E-mail:stephensong1。05@sina.
corn.cn。 66 探测与控制学报 仅能够给出近似正确的频谱,还具有较小的运算 量E。]和更高的频率分辨力。 1.1傅里叶变换 在实际应用中受器件和环境等因素的影响,所 得到的差频信号的信噪比较低。由于傅里叶变换对 噪声抑制能力强,所以一般用其获得信号频谱信息。 根据傅里叶变换的定义,连续非周期信号s(£)的傅 里叶变换可以表示为E :
SOw)一 £)e--i d (1) 将式(1)展开,得到 SOw)=J s(£)COS(wt)dt+J J s(£)sin(叫£)dt (2) 对上式取模,即得到信号的频谱。由(2)式可知:将 信号s( )分别与各种频率下的余弦和正弦信号进行 混频,再将每一个频率下的两个混频结果取模就得 到了该频率下的频谱幅值。由于连续非周期信号等 同于周期无限大的周期信号,所以得到的频谱应该 被理解为频谱密度。信号s(£)中包含的任一频率分 量的初始相位都是未知的,频谱分析不应受到未知 初始相位的影响,所以傅里叶变换采用正交混频并 取模的方式,使得只要信号s(f)中存在该频率分量, 计算结果就会在该频率点上得到峰值且不会受到其 初始相位的影响。 对频率为 ,时长为T的余弦信号,无论其初 始相位如何,对其进行傅里叶变换后,其频域将呈现 一个峰值在 处的SINC函数,如图1所示。 越 馨 r | 1 .| } |’ | \ 图1 1 ms时长矩形窗函数的傅立叶变换频谱图 Fig.1 The frequency spectrum of 1 ms-lasting rectangular window in Fourier transform 1.2余弦变换 连续非周期信号s 的余弦变换为 引: S(jw)一I S (t)cos(wt)dt (3) 在余弦变换下,由于没有涉及正交混频,所以信 号的初始相位不同会引起频谱误差,即通过余弦变 换得到的频谱会因为信号的初始相位而出现频谱偏 移和畸变。例如对一时长为T、频率为厂1且初始相 位 。不为0的余弦信号 5(£)一cos(2丌 t+ ),0≤t≤T (4) 作余弦变换,得到信号频谱 s(D== 格 (5) 由于: sin 。)一 0 1 , 兀 .,一.厂 』 (6) 故有: S(厂1)一Tsin ( )一Tcos( ̄o) (7) 由式(7)可知用余弦变换得到的频谱函数在差频信 号频率点上的幅度会受到初始相位的影响。只有当 信号初始相位为0(或近似为0)时,才能得到和傅里 叶变换一致(或近似一致)的结果,即在频域呈现一 个峰值在 处的SINC函数,如图2所示。
】晕 | J / \ l f.
图2 1 ms时长矩形窗函数的余弦变换频谱图 Fig.2 The frequency spectrum of 1 ms-lasting rectangular window in cosine transfoITn
2线性调频连续波时频分析的余弦变 换原理
LFM/CW体制测距系统将回波信号与本振信 号混频得到差频信号,该差频信号的频率与目标距 离间存在线性关系Ⅲ。在实际应用中,综合考虑信 号信噪比和抗干扰能力等因素,一般利用傅里叶变 换提取差频信号的频率。如果在一次测量中存在两
\ 赵继广等:线性调频连续波时频分析中的余弦变换方法 67 个或以上不同距离的目标,那么得到的差频信号中 也含有与这些目标距离对应的频率。分辨开这些频 率就分辨开了这些不同的距离。由第一节中傅里叶 变换和余弦变换的性质可知,对于时长为T的余弦 信号,两种变换下的频率分辨力分别为丁L 和 0.5,r ,但使用余弦变换时要求信号的初始相位近 似为零以避免频谱偏移和失真。LFM/CW体制测 距系统得到的差频信号由一个或多个余弦信号组 成,通过改变系统参数,这些余弦信号的初始相位在
一些距离范围内近似为O,此时利用余弦变换可得 到近似正确的信号频谱。这使余弦变换在LFM/ CW测距中的应用成为可能,即可利用余弦变换处 理差频信号,使得在差频信号时长不变的情况下,将 频率分辨力提高到使用傅里叶变换时的两倍。
3余弦变换在LFM/CW体制测距系 统中的应用
3.1余弦变换下LFM/CW体制测距系统的测距分 辨力 具体到LFM/CW体制测距系统[6],由于一个 周期内观察到的差频信号的频率为 ,时长约等于 扫频周期T,故对其进行傅里叶变换后,其频域将呈 现一个峰值在. 处的SINC函数,此时SINC函数 的主瓣宽度为r ,频率分辨力为TL ,即如果两个 差频信号相差小于r 则会造成频谱叠加而无法分 辨。所以如果发射信号扫频带宽为B,则利用傅里叶 变换处理被矩形窗截短的差频信号时,LFM/CW体 制测距系统的测距分辨力为: △R一0.5cB (8) 这说明如果系统探测到的两个目标之间的距离差小 于0.5cB~,则不能正确分辨两个目标。相比在傅里 叶变换下得到的结果,利用余弦变换得到的SINC函 数主瓣宽度不再是丁L ,而是0.5了L 。即对于初始相 位为0(或近似为0)的余弦信号,在信号时长为T的 情况下,其频率分辨力为0.5TL ,比傅里叶变换提 高了一倍,相应的测距分辨力也提高到 △R一0.25cB (9) 3.2差频信号分析 LFM/CW体制测距系统得到的差频信号由回 波信号与本振信号经混频滤波后得到,在r≤t≤T 时间内,其形式由式(10)给出l_6]。