QAM盲载波恢复算法---DD算法(频率捕获范围代码)
- 格式:docx
- 大小:13.25 KB
- 文档页数:5

数字调制信号接收技术孙海祥;刘杰【摘要】为了实现时多种数字信号的解调,设计了一种全数字接收机体制.对通用环载波同步方法及内插滤波码元同步方法进行了深入分析和设计.仿真结果表明,在误比特率为10-4时,所需Eb/N0比理论值高2 dB.基于通用环和内插定时技术的全数字接收机适用于对PSK,QAM数字调制信号的接收解调,满足数字VSLI硬件实现高集成度、小型化接收机的要求.【期刊名称】《现代电子技术》【年(卷),期】2008(031)015【总页数】4页(P171-173,177)【关键词】载波恢复;定时恢复;内插滤波;全数字接收【作者】孙海祥;刘杰【作者单位】中国电子科技集团公司,第54研究所,河北,石家庄,050081;中国电子科技集团公司,第54研究所,河北,石家庄,050081【正文语种】中文【中图分类】TN911.3近年来,数字无线电技术日益受到人们的重视。
数字无线电技术因采用软件化数字化设计,工作稳定可靠,可生产性好,设备小巧,因而在通信中应用越来越广泛。
随着大规模集成电路的发展以及对通信设备小型化、智能化的要求,数字无线电技术已经成为发展趋势。
全数字接收机的概念被提出后立刻引起了人们的兴趣与关注,它和传统的数字接收机不同,其解调和采样所用的本地参考时钟振荡于固定的频率,且不需要反馈控制,滤波、载波同步、时钟同步、数据判决等全由采样后的数字信号处理器来完成。
本文设计提出了适于中频数字化接收机的体制结构和实现方法。
1 全数字接收机组成全数字接收机对中频信号进行采样后,全部采用数字器件和数字处理方法,是一种全数字实现方案。
因其采用数字解调方法,克服了由模拟器件构成的解调器同相与正交两支路参数不一致的缺点。
虽然对已调信号采样要求ADC的采样率较高,但现今的高速ADC器件已足够满足要求。
全数字接收机结构如图1所示。
数字中频信号分别与两路正交载波相乘,然后低通滤波抽取,滤除二次频项,完成数字正交下变频,得到I,Q两路信号。
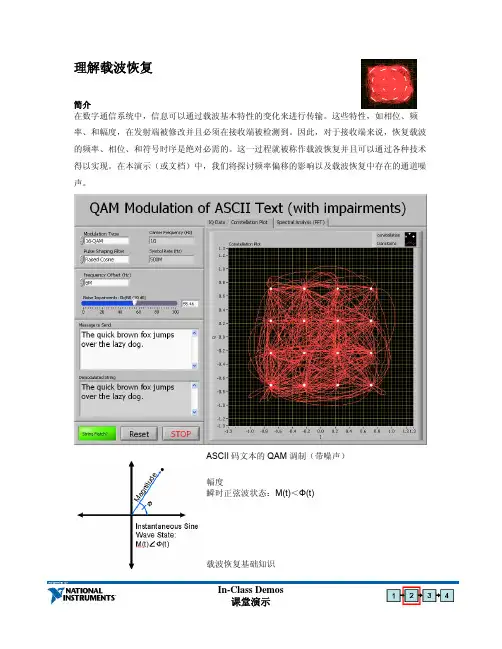
理解载波恢复简介在数字通信系统中,信息可以通过载波基本特性的变化来进行传输。
这些特性,如相位、频率、和幅度,在发射端被修改并且必须在接收端被检测到。
因此,对于接收端来说,恢复载波的频率、相位、和符号时序是绝对必需的。
这一过程就被称作载波恢复并且可以通过各种技术得以实现。
在本演示(或文档)中,我们将探讨频率偏移的影响以及载波恢复中存在的通道噪声。
ASCII 码文本的QAM 调制(带噪声)幅度瞬时正弦波状态:M(t)<Φ(t)载波恢复基础知识In-Class Demos一个QAM 发送端使用特定的相位和幅度来调制载波信号,而另一方面,如果接收器能够确定原始信号的相位和频率,那它就能准确地检测到这个信号。
因此,两者之间的同步是必需的。
在理想情况下,发送端和接收端将会完美地同步工作。
换句话说,两者将会以同样的方式解释信号的相位和频率。
然而,实际的硬件并不是完美的,而且即使利用某种纠错机制,接收端也不可能精确地锁定到与发送端完全相同的相位和频率。
为了弥补这些不尽完美的特性,采用锁相环或PLL 来匹配接收端和发送端之间的频率(1)。
利用星座图,我们可以表示出每个符号的幅度和相位。
此外,每个符号覆盖在另一个符号之上是为了说明与我们所能恢复载波的相位和幅度之间的一致性。
理想情况下,当接收端的PLL 能够恢复载波,那么每个符号就会在星座图上清楚地分布。
然而,当载波由于通道噪声或频率误差的原因而无法恢复时,星座图也能表示来了。
在右边,我们示出了一幅符号出现在正确幅度处,但其相位正持续变化的星座图。
因为:Frequency = d Θ / dt频率= d Θ / dt所以,当星座图的相位持续变化时,我们能够确定频率估计是错误的。
在这个特定的实例中,我们已经通过在系统中引入足够的噪声来仿真频率误差,从而得以干扰PLL ,甚至将噪声去除之后,PLL 仍然可能无法锁定正确的频率。
载波恢复步骤解决这个载波恢复问题的方法有两个部分,它们可以粗略地分为以下两个部分:频率恢复和符号时序(相位)恢复。


DTMB接收机定时恢复算法及其高效VLSI实现
张阳;陈赟;巫建明;曾晓洋
【期刊名称】《小型微型计算机系统》
【年(卷),期】2008(29)10
【摘要】提出一种基于中国数字电视标准DTMB(Digital Terrestrial/Television Multimedia Broadcasting)的时域定时恢复方案.该方案采用全数字延迟锁定环来跟踪定时误差,与传统的时域鉴相器相比,本文提出的鉴相算法能实现增益的自动归一化,且捕获范围为原算法的三倍,能纠正采样频率偏差达到±90ppm.此外本方案能实现环路带宽的自动调整,以兼顾较快的收敛速度和较小的抖动.本文最后给出了此方案的性能仿真及VLSI实现结果.
【总页数】4页(P1944-1947)
【作者】张阳;陈赟;巫建明;曾晓洋
【作者单位】复旦大学,专用集成电路与系统国家重点实验室,上海,201203;复旦大学,专用集成电路与系统国家重点实验室,上海,201203;复旦大学,专用集成电路与系统国家重点实验室,上海,201203;复旦大学,专用集成电路与系统国家重点实验室,上海,201203
【正文语种】中文
【中图分类】TP331
【相关文献】
1.基于DVB-C的QAM接收机定时恢复算法 [J], 谭泽富;廖明霞;晏先伟;吴婷婷
2.基于DSP Builder全数字接收机定时载波同步算法的实现 [J], 陈舒;刘奇佳;刘昌清;赵克明
3.全数字接收机中定时同步算法和实现 [J], 晏蕾;余荣;梅顺良
4.全数字接收机定时恢复算法的FPGA实现 [J], 赵毅;梁淮宁;程晓军
5.dPMR接收机定时估计算法及FPGA实现 [J], 朱子文;张涛;关汉兴
因版权原因,仅展示原文概要,查看原文内容请购买。



改进的16QAM载波频偏估计算法向劲松;刘飞;马圣明;杨松【期刊名称】《电视技术》【年(卷),期】2013(37)15【摘要】Aiming at the carrier frequency offset estimation algorithm with the small estimated range and the high computational complexity problem,a new FFT frequency offset estimation algorithm based on training symbols is proposed for QAM coherent optical transmission system,which removes the modulated phase information from the received signal accurately using training sequence.Then a estimation value by using the peak of a period gram,which is employing FFT transform is got.The computing divided by 4 in the original offset estimation algorithm is eliminated to expand the range of frequency offset estimation,and the computational complexity is reduced by decreasing the FFT transform length.The simulation results show that the improved algorithm has a higher frequency offset estimation accuracy and larger estimation range,and its estimation range is about 50% of the symbol rate.%针对QAM相干光传输系统中载波频偏估计算法存在估计范围小、计算复杂度高的问题,提出一种基于训练符号的FFT频偏估计算法.利用训练符号相位信息消除部分采样信号调制相位,取该部分信号的幅角进行FFT变换,最终得到频偏估计值.消除了原频偏估计算法中除以4的运算,从而扩大了频偏估计范围,同时由于减少了FFT长度进而降低计算复杂度.仿真结果表明,改进后的算法在QAM相干检测系统保持较高精度的频偏估计情况下,其估计范围可以达到±50%符号速率.【总页数】3页(P156-158)【作者】向劲松;刘飞;马圣明;杨松【作者单位】重庆邮电大学光纤通信技术重点实验室,重庆400065;重庆邮电大学光纤通信技术重点实验室,重庆400065;重庆邮电大学光纤通信技术重点实验室,重庆400065;重庆邮电大学光纤通信技术重点实验室,重庆400065【正文语种】中文【中图分类】TN911【相关文献】1.适用于16QAM信号的载波频偏估计算法 [J], 周庆龙;肖龙;江桦2.协作OFDM系统中改进的载波频偏估计算法 [J], 鲍晶晶;赵兴华3.一种基于16QAM调制系统的LDPC改进算法 [J], 邓洪高;黄宇仁;孙少帅4.OFDM系统中改进的16QAM软判决解调算法 [J], 张力;施玉松;姜建;李甲;王营冠5.一种适用于16QAM的自适应阈值载波锁定检测算法 [J], 刘洋因版权原因,仅展示原文概要,查看原文内容请购买。


QAM是一种在两个正交载波上进行幅度调制的调制方式。
这两个载波通常是相位差为90度(π/2)的正弦波,因此被称作正交载波。
这种调制方式因此而得名。
概述同其它调制方式类似,QAM通过载波某些参数的变化传输信息。
在QAM中,数据信号由相互正交的两个载波的幅度变化表示。
模拟信号的相位调制和数字信号的PSK可以被认为是幅度不变、仅有相位变化的特殊的正交幅度调制。
由此,模拟信号频率调制和数字信号FSK也可以被认为是QAM的特例,因为它们本质上就是相位调制。
这里主要讨论数字信号的QAM,虽然模拟信号QAM也有很多应用,例如NTSC和PAL制式的电视系统就利用正交的载波传输不同的颜色分量。
类似于其他数字调制方式,QAM发射信号集可以用星座图方便地表示。
星座图上每一个星座点对应发射信号集中的一个信号。
设正交幅度调制的发射信号集大小为N,称之为N-QAM。
星座点经常采用水平和垂直方向等间距的正方网格配置,当然也有其他的配置方式。
数字通信中数据常采用二进制表示,这种情况下星座点的个数一般是2的幂。
常见的QAM形式有16-QAM、64-QAM、256-QAM等。
星座点数越多,每个符号能传输的信息量就越大。
但是,如果在星座图的平均能量保持不变的情况下增加星座点,会使星座点之间的距离变小,进而导致误码率上升。
因此高阶星座图的可靠性比低阶要差。
当对数据传输速率的要求高过8-PSK能提供的上限时,一般采用QAM的调制方式。
因为QAM的星座点比PSK的星座点更分散,星座点之间的距离因之更大,所以能提供更好的传输性能。
但是QAM星座点的幅度不是完全相同的,所以它的解调器需要能同时正确检测相位和幅度,不像PSK解调只需要检测相位,这增加了QAM解调器的复杂性。
M-QAM信号波形的表达式为:其中g(t)为码元信号脉冲。
因此QAM可以分解为分别在两个正交的载波cos2πfct与sin2πfct上的M1-PAM与M2-PAM的叠加,其中M1M2 = M。


8qam 调制符号计算公式
8QAM(Quadrature Amplitude Modulation)是一种调制方式,用于数
字信号的传输。
QAM是一种振幅和相位联合调制的方式,它同时利用了载
波的幅度和相位来传输信息。
8QAM的调制符号计算公式如下:
1. 归一化因子公式:μ = 32EsM−1\mu = \sqrt{\frac{3}{2}\frac{E_s}{M-1}}μ=23M−1Esμμ。
其中,μ 是归一化因子,M 是调制阶数(这里 M=8),Es 是每个符号的平均能量。
2. 比特数计算:k = log2(M)k = \log_2(M)k=log2(M)。
其中,k 是每个码元的比特数(这里 k=3)。
3. 符号数计算:n = 9999n = 9999n=9999(因为是8QAM调制,所以不能使用10000,因为10000不能被3整除,在航类转换时会出错)。
4. 重复取样速率:nsamp = 1nsamp = 1nsamp=1。
5. 随机数组生成:x = randint(n,1)x = \randint(n,1)x=randint(n,1)。
这会生成一个 n 列 1 行的取值为 0 或 1 的随机数组。
以上信息仅供参考,如需获取更多详细信息,建议咨询通信工程专家或查阅通信工程相关书籍。
在MATLAB中,QPSK解调算法的实现通常包括以下几个步骤:1. 载波恢复:首先,需要从接收到的信号中恢复出载波。
这通常是通过相乘或相除的方式完成的,即通过将接收到的信号与恢复的载波相乘或相除来去除载波。
2. 符号解调:在恢复载波之后,需要进行符号解调。
这通常是通过比较接收到的信号与参考信号的相位差来实现的。
根据比较结果,可以确定接收到的符号是0还是1。
3. 解调后的信号处理:在解调之后,通常需要对解调后的信号进行一些处理,例如去除直流分量、低通滤波等。
下面是一个简单的MATLAB代码示例,演示了如何实现QPSK解调:生成QPSK信号M = 4; % QPSK的调制阶数data = randi([0 M-1], 1000, 1); % 生成1000个随机数据modData = qammod(data, M); % QPSK调制加入高斯白噪声SNR = 10; % 信噪比noise = sqrt(1/2)*(randn(size(modData)) + 1i*randn(size(modData))); % 生成高斯白噪声receivedSignal = modData + noise; % 加入噪声QPSK解调demodData = qamdemod(receivedSignal, M, 'Peak'); % QPSK解调计算误码率errors = sum(abs(data - demodData)) / length(data); % 计算误码率fprintf('误码率为: %f\n', errors);请注意,这只是一个简单的示例代码,实际应用中可能需要更复杂的处理和优化。
此外,上述代码中使用的`qammod`和`qamdemod`函数是MATLAB中提供的QAM调制和解调函数,对于QPSK来说,它们可以正常工作。
多载波调制技术概述多载波调制技术是一种通过同时将多个载波进行调制,将数字信号转换为模拟信号进行传输的技术。
在数字通信系统中,通过多载波调制技术可以有效地提高信号传输的效率和带宽利用率,同时也能减少信号传输过程中的误码率,提高通信质量。
多载波调制技术主要包括正交频分复用(OFDM)、正交振幅调制(QAM)、正交相移键控(QPSK)等技术。
这些技术在数字通信系统中广泛应用,其中OFDM技术更是在无线通信系统中得到了广泛应用,如Wi-Fi、4G、5G等。
正交频分复用(OFDM)是一种将高速数字数据流分割成多个低速子载波进行同时传输的技术。
通过将子载波频率间隔设置为互不干扰的正交频率,可以有效地提高频谱利用率,并且抵抗多径效应和频率选择性衰落。
这种技术不仅可以提高信号传输速率,还可以降低信号传输时的功耗,实现高效的数据传输。
正交振幅调制(QAM)是一种通过改变振幅和相位来传输数据的调制技术。
QAM技术将信号分解成实部和虚部进行传输,通过改变振幅和相位的组合来表示不同的数据位,从而提高信号传输的效率和可靠性。
QAM技术可以在有限的带宽内传输更多的数据,具有很高的频谱利用率。
正交相移键控(QPSK)是一种将数字信号转换为相位信号的调制技术。
QPSK技术将每个信号符号分为4个相位进行传输,每个相位代表2个比特信息。
通过改变相位的组合,可以表示不同的数字信息,从而提高信号传输效率和可靠性。
QPSK技术在数字通信系统中得到广泛应用,尤其在卫星通信、光纤通信等方面有着重要的作用。
总的来说,多载波调制技术在数字通信系统中发挥着重要的作用,可以提高信号传输的效率、带宽利用率和通信质量。
随着通信技术的不断发展,多载波调制技术将会继续完善和应用,为通信领域的发展带来更多的创新和进步。
用于深空通信的载波同步技术魏苗苗;刘洲峰;王竹刚【摘要】为了适应极低信噪比高动态的深空通信条件,采用去符号频域移位平均周期图法和分区搜索法完成高动态环境下的载波频偏、频偏变化率和相偏的粗同步过程,并采用译码辅助的载波同步算法实现载波细同步过程.仿真表明,在信噪比为1.5 dB,相偏(-180°,180°),频偏(-300,300)kHz,频偏变化率(-800,800)Hz/s时,该算法方案能够有效纠正载波偏差以及相位模糊,获得了BPSK译码结果距离理想同步0.1 dB以内的误码性能.【期刊名称】《电子设计工程》【年(卷),期】2018(026)020【总页数】5页(P93-97)【关键词】高动态;低信噪比;LDPC码;迭代载波同步;频域移位平均周期图法【作者】魏苗苗;刘洲峰;王竹刚【作者单位】中原工学院电子信息学院河南郑州451191;中原工学院电子信息学院河南郑州451191;中国科学院国家空间科学中心,北京100190【正文语种】中文【中图分类】TN911深空通信[1]由于其遥远的传输距离和特殊的运动情况,对通信接收机系统有着很高的要求。
在接收和遥测的过程中,首先要克服深空信道中的各种噪声带来信噪比极低的问题,其次火星EDL(Entry,Descent and Landing)阶段探测器会处于较高的运动状态[2-3],因此还需解决高动态适应性问题。
针对低信噪比的问题,近年来国内外学者提出了多种利用译码辅助同步算法[4-11],但是该类算法的同步范围有限;为提高该类算法的动态适用性,文中将改进的频域移位周期图法与译码辅助算法相结合,设计了一种针对深空通信条件下的同步系统并根据算法特点完成参数设计,实现在低信噪比高动态环境下对载波相偏、频偏以及频偏变化率的估计。
经仿真,该算法在信噪比1.5 dB、火星EDL动态模型下系统可以实现误码率达到10-3以下。
1 系统模型系统采用LDPC(Low density Parity Check Code,低密度奇偶校验)编码方式,译码算法使用置信传播(BP)译码方式,调制方式为BPSK,噪声选择高斯白噪声(AWGN)。
全数字QAM解调器的设计与FPGA实现张华冲;王晓亚【摘要】正交幅度调制(QAM)是一种频谱利用率较高的调制方式.分析了影响解调性能的主要因素以及解决方法,提出了一种QAM解调器的全数字实现结构.介绍了符号同步环路的构成,在设计中采用FARROW结构立方内插器,内插控制器为内插器提供控制变量,对内插控制器的实现进行了详细介绍,定时误差提取采用Gardner 算法.采用结合均衡的载波恢复混合结构,显著提高了载波恢复的性能.所设计的解调器可以应用于通信、侦察接收机中.【期刊名称】《无线电工程》【年(卷),期】2010(040)006【总页数】4页(P27-30)【关键词】全数字接收机;内插滤波器;符号同步【作者】张华冲;王晓亚【作者单位】中国电子科技集团公司第五十四研究所,河北,石家庄,050081;中国电子科技集团公司第五十四研究所,河北,石家庄,050081【正文语种】中文【中图分类】TN9110 引言QAM是一种频谱利用率较高的调制方式。
在频谱资源日益紧张的今天,越来越多的领域采用了这一调制方式,如有线视频广播(DVB-C)、宽带接入和SDH等许多高速通信系统中。
由于收发双方本振频率存在必然的差异,这样就导致收发双方载波频率会有微小的偏差,传播延时还会造成载波相位的偏移。
在接收机中收发双方的延时一般是未知的,并且AD采样还会产生采样频偏与相偏,这些是解调器中的载波同步与符号同步需要解决的问题。
信道衰减、多径、白噪声干扰和回波叠加等非理想因素的影响使得QAM信号经过信道传输后产生了幅度、频率和相位失真,造成码间串扰(ISI),严重的码间串扰甚至使通信中断。
QAM调制信号、幅度和相位上都携带有信息,对信道失真尤其敏感,所以QAM信号的解调还应当包含自动增益控制(AGC)和均衡等环节。
1 QAM解调器总体结构随着ADC采样频率的提高以及高速数字信号处理芯片的发展,模数转换模块的位置逐渐向着射频方向移动。
%%DD算法---频率捕获范围
%仿真参数
N = 500000;
M = 256;
SNR = 30;
samplingFreq = 5000000;
carrFreqOffset = -300000:20000:300000;
carrPhsOffset = 0;
h1 = modem.qammod('M',2^8, 'SymbolOrder', 'Gray');
h2 = modem.qamdemod('M', 2^8, 'SymbolOrder', 'Gray');
%鉴相器参量
DifferOfPha = zeros(1,N);
DD_bitsOutput = zeros(1,N);
DD_DifferOfPha = zeros(1,N);
Z = zeros(1,N);
Y = zeros(1,256);
%锁定检测器参量
lamuda = 0.7;
beita = 0.6;
Ncounter = 0;
Track_sign = 0;
MeanOfY = 0;
Lock_N = zeros(1,length(carrFreqOffset));
%环路滤波器及NCO参量
fs = samplingFreq;
fn = 50000;
yita = 0.5;
wn = 2*pi*fn/fs;
Kp = 2*yita*wn;
Ki = wn^2;
PraZ = 0;
PhasControl = 0;
PhaseOfNCO = 0;
%环路捕获频率
PreAcqFreq = 0;
RealAcqFreq = zeros(1,length(carrFreqOffset));
%通信过程仿真
for fre = 1:1:length(carrFreqOffset)
bitSrc = randi([0 M-1],1,N);
bitsTransmit = modulate(h1,bitSrc);
phaseStep = carrFreqOffset(fre) / samplingFreq;
phaseVar = phaseStep * (0:1:length(bitsTransmit)-1);
aftFreOffset = bitsTransmit .* exp(1j*(2*pi*phaseVar+carrPhsOffset));
bitsnoise = awgn(aftFreOffset,SNR,'measured');
for m=1:N
%%PD
DifferOfPha(m) = bitsnoise(m)*exp(-1j*PhaseOfNCO);
DD_bitsOutput(m) = demodulate(h2,DifferOfPha(m));
DD_DifferOfPha(m) = modulate(h1,DD_bitsOutput(m));
Ncounter=Ncounter+1;
if(abs(DD_DifferOfPha(m)-DifferOfPha(m))
else
Y(Ncounter)=0;
end
if(Ncounter==256)
MeanOfY = mean(Y);
Ncounter = 0;
end
if(Track_sign==0)
Z(m) = imag(DifferOfPha(m)/DD_DifferOfPha(m));
if(MeanOfY>yita)
Track_sign = 1;
Lock_N(fre) = m;
end
else
Z(m) = imag(DifferOfPha(m)/DD_DifferOfPha(m));
end
%%Loop Filter
Phaz = Kp*Z(m) + PhasControl;
PhasControl = Ki*Z(m) + PhasControl;
%%NCO
PhaseOfNCO = PhaseOfNCO + Phaz;
%%acqucisition frequency
Acqfreq = 0.01*PhasControl + 0.99*PreAcqFreq;
PreAcqFreq = Acqfreq;
RealAcqFreq(fre) = PreAcqFreq/2/pi*5000000;
end
end
%figure
figure(1);
i1 = 1:1:length(carrFreqOffset);
plot((i1-16)*20000,RealAcqFreq,'k-*','linewidth',2);
xlabel('实际频率偏移/Hz');
ylabel('环路捕获频率/Hz');
grid on;
if 0
figure(2);
i2 = 1:1:length(carrFreqOffset);
plot((i1-16)*20000,Lock_N,'k-*','linewidth',2);
xlabel('实际频率偏移/Hz');
ylabel('环路工作时间/T');
end