典型光学系统部分例题
- 格式:ppt
- 大小:916.00 KB
- 文档页数:10
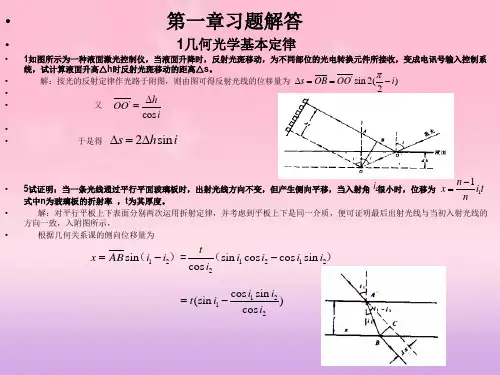

第一章1、已知真空中的光速c =3 m/s ,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s, 当光在冕牌玻璃中,n=1.51时,v=1.99 m/s, 当光在火石玻璃中,n =1.65时,v=1.82 m/s , 当光在加拿大树胶中,n=1.526时,v=1.97 m/s , 当光在金刚石中,n=2.417时,v=1.24 m/s 。
(例题)2、一物体经针孔相机在 屏上成一60mm 大小的像,若将屏拉远50mm ,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x ,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm 。
(例题)3、一厚度为200mm 的平行平板玻璃(设n=1.5),下面放一直径为1mm 的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?1mmI 1=90n 1 n 2 200mmLI 2x解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。


工程光学-1-4章例题分析(总22页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第一章1、已知真空中的光速c =3 m/s ,求光在水(n=)、冕牌玻璃(n=)、火石玻璃(n=)、加拿大树胶(n=)、金刚石(n=)等介质中的光速。
解:则当光在水中,n=时,v= m/s, 当光在冕牌玻璃中,n=时,v= m/s, 当光在火石玻璃中,n =时,v= m/s , 当光在加拿大树胶中,n=时,v= m/s , 当光在金刚石中,n=时,v= m/s 。
(例题)2、一物体经针孔相机在 屏上成一60mm 大小的像,若将屏拉远50mm ,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x ,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm 。
(例题)3、一厚度为200mm 的平行平板玻璃(设n=),下面放一直径为1mm 的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少解:令纸片最小半径为x, 则根据全反射原理,光束由玻璃射向空气中时满1mmI 1=90n 1 n 2 200mmLI 2x足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=, 同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=,所以纸片最小直径为。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n,求光纤的数值孔径(即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有:n0sinI1=n2sinI2(1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到nsinI1 .(例题)5、一束平行细光束入射到一半径r=30mm、折射率n=的玻璃球上,求其会聚点的位置。
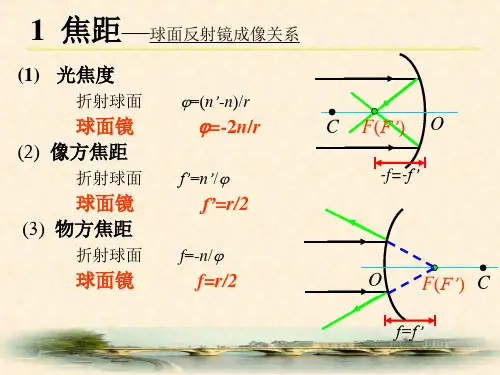

近轴光学系统例1.一厚度为200mm的平行平板玻璃(n=1.5)下面放着一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片的最小直径为多少?例2.用费马定理证明光的折射定律和反射定律。
例3.如图有两个平面反射镜,M1、M2夹角为α,今在两反射镜之间有一光线以50°角入射,入射到M1的反射镜上,经M1、M2四次反射后,起反射光线与M1平行,求其夹角α。
例4.设计一个在空气中和某种玻璃之间的单个折射表面构成的光学系统,希望物在空气中离表面15.0cm。
实像在玻璃中,离表面45.0cm,放大率为2.0。
那么玻璃的折射率应为多少?表面的曲率半径为多少?例5.直径为100mm的球形玻璃缸,将半面镀银,内有一条鱼在镀银面前25mm处。
问缸外的观察者看到几条鱼?位置在何处?相对大小事多少?(水的折射率为4/3)例6.在一张报纸上放一个平凹透镜,通过镜面看报纸。
当平面朝着眼睛时,报纸的虚像在平面下13.3mm处。
当凸面朝着眼睛时,报纸的虚像在凸面下14.6mm处。
若透镜中央厚度为20mm。
求透镜的折射率和凸球面的曲率半径。
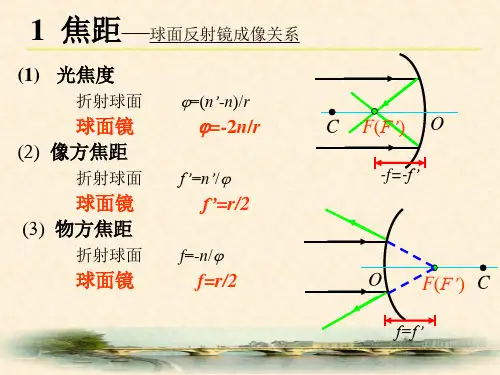
例7.一凹球面镜将一实物成一实像,物与像的距离为1m,物高为像高的4倍,求凹面镜的曲率半径。
例8.①一束平行光入射到一半径r=30mm,折射率n=1.5的玻璃球上,求其汇聚点的位置。
②如果在凸面上镀反射膜,其汇聚点应在何处?③如果凹面镀反射膜,则反射光束在玻璃中的汇聚点在何处?④反射光束经前表面折射后,汇聚点在何处?说明各汇聚点的虚实。
(2)(3)(4)例9.一直径为400mm,折射率为1.5的玻璃球中有两个小气泡,一个位于球心,另一个在1/2半径处。
沿两气泡连线方向在球两边观察,问看到的气泡在何处?如果在水中观察者看到的气泡又在何处?例10.位于空气中的等腰直角棱镜折射率n=1.54,问当光线在斜边上发生全反射时直角边1上入射光线的入射角I1应为多大?若棱镜折射率增大,I1增大还是减小?又问若棱镜放入水中,按图中光轴方向入射的光线是否会发生全反射。
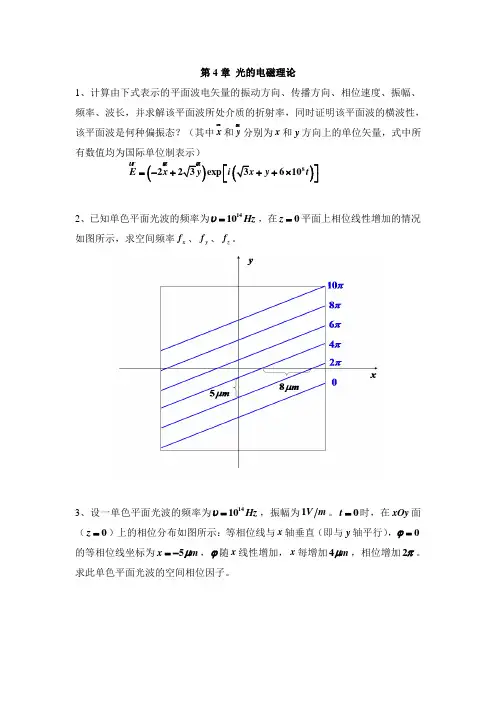
第4章 光的电磁理论1、计算由下式表示的平面波电矢量的振动方向、传播方向、相位速度、振幅、频率、波长,并求解该平面波所处介质的折射率,同时证明该平面波的横波性,该平面波是何种偏振态?(其中x 和y 分别为x 和y 方向上的单位矢量,式中所有数值均为国际单位制表示)())8223exp 610E x y i y t ⎡⎤=-+++⨯⎣⎦ 2、已知单色平面光波的频率为1410Hz υ=,在0z =平面上相位线性增加的情况如图所示,求空间频率x f 、y f 、z f 。
3、设一单色平面光波的频率为1410Hz υ=,振幅为1V m 。
0t =时,在xOy 面(0z =)上的相位分布如图所示:等相位线与x 轴垂直(即与y 轴平行),0ϕ=的等相位线坐标为5x m μ=-,ϕ随x 线性增加,x 每增加4m μ,相位增加2π。
求此单色平面光波的空间相位因子。
4、试确定下列各组光波表达式所代表的偏振态:(1)、()0si n x E E t k z ω=-,()0cos y E E t kz ω=- (2)、()0co s x E E t k z ω=-,()0cos 4y E E t kz ωπ=-+ (3)、()0si n x E E t kz ω=-,()0sin y E E t kz ω=--5、若要使自然光经过红宝石( 1.76n =)表面反射后成为完全偏振光,入射角应等于多少?求在此入射角的情况下,折射光的偏振度t P 。
6、如图所示,玻璃块周围介质(水)的折射率为1 1.33n =。
若光束射向玻璃块的入射角为45,问玻璃块的折射率至少应为多大才能使透入光束发生全反射。
7、如图所示,光束垂直入射到45直角棱镜的一个侧面,经斜面反射后从第二个侧面透出。
若入射光强为0I ,问从棱镜透出的光束的强度为多少?(设棱镜的折射率为1.52,棱镜周围为空气,并且不考虑棱镜的吸收)8、穆尼棱体能将偏振方向与入射面成45的线偏振光变成圆偏振光,如图所示。



应用光学习题本习题供学习、复习使用。
精练这些习题及作业和课件上的例题有助于掌握、理解应用光学课程的基本知识、理论和规律。
应用光学的基本问题包括在本习题内,但不仅限于本习题。
本习题仅供课程学习时参考。
习题中一些问题提供了解答,限于时间,其它则略去。
一、筒答题1、几何光学的基本定律及其内容是什么?答:几何光学的基本定律是自钱传播定律、独立传播定W:、反射定律和折射定律。
直线传播定律:光线在均匀透明介质中按直线传播。
独立传播定律:不同光源的光在通过介质某点时互不影响。
反射定律:反射光线位于入射面内;反射角等于入射角:折射定律:折射光线位于入射面内:入射角和折射角正弦之比,对两种定的介j员来说,是=个和入射角无关的常数n isin/,-msin/。
22、理想光学系统的基点和基面有哪些?理想光学系统的基点包指物方焦点、{象方焦点;物方主点、像方主点:物方节点、像方节点。
基面包括:物方焦平丽、像方然平面:物方主平丽、像方主平面;物方节平面、像方节平面。
3、什么是光学系统的孔役光阑和视场光阙?答:孔径光阑是限制轴上物点成像光束立体角的光阔。
晴荡艾丽王辅前有字亩7茧事宝肯车夜夜古国的光册J。
4、常见非正常跟有哪两种?如何校正常见非正常1'常见正常目艮包括近视酬远视盹近视眼将工二(远附近点)矫正到无限远,远视眼,将一丘丛(远点就近点)矫正到明视距离。
3、光'于系统极限分辨角为多大?采取什么途径可以提岗极限分辨角?答:衍射决定的极限分辨角为0=3®。
可见其与波长和孔役有关。
订蔬小波长D和增大孔径可以提高光学系统的分辨率。
I什么是共和1)也学系统、元学系统物空间、像空间?答:光学系统以一条公共制线通过系统各表面的幽率中心,该轴线称为光轴,这样的系统称为共轴光学系统。
物体所在的空间称为物空间,像所在的空间称为像空间。
、如何确定光学系统的视场Jt阙?答:将系统中除孔径光阑以外的所有光阑对其前面所有的光学零件成像到物空间;这些像中,孔径对入暗中心张角最小的一个像所对应的光阑即为光学系统的视场光阙。
一、填空题1、光学系统中物和像具有共轭关系的原因是 光路可逆 。
2、发生全反射的条件是 光从光密媒质射向光疏媒质,且入射角大于临界角I 0,其中,sinI 0=n 2/n 1 。
3、 光学系统的三种放大率是 垂轴放大率 、 角放大率 、轴向放大率 ,当物像空间的介质的折射率给定后,对于一对给定的共轭面,可提出 一 种放大率的要求。
4、 理想光学系统中,与像方焦点共轭的物点是 轴上无穷远的物点 。
5、物镜和目镜焦距分别为mm f 2'=物和mm f 25'=目的显微镜,光学筒长△= 4mm ,则该显微镜的视放大率为 -20 ,物镜的垂轴放大率为 -2 ,目镜的视放大率为 10 。
6、某物点发出的光经理想光学系统后对应的最后出射光束是会聚同心光束,则该物点所成的是 实 (填“实”或“虚”)像。
7、人眼的调节包含 视度 调节和 瞳孔 调节。
8、复杂光学系统中设置场镜的目的是 在不影响系统光学特性的的情况下改变成像光束的位置,使后面系统的通光口径不致过大。
9、要使公共垂面内的光线方向改变60度,则双平面镜夹角应为30 度。
10、近轴条件下,折射率为1.4的厚为14mm 的平行玻璃板,其等效空气层厚度为 10 mm 。
11、设计反射棱镜时,应使其展开后玻璃板的两个表面平行,目的是 保持系统的共轴性 。
12、有效地提高显微镜分辨率的途径是 提高数值孔径和减小波长 。
13、近轴情况下,在空气中看到水中鱼的表观深度要比实际深度 小 。
二、简答题1、几何光学的基本定律及其内容是什么?答:几何光学的基本定律是直线传播定律、独立传播定律、反射定律和折射定律。
直线传播定律:光线在均匀透明介质中按直线传播。
独立传播定律:不同光源的光在通过介质某点时互不影响。
反射定律:反射光线位于入射面内;反射角等于入射角;折射定律:折射光线位于入射面内;入射角和折射角正弦之比,对两种一定的介质来说,是一个和入射角无关的常数2111sin sin I n I n =。