小波变换降噪处理及其Matlab实现

轧制信号消噪的小波处理方法及matlab实现针对轧制信号消噪，可以采用小波去噪处理方法。

小波变换有抽取信
号的时域特征的能力，将信号的振幅与频率分离成多个子带，并确定出低
频范围和高频范围，对各个小带内部信号分别进行滤波，消除噪声，提高
了信号清洁度。

matlab实现小波变换消噪处理，首先要选择一种小波变
换函数，例如“db4”，然后调用matlab中内嵌的小波变换函数waverec，再调用wavelet transform函数，将轧制信号进行层次小波分解，将低频
成分设定为阈值，可以按照特定的比例将高频分量归零，从而消除噪音。

最终调用函数iwavelet，将轧制信号进行小波反变换，实现小波消噪处理，完成信号消噪任务。

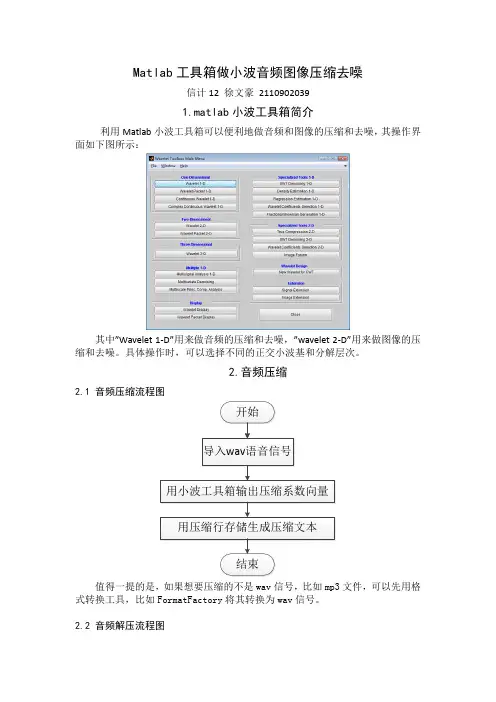
Matlab工具箱做小波音频图像压缩去噪信计12 徐文豪21109020391.matlab小波工具箱简介利用Matlab小波工具箱可以便利地做音频和图像的压缩和去噪，其操作界面如下图所示：其中”Wavelet 1-D”用来做音频的压缩和去噪，”wavelet 2-D”用来做图像的压缩和去噪。

具体操作时，可以选择不同的正交小波基和分解层次。

2.音频压缩2.1 音频压缩流程图值得一提的是，如果想要压缩的不是wav信号，比如mp3文件，可以先用格式转换工具，比如FormatFactory将其转换为wav信号。

2.2 音频解压流程图2.3 音频压缩效果比较考虑到正交小波基种类繁多，因而只比较较常用的haar、db和sym。

（1）量化音频压缩效果为了比较用不同正交小波基在不同分解层次下的压缩效果，有必要做一些量化处理。

考虑到，对同一音频信号，在取0率相同的情况下，压缩效果越好的正交小波基，其能量保留的应该越多。

因而，可先固定取0率，然后以能量保留百分比作为压缩效果的衡量指标。

（2）不同分解层次音频压缩效果比较不失一般性，考虑db4在取0率为95%的情况下在不同分解层次下的压缩效果，结果如下图：从图中可以看出，压缩效果随着分解层次的增加而增大，且增大速度先快后慢，最终压缩效果趋于稳定。

从理论上看，分解层次越多，出现小系数比率就越大，因而实验所得结果是与理论相符的。

可惜的是，在分解层次小于5时，可能是因为压缩效果已经太差，小波工具箱没给出其取0率为95%的情况，不然图像可以更加细致。

然而，也不能说分解层次越多越好，因为随着分解层次的增加，用于压缩和解压的时间会明显增加，因而这需要有一个折中。

（3）不同连续等级音频压缩效果比较对同种正交小波基，在分解层次固定时，可以比较不同连续等级对压缩效果的影响，考虑分解层次为5，取0率为95%，连续等级从1到7的db小波，结果如下图所示：从图中可以看出，随着小波基越来越连续，压缩效果是逐渐变大的，但增长速度也是先快后慢，且最终趋于平稳。

4.6 小波去噪举例[4,6]4.6.1 MATLAB中用wnoise函数测试去噪算法％ waveletnoise.msqrt_snr=3;init=231434;[x,xn]=wnoise(3,11,sqrt_snr,init); % WNOISE generate noisy wavelet test data.% X= WNOISE(FUN,N) returns values of the test function given by FUN, on a % 2^N sample of [0,1].% [X,XN] = WNOISE(FUN,N,SQRT_SNR) returns values of the test function% given by FUN and rescaled such that std(x) = SQRT_SNR (standard% deviation). The returned vector XN contains the same test vector X corrupted% by an additive Gaussian white noise N(0,1).% Then XN has a signal-to-noise ratio of (SQRT_SNR^2).% [X,XN] = WNOISE(FUN,N,SQRT_SNR,INIT) returns previous vectors X % and XN, but the generator seed is set to INI value.subplot(3,2,1),plot(x)title('original test function')subplot(3,2,2),plot(xn)title('noised function')% 产生一个长为2**11点，包含高斯白噪声的正弦信号，噪声的的标准％偏差为3。

matlab小波包分解降噪小波包分解是一种信号处理方法，可以用于降噪。

在MATLAB中，我们可以利用小波包分解对信号进行降噪处理。

让我们来了解一下什么是小波包分解。

小波包分解是一种将信号分解成不同频率分量的方法，它通过将信号分解成一系列小波包基函数来实现。

在小波包分解中，我们可以选择不同的小波基函数和不同的分解层数来得到不同精度的分解结果。

在MATLAB中，我们可以使用wavelet包中的函数来进行小波包分解。

首先，我们需要将信号加载到MATLAB中，并选择一个合适的小波基函数。

常用的小波基函数有haar、db、sym等，它们具有不同的性质，可以根据实际需求选择合适的函数。

在加载信号和选择小波基函数之后，我们可以使用wavedec函数对信号进行小波包分解。

该函数的参数包括信号、小波基函数和分解层数。

通过调整分解层数，我们可以得到不同精度的分解结果。

得到小波包分解结果后，我们可以对分解系数进行阈值处理，以实现降噪效果。

阈值处理是指将分解系数中小于某个阈值的值设置为零，从而达到降噪的目的。

常用的阈值处理方法有固定阈值、自适应阈值等，可以根据具体情况选择合适的方法。

在MATLAB中，我们可以使用wthresh函数来实现阈值处理。

该函数的参数包括分解系数、阈值和阈值处理方法。

通过调整阈值和阈值处理方法，我们可以得到不同的降噪效果。

完成阈值处理后，我们可以使用waverec函数对降噪后的信号进行重构，从而得到降噪后的信号。

重构后的信号可以用于后续的分析和处理。

小波包分解是一种有效的降噪方法，在MATLAB中可以很方便地实现。

通过选择合适的小波基函数、调整分解层数和阈值处理方法，我们可以得到满足要求的降噪效果。

在实际应用中，我们可以根据信号的特点和需求选择合适的参数，从而得到最佳的降噪效果。

小波包分解是一种在MATLAB中实现降噪的有效方法。

通过合理选择参数和方法，我们可以得到满足要求的降噪效果。

希望本文能对读者理解和应用小波包分解降噪方法有所帮助。

函数wdencmp功能：小波去噪，得到去噪后的图像[XC,CXC,LXC,PERF0,PERFL2] = WDENCMP('gbl',X,'wname',N,THR,SORH,KEEPAPP) 其中XC为去噪后的图像信号在wdencmp中通过xc = waverec2(cxc,lxc,w) ，重构函数得到信号xcWaverec2如何工作的呢？X = W A VEREC2(C,S,'wname') reconstructs the matrix Xbased on the multi-level wavelet decomposition structure[C,S]利用经过阈值处理过得系数C和它对应的长度S按照分解时选择的小波来重构；Waverec2涉及到的函数x = appcoef2(c,s,varargin{:},0)Appcoef2函数得到x的方法：x= idwt(a,d,Lo_R,Hi_R,l(imax-p)),综合滤波器重构Idwt中包含了上采用和卷积函数upsconv1x = upsconv1(a,Lo_R,lx,dwtEXTM,shift) + upsconv1(d,Hi_R,lx,dwtEXTM,shift);里面分别调用了采样函数和卷积函数完成！！函数wavedec2功能：返回N层小波分解系数，使用指定滤波器[C,S] = WA VEDEC2(X,N,'wname') returns the wavelet decomposition of the matrix X at level N，using the wavelet named in string 'wname' ，输出C小波系数，S是对应的系数长度；Wavedec2中通过dwt获得低频系数和小波系数for i=1:n[x,h,v,d] = dwt2(x,Lo_D,Hi_D); % decompositionc = [h(:)' v(:)' d(:)' c]; % store detailss = [size(x);s]; % store sizeend% Last approximation.c = [x(:)' c];s = [size(x) ; s];Dwt2函数如何实现此功能？包含卷积conv2和下采样convdown函数根据二维mallat变换输入信号先与滤波器卷积conv2，再下采样得到系数[x,h,v,d] ;Mallat算法，图像先小波分解。

matlab小波函数Matlab小波函数一、Matlab小波去噪基本原理1、带噪声的信号一般是由含有噪声的高频信号和原始信号所在的低频信号。

利用多层小波，将高频噪声信号从混合信号中分解出来。

2、选择合适的阈值对图像的高频信号进行量化处理3、重构小波图像：依据图像小波分解的低频信号与处理之后的高频信号来重构图像的信息。

二、第二代小波变换1、构造方法特点：（1）继承了第一代小波的多分辨率的特性。

（2）不依赖fourior变换，直接在时域完成小波变换。

（3）变换之后的系数可以是整数。

（4）图像恢复质量与变换是边界采用何种延拓方式无关。

2、优点：算法简单，速度快，适合并行处理。

对内存需求量小，便于DSP芯片实现、可用于本位操作运算。

3、提升原理:构造紧支集双正交小波（1）步骤：分裂—预测—更新（2）分解与重构三、matlab小波函数库1、matlab小波通用函数：（1）wavemngr函数【小波管理器（用于小波管理，添加、删除、储存、读取小波）】wavemngr(‘add’,FN,FSN,WT,NUMS,FILE)wavemngr(‘add’,FN,FSN,WT,NUMS,FILE,B)% 添加小波函数，FN为family name，FSN为family shortname WT为小波类型：WT=1表示正交小波，=2表示非正交小波，=3表示带尺度函数的小波，=4表示无尺度函数的小波，=5表示无尺度函数的复小波。

小波族只有一个小波，则NUMS=“，否则NUMS表示小波参数的字符串FILE表示文件名B=[lb ub]指定小波有效支撑的上下界wavemngr(‘del’,N) %删除小波wavemngr(‘restore’)/ wavemngr(‘restore’,IN2) %保存原始小波OUT1= wavemngr(‘read’) %返回小波族的名称OUT1= wavemngr(‘read’,IN2) %返回所有小波的名称OUT1= wavemngr(‘read_asc’)%读取wavelets.asc文件并返回小波信息（2）scal2frq函数【尺度转换频率】F=scal2frq(A,’wname’,DELTA)%返回由尺度A，小波函数“wname”和采样周期DELTA决定的准频率。

小波去噪的matlab程序-回复如何使用Matlab进行小波去噪。

小波去噪是数值信号处理中常用的一种方法，它可以有效地去除信号中的噪声，保留有用的信号部分。

Matlab是一个强大的数值计算和数据可视化工具，也提供了丰富的信号处理工具箱，其中包括小波去噪算法。

本文将介绍如何使用Matlab进行小波去噪，以帮助读者更好地理解和应用这一方法。

首先，我们需要定义被噪声污染的信号。

在Matlab中，可以通过生成具有噪声的信号来模拟实际应用。

以下是一段生成具有高斯白噪声的正弦信号的代码：fs = 1000; 采样频率T = 1/fs; 采样间隔L = 1000; 信号长度t = (0:L-1)*T; 时间向量f = 50; 正弦信号频率A = 0.7; 正弦信号幅度x = A*sin(2*pi*f*t); 生成正弦信号添加高斯白噪声mu = 0; 噪声均值sigma = 0.5; 噪声标准差n = sigma*randn(size(t)); 生成高斯白噪声x_noisy = x + n; 带噪声的信号上述代码中，我们生成了一个频率为50 Hz的正弦信号，并添加了均值为0、标准差为0.5的高斯白噪声。

生成的带噪声的信号存储在变量`x_noisy`中。

接下来，我们需要选择一种小波基函数以分析信号，并选择合适的小波系数阈值来进行去噪。

Matlab提供了多种小波基函数和小波系数阈值选择方法，如Daubechies小波基函数和固定阈值法、SureShrink方法等。

以下是一段使用Daubechies小波基函数和可视化小波系数阈值选择结果的代码：执行小波变换[c, l] = wavedec(x_noisy, 5, 'db4'); 小波分解可视化小波系数figure;subplot(2,1,1);plot(x_noisy);title('原始信号');subplot(2,1,2);plot(c);title('小波系数');小波系数阈值选择thr = wthrmngr('dw1ddenoLVL','penalhi',c,l); 阈值选择sorh = 's'; 阈值类型，s代表软阈值，h代表硬阈值keepapp = 1; 保留近似系数X = wdencmp('gbl',c,l,'db4',5,thr,sorh,keepapp); 小波去噪可视化去噪结果figure;subplot(2,1,1);plot(x_noisy);title('带噪声的信号');subplot(2,1,2);plot(X);title('去噪后的信号');上述代码中，我们使用了Daubechies小波基函数对信号进行了5级小波分解，并可视化了小波系数。

小波变换原理matlab摘要：I.引言- 介绍小波变换的基本概念- 介绍小波变换在信号处理中的应用- 引入MATLAB 工具在实现小波变换中的作用II.小波变换原理- 傅里叶变换与小波变换的对比- 小波基函数的概念和性质- 小波变换的分解与重构过程III.MATLAB 中小波变换的实现- MATLAB 中常用的小波函数介绍- 使用MATLAB 实现小波变换的步骤和示例- MATLAB 中实现小波变换的优势和应用案例IV.小波变换在信号处理中的应用- 去噪和压缩信号- 特征提取和模式识别- 其他应用案例V.总结- 总结小波变换的原理和应用- 强调MATLAB 在实现小波变换中的重要性正文：I.引言小波变换是一种在时频域上同时进行的信号分析方法，相较于傅里叶变换，它能够更好地处理非平稳信号。

在实际应用中，小波变换被广泛应用于信号处理、图像处理、语音识别等领域。

MATLAB 作为一种功能强大的数学软件，提供了丰富的工具箱和函数，可以方便地实现小波变换。

II.小波变换原理小波变换是一种多尺度分析方法，其基本原理是将信号分解成不同尺度的小波基函数的线性组合。

小波基函数是一类具有局部特性、具有不同尺度和位置参数的函数。

小波变换包括两个过程：分解和重构。

分解是将原始信号分解成一系列小波系数，每个小波系数对应信号的一个尺度；重构是将小波系数重新组合，得到重构信号。

III.MATLAB 中小波变换的实现MATLAB 提供了丰富的函数和工具箱用于实现小波变换，其中最常用的是小波分析工具箱(Wavelet Toolbox)。

在MATLAB 中实现小波变换主要包括以下步骤：1.选择合适的小波基函数和分解层数；2.使用dwt 函数进行小波分解；3.对分解得到的小波系数进行处理，如阈值去噪、特征提取等；4.使用wavedec 函数进行小波重构；5.分析重构信号与原始信号的差异，评估小波变换的效果。

MATLAB 中实现小波变换的优势在于，可以方便地调整小波基函数、分解层数等参数，以及实现各种小波变换后的信号处理。

在MATLAB中使用小波变换进行信号处理引言信号处理是一个非常重要的研究领域，它涉及到从传感器、通信系统、音频、视频等领域中提取、分析和处理信号的各种技术和方法。

小波变换作为一种强大的数学工具，被广泛应用于信号处理中，特别是在时频分析、信号压缩、噪声去除等方面。

本文将介绍在MATLAB中使用小波变换进行信号处理的基本原理和实际应用。

一、小波变换的基本原理小波变换是一种时频分析方法，它可以将时域信号通过一系列基函数进行分解，得到不同尺度和频率的信号分量。

在MATLAB中，可以使用Wavelet Toolbox来进行小波变换。

1. 小波函数族小波函数族是指一组基函数，它们具有尺度变换和平移变换的特性。

常用的小波函数族有Daubechies小波、Haar小波、Coiflet小波等。

这些小波函数族根据不同的尺度和频率特性，在信号处理中具有不同的应用。

2. 小波变换的计算在MATLAB中，可以使用函数``cwt(x,scales,'wavelet',wavename)``来进行小波变换的计算，其中x是输入信号，scales是尺度（尺度越大表示观测时间越长，对应低频成分），wavename是小波函数族的名称。

二、小波变换的实际应用小波变换在信号处理中有广泛的应用，下面将介绍一些常见的实际应用场景。

1. 信号去噪噪声是信号处理中一个常见的问题，它会影响信号的质量和可靠性。

小波变换可以将信号分解为不同尺度的成分，通过分析各个尺度的能量分布，可以有效地去除噪声。

通过调整小波变换的尺度参数，可以对不同频率和尺度的噪声进行去除。

2. 信号压缩信号压缩是在信号处理中另一个重要的应用，它可以减少数据存储和传输的成本。

小波变换可以将信号分解为不同尺度的成分，在某些尺度上，信号的能量可能会很小，可以将这些尺度上的系数设置为0，从而实现信号的压缩。

同时，小波变换还可以使用压缩算法如Lempel-Ziv-Welch（LZW）对小波系数进行进一步的编码压缩。

5 总结
小波变换对平稳信号的去噪声，要比传统的滤波去噪声得到的效果好．用小波变换 进行信号降噪处理， 既降低了噪声同时又提高了信噪比，这说明小波降噪方法是切实 可行的方案， 但是由于小波函数很多，采用不同的小波进行分解， 得到的结果可能相 差很大， 而变换前并不能预知哪一种小波降噪效果更好，需反复试验比较才能得到良 好的效果，这也是小波变换的困难之处之一。另外信号降噪过程中阀值的选取是十分重 要的。本文利用两个小波( sym8 ，db 10 )以及将信号中的信噪分离开来，更加直观可 行，通过分别进行信号降噪处理对所得结果与原始信号进行比较可以得出 Sym8 小波以 及默认阈值处理后的重构信号与原始信号最为接近，与分离的结果相同。 小波分析是一种信号的视频分析方法,它具有多分辨率分析的特点 ,很适合探测正 常信号中夹带的瞬态反常现象并展示其成分,有效区分信号中的突变部分和噪声。通过 MATLAB 编制程序进行给定信号的噪声抑制和非平稳信号的噪声消除实验表明:基于小波 分析的消噪方法是一种提取有用信号、 展示噪声和突变信号的优越方法 ,具有广阔的实 用价值。在这个越来月信息化的社会中，基于小波分析的应用前景必将越来越广泛。
图1
图2
图3 图 1-1 为原始信号图形，1-2 为叠加随机噪声后的图形，而 1-3 和 1-4 为利用 db10 和 sym8 小波默认阈值降噪后的信号图形。从图 1-3 和 1-4 可以看出利用 db10 和 sym8 小波降噪后的信号基本上恢复了原始信号，去噪效果明显。但是滤波后的信号与原始信 号也有不同， 从图中可以很直观地看到采用阈值消噪后信号特征值较少无法准确还原原 始信号 这是由于为降噪过程中所用的分析小波和细节系数的阈值不恰当所致，如需要 更好的恢复信号，还可以采用其它种类小波对其进行分析，通过选取不同的阈值，分析 结果，得到一个合适的阈值。 从图 2 和图 3 中看出， 在经过用 db10 对信号进行 5 层分解， 然后分别对分解的第 5 层到第 1 层的低频系数和高频系数进行重构。 可以得出其主要基波函数和高频噪声函数 的图形，其中小分波分解的细节信号是有白噪声分解得到的，而正弦信号可以在图 2 中 的近似信号 a5 得到。因为在这一层的影响已经可以忽略了，所以获得的信号就是初始 信号的波形，从而把淹没在噪声中的有用信号有效地分离出来。

小波去噪MATLAB实现第二章图像小波去噪理论第4章医学图像小波去噪的MATLAB实现4.1 小波基的确定不同的小波基具有不同的时频特征，用不同的小波基分析同一个问题会产生不同的结果，故小波分析在应用中便存在一个小波基或小波函数的选取和优化问题。

我们在应用中要把握小波函数的特征，根据应用需要，选择合适的小波基。

在小波分析应用中要考查小波函数或小波基的连续性、正交性、对称性、消失矩、线性相位、时频窗口的中心和半径以及时频窗的面积等，这些特征关系到如何选择合适的小波基。

本节选取了一些常见的小波基，首先固定小波分解层数和阈值，然后改变小波基，运行结果。

通过计算峰值信噪比(PSNR)来判定哪个小波基对医学图像去噪效果好。

下表为不同小波基去噪前带噪图像的峰值信噪比（PSNR）和去噪后图像的峰值信噪比（PSNR），通过峰值信噪比对不同小波基的去噪效果进行评价，从而选出对图像去噪效果较好的小波基。

通过去噪效果图4-1和表4-1以及图像评价原则我们可以很容易选出对图像去噪效果好，而又很好的保持图像细节的小波基。

从图4-1中我们可以看出选用sym3小波基去噪后噪声得到了明显的抑制，但是图像的细节被弱化了，读图有所影响。

选用sym5小波基去噪后，噪声没有得到很好的抑制，而且图像细节已明显消损，对读图有所影响。

选用coif2小波基对图像进行去噪后，噪声得到一定的抑制，图像的细节保持的也很好。

选用coif5小波基对图像去噪后，图像细节明显消损，对读图有所影响。

选用db2小波基对图像去噪后图像的噪声虽然得到抑制但细节变得模糊，很难辨别。

选用db6小波基对图像进行去噪后，图像失真比较明显。

综上所述，coif2小波基去噪效果很好，所以本次课程设计中我选择coif2小波基进行医学图像小波去噪方法研究。

相应小波变换语句：[c,s]=wavedec2(A,n,wname);其中：wname为小波基变量，通过改变它来变换程序中运用的小波基。

小波去噪matlab代码以下是一段使用小波去噪的 Matlab 示例代码：% 载入待处理的信号，这里将代表信号命名为 Sload signal.mat% 将信号做小波变换，将小波变换结果保存在 A 中[C,L] = wavedec(S,4,'db4');A = wrcoef('a',C,L,'db4',4);% 计算小波图形的阈值，使用一个固定值或自适应阈值thr = 0.15; % 使用一个固定的阈值，可以根据实际情况调整% 定义阈值类型，默认使用定值阈值thresholdType = 's';% 根据阈值将 A 中的小波系数进行阈值处理switch thresholdTypecase 's' % 定值阈值A(abs(A) < thr) = 0;case 'h' % 硬阈值A = wthcoef('h',A,thr);case 's' % 软阈值A = wthcoef('s',A,thr);end% 将处理后的小波系数进行重构，得到去噪效果更好的信号S_denoise = waverec(A,L,'db4');% 显示原始信号和处理后的信号subplot(2,1,1)plot(S)title('Original Signal')subplot(2,1,2)plot(S_denoise)title('Denoised Signal')该代码载入一个信号，执行小波变换，然后使用固定阈值处理小波系数，最后通过逆小波变换方式重构信号。

在具体应用中，可以根据需要调整使用方法和阈值数值，以达到更好的去噪效果。

matlab实现小波变换小波变换（Wavelet Transform）是一种信号处理技术，可以将信号分解成不同频率和时间分辨率的成分。

在Matlab中，可以利用小波变换函数实现信号的小波分析和重构。

本文将介绍小波变换的原理和在Matlab中的使用方法。

一、小波变换原理小波变换是一种时频分析方法，通过对信号进行多尺度分解，可以同时观察信号的时间和频率信息。

小波变换使用小波函数作为基函数，将信号分解成不同频率的子信号。

小波函数是一种具有有限长度的波形，可以在时间和频率上进行局部化分析。

小波变换的主要步骤包括：选择小波函数、信号的多尺度分解、小波系数的计算和重构。

1. 选择小波函数：小波函数的选择对小波变换的结果有重要影响。

常用的小波函数有Haar小波、Daubechies小波、Symlet小波等。

不同的小波函数适用于不同类型的信号，选择合适的小波函数可以提高分析的效果。

2. 信号的多尺度分解：信号的多尺度分解是指将信号分解成不同尺度的成分。

小波变换采用层级结构，每一层都将信号分解成低频和高频两部分。

低频表示信号的平滑部分，高频表示信号的细节部分。

3. 小波系数的计算：小波系数表示信号在不同尺度和位置上的强度。

通过计算每一层的小波系数，可以得到信号在不同频率上的能量分布。

4. 信号的重构：信号的重构是指将分解得到的小波系数合成为原始信号。

小波重构的过程是小波分析的逆过程，通过将每一层的低频和高频合并，可以得到原始信号的近似重构。

二、Matlab中的小波变换在Matlab中，可以使用wavedec函数进行小波分解，使用waverec 函数进行小波重构。

具体步骤如下：1. 加载信号：需要加载待处理的信号。

可以使用load函数从文件中读取信号，或者使用Matlab中自带的示例信号。

2. 选择小波函数：根据信号的特点和分析目的，选择合适的小波函数。

Matlab提供了多种小波函数供选择。

3. 进行小波分解：使用wavedec函数进行小波分解，指定分解的层数和小波函数名称。

·54·文章编号：1006-1576（2006）02-0054-02小波变换降噪技术及其在Matlab 中的实现赵海英，纪超辉（海军潜艇学院 研究生队，山东 青岛 266071）摘要：小波降噪含模极大值、尺度空间滤波、域值滤波三种方法。

域值滤波法只对低频部分进一步分解，不考虑高频部分，因而用小波函数进行处理。

域值滤波方法的处理过程为：对信号进行小波分解；小波分解高频系数的域值量化；信号重组。

对潜艇获得的测量方位信号仿真结果分析表明，该方法可行。

关键词：小波变换；降噪；Matlab中图分类号：TP312 文献标识码：BNoise Reduction Technology Based on Wavelet Transform and Realization in MatlabZHAO Hai-ying, JI Chao-hui(Brigade of Graduate, Submarine Academy of PLA Navy, Qingdao 266071, China)Abstract: Modular maximum, scale space filtering and domain value filtering are three methods of wavelet noise reduction. Domain value filtering method only decompounded the low frequency, without considering the high frequency, so it can be disposed through wavelet function. The disposing process of domain value filtering method as follows: the wavelet decomposition of signals; the domain value quantification of high frequency coefficient in wavelet decomposition; recombination of signals. The simulation result of the submarine measure orientation proves that this method is reliable.Keywords: Wavelet transform; Noise reduction; Matlab1 引言傅里叶变换是降噪处理手段，对处理非平稳信号和暂态信号，傅里叶变换会忽略暂态信息。

光谱小波去噪是指利用小波变换对光谱信号进行去噪处理，以提高信号的质量和可读性。

Matlab作为一种强大的科学计算软件，提供了丰富的工具和函数来进行光谱小波去噪处理。

本文将详细介绍光谱小波去噪的原理与方法，并结合Matlab的实际操作来演示该过程。

一、光谱小波去噪的原理光谱信号是通过测量目标物体的反射、散射或发射光的波长分布来描述物质的性质。

然而，由于各种噪声的干扰，光谱信号往往存在着不同程度的随机波动和干扰，影响了信号的准确性和可靠性。

光谱信号的去噪处理变得十分重要。

小波变换是一种时频分析的方法，能够将信号分解成不同尺度和频率的小波系数，从而更好地揭示信号的时频特性。

光谱小波去噪正是基于小波变换的理论，利用小波分析和重构信号，实现对光谱信号的有效去噪。

二、光谱小波去噪的方法1. 数据准备在进行光谱小波去噪之前，首先需要准备好光谱信号的数据。

通常情况下，光谱信号通过光谱仪或其他光谱测量设备获取，可以是吸收光谱、荧光光谱、拉曼光谱等不同类型的光谱数据。

在Matlab中，可以通过导入数据的方式将光谱信号加载到工作空间中，以便进行下一步的处理。

2. 小波变换利用Matlab提供的小波工具箱，可以很方便地对光谱信号进行小波变换。

小波变换将光谱信号分解成不同频率和尺度的小波系数，利用这些系数可以更好地理解和处理光谱信号中的信息。

在Matlab中，可以使用“wavedec”函数进行小波分解，得到各级小波系数和近似系数。

3. 去噪处理在得到小波系数之后，可以通过滤波的方式对小波系数进行去噪处理。

常用的去噪方法包括阈值去噪、软硬阈值去噪等。

阈值去噪是指按照一定的规则，将小于某个阈值的小波系数置零，从而实现去除噪声的目的。

而软硬阈值去噪则是在阈值去噪的基础上引入了软硬阈值的概念，更加灵活和精细地控制去噪效果。

4. 信号重构经过去噪处理的小波系数需要进行信号重构，以得到去噪后的光谱信号。

在Matlab中，可以利用“waverec”函数将去噪后的小波系数重构成信号，并进一步进行可视化展示和分析。

小波变换图像降噪的matlab代码求小波变换图像降噪的matlab代码load wbarb; % 装载原始图像subplot(221); % 新建窗口image(X); % 显示图像colormap(map); % 设置色彩索引图title('原始图像'); % 设置图像标题axis square; % 设置显示比例,生成含噪图像并图示init=2055615866; % 初始值randn('seed',init); % 随机值XX=X+8*randn(size(X)); % 添加随机噪声subplot(222); % 新建窗口image(XX); % 显示图像colormap(map); % 设置色彩索引图title('含噪图像'); % 设置图像标题axis square; %用小波函数coif2 对图像XX 进行2 层分解[c,l]=wavedec2(XX,2,'coif2'); % 分解n=[1,2]; % 设置尺度向量p=[10.28,24.08]; % 设置阈值向量,对高频小波系数进行阈值处理%nc=wthcoef2('h',c,l,n,p,'s');%nc=wthcoef2('v',c,l,n,p,'s');nc=wthcoef2('d',c,l,n,p,'s');X1=waverec2(nc,l,'coif2'); % 图像的二维小波重构subplot(223); % 新建窗口image(X1); % 显示图像colormap(map); %设置色彩索引图title('第一次消噪后的图像'); % 设置图像标题axis square; % 设置显示比例,再次对高频小波系数进行阈值处理%mc=wthcoef2('h',nc,l,n,p,'s');mc=wthcoef2('v',nc,l,n,p,'s');mc=wthcoef2('d',nc,l,n,p,'s');X2=waverec2(mc,l,'coif2'); % 图像的二维小波重构subplot(224); % 新建窗口image(X2); % 显示图像colormap(map); % 设置色彩索引图title('第二次消噪后的图像'); % 设置图像标题axis square; % 设置显示比例。